Похожие презентации:
ANSYS в инженерных задачах
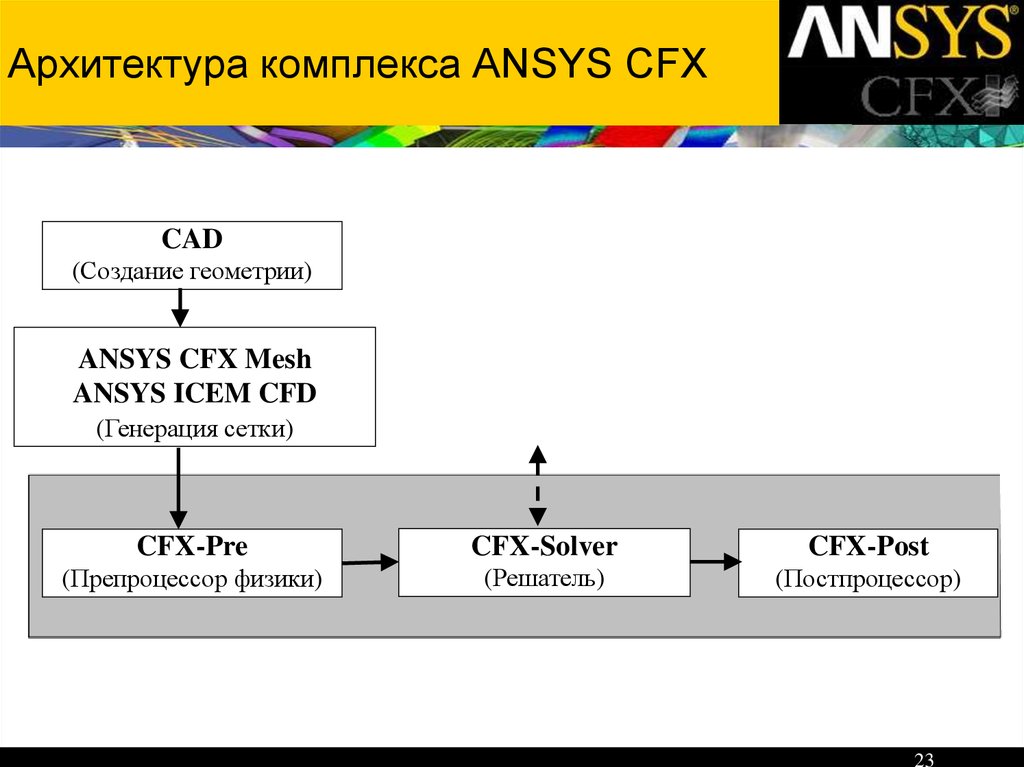
1. ANSYS в инженерных задачах
Наталья Анатольевна Лыкова2. Система уравнений Навье-Стокса
Уравнение неразрывности (сохранения массы)Уравнение количества движения (сохранения импульса)
3. Система уравнений Навье-Стокса
Уравнение энергии (сохранения энергии)htot p
Vhtot T V V SM S E
t
t
htot hstat
2
V
2
hstat hstat T , p
Уравнение состояния
T , p
p
V
T
t
htot
hstat
SM
SE
- давление;
- плотность;
- скорость;
- температура;
- время;
- полная энтальпия;
- статическая энтальпия;
- источниковый член для импульса;
- источниковый член для энергии;
- коэффициент динамической вязкости;
- коэффициент теплопроводности;
- оператор Гамильтона (набла);
- обозначает векторную величину
3
4. Анализ системы уравнений Навье-Стокса
дифференциальные уравнения в частных производных какпервого, так и второго порядка
наличие нелинейной зависимости членов уравнений от
переменных
4
5.
«Проблема тысячелетия»Необходимо доказать или опровергнуть существование глобального
гладкого решения задачи Коши для трёхмерных уравнений Навье — Стокса.
Найти вектор скорости и давление, которые удовлетворяют системе
уравнений Навье-Стокса и начальному условию
за решение Математический институт Клэя
назначил премию в 1 млн долларов США
5
6.
Решение уравнений10 января 2014 года математик Мухтарбай Отелбаев опубликовал статью, в
которой утверждает, что дал полное решение проблемы.
6 февраля 2014 года Лауреатом Филдсовской медали Теренсом Тао была
опубликована работа, доказывающая невозможность решения проблемы
тысячелетия, посвященной задаче Навье-Стокса, существующими на
настоящий момент средствами [2].
По состоянию на 2014 год подтверждённые решения этих уравнений
найдены лишь в некоторых частных случаях.
В остальных случаях используется численное моделирование.
6
7. Пример точного решения
Течение Пуазейляламинарное течение жидкости через каналы в виде прямого кругового
цилиндра или слоя между параллельными плоскостями
7
8. Структура численного решения
Дискретизацияметод конечных разностей (МКР)
метод конечных элементов (МКЭ)
метод конечных объемов (МКО)
8
9. Метод конечных объёмов
Уравнение неразрывности и количества движения в координатной формеVi 0
t xi
P
V j Vi
V j
ViV j
t
xi
x j xi xi x j
Интегрирование по контрольному объему
d
d Vi dni 0
dt
S
V j V
d
V
d
V
V
dn
Pdn
i dni SV j d
j
i j i
i
dt
x
x j
S
S
S i
- контрольный объем
S
- контрольная поверхность, ограничивающая контрольный объем
dni
- дифференциал декартовой составляющей вектора внешней нормали к поверхности
9
10. Метод конечных объёмов
Дискретная форма интегральных соотношений0
Vi ni ip 0
t
ip
V 0V i
V
j
j
V
mip V j P n j j i
ip
ip
t
x
ip
x j
ip
ip i
ni SV j
t
- шаг по времени;
ni
- приращение декартовой составляющей вектора внешней нормали к поверхности
ip
- вычисление для точки интегрирования и суммирование по всем точкам интегрирования данного
контрольного объема
0
- величина соответствует предыдущему значению времени
mip Vi ni ip
- изменение массы через поверхность элемента
10
11. Метод конечных элементов
Переменнаяn
внутри объема
Ni i
i 1
n
Ni 1
i 1
В МКО заложено точное интегральное сохранение таких величин,
как масса, количество движения и энергия на всей расчетной
области
11
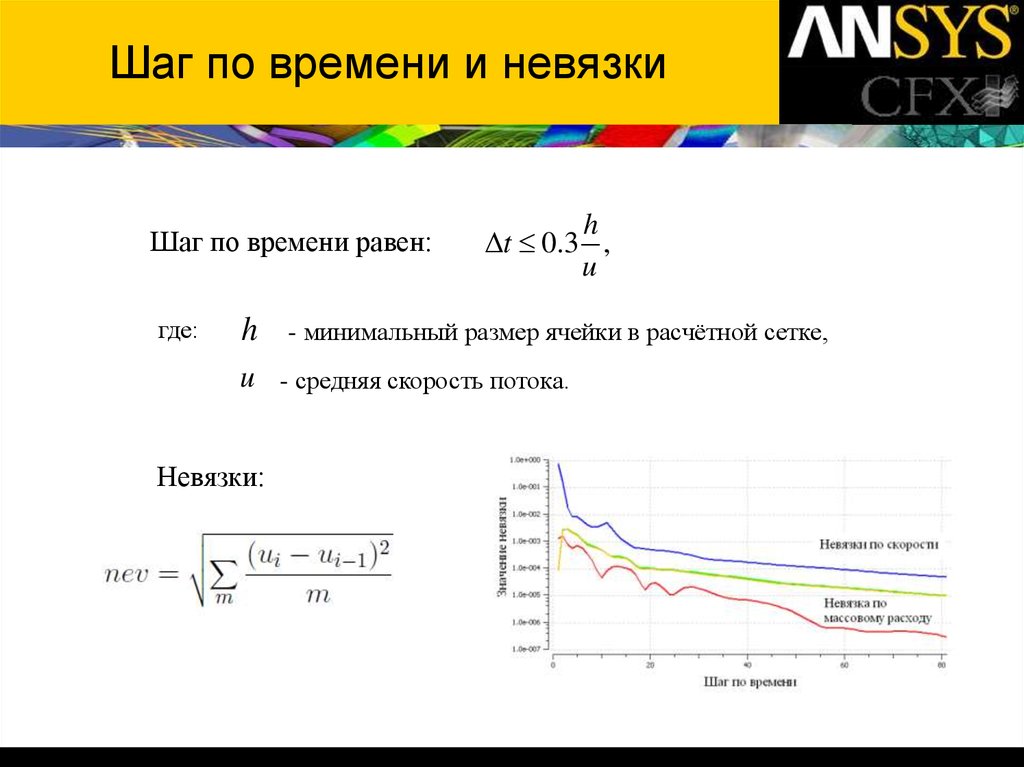
12. Шаг по времени и невязки
Шаг по времени равен:где:
h
h
t 0.3 ,
u
- минимальный размер ячейки в расчётной сетке,
u - средняя скорость потока.
Невязки:
13. Уравнения Рейнольдса
Уравнения Навье-Стокса, осреднённые по Рейнольдсу- напряжения Рейнольдса
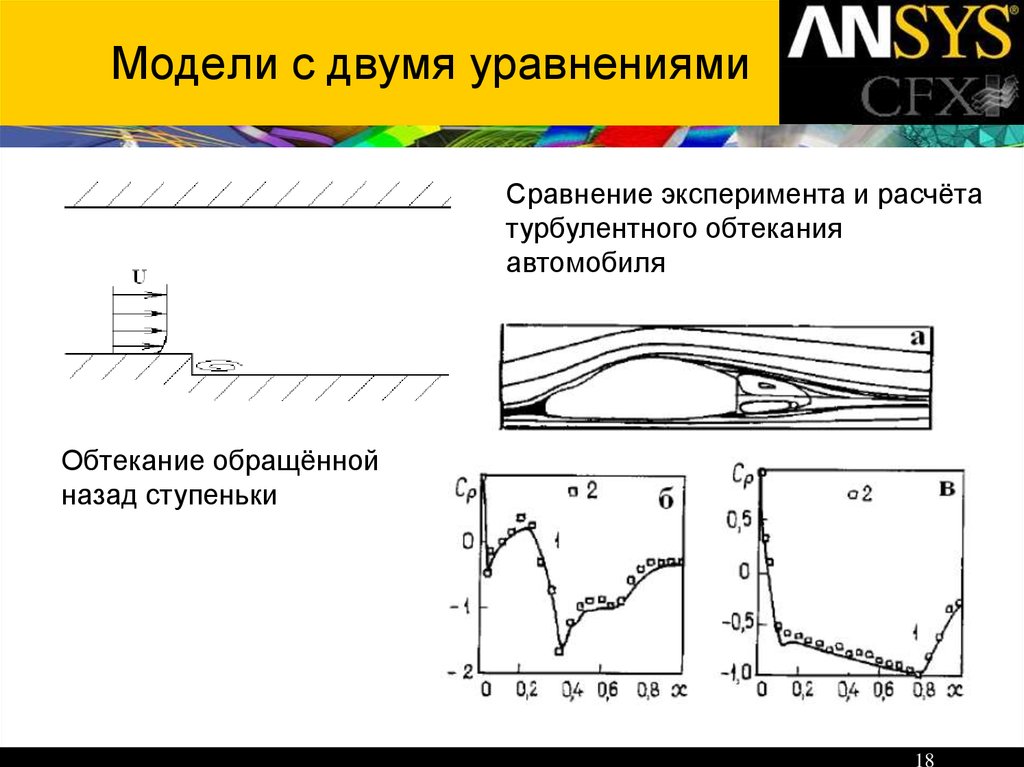
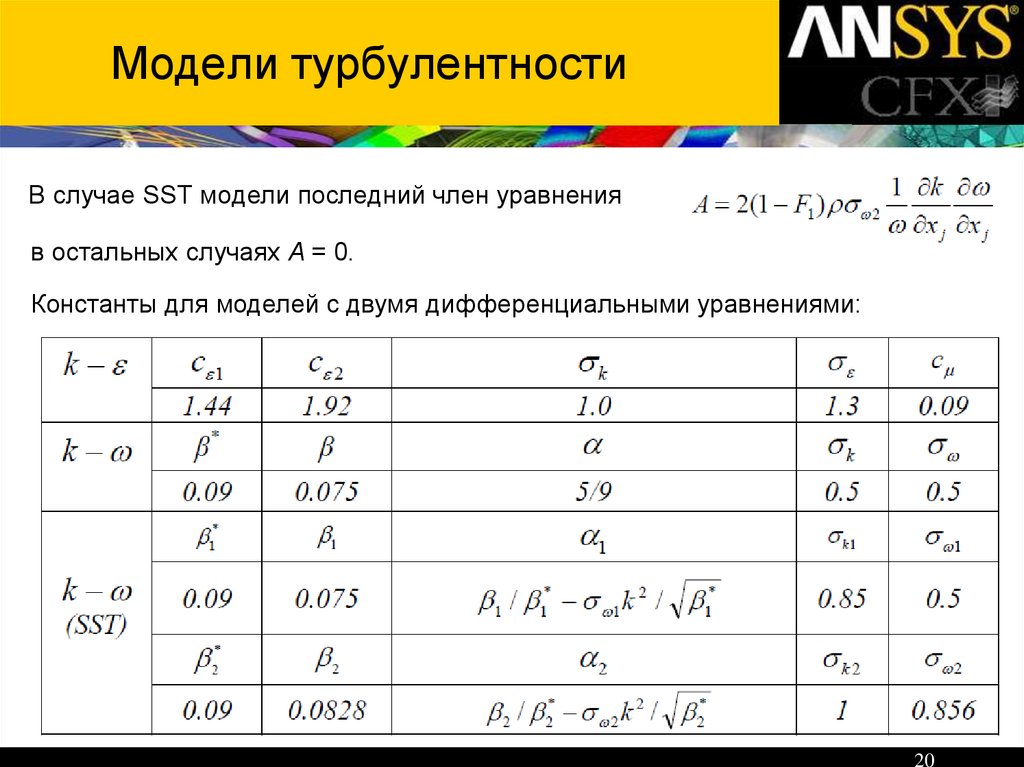
14. Модели турбулентности
Модели вихревой вязкости:Однопараметрическая модель Колмогорова-Прандтля
Стандартная модель k
RNG k модель
Стандартная модель k
Зонная модель BSL k
Зонная модель SST k
Модель k
1E
Модели напряжений Рейнольдса:
Изотропная модель Launder-Reece-Rodi (LRR Reynolds Stress)
Квазиизотропная модель Launder-Reece-Rodi (QI Reynolds Stress)
Модель Speziale-Sarka-Gatski (SSG Reynolds Stress)
Модель SMC (Omega Reynolds Stress)
Модель BSL-RSS
Переходная модель ANSYS CFX Transition Model
Вихревые модели:
Модель крупных вихрей LES
Модель дискретных вихрей DES
Модель адаптивного масштаба SAS
14
15. Алгебраические модели
Алгебраические модели - это простейший тип моделей турбулентности, согласнокоторым значение турбулентной вязкости































 Инженерная графика
Инженерная графика








