Теоретичні, фізичні та інформаційні основи галузевого знання

Приклади інженерних завдань, оптимальне вирішення яких вимагає відновлення функцій багатьох змінних і сучасних комп'ютерних технологій

5.20M

Категория:

Информатика

Похожие презентации:

Теоретичні основи інформатики

Паралельні та розподілені обчислювальні системи. Лекція 1

Вступ до паралельних та розподілених обчислень. Лекція 1

Теорія інформаційних систем. Тема 2. Інформаційні системи та технології

Інформаційні технології та інформаційні системи

Професійна підготовка фахівців з інформаційних технологій для викладання освітнього модуля "Алгоритми та методи обчислень"

Інформаційні системи та технології

Інформаційні технології математичного аналізу систем

Лекція 1. Алгоритми та основні поняття

Інформація. Інформаційні процеси та системи. Етапи розвитку та сфери застосування інформаційних технологій. (Урок 2)

Теоретичні, фізичні та інформаційні основи галузевого знання. (Лекція 1)

1. Теоретичні, фізичні та інформаційні основи галузевого знання

Лекція 1
Українська інженерно-педагогічна
академія

2. ВСТУП

2
ВСТУП
Мета курсу: Забезпечити системність фахових знань
отриманих на попередніх курсах навчання, зв'язок з
математичними та комп’ютерними розділами знань, та
їх використання при розв’язанні практичних задач за
фахом. Виробити навики складання математичних
моделей, допомогти оволодінням чисельним методам
обчислювальної математики, їх реалізаціями на ПЕОМ
та набути вміння використовувати їх для розв’язання
практичних
задач
з
використанням
системи
комп’ютерної математики MathCad.

3. ВСТУП

3
ВСТУП

4. Вступ

4
Вступ

5. Вступ

5
Вступ

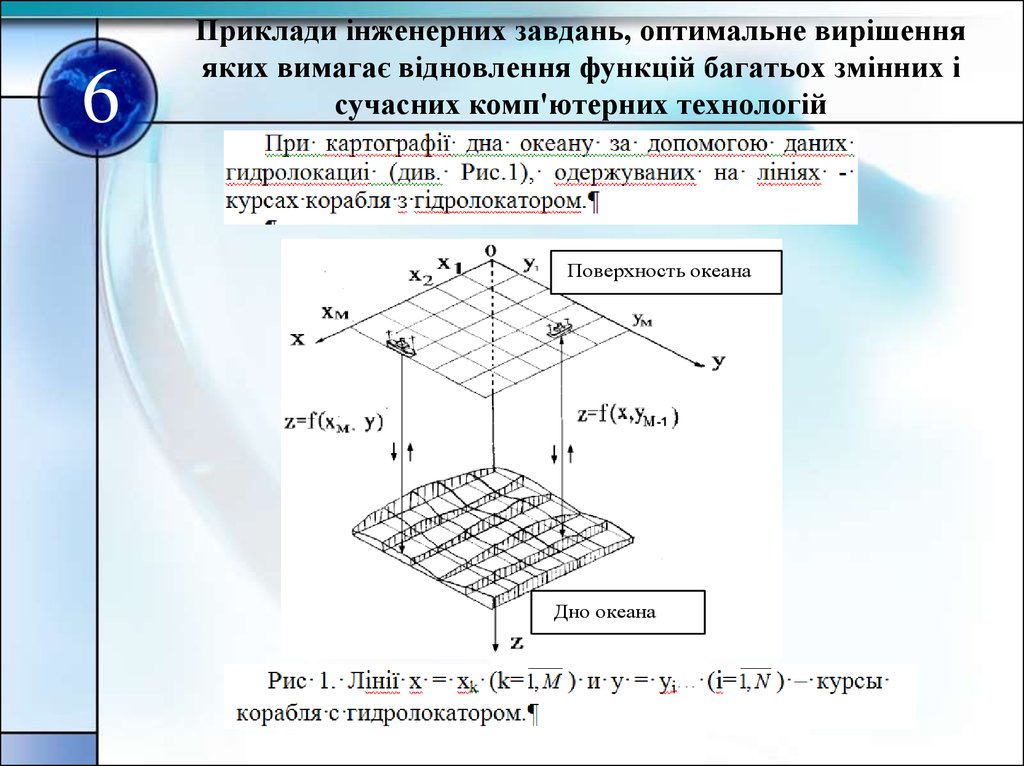
6. Приклади інженерних завдань, оптимальне вирішення яких вимагає відновлення функцій багатьох змінних і сучасних комп'ютерних технологій

6
Приклади інженерних завдань, оптимальне вирішення
яких вимагає відновлення функцій багатьох змінних і
сучасних комп'ютерних технологій
Поверхность океана
Дно океана

7.

7
Приклади інженерних завдань, оптимальне вирішення
яких вимагає відновлення функцій багатьох змінних і
сучасних комп'ютерних технологій

8.

8
Приклади інженерних завдань, оптимальне вирішення
яких вимагає відновлення функцій багатьох змінних і
сучасних комп'ютерних технологій

9.

9
Приклади інженерних завдань, оптимальне вирішення
яких вимагає відновлення функцій багатьох змінних і
сучасних комп'ютерних технологій

10.

10
Приклади інженерних завдань, оптимальне вирішення
яких вимагає відновлення функцій багатьох змінних і
сучасних комп'ютерних технологій

11.

11
Приклади інженерних завдань, оптимальне вирішення
яких вимагає відновлення функцій багатьох змінних і
сучасних комп'ютерних технологій

12.

12
Приклади інженерних завдань, оптимальне вирішення
яких вимагає відновлення функцій багатьох змінних і
сучасних комп'ютерних технологій

13.

13
Математичні моделі.
Теорія похибок
наближених обчислень.

14.

14
Поняття математичної моделi

15.

15
Поняття математичної моделi

16.

16
Поняття математичної моделi

17.

17
Поняття математичної моделi

18.

18
Приклад математичної моделi
Розглянемо приклад побудови математичної моделі. Нехай
вивчається процес падіння якого-небудь тіла з висоти. Існує
багато математичних моделей цього процесу. Ще Аристотель
побудував математичну модель падіння тіла. Він вважав, що
швидкість вільно падаючого тіла пропорційна його ваги. Тобто,
якщо т — вага тіла, v — його швидкість, то v = k ∙ т, де k —
деякий коефіцієнт.
Ця модель активно обговорювалася поколіннями філософів,
були знайдені спростування і запропоновані інші моделі, що,
однак, також не витримували критики. Була потрібна більш
адекватна нова модель. Вона була побудована Галилеєм, і ми
дотепер користуємося нею: швидкість вільно падаючого тіла
пропорційна часу v = at, де а — коефіцієнт пропорційності.
Ця модель була отримана Галилеєм методом проб і помилок
після чисельних експериментів і міркувань, а потім доповнена
й уточнена Ньютоном, що установив, що коефіцієнт
пропорційності а = g ~ 9,8 м/с — прискорення вільного