Методы решения задач теплопроводности

1. Проблемы энерго- и ресурсосбережения

● Приближенные методы решения
задач теплопроводности

2. Приближенные методы решения задач теплопроводности

Точное аналитическое решение позволяет
рассчитать температуру в любой точке
тела, однако, не любую задачу
теплопроводности можно решить
аналитически. В том случае, когда тело
имеет сложную форму и коэффициент
теплоотдачи является величиной
переменной, задачу по теплообмену
аналитически решить невозможно. В этом
случае используют приближенные методы
решения задач (численные методы).

3. Приближенные методы решения задач теплопроводности

Дифференциальное уравнение
теплопроводности заменяется
системой алгебраических уравнений.
Температура рассчитывается в
отдельных фиксированных точках
тела, точность расчета зависит от
выбранного шага разбиения тела на
отдельные участки.

4. Приближенные методы решения задач теплопроводности

Наибольшее распространение
получили два метода расчета:
Метод элементарных тепловых
балансов.
Метод конечных разностей.

5. Метод элементарных тепловых балансов

Тело разбивается на отдельные объемы.
Центральным точкам каждого объема присваивается
отдельный номер.
Эти точки обладают определенной массой и
теплоемкостью.
К каждой точке теплота подводится или отводится
через стержни, с помощью которых точки условно
соединены друг с другом.
При этом внутренняя энергия точки может
увеличиваться или уменьшаться.

6. Метод элементарных тепловых балансов

Пусть температурное поле описывается
уравнением:
2
t
t
a 2
x
Разбиваем стенку на элементарные объемы:
V 1
2

7. Метод элементарных тепловых балансов

Изменение внутренней энергии в рассматриваемой
узловой точке:
U c V t0 t0 ,
c, Дж / (кг К ) - удельная массовая теплоемкость;
, кг / м3
- плотность;
t0 - начальная температура точки 0;
t0 - температура этой точки через время
(1)

8. Метод элементарных тепловых балансов

Теплота к точке 0 подводится от точки 1 и точки 2 за
счет теплопроводности:
t1 t0
Q1 0
f
t 2 t0
Q2 0
f
(2)
(3)
Уравнение теплового баланса:
U Q1 0 Q2 0
(4)

9. Метод элементарных тепловых балансов

С учетом (1), (2), (3) уравнение (4) примет вид
c
2
t t
0
0
t t
1
0
t2 t0
t0 t0
t
t
t
t
.
1
0
2
0
2
c
(5)

10. Метод элементарных тепловых балансов

a, м 2 / с - коэффициент температуропроводности.
с
a
2
Fo
- критерий Фурье.
При фиксированном значении шага разбиения по
пространству и по времени критерий Фурье
является величиной постоянной .

11. Метод элементарных тепловых балансов

Уравнение (5) принимает вид:
t0 t0 Fo t1 t2 2t0
(6)
t0
t0 Fo t1 t2 2t0
Fo
1
t0 Fo t1 t2 t0
2
Fo
(7)

12. Метод элементарных тепловых балансов

Из рассмотрения (7) следует, что
будущая температура в
рассматриваемой точке является
функцией настоящей
температуры в этой точке и
настоящих температур в соседних
точках.

13. Метод элементарных тепловых балансов

Частные случаи:
Пусть
1
Fo
2
t1 t2
t0 Fo t1 t2 t0
2
Будущая температура в рассматриваемой точке не
зависит от настоящей температуры в этой точке.

14. Метод элементарных тепловых балансов

1
Fo
3
1
t0 t1 t2 t0 .
3
1
Пусть Fo
4
Пусть
1
t0 t1 t2 2t0 .
4

15. Метод элементарных тепловых балансов

Установлено, что устойчивость решения достигается
лишь при
1
Fo
2
Fo
a
2
1
2

16. Метод элементарных тепловых балансов

Аналогично можно получить решение для двухмерной
задачи:
1
t0 Fo t1 t2 t3 t4 t0
4
Fo

17. Метод элементарных тепловых балансов

Установлено, что устойчивость решения достигается лишь при
1
Fo
4
Fo
a
2
1
4

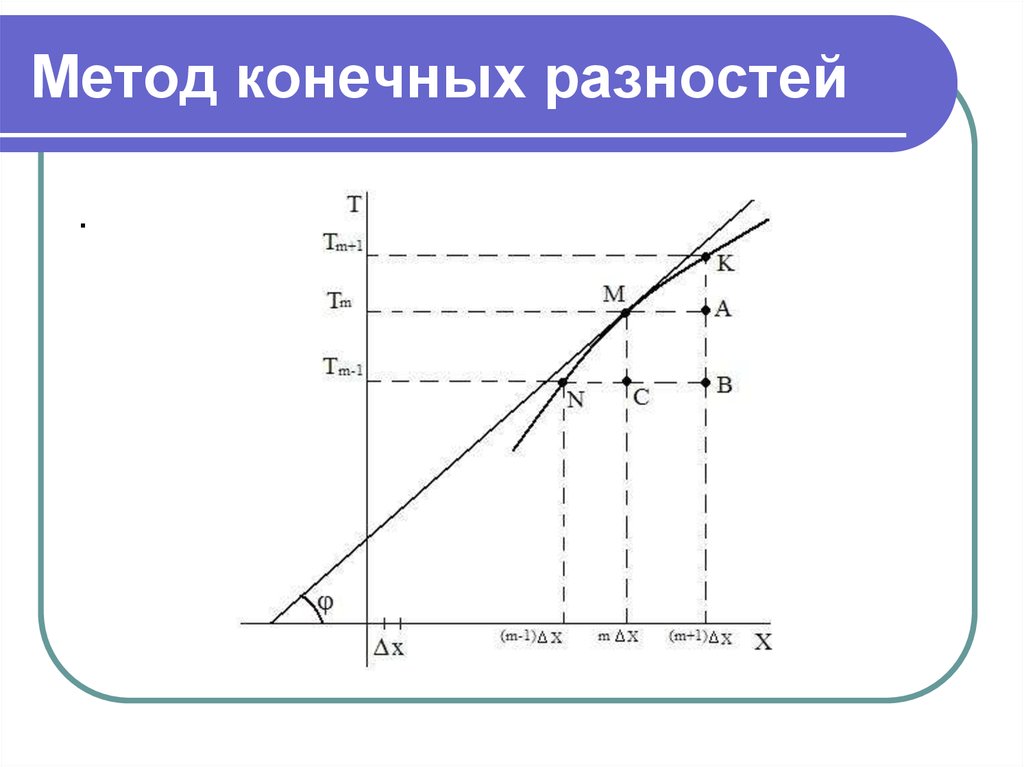
18. Метод конечных разностей

В этом методе производные,
входящие в дифференциальное
уравнение теплопроводности,
замещаются разностными
соотношениями:
/
t m x tg

19. Метод конечных разностей

.

20. Метод конечных разностей

Приближенные значения производных
Предыдущие значения производных:
MC tm tm 1
t m x
NC
x
Последующие значения производных:
/
KA tm 1 tm
t m x
MA
x
/

21. Метод конечных разностей

Симметричные значения производных:
KB tm 1 tm 1
t m x
NB
2 x
/

22. Метод конечных разностей

Вторая производная:
tm 1 tm tm tm 1 1
t m x
x x
x
//
1
t m x 2 t m 1 tm 1 2tm
x
//

23. Метод конечных разностей

Пусть температурное поле описывается
дифференциальным уравнением:
t
t
a 2
x
2
(1)

24. Метод конечных разностей

Поскольку температура является функцией
двух переменных, удобно выбрать
прямоугольную сетку. Интервал изменения
разделим на одинаковые интервалы x , а
отрезок времени разделим на
равномерные интервалы
Восстановленные перпендикуляры к
координатным осям в точках деления при
пересечении образуют расчетные узловые
точки.
x

25. Метод конечных разностей

Расчетная сетка:

26. Метод конечных разностей

Координаты точек:
1: m x, k ;
m 1 x, k ;
2:
m 1 x, k ;
4: m x, k 1 ;
5: m x, k 1 ;
3:

27. Метод конечных разностей

Заменим производные разностными соотношениями:
t
1
t k 1 ,m tk ,m
1 ;
t
1
2 t m 1 ,k t m 1 ,k 2tm,k 2 ;
2
x
x
2

28. Метод конечных разностей

Формула (1) примет вид:
t
m , k 1
tm , k
1
1
tm, k 1
a
2 t m 1 ,k t m 1 ,k 2tm,k 2 a;
x
1 2 a
a
2 t m 1 ,k t m 1 ,k 2tm,k tm,k ;
x

29. Метод конечных разностей

Или:
tm, k 1
tm, k 1
1
Fo t m 1 ,k t m 1 ,k 2tm,k
tm,k 2 a 1
Fo
1
Fo t m 1 ,k t m 1 ,k tm,k
2 2 a 1 (2)
Fo

30. Метод конечных разностей

Уравнение (2) составляется для каждой узловой
точки включая пограничные точки.
Погрешность расчета уменьшается при 0 .
Устойчивость решения обеспечивается лишь при
условии:
1
1
2 0 Fo
Fo
2
a 1
x
Fo
2
x
2
2a
2

31. Метод конечных разностей

Пусть температурное поле описывается
дифференциальным уравнением вида:
t t
t
a 2 2
x y
2
2
(3)

32. Метод конечных разностей

Заменим производные разностными соотношениями:
t
1 k
k
k
2 t m 1 ,n t m 1 ,n 2tm,n 1 ;
2
x
x
2
t
1 k
k
k
2 tm, n 1 tm, n 1 2tm,n 2 ;
2
y
y
2
t
1 k 1 k
tm , n tm , n 3 ;

33. Метод конечных разностей

Уравнение (3) примет вид:
1 k 1 k
tm , n tm , n 3
a k
k
k
2 t m 1 ,n t m 1 ,n 2tm,n 1a
x
a k
k
k
2 tm, n 1 tm, n 1 2tm,n 2 a
y

34. Метод конечных разностей

1 , 2 , 3 0
Пусть
t
k 1
m,n
t
k
m ,n
a k
k
k
2 t m 1 ,n t m 1 ,n 2tm ,n
x
a k
k
k
2 tm, n 1 tm, n 1 2tm,n
y

35. Метод конечных разностей

Обозначают числа Фурье:
a
a
Fox
;
Fo
y
2
2
x
y
Часто принимают
x y Fox Fo y Fo

36. Метод конечных разностей

Тогда формула примет вид:
tmk ,n1 tmk ,n Fo t km 1 ,n t km 1 ,n 4tmk ,n tmk , n 1 tmk , n 1
t
k 1
m,n
k
k
k
k
k 1
Fo t m 1 ,n t m 1 ,n tm, n 1 tm, n 1 tm,n
4
Fo

37. Метод конечных разностей

Устойчивость решения обеспечивается
при условии:
1
1
4 0 Fo
Fo
4

38. Вопросы к экзамену

Метод элементарных тепловых
балансов.
2. Метод конечных разностей.
1.