Похожие презентации:
Методы статистического анализа
1.
Состояние проблемы на современном этапеЯрко выраженный примитивизм математической обработки в научных
медицинских исследованиях, которая в лучшем случае характеризуется
параметрическими показателями, критерием Стьюдента и
коэффициентом линейной парной корреляции Браве-Пирсона
Практически отсутствует системный подход к статистическому анализу:
применение той или иной его разновидности ничем специально не
обосновывается и не диктуется логикой научного исследования
Игнорируется предшествующее любой научной работе статистическое
планирование, которое само может и должно определять структуру
исследовательской работы и оптимальный методический минимум
Низкая культура преподавания высшей математики и информатики
особенно в медицинских вузах, которая постепенно трансформируется в
научные исследования с неэффективными практическими
рекомендациями
2.
БиометрияCистема знаний, опирающаяся на союз математики, биологии и
информатики, составляют суть биометрии - науки, вспомогательной в
медико-биологических исследованиях, но придающей им законченный
описательный и достоверный смысл
Основные задачи биометрии - описание явления, оценка его
достоверности (воспроизводимости), изучение механизмов его развития
(во взаимосвязи с другими процессами и явлениями) и условий его
максимального проявления, принятие решения (прогноз,
предсказание, экстраполяция)
Ученый, который открыл некоторые новые явления, зависимости,
тенденции, на этом построил рабочую гипотезу должен защитить ее от
предположения, что все эти явления и эффекты не обусловлены
случаем. Он должен оценить, сколько необходимо провести
наблюдений, чтобы доказать наличие достоверного результата
3.
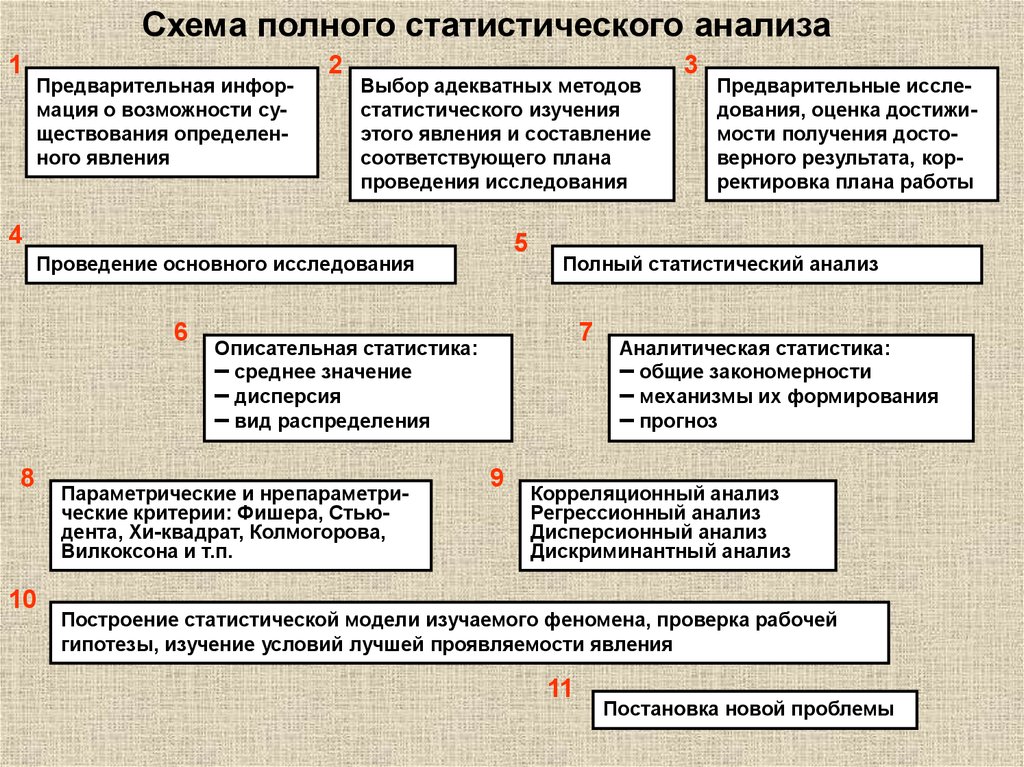
Схема полного статистического анализа1
Предварительная информация о возможности существования определенного явления
2
Выбор адекватных методов
статистического изучения
этого явления и составление
соответствующего плана
проведения исследования
4
5
Проведение основного исследования
6
8
10
7
9
Предварительные исследования, оценка достижимости получения достоверного результата, корректировка плана работы
Полный статистический анализ
Описательная статистика:
– среднее значение
– дисперсия
– вид распределения
Параметрические и нрепараметрические критерии: Фишера, Стьюдента, Хи-квадрат, Колмогорова,
Вилкоксона и т.п.
3
Аналитическая статистика:
– общие закономерности
– механизмы их формирования
– прогноз
Корреляционный анализ
Регрессионный анализ
Дисперсионный анализ
Дискриминантный анализ
Построение статистической модели изучаемого феномена, проверка рабочей
гипотезы, изучение условий лучшей проявляемости явления
11
Постановка новой проблемы
4.
40Основные параметры нормального распределения
35
Х = (х1+ х2 + … +хn) / n
σ=
30
√(∑x2i - (∑xi)2/n) / (n-1)
m = σ / √n
25
20
15
10
5
0
-5
-3 σ
-2 σ
-1σ
Х
68,3%
95,5%
99,9%
+1 σ
+2 σ
+3 σ
5.
Арифметическая точность в представлении данныхНеправильно
Правильно
0,4±0,022
0,412±0,0217
7,0±0,063
7,03±0,063
12,33±0,15
12,3±0,15
384,54±18,608
385±18,6
Правило 1
Точность представления среднего значения зависит от его величины
До 1 – три знака после запятой
От 1 до 10 – два знака после запятой
От 10 до 100 – один знак после запятой
Свыше 100 – целое число.
Правило 2
Ошибка среднего значения пишется на один знак точнее среднего
значения
6.
7.
8.
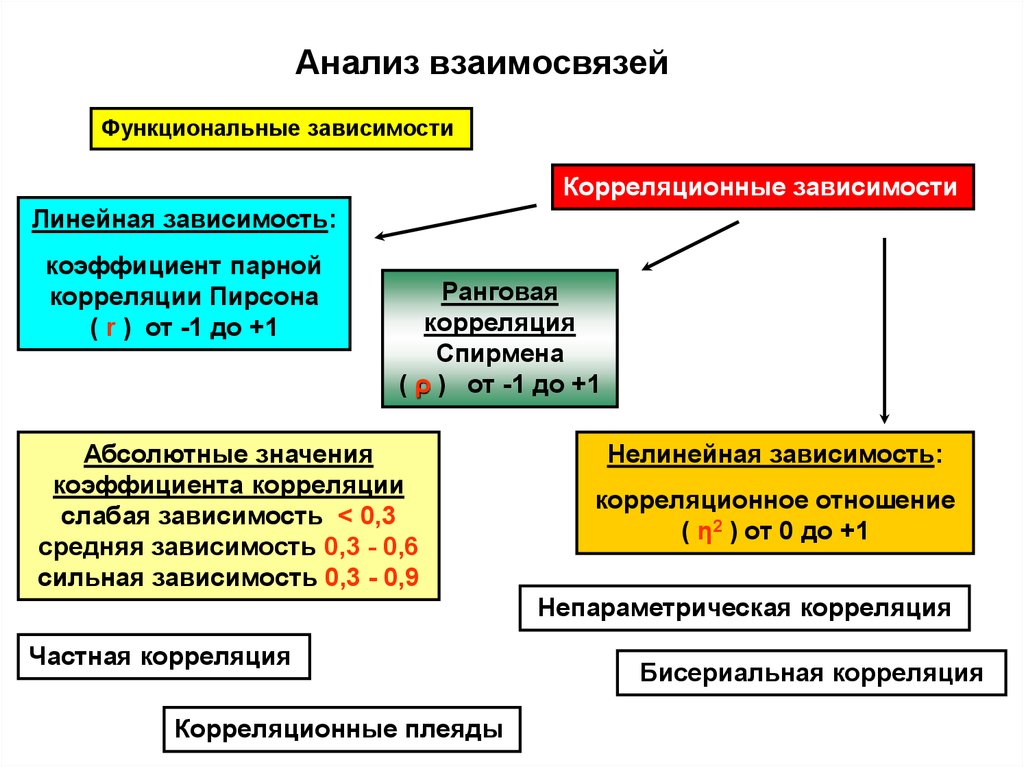
Анализ взаимосвязейФункциональные зависимости
Корреляционные зависимости
Линейная зависимость:
коэффициент парной
корреляции Пирсона
( r ) от -1 до +1
Ранговая
корреляция
Спирмена
( ρ ) от -1 до +1
Абсолютные значения
коэффициента корреляции
слабая зависимость < 0,3
средняя зависимость 0,3 - 0,6
сильная зависимость 0,3 - 0,9
Нелинейная зависимость:
корреляционное отношение
( η2 ) от 0 до +1
Непараметрическая корреляция
Частная корреляция
Корреляционные плеяды
Бисериальная корреляция
9.
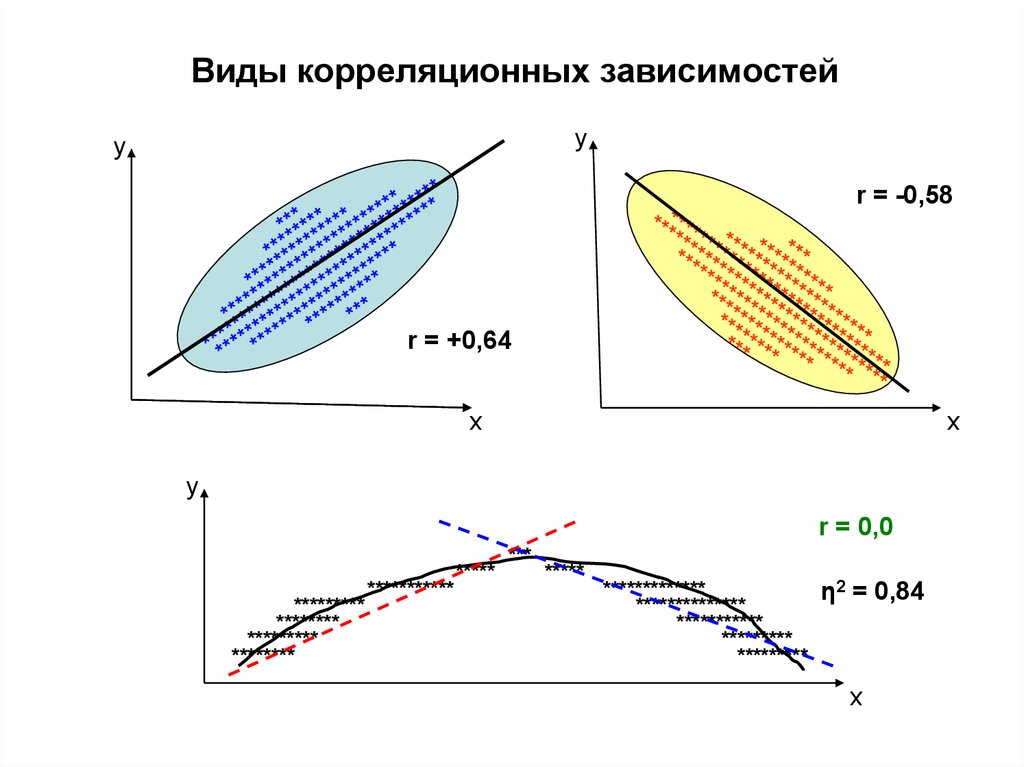
Виды корреляционных зависимостейy
y
r = -0,58
r = +0,64
х
х
y
r = 0,0
*********
********
*********
********
***********
*****
***
*****
*************
**************
***********
*********
*********
η2 = 0,84
х
10.
Регрессионный анализНа основе корреляционного анализа и анализа дисперсий
строится математическая модель влияния одного параметра
на другой
Парная регрессия
Множественная регрессия
Y = aX + b
Y = a1X1 + a2X2 + … anXn + b
Регрессионный анализ позволяет строить прогностические
модели - по изменению одного (или нескольких) показателей
предсказывать изменение какого-либо параметра
11.
Дисперсионный анализИзменение параметра во время воздействия
является результатом действия факторов, часть из
которых врач контролирует, а часть – нет (т.е.
влияние могут оказать случайные факторы)
η2 = η2контр. + η2случайн.
Дисперсионный анализ применяют в многофакторных моделях; он
позволяет выделить ту часть динамических процессов, которая
определяется тем или иным контролируемым фактором. Главное
условие применения этого вида анализа – необходимость
выделения градаций внутри каждого фактора
12.
Факторный анализДальнейшее развитие дисперсионного анализа, который позволяет
выделить из суммы случайных влияний скрытые факторы, которые
по тем или иным причинам врач не контролирует.
Типичный вывод после проведения факторного анализа: изменение
параметра Х в процессе лечения на 12% объясняется выбранной
методикой лечения, 39% изменений – результат случайных
воздействий, но другие 49% объясняются влиянием, например,
трех неучтенных факторов (F1 – 25%; F2 – 11%’ F3 – 13%)
13.
Классификационный анализКластерный анализ
Корреляционные плеяды
Дискриминантный
анализ
Математическое
обоснование группировки
параметров в
гипотетические
функциональные системы
Построение уравнения
разграничительной функции для
разделения пациентов на различные
классы (диагностика)
Выделение из суммы параметров
важнейших, которые вносят
значимый вклад в уравнение
разграничительной функции
14.
Непараметрическая статистикаНепараметрическая оценка изменения средних значений
критерий Вальда-Вольфовица
критерий Диксона-Муди
критерий Вилкоксона
Непараметрическая корреляция
Ранговая корреляция Спирмена
Корреляция Кендала
Критерий ассоциации Пирсона
Оценка формы распределения встречаемости признака
Критерий Пирсона χ2











 Математика
Математика








