Похожие презентации:
Численные методы решения задач
1. ИНФОРМАТИКА
Тема 6.Численные методы решения задач.
2.
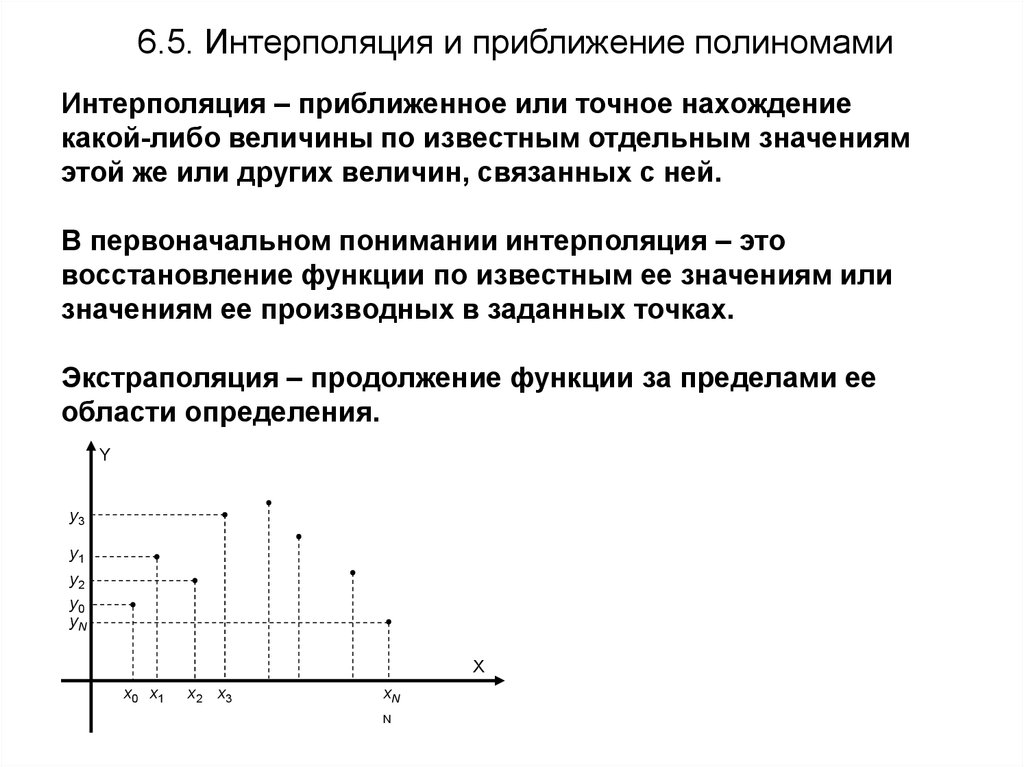
6.5. Интерполяция и приближение полиномамиИнтерполяция – приближенное или точное нахождение
какой-либо величины по известным отдельным значениям
этой же или других величин, связанных с ней.
В первоначальном понимании интерполяция – это
восстановление функции по известным ее значениям или
значениям ее производных в заданных точках.
Экстраполяция – продолжение функции за пределами ее
области определения.
Y
y3
y1
y2
y0
yN
X
x0 x1
x2 x3
xN
N
3.
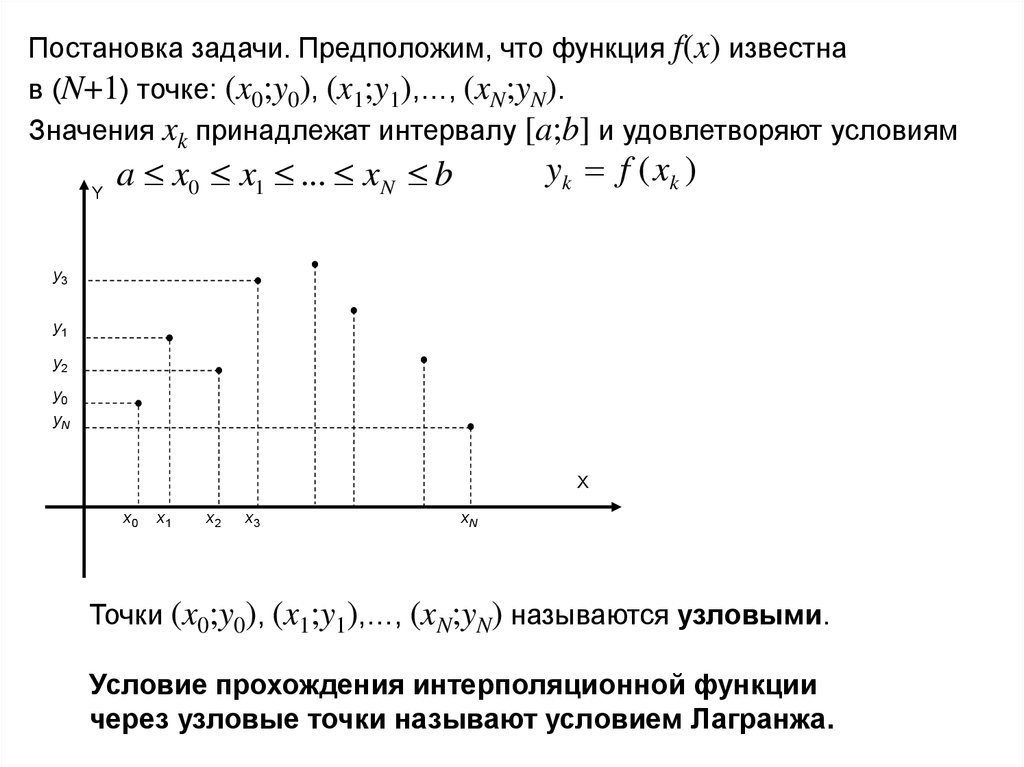
Постановка задачи. Предположим, что функция f(x) известнав (N+1) точке: (x0;y0), (x1;y1),…, (xN;yN).
Значения xk принадлежат интервалу [a;b] и удовлетворяют условиям
Y
yk f ( xk )
a x0 x1 ... xN b
y3
y1
y2
y0
yN
X
x0
x1
x2
x3
xN
Точки (x0;y0), (x1;y1),…, (xN;yN) называются узловыми.
Условие прохождения интерполяционной функции
через узловые точки называют условием Лагранжа.
4.
6.5.1. Интерполяция алгебраическим полиномомИнтерполяционная функция φ(x) имеет вид многочлена
( x ) c0 c1 x c2 x 2 c3 x 3 ...cN x N
2
3
N
c
c
x
c
x
c
x
...
c
x
( x0 ) y0
0
1
0
2
0
3
0
N
0 y0
(x ) y
2
3
N
c
c
x
c
x
c
x
...
c
x
0 1 1 2 1
1
1
3
1
N
1 y1
( xN ) y N
c c x c x 2 c x 3 ...c x N y
0 1 N
2
N
3
N
N
N
N
X C Y
C X 1 Y
1
1
X 1
1
x0
x1
x2
x02
x12
x22
xN
x N2
c0
y0
x0N
c
y
x1N
1
1
x2N C c2 Y y2
cN
y N
x NN
5.
Схема Горнера( x) c0 c1 x c2 x c3 x ...cN x
2
3
N
c0 x (c1 x (c2 x (c3 x (... cN x)...)))
Количество
операций
Обычный способ
Сложение
N
Умножение
N ( N 1) ( N 2) ... 2 1 0
Фрагмент программы на языке Си
p=c[n];
for(i=n-1; i>=0; i--)
p=c[i]+p*x;
Схема
Горнера
N ( N 1)
2
N
N
6.
6.5.2. Интерполяционный полином ЛагранжаИнтерполяционный полином Лагранжа имеет вид:
x x1 x x2
x xN
x x0 x x2
x xN
P ( x ) y0
...
y1
...
x0 x1 x0 x2
x0 x N
x1 x0 x1 x2
x1 x N
N
N x x
x x0 x x1
x xN 1
j
yN
...
yi
xN x0 x0 x1
xN xN 1 i 0
j 0 xi x j
j i
x0 x1 x0 x2
x0 x N
x0 x0 x0 x2
x0 x N
P( x0 ) y0
...
y1
...
x0 x1 x0 x2
x0 x N
x1 x0 x1 x2
x1 x N
yN
x0 x0 x0 x1
x x N 1
... 0
y0 0 ... 0 y0 f ( x0 )
xN x0 x0 x1
xN xN 1
Достоинством полинома Лагранжа является то, что не требуется
предварительного определения коэффициентов полинома.
7.
6.5.3. Интерполяционный полином НьютонаИнтерполяционный полином Ньютона имеет вид:
PN ( x) a0 a1 ( x x0 ) a2 ( x x0 ) ( x x1 ) ... aN ( x x0 ) ( x x1 ) ... ( x xN )
a0 , a1 , a2 ,..., aN
– коэффициенты полинома Ньютона.
Коэффициенты полинома Ньютона находятся исходя из
выполнения условия Лагранжа. PN ( xi ) yi i 0,1,2,..., N
PN ( x0 ) y0
PN ( x0 ) a0 a1 ( x0 x0 ) a2 ( x0 x0 ) ( x0 x1 ) ... aN ( x0 x0 ) ( x0 x1 ) ... ( x0 xN ) y0
PN ( x1 ) y1
a0 y0
PN ( x1 ) a0 a1 ( x1 x0 ) a2 ( x1 x0 ) ( x1 x1 ) ... aN ( x1 x0 ) ( x1 x1 ) ... ( x1 xN ) y1
y0 a1 ( x1 x0 ) y1
a1
y1 y0
x1 x0
8.
Аналитическая формула, по которой находятся коэффициентыполинома, имеет сложный вид
f xK J 1 ,..., xK f xK J ,..., xK 1
f xK J , xK J 1 ,..., xK
xK xK J
Итерационная процедура очень простая.
f[ , , ]
f[ , , , ]
xK
f [ xK ]
x0
f [ x0 ]
x1
f [ x1 ]
f [ x0 , x1 ]
x2
f [ x2 ]
f [ x1 , x2 ]
f [ x0 , x1 , x2 ]
x3
f [ x3 ]
f [ x2 , x3 ]
f [ x1 , x2 , x3 ]
f [ x0 , x1 , x2 , x3 ]
x4
f [ x4 ]
f [ x3 , x4 ]
f [ x2 , x3 , x4 ]
f [ x1 , x2 , x3 , x4 ]
f[ , ]
f[ , , , , ]
f [ x0 , x1 , x2 , x3 , x4 ]
9.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
15
4
48
5
105
6
192
f[,,,,,]
10.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
15
4
48
5
105
6
192
3
f[,,,,,]
11.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
4
48
5
105
6
192
f[,,,,,]
12.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
4
48
33
5
105
6
192
f[,,,,,]
13.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
4
48
33
5
105
57
6
192
f[,,,,,]
14.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
4
48
33
5
105
57
6
192
87
f[,,,,,]
15.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
4
48
33
5
105
57
6
192
87
6
f[,,,,,]
16.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
6
4
48
33
9
5
105
57
6
192
87
f[,,,,,]
17.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
6
4
48
33
9
5
105
57
12
6
192
87
f[,,,,,]
18.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
6
4
48
33
9
5
105
57
12
6
192
87
15
f[,,,,,]
19.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
6
4
48
33
9
5
105
57
12
6
192
87
15
1
f[,,,,,]
20.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
6
4
48
33
9
1
5
105
57
12
1
6
192
87
15
f[,,,,,]
21.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
6
4
48
33
9
1
5
105
57
12
1
6
192
87
15
1
f[,,,,,]
22.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
6
4
48
33
9
1
5
105
57
12
1
6
192
87
15
1
0
f[,,,,,]
23.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
x0 1
x1 2
y0 3 y1 0
x2 3 x3 4 x4 5
y2 15 y3 48 y4 105
x5 6
y5 192
f ( x) x 3 4 x
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
6
4
48
33
9
1
5
105
57
12
1
0
6
192
87
15
1
0
f[,,,,,]
24.
Пример. Найти значения коэффициентов полинома Ньютона дляшести узловых – точек.
xk f [xk] f [ , ] f [ , , ] f [ , , , ] f [ , , , , ]
1
–3
2
0
3
3
15
15
6
4
48
33
9
1
5
105
57
12
1
0
6
192
87
15
1
0
a0 3
a1 3
a2 6 a3 1
f[,,,,,]
0
a4 a5 0
P5 ( x) a0 a1 ( x x0 ) a2 ( x x0 ) ( x x1 ) a3 ( x x0 ) ( x x1 ) ( x x2 )
25.
Проверка.P5 ( x) a0 a1 ( x x0 ) a2 ( x x0 ) ( x x1 ) a3 ( x x0 ) ( x x1 ) ( x x2 )
a0 3
a1 3
a2 6 a3 1
x0 1
x1 2
x2 3
P5 ( x) 3 3 ( x 1) 6 ( x 1) ( x 2) ( x 1) ( x 2) ( x 3)
3 3x 3 6 x 2 18 x 12 x3 3 x 2 2 x 3 x 2 9 x 6 x 3 4 x
К достоинствам данного метода можно отнести
• меньшая погрешность интерполяции при близкорасположенных узлах;
• возможность использования вложенных умножений при вычислении
значений полинома;
• коэффициенты полинома получаются более простым способом, чем
при интерполяции алгебраическим полиномом.
Недостатком является проведение предварительных расчетов
коэффициентов.
26.
6.5.4. Интерполяция параболическим сплайномСплайном называется функция, определенная на отрезке [a; b],
совпадающая на частичных отрезках [xi; xi+1] с некоторым
алгебраическими многочленами степени не выше m и имеющая
непрерывную (m–1)-ю производную.
Параболическим сплайном называют совокупность многочленов
второй степени вида
i ( x) ai bi ( x xi ) ci ( x xi )2
ai , bi , ci – коэффициенты параболических полиномов i 0,1,..., N 1
N – число узловых точек
27.
Коэффициенты ai, bi, ci находятся при решении системы линейныхуравнений, которые получаются из выполнения трех условий:
• равенство значений сплайна и аппроксимируемой функции в узлах
(условие Лагранжа)
(x ) y
(x ) y
i
i
i
i
i 1
i 1
• непрерывность первой производной в узловых точках:
i ( xi 1 ) i 1 ( xi 1 )
• равенство некоторому значению D первой производной в начале
или на конце интервала: 0 ( x0 ) D или N 1 ( xN ) D
i ( x) bi 2ci ( x xi )
– первая производная
параболического многочлена
28.
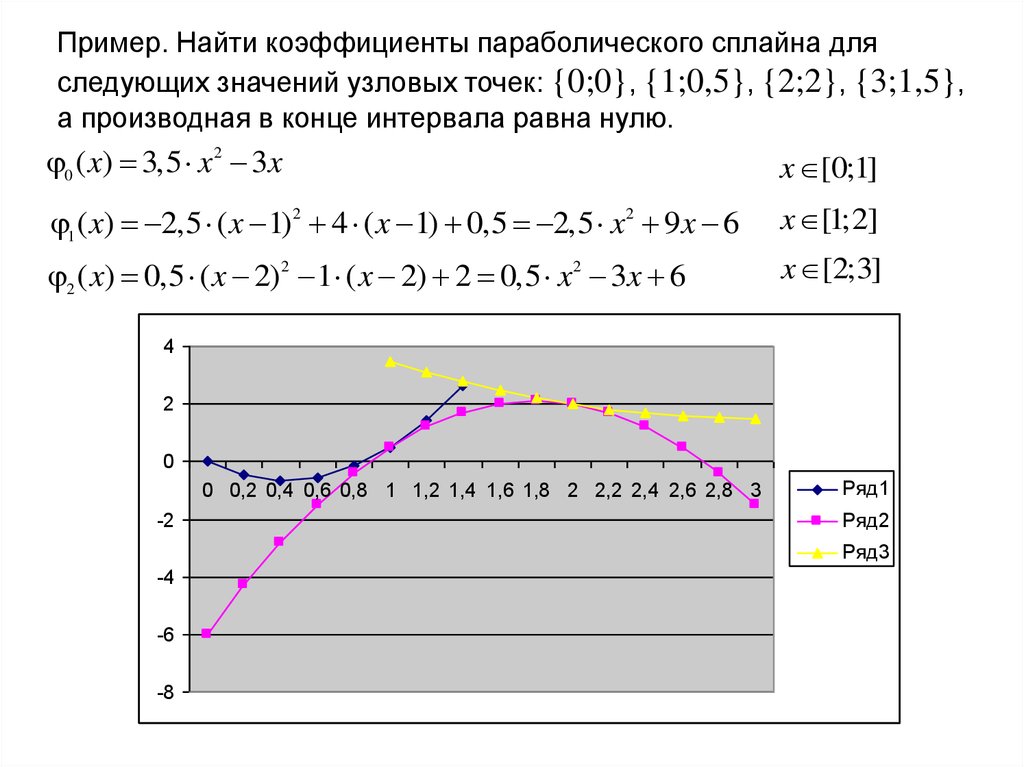
Пример. Найти коэффициенты параболического сплайна дляследующих значений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5},
а производная в конце интервала равна нулю.
0 ( x0 ) y0
( x ) y
1
0 1
1 ( x1 ) y1
1 ( x2 ) y2
2 ( x2 ) y2
( x ) y
3
2 3
0 ( x1 ) 1 ( x1 )
1 ( x2 ) 2 ( x2 )
2 ( x3 ) 0
29.
Пример. Найти коэффициенты параболического сплайна дляследующих значений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5},
а производная в конце интервала равна нулю.
a0 0
2
a
b
(1
0)
c
(1
0)
0,5
0
0 0
a1 0,5
2
a
b
(2
1)
c
(2
1)
2
1 1
1
a2 2
a b (3 2) c (3 2) 2 1,5
2
2 2
b0 2c0 (1 0) b1
b1 2c1 (2 1) b2
b2 2c2 (3 2) 0
0 ( x0 ) y0
( x ) y
1
0 1
1 ( x1 ) y1
1 ( x2 ) y2
2 ( x2 ) y2
( x ) y
3
2 3
0 ( x1 ) 1 ( x1 )
1 ( x2 ) 2 ( x2 )
2 ( x3 ) 0
a0 0
a1 0,5
a2 2
30.
Пример. Найти коэффициенты параболического сплайна дляследующих значений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5},
а производная в конце интервала равна нулю.
b0 c0 0,5
0,5 b c 2
1
1
2 b2 c2 1,5
b0 2c0 b1
b1 2c1 b2
b2 2c2 0
a0 0
a1 0,5
a2 2
b0 c0 0,5
b c 1,5
1 1
b2 c2 0,5
b0 2c0 b1
b1 2c1 b2
b2 2c2 0
c2 0,5
b2 1
31.
Пример. Найти коэффициенты параболического сплайна дляследующих значений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5},
а производная в конце интервала равна нулю.
b0 c0 0,5
b c 1,5
1 1
b2 c2 0,5
b0 2c0 b1
b1 2c1 b2
b2 2c2 0
a0 0
a1 0,5
a2 2
c1 b2 1,5 2,5
c0 b1 0,5 3,5
b1 1,5 c1 4
b0 0,5 c0 3
c2 0,5
b2 1
32.
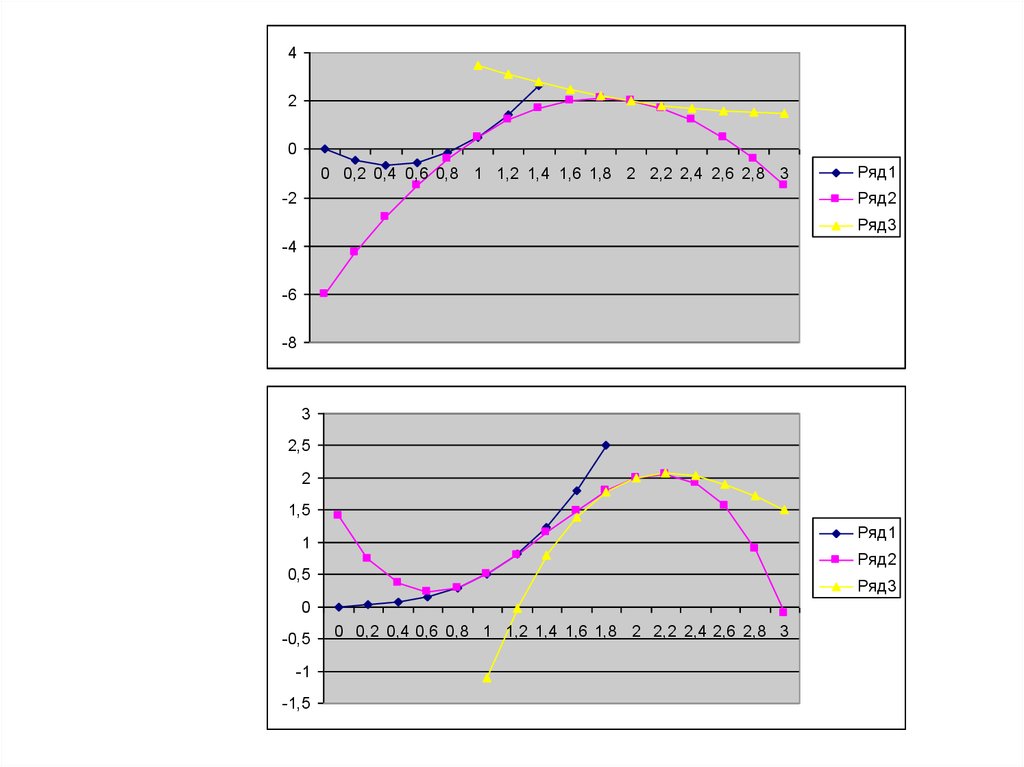
Пример. Найти коэффициенты параболического сплайна дляследующих значений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5},
а производная в конце интервала равна нулю.
0 ( x) 3,5 x2 3x
x [0;1]
1 ( x) 2,5 ( x 1)2 4 ( x 1) 0,5 2,5 x2 9 x 6
x [1;2]
2 ( x) 0,5 ( x 2)2 1 ( x 2) 2 0,5 x2 3x 6
x [2;3]
4
2
0
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 2,2 2,4 2,6 2,8 3
-2
Ряд1
Ряд2
Ряд3
-4
-6
-8
33.
В общем случае итерационная процедура нахождениякоэффициентов параболического сплайна следующая:
1. Находятся значения hK при K=0, 1, 2,…, (N–1) по формуле
hK xK 1 xK
2. Находятся значения zK при K=0, 1, 2,…, (N–1) по формуле
yK 1 yK
zK
hK
3. Находятся значения aK, bK, cK при K=0, 1, 2,…, (N–1) по формулам
• если задано значение первой производной D в начале интервала
интерполяции
b b
aK yK bK 2 z K bK 1 b0 D
cK
K 1
K
2 hK
• если задано значение первой производной D в конце интервала
bK 1 bK
интерполяции
aK yK bK 2 zK bK 1 bN D
cK
2 hK
34.
Пример. Найти коэффициенты параболического сплайна дляследующих значений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5},
а производная в конце интервала равна нулю.
hK xK 1 xK
aK y K
yK 1 yK
zK
hK
bK 2 z K bK 1
i xi yi hi
bK 1 bK
cK
2 hK
bN D
zi
0
1
0
1
0
0,5
1
1
0,5
1,5
2
2
2
1
-0,5
3
3
1,5
ai
bi
0 -3
0,5 4
2
-1
0
ci
3,5
-2,5
0,5
35.
6.5.5. Интерполяция кубическим сплайномКубическим сплайном называют совокупность многочленов
третьей степени вида
i ( x) ai bi ( x xi ) ci ( x xi ) di ( x xi )
2
3
ai , bi , ci , di – коэффициенты кубических полиномов i 0,1,..., N 1
N – число узловых точек
36.
i ( x) ai bi ( x xi ) ci ( x xi )2 di ( x xi )3Коэффициенты ai, bi, ci, di находятся при решении системы линейных
уравнений, которые получаются из выполнения трех условий:
• равенство значений сплайна и аппроксимируемой функции в узлах
(условие Лагранжа)
i ( xi ) yi i ( xi 1 ) yi 1
• непрерывность первой и второй производной в узловых точках:
i ( xi 1 ) i 1 ( xi 1 )
i ( xi 1 ) i 1 ( xi 1 )
• равенства нулю вторых производных на концах интервала:
0 ( x0 ) 0
N 1 ( xN 1 ) 0
i ( x) bi 2ci ( x xi ) 3di ( x xi )2 – первая производная
кубического многочлена
i ( x) 2ci 6di ( x xi )
– вторая производная
кубического многочлена
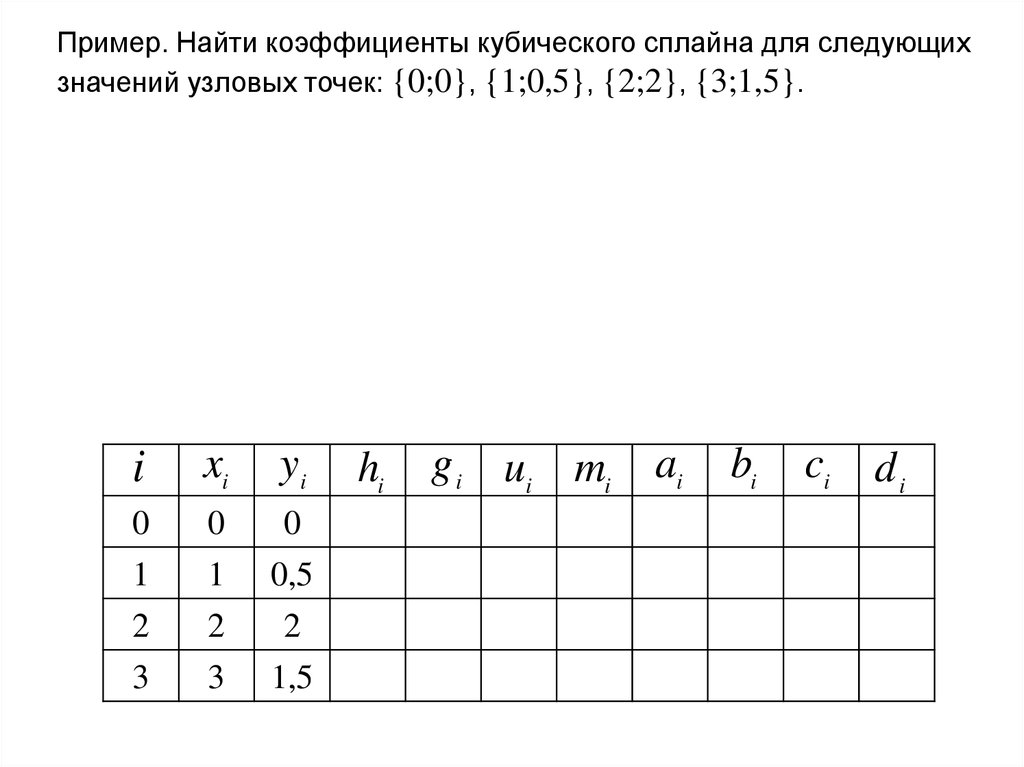
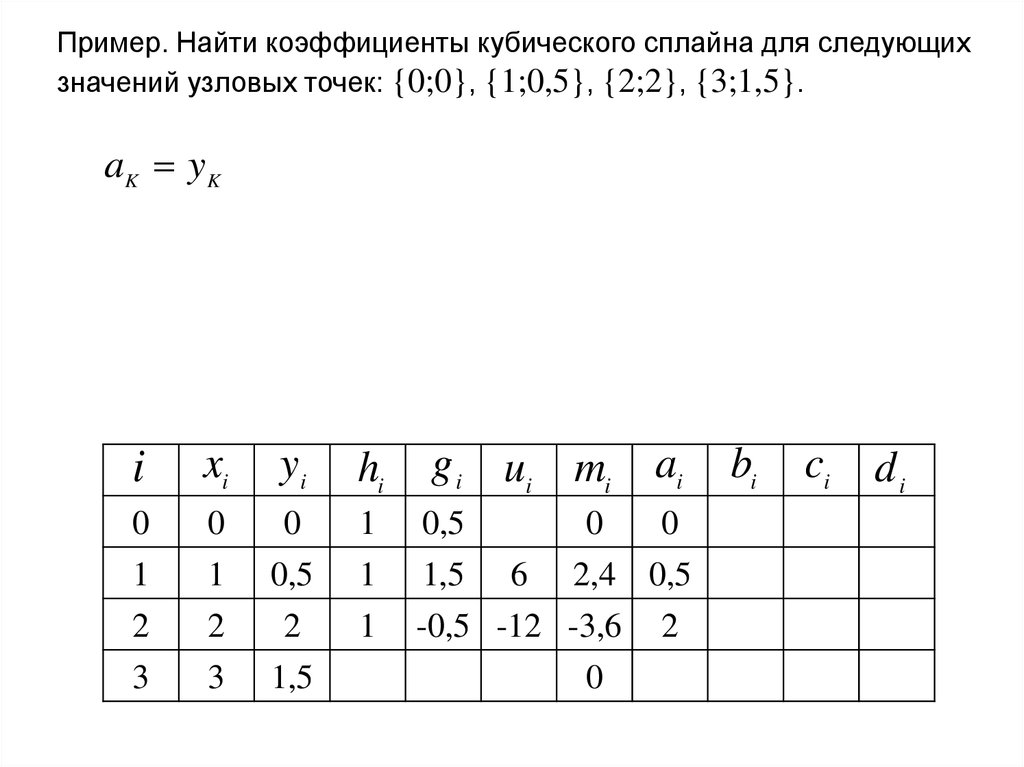
37.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
0 ( x0 ) y0
( x ) y
1
0 1
1 ( x1 ) y1
1 ( x2 ) y2
2 ( x2 ) y2
2 ( x3 ) y3
0 ( x1 ) 1 ( x1 )
1 ( x2 ) 2 ( x2 )
0 ( x1 ) 1 ( x1 )
( x ) ( x )
2
2
1 2
0 ( x0 ) 0
2 ( x3 ) 0
38.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
0 ( x0 ) y0
( x ) y
1
0 1
1 ( x1 ) y1
1 ( x2 ) y2
2 ( x2 ) y2
2 ( x3 ) y3
0 ( x1 ) 1 ( x1 )
1 ( x2 ) 2 ( x2 )
0 ( x1 ) 1 ( x1 )
( x ) ( x )
2
2
1 2
0 ( x0 ) 0
2 ( x3 ) 0
a0 0
2
3
a
b
(1
0)
c
(1
0)
d
(1
0)
0,5
0
0
0
0
a1 0,5
2
3
a1 b1 (2 1) c1 (2 1) d1 (2 1) 2
a 2
2
a2 b2 (3 2) c2 (3 2) 2 d 2 (3 2) 3 1,5
2
b
2
c
(1
0)
3
d
(1
0)
b1
0
0
0
b 2c (2 1) 3d (2 1) 2 b
1
1
2
1
2c0 6d 0 (1 0) 2c1
2c1 6d1 (2 1) 2c2
2c0 6d 0 (0 0) 0
2c2 6d 2 (3 2) 0
a0 0 a1 0,5 a2 2 c0 0
39.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
a0 0
2
3
a
b
(1
0)
c
(1
0)
d
(1
0)
0,5
0
0
0
0
a1 0,5
2
3
a1 b1 (2 1) c1 (2 1) d1 (2 1) 2
a 2
2
a2 b2 (3 2) c2 (3 2) 2 d 2 (3 2) 3 1,5
2
b
2
c
(1
0)
3
d
(1
0)
b1
0
0
0
b 2c (2 1) 3d (2 1) 2 b
1
1
2
1
2c0 6d 0 (1 0) 2c1
2c1 6d1 (2 1) 2c2
2c0 6d 0 (0 0) 0
a0 0 c0 0
2c2 6d 2 (3 2) 0
a1 0,5
a2 2
b0 d 0 0,5
0,5 b c d 2
1
1
1
2 b2 c2 d 2 1,5
b0 3d 0 b1
b1 2c1 3d1 b2
6d 0 2c1
2c1 6d1 2c2
2c 6d 0
2
2
40.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
b0 d 0 0,5
0,5 b c d 2
1
1
1
2 b2 c2 d 2 1,5
b0 3d 0 b1
b1 2c1 3d1 b2
6d 0 2c1
2c1 6d1 2c2
2c 6d 0
2
2
a0 0
a1 0,5
a2 2
c0 0
6d 0 6d1 6d 2
d 2 d0 d1
c2 3d 2 3 (d0 d1 )
41.
c2 3d 2 3 (d0 d1 )b0 0,5 d 0
b c d 1,5
1 1 1
b2 c2 d 2 0,5
c1 3d 0
c2 3d 2
b1 b0 3d 0 0,5 d 0 3d 0 0,5 2d 0
b2 b1 2c1 3d1 0,5 2d 0 6d 0 3d1 0,5 8d 0 3d1
6d 6d 6d
0
1
2
a0 0
a1 0,5
a2 2
c0 0
42.
b0 0,5 d 0b c d 1,5
1 1 1
b2 c2 d 2 0,5
c1 3d 0
c2 3d 2
b1 b0 3d 0 0,5 d 0 3d 0 0,5 2d 0
b2 b1 2c1 3d1 0,5 2d 0 6d 0 3d1 0,5 8d 0 3d1
6d 6d 6d
0
1
2
0,5 2d0 3d0 d1 1,5
0,5 8d0 3d1 3d 2 d 2 0,5
d d d
0
1
2
5d0 d1 1
8d0 3d1 2d 2 1
d d d
0
1
2
43.
5d0 d1 18d0 3d1 2d 2 1
d d d
0
1
2
d1 1 5d 0
d 2 d 0 d1 d 0 1 5d 0 4d 0 1
8d 0 3 (1 5d 0 ) 2 (4d 0 1) 1
15d 0 6
d 0 0, 4
d1 1 5 0,4 1
d 2 4 0,4 1 0,6
44.
b0 0,5 d 0d 0 0,4
b c d 1,5
1 1 1
d1 1
b2 c2 d 2 0,5
d 2 0,6
c1 3d 0
c2 3d 2
b1 b0 3d 0 0,5 d 0 3d 0 0,5 2d 0
b2 b1 2c1 3d1 0,5 2d 0 6d 0 3d1 0,5 8d 0 3d1
6d 6d 6d
0
1
2
c1 3 0,4 1,2
b0 0,5 0,4 0,1
c2 3 0,6 1,8
b1 0,5 2 0,4 1,3
b2 0,5 8 0,4 3 ( 1) 0,7
45.
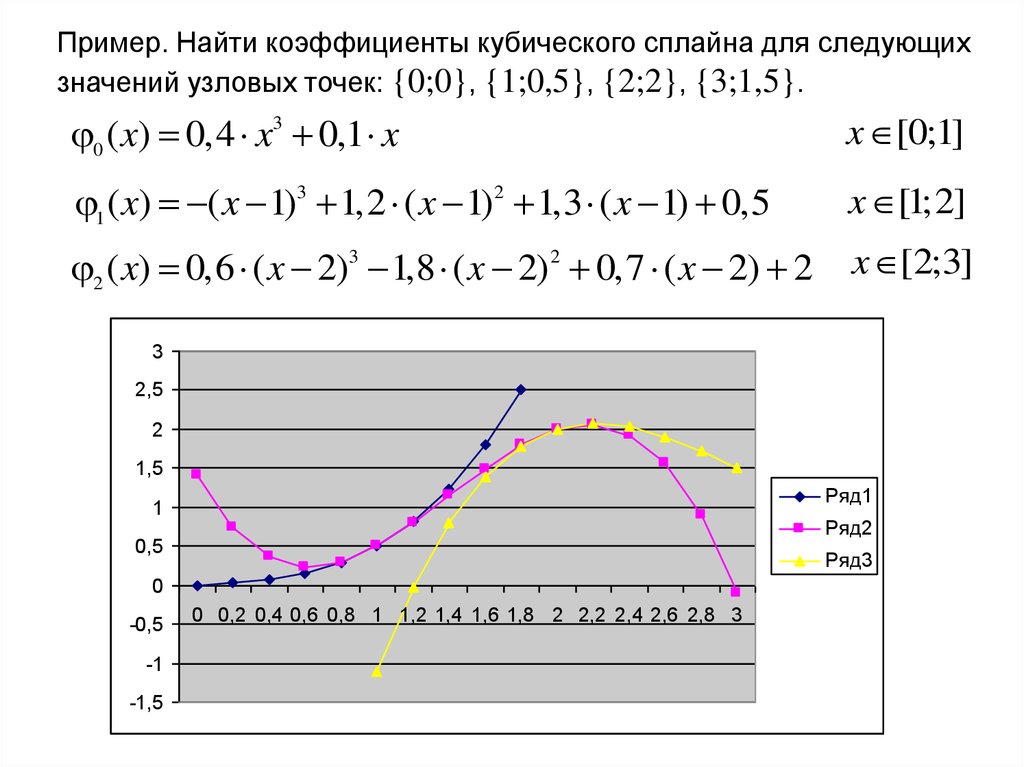
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
0 ( x) 0,4 x3 0,1 x
x [0;1]
1 ( x) ( x 1)3 1,2 ( x 1)2 1,3 ( x 1) 0,5
x [1;2]
2 ( x) 0,6 ( x 2)3 1,8 ( x 2)2 0,7 ( x 2) 2
x [2;3]
3
2,5
2
1,5
Ряд1
1
Ряд2
0,5
Ряд3
0
-0,5
-1
-1,5
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 2,2 2,4 2,6 2,8 3
46.
42
0
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 2,2 2,4 2,6 2,8 3
-2
Ряд1
Ряд2
Ряд3
-4
-6
-8
3
2,5
2
1,5
Ряд1
1
Ряд2
0,5
Ряд3
0
-0,5
-1
-1,5
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 2,2 2,4 2,6 2,8 3
47.
В общем случае итерационная процедура нахождениякоэффициентов кубического сплайна следующая:
1. Находятся значения hK при K=0, 1, 2,…, (N–1) по формуле
hK xK 1 xK
2. Находятся значения gK при K=0, 1, 2,…, (N–1) по формуле
yK 1 yK
gK
hK
3. Находятся значения uK при K=0, 1, 2,…, (N–1) по формуле
uK 6 ( g K g K 1 )
4. Находятся значения mK при решении системы линейных уравнений
2 (h0 h1 ) m1 h1 m2 u1
hK 1 mK 1 2 (hK 1 hK ) mK hK mK 1 uK , K 2,3,...,( N 2)
h m 2 (h h ) m u
N 2
N 1
N 1
N 1
N 2 N 2
48.
В общем случае итерационная процедура нахождениякоэффициентов кубического сплайна следующая:
5. Принимается m0 = mN = 0
6. Находятся значения коэффициентов aK, bK, cK, dK кубических
полиномов при K=0, 1, 2,…, (N–1) по формулам
aK y K
mK
cK
2
hK (2 mK mK 1 )
bK g K
6
mK 1 mK
dK
6 hK
49.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
i
xi
yi
0
1
2
3
0
1
2
3
0
0,5
2
1,5
hi
g i ui mi
ai
bi
ci
di
50.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
hK xK 1 xK
i
xi
yi
hi
0
1
2
3
0
1
2
3
0
0,5
2
1,5
1
1
1
g i ui mi
ai
bi
ci
di
51.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
yK 1 yK
gK
hK
hK xK 1 xK
i
xi
yi
hi
0
1
2
3
0
1
2
3
0
0,5
2
1,5
1
1
1
g i ui mi
0,5
1,5
-0,5
ai
bi
ci
di
52.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
yK 1 yK
gK
hK
hK xK 1 xK
i
xi
yi
hi
0
1
2
3
0
1
2
3
0
0,5
2
1,5
1
1
1
g i ui mi
0,5
1,5 6
-0,5 -12
uK 6 ( g K g K 1 )
ai
bi
ci
di
53.
2 (h0 h1 ) m1 h1 m2 u1hK 1 mK 1 2 (hK 1 hK ) mK hK mK 1 uK , K 2,3,...,( N 2)
h m 2 (h h ) m u
N 2
N 1
N 1
N 1
N 2 N 2
4 m1 m2 6
m1 4 m2 12
4 1
1 4
1
15
2
1 36
2 54
m1
2,4 m2
3,6
15
15
i
xi
yi
hi
g i ui mi
0
1
0
1
0
0,5
1
1
0,5
1,5
2
3
2
3
2
1,5
1
-0,5 -12 -3,6
0
6
0
2,4
6
1
12 4
4
6
1 12
ai
24 12 36
48 6 54
bi
ci
di
54.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
aK y K
i
xi
yi
hi
0
1
2
3
0
1
2
3
0
0,5
2
1,5
1
1
1
g i ui mi
ai
0,5
0
0
1,5 6 2,4 0,5
-0,5 -12 -3,6 2
0
bi
ci
di
55.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
mK
cK
2
aK y K
i
xi
yi
hi
0
1
2
3
0
1
2
3
0
0,5
2
1,5
1
1
1
g i ui mi
ai
0,5
0
0
1,5 6 2,4 0,5
-0,5 -12 -3,6 2
0
bi
ci
0
1,2
-1,8
di
56.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
mK
cK
2
aK y K
i
xi
yi
hi
0
1
2
3
0
1
2
3
0
0,5
2
1,5
1
1
1
mK 1 mK
dK
6 hK
g i ui mi
ai
0,5
0
0
1,5 6 2,4 0,5
-0,5 -12 -3,6 2
0
bi
ci
di
0 0,4
1,2 -1
-1,8 0,6
57.
Пример. Найти коэффициенты кубического сплайна для следующихзначений узловых точек: {0;0}, {1;0,5}, {2;2}, {3;1,5}.
mK
cK
2
aK y K
mK 1 mK
dK
6 hK
hK (2 mK mK 1 )
bK g K
6
i
xi
yi
hi
0
1
2
3
0
1
2
3
0
0,5
2
1,5
1
1
1
g i ui mi
ai
bi
ci
di
0,5
0
0 0,1 0 0,4
1,5 6 2,4 0,5 1,3 1,2 -1
-0,5 -12 -3,6 2 0,7 -1,8 0,6
0
58.
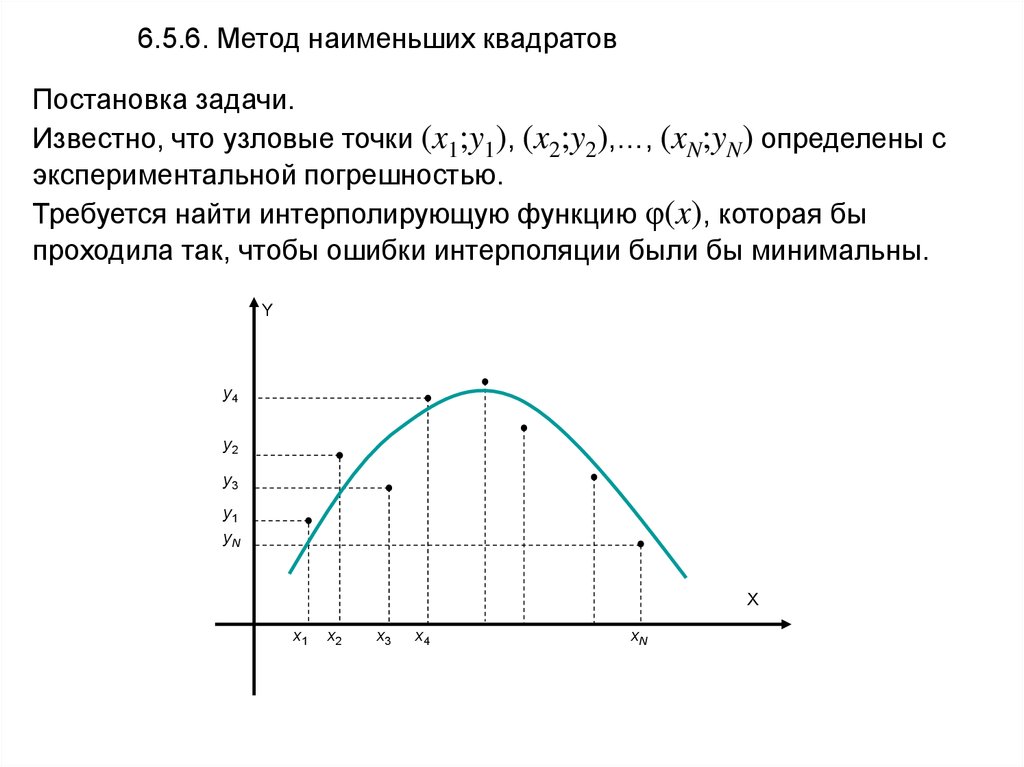
6.5.6. Метод наименьших квадратовПостановка задачи.
Известно, что узловые точки (x1;y1), (x2;y2),…, (xN;yN) определены с
экспериментальной погрешностью.
Требуется найти интерполирующую функцию φ(x), которая бы
проходила так, чтобы ошибки интерполяции были бы минимальны.
Y
y4
y2
y3
y1
yN
X
x1
x2
x3
x4
xN
59.
6.5.6. Метод наименьших квадратов( x) c1 1 ( x) c2 2 ( x) ... cm m ( x)
1 ( x), 2 ( x),..., m ( x)
– базисные функции.
1 N
[ ( xi ) yi ]2
N i 1
– среднеквадратичная ошибка
интерполяции.
N
Q [ ( xi ) yi ]2
i 1
Задача интерполяции по методу наименьших квадратов сводится
к нахождению значений коэффициентов c1, c2,…, cm, при которых
величина Q получает минимальное значение.
60.
6.5.6. Метод наименьших квадратов( x) c1 1 ( x) c2 2 ( x) ... cm m ( x)
Q
c 0
1
Q
0
c2
Q
c 0
m
61.
6.5.6. Метод наименьших квадратов( x) c1 1 ( x) c2 2 ( x) ... cm m ( x)
2 n c ( x ) c ( x ) ... c ( x ) y ( x ) 0
1 1 i 2 2 i
m m
i
i
1
i
i 1
n
2 c1 1 ( xi ) c2 2 ( xi ) ... cm m ( xi ) yi 2 ( xi ) 0
i 1
n
2 c ( x ) c ( x ) ... c ( x ) y ( x ) 0
2 2
i
m m
i
i
m
i
i 1 1 1 i
62.
2 n c ( x ) c ( x ) ... c ( x ) y ( x ) 01 1 i 2 2 i
m m
i
i
1
i
i 1
n
2 c1 1 ( xi ) c2 2 ( xi ) ... cm m ( xi ) yi 2 ( xi ) 0
i 1
n
2 c ( x ) c ( x ) ... c ( x ) y ( x ) 0
2 2
i
m m
i
i
m
i
i 1 1 1 i
n c ( x ) ( x ) c ( x ) ( x ) ... c ( x ) ( x ) N y ( x )
1 1 i 1 i 2 2 i 1 i
m m
i
1
i
i
1
i
i 1
i 1
n
N
c1 1 ( xi ) 2 ( xi ) c2 2 ( xi ) 2 ( xi ) ... cm m ( xi ) 2 ( xi ) yi 2 ( xi )
i 1
i 1
n
N
c ( x ) ( x ) c ( x ) ( x ) ... c ( x ) ( x ) y ( x )
m
i
2 2
i
m
i
m m
i
m
i
i
m
i
i 1 1 1 i
i 1
63.
n c ( x ) ( x ) c ( x ) ( x ) ... c ( x ) ( x ) N y ( x )1 1 i 1 i 2 2 i 1 i
m m
i
1
i
i
1
i
i 1
i 1
n
N
c1 1 ( xi ) 2 ( xi ) c2 2 ( xi ) 2 ( xi ) ... cm m ( xi ) 2 ( xi ) yi 2 ( xi )
i 1
i 1
n
N
c ( x ) ( x ) c ( x ) ( x ) ... c ( x ) ( x ) y ( x )
m
i
2 2
i
m
i
m m
i
m
i
i
m
i
i 1 1 1 i
i 1
( 1 1 ) ( 1 2 )
( ) ( )
2 2
1 2
( 1 m ) ( 2 m )
n
( 1 m ) c1 ( 1 y )
( 2 m ) c2 ( 2 y )
( m m ) cm ( m y)
( j k ) j ( xi ) k ( xi )
i 1
n
( j y) j ( xi ) yi
i 1
64.
( 1 1 ) ( 1 2 )( ) ( )
2 2
1 2
( 1 m ) ( 2 m )
( 1 m ) c1 ( 1 y )
( 2 m ) c2 ( 2 y )
( m m ) cm ( m y)
n
n
( j k ) j ( xi ) k ( xi )
( j y) j ( xi ) yi
i 1
i 1
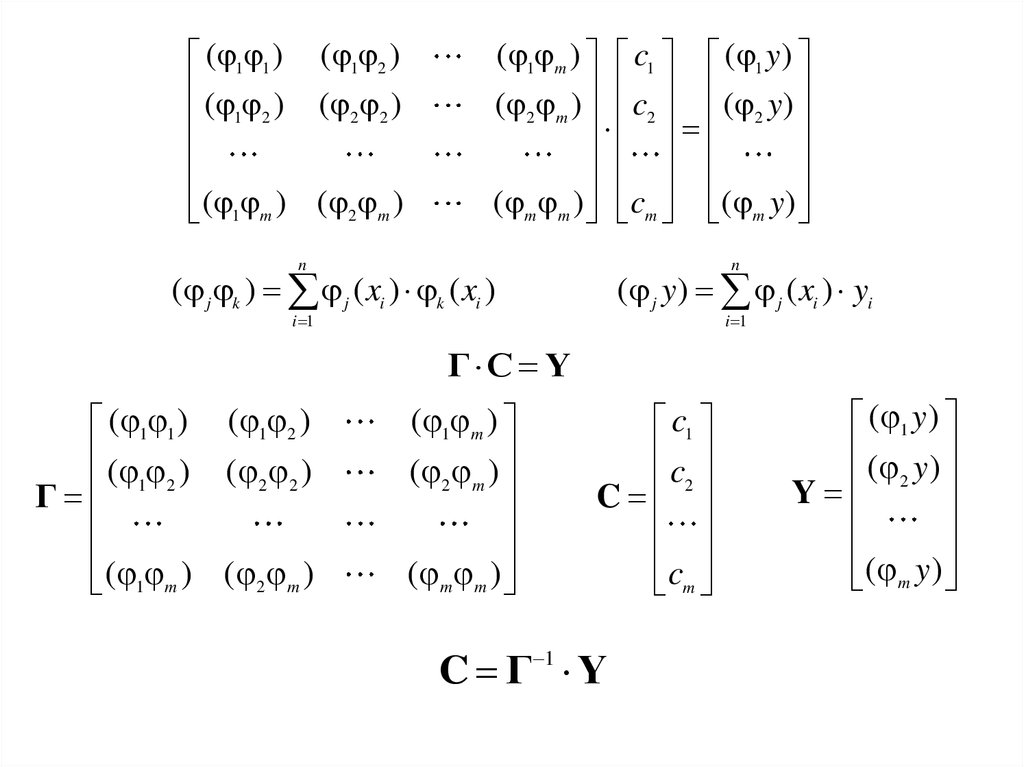
Γ C Y
( 1 1 ) ( 1 2 )
( ) ( )
2 2
Γ 1 2
( 1 m ) ( 2 m )
( 1 m )
( 2 m )
( m m )
c1
c
C 2
cm
C Γ 1 Y
( 1 y )
( y )
Y 2
(
y
)
m
65.
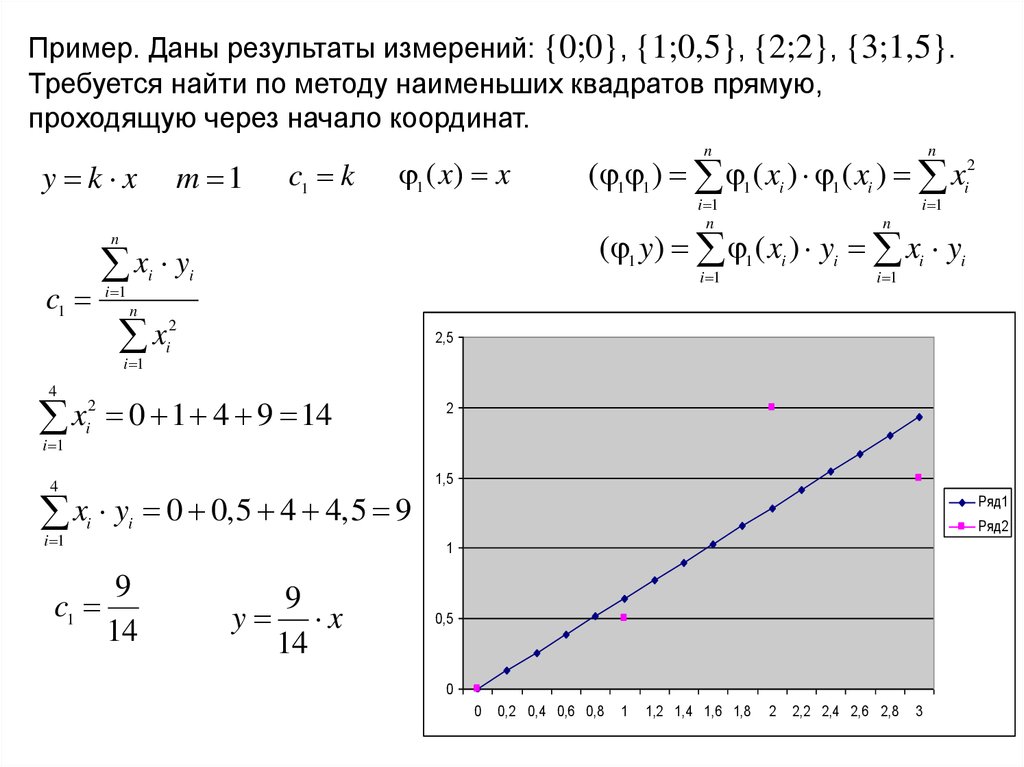
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется найти по методу наименьших квадратов прямую,
проходящую через начало координат.
( x) c1 1 ( x) c2 2 ( x) ... cm m ( x)
66.
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется найти по методу наименьших квадратов прямую,
проходящую через начало координат.
y k x
m 1
c1 k
1 ( x) x
c1
x y
i
x
i 1
2
i
2
i
i 1
n
n
i 1
i 1
i 1
2,5
0 1 4 9 14
x y
i 1
i
x
4
i
( 1 1 ) 1 ( xi ) 1 ( xi ) xi2
n
i 1
4
n
( 1 y) 1 ( xi ) yi xi yi
n
i 1
n
i
9
c1
14
2
1,5
0 0,5 4 4,5 9
Ряд1
Ряд2
1
9
y x
14
0,5
0
0
0,2 0,4 0,6 0,8
1
1,2 1,4 1,6 1,8
2
2,2 2,4 2,6 2,8
3
67.
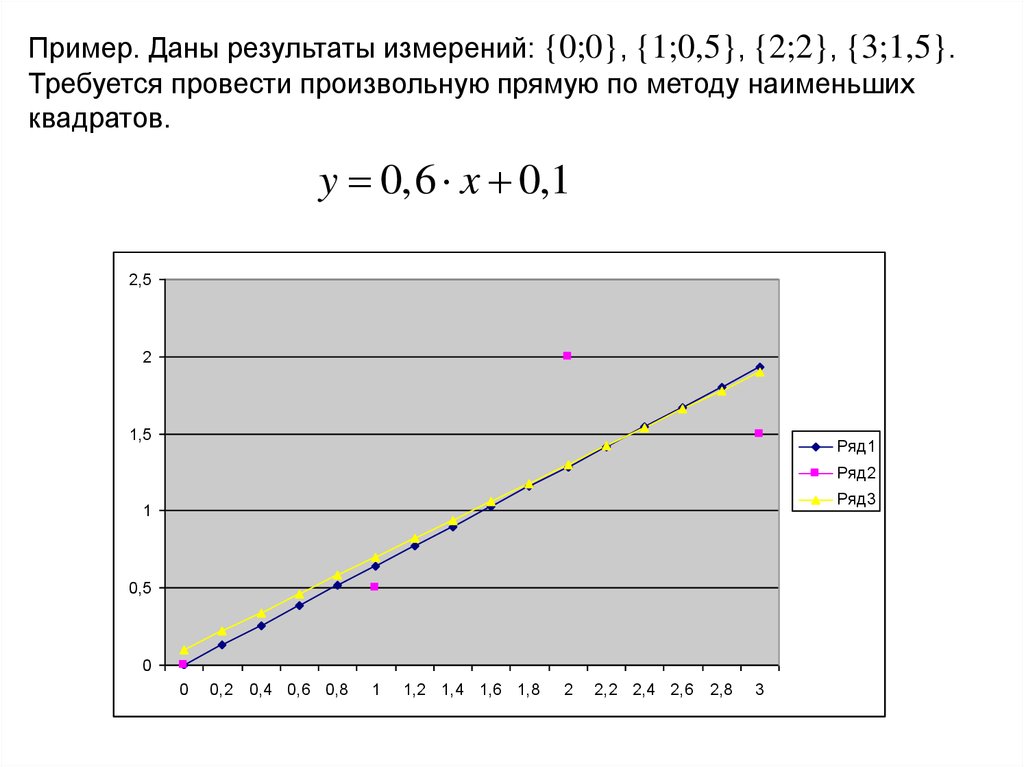
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется провести произвольную прямую по методу наименьших
квадратов.
( x) c1 1 ( x) c2 2 ( x) ... cm m ( x)
68.
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется провести произвольную прямую по методу наименьших
квадратов.
m 2
c1 k
n
( 1 1 ) x
2
i
i 1
n
( 1 y) xi yi
i 1
n x2
i
i 1
Γ n
xi
i 1
c2 b
1 ( x) x
n
( 1 2 ) xi
2 ( x ) 1
( 2 2 ) n
i 1
n
( 2 y) yi
x
i
14 6
i 1
6
4
n
i 1
n
c1
C
c2
n x y
i
i
9
i 1
Y n
yi 4
i 1
69.
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется провести произвольную прямую по методу наименьших
квадратов.
n x2
i
i 1
Γ n
xi
i 1
14 6
6
1
2
x
i
14 6
i 1
6
4
n
n
4
9 6
4 4
14 9
6
4
c1
C
c2
14 4 6 6 56 36 20
9 4 4 6 36 24 12
14 4 6 9 56 54 2
n x y
i
i
9
i 1
Y n
yi 4
i 1
c1 12 : 20 0,6
c2 2 : 20 0,1
y 0,6 x 0,1
70.
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется провести произвольную прямую по методу наименьших
квадратов.
y 0,6 x 0,1
2,5
2
1,5
Ряд1
Ряд2
Ряд3
1
0,5
0
0
0,2 0,4 0,6 0,8
1
1,2 1,4 1,6 1,8
2
2,2 2,4 2,6 2,8
3
71.
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется провести параболу по методу наименьших квадратов.
( x) c1 1 ( x) c2 2 ( x) ... cm m ( x)
72.
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется провести параболу по методу наименьших квадратов.
y a0 a1 x a2 x
2
73.
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется провести параболу по методу наименьших квадратов.
y a0 a1 x a2 x
2
m 3
c1 a0
1 ( x) 1
c2 a1
2 ( x ) x
c3 a2
3 ( x) x
2
74.
Пример. Даны результаты измерений: {0;0}, {1;0,5}, {2;2}, {3;1,5}.Требуется провести параболу по методу наименьших квадратов.
y a0 a1 x a2 x
m 3
c1 a0
c2 a1
c3 a2
1 ( x) 1
n
( 1 y) yi
( 1 1 ) n
n
( 2 2 ) xi2
2 ( x ) x
3 ( x) x
2
i 1
n
2
( 3 3 ) xi4
i 1
n
( 1 2 ) xi
i 1
n
( 1 3 ) xi2
i 1
n
( 2 3 ) xi3
i 1
i 1
n
( 2 y) xi yi
i 1
n
( 3 y) xi2 yi
i 1
75.
( 1 1 ) nn 4
n
( 2 2 ) xi2
i 1
n
( 3 3 ) x
i 1
n
4
i
( 1 2 ) xi
i 1
n
( 1 3 ) xi2
i 1
n
( 2 3 ) xi3
i 1
n
( 1 y) yi
i 1
n
( 2 y) xi yi
i 1
n
( 3 y) xi2 yi
i 1
4
4
xi 6
2
x
i 14
i 1
4
x
i 1
3
i
4
y
i 1
i
i 1
36
4
4
4
4
x
i 98
i 1
4
x y
i 1
i
2
x
i yi 22
i 1
i
9
76.
44
xi 6
n 4
x 14
i 1
4
yi 4
i 1
i 1
2
i
4
xi yi 9
i 1
4 6 14
Γ 6 14 36
14 36 98
4
x 36
i 1
3
i
4
4
x
i 98
i 1
4
2
x
i yi 22
i 1
c1
C c2
c3
4
Y 9
22
77.
4 6 14Γ 6 14 36
14 36 98
4
Y 9
22
c1
C c2
c3
4 6 14
6 14 36 80
14 36 98
4 6 14
1 9 14 36 12
22 36 98
4 4 14
2 6 9 36 108
14 22 98
4 6 4
3 6 14 9 20
14 36 22
c1 12 :80 0,15
c2 108 :80 1,35
c3 20 :80 0,25
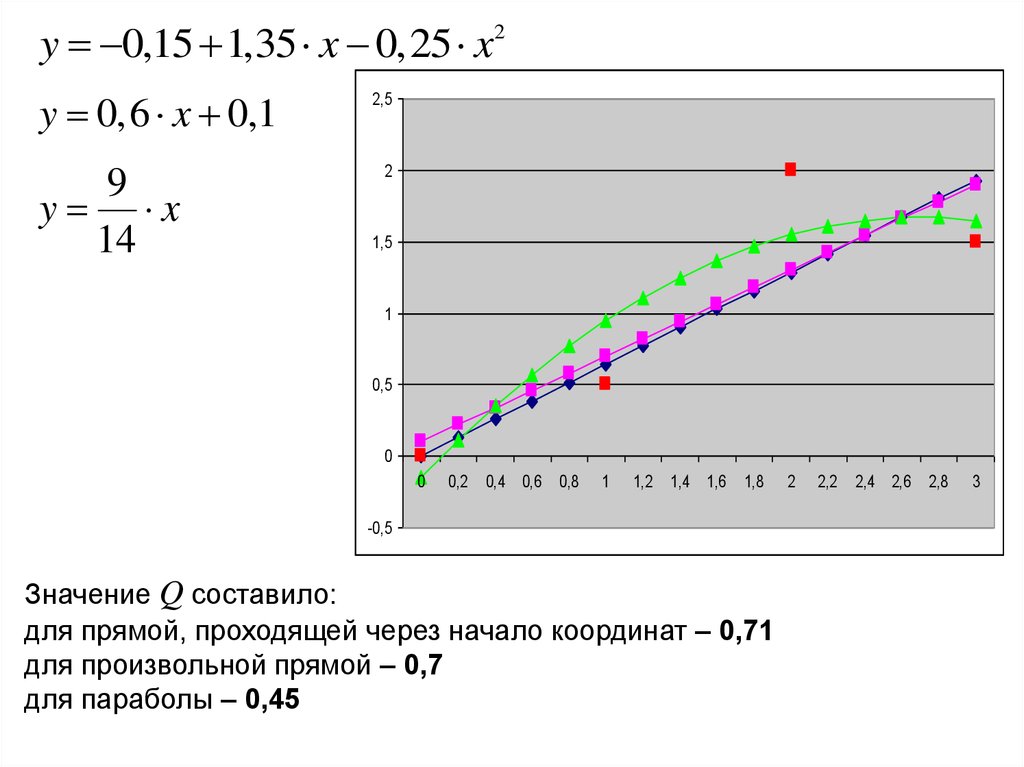
y 0,15 1,35 x 0,25 x
2
78.
y 0,15 1,35 x 0,25 x2y 0,6 x 0,1
9
y x
14
2,5
2
1,5
1
0,5
0
0
0,2
0,4 0,6
0,8
1
1,2
1,4 1,6
1,8
-0,5
Значение Q составило:
для прямой, проходящей через начало координат – 0,71
для произвольной прямой – 0,7
для параболы – 0,45
2
2,2
2,4 2,6
2,8
3
79.
Увеличение степени полинома приводит, с одной стороны, куменьшению суммарной ошибки Q, а с другой стороны, к
увеличению времени вычисления неизвестных
коэффициентов c1, c2, cm.
Для оценки приемлемого значения числа степени многочлена
используют величину
n
1
2
m
Pm ( xi ) yi
n m i 1
За оптимальное значение степени многочлена следует принять
то значение m, начиная с которого величина σm стабилизируется
или начинает возрастать.
80.
6.5.7. Интерполяция тригонометрическим полиномомЕсли требуется провести интерполяцию данных, имеющий
периодический характер, то в качестве базисных функций
φ1(x), φ2(x),…, φm(x) выбираются периодические функции.
Тригонометрический полином порядка M имеет вид
a0 M
TM ( x) a j cos( j x) b j sin( j x)
2 j 1
Коэффициенты тригонометрического полинома находятся
по методу наименьших квадратов.
2 N
a j yi cos( j xi )
N i 1
j 0,1,2,..., M
2 N
b j yi sin( j xi )
N i 1
j 1,2,..., M
81.
Пример. Аппроксимировать функцию y=5·x на интервале [–π; π]тригонометрическими полиномами порядка 1, 2 и 3. Тринадцать
узловых точек расположены равномерно на данном интервале.
82.
Пример. Аппроксимировать функцию y=5·x на интервале [–π; π]тригонометрическими полиномами порядка 1, 2 и 3. Тринадцать
узловых точек расположены равномерно на данном интервале.
a0 a1 a2 a3 0
2 N
b j yi sin( j xi )
N i 1
b1 9,01891
b2 4,18569
b3 2,41661
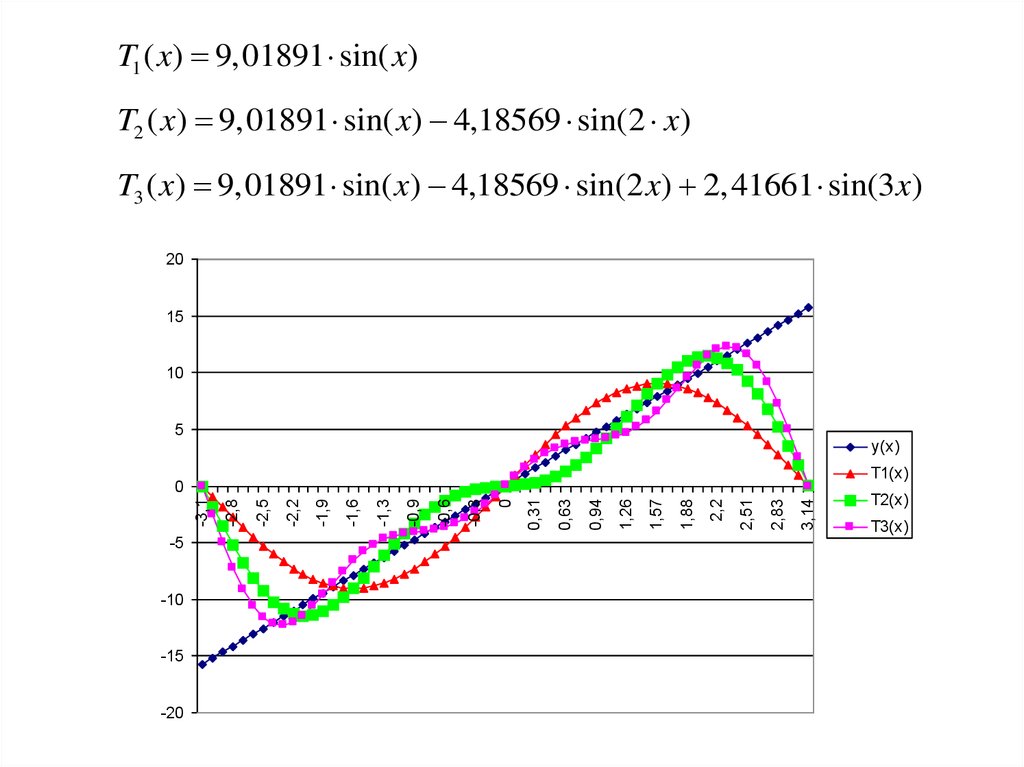
T1 ( x) 9,01891 sin( x)
T2 ( x) 9,01891 sin( x) 4,18569 sin(2 x)
T3 ( x) 9,01891 sin( x) 4,18569 sin(2 x) 2,41661 sin(3 x)
83.
T1 ( x) 9,01891 sin( x)T2 ( x) 9,01891 sin( x) 4,18569 sin(2 x)
T3 ( x) 9,01891 sin( x) 4,18569 sin(2 x) 2,41661 sin(3 x)
20
15
10
5
y(x)
T1(x)
-5
-10
-15
-20
3,14
2,83
2,51
2,2
1,88
1,57
1,26
0,94
0,63
0,31
0
-0,3
-0,6
-0,9
-1,3
-1,6
-1,9
-2,2
-2,5
-2,8
-3,1
0
T2(x)
T3(x)
84.
6.5.8. Интерполяция кривой БезьеПьер Безье – французский
инженер компании Рено,
разработчик системы
проектирования UNISURF
Поль де Фаже де Кастельжо –
французский математик и физик,
автор рекурсивного способа
построения кривых Безье
85.
6.5.8. Интерполяция кривой БезьеКривая Безье – это параметрическая кривая, задаваемая
выражением
n
B(t ) Pi bi ,n (t )
0 t 1
i 0
Pi
– функция компонент векторов опорных вершин
bi ,n
– базисные функции кривой Безье.
n i
bi ,n (t ) t (1 t )n i
i
n
n!
i i ! (n i)!
86.
Кубические кривые Безье (n=3) широко используются вграфических редакторах
B(t ) P0 (1 t )3 3 P1 t (1 t )2 3 P2 t 2 (1 t ) P3 t 3
0 t 1
B(t ) t 3 t 2
P0
P
1
t 1 M
P2
P3
1 3 3
3 6 3
M
3 3 0
1 0 0
1
0
0
0
87.
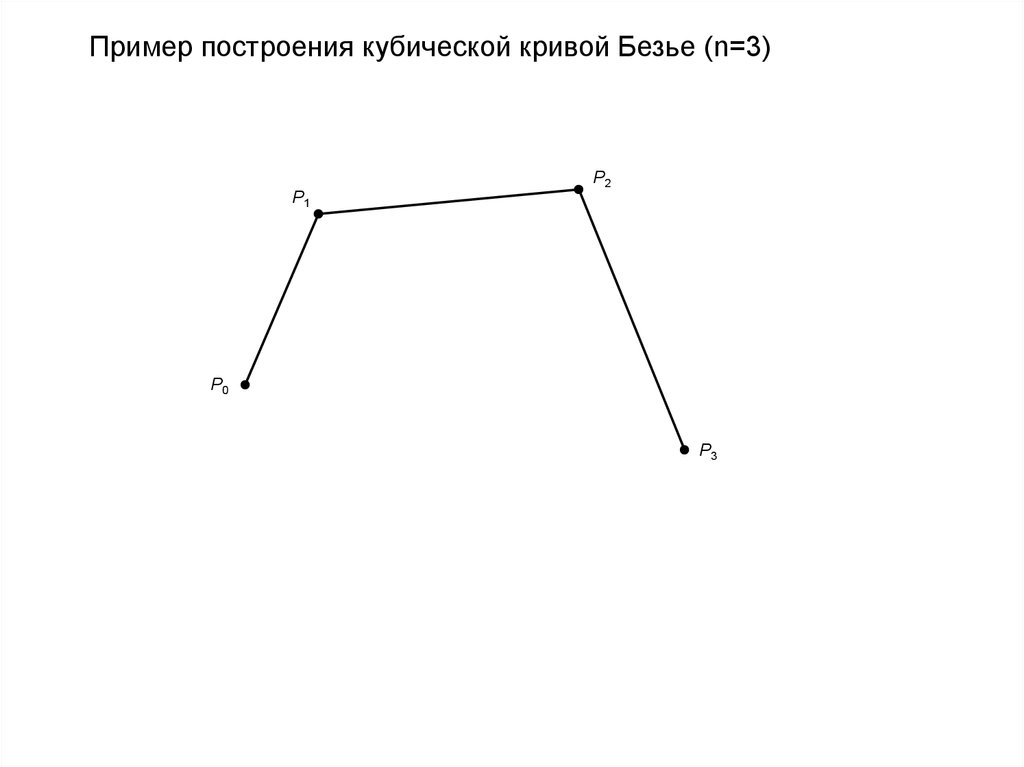
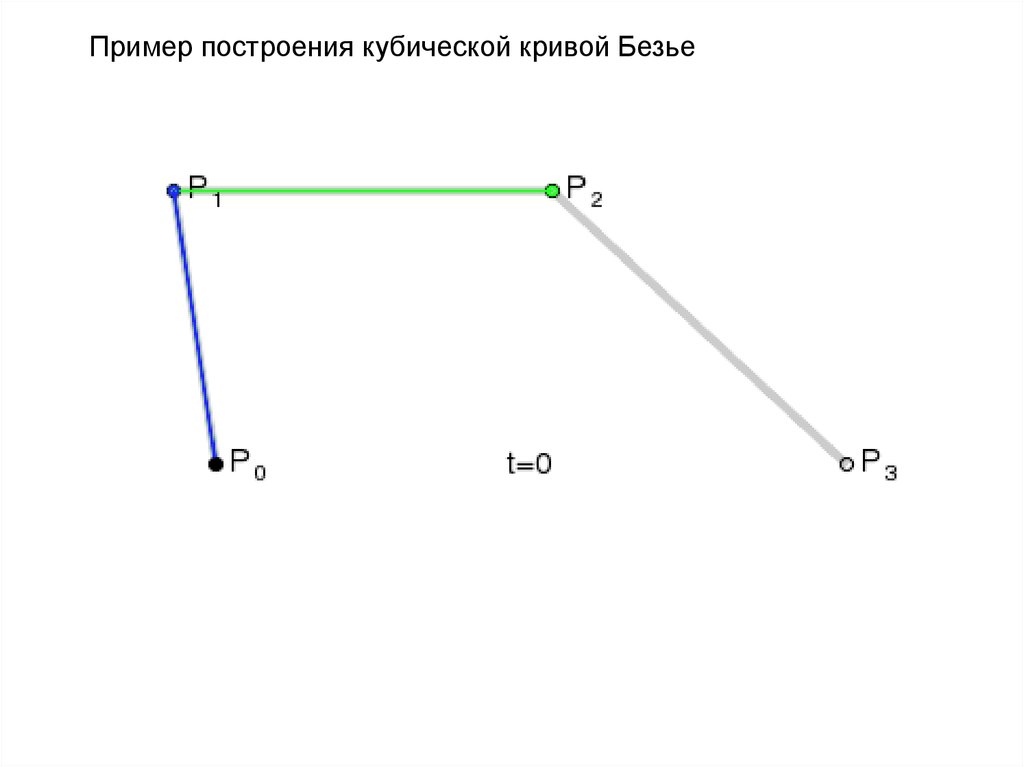
Пример построения кубической кривой Безье (n=3)P2
P1
P0
P3
88.
Пример построения кубической кривой Безье (n=3)P2
P1
P0
P3
89.
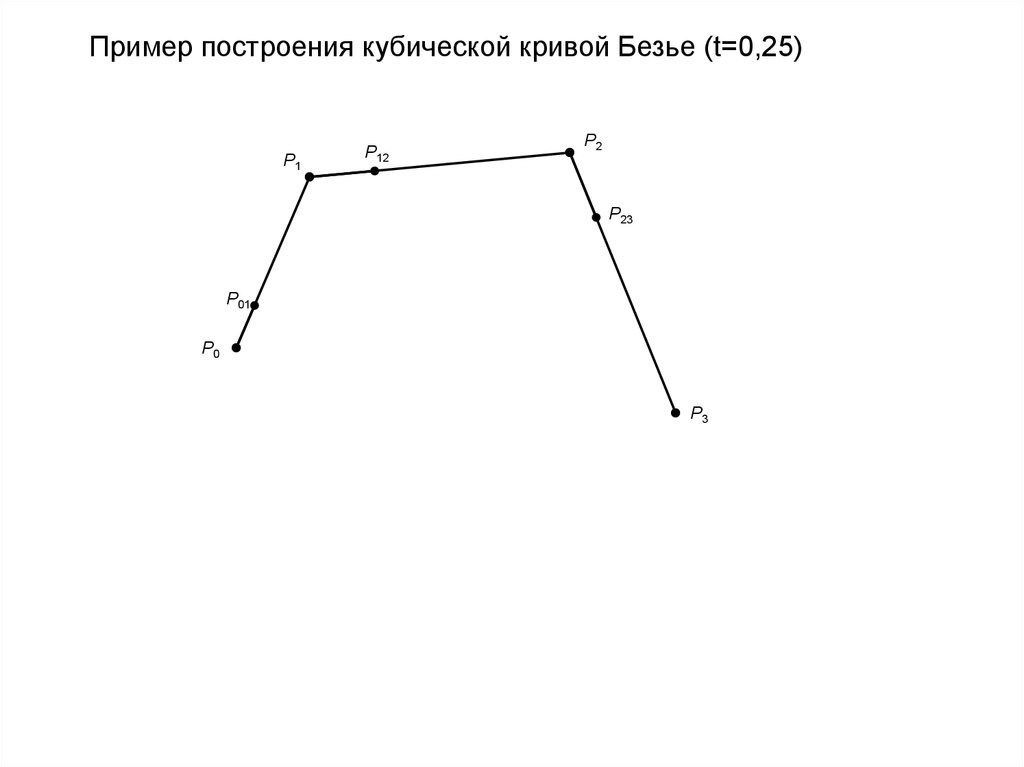
Пример построения кубической кривой Безье (t=0,25)P1
P12
P2
P23
P01
P0
P3
90.
Пример построения кубической кривой Безье (t=0,25)P1
P12
P2
P23
P01
P0
P3
91.
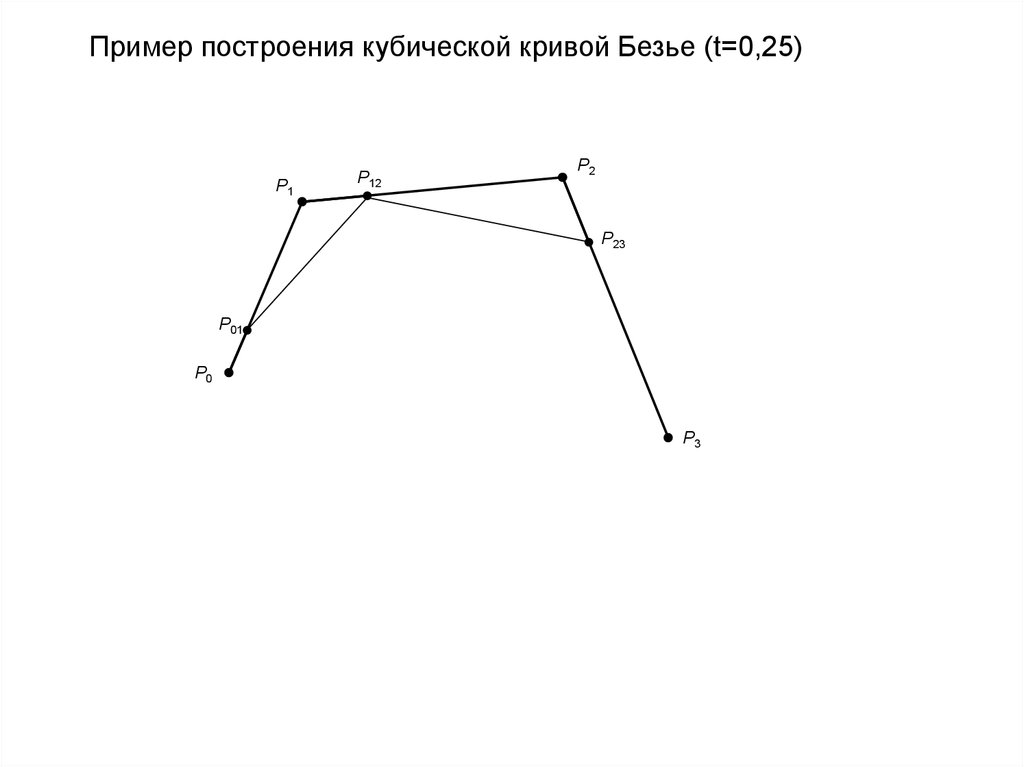
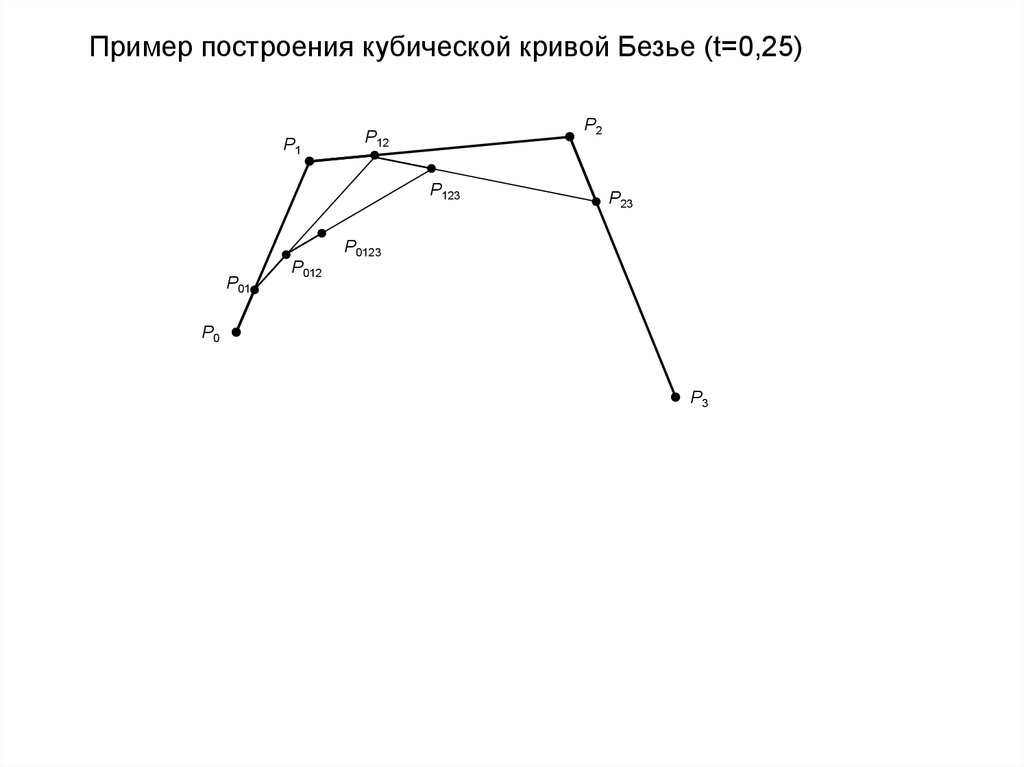
Пример построения кубической кривой Безье (t=0,25)P1
P2
P12
P123
P01
P23
P012
P0
P3
92.
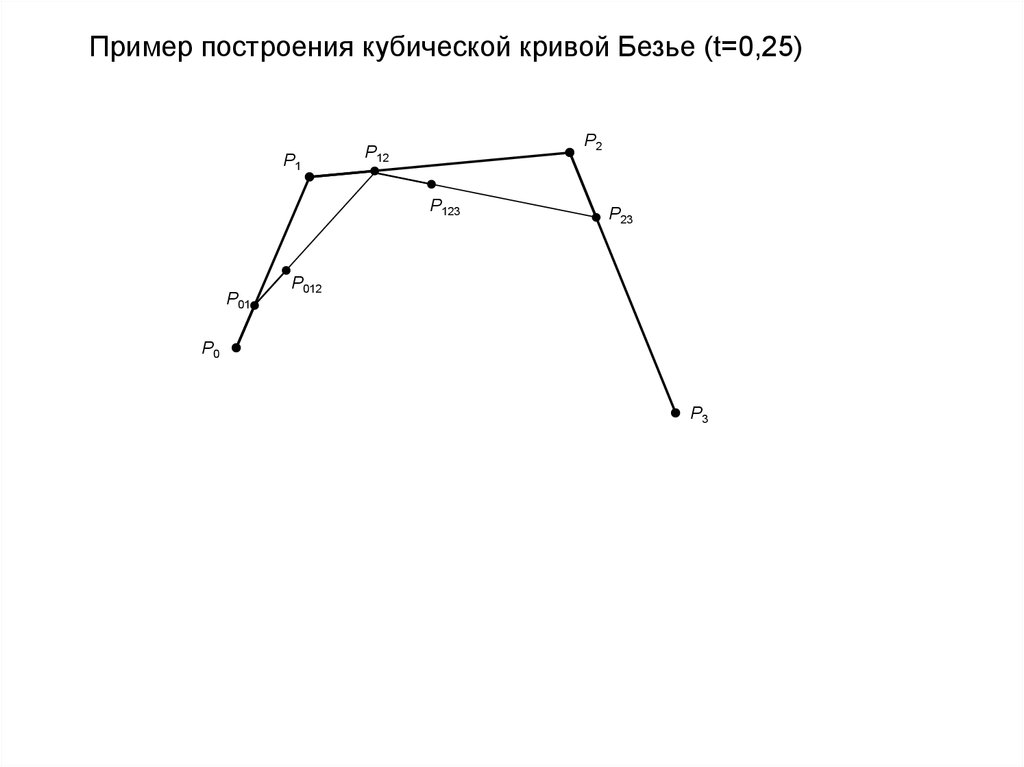
Пример построения кубической кривой Безье (t=0,25)P1
P2
P12
P123
P23
P0123
P01
P012
P0
P3
93.
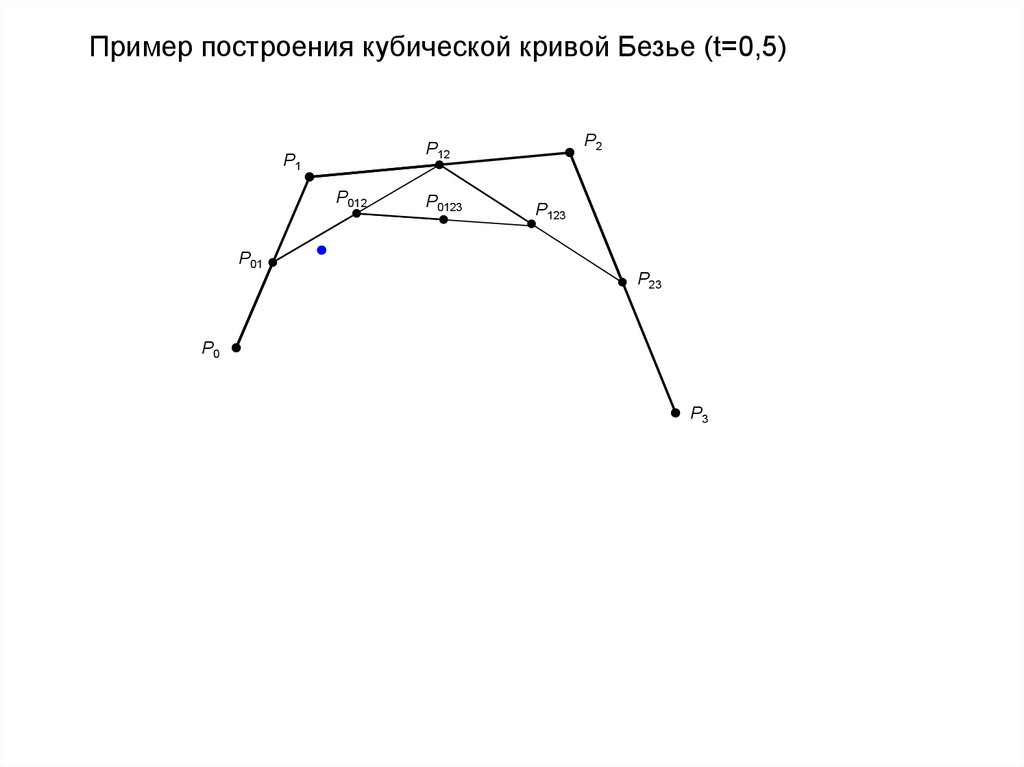
Пример построения кубической кривой Безье (t=0,5)P2
P12
P1
P012
P0123
P123
P01
P23
P0
P3
94.
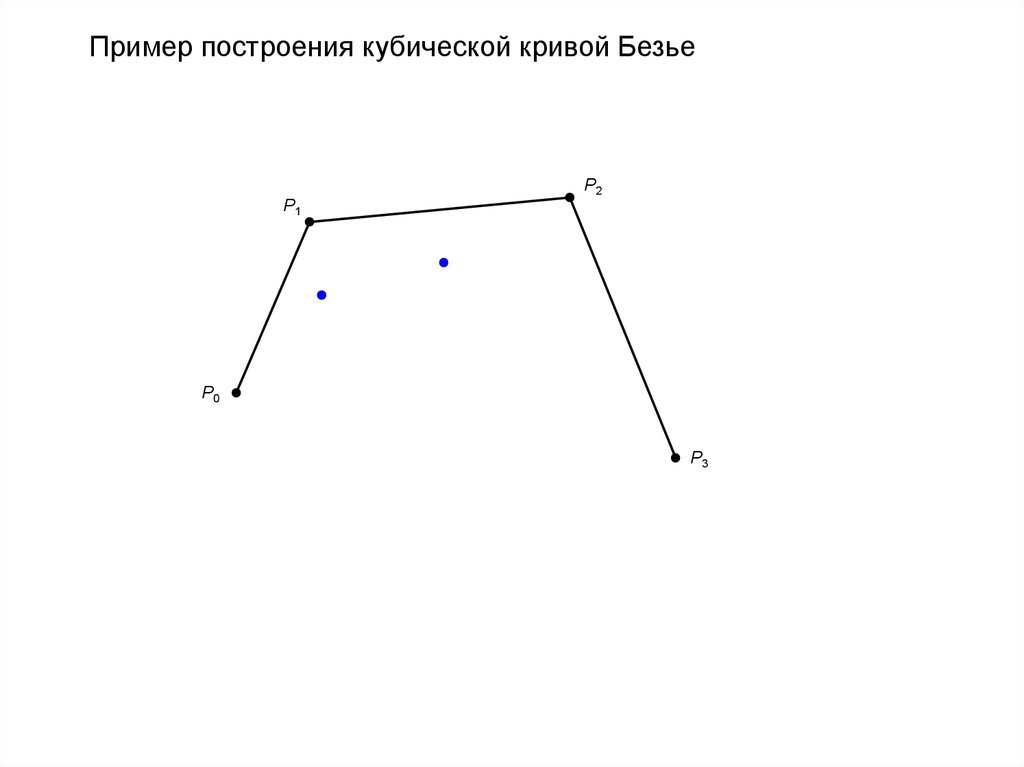
Пример построения кубической кривой БезьеP2
P1
P0
P3





































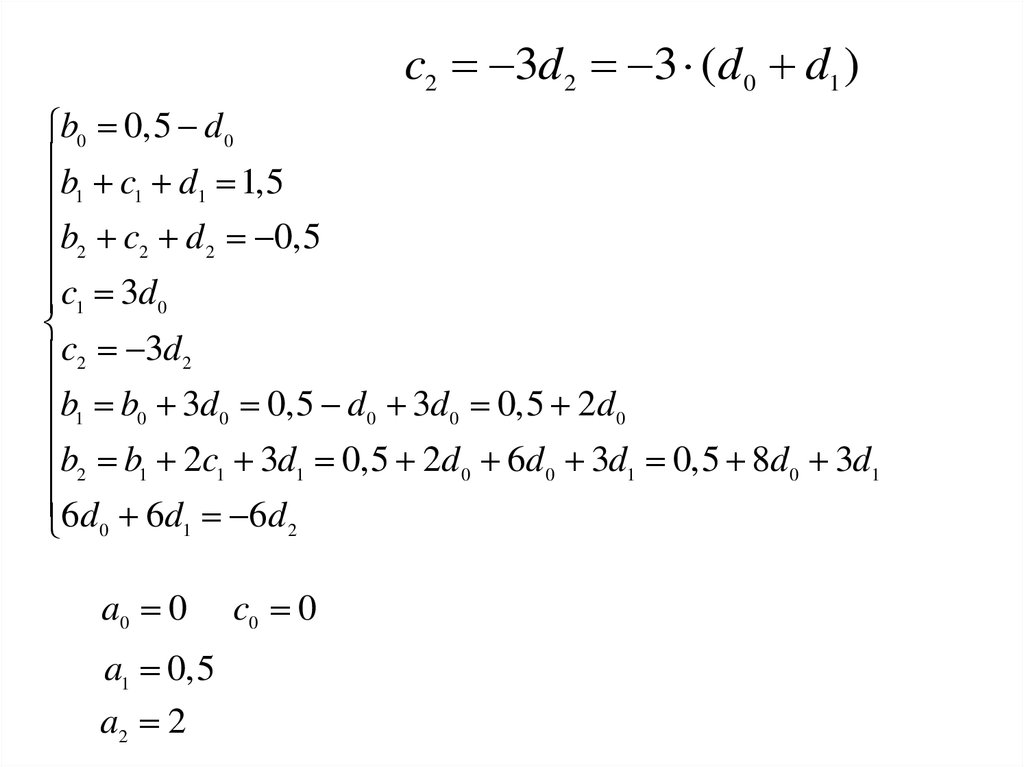
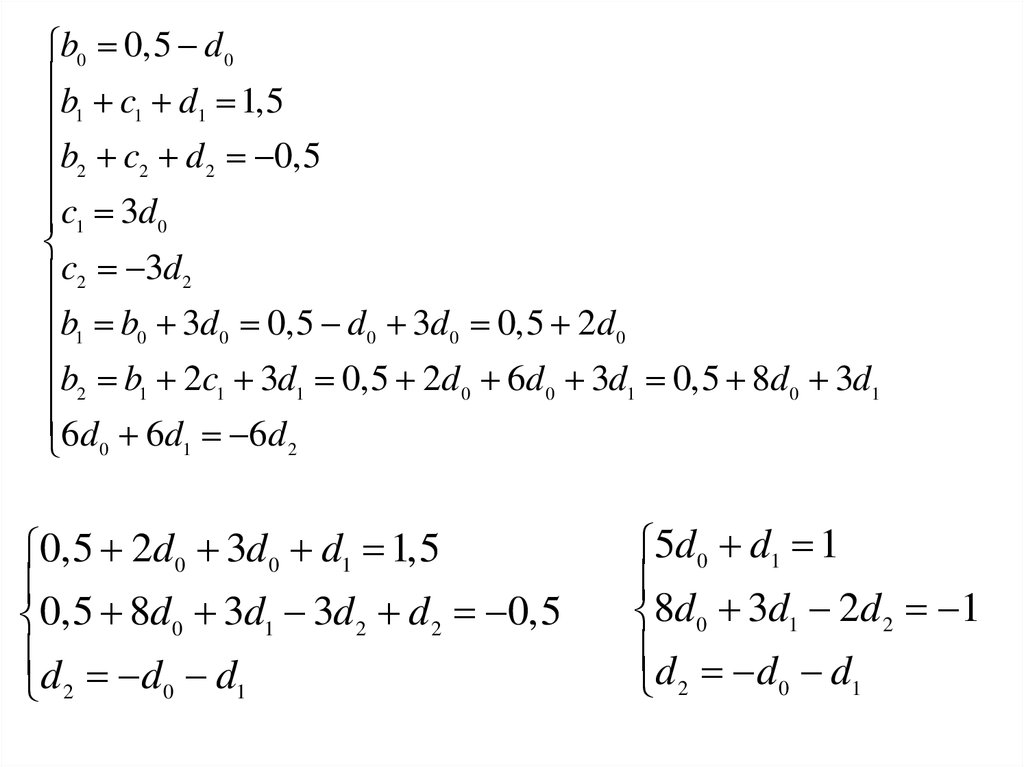
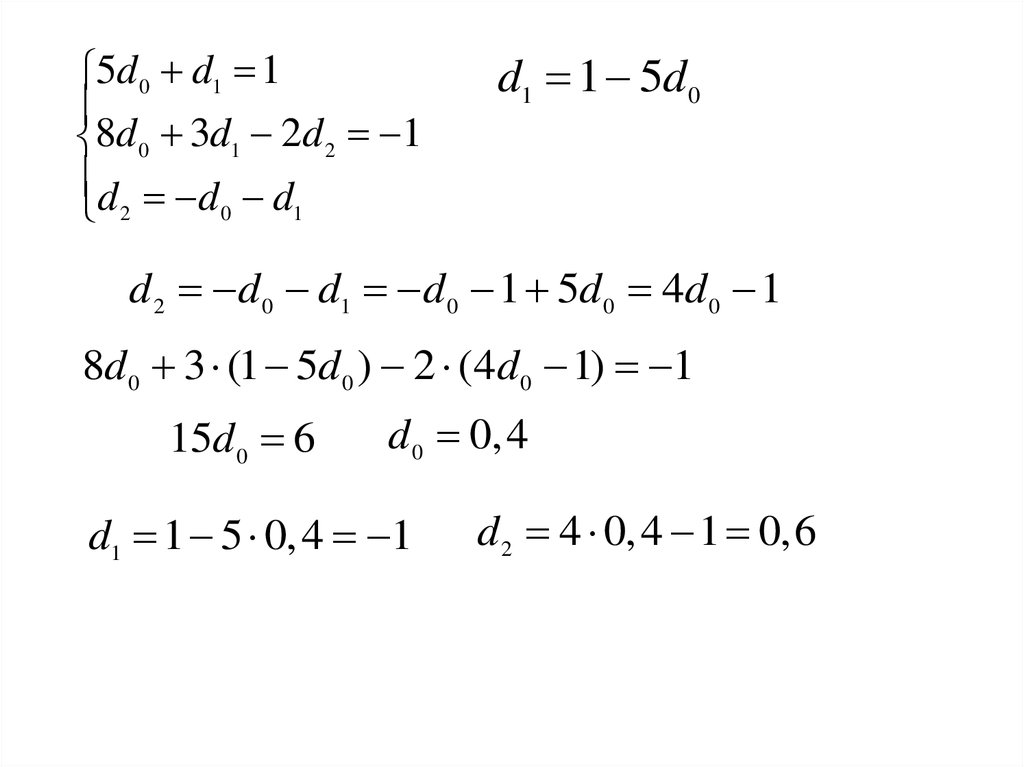
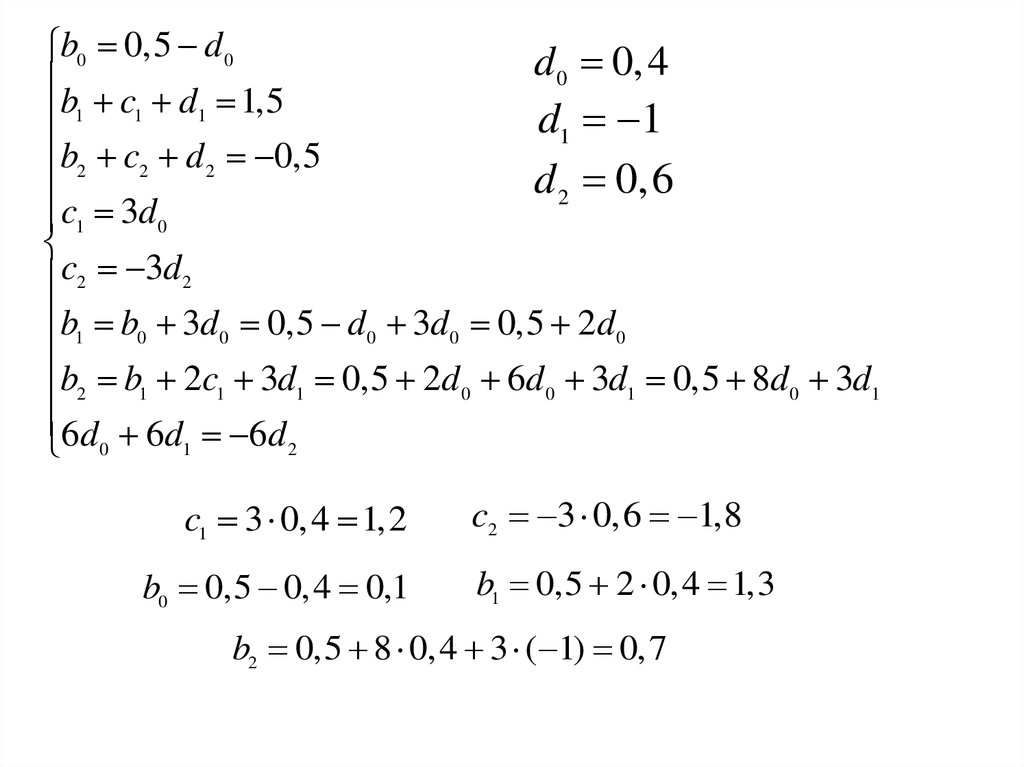












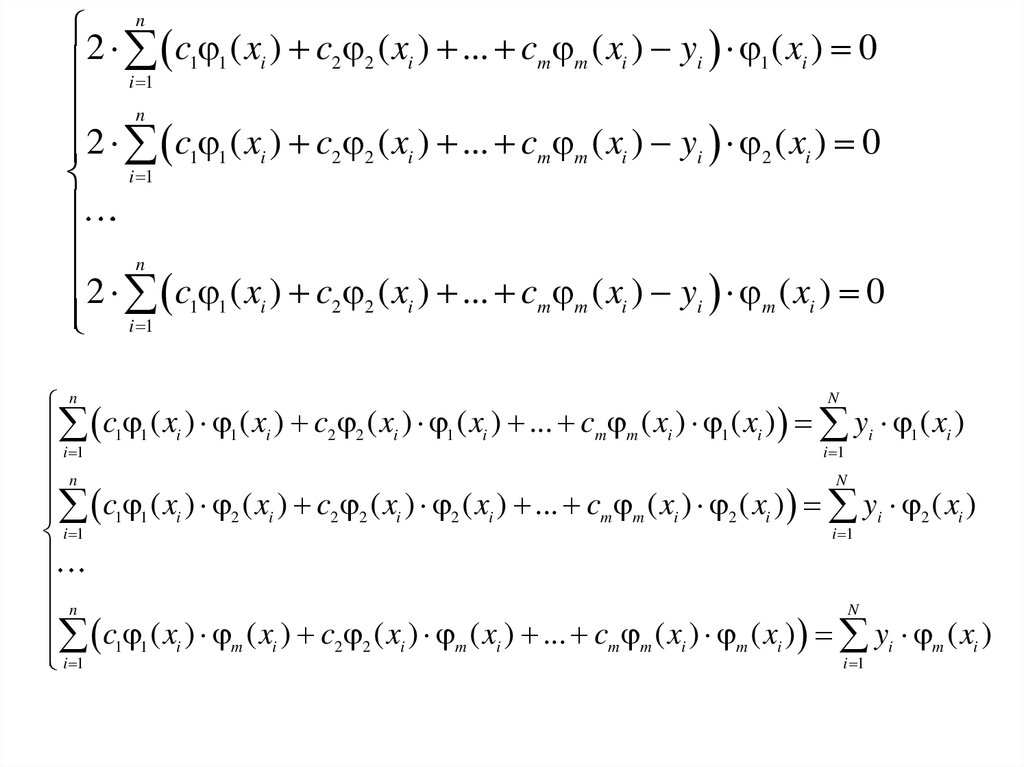
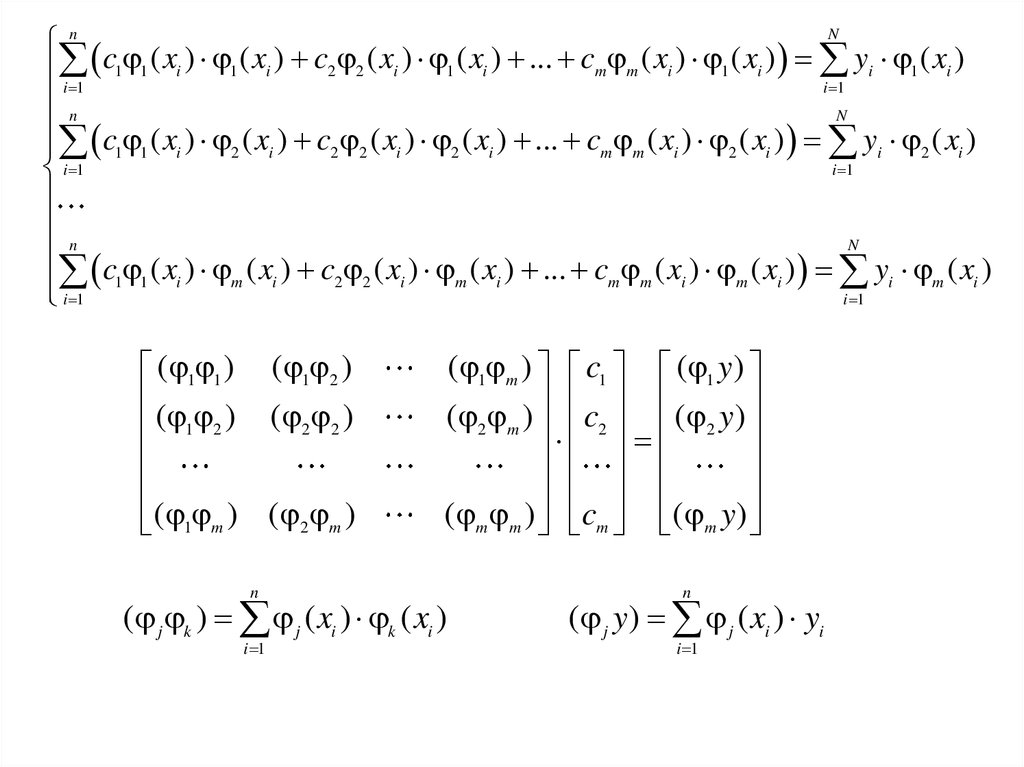








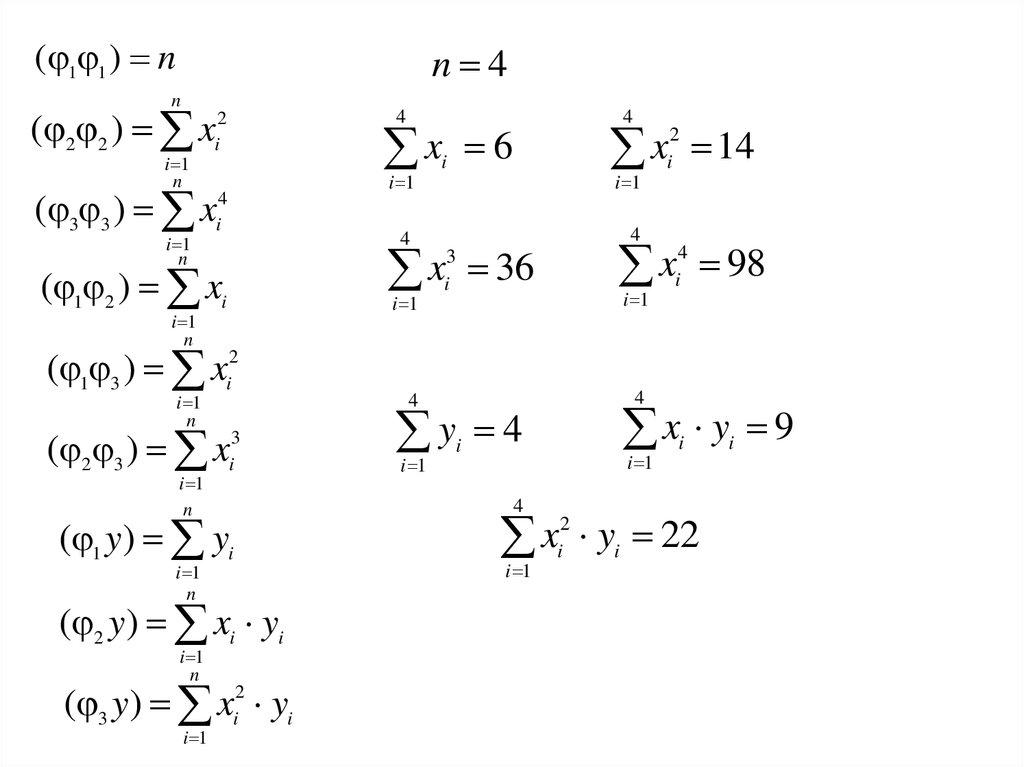










 Информатика
Информатика








