Похожие презентации:
Выбор в условиях неопределенности
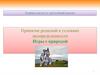
1.
С2D
E
С1
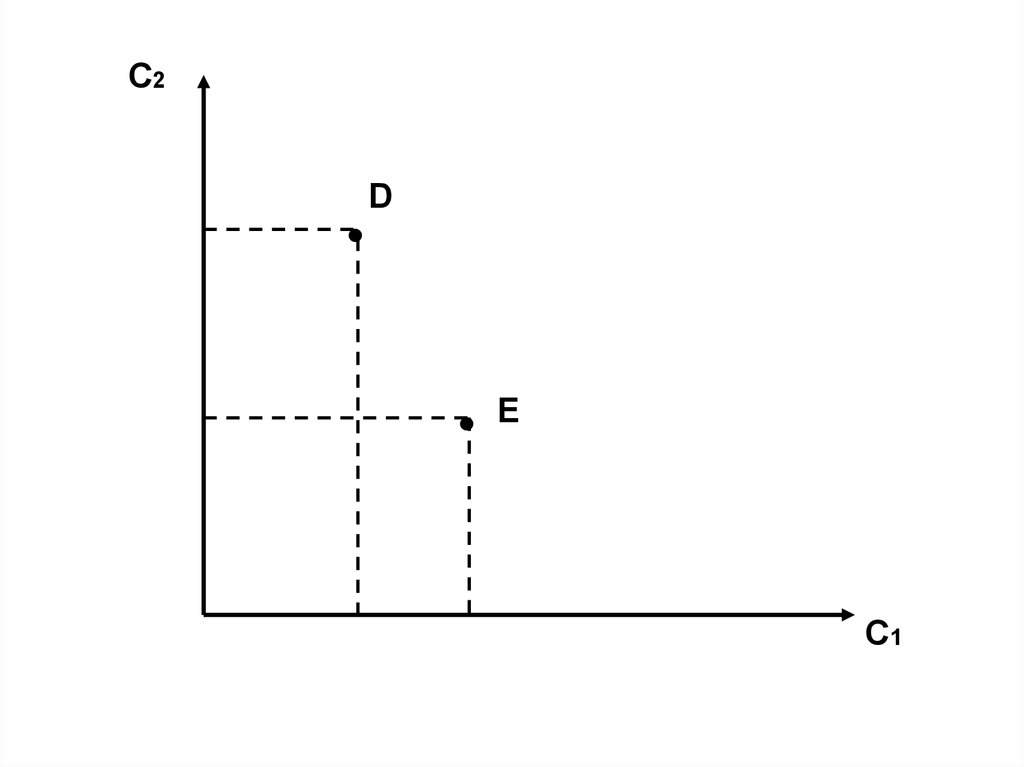
2.
С2100000
75000
45000
25000
55000
100000
С1
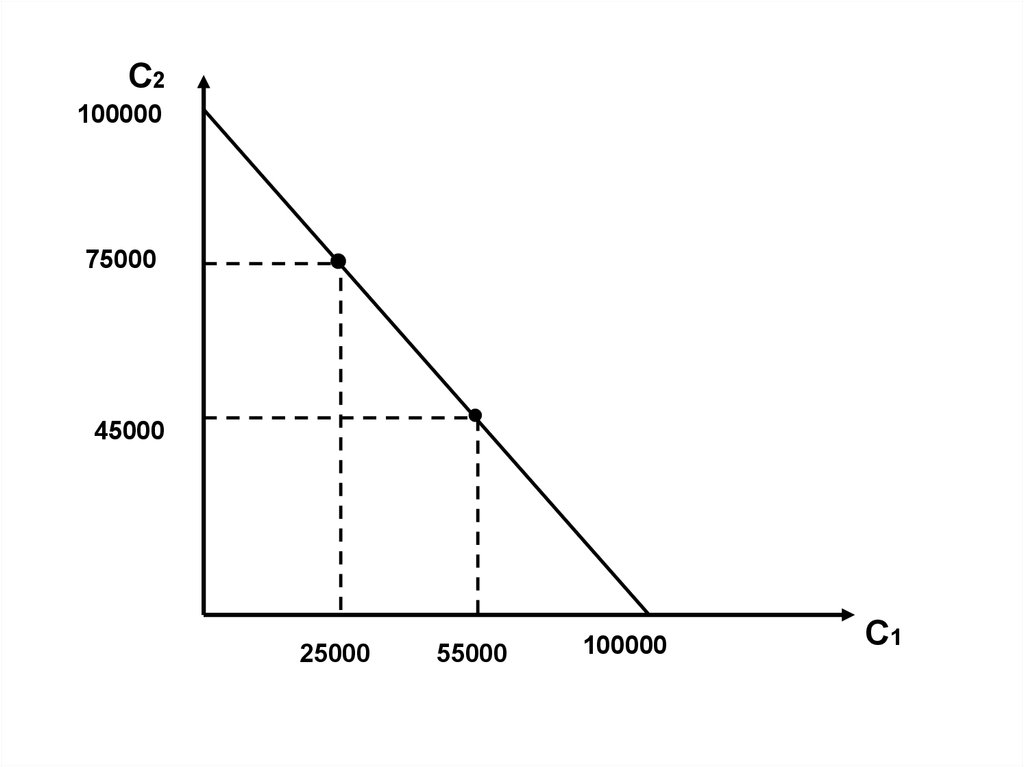
3.
С2110000
100000
Наклон = - 1.1
100000
С1
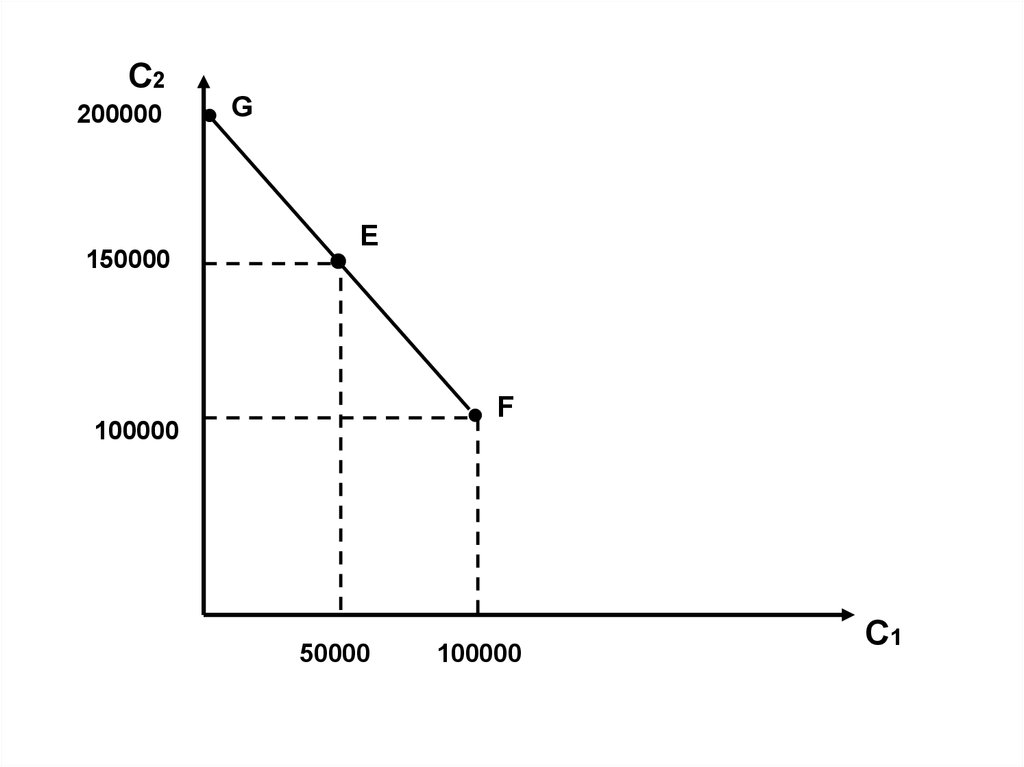
4.
С2200000
150000
G
E
F
100000
50000
100000
С1
5.
M1(1+r)M1(1+r) + M2
6.
Текущая стоимость (сегодняшняяценность платежа)
PV(M2).
PV(M2)(1+r)=M2.
PV(M2)= M2:(1+r.)
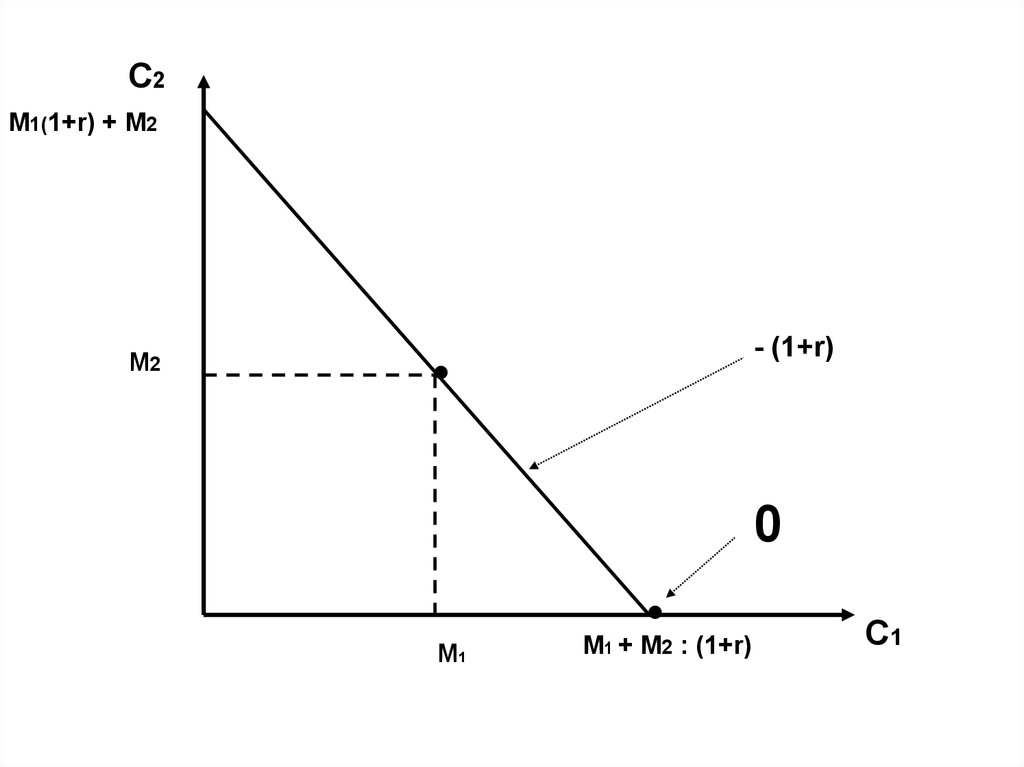
7.
С2М1(1+r) + М2
- (1+r)
М2
0
М1
М1 + М2 : (1+r)
С1
8.
Совершенный рынок заёмных средств –рынок, на котором действует единая ставка
процента и по кредитованию, и по депозитам.
Теорема о разделении – возможность четко
разделять межвременной выбор потоков доходов и
межвременной выбор расходов на потребление.
*индивиды выбирают из различающихся по времени
потоков доходов поток с наибольшей текущей
стоимостью;
*индивиды выбирают во времени тот вариант
осуществления расходов на потребление, который
максимизирует их полезность при ограничении,
состоящем в непревышении текущей стоимостью
дохода текущей стоимости расхода на потребление.
9.
Критерием выбора потока дохода выступаетвеличина текущей стоимости (PV).
На совершенном рынке заёмных средств ему
эквивалентен критерий будущей стоимости (FV).
Бессрочный аннуитет.
PV = М2 : r
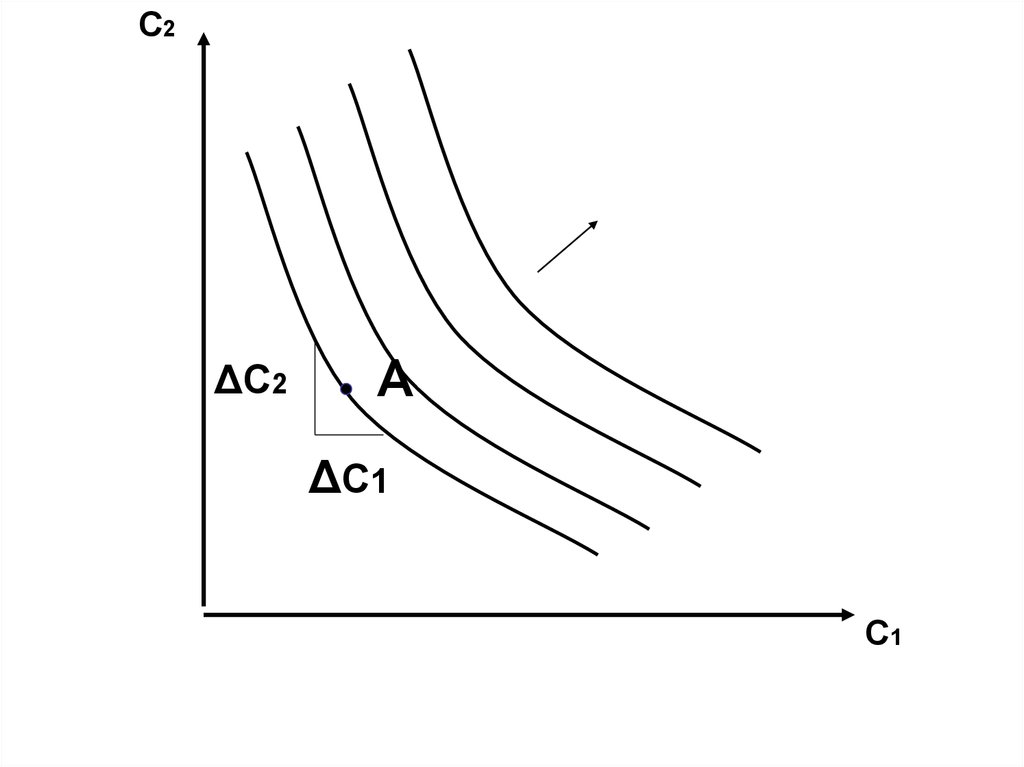
10.
С2ΔС2
А
ΔС1
С1
11.
MRTP=ΔС2/ΔC112.
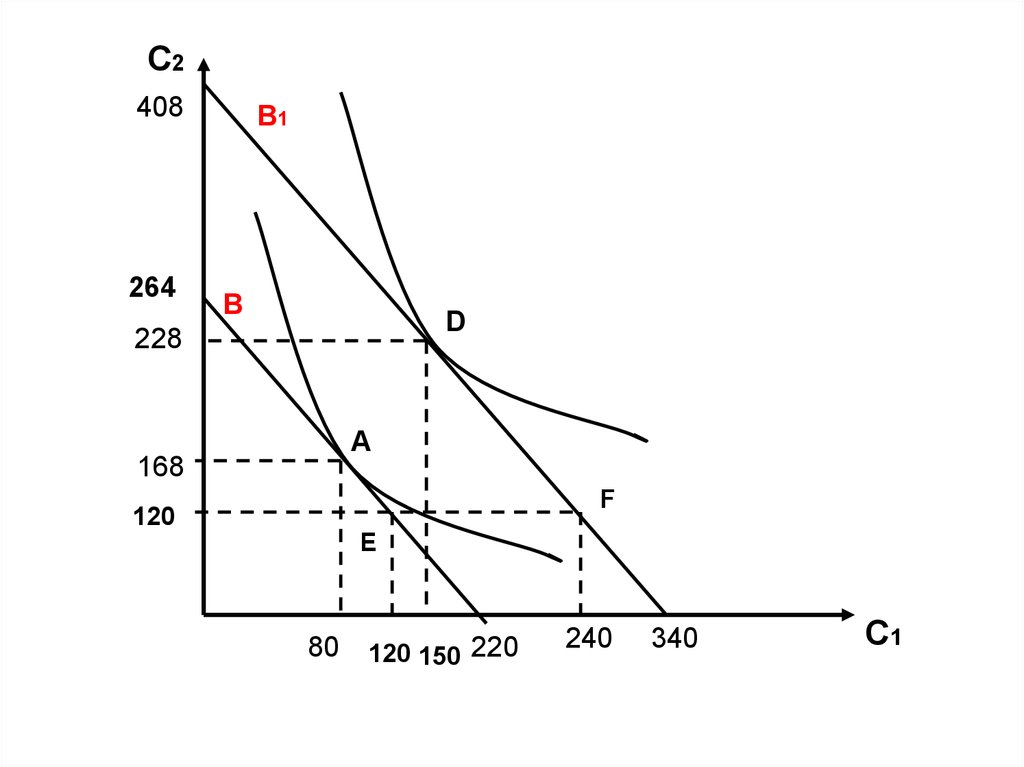
С2408
264
B1
B
D
228
A
168
F
120
E
80
120 150 220
240
340
С1
13.
Выбор в условияхнеопределённости
14. Вероятность, ожидаемая стоимость и отклонения от нее
• Если возможно n исходов какого-либособытия, сумма вероятностей реализации
этих исходов равна 1:
n
pi 1
i 1
• Ожидаемая стоимость (математическое
ожидание):
n
E X X p1 X 1 p2 X 2 ... pn X n pi X i
i 1
15. Вероятность, ожидаемая стоимость и отклонения от нее
• Дисперсия:X2
n
pi X i X
2
i 1
• Стандартное отклонение:
X X2
• Чему равны ожидаемая стоимость,
дисперсия и стандартное отклонение, если
существует только два возможных исхода:
X1=100, X2=200; и их вероятности,
соответственно: p1=0,4 и p2=0,6?
16. Актуарно справедливые игры
• Актуарно справедливые игры: игры снулевой ожидаемой стоимостью или игры, за
участие в которых игроки готовы заплатить
их ожидаемую стоимость
p1 X1 p2 X 2 0,5 1000 0,5 1000 0
p1 X1 p2 X 2 0,6 1000 0,4 1000 200
17.
49.75EV1 = 1/2 *100руб. + 1/2 *(-0.5руб.)=
EV2 =1/2*200руб. +1/2*(-100руб.)=
руб.
50 руб.
EV3 =1/2*20000руб. +1/2*(-10000руб.)=
5000
руб.
18. Гипотеза ожидаемой полезности
• Санкт-Петербургский парадокс:X1 2, X 2 4, ...X n 2
1
1
1
p1 , p2 , ... pn n
2
4
2
n
E X pi X i 2
i 1
i 1
i
1
2
i
1 1 ... 1
• Гипотеза ожидаемой полезности:
индивиды оценивают игру не по ее
ожидаемой стоимости, а по ожидаемой
полезности
n
E U U U X i pi
i 1
19.
EU1 = 1/2*U(M0+100) + 1/2*U(M0 - 0.5)EU1 > U(M0)
20. Функция полезности фон Неймана – Моргенштерна и типы отношения к риску
• Риск: понятие, характеризующееизменчивость исходов в ситуации
неопределенности.
• Несклонные к риску индивиды выберут
из двух игр с одинаковой ожидаемой
стоимостью ту, которая характеризуется
меньшей изменчивостью доходности.
• Склонные к риску индивиды, наоборот,
выберут игру с большей изменчивостью
доходности.
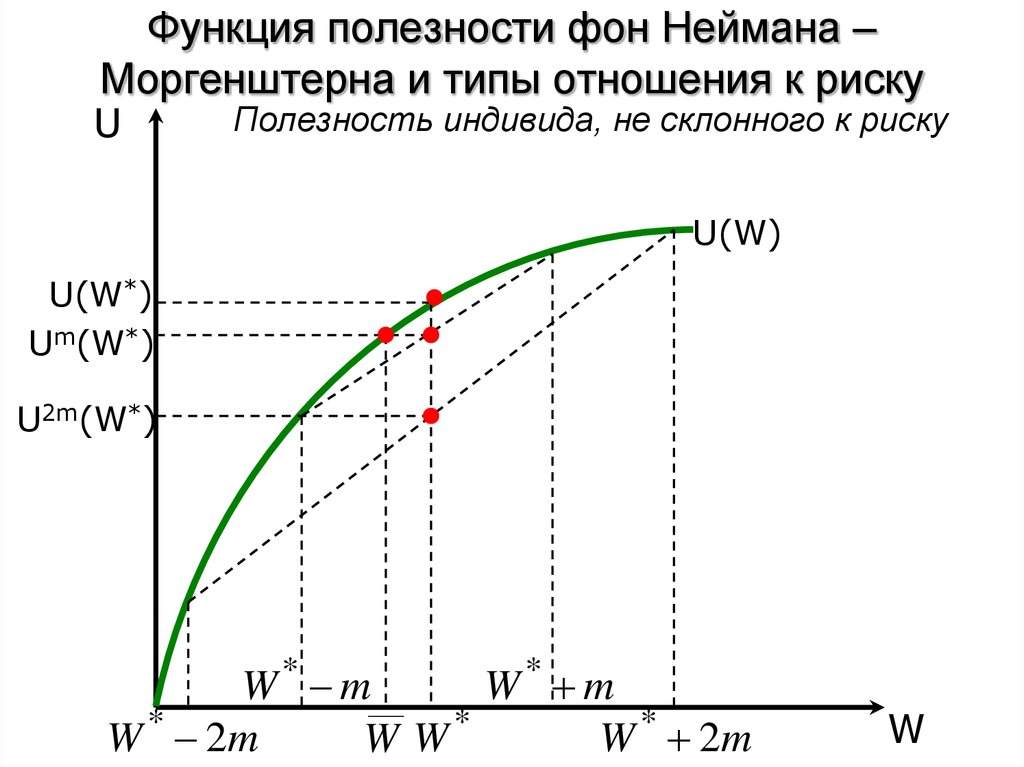
21. Функция полезности фон Неймана – Моргенштерна и типы отношения к риску
UПолезность индивида, не склонного к риску
U(W)
U(W*)
Um(W*)
U2m(W*)
W* m
W* m
W * 2m
W * 2m
W W*
W
22. Функция полезности фон Неймана – Моргенштерна и типы отношения к риску
• Ожидаемая полезность 1-й игры:m
U W
*
1
1
*
*
U W m U W m
2
2
• Ожидаемая полезность 2-й игры:
U
2m
W
*
1
1
*
*
U W 2m U W 2m
2
2
• Для несклонного к риску индивида:
U W U W
UW
*
m
*
2m
*
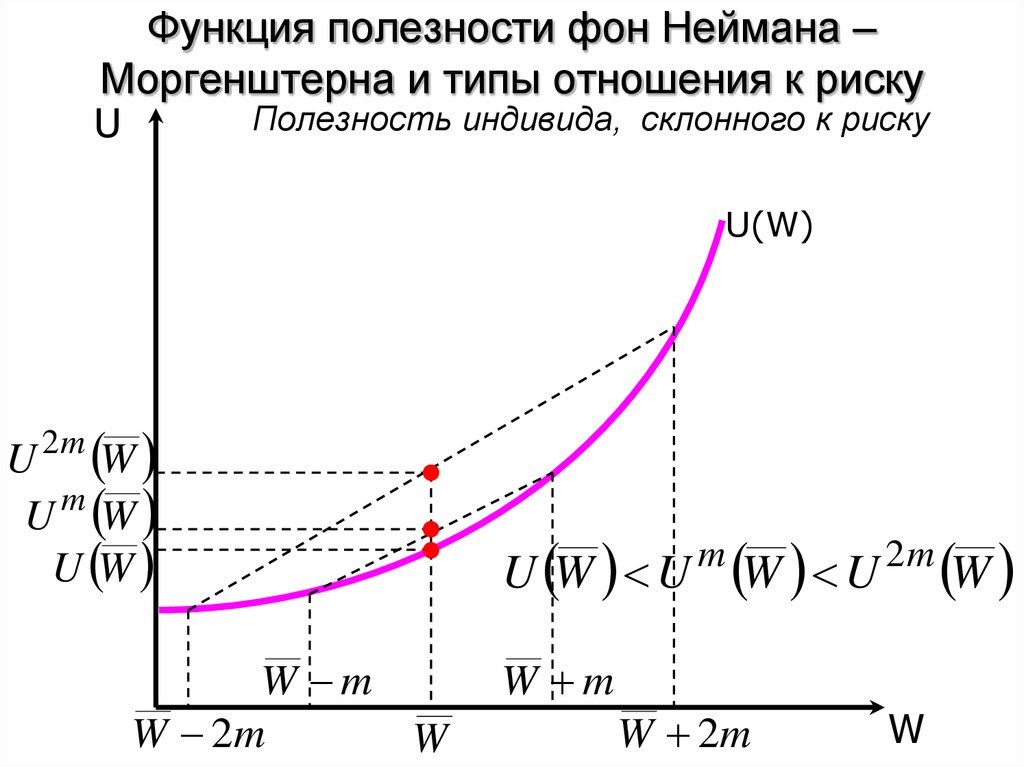
23. Функция полезности фон Неймана – Моргенштерна и типы отношения к риску
UПолезность индивида, склонного к риску
U(W)
U W
U m W
U W
2m
W m
W 2m
W
U W U
W m
m
W U W
W 2m
2m
W
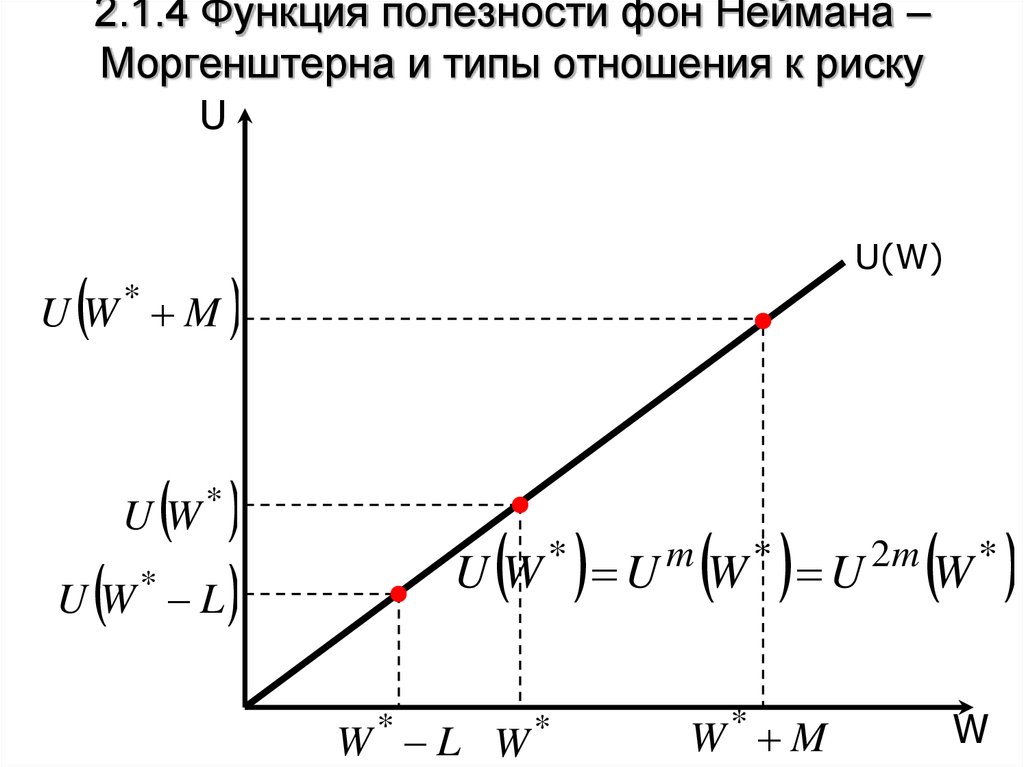
24. 2.1.4 Функция полезности фон Неймана – Моргенштерна и типы отношения к риску
UU W* M
U(W)
U W * L
U W*
U W U W
UW
W L W
*
*
*
m
*
W* M
2m
*
W
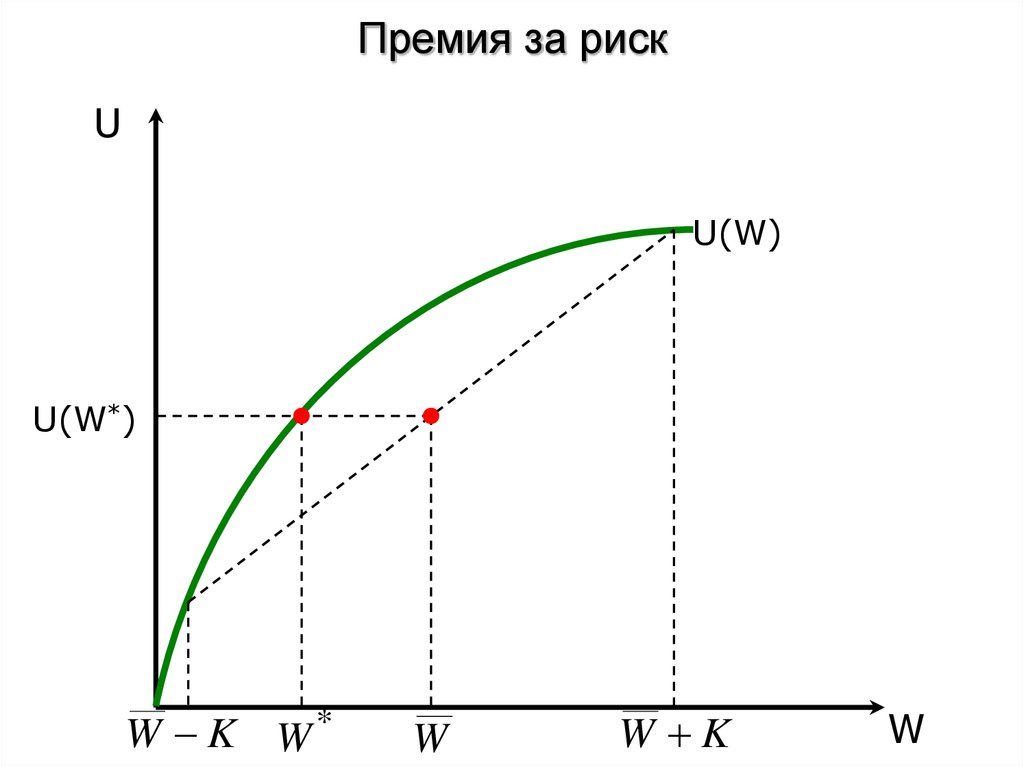
25. Премия за риск
UU(W)
U(W*)
W K W*
W
W K
W
26.
Наибольшее признание получила разработанная всередине 1960-х гг. модель оценки
долгосрочных активов (capital asset princing model –
CAPM). Модель утверждает, что на
конкурентных рынках капитала в состоянии
равновесия (когда все ценные бумаги и активы
оцениваются рынком верно) премия за риск
инвестирования в актив) находится в прямой
зависимости от чувствительности этого актива к
движению рынка
27. Вероятностные состояния как обусловленные блага
• Wg – богатство индивида при «хорошем»исходе
• Wb – богатство индивида при «плохом»
исходе
• Ожидаемая полезность индивида:
EU Wg ,Wb u pU Wg 1 p U Wb
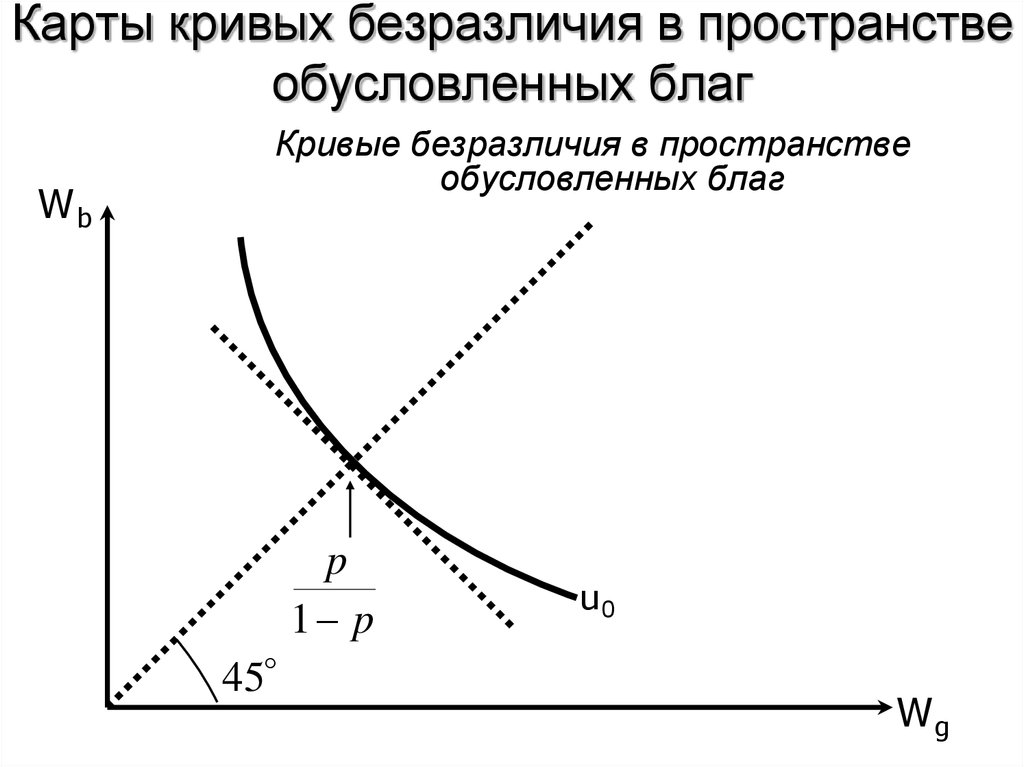
28. Карты кривых безразличия в пространстве обусловленных благ
Кривые безразличия в пространствеобусловленных благ
Wb
p
1 p
u0
45
Wg
29. Карты кривых безразличия в пространстве обусловленных благ
• Предельная норма замещенияпоказывает пропорцию, в которой индивид
готов заместить товар, количество которого
отложено по вертикальной оси (богатство
при «плохом» исходе), товаром, количество
которого отложено по горизонтальной оси
(богатство при «хорошем» исходе):
pu' Wg
MRS
• При Wg=Wb:
1 p u' Wb
p
MRS
1 p
30. Построение деревьев решений
• Узел решения – точка дерева решений, вкоторой индивид сталкивается с
необходимостью выбора.
• Узел случая – точка дерева решений,
движение из которой по исходящим ветвям
обусловлено случайным процессом.
• Конечный узел – точка дерева решений,
представляющая конечный исход,
связываемый с данной ветвью дерева
решений.
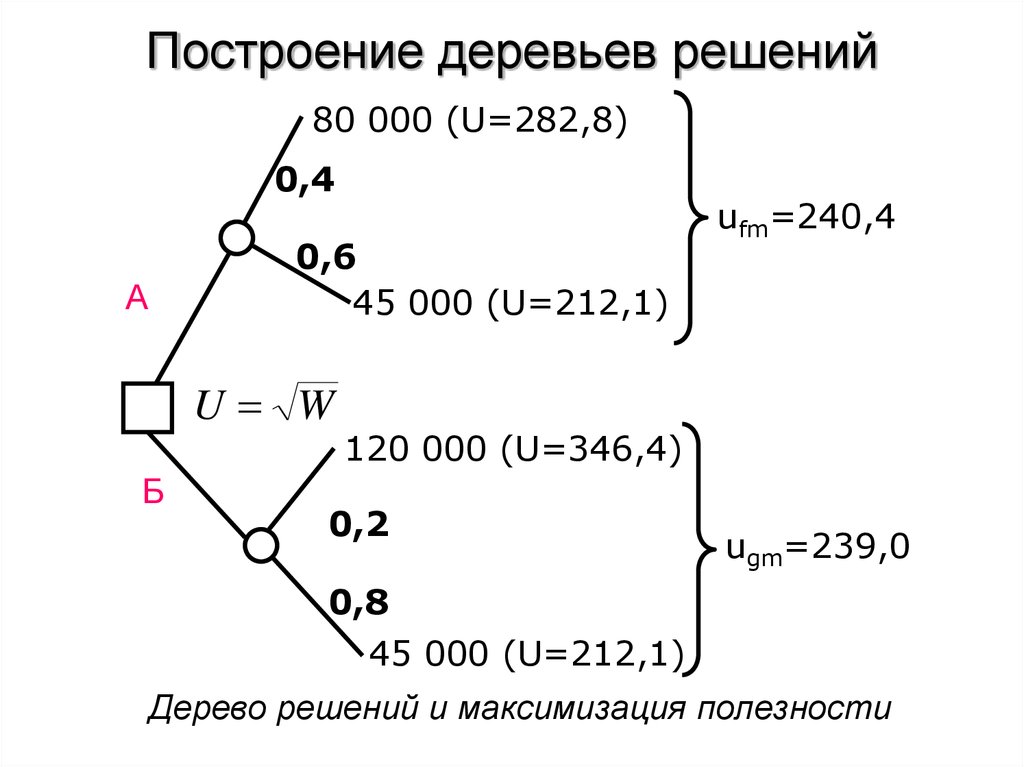
31. Построение деревьев решений
80 000 (U=282,8)0,4
0,6
45 000 (U=212,1)
А
U W
Б
ufm=240,4
120 000 (U=346,4)
0,2
ugm=239,0
0,8
45 000 (U=212,1)
Дерево решений и максимизация полезности
32.
Выбор в условиях ограниченнойрациональности
33.
34.
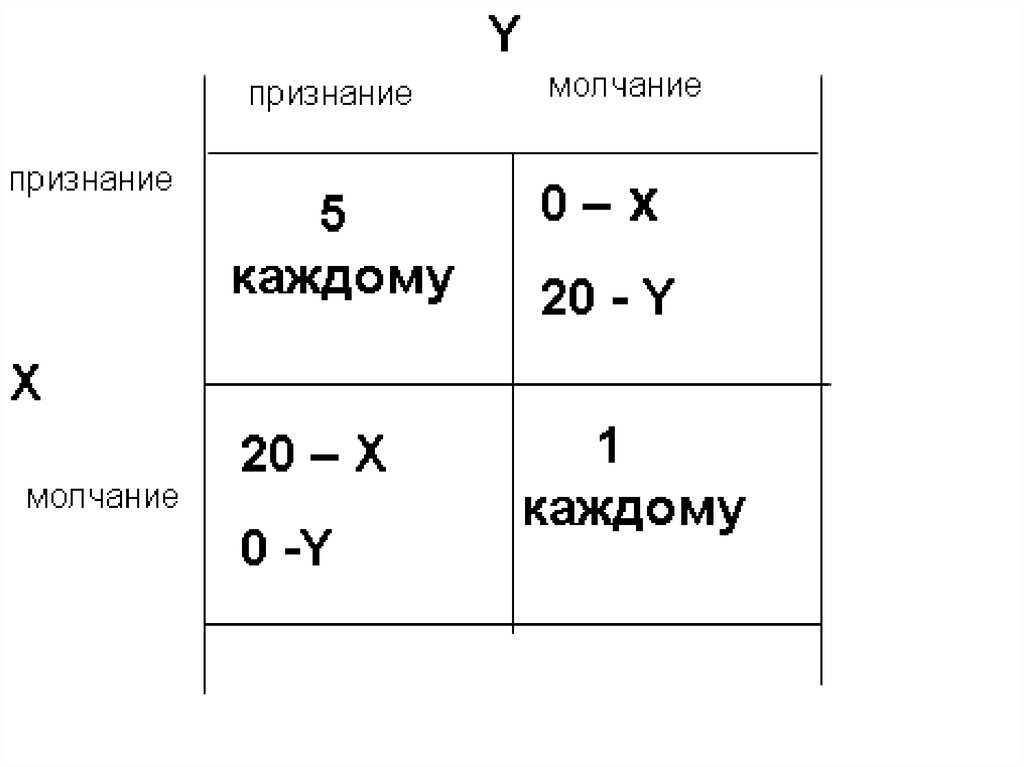
1. Проблема обязательств.(дилемма заключённого)
35.
36.
2. Механизм вознаграждения3. Проблема мимикрии.
4. Различие вкусов.
5. Альтруистические предпочтения
6. Забота о справедливости
37.
Познавательные ограничения иповедение потребителя.
1. Ограниченная рациональность.
2. Асимметричная функция ценности.
3. Невозвратные издержки.
4. Прямые и вменённые издержки
5. Гедоническое «обрамление»
38.
6. Эвристика суждений и ошибки7. Психофизика восприятия.
8. Трудности практических
решений.
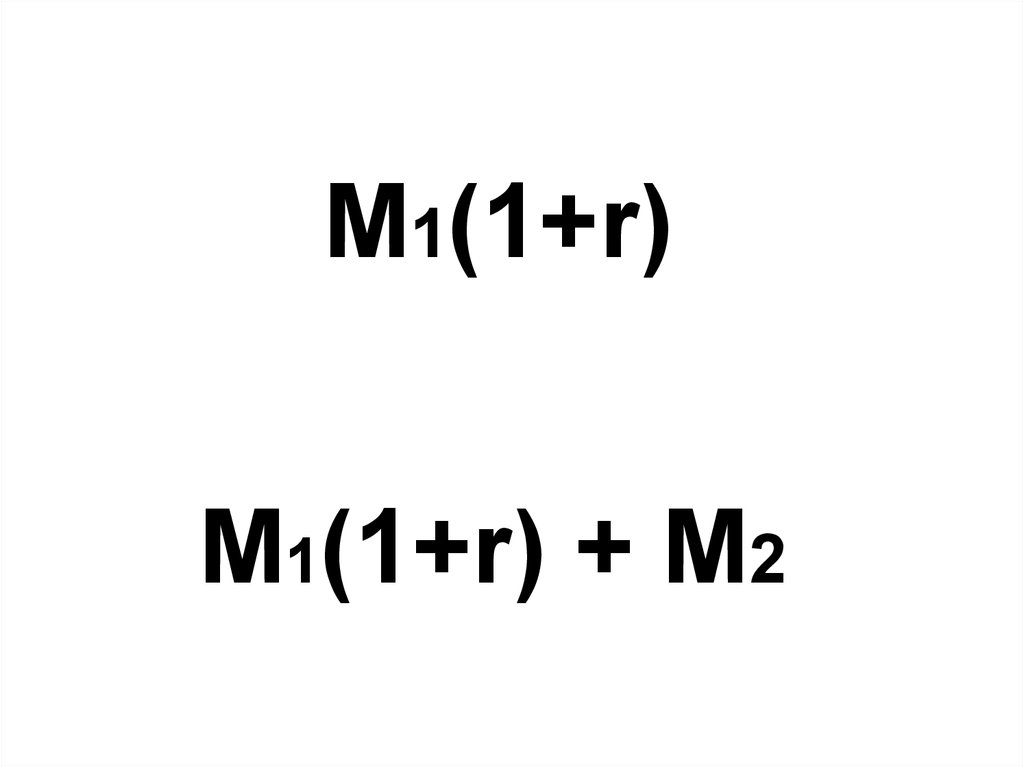






















 Математика
Математика