Эйлеровы графы. Гамильтоновы графы

1. Эйлеровы графы. Гамильтоновы графы

2.

Эйлеровы графы.
Определение 1
Цикл называется эйлеровым, если он содержит все ребра графа.
Определение 2
Граф называется эйлеровым, если в нем найдется эйлеров цикл.
Пример
Граф “Сабли Магомета” является эйлеровым,
так как в нем есть эйлеров цикл 123475287651.
1
2
5
3
4
7
6
8

3.

Теорема 3
(Эйлера)
Связный граф является эйлеровым тогда и только тогда, когда он не
содержит вершин нечетной степени.
Определение 4
Цепь, содержащая все ребра графа, называется эйлеровой.
Определение 5
Граф, обладающий эйлеровой цепью, называется квазиэйлеровым.
Теорема 6
Граф является квазиэйлеровым, если в нем не более двух
вершин нечетной степени.
Замечание
В квазиэйлеровом графе существующие у него две вершины
нечетной степени всегда будут являться концами любой эйлеровой
цепи.

4.

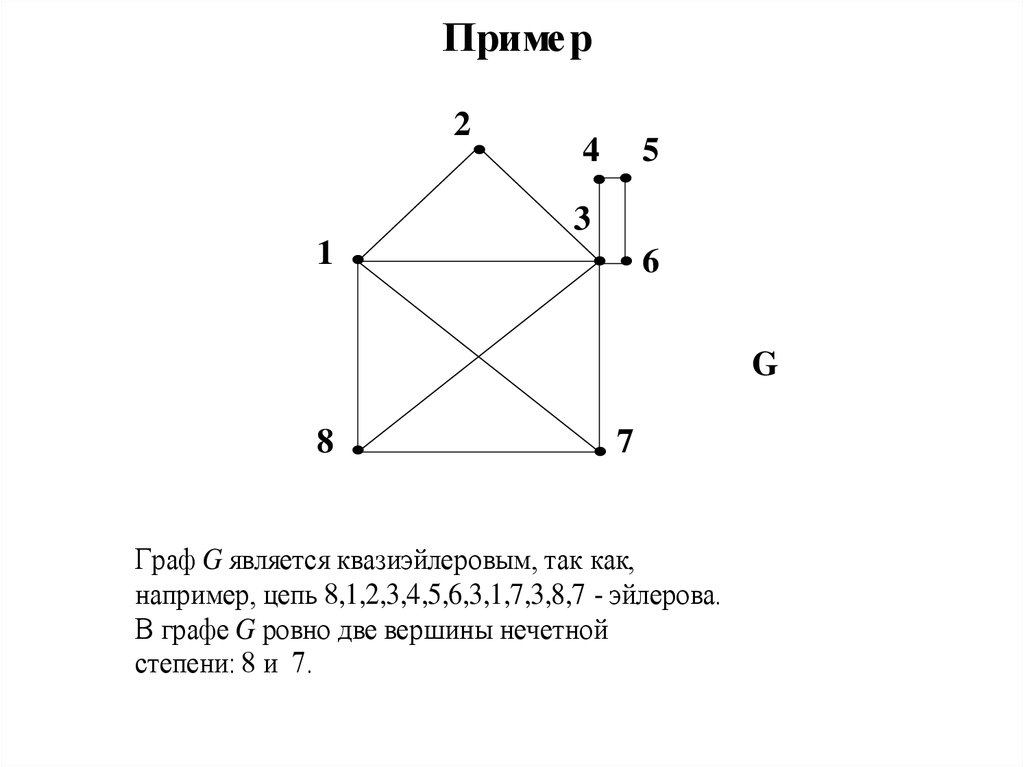
Пример
2
4
5
3
1
6
G
8
7
Граф G является квазиэйлеровым, так как,
например, цепь 8,1,2,3,4,5,6,3,1,7,3,8,7 - эйлерова.
В графе G ровно две вершины нечетной
степени: 8 и 7.

5.

Гамильтоновы
графы.
Определение 1
Цикл называется гамильтоновым, если он проходит через каждую
вершину графа (за исключением крайней) в точности один раз.
Цепь называется гамильтоновой, если она проходит через каждую
вершину графа в точности один раз.
Замечание
Гамильтонов цикл и гамильтонова цепь всегда являются простыми.
Они могут не содержать всех ребер графа.
Определение 2
Граф называется гамильтоновым, если он обладает гамильтоновым
циклом.

6.

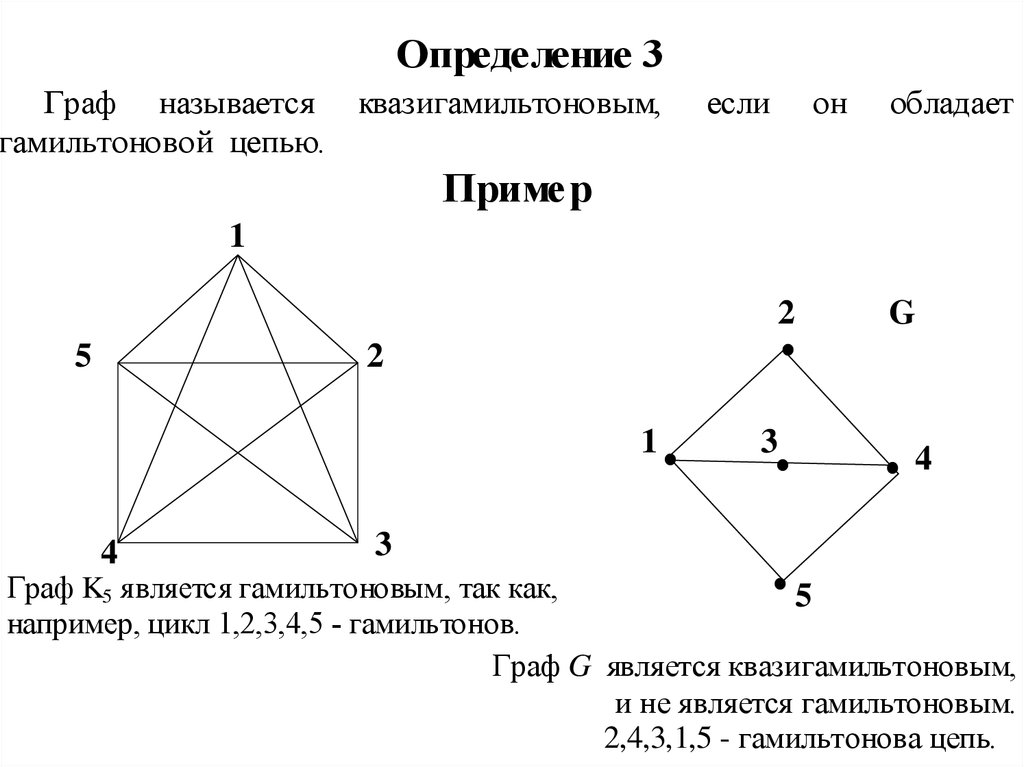
Определение 3
Граф называется квазигамильтоновым,
гамильтоновой цепью.
если
он
обладает
Пример
1
2
5
G
2
1
4
3
4
3
Граф K5 является гамильтоновым, так как,
5
например, цикл 1,2,3,4,5 - гамильтонов.
Граф G является квазигамильтоновым,
и не является гамильтоновым.
2,4,3,1,5 - гамильтонова цепь.

7.

Уи́льям Ро́уэн Га́мильтон –
(4 августа 1805 — 2 сентября
1865) — выдающийся ирландский
математик, механик и физик .
Задача «кругосветного
путешествия» по додекаэдру,
узловые вершины которого
символизировали крупнейшие
города Земли

8.

Достаточные условия гамильтоновости графа
Теорема Дирака. Пусть G - неориентированный граф
порядка n и
m - минимальная степень его вершин. Если n≥3 и m ≥n/2,
то G - гамильтонов граф.
Теорема Оре. Пусть G - неориентированный граф порядка n.
Если n≥3 и deg(u)+deg(v) ≥ n для любых двух различных
несмежных вершин u и v , то G - гамильтонов граф.
Необходимое условие гамильтоновости графа
Если неориентированный граф G содержит гамильтонов
цикл, тогда в нём не существует ни одной вершины u со
степенью u < 2.

9. Задание

• Построить эйлеров, квазиэйлеров,
гамильтонов, квазигамильтонов графы
порядка n=F+N, p>n, где F-количество
букв в Вашей фамилии, N-количество
букв в Вашем полном имени. Описать
полученные графы матрицами
смежности вершин, смежности ребер,
инцидентности, Кирхгофа
соответственно.