Похожие презентации:
Hydrostatic Pressure. Communicating Vessels. Pascal's Principle. Hydraulic Press
1.
Hydrostatic PressureCommunicating Vessels
Pascal's Principle
Hydraulic Press
2.
LEARNING OBJECTIVES:1. Describe hydrostatic pressure and recall,
rearrange and use the equation
р = ρgh;
2. Compare the effects of applying a force to
a compressible fluid and an incompressible
fluid;
3. Describe Pascal’s law and apply it to
connecting vessels and hydraulic presses.
3.
DENSITYThe mass density of a substance
is the mass of a substance
divided by its volume:
m
V
SI Unit of Density: g/cm3 or kg/m3
4.
5.
Example - Blood as a Fraction ofBody Weight
The body of a man whose weight is
690 N contains about 5.2x10-3 m3
of blood.
(a) Find the blood’s weight and (b)
express it as a percentage of the
body weight.
m V 5.2 10 m
3
3
1060 kg
m 5.5 kg
3
6.
(a)W mg 5.5 kg 9.80 m s 54 N
2
(b)
54 N
Percentage
100% 7.8%
690 N
7.
FP
A
SI Unit
of Pressure:
1 N/m2 = 1 Pa
Pascal
8.
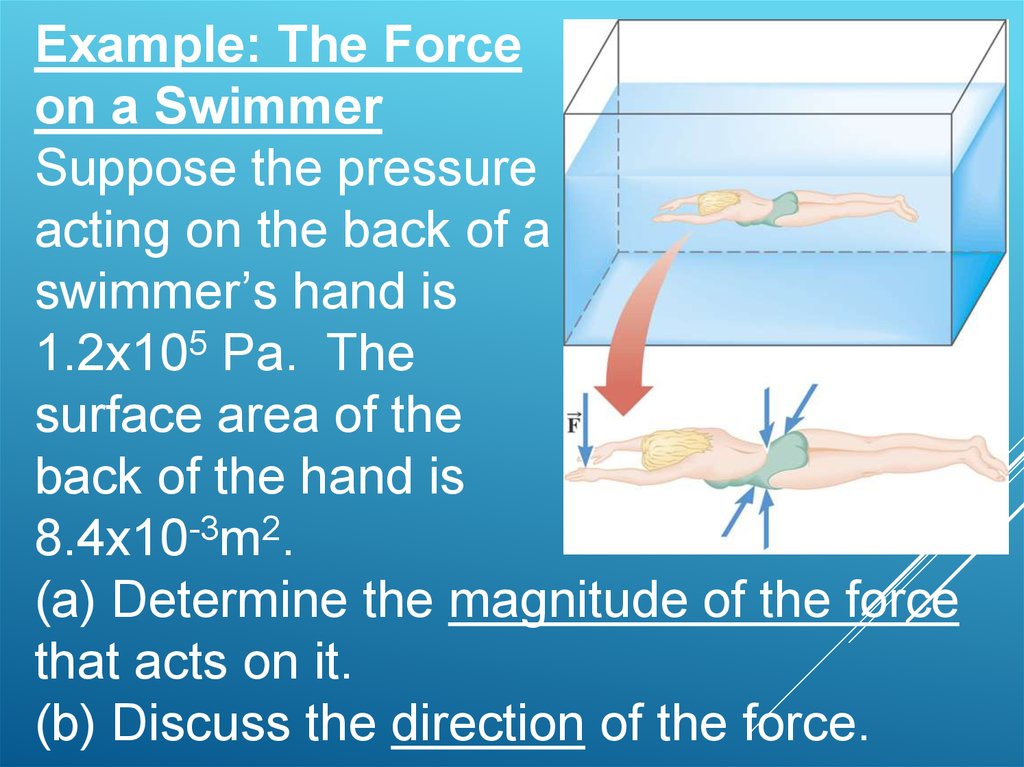
Example: The Forceon a Swimmer
Suppose the pressure
acting on the back of a
swimmer’s hand is
1.2x105 Pa. The
surface area of the
back of the hand is
8.4x10-3m2.
(a) Determine the magnitude of the force
that acts on it.
(b) Discuss the direction of the force.
9.
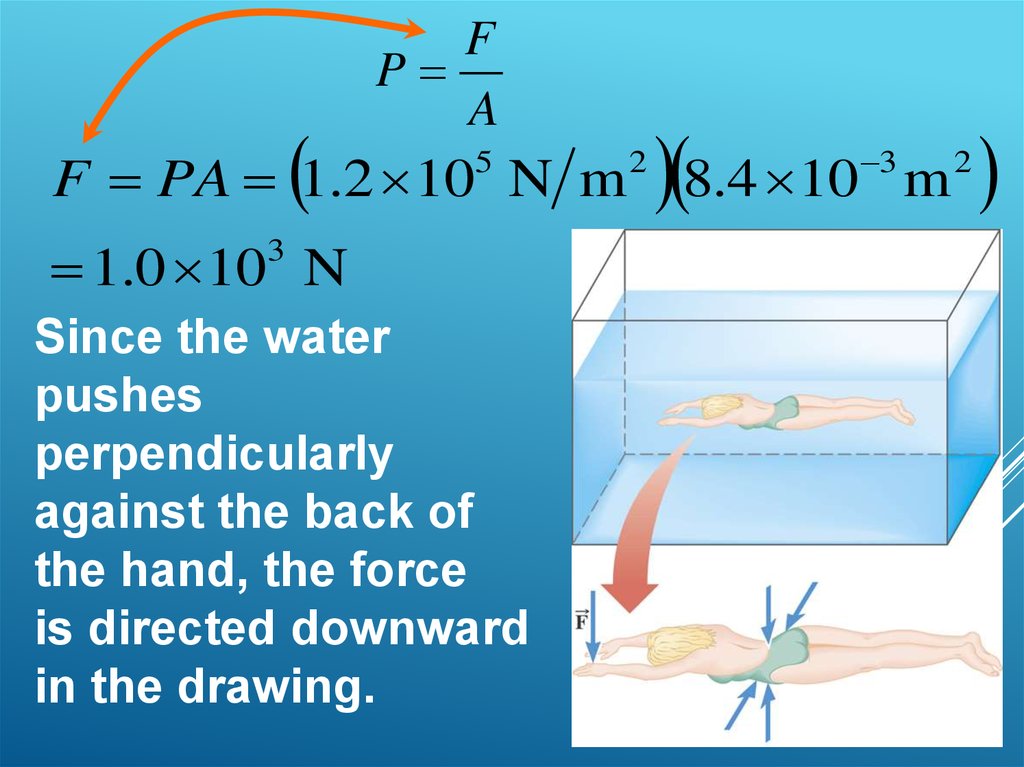
FP
A
F PA 1.2 10 N m
5
1.0 10 N
3
Since the water
pushes
perpendicularly
against the back of
the hand, the force
is directed downward
in the drawing.
2
8.4 10
3
m
2
10.
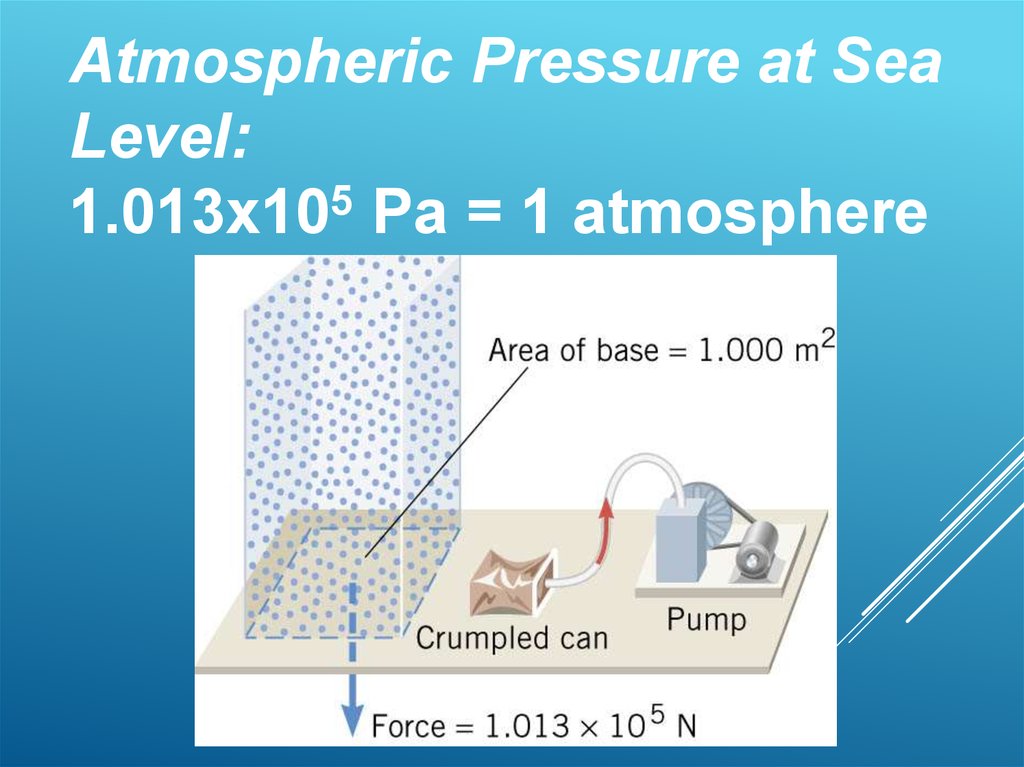
Atmospheric Pressure at SeaLevel:
5
1.013x10 Pa = 1 atmosphere
11.
Why do tetra packscrush or squeeze
itself when you sip
too much air
inside?
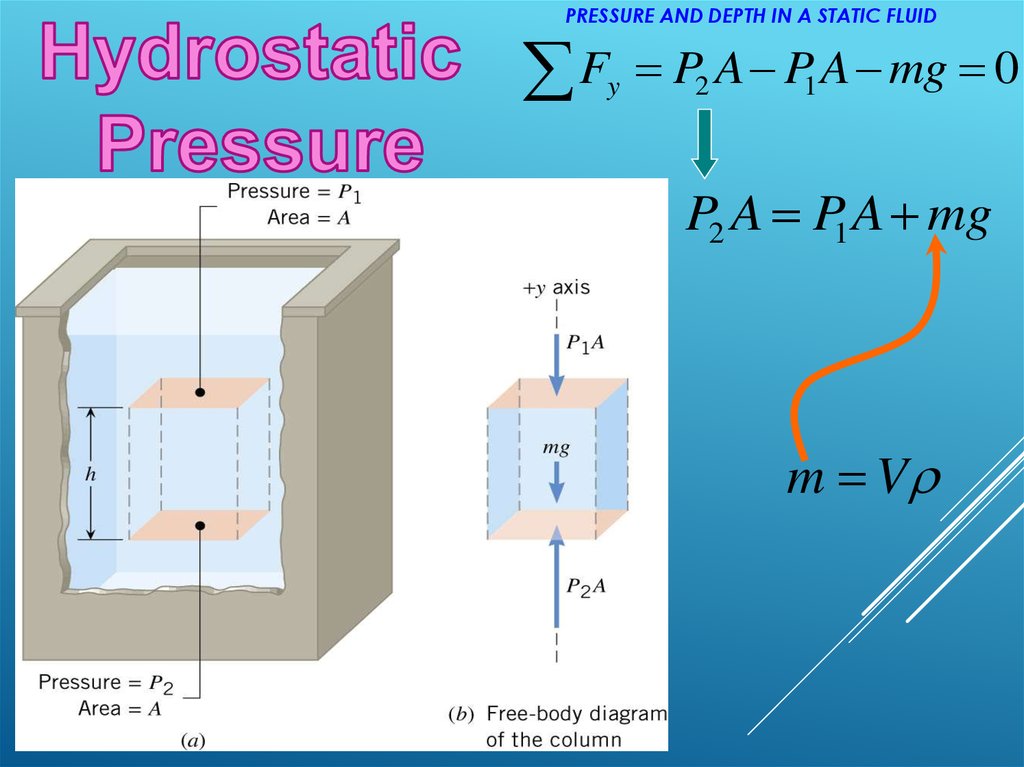
12. Pressure and Depth in a Static Fluid
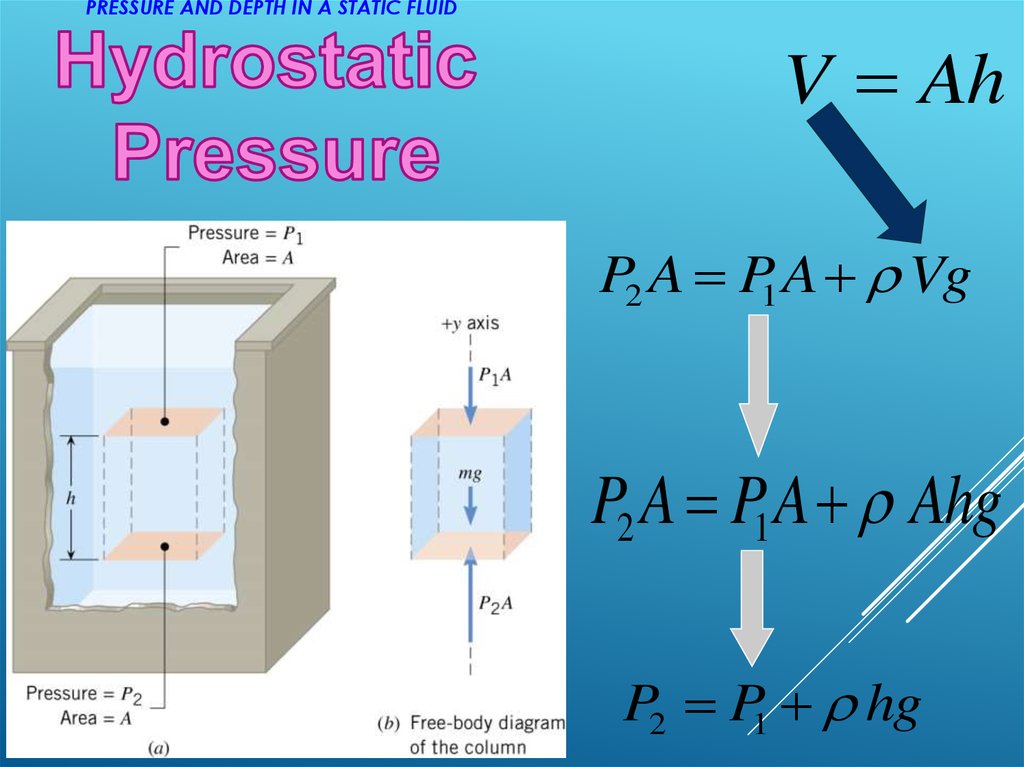
PRESSURE AND DEPTH IN A STATIC FLUIDF
y
P2 A P1 A mg 0
P2 A P1 A mg
m V
13. Pressure and Depth in a Static Fluid
PRESSURE AND DEPTH IN A STATIC FLUIDV Ah
P2 A P1 A Vg
P2 A P1 A Ahg
P2 P1 hg
14. Pressure and Depth in a Static Fluid
PRESSURE AND DEPTH IN A STATIC FLUIDConceptual Example - The Hoover Dam
Lake Mead is the largest wholly
artificial reservoir in the United
States. The water in the reservoir
backs up behind the dam for a
considerable distance (120 miles).
Suppose that all the water in Lake
Mead were removed except a
relatively narrow vertical column.
Would the Hoover Same still be
needed to contain the water, or
could a much less
massive structure do the job?
15.
Answer:The force exerted on a given section of
the dam depends only on how far that
section is located vertically below the
surface. As we go deeper, the water
pressure and force becomes greater.
The force that water applies on the
dam does not depend on the amount of
water backed up behind the dam. Thus,
an EQUALLY MASSIVE HOOVER DAM
WOULD STILL BE NEEDED.
PRESSURE AND DEPTH IN A STATIC FLUID
16. Pressure and Depth in a Static Fluid
PRESSURE AND DEPTH IN ASTATIC FLUID
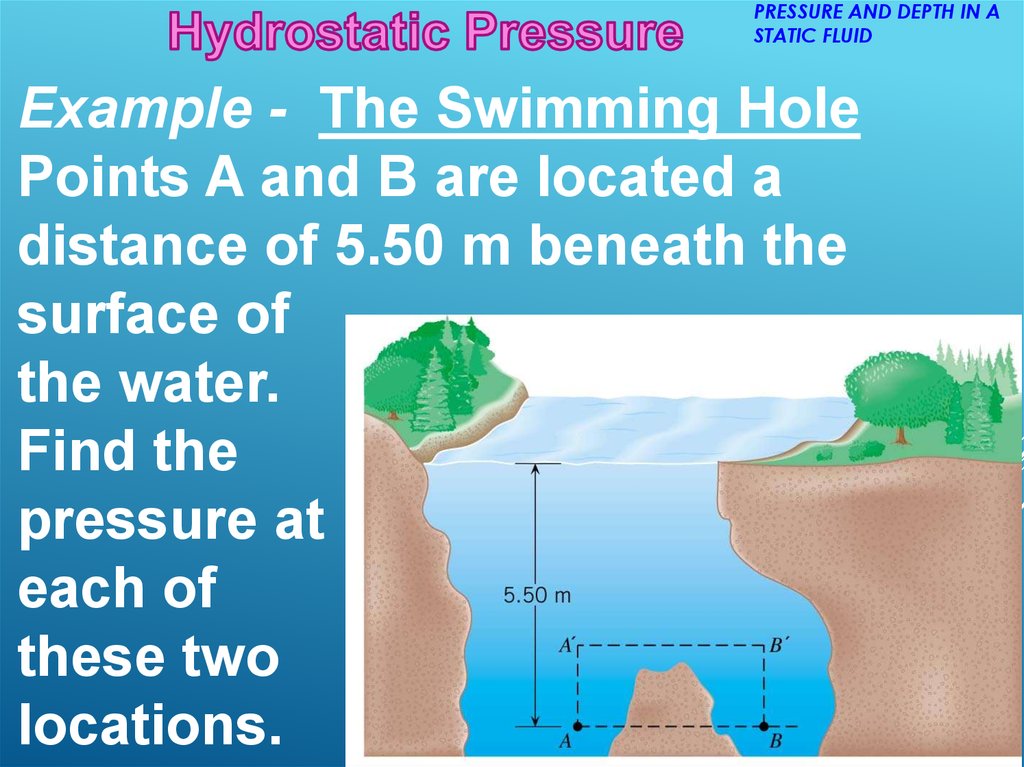
Example - The Swimming Hole
Points A and B are located a
distance of 5.50 m beneath the
surface of
the water.
Find the
pressure at
each of
these two
locations.
17. Pressure and Depth in a Static Fluid
PRESSURE AND DEPTH IN A STATIC FLUIDP2 P1 gh
atmospheric pressure
P2 1.01 105 Pa 1.00 103 kg m 3 9.80 m s 2 5.50 m
1.55 105 Pa
18.
Pressure Gauges19. Pressure Gauges
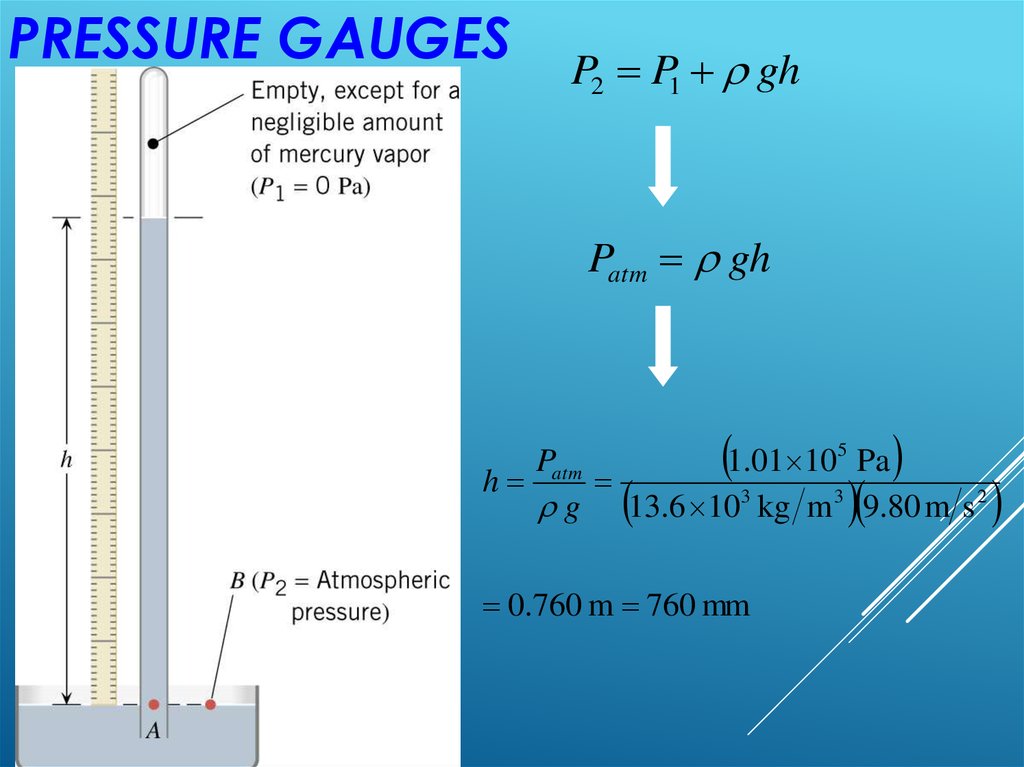
PRESSURE GAUGESP2 P1 gh
Patm gh
Patm
1.01 105 Pa
h
g 13.6 103 kg m 3 9.80 m s 2
0.760 m 760 mm
20. 11.4 Pressure Gauges
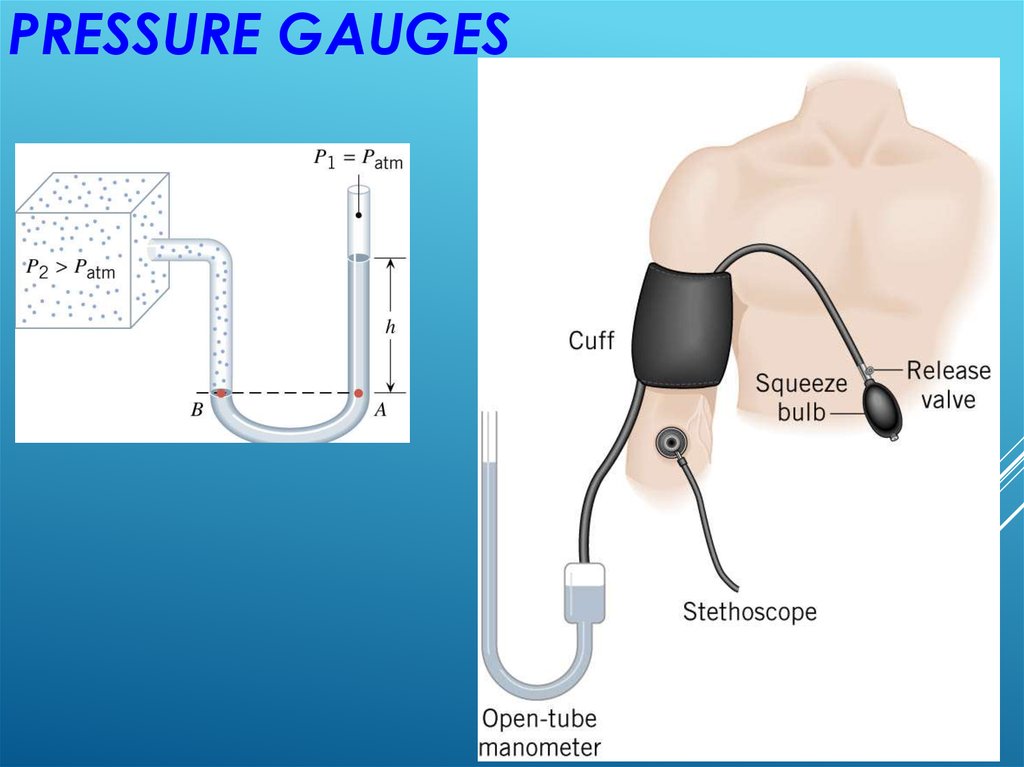
11.4 PRESSURE GAUGESP2 PB PA
PA P1 gh
absolute pressure
P2 Patm gh
gauge pressure
21. Pressure Gauges
PRESSURE GAUGES22. Pascal’s Principle
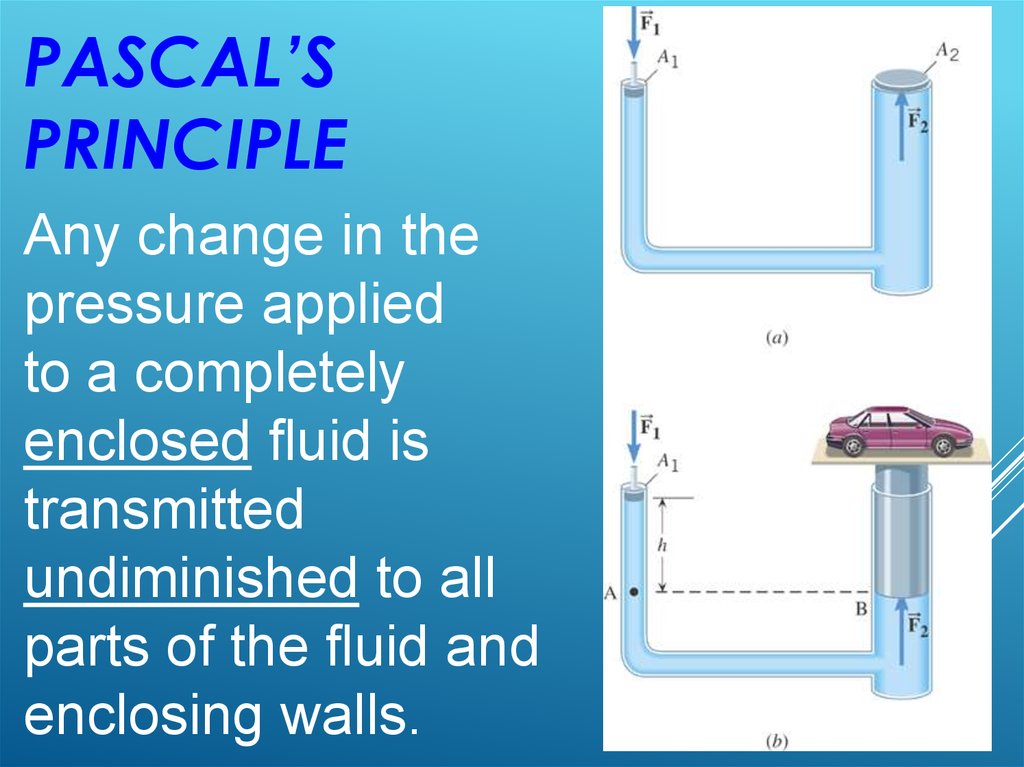
PASCAL’SPRINCIPLE
Any change in the
pressure applied
to a completely
enclosed fluid is
transmitted
undiminished to all
parts of the fluid and
enclosing walls.
23. Pascal’s Principle
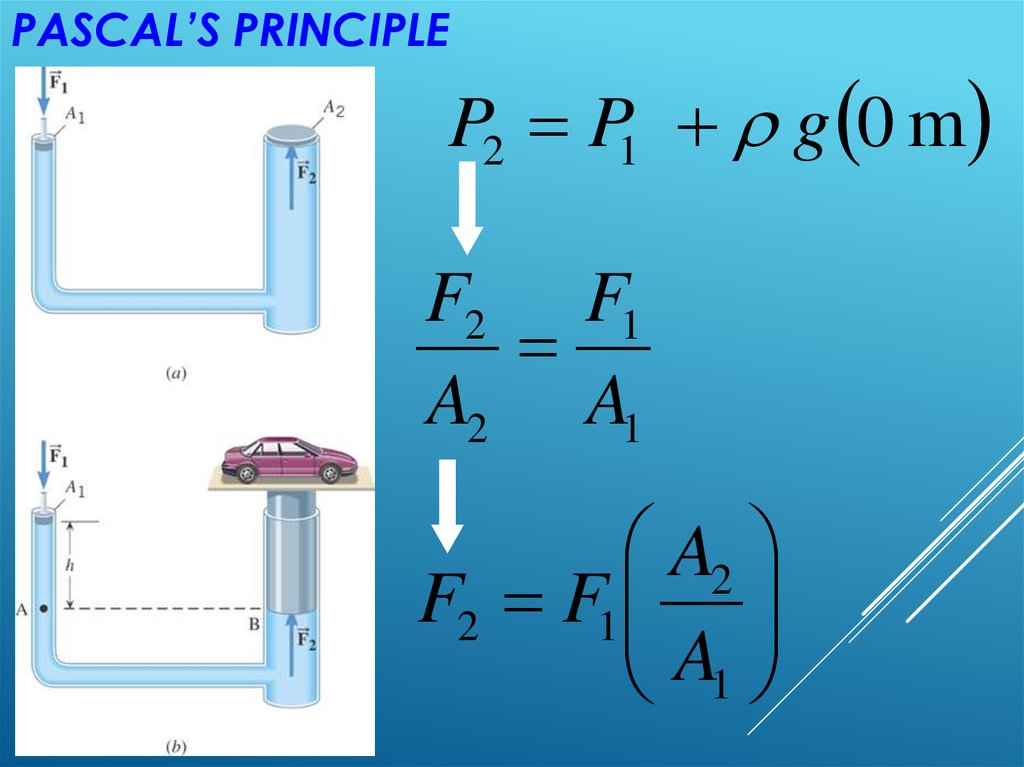
PASCAL’S PRINCIPLEP2 P1 g 0 m
F2 F1
A2 A1
A2
F2 F1
A1
24. Pascal’s Principle
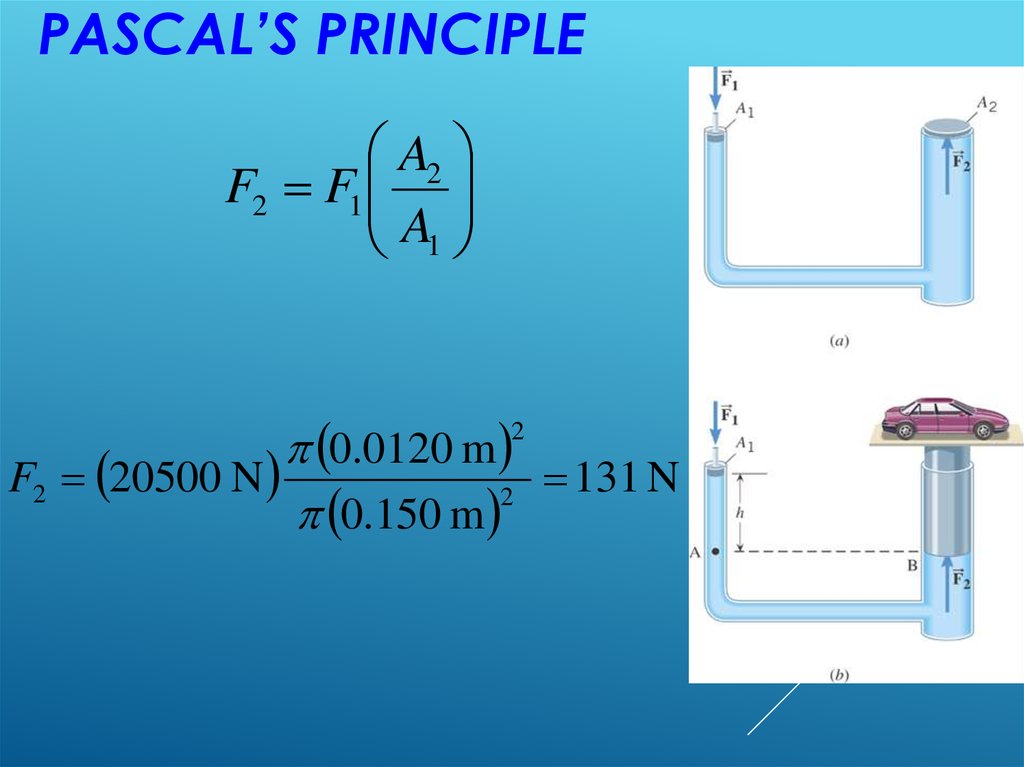
PASCAL’S PRINCIPLEExample - A Car Lift
The input piston has a radius
of 0.0120 m and the output
plunger has a radius of 0.150
m. The combined weight of
the car and the plunger is
20,500 N. Suppose that the
input piston has a negligible
weight and the bottom surfaces
of the piston and plunger are
at the same level. What is the required input
force?
25. Pascal’s Principle
PASCAL’S PRINCIPLEA2
F2 F1
A1
0.0120 m
F2 20500 N
131 N
2
0.150 m
2
26.
Communicating Vesselset
of
containers
containing
a
homogeneous fluid: when the liquid
settles, it balances out to the same level
in all of the containers regardless of the
shape and volume of the containers. If
additional liquid is added to one vessel,
the liquid will again find a new equal
level in all the connected vessels. This
occurs because gravity and pressure
are constant in each vessel (hydrostatic
pressure).
27.
Containing homogeneous fluid: when the liquid settles, itbalances out to the same level in all of the containers
regardless of the
shape and volume
of the containers.
This occurs
because gravity
and pressure are
constant in each
vessel (hydrostatic
pressure).
















 Физика
Физика








