Похожие презентации:
Геодезия. Топография
1. Геодезия "ge" - земля и "dazomai" - разделяю, делю на части "землеразделение".
Геодезия"ge" - земля и "dazomai" - разделяю, делю на
части "землеразделение".
- это наука о методах определения фигуры и размеров
Земли, методах изображения ее поверхности на картах
и планах, а также о способах проведения различных
измерений на поверхности Земли (на суше и
акваториях), под землей, в околоземном пространстве и
на других планетах.
2.
Топография(от греч. tópos – место и греч. gráphō – пишу, описание местности)
Картография
Высшая геодезия
Фотограмметрия
Инженерная геодезия
Маркшейдерия
Спутниковая геодезия
Космическая геодезия
3.
Доказательства шарообразности Земли: с древних времёндо современности
О том, что форма у нашей планеты шарообразная, люди
узнали не сразу. Давайте плавно перенесёмся в древниедревние времена, когда люди считали, что Земля плоская, и
попробуем вместе с древними мыслителями, философами и
путешественниками прийти к идее шарообразности Земли...
Представления наших далёких предков о Земле в основном
опирались на мифы, предания
4.
Древние греки считали, что планета - это выпуклый диск, похожий на щитвоина, омываемый со всех сторон рекой Океан.
В Древнем Китае существовало представление, согласно которому Земля
имеет форму плоского прямоугольника, над которым на столбах
поддерживается круглое выпуклое небо. Разъяренный дракон будто бы
согнул центральный столб, вследствие чего Земля наклонилась к востоку.
Поэтому все реки в Китае текут на восток. Небо же наклонилось на запад,
поэтому все небесные светила движутся с востока на запад.
Греческий философ Фалес (VI в. до н. э.) представлял Вселенную в виде
жидкой массы, внутри которой находится большой пузырь, имеющий форму
полушария. Вогнутая поверхность этого пузыря — небесный свод, а на
нижней, плоской поверхности, наподобие пробки, плавает плоская Земля.
Нетрудно догадаться, что представление о Земле как о плавающем
острове Фалес основывал на том факте, что Греция расположена на
островах.
5.
А вот мир в представлении древнихегиптян:
внизу - Земля, над ней - богиня неба;
слева и справа корабль бога Солнца, показывающий путь Солнца по небу
от восхода до заката.
6.
Древние индийцы представляли Землю в виде полусферы,опирающейся на слонов.
Слоны стоят на панцире огромной черепахи, стоящей на змее и плывущей в
бескрайнем Океане из молока. Змея, свернувшись кольцом, замыкает
околоземное пространство.
Обратите внимание, до истины ещё далеко, но первый шаг к ней уже сделан!
7.
Жители Вавилона представляли Землю в виде горы, на западном склонекоторой находится Вавилония.
Они знали, что к югу от Вавилона раскинулось море, а на востоке
расположены горы, через которые не решались переходить. Поэтому им и
казалось, что Вавилония расположена на западном склоне «мировой»
горы. Гора эта окружена морем, а на море, как опрокинутая чаша,
опирается твердое небо - небесный мир, где, как и на Земле, есть суша,
вода и воздух.
8.
А на Руси считали, что Земля плоская и держится на трех китах, которыеплавают и безбрежном всемирном океане.
9.
Современник Фалеса –Анаксима́ндрМиле́тский древнегреческий философ
представлял Землю отрезком колонны
или цилиндра, на одном из оснований
которого мы живем. Середину Земли
занимает суша в виде большого
круглого острова Ойкумены
(«населенной Земли»), окруженного
океаном. Внутри Ойкумены находится
морской бассейн, который делит ее на
две приблизительно равные части:
Европу и Азию:
10.
Пифагор ( ок. 540-х г. до н. э.),«В природе все должно быть
совершенным, а наиболее
совершенным из геометрических тел
является шар»
ПАРМЕНИД (период расцвета
504–501 до н. э.),
основатель элейской школы.
Первым высказал мысль о
шарообразности Земли исходя из
астрономических наблюдений.
11.
АНАКСАГОР (ок. 500–428 до н. э.),Считал, что Луна попадает в тень
Земли и происходит лунное
затмение. Первым оценил размеры
Земли по лунным затмениям.
АРИСТОТЕЛЬ (384–322 до н. э.),
«Земля – это всюду выпуклое тело»
Ввел понятие геодезии –
практическая часть геометрии
12.
ЭРАТОСФЕН Киренский(ок. 276–194 до н. э.),
Определил длину окружности земного шара в
250 тысяч стадиев (39 250 километров)
S=0,5 (158+185) 5000=857500 м,
Δφ =7°12‘ = 7.2 °,
S/2 R = /360º
имеем R=6823,8 км
13. Геодезические измерения
Жан Френель (1497 -1558 гг.),французский ученый и придворный врач
определил дугу меридиана между
Парижем и Амьеном,
длина дуги в 1° оказалась равной 56747
тоазам
(1 тоаз = 1,94904 м), т.е. 110,6 км
14. Снеллиус (1580 - 1626 гг.) голландский астроном и математик
разработал метод триангуляцииЖак Пикар (1620 - 1682 гг.)
Французский
академик
впервые
использовал
геодезические приборы со зрительными трубами и сеткой
нитей и в 1669 - 1670 гг. повторил градусные измерения
Френеля между Парижем и Амьеном, создав цепь из 13
треугольников,
определил длину одного градуса дуги парижского
меридиана, равную 111,212 км
(по современным данным 111,221 км)
15. Д’Аламбер Жан Лерон (Франция. Париж. 1717 – 1783)
за 6 лет измерили дугупарижского меридиана
длиной в 9°40' (1000 км)
от Дюнкерка до
Барселоны,
проложив цепь из 115
треугольников через
всю Францию и часть
Испании.
16.
И.Ньютон - 1687«Математические начала
натуральной философии»
m1m 2
F G
2
r
G 6.674 10 11 м 3 / кг с 2
17. Основные этапы определения формы и размеров Земли
1.2.
3.
4.
с древнейших времен до конца XVII в., когда Землю принимали
за шар;
с конца XVII в. до второй половины XIX в, когда считали, что
Земля является сплюснутым у полюсов шаром, т.е. сфероидом,
близким к эллипсоиду вращения;
со второй половины XIX в до сороковых годов XX в.,когда
установили, что более правильно представлять Землю трехосным
эллипсоидом, который является моделью более сложной формы
Земли - геоида;
с сороковых годов XX в до настоящего времени, когда за фигуру
Земли принимают тело, ограниченное физической поверхностью
Земли.
18.
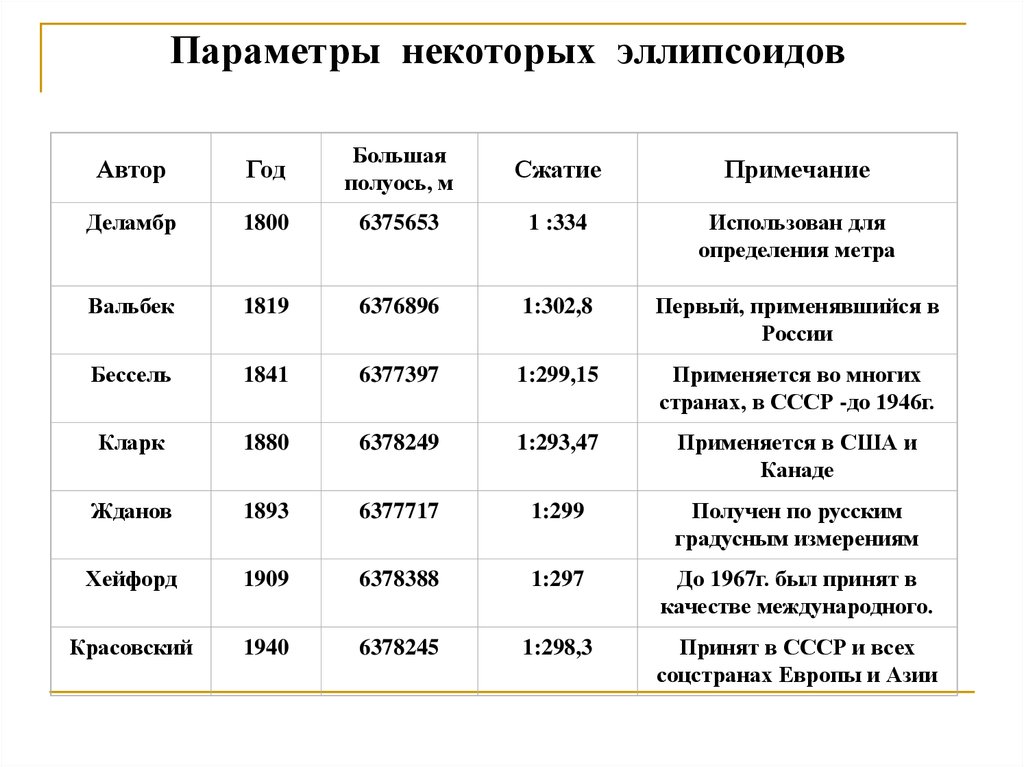
Параметры некоторых эллипсоидовАвтор
Год
Большая
полуось, м
Сжатие
Примечание
Деламбр
1800
6375653
1 :334
Использован для
определения метра
Вальбек
1819
6376896
1:302,8
Первый, применявшийся в
России
Бессель
1841
6377397
1:299,15
Применяется во многих
странах, в СССР -до 1946г.
Кларк
1880
6378249
1:293,47
Применяется в США и
Канаде
Жданов
1893
6377717
1:299
Получен по русским
градусным измерениям
Хейфорд
1909
6378388
1:297
До 1967г. был принят в
качестве международного.
Красовский
1940
6378245
1:298,3
Принят в СССР и всех
соцстранах Европы и Азии
19. Красовский Феодосий Николаевич (1878 — 1948 гг.)
Окончил физ.-мат. факультет МГУ.Работал доцентом кафедры
гравиметрии и геофизики в
МИИГАиК, был руководителем
лаборатории гравиметрии в
ЦНИИГиК.
С 1956г перешел на работу в
Институт физики Земли ( ИФЗ) АН
СССР. Ему дважды была
присуждена Сталинская премия и
Ленинская премия
астроном-геодезист, член-корреспондент АН СССР,
заслуженный деятель науки и техники РСФСР.
В конце 1928 г. по его инициативе был создан
Центральный научно-исследовательский институт
геодезии, аэросъёмки и картографии,
в котором он был директором.
В 1924–1930 гг. руководил астрономо-геодезическими
и картографическими работами в СССР
Молоденский
Михаил
Сергеевич
(15.06.1909 –
12.11.1991)
20.
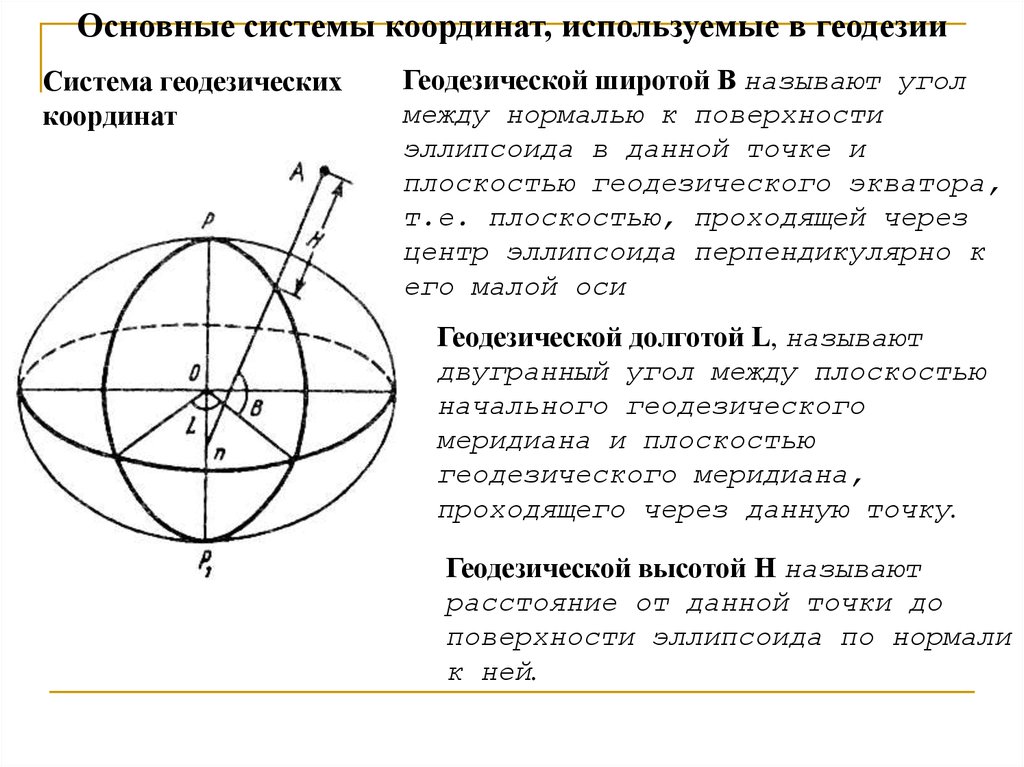
Основные системы координат, используемые в геодезииСистема геодезических
координат
Геодезической широтой В называют угол
между нормалью к поверхности
эллипсоида в данной точке и
плоскостью геодезического экватора,
т.е. плоскостью, проходящей через
центр эллипсоида перпендикулярно к
его малой оси
Геодезической долготой L, называют
двугранный угол между плоскостью
начального геодезического
меридиана и плоскостью
геодезического меридиана,
проходящего через данную точку.
Геодезической высотой Н называют
расстояние от данной точки до
поверхности эллипсоида по нормали
к ней.
21.
PM
Земная ось
ы
Меридиан т
очк
и
Нач
ал
ьн
М
иан
д
и
ер
м
й
D
P
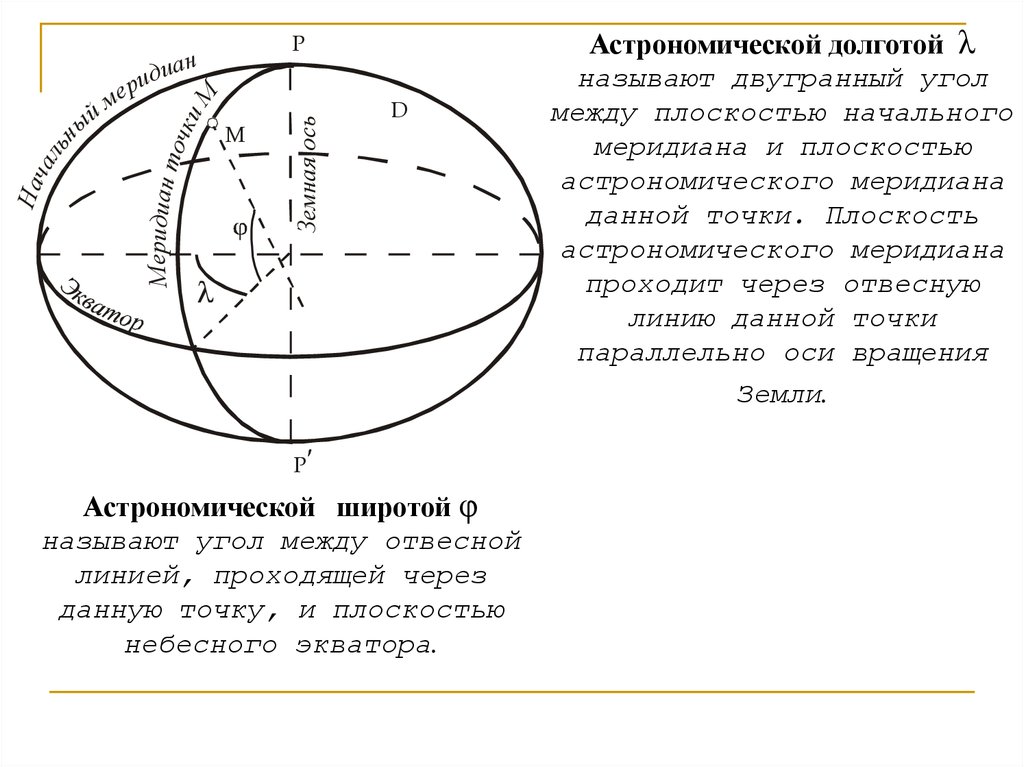
Астрономической широтой φ
называют угол между отвесной
линией, проходящей через
данную точку, и плоскостью
небесного экватора.
Астрономической долготой λ
называют двугранный угол
между плоскостью начального
меридиана и плоскостью
астрономического меридиана
данной точки. Плоскость
астрономического меридиана
проходит через отвесную
линию данной точки
параллельно оси вращения
Земли.
22.
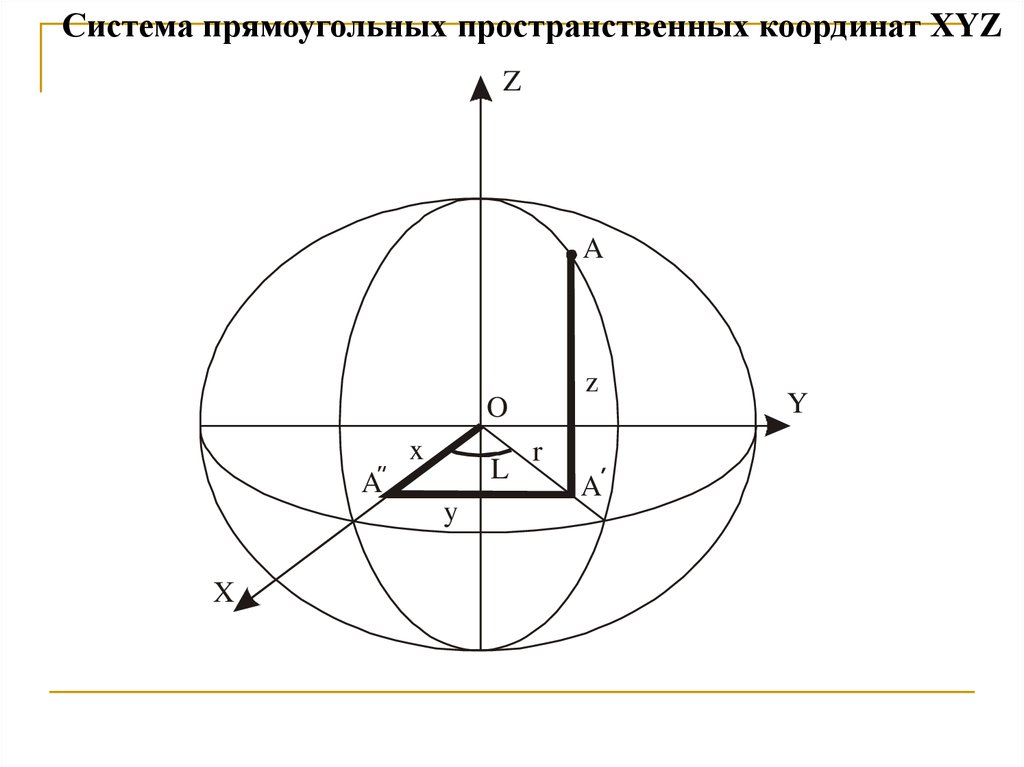
Система прямоугольных пространственных координат XYZZ
A
z
O
x
L
A
y
X
r
A
Y
23.
Плоские прямоугольные координаты+X
IV
I
Ya
A
Yd
D
Xa
Xd
0
-Y
Xb
Xc
III
C
+Y
Yb
Yc
-X
Рис. 8
B
II
24.
Полярные координатыX
M
r
1
N
1
2
r
2
O
Р ис. 9
25.
Связь плоской прямоугольной и полярной систем координатX
Xb-Xa
B
Yb
XB = XA + ΔXAB
Yab
Xab
С
Прямая геодезическая задача состоит в
определении координат конечной точки
линии по длине ее горизонтального
проложения, направлению и координатам
начальной точки
YB = YA + ΔYAB
S
Ya
А
Xb
XAB = S cos α, YAB = S sin α
Xa
Y
0
Yb-Ya
Рис. 10
XB = XA + S cos α,
YB = YA + S sin α
26.
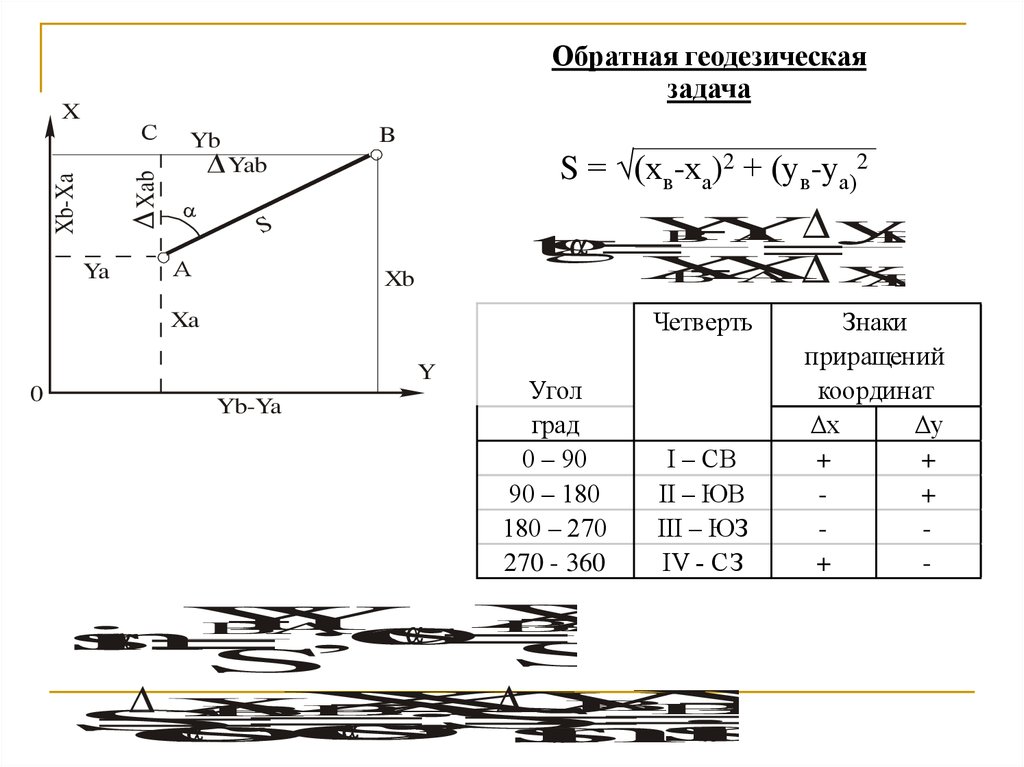
Обратная геодезическаязадача
X
Xb-Xa
B
Yb
S = √(хв-ха)2 + (ув-уа)2
Yab
Xab
С
y
Y
Y
B
А
А
t
g
=
= B
X
X
B
А
x
B
А
S
Ya
А
Xb
Четверть
Xa
Y
0
Yb-Ya
Рис. 10
Угол
град
0 – 90
90 – 180
180 – 270
270 - 360
I – СВ
II – ЮВ
III – ЮЗ
IV - СЗ
Знаки
приращений
координат
Δх
Δу
+
+
+
+
-
X
X
Y
Y
А
B
B
А
c
o
s
=
;
s
i
n
=
S
S
y
Y
Y
А
B
x
X
X
B
А
А
B
А
B
;
=
S
=
=
S
=
o
s
s
i
n
c
o
sc
s
i
n
27.
Понятие о фигуре Земли. Уровенная поверхность.Отвесная линия. Геоид, земной эллипсоид, референц-эллипсоид
Уровенной называют поверхность, в каждой точке
которой потенциал силы тяжести имеет одинаковое
D
значение.
Ур
о ве н
B
b’
A
a’
a
b
ная
точ повер
C
ки D хн о
Уро
ст
вен
ь
ная
H
т о п о ве
ч к и рх
c“
C нос
Уро
ть
в
енн
c’
ая
Уро
п
вен точк овер
и B хн
на
ос
яп
т
ть
c Ур
ов
о
ч
ове
ки ерх
нн
A но
ая
ст
п
ь
ок ове
еа р х
на но
ст
ь
28.
ФИГУРА ГЕОИДА29. Фигура геоида по данным ИСЗ CHAMP
30.
Касательная к точкесиловой линии называется
отвесной линией
Физическа поверхность Земли
Геоид
Эллипсои
д
31. Поверхность относимости
Поверхность относимости – правильнаяматематическая поверхность, на которую
проектируют геодезические измерения (плоскость,
шар, эллипсоид).
Метод проектирования – это способ переноса
измеренных на физической поверхности Земли
величин на поверхность относимости. В геодезии
применяют проектирование по линиям,
перпендикулярным к поверхности относимости.
32. Поверхность относимости
Земной эллипсоид (общий земной эллипсоид,сфероид) – математически правильная поверхность,
образованная вращением эллипса вокруг малой оси,
близкая к поверхности геоида в целом.
Референц-эллипсоид – эллипсоид, ориентированный в
теле Земли для близости к геоиду на определенной
территории. Его центр может не совпадать с центром
масс Земли, а ось вращения не совпадать с осью
вращения Земли, но быть параллельна ей.
33. Поверхность относимости
В России принят общий земной эллипсоид ПЗ-90(а = 6378136 м, f = 1/298,257839303), на нем задаются
координаты для глобальной навигационной системы
ГЛОНАСС, и референц-эллипсоид Красовского
(а = 6378245 м, b = 6356863 м, f =1/298,3), на котором
определяются государственные референцные
системы координат СК-42 и СК-95.
Для американской глобальной навигационной системы
GPS используется эллипсоид WGS-84 (а = 6378137 м,
f = 1/298,2572235бЗ).
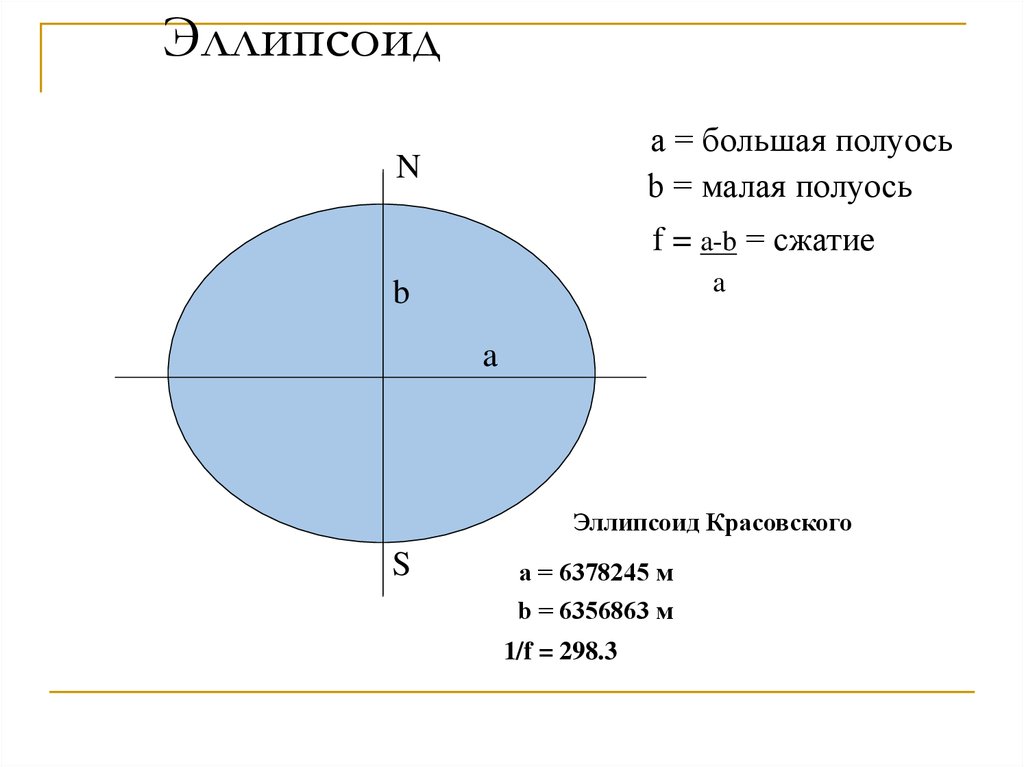
34. Эллипсоид
a = большая полуосьb = малая полуось
N
f = a-b = сжатие
a
b
a
Эллипсоид Красовского
S
a = 6378245 м
b = 6356863 м
1/f = 298.3
35.
ЭллипсоидКрасовского
Эллипсоид
WGS 84
Эллипсоид
Геоид
36.
37.
38.
39.
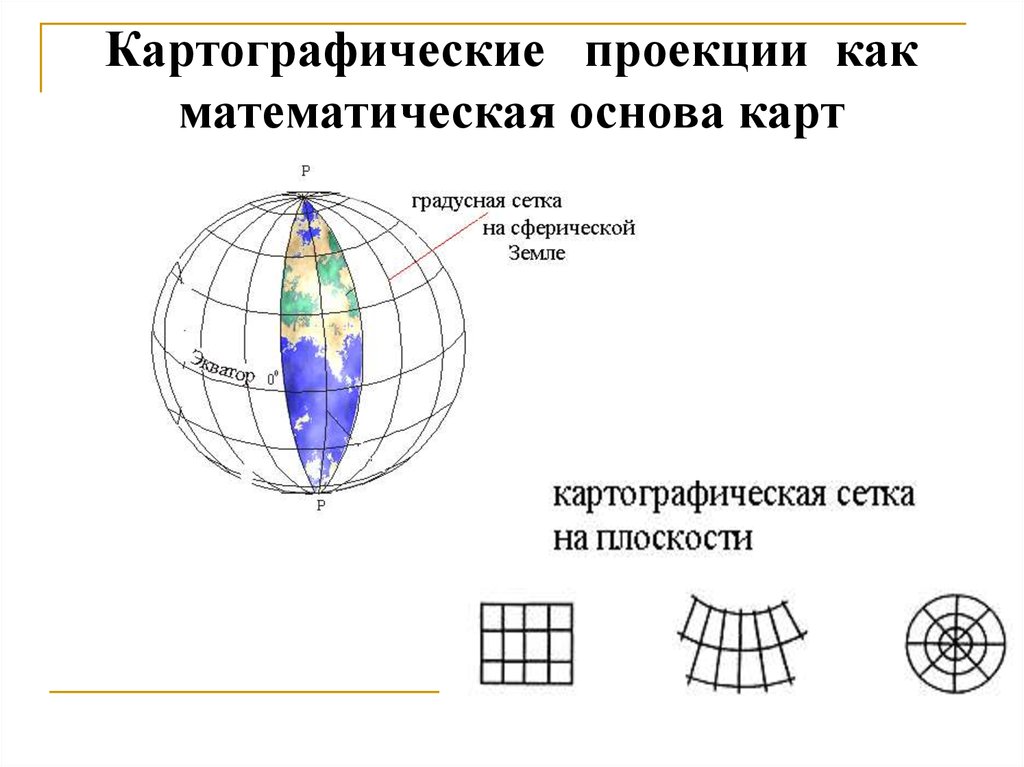
Картографические проекции какматематическая основа карт
40. Классификация картографических проекций
1) по характеру искажений:равноугольные
равновеликие
произвольные;
2) по виду сетки меридианов и параллелей или по способу
проектирования:
азимутальные
конические
цилиндрические
3) положению полюса сферических координат
нормальные
поперечные
косые
41. Азимутальные проекции
вспомогательной поверхностью являетсякартографическая сетка:
касательная или секущая плоскость
меридианы –прямые линии,
параллели – окружности
псевдоазимутальные
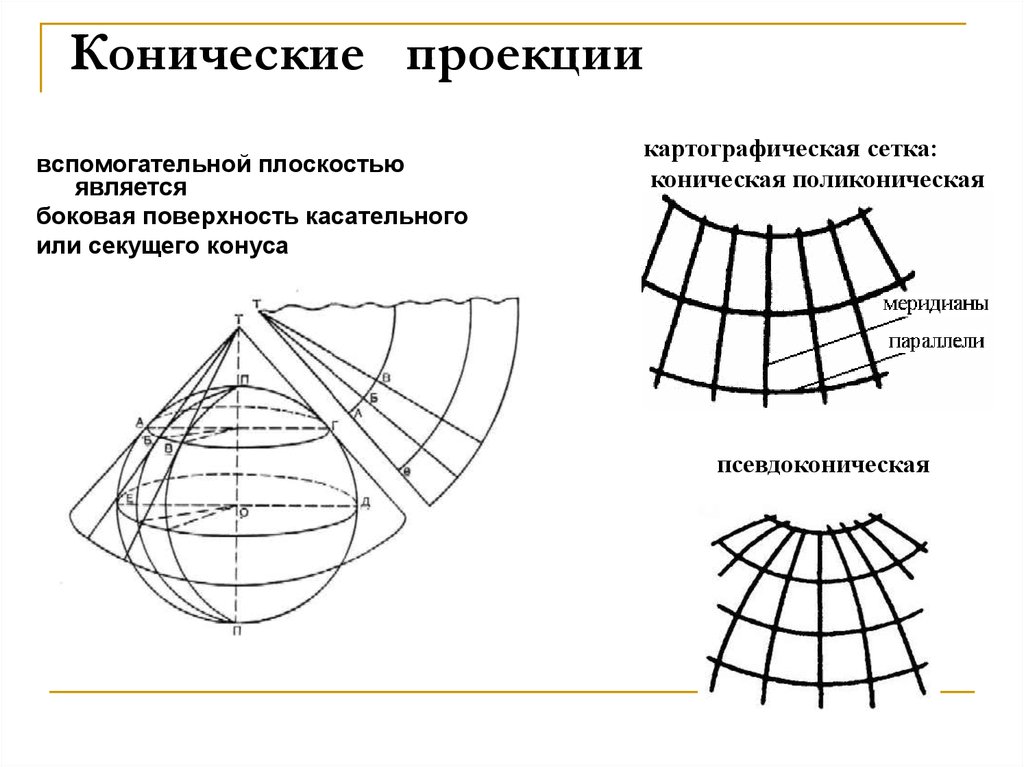
42. Конические проекции
вспомогательной плоскостьюявляется
боковая поверхность касательного
или секущего конуса
картографическая сетка:
коническая поликоническая
псевдоконическая
43. Цилиндрические проекции
вспомогательной поверхностью служит боковая поверхность цилиндра,касательного к эллипсоиду или секущего эллипсоид
картографическая
сетка
проекция
Меркатора
44.
Картографическая проекция Гаусса6-тиградусная зона
P
Эк
ват
6
ор 0
0
P
2-я зона
P
1-я зона
60-я зона
P
Э к в а т о р
0
0
6
0
0
6
0
P
P
Осевой
меридиан
P
P
12
0
45.
План и картаПлан
– это уменьшенное, подобное изображение на
горизонтальной плоскости небольшого плоского участка
местности
(признаки плана: уменьшенное, подобное, плоское)
Карта
– это уменьшенное, обобщенное изображение на
горизонтальной плоскости сферической поверхности
Земли, выполненное в определенной картографической
проекции
(признаки карты: уменьшенное, обобщенное, с учетом
сферичности Земли)
Масштаб – это степень уменьшения изображения участка
местности на плане или карте (1: 10000, в 1 см – 100 м)
46.
Размеры участков земной поверхности,принимаемые за плоские.
Топографический план
a
T
b
s
h
S
A
3
2
2
S
h=
2R
S= S2
3R
B
S, км
R
O
Δ S, м
1
5
10
20
50
100
0
0
0,01
0,07
1,02
8,21
Δ h, м
0,08
1,96
7,85
31,39
196,2
784,81
47.
Основные свойства картографического изображения земнойповерхности – наглядность и измеримость
Наглядность и измеримость карты обусловливаются:
1) наличием математически определенной связи между многомерными
объектами окружающего нас мира и их плоским картографическим
изображением; она осуществляется с помощью картографических проекций;
2) известной степенью уменьшения линейных размеров изображенных объектов,
которая зависит от масштаба;
3) выделением типических черт местности, определяющих ее отличительные
особенности, путем картографической генерализации;
4)
применением для изображения земной поверхности особой
системы - картографических условных знаков
знаковой
48.
Элементами карты, ее составными частями, являются:математическая основа, включающая масштаб, геодезическую
основу и картографическую проекцию;
содержание, под которым понимается совокупность показанных
объектов и сообщаемых сведений;
вспомогательное оснащение (название, легенда — свод условных
знаков и пояснений, раскрывающих их содержание, различные
графики, справочные данные и др.
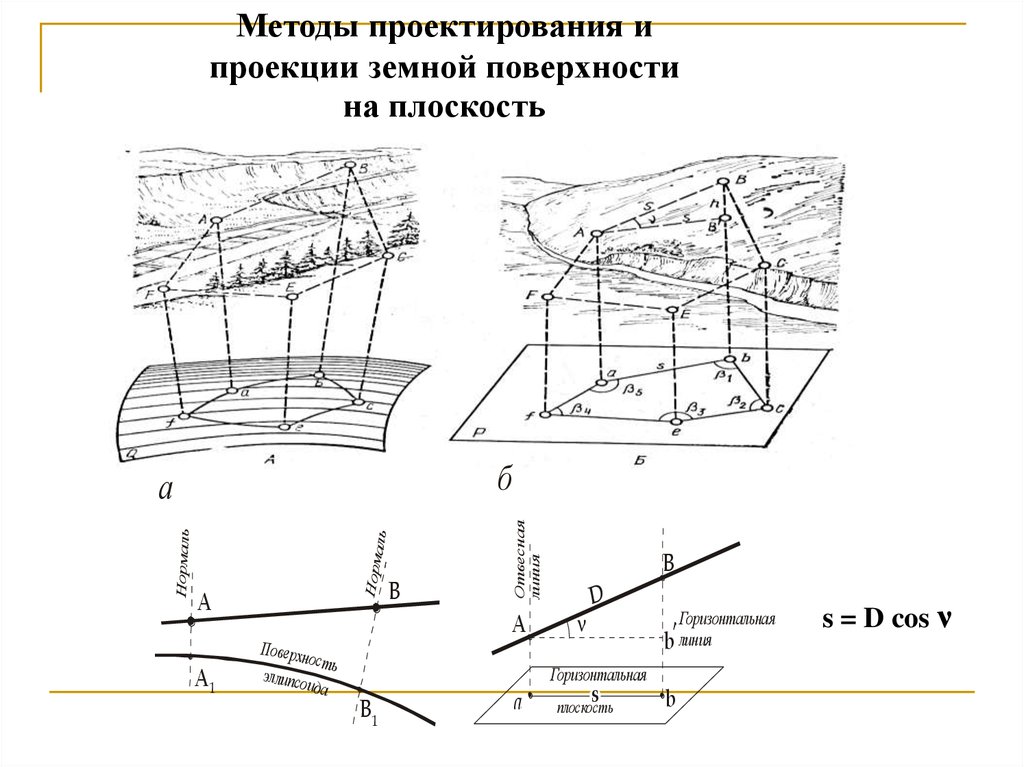
49.
Методы проектирования ипроекции земной поверхности
на плоскость
Норм
аль
Нормаль
A
A1
Поверхн
ость
эллипсои
да
B
Отвесная
линия
б
а
A
B
D
Горизонтальная
B1
a
s
плоскость
Горизонтальная
b линия
b
s = D cos ν
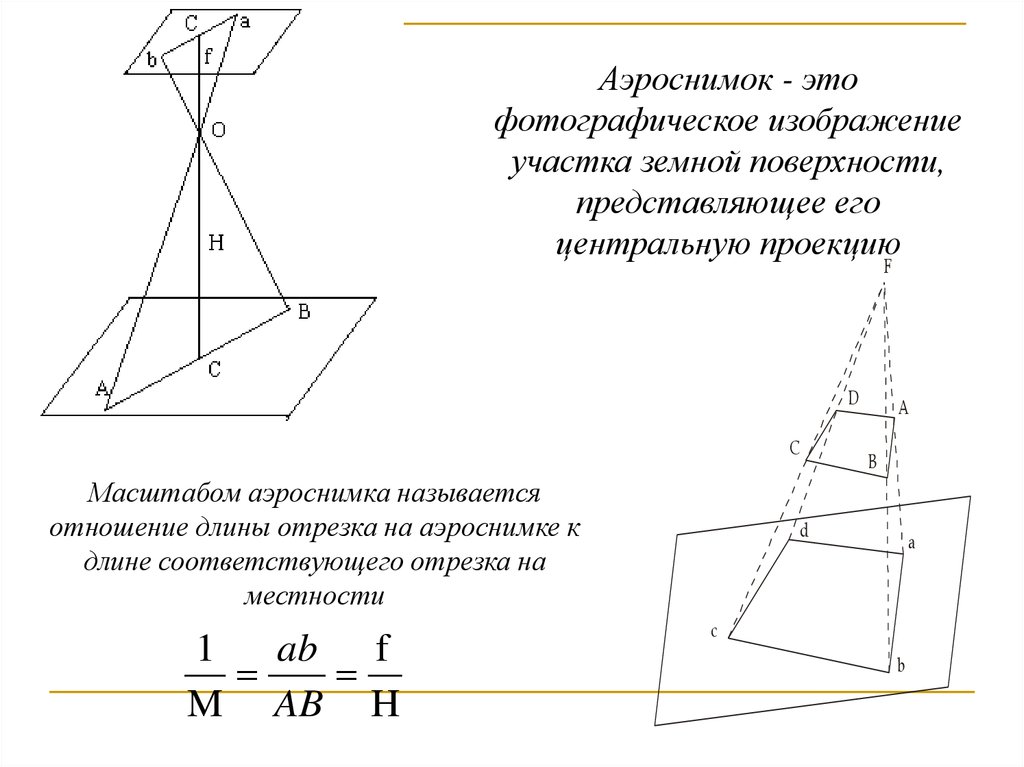
50.
Аэроснимок - этофотографическое изображение
участка земной поверхности,
представляющее его
центральную проекцию
F
D
C
Масштабом аэроснимка называется
отношение длины отрезка на аэроснимке к
длине соответствующего отрезка на
местности
1
ab f
M AB H
A
B
d
a
c
b
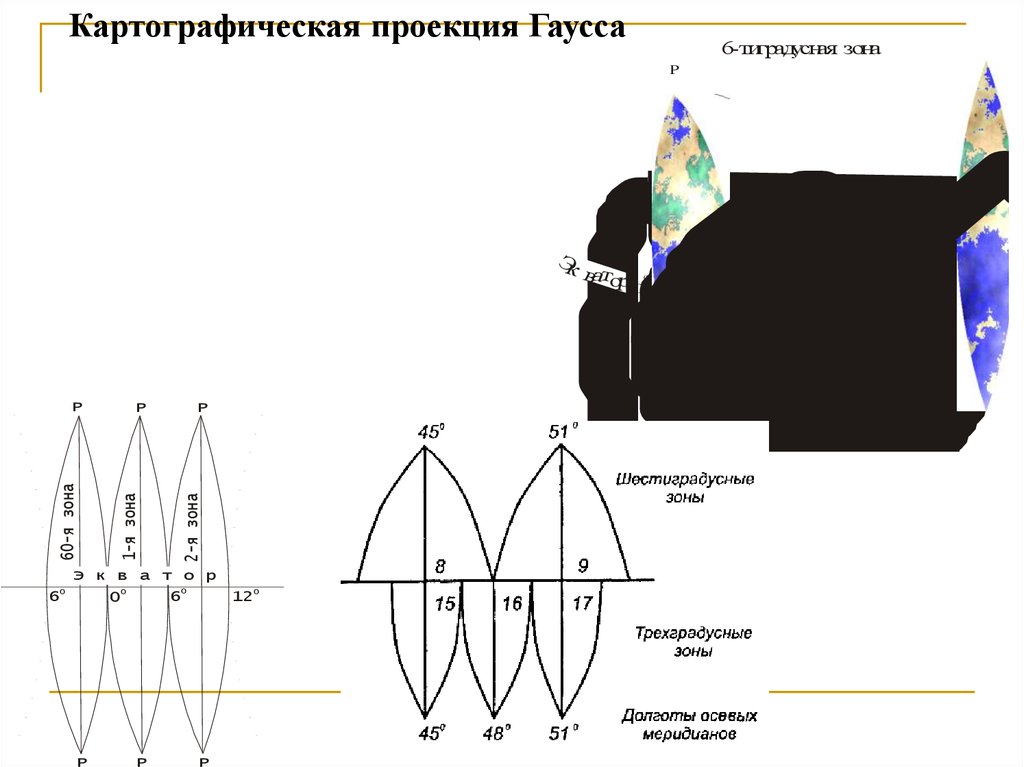
51.
Картографическая проекция Гаусса6-тиградусная зона
P
Эк
ват
ор 0
P
Э к в а т о р
0
0
6
6
0
0
P
P
P
2-я зона
P
1-я зона
60-я зона
P
P
0
6
0
12
0
Осевой
меридиан
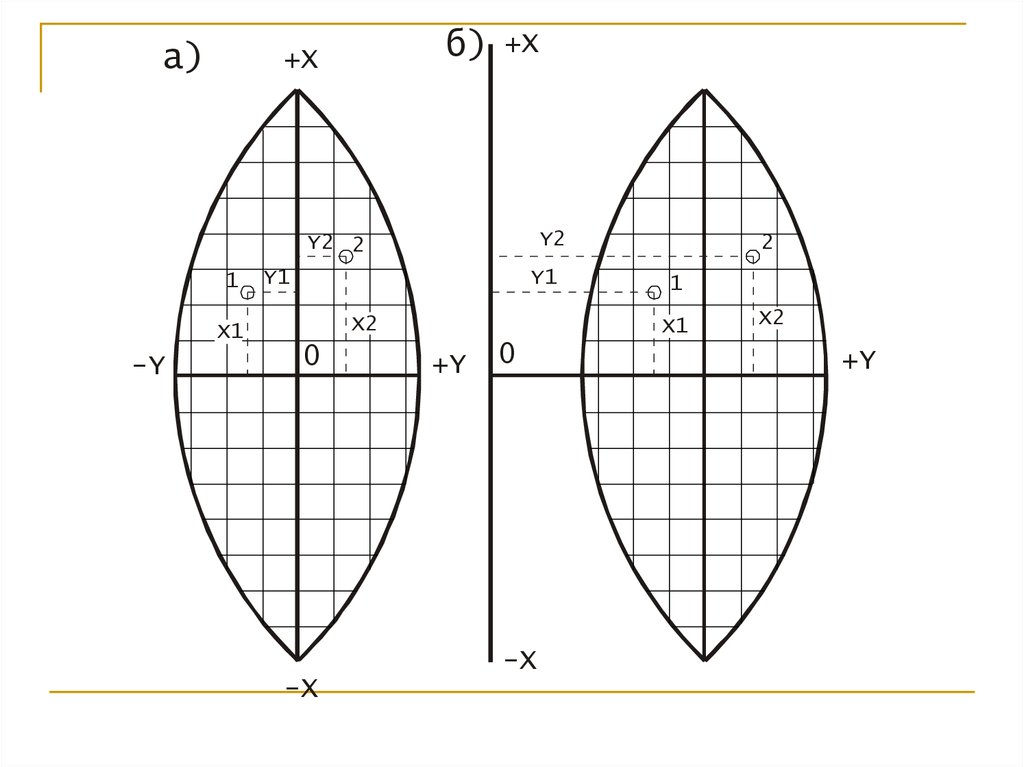
52.
а)б)
+X
+X
Y2
Y2 2
1
X1
-Y
Y1
Y1
X2
0
1
X1
+Y
0
-X
-X
2
X2
+Y
53.
ианд
и
р
е
м
меридиа
н
5-я
Зона
6- я
й
Осево
Осевой
Зо на
0
24
0
27
300
33
0
36 0
54.
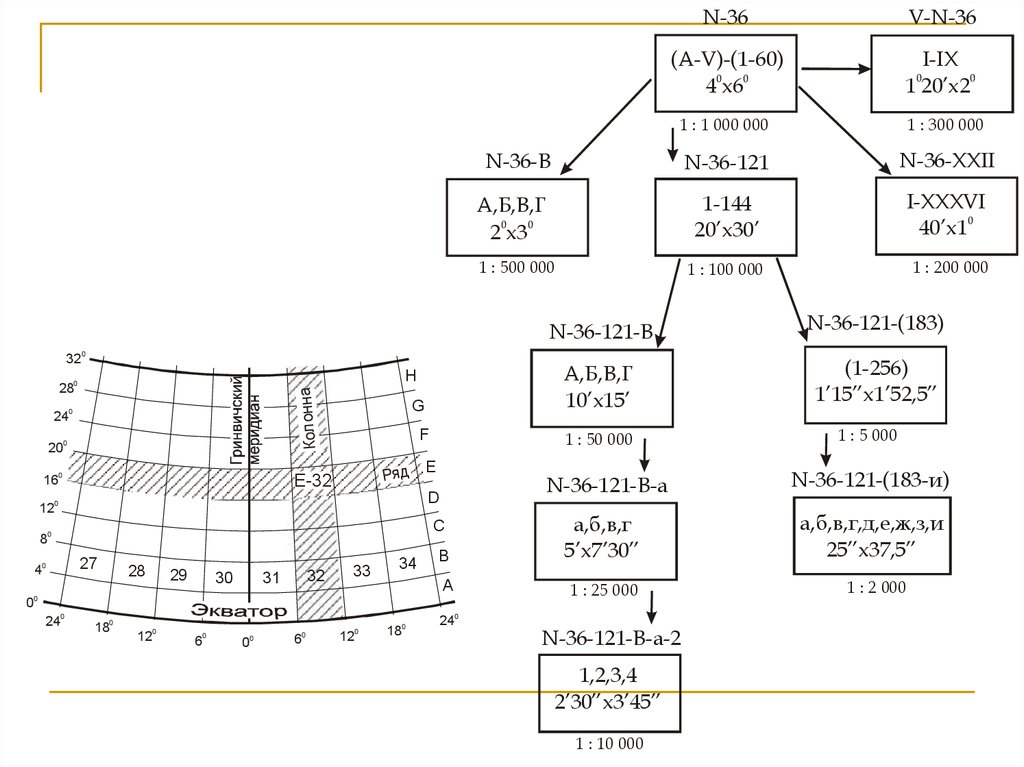
Разграфка и номенклатураРазграфкой называется разделение многолистной карты на отдельные листы.
Обозначение отдельных листов такой карты по определенной системе называется
номенклатурой
55.
N-36V-N-36
(A-V)-(1-60)
40x60
I-IX
0
1 20’x2
1 : 1 000 000
1 : 300 000
N-36-121
N-36-XXII
1-144
20’x30’
I-XXXVI
40’x10
1 : 100 000
1 : 200 000
N-36-В
А,Б,В,Г
0
0
2 х3
1 : 500 000
32
H
Колонна
28
240
0
20
16
12
8
0
G
F
Ряд
Е-32
0
E
27
(1-256)
1’15”x1’52,5”
28
29
30
32
31
33
34
180
12
0
6
0
00
6
0
12
0
180
1 : 5 000
N-36-121-(183-и)
B
а,б,в,г
5’x7’30”
а,б,в,г,д,е,ж,з,и
25”x37,5”
A
1 : 25 000
0
0
А,Б,В,Г
10’x15’
N-36-121-В-а
C
0
24
N-36-121-(183)
1 : 50 000
D
0
40
N-36-121-В
0
0
0
240
N-36-121-В-а-2
1,2,3,4
2’30”x3’45”
1 : 10 000
1 : 2 000
56.
1:300 000I-N-36
1
2
N-36
3
I
4
14
15
I
25
26
37
28
А
39
40
50
51
XIII
52
63
64
IV
74
76
XX
85
86
87
97
98
99
30
88
В
XXVI
109
110
111
121
122
123
VII
XXXI
134
112
124
XXXII
135
20
21
31
32
33
IX
III
XI
41
42
43
44
45
53
54
55
56
57
XVI
65
67
66
68
77
78
136
XII
Б
48
47
46
60
59
58
XVIII
XVII
69
70
81
82
71
72
83
84
VI
79
80
XXII
1:200 000
N-36-XII
36
35
34
X
XV
24
23
22
19
XXI
100
XXV
II
VI
V
V
75
XIX
133
29
XIV
62
73
18
VIII
38
61
17
12
11
10
9
IV
III
16
27
VII
8
7
6
II
13
49
5
1:100 000
N-36-12
XXIV
XXIII
89
90
91
92
93
94
95
96
101
102
103
104
105
Г106
107
108
119
XXVII
XXVIII
113
114
115
116
117
118
125
126
127
128
129
130
VIII
XXXIII
137
138
XXXIV
139
140
1:1 000 000
XXX
XXIX
IX
XXXV
141
142
131
120
132
XXXVI
143
144
1:500 000
N-36-Г
57.
N-36-12б
а
А
г
в
1
3
1
3
а
в
2
1
4
3
Б
2
1
4
3
Г
В
1:100000
б
г
2
1:10000
N-36-12-Б-б-2
4
2
4
1:25000
N-36-12-Б-г
1:50000
N-36-12-г
58.
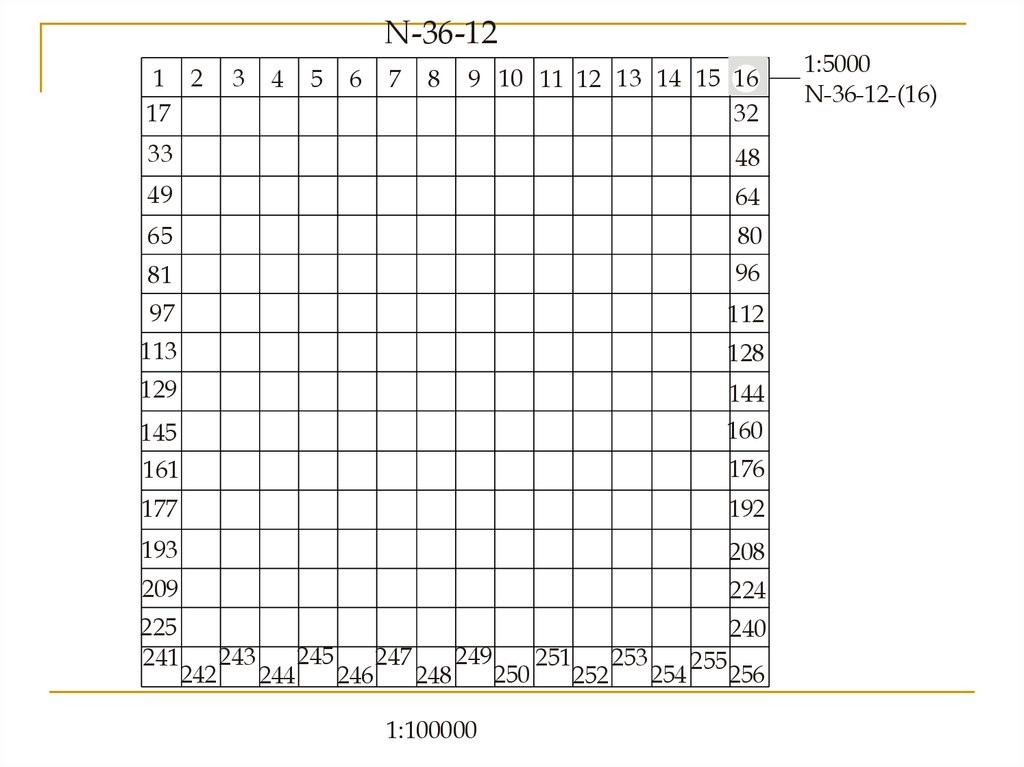
N-36-121 2
17
3
4
5
6
7
8
9 10 11 12 13 14 15 16
32
33
48
49
64
65
80
81
96
97
112
113
128
129
144
145
160
161
176
177
192
193
208
209
224
225
241
240
242
243
244
245
246
247
248
249
1:100000
250
251
252
253
254
255
256
1:5000
N-36-12-(16)
59.
N-36-12-(16)а
б
в
г
д
е
ж
з
и
1:5000
1:2000
N-36-12-(16-в)
60.
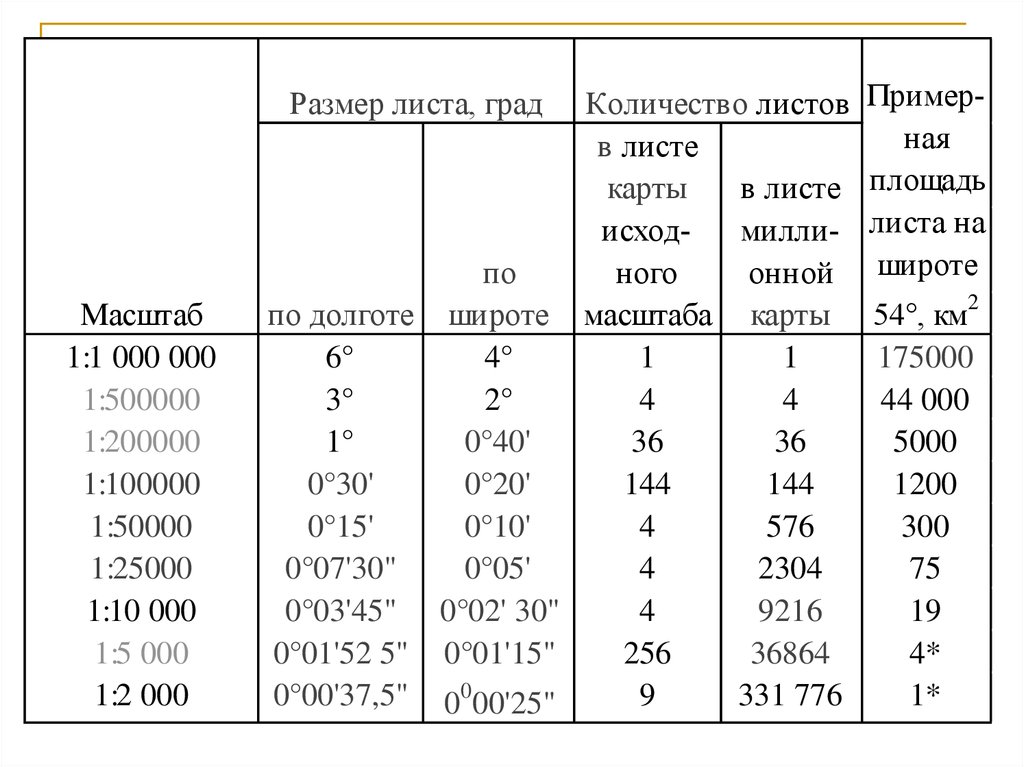
Размер листа, градМасштаб
1:1 000 000
1:500000
1:200000
1:100000
1:50000
1:25000
1:10 000
1:5 000
1:2 000
Количество листов
в листе
карты
в листе
исходмиллипо
ного
онной
по долготе широте масштаба карты
6°
4°
1
1
3°
2°
4
4
1°
0°40'
36
36
0°30'
0°20'
144
144
0°15'
0°10'
4
576
0°07'30"
0°05'
4
2304
0°03'45" 0°02' 30"
4
9216
0°01'52 5" 0°01'15"
256
36864
0°00'37,5" 00 00'25"
9
331 776
Примерная
площадь
листа на
широте
2
54°, км
175000
44 000
5000
1200
300
75
19
4*
1*
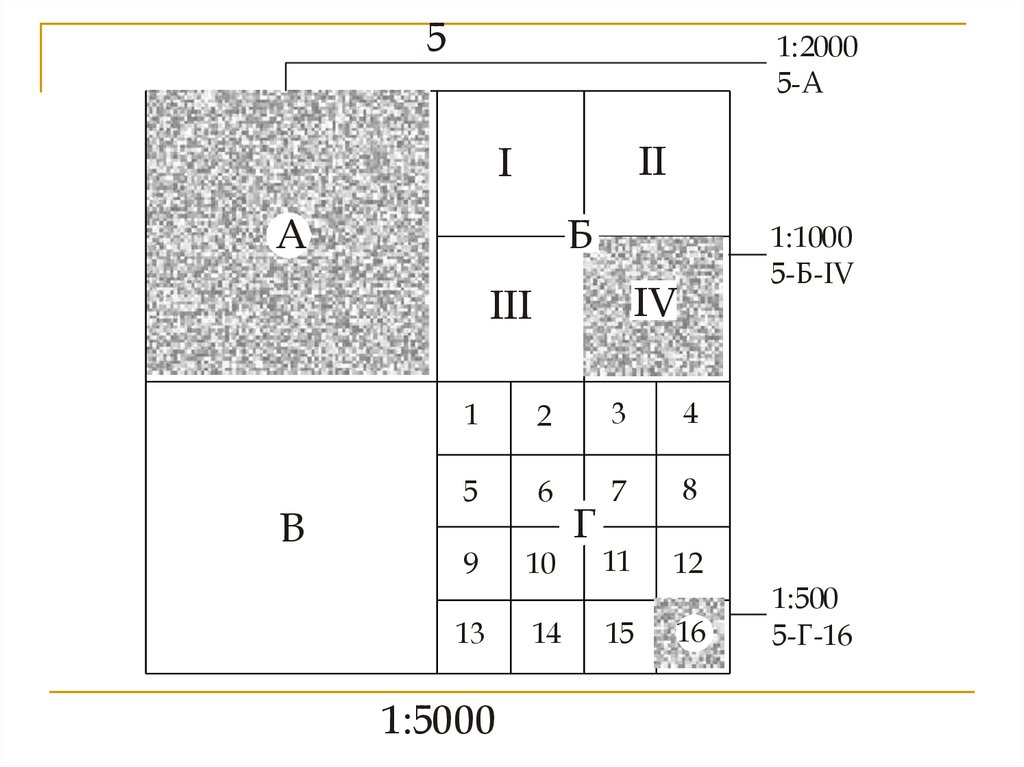
61.
51:2000
5-А
II
I
А
Б
IV
III
В
1:1000
5-Б-IV
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1:5000
Г
15
16
1:500
5-Г-16
62.
Размеррамок
Масштаб
1:5000
1:2000
1:1000
1:500
Обозначение
листов
листа, см
Площадь листа
га
км
40X40
400
4
50X50
I, II, ///, IV 50X50
1, 2, 3...
50X50
100
25
1
/, 2, 3...
А, Б, В, Г
6,25
2
0,25
0,0625
63.
Карта64.
Картографические условные знаки – это применяемыена картах обозначения различных объектов и их качественных
и количественных характеристик.
Условные знаки – это система графических,
цветовых и буквенно-цифровых обозначений.
Площадные
Линейные
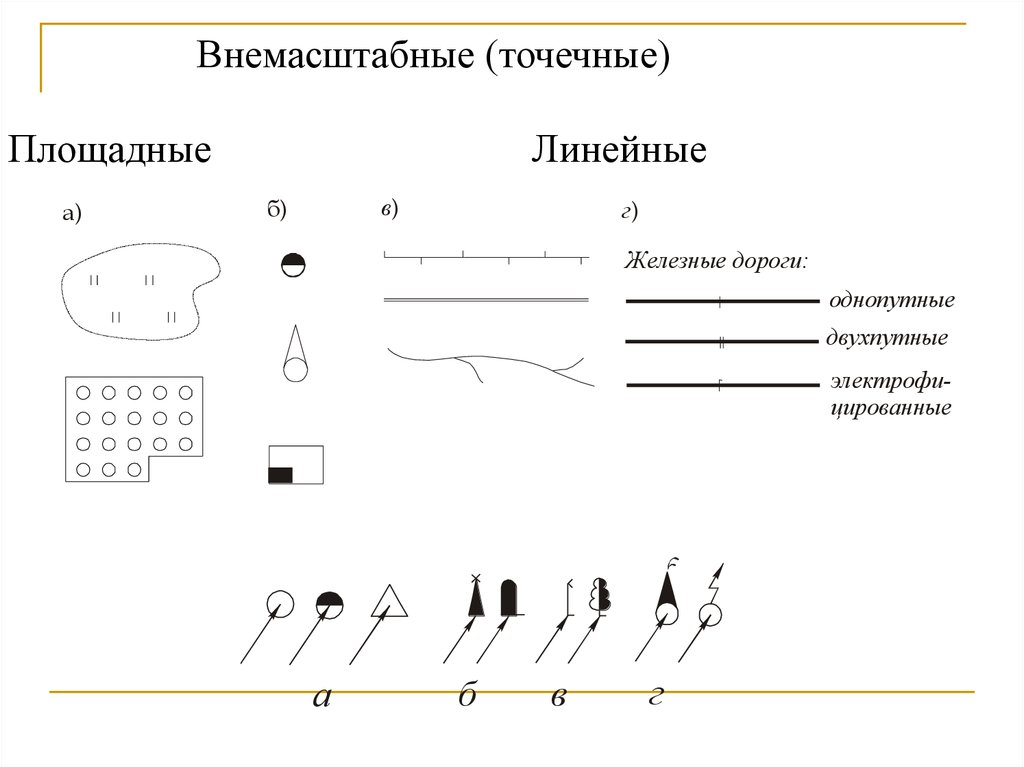
Внемасштабные (точечные)
65.
Внемасштабные (точечные)Площадные
а)
Линейные
в)
б)
г)
Железные дороги:
однопутные
двухпутные
электрофицированные
а
б
в
г
66. Картографическая генерализация
- это процесс отбора и обобщения, выделения главного иснятия второстепенного в зависимости от назначения
карты при картографировании поверхности Земли.
Факторы генерализации:
масштаб карты;
назначение карты;
тематика карты;
особенности и изученность объектов;
способы графического оформления карты.
-
-
67. Виды и формы генерализации
1. Обобщение качественных характеристик;2. Обобщение количественных характеристик;
3. Переход от простых понятий к сложным;
4. Отбор (исключение) объектов (ценз и норма);
5. Обобщение очертаний контуров;
6. Объединение контуров;
7. Смещение элементов отображения;
8. Утрирование.
68.
69.
φ 54 40 42λ 18 02 03
70.
Плоские прямоугольные координаты+X
IV
I
Ya
A
Yd
D
Xa
Xd
0
-Y
Xb
Xc
III
C
+Y
Yb
Yc
-X
Рис. 8
B
II
71.
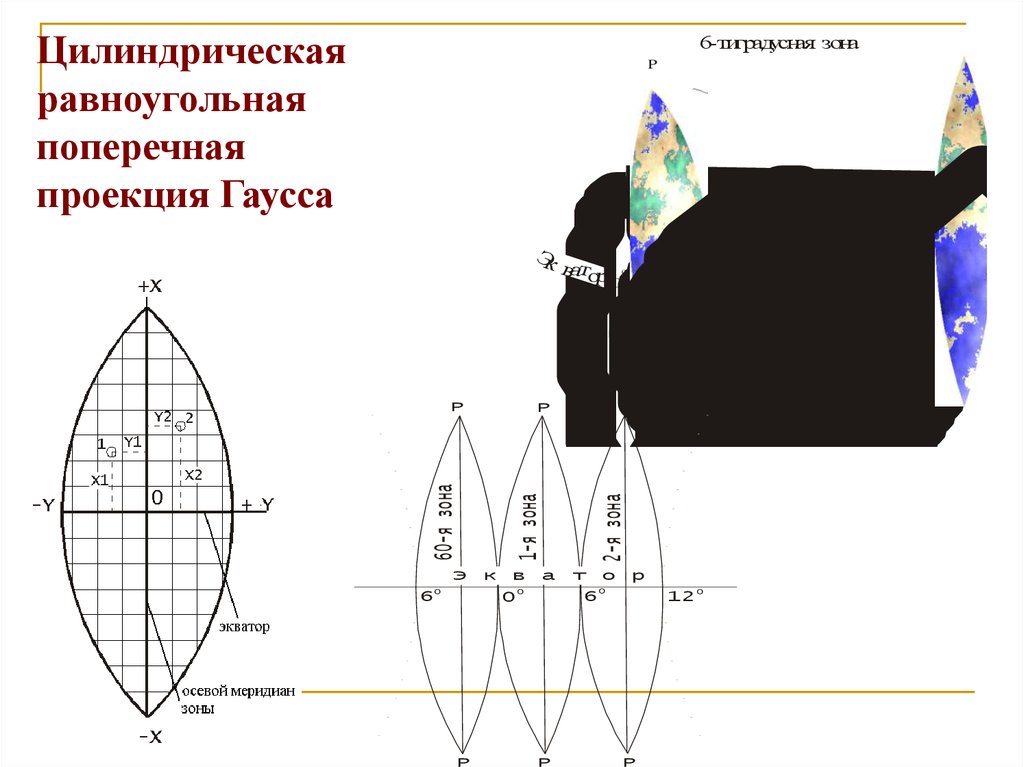
Цилиндрическаяравноугольная
поперечная
проекция Гаусса
6-тиградусная зона
P
Эк
ват
ор 0
P
P
6
к
в
0
P
P
P
Осевой
меридиан
2-я зона
1-я зона
60-я зона
Э
0
0
6
0
а
0
P
т о
0
6
р
12
P
0
72.
а)б)
+X
+X
Y2
Y2 2
1
X1
-Y
Y1
Y1
X2
0
1
X1
+Y
0
-X
-X
2
X2
+Y
73.
ианд
и
р
е
м
меридиа
н
5-я
Зона
6- я
й
Осево
Осевой
Зо на
0
24
0
27
300
33
0
36 0
74.
X = 6065540 мY = 4 308 620 м
ΔX
ΔY
75.
0 40 0
1
6
01
2
08
м
2
0
0
q
1
0
0
3
0
0
2
0
0
4
0
0
q
a
a b
N
b
a3
a2
a1
M
2
0
2
4
0
2
4
10
8
6
4
2
0
2
6
3q
2q
q
b3
b2
b1
0
76. Ориентирование линий
Ориентировать линию найти ее направлениеотносительно какого-либо
другого направления,
принимаемого за исходное
(известное) направление.
Для этого необходимо
определить значение
горизонтального угла между
исходным и определяемым
направлениями.
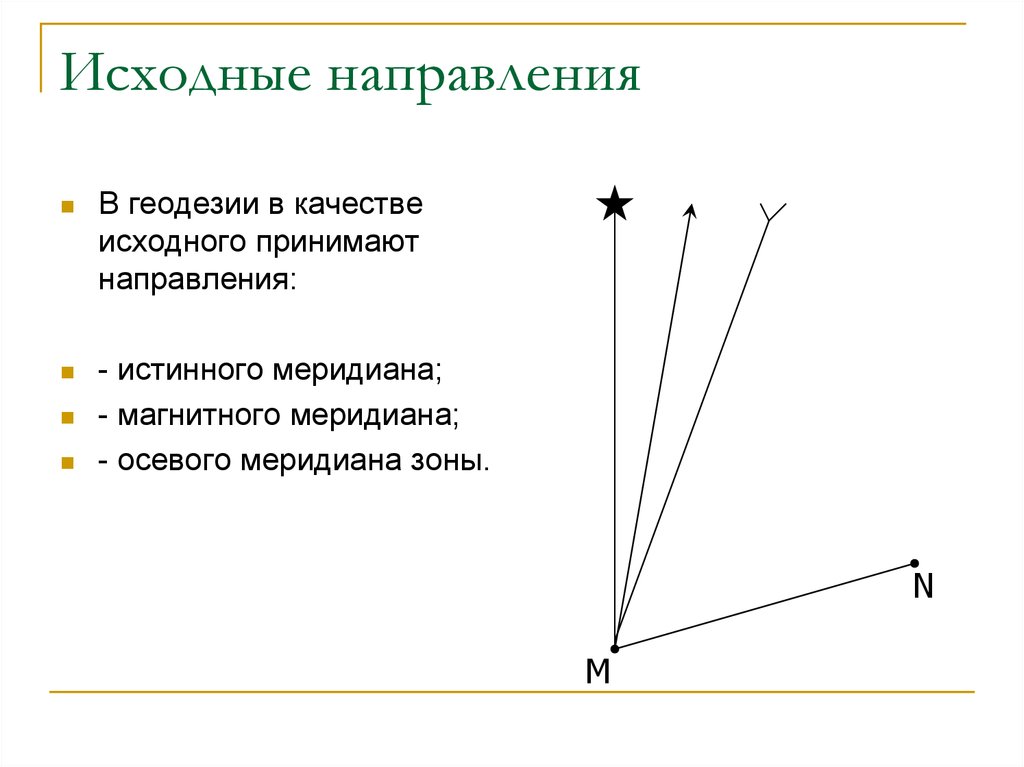
77. Исходные направления
В геодезии в качествеисходного принимают
направления:
- истинного меридиана;
- магнитного меридиана;
- осевого меридиана зоны.
N
M
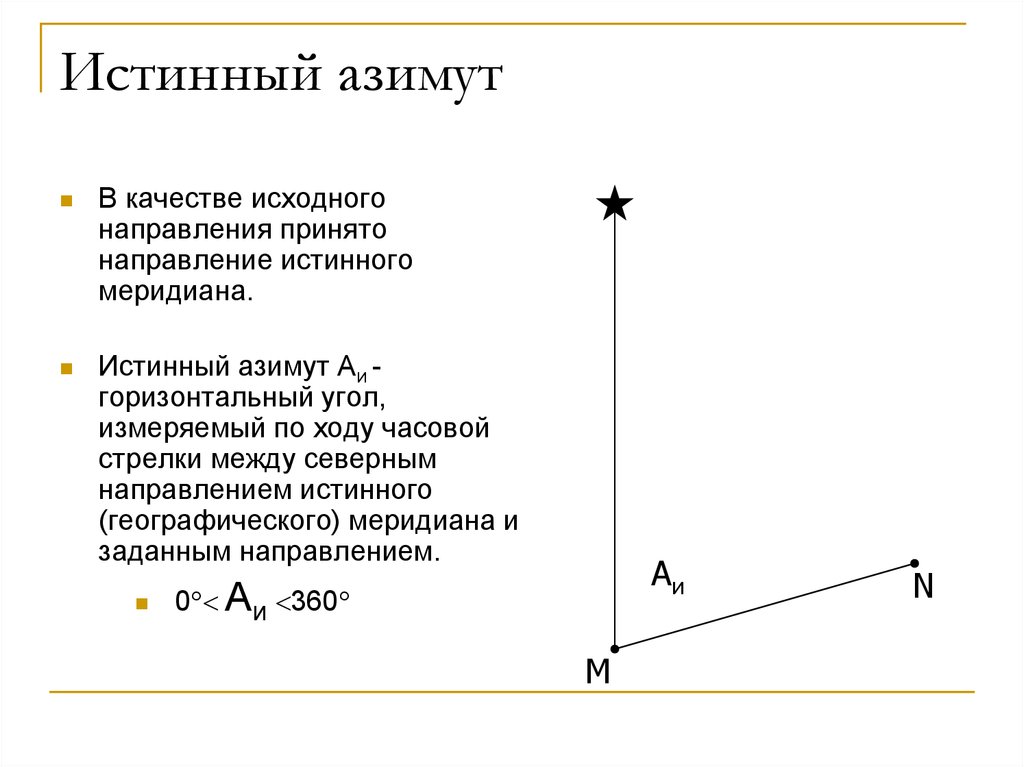
78. Истинный азимут
В качестве исходногонаправления принято
направление истинного
меридиана.
Истинный азимут Аи горизонтальный угол,
измеряемый по ходу часовой
стрелки между северным
направлением истинного
(географического) меридиана и
заданным направлением.
Аи
0 Аи 360
M
N
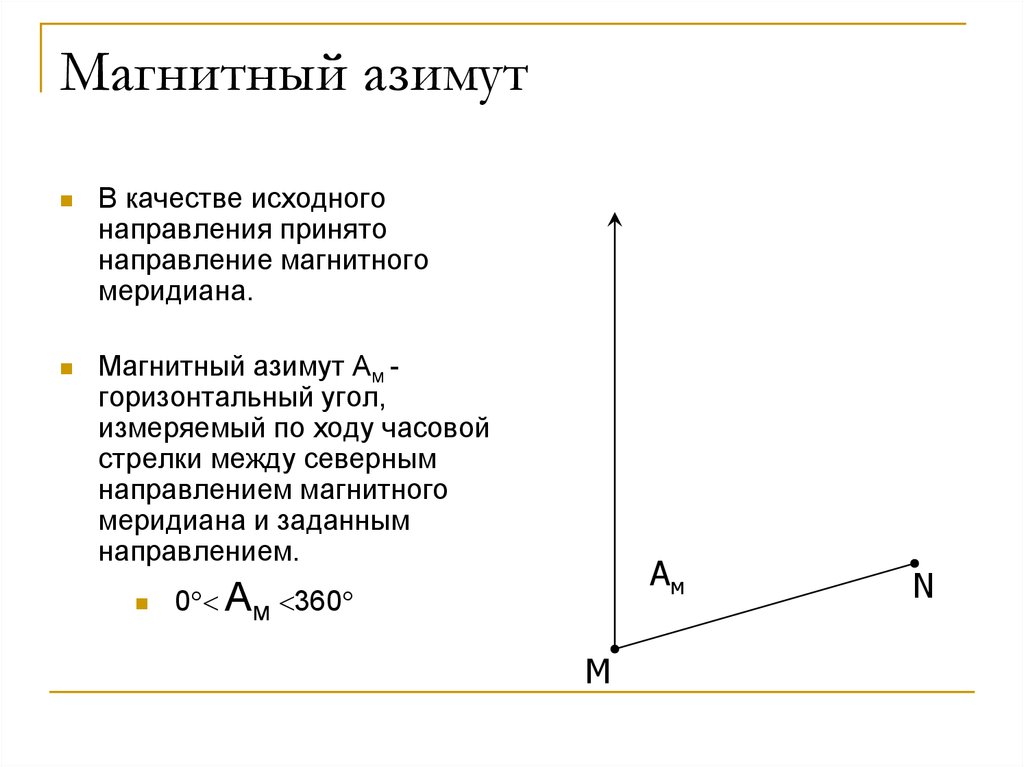
79. Магнитный азимут
В качестве исходногонаправления принято
направление магнитного
меридиана.
Магнитный азимут Ам горизонтальный угол,
измеряемый по ходу часовой
стрелки между северным
направлением магнитного
меридиана и заданным
направлением.
Ам
0 Ам 360
M
N
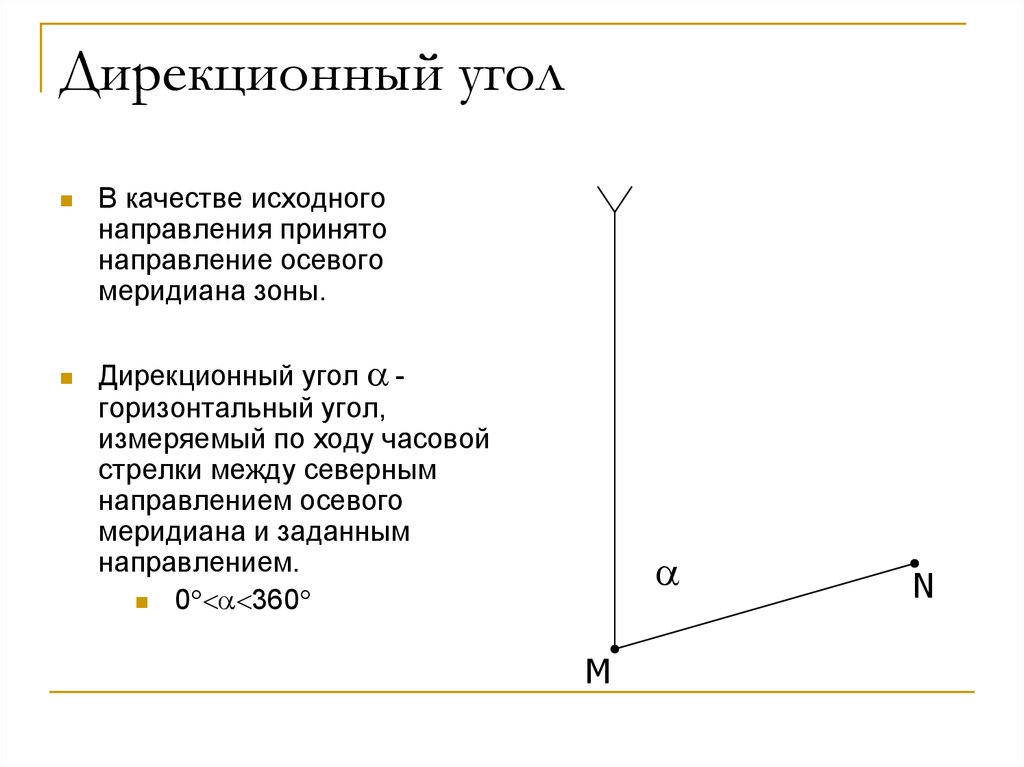
80. Дирекционный угол
В качестве исходногонаправления принято
направление осевого
меридиана зоны.
Дирекционный угол горизонтальный угол,
измеряемый по ходу часовой
стрелки между северным
направлением осевого
меридиана и заданным
направлением.
0 360
M
N
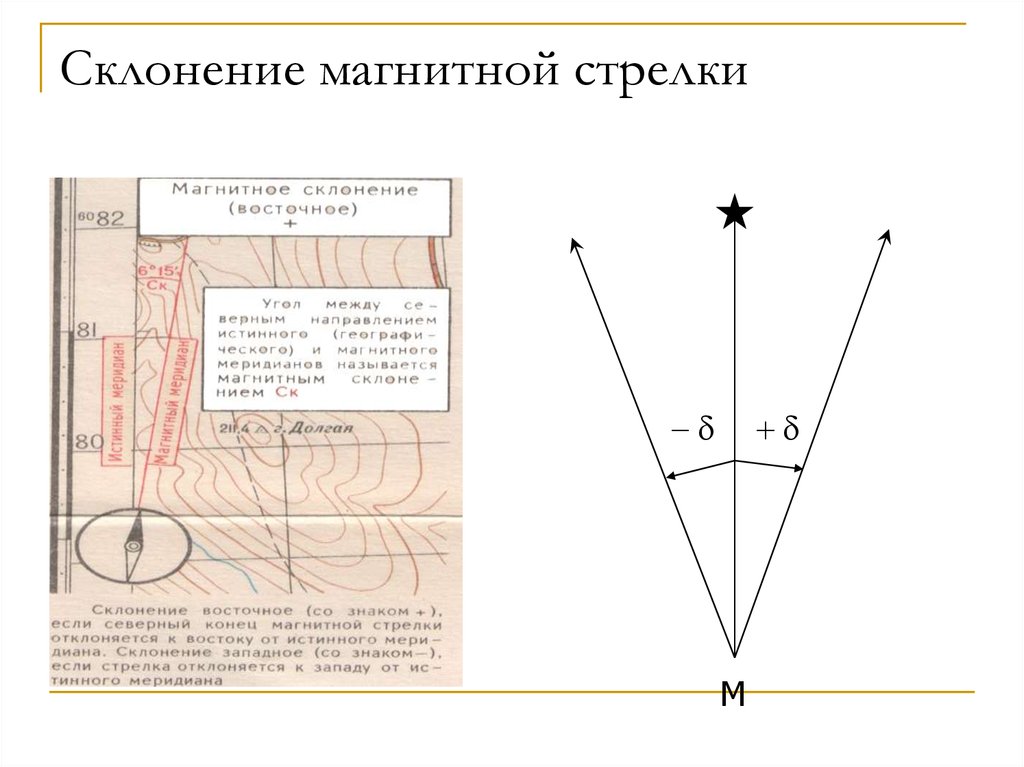
81. Склонение магнитной стрелки
+M
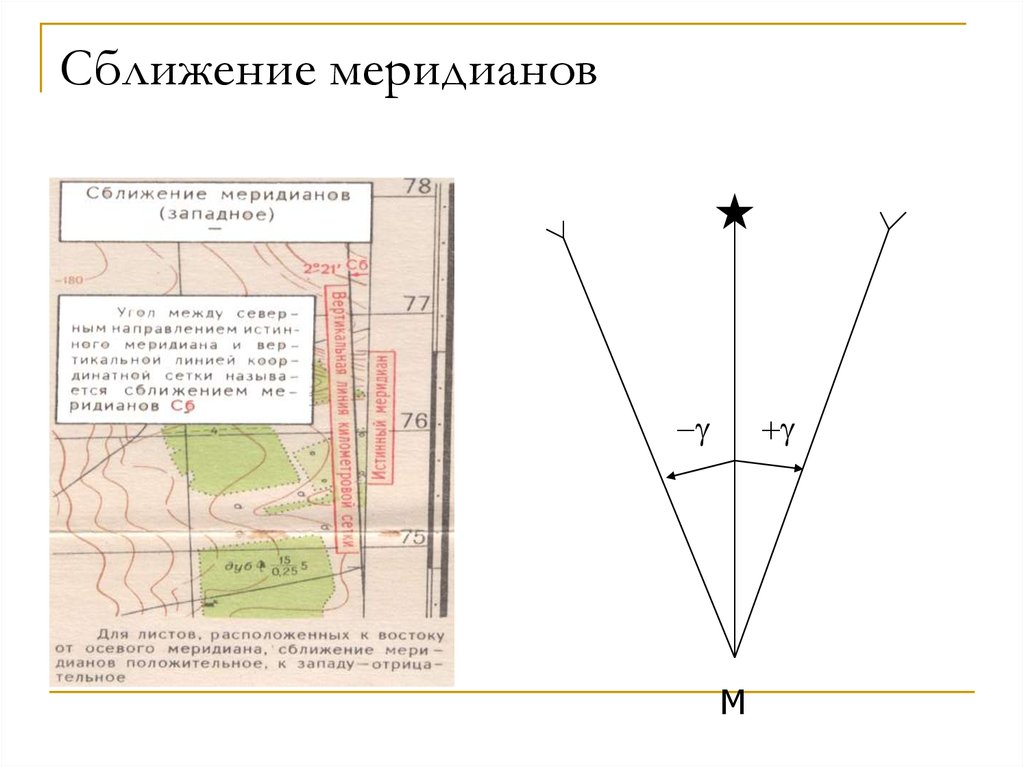
82. Сближение меридианов
+M
83. Исходные направления на карте
84.
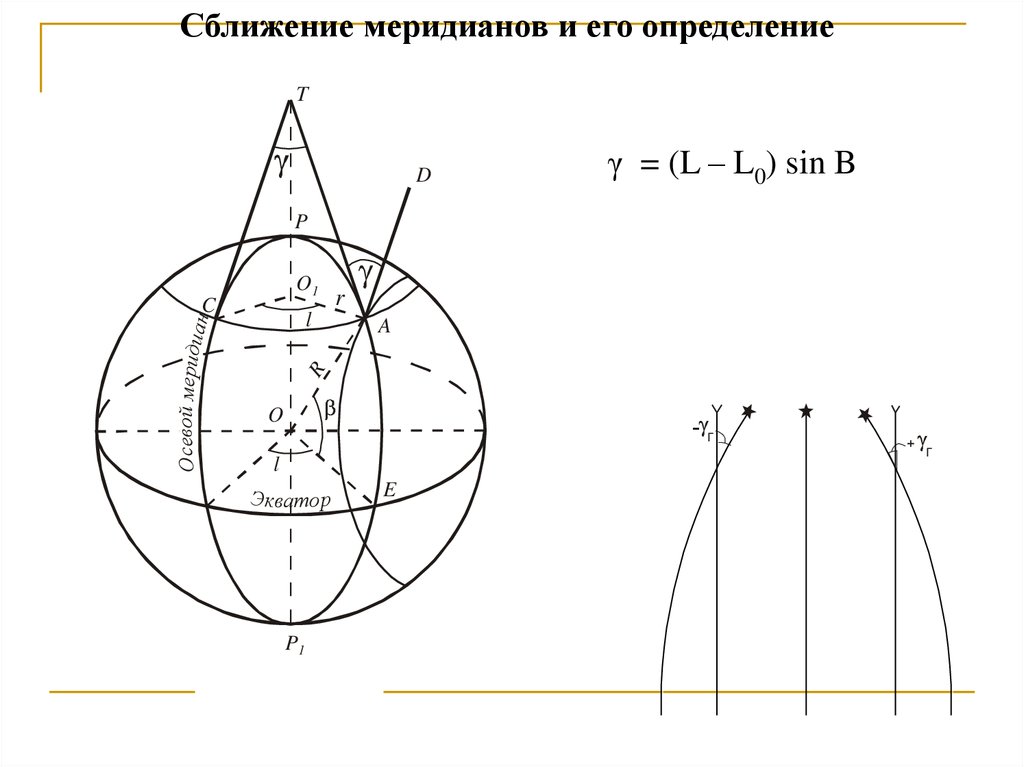
Сближение меридианов и его определениеT
D
γ = (L – L0) sin B
P
O1
C
l
A
R
н
Осевой мериди а
r
O
-
l
Экватор
P1
Рис. 11
E
Г
+ Г
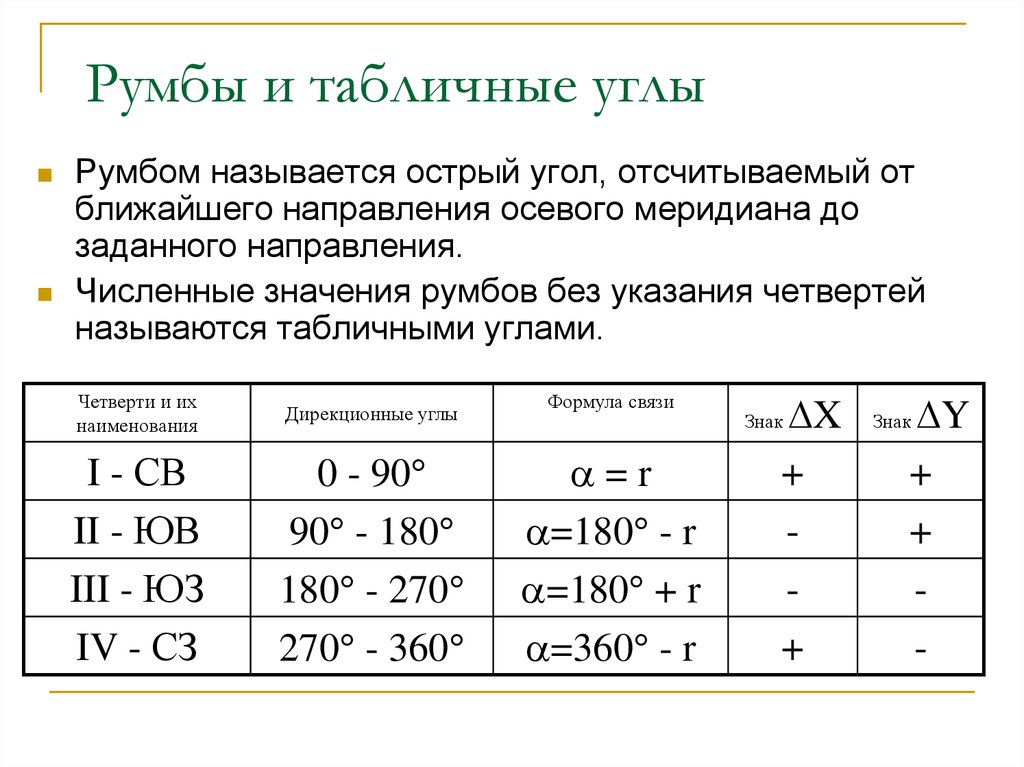
85. Румбы и табличные углы
Румбом называется острый угол, отсчитываемый отближайшего направления осевого меридиана до
заданного направления.
Численные значения румбов без указания четвертей
называются табличными углами.
Четверти и их
наименования
Дирекционные углы
I - СВ
II - ЮВ
III - ЮЗ
IV - СЗ
0 - 90
90 - 180
180 - 270
270 - 360
Формула связи
=r
=180 - r
=180 + r
=360 - r
X
+
+
Знак
Y
+
+
-
Знак
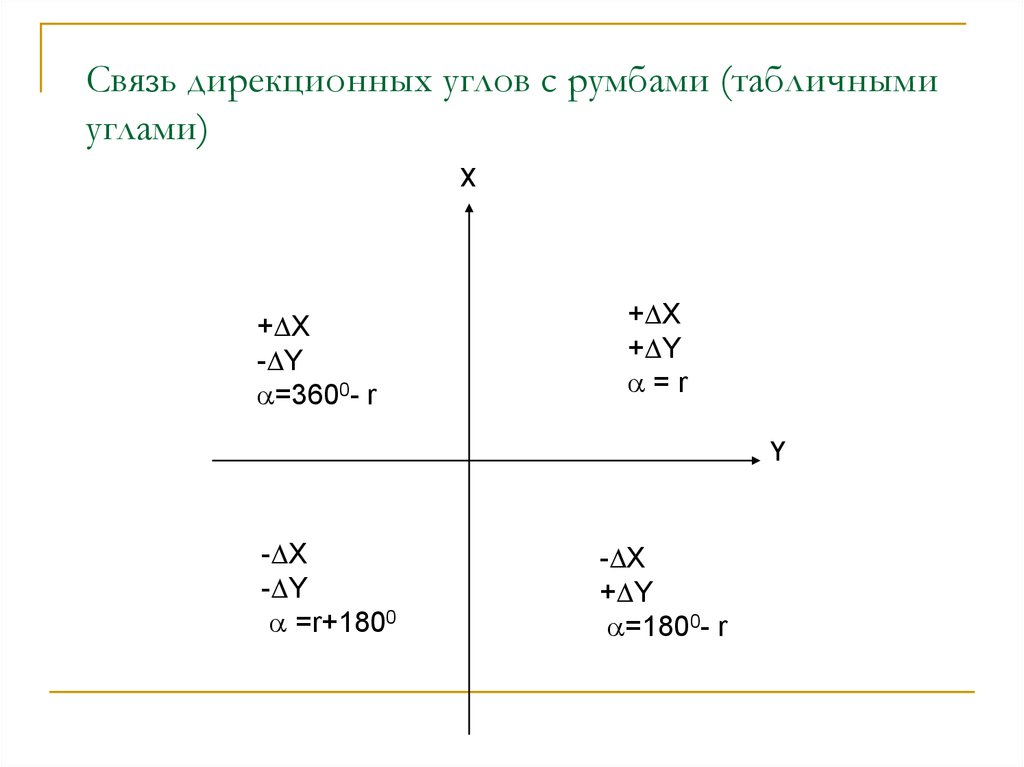
86. Связь дирекционных углов с румбами (табличными углами)
X+ X
- Y
=3600- r
+ X
+ Y
=r
Y
- X
- Y
=r+1800
- X
+ Y
=1800- r
87. Маршрут по карте
88.
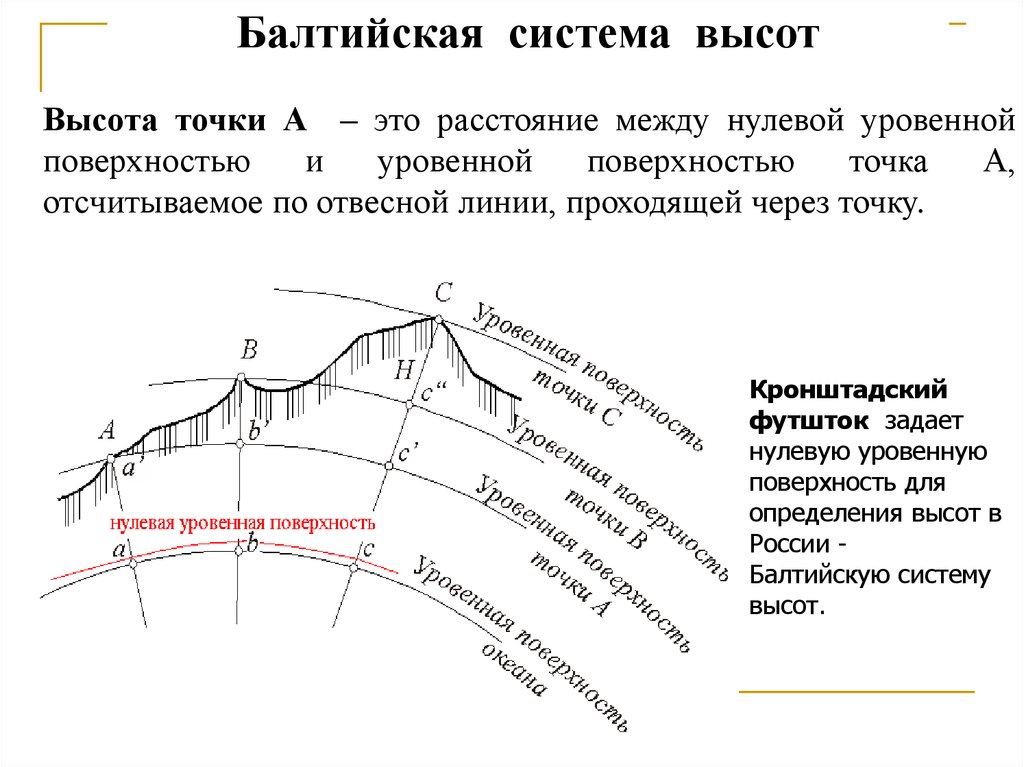
Балтийская система высотВысота точки А – это расстояние между нулевой уровенной
поверхностью
и
уровенной
поверхностью
точка
А,
отсчитываемое по отвесной линии, проходящей через точку.
Кронштадский
футшток задает
нулевую уровенную
поверхность для
определения высот в
России Балтийскую систему
высот.
89.
90.
91.
92. Эллипсоид, геоид
H = ортометрическая высотаh = геодезическая (эллипсоидальная) высота
N = аномалия высоты
H
Топографическая
(физическая)
поверхность
h
A
Эллипсоид
Геоид
H
=h-N
N
Аномалия
высоты
B
93.
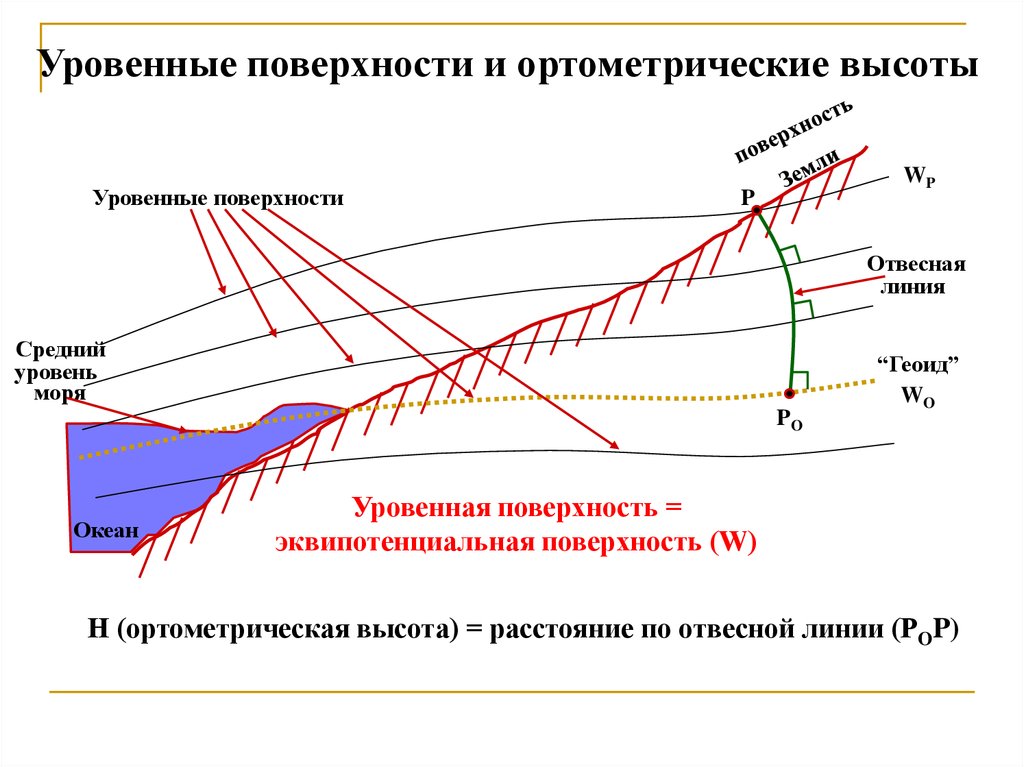
Уровенные поверхности и ортометрические высотыУровенные поверхности
WP
P
Отвесная
линия
Средний
уровень
моря
PO
Океан
“Геоид”
WO
Уровенная поверхность =
эквипотенциальная поверхность (W)
H (ортометрическая высота) = расстояние по отвесной линии (POP)
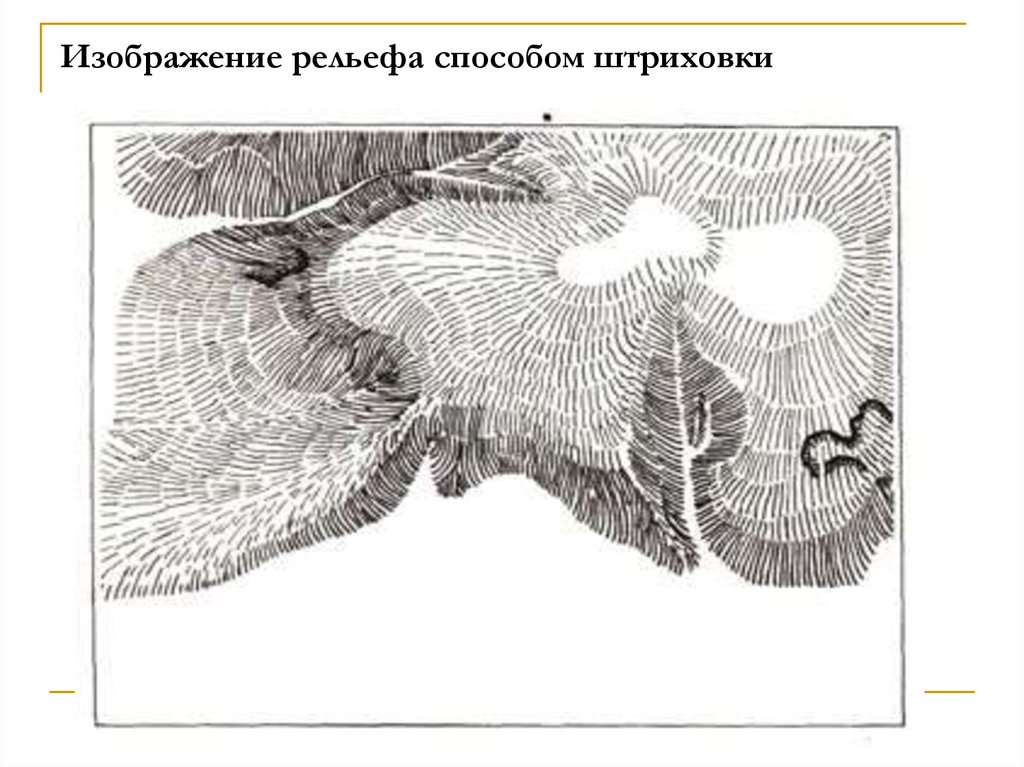
94. Изображение рельефа способом штриховки
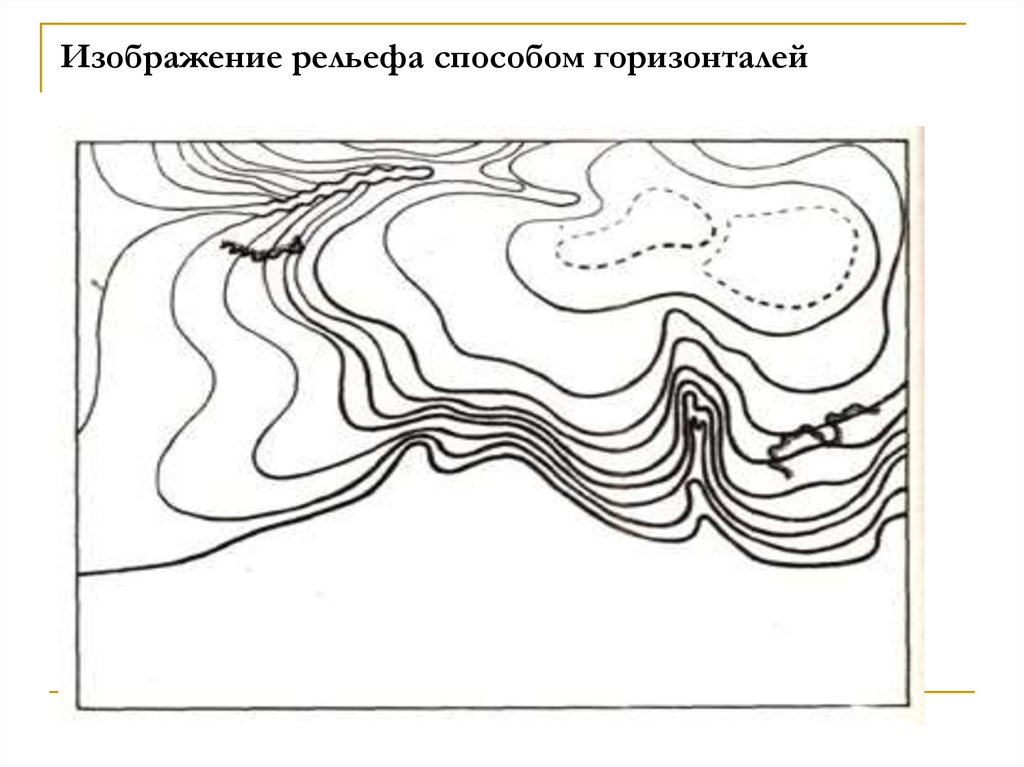
95. Изображение рельефа способом горизонталей
96.
97.
98.
водоразделтальвег
A
99.
167.2Секущие
плоскости
a
ат
Ск
d
b
Карта
150
d
h=5 м
Горизонтали
I
II
10
0
2
0
3
4
0
50
h







































































 География
География








