Похожие презентации:
Дискриминантный анализ
1. ДИСКРИМИНАНТНЫЙ АНАЛИЗ
Cтат. методы впсихологии
(Радчикова Н.П.)
Trisha Klass Illinois State University
2. Цели
В каких случаях применяетсядискриминантный анализ
Как применить дискриминантный анализ
Как интерпретировать результаты
дискриминантного анализа
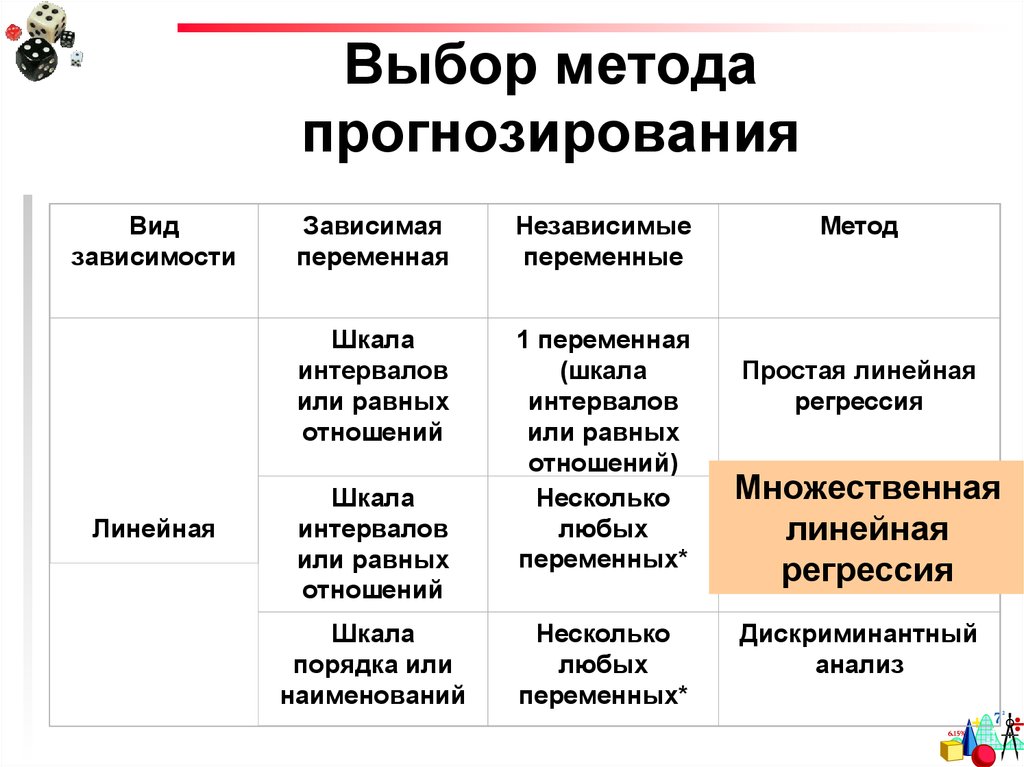
3. Выбор метода прогнозирования
Видзависимости
Линейная
Зависимая
переменная
Независимые
переменные
Шкала
интервалов
или равных
отношений
1 переменная
(шкала
интервалов
или равных
отношений)
Несколько
любых
переменных*
Шкала
интервалов
или равных
отношений
Шкала
порядка или
наименований
Несколько
любых
переменных*
Метод
Простая линейная
регрессия
Множественная
линейная
регрессия
Дискриминантный
анализ
4. Выбор метода прогнозирования
Видзависимости
Линейная
Зависимая
переменная
Независимые
переменные
Шкала
интервалов
или равных
отношений
1 переменная
(шкала
интервалов
или равных
отношений)
Несколько
любых
переменных*
Шкала
интервалов
или равных
отношений
Шкала
порядка или
наименований
Несколько
любых
переменных*
Метод
Простая
Простая линейная
линейная
регрессия
регрессия
Множественная
линейная
регрессия
Дискриминантный
анализ
5. Выбор метода прогнозирования
Видзависимости
Линейная
Зависимая
переменная
Независимые
переменные
Шкала
интервалов
или равных
отношений
1 переменная
(шкала
интервалов
или равных
отношений)
Несколько
любых
переменных*
Шкала
интервалов
или равных
отношений
Шкала
порядка или
наименований
Несколько
любых
переменных*
Метод
Простая линейная
регрессия
Множественная
Множественная
линейная
линейная
регрессия
регрессия
Дискриминантный
анализ
6. Выбор метода прогнозирования
Видзависимости
Линейная
Зависимая
переменная
Независимые
переменные
Шкала
интервалов
или равных
отношений
1 переменная
(шкала
интервалов
или равных
отношений)
Несколько
любых
переменных*
Шкала
интервалов
или равных
отношений
Шкала
порядка или
наименований
Несколько
любых
переменных*
Метод
Простая линейная
регрессия
Множественная
линейная
регрессия
Дискри-
Дискриминантный
минантный
анализ
анализ
7. Шкалы наименований
Мы уже знаем, что можно использоватьдихотомические шкалы.
А что делать, если попалась шкала
наименований?
Не спешите расстраиваться! Надо ее
просто перекодировать!
8. Дискриминантный анализ
Альтернатива множественногорегрессионного анализа для случая,
когда зависимая переменная
качественная (категориальная).
9. Дискриминантный анализ
Основная цель:Выявление структуры исследуемого
множества объектов
(структура – набор основных
факторов (шкал), по которым
различаются и могут быть описаны
объекты)
10. Основная задача
По значениям дискриминантныхпеременных для объектов получить
значения классифицирующей
переменной, то есть определить
классы, в которые попадают эти
объекты.
11. Основная задача
На основании некоторых признаков(независимых переменных) объект или
индивидуум может быть причислен к
одной из двух (или к одной из
нескольких) заранее заданных групп.
12. Ограничения
В случае дискриминантного анализапредполагается, что
• зависимая переменная одна и
представлена в шкале наименований
• независимых переменных несколько
13. Представление данных
группаХ1
Х2
…
Гр1
23
2,5
123
Гр1
21
1,7
131
…
…
…
Гр2
24
1,5
148
Гр2
21
2,1
133
…
…
…
…
…
Х34
…
…
14. Основная идея
Дискриминантная функцияz=b1 x1+b2 x2+b3 x3+…+bn xn+b0
15. Основная идея
Наша цель:Определить коэффициенты b,
чтобы по значениям
дискриминантной функции можно
было с максимальной четкостью
провести разделение по группам.
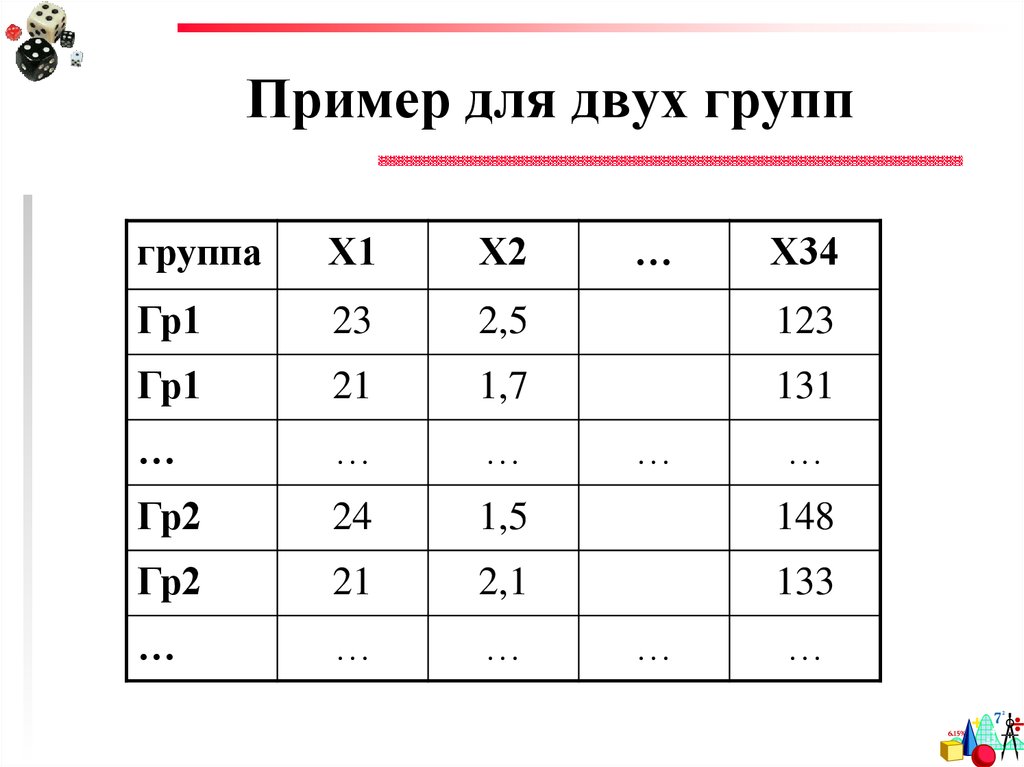
16. Пример для двух групп
группаХ1
Х2
…
Гр1
23
2,5
123
Гр1
21
1,7
131
…
…
…
Гр2
24
1,5
148
Гр2
21
2,1
133
…
…
…
…
…
Х34
…
…
17. Основная идея
Строим дискриминантную функциюz=b1 x1+b2 x2+b3 x3+…+bn xn+b0,
такую, что разница между средними
значениями z1 и z2, полученными на
множествах значений НП для разных
групп максимальна.
18. Основная идея
z1 - z2 максимумФишер показал, что
b=S-1 (x1-x2),
где S – ковариационная матрица
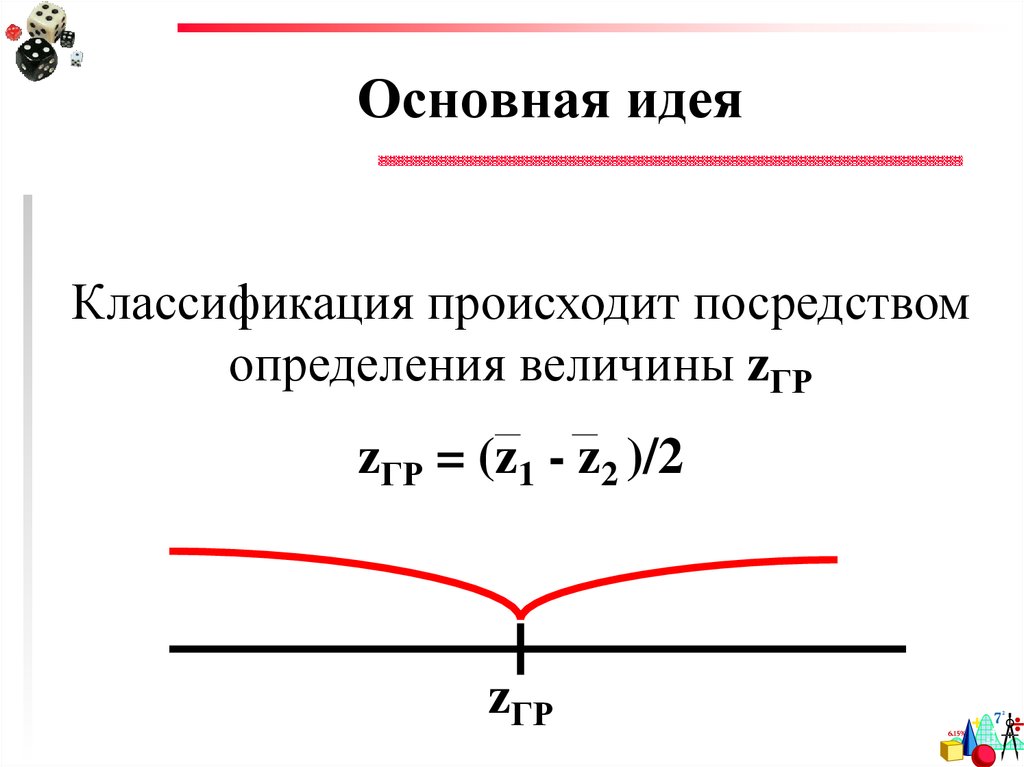
19. Основная идея
Классификация происходит посредствомопределения величины zГР
zГР = (z1 - z2 )/2
zГР
20. Основная идея
Предположив, что z1 – большее их двухсредних, получаем правило:
Случай относится к группе 1, если zi - zГР >0
Случай относится к группе 2, если zi - zГР 0
21. Основная идея
z1 и z2 называются центроидамигрупп
22. Пример для двух групп
ДанныеGENDER – пол испытуемого;
EDUC – образование испытуемого
(количество лет, которые бедняга потратил на
учебу);
JCAT – вид профессиональной деятельности
(1 – клерк, 2- охранник, 3 – менеджер);
SALARY – зарплата в настоящий момент;
23. Пример для двух групп
ДанныеSAL_BEG – начальная зарплата на этой
работе;
JTIME – трудовой стаж на данном рабочем
месте (число месяцев);
PREVEX – предыдущий опыт – стаж до
поступления на данную работу;
MINORITY – принадлежит ли испытуемый к
национальному меньшинству (0 – нет, 1 – да).
24. Пример для двух групп
Попробуем предсказать,принадлежит ли человек к
национальному меньшинству на
основании его зарплаты и
образования
25. Пример для двух групп
•Что мы получим в результатеприменения дискриминантного
анализа?
•Как это интерпретировать?
26. Модуль дискриминантного анализа
Discriminant AnalysisStatistics
Multivariate Exploratory Techniques
Discriminant Analysis
27. Модуль дискриминантного анализа
28. Модуль дискриминантного анализа
29. Модуль дискриминантного анализа
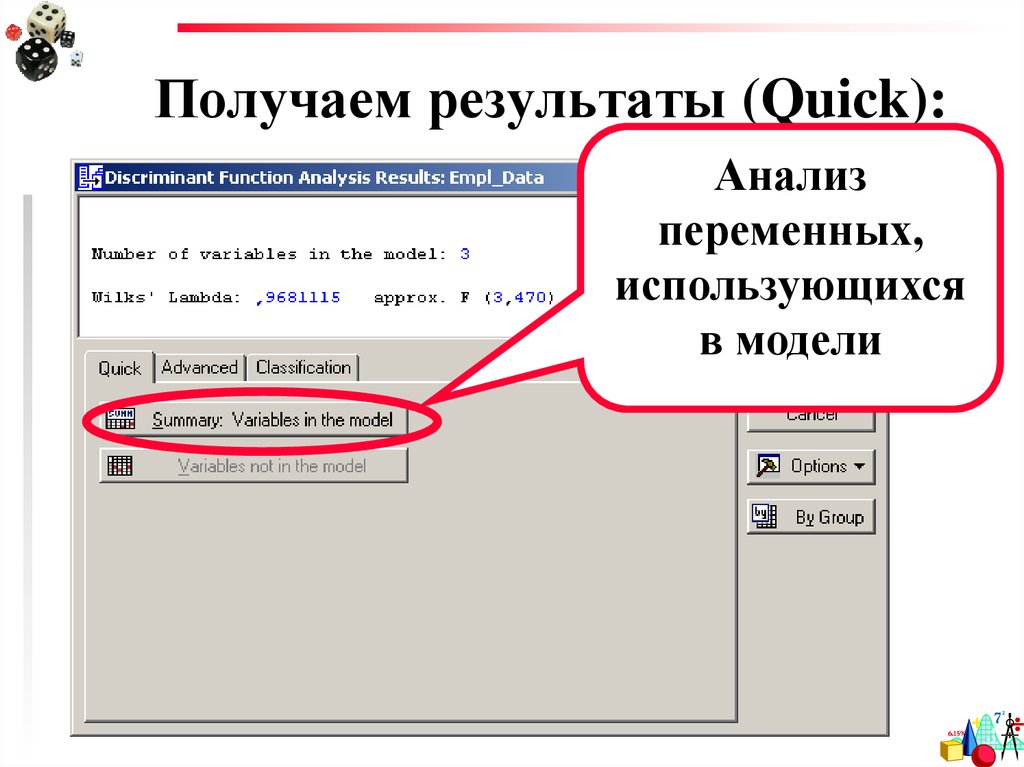
30. Получаем результаты (Quick):
Анализпеременных,
использующихся
в модели
31. Variables in the Model:
Лямбда Уилкса длямодели с исключенной
данной переменной.
Изменяется от 0
(совершенное
различение) до 1
(никакого различия)
32. Variables in the Model:
Эта лямбда связанас вкладом данной
переменной в
различительную
силу модели
33. Variables in the Model:
Статистикадисперсионного
анализа,
показывающая вклад
данной переменной в
общее «дело»
различения групп.
34. Variables in the Model:
Толерантность– измеряет
избыточность
данной
переменной.
Толерантность 0,34 означает, что
переменная на 66% объясняет то, что и
другие переменные модели
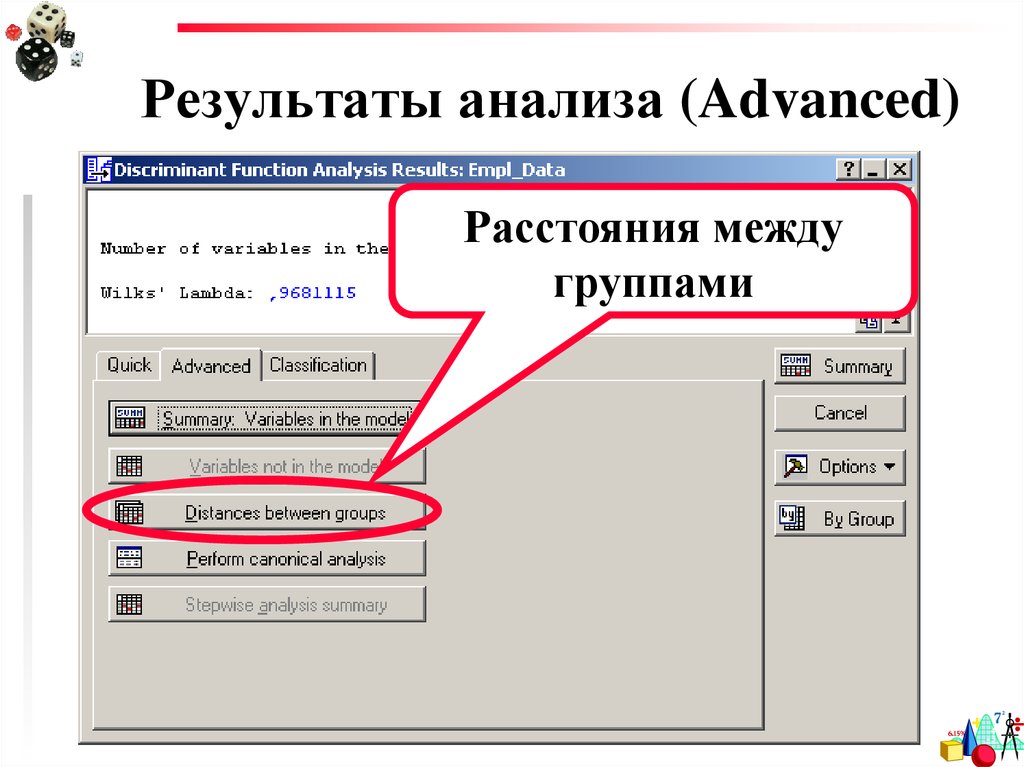
35. Результаты анализа (Advanced)
Расстояния междугруппами
36. Distances between groups
Расстояние Махаланобисамежду группами
37. Distances between groups
Значение дисперсионного анализа исоответствующий уровень значимости для
оценки расстояния между группами
38. Результаты анализа (Advanced)
Канонический анализи графики
39. Canonical Analysis:
40. Canonical Analysis (Advanced):
41. Canonical Analysis (Advanced):
Коэффициентыдискриминантной
функции
42. Canonical Analysis (Advanced):
z=0,043*educ+0,044*salary++0,030*sal_beg-2,605
43. Canonical Analysis (Advanced):
z=0,124*educ+0,720*salary++0,230*sal_beg
44. Canonical Analysis (Advanced):
45. Canonical Analysis (Advanced):
Корреляция переменных сдискриминантной фукцией
46. Canonical Analysis (Advanced):
Центроиды групп(ненормированные)
47. Canonical Analysis (Advanced):
zГР=(0,096-0,342)/248. Пример для двух групп
zГР=(0,096-0,342)/2 = -0,123цветной
белый
-0,123
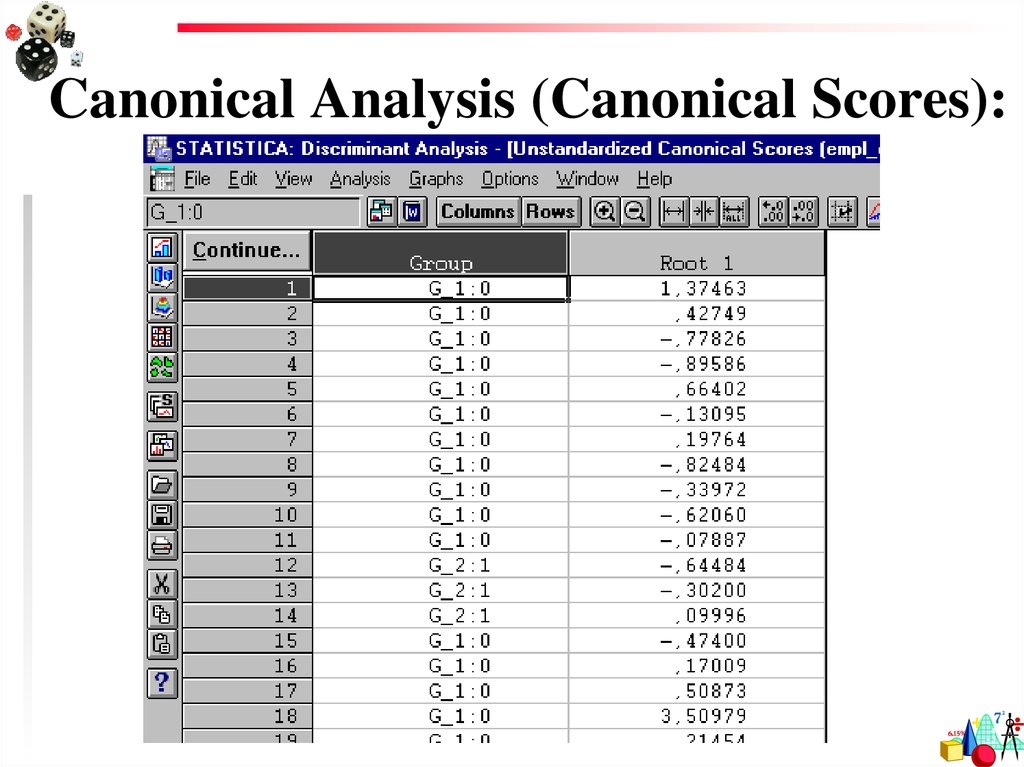
49. Canonical Analysis (Canonical Scores):
Значениядискриминантной
функции для каждого
случая
50. Canonical Analysis (Canonical Scores):
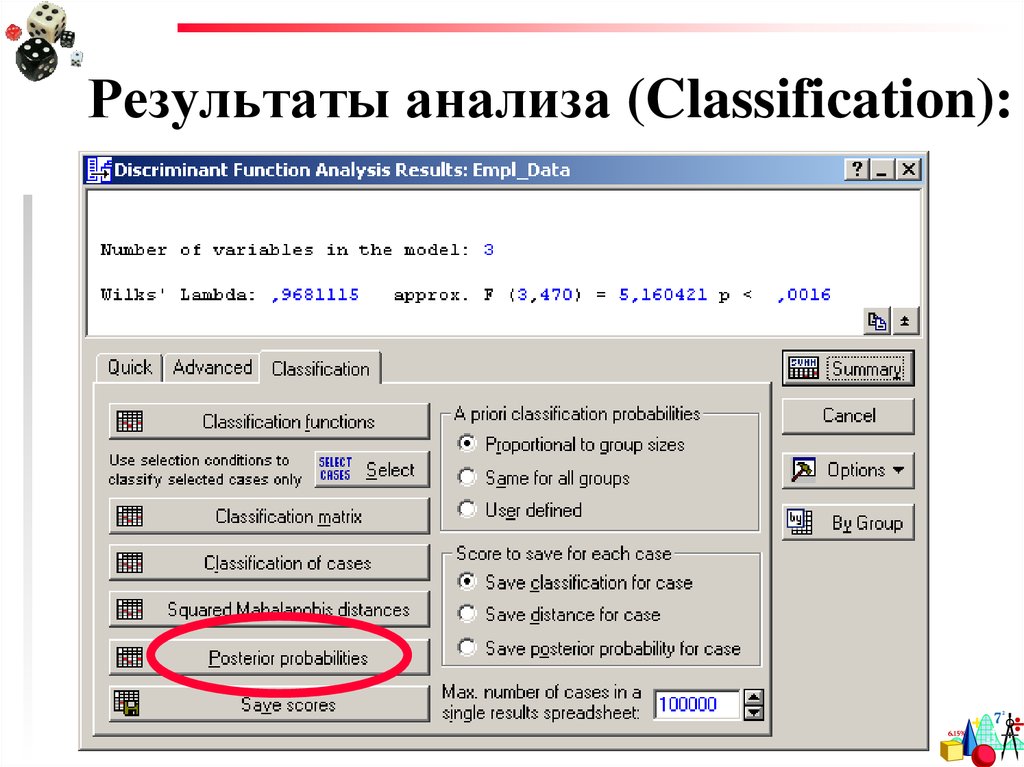
51. Результаты анализа (Classification):
Функцииклассификации
52. Результаты анализа (Classification):
Значения этих функций вычисляются длякаждой группы и служат для прямой
классификации. Случай попадает в группу,
для которой у него получается наибольшее
значение
53. Результаты анализа(Classification):
Априорные вероятности попасть к даннуюгруппу (по умолчанию вычисляются исходя
из размеров группы)
54. Результаты анализа:
Это очень полезнаяматрица!
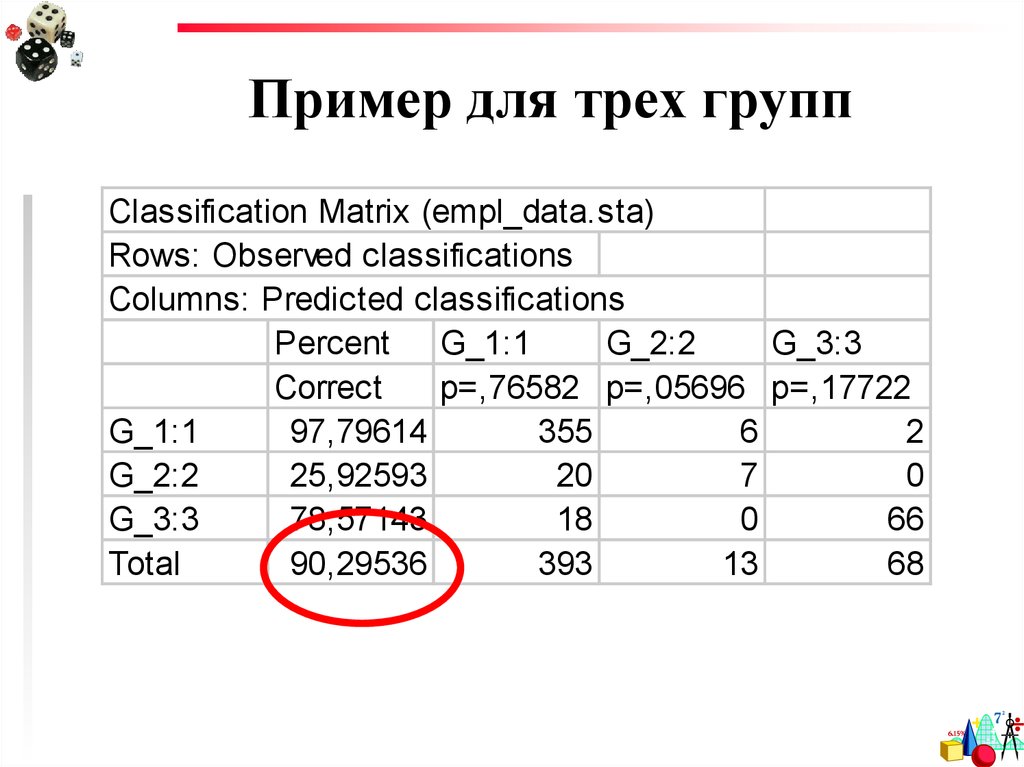
55. Результаты анализа (Classification):
Очень важный показатель! Процентправильно предсказанных значений
56. Результаты анализа (Classification):
57. Результаты анализа (Classification):
58. Результаты анализа (Classification):
59. Пример для двух групп
60. Пример для трех групп
Посмотрим, можем ли мыпредсказать, на какой должности
работает человек по его зарплате,
образованию и принадлежности к
национальному меньшинству.
61. Пример для трех групп
В этом случае однойдискриминантной функцией не
обойдешься!
Их будет две.
62. Пример для трех групп
Группа 3Группа 2
Группа 1
63. Пример для трех групп
Classification Matrix (empl_data.sta)Rows: Observed classifications
Columns: Predicted classifications
Percent G_1:1
G_2:2
G_3:3
Correct
p=,76582 p=,05696 p=,17722
G_1:1
97,79614
355
6
2
G_2:2
25,92593
20
7
0
G_3:3
78,57143
18
0
66
Total
90,29536
393
13
68
64. Пример для трех групп
Discriminant Function Analysis Summary (empl_data.sta)No. of vars in model: 4; Grouping: JCAT (3 grps)
Wilks' Lambda: ,25680 approx. F (8,936)=113,88 p<0,0000
Wilks'
Partial
F-remove
Lambda Lambda (2,468)
p-level
Toler.
EDUC
0,290012 0,885496 30,25871 4,38E-13 0,805286
SALARY 0,324602 0,791136 61,77707 1,55E-24 0,731865
SAL_BEG 0,299848 0,85645 39,22078 1,79E-16 0,765182
MINORITY 0,264071 0,972483 6,62129 0,00146 0,996228
1-Toler.
(R-Sqr.)
0,194714
0,268135
0,234818
0,003772
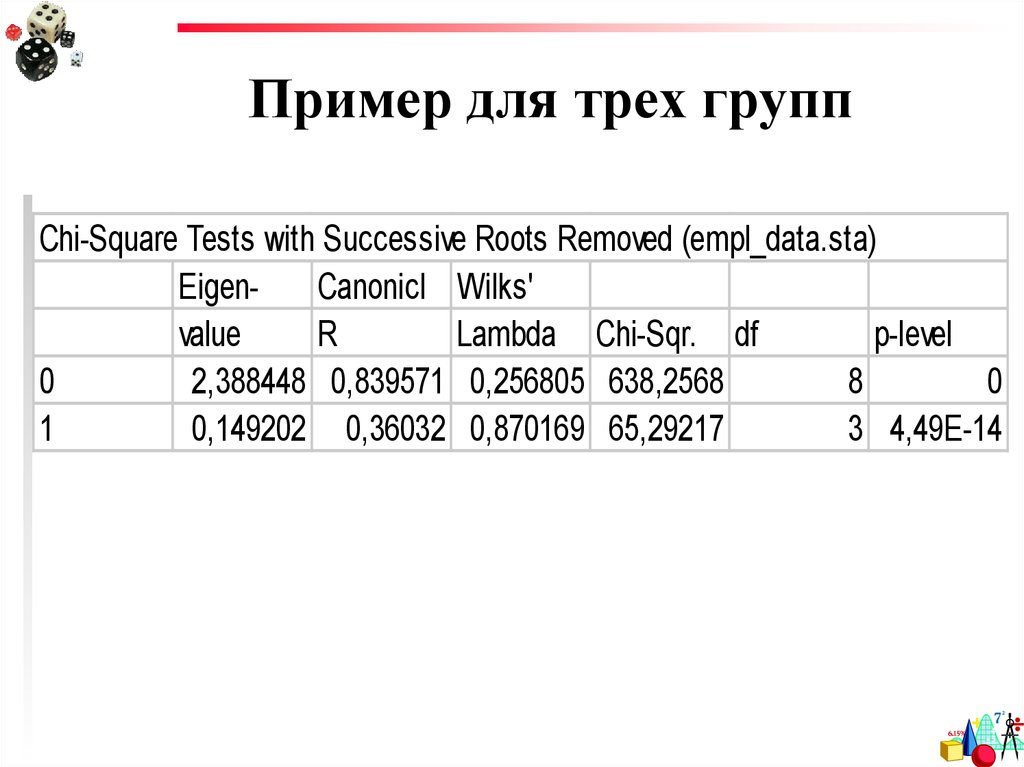
65. Пример для трех групп
Chi-Square Tests with Successive Roots Removed (empl_data.sta)EigenCanonicl Wilks'
value
R
Lambda Chi-Sqr. df
p-level
0
2,388448 0,839571 0,256805 638,2568
8
0
1
0,149202 0,36032 0,870169 65,29217
3 4,49E-14
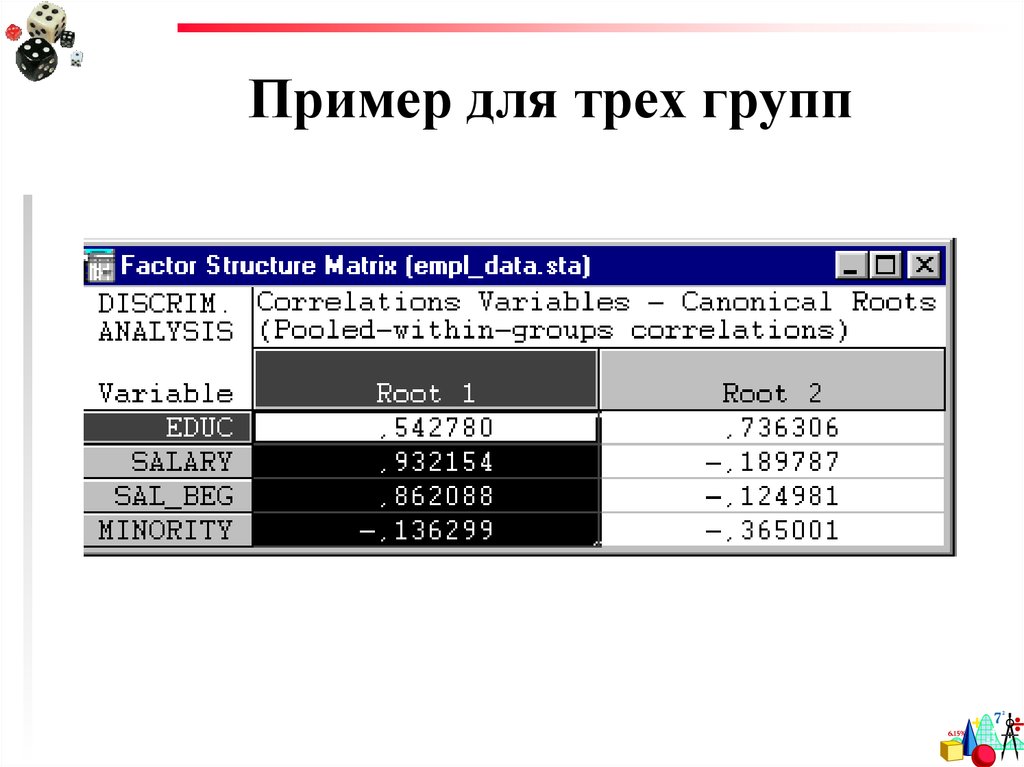
66. Пример для трех групп
67. Пример для трех групп
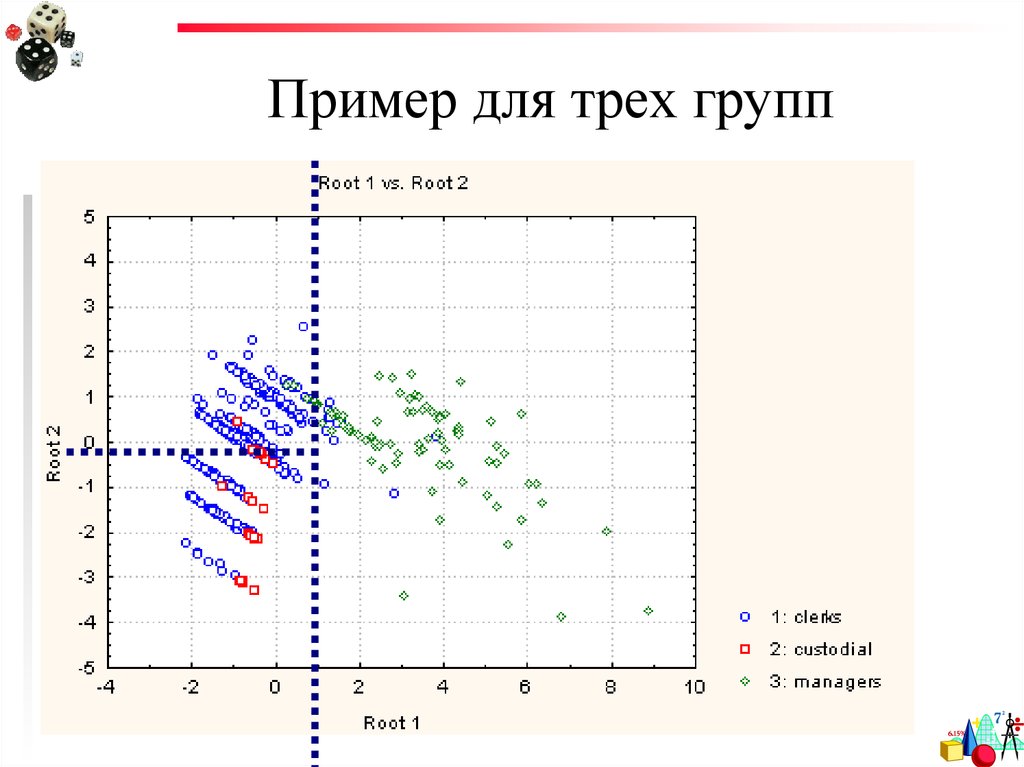
Теперь можно посмотретькрасивый график
68. Пример для трех групп
69. Пример для трех групп
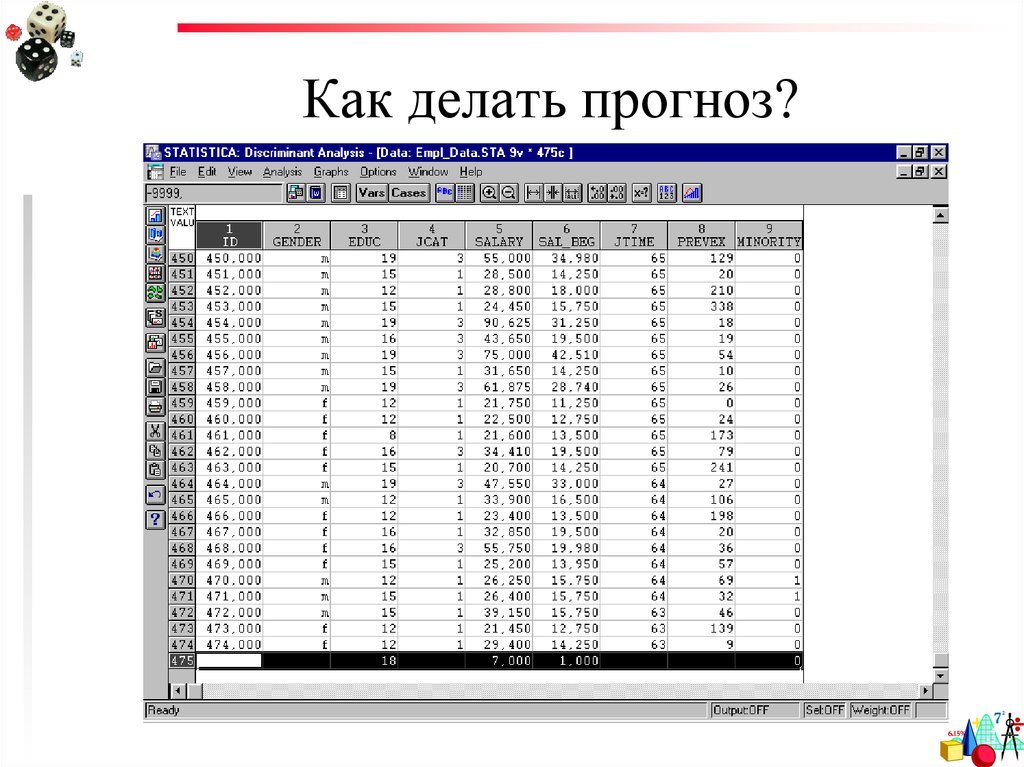
70. Результаты анализа
Мы можем1) оценить, насколько НП определяют ЗП
(т.е оценить нашу модель)
2) делать предсказания (по значениям НП
определять, в какую группу попадет
объект или индивид)
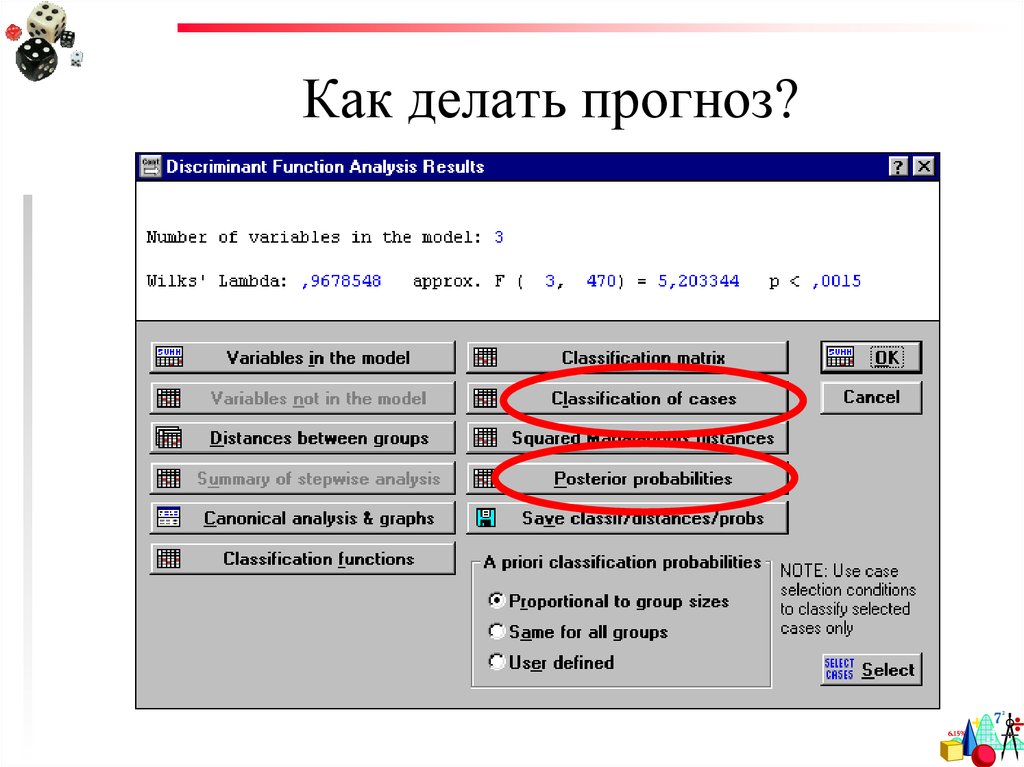
71. Как делать прогноз?
72. Как делать прогноз?
73. Как делать прогноз?
74. Пример (реальный)
Проект: Можно ли предсказать типпреступника (насильственный,
корыстный или корыстнонасильственный) по результатам
тестов Кеттела и ЛеонгардаШмишека?
75. Пример
1) дискриминантный анализ по всемпеременным.
2) прямой пошаговый дискриминантный
анализ.
Получились совершенно потрясающие
результаты:
76. Пример (результаты)
77. Пример (результаты)
Chi-Square Tests with Successive Roots Removed (issled.sta)Eigen-
Canonicl Wilks'
value
R
Lambda Chi-Sqr. df
0 19,02697 0,974714 0,003411 96,57309
1 13,63901 0,965241 0,068311 45,62273
p-level
42
20
0
0,00091
78. Пример (результаты –гм!)
Standardized Coefficients (issled.sta)for Canonical Variables
Correlations Variables - Canonical Roots
Factor Structure Matrix (issled.sta)
(Pooled-within-groups correlations)
F3
A
F4
H
EKZ
F
Root 1
0,11
0,08
-0,11
0,08
-0,02
0
Root 2
0,19
0,21
0,07
0,13
-0,01
0,02
Q3
0,04
0
Q1
0,01
0,11
TREV
DEM
VOZB
O
PED
MD
ZASTR
N
B
M
L
EMOT
CIKL
0,03
0,06
0,03
-0,03
0,03
0,05
0
0,05
0,03
-0,11
0,04
-0,04
0
-0,03
0,08
-0,08
0,07
0,01
-0,08
0
0,11
-0,01
0,01
-0,03
-0,02
0,01
F3
A
F4
H
EKZ
F
Q3
Q1
TREV
DEM
VOZB
O
PED
MD
ZASTR
N
B
M
L
EMOT
CIKL
Root 1
0,47
-1
-1,34
3,88
1,04
0,12
-1,33
0,75
1,94
-0,63
-0,46
-3,32
-5,26
6,32
3,09
4,6
0,69
-3,13
-1,7
2,29
-1,16
Root 2
0,27
2,96
2,94
0,31
-1,15
-1,02
1,64
-1,49
0,29
1,79
-1,06
1,82
-0,11
-0,85
-0,6
-1,4
-0,49
-0,14
0,79
-0,64
0,54
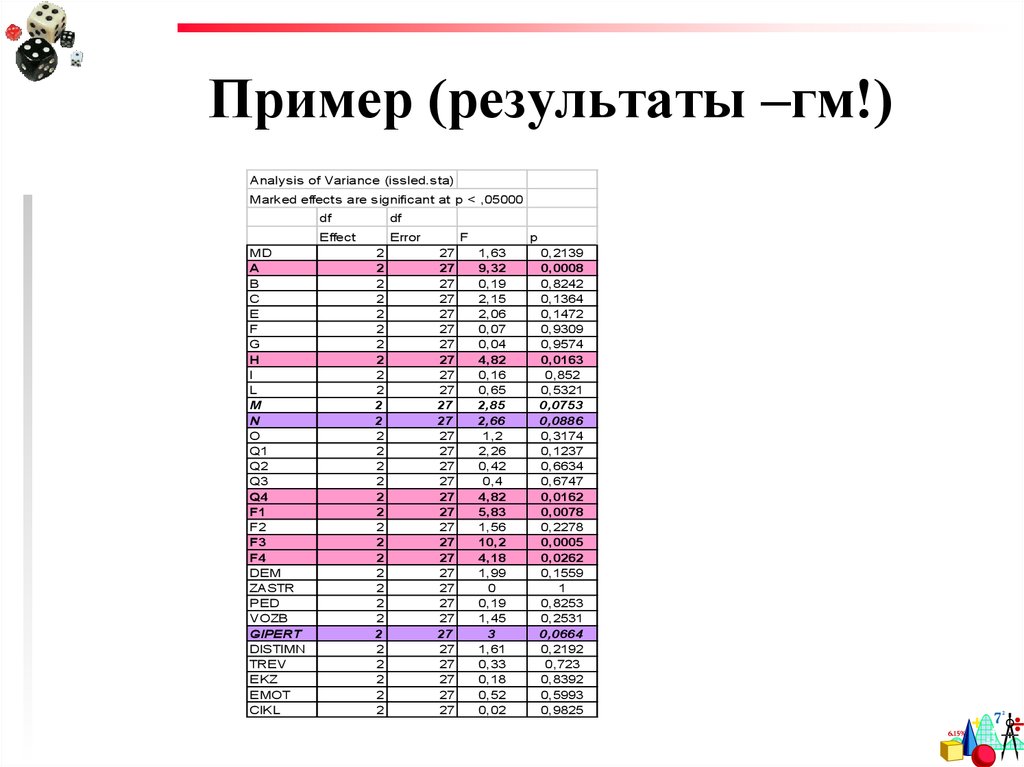
79. Пример (результаты –гм!)
Analysis of Variance (issled.sta)Marked effects are significant at p < ,05000
df
df
Effect
MD
A
B
C
E
F
G
H
I
L
M
N
O
Q1
Q2
Q3
Q4
F1
F2
F3
F4
DEM
ZASTR
PED
VOZB
GIPERT
DISTIMN
TREV
EKZ
EMOT
CIKL
Error
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
F
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
27
p
1,63
9,32
0,19
2,15
2,06
0,07
0,04
4,82
0,16
0,65
2,85
2,66
1,2
2,26
0,42
0,4
4,82
5,83
1,56
10,2
4,18
1,99
0
0,19
1,45
3
1,61
0,33
0,18
0,52
0,02
0,2139
0,0008
0,8242
0,1364
0,1472
0,9309
0,9574
0,0163
0,852
0,5321
0,0753
0,0886
0,3174
0,1237
0,6634
0,6747
0,0162
0,0078
0,2278
0,0005
0,0262
0,1559
1
0,8253
0,2531
0,0664
0,2192
0,723
0,8392
0,5993
0,9825
80. Пример (результаты –гм!)
81. Пример (результаты –гм!)
Classification Matrix (issled.sta)Rows: Observed classifications
Columns: Predicted classifications
kn
n
k
Total
Percent
kn
Correct
p=,33333 p=,33333 p=,33333
6
3
1
1
9
0
0
2
8
7
14
9
60
90
80
76,66666
n
k
82. Пример
Classification Matrix (issled.sta)Rows: Observed classifications
Columns: Predicted classifications
kn
n
k
Total
Percent
kn
Correct
p=,33333 p=,33333 p=,33333
8
1
1
1
9
0
0
1
9
9
11
10
80
90
90
86,66666
n
k
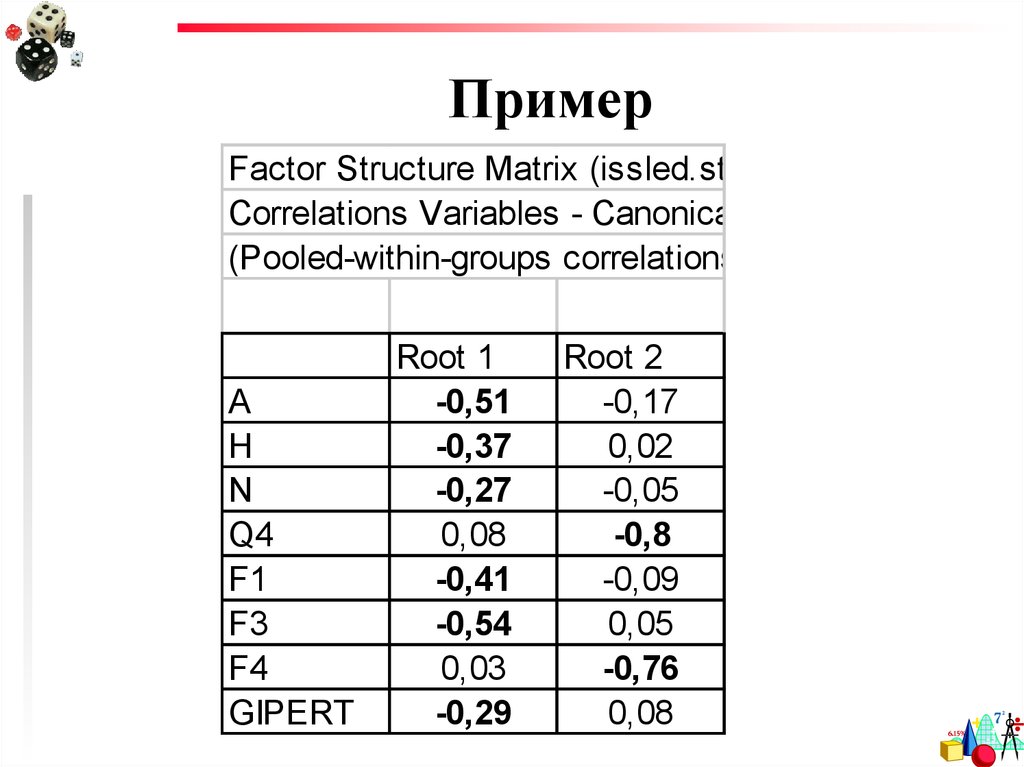
83. Пример
Factor Structure Matrix (issled.sta)Correlations Variables - Canonical Roots
(Pooled-within-groups correlations)
A
H
N
Q4
F1
F3
F4
GIPERT
Root 1
-0,51
-0,37
-0,27
0,08
-0,41
-0,54
0,03
-0,29
Root 2
-0,17
0,02
-0,05
-0,8
-0,09
0,05
-0,76
0,08
84. Полезная литература
ПРОГРАММА STATISTICAБоровиков В. Программа STATISTICA для студентов и
инженеров. - Компьютер Пресс: Москва, 2001.
Электронный учебник по программе (StatSoft)
ПРОГРАММА SPSS
Наследов А.Д. Математические методы психологического
исследования. Анализ и интерпретация данных. – СПб. –
Речь. – 2004.
Бююль А., Цефель П. SPSS: Искусство обработки
информации. – СПб, «ЛиаСофтЮп». –2001.
85.
К практическому занятию по регрессионному анализунадо прочитать:
•Нестеренко А.И. и др. Прогноз тревожности
у студенток на основании их типологических
различий// ПЖ, 2003, т.24, № 6, с. 37-46
86. Дискриминантный анализ
СПАСИБОЗА ВНИМАНИЕ!







































































 Математика
Математика








