Похожие презентации:
Логические основы ЭВМ
1. ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ
Лабораторная работаLOGO
2. Основные термины и понятия
Логическое высказывание – это любое утверждение,относительно которого можно сказать истинно оно или
ложно, т.е. соответствует оно действительности или нет.
Логические переменные – переменные, которые
принимают только два значения –"истина" или
"ложь", обозначаемые, соответственно, "1" и "0".
www.themegallery.com
Company Name
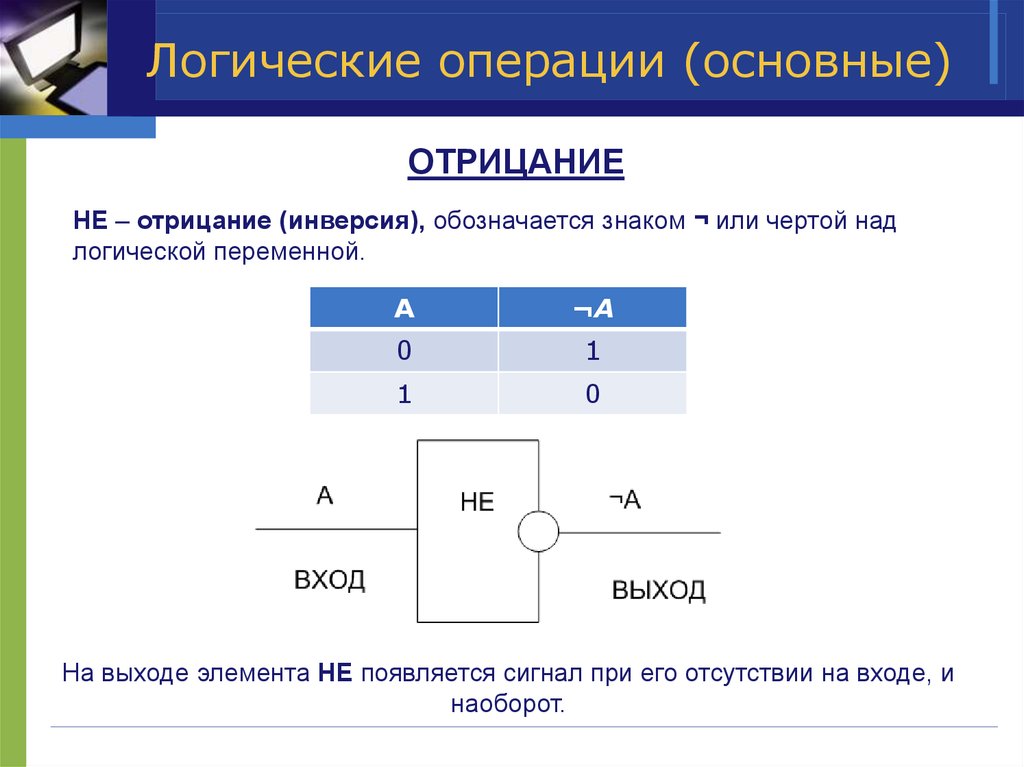
3. Логические операции (основные)
ОТРИЦАНИЕНЕ – отрицание (инверсия), обозначается знаком ¬ или чертой над
логической переменной.
A
¬A
0
1
1
0
На выходе элемента НЕ появляется сигнал при его отсутствии на входе, и
наоборот.
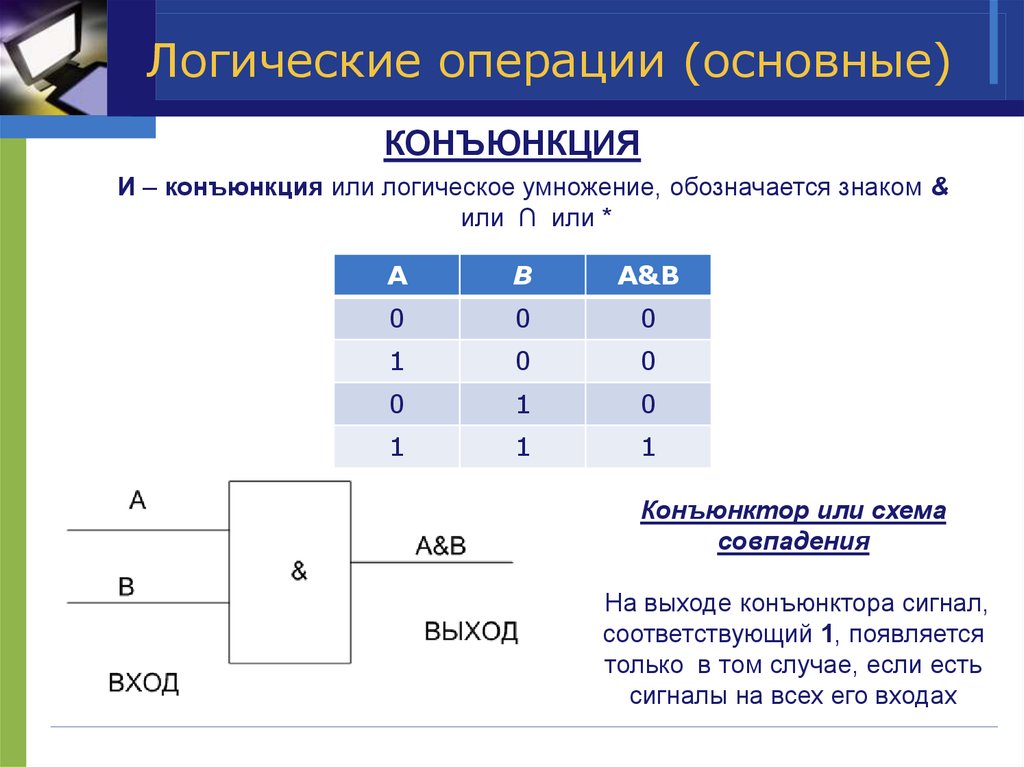
4. Логические операции (основные)
КОНЪЮНКЦИЯИ – конъюнкция или логическое умножение, обозначается знаком &
или ∩ или *
A
B
A&B
0
0
0
1
0
0
0
1
0
1
1
1
Конъюнктор или схема
совпадения
На выходе конъюнктора сигнал,
соответствующий 1, появляется
только в том случае, если есть
сигналы на всех его входах
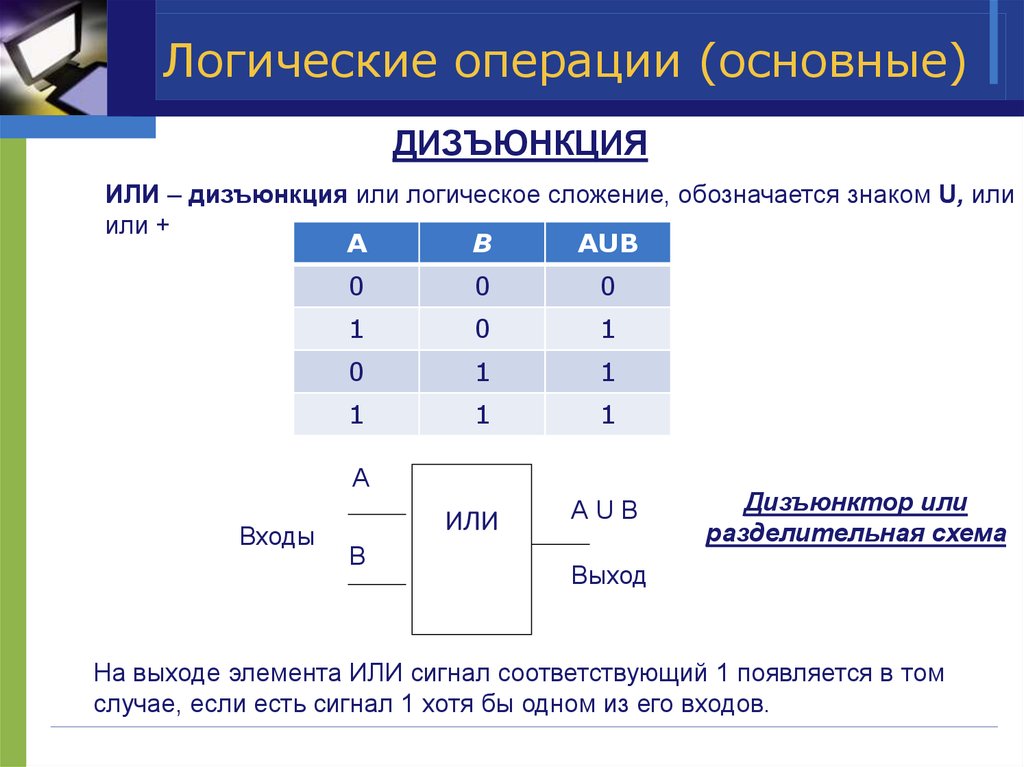
5. Логические операции (основные)
ДИЗЪЮНКЦИЯИЛИ – дизъюнкция или логическое сложение, обозначается знаком U, или
или +
A
B
AUB
0
0
0
1
0
1
0
1
1
1
1
1
А
Входы
ИЛИ
B
АUB
Дизъюнктор или
разделительная схема
Выход
На выходе элемента ИЛИ сигнал соответствующий 1 появляется в том
случае, если есть сигнал 1 хотя бы одном из его входов.
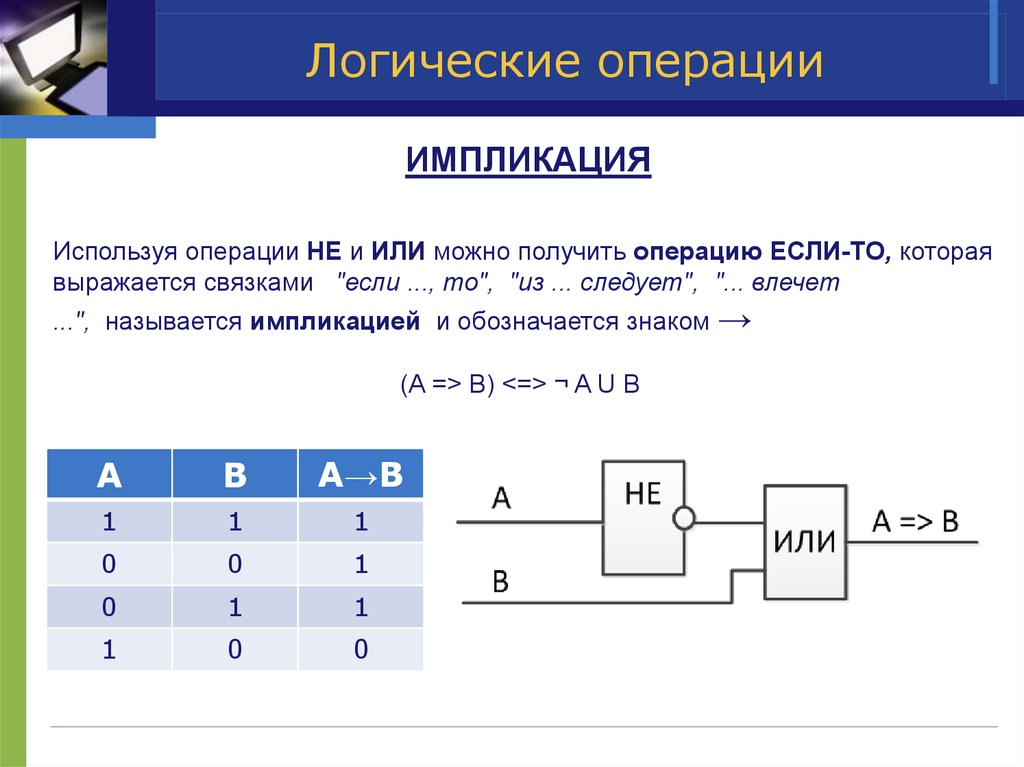
6. Логические операции
ИМПЛИКАЦИЯИспользуя операции НЕ и ИЛИ можно получить операцию ЕСЛИ-ТО, которая
выражается связками "если ..., то", "из ... следует", "... влечет
...", называется импликацией и обозначается знаком →
(A => B) <=> ¬ A U B
A
B
A→B
1
1
1
0
0
1
0
1
1
1
0
0
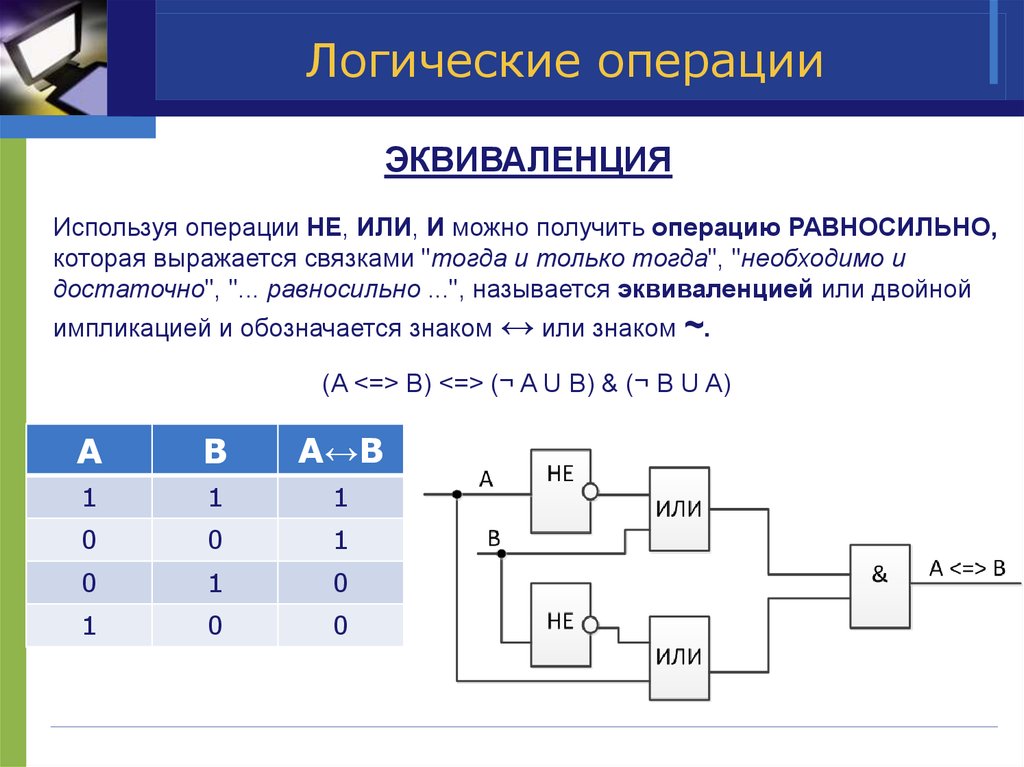
7. Логические операции
ЭКВИВАЛЕНЦИЯИспользуя операции НЕ, ИЛИ, И можно получить операцию РАВНОСИЛЬНО,
которая выражается связками "тогда и только тогда", "необходимо и
достаточно", "... равносильно ...", называется эквиваленцией или двойной
импликацией и обозначается знаком ↔ или знаком ~.
(A <=> B) <=> (¬ A U B) & (¬ B U A)
A
B
A↔B
1
1
1
0
0
1
0
1
0
1
0
0
8. Пример записи высказываний
"Быть иль не быть - вот в чем вопрос.«(В. Шекспир)
А U ¬ A <=> В
"Если хочешь быть красивым, поступи в гусары."
(К. Прутков)
А => В
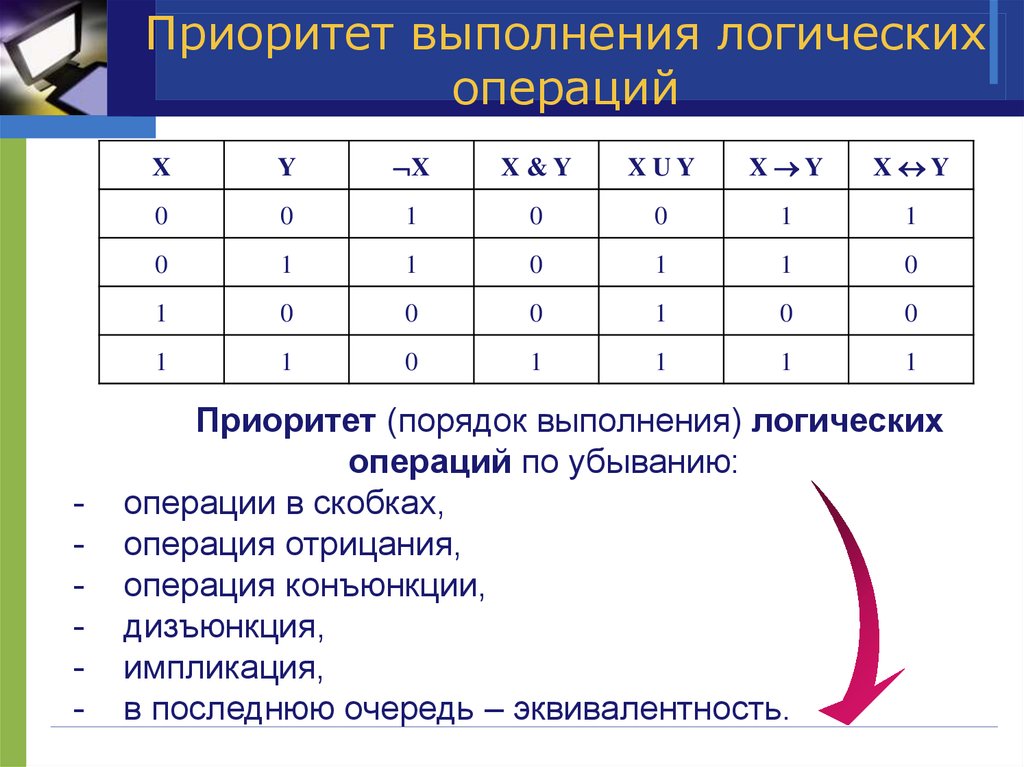
9. Приоритет выполнения логических операций
-X
Y
X
X&Y
XUY
X Y
X Y
0
0
1
0
0
1
1
0
1
1
0
1
1
0
1
0
0
0
1
0
0
1
1
0
1
1
1
1
Приоритет (порядок выполнения) логических
операций по убыванию:
операции в скобках,
операция отрицания,
операция конъюнкции,
дизъюнкция,
импликация,
в последнюю очередь – эквивалентность.
10. Таблицы истинности
Таблица истинности представляет собой таблицу,устанавливающую соответствие между всевозможными наборами
значений переменных и значениями функций.
Функция, которая принимает:
• значение "истина" для всех наборов значений переменных,
называется
тождественно
истинной
функцией
или
тавтологией;
• значение "ложь" для всех наборов значений переменных,
называется
тождественно
ложной
функцией
или
противоречием;
• для некоторых наборов значений переменных значение
"истина", а для других – значение "ложь", называется выполнимой
логической функцией.
Если две функции А и В при одинаковых наборах значений
входящих в них переменных, принимают одинаковые значения, то
они называются равносильными.
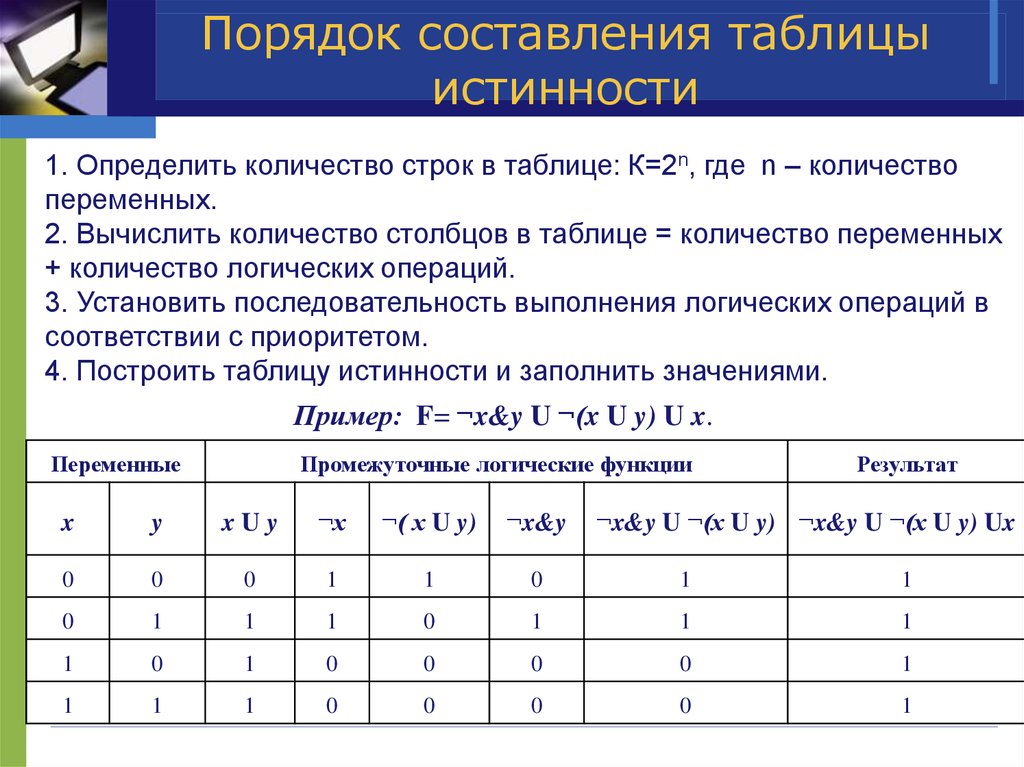
11. Порядок составления таблицы истинности
1. Определить количество строк в таблице: К=2n, где n – количествопеременных.
2. Вычислить количество столбцов в таблице = количество переменных
+ количество логических операций.
3. Установить последовательность выполнения логических операций в
соответствии с приоритетом.
4. Построить таблицу истинности и заполнить значениями.
Пример: F= ¬x&y U ¬(x U y) U x.
Переменные
Промежуточные логические функции
Результат
x
y
xUy
¬x
¬( x U y)
¬x&y
¬x&y U ¬(x U y) ¬x&y U ¬(x U y) Ux
0
0
0
1
1
0
1
1
0
1
1
1
0
1
1
1
1
0
1
0
0
0
0
1
1
1
1
0
0
0
0
1
12. Законы булевой алгебры (законы логики)
1. ¬¬ А <=> A закон двойного отрицания;2. A&B <=> B&A коммутативность конъюнкции;
3. AUB <=> BUA коммутативность дизъюнкции;
4. A&(B&C) <=> (A&B)&C ассоциативность конъюнкции;
5. AU(BUC) <=> (AUB)UC
ассоциативность дизъюнкции;
6. A&(BUC) <=> (A&B)U(A&C)
дистрибутивность конъюнкции
относительно дизъюнкции;
7. AU(B&C) <=> (AUB)&(AUC)
дистрибутивность дизъюнкции
относительно конъюнкции;
8. A&A <=> A
9. AUA <=> A
10. AU¬A <=> И
закон исключенного третьего;
11. A&¬A <=> Л
закон непротиворечия;
12. A&И <=> A
13. AUИ <=> И
14. A&Л <=> Л
15. AUЛ <=> A
16. ¬(A&B) <=> ¬ A U ¬ B
законы де Моргана;
17. ¬(AUB) <=> ¬ A & ¬ B
18. A => B <=> ¬ A U B
замена импликации.
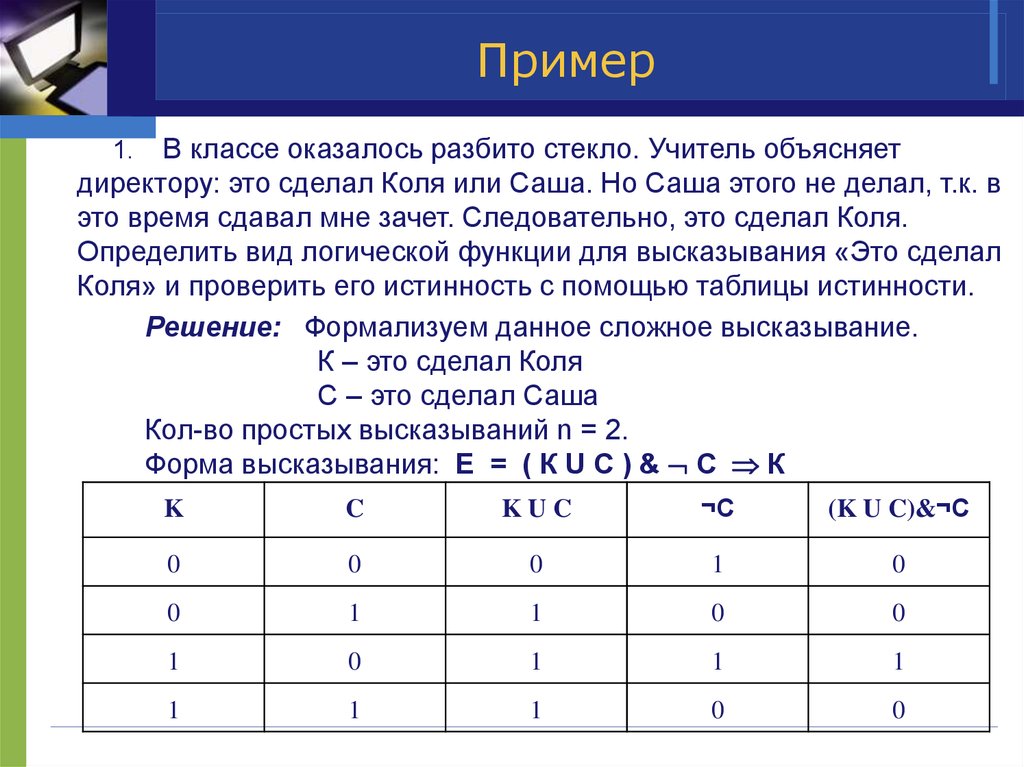
13. Пример
В классе оказалось разбито стекло. Учитель объясняетдиректору: это сделал Коля или Саша. Но Саша этого не делал, т.к. в
это время сдавал мне зачет. Следовательно, это сделал Коля.
Определить вид логической функции для высказывания «Это сделал
Коля» и проверить его истинность с помощью таблицы истинности.
Решение: Формализуем данное сложное высказывание.
К – это сделал Коля
С – это сделал Саша
Кол-во простых высказываний n = 2.
Форма высказывания: Е = ( К U C ) & С К
1.
K
C
KUC
¬C
(K U C)&¬C
0
0
0
1
0
0
1
1
0
0
1
0
1
1
1
1
1
1
0
0
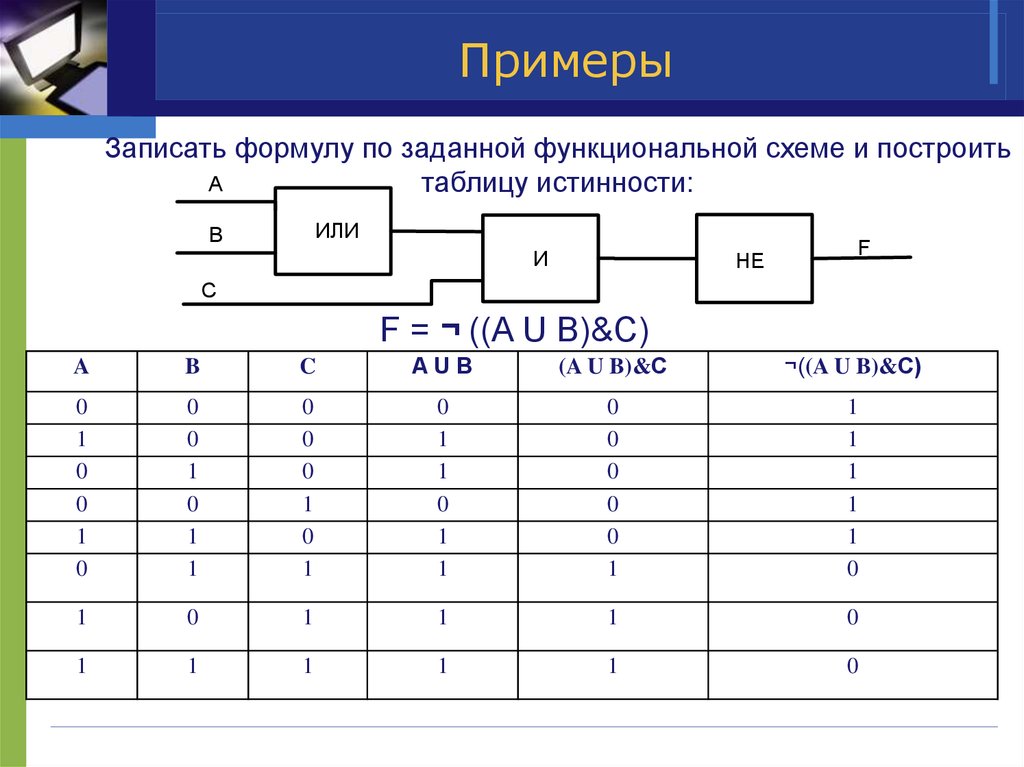
14. Примеры
Записать формулу по заданной функциональной схеме и построитьA
таблицу истинности:
ИЛИ
B
И
НЕ
F
С
F = ¬ ((A U B)&C)
A
B
C
AUB
(A U B)&C
¬((A U B)&C)
0
1
0
0
1
0
0
0
1
0
1
1
0
0
0
1
0
1
0
1
1
0
1
1
0
0
0
0
0
1
1
1
1
1
1
0
1
0
1
1
1
0
1
1
1
1
1
0
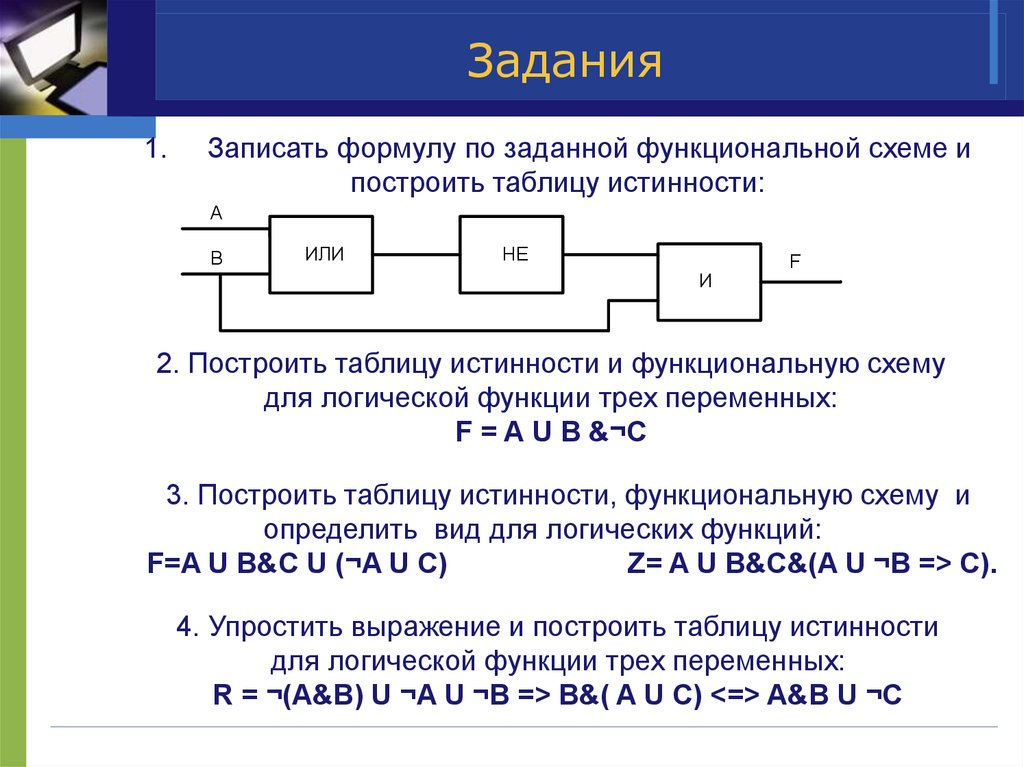
15. Задания
1.Записать формулу по заданной функциональной схеме и
построить таблицу истинности:
A
B
ИЛИ
НЕ
И
F
2. Построить таблицу истинности и функциональную схему
для логической функции трех переменных:
F = A U B &¬C
3. Построить таблицу истинности, функциональную схему и
определить вид для логических функций:
F=A U B&C U (¬A U C)
Z= A U B&C&(A U ¬B => C).
4. Упростить выражение и построить таблицу истинности
для логической функции трех переменных:
R = ¬(A&B) U ¬A U ¬B => B&( A U C) <=> A&B U ¬C
16. Задания
Построить таблицу истинности и схему для логической функции№
Логическая функция
№
Логическая функция
1
((X& Y) Y) (XUY)
13 ( ( A U B ) & ( A U B ) ) A
2
(XUY) ( X& Y)
14 ( A & B ) ( A U B )
3
(X&(YU X)) (X&Y)
15 ( A & B ) U ( A ( B & A ) )
4
((XUY) X) (Y&X))
16 A & ( ( B & A ) ( A U B ) )
5
(XU( X&Y)) (XUY)
17 ( A U ( A & B ) ) ( A U B )
6
((X Y)& X) (XU Y)
18 ( ( A B ) & A ) ( A U B )
7
((XUY)&(XU Y)) X
19 ( ( R U S ) & ( R U S ) ) R
8
(X&Y)U( X (Y&X))
20 ( R U ( R & S ) ) ( R U S )
9
X&( ( Y&X) (XUY))
21 R & ( ( S & R ) (R U S ) )
10 ( X & Y ) ( X U Y )
22 ( ( R & S ) S ) ( R U S )
11 A U ( B & A ) ( A & B )
23 ( R U S ) ( R & S )
12 ( A U B ) ( A & B )
24 ( R & S ) U ( R ( S & R ) )
17.
Катков К.А.LOGO







 Информатика
Информатика








