Операции с множествами. Основные понятия графов. Комбинаторика

1. Операции с множествами. Основные понятия графов. Комбинаторика.

2. Основные вопросы

• Элементы и множества. Операции над
множествами и их свойства.
• Графы. Элементы графов. Виды графов
и операции над ними.
• Обоснование основных понятий
комбинаторики: факториал,
перестановки, размещения, сочетания.

3. Элементы и множества. Операции над множествами и их свойства.

4.

«Множество есть многое, мыслимое
нами как единое»
основатель теории множеств – Георг Кантор
(1845—1918) — немецкий
математик, логик, теолог, создатель
теории бесконечных множеств,
оказавшей определяющее влияние
на развитие математических наук на
рубеже 19— 20 вв.

5. Понятия теории множеств

Понятие множества является одним из
наиболее общих и наиболее важных
математических понятий. Оно было введено
в математику немецким ученым Георгом
Кантором (1845-1918).Следуя Кантору,
понятие "множество" можно определить так:
Множество - совокупность объектов,
обладающих определенным свойством,
объединенных в единое целое.

6.

• С понятием множества мы соприкасаемся
прежде всего тогда, когда по какой-либо
причине объединяем по некоторому признаку
в одну группу какие-то объекты и далее
рассматриваем эту группу или совокупность
как единое целое.
• Множества принято обозначать
заглавными латинскими буквами: А, В, С, D .
• Объекты, которые образуют множество,
называют элементами множества и для
обозначения элементов используют, как
правило, малые буквы латинского алфавита.

7. Примеры множеств:

множество учащихся в данной аудитории;
множество людей, живущих на нашей планете в
данный момент времени;
множество точек данной геометрической фигуры;
множество чётных чисел;
множество корней уравнения х2-5х+6=0;
множество действительных корней уравнения
х2+9=0;

8.

• Если элемент x принадлежит
множеству X, то записывают x Х
( — принадлежит).
• В противном случае, если a не
принадлежит множеству А, будем
использовать обозначение :
• Если множество А является частью
множества В, то записывают А В
( — содержится).

9.

множество
Множество
четырехугольников
Пространственные тела
Натуральные числа
элемент
Трапеция, параллелограмм, ромб,
квадрат, прямоугольник
Шар, прямоугольный
параллелепипед, призма,
пирамида, октаэдр
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
Квадраты чисел
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ..
Цифры десятичной системы
счисления
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двузначные четные числа
10, 12, 14, 16 … 96, 98

10.

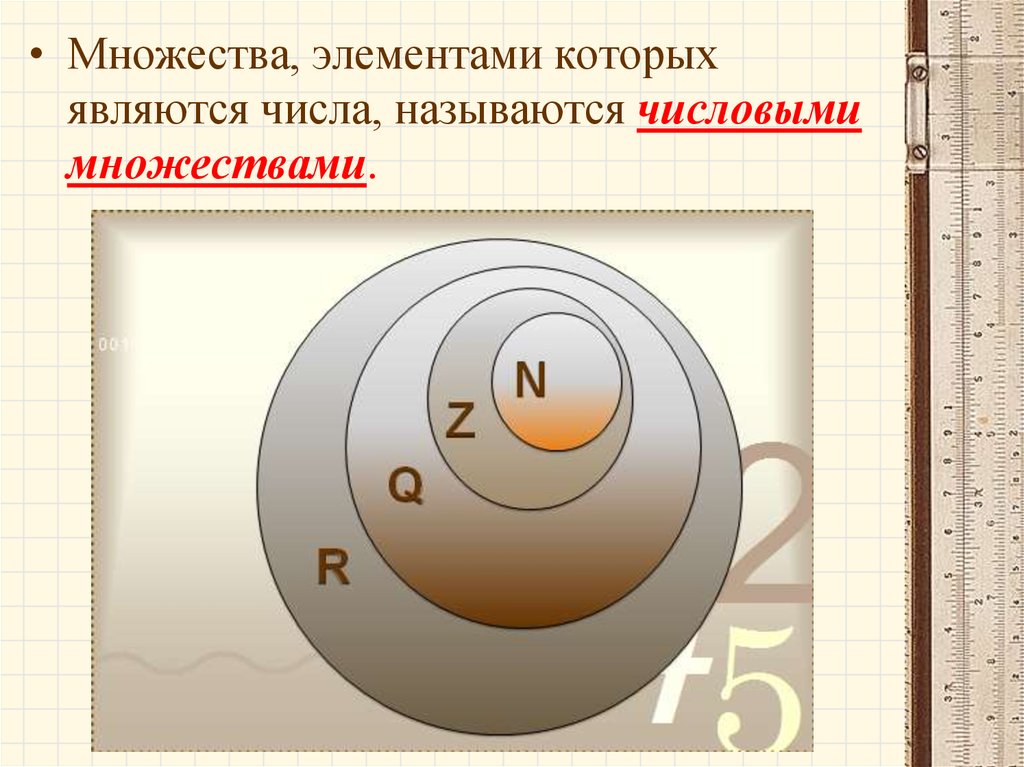
• Множества, элементами которых
являются числа, называются числовыми
множествами.

11.

N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел.

12. Способы задания множеств

Множество может быть задано перечислением всех его
элементов или списком. В этом случае элементы множества
записывают внутри фигурных скобок, например: A={студент
А., рабочий Л., школьник М.}.
2. Множество может быть задано описанием свойств его
элементов. Чаще всего при этом используют запись, которую
читают следующим образом: «A есть множество элементов b
таких, что для них выполняется свойство B». Например, а –
четное натуральное число.
3. Множество может быть задано указанием характеристического
свойства его элементов , то есть такого свойства, которым
обладают все элементы данного множества, и только они:
1.
A x | x M , P( x)
Здесь x М означает, что элемент х является элементом
известного множества .
Запись Р(х) означает, что элемент х обладает свойством Р.
Свойство Р(х) формулируется словами, символами или
выражается с помощью уравнения или неравенства.

13. Примеры

A x | x Z , 3 x 4 2, 1, 0, 1, 2, 3

14. Примеры

15. Виды множеств:

Множества
Виды множеств:
Конечные
Бесконечные
Пустые

16. Если элементы множества можно сосчитать, то множество является КОНЕЧНЫМ

Пример
Множество гласных букв в слове
“математика” состоит из трёх
элементов – это буквы “а”, “е”, “и”,
причем, гласная считается только один
раз, т.е. элементы множества при
перечислении не повторяются.

17. Если элементы множества сосчитать невозможно, то множество БЕСКОНЕЧНОЕ

Пример
• Множество натуральных чисел
бесконечно.
Пример
• Множество точек отрезка [0;1]
бесконечно.
Пример
• Множество атомов во Вселенной

18. Множество, не содержащее ни одного элемента, называется ПУСТЫМ. Символически оно обозначается знаком 

Множество, не содержащее ни
одного элемента, называется
ПУСТЫМ.
Символически оно обозначается
знаком
Пример
• Множество действительных корней
уравнения x2 +1=0.
Пример
• Множество людей, проживающих на
Солнце.

19. Мощность множества

• Число элементов конечного множества
называют мощностью этого множества и
обозначают символом m (A) или |A|.
• Количество элементов в конечном
множестве естественно характеризовать их
числом.
• В этом смысле множество чисел {-2, 0, 3,8}
и множество букв {с, х, ф, а}
эквивалентны, так как они содержат
одинаковое число элементов.

20. Пример . Определите мощность какого из множеств A = {1, 3, 5, 7, 9} или B = {2, 4, 6, 8} больше.

• Решение. Понятие мощности конечных
множеств позволяет сравнивать их по
количеству элементов.
Так, если A = {1, 3, 5, 7, 9}, а
B = {2, 4, 6, 8}, то m (A) = 5, а m (B) = 4 и
потому m (A) > m (B).

21. Отношения между множествами

• Наглядно отношения между множествами
изображают при помощи особых чертежей,
называемых КРУГАМИ ЭЙЛЕРА (или
диаграммами Эйлера – Венна).
• Для этого множества, сколько бы они ни
содержали элементов, представляют в виде
кругов или любых других замкнутых кривых
(фигур)

22.

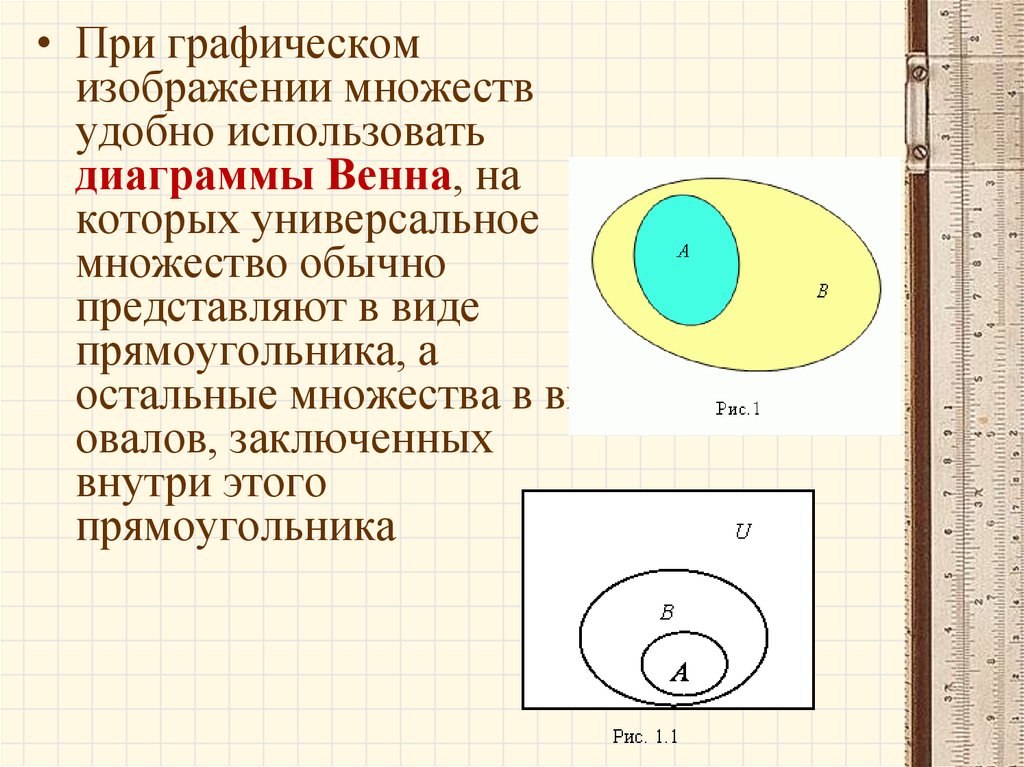
• При графическом
изображении множеств
удобно использовать
диаграммы Венна, на
которых универсальное
множество обычно
представляют в виде
прямоугольника, а
остальные множества в виде
овалов, заключенных
внутри этого
прямоугольника

23.

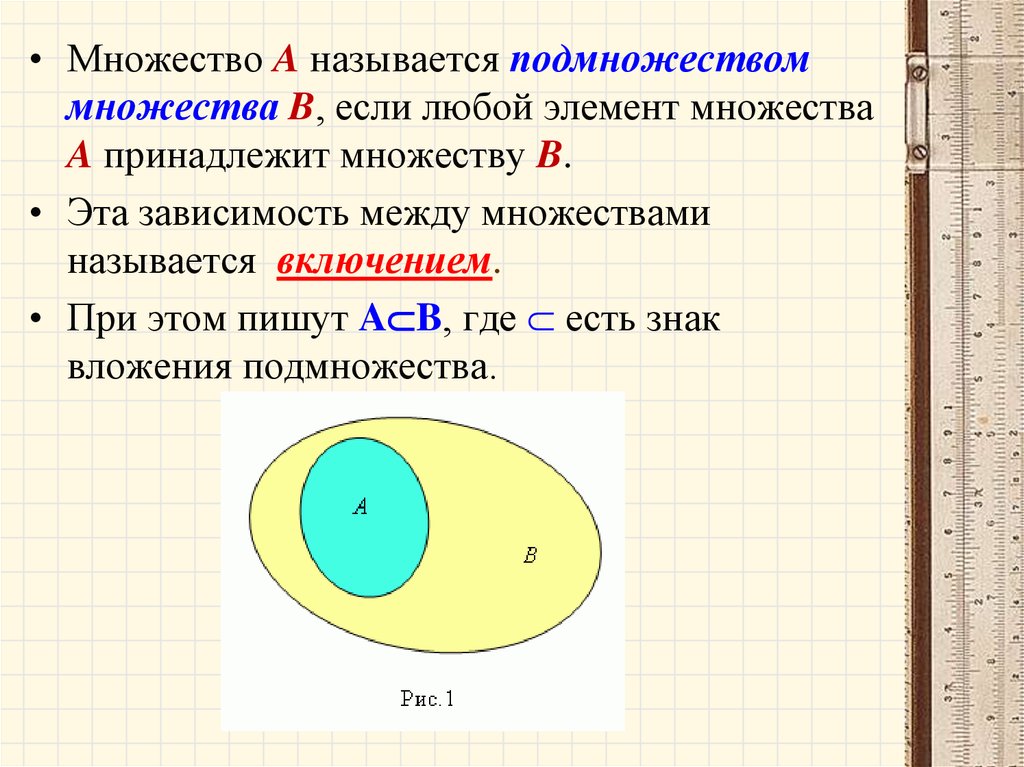
• Множество A называется подмножеством
множества B, если любой элемент множества
A принадлежит множеству B.
• Эта зависимость между множествами
называется включением.
• При этом пишут A B, где есть знак
вложения подмножества.

24. Свойства множеств

• Любое множество является
подмножеством самого себя
(рефлексивность): A B.
• Для любых множеств А,В,С справедливо
свойство транзитивности: если A B
и B C , то A C .
• Для всякого множества А пустое
множество является его
подмножеством: А

25.

Два множества А и В называются равными ( А =
В ), если они состоят из одних и тех же
элементов, то есть каждый элемент
множества А является элементом
множества В и наоборот, каждый элемент
множества В является элементом множества А .
Примеры
1. A 1, 3 , B 3, 1 . Множества и состоят из одних и
тех же элементов, поэтому они равные: А = В .
2. Множество решений уравнения x 2 5 x 6 0
есть множество чисел 2 и 3, то есть A 2, 3
.
Множество В простых чисел, меньших 5, также
состоит из чисел 2 и 3, то есть B 2, 3
.

26. Количество подмножеств

Если мощность множества n,
то у этого множества 2n
подмножеств.
А={1,2}
Подмножества А:
{ }, {1}, {2}, {1,2}.

27.

Количество подмножеств
В={1,3,5}
Подмножества В:
{ }, {1}, {3}, {5},
{1,3}, {1,5}, {5,3},
{1,3,5}
С={а,и,е,о}
Подмножества С:
{ }, {а}, {и}, {е}, {о},
{а,и}, {а,е}, {а,о},
{и,е}, {и,о}, {е,о},
{а,и,е}, {а,и,о},
{а,е,о}, {и,е,о},
{а,и,е,о}.

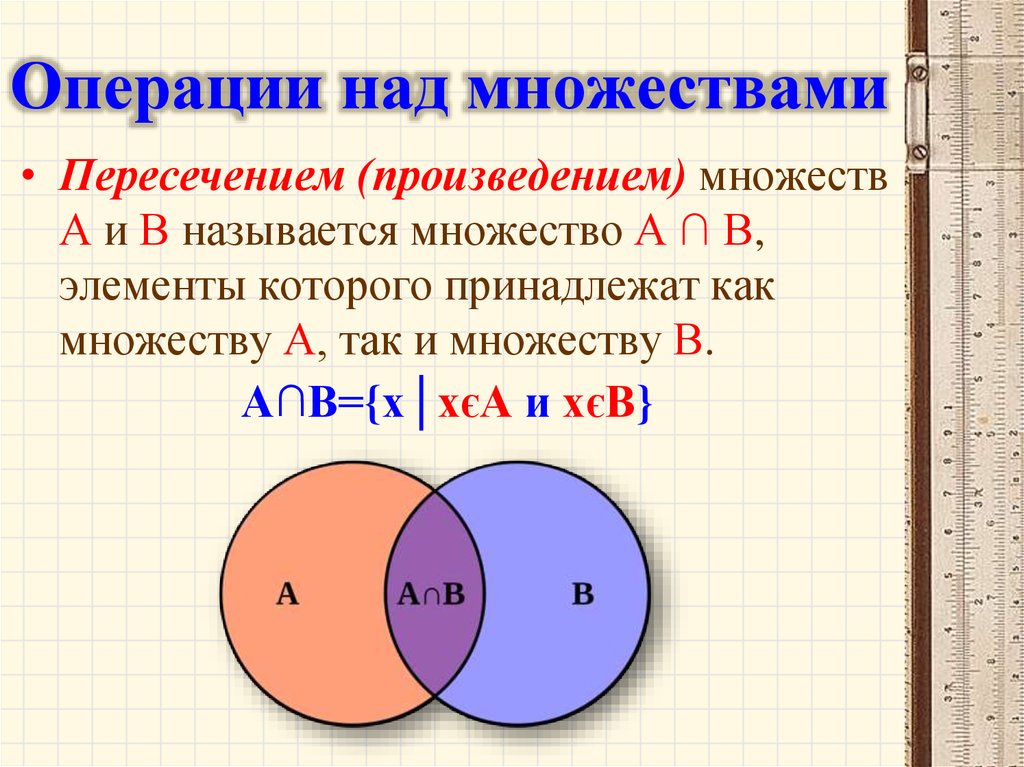
28. Операции над множествами

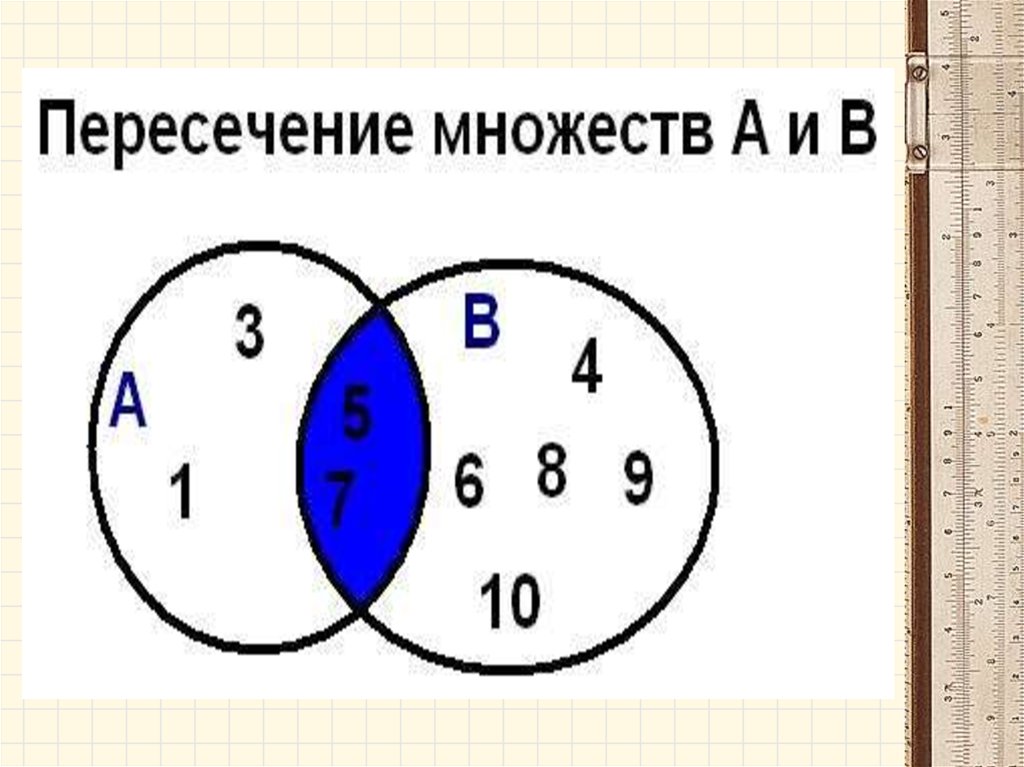
• Пересечением (произведением) множеств
А и В называется множество А ∩ В,
элементы которого принадлежат как
множеству А, так и множеству В.
А∩В={х│хєА и хєВ}

29.

Операции над множествами
пересечение
Например, если А={a,b,c}, B={b,c,f,e},
то А ∩ В = {b}

30. Операции над множествами

31.

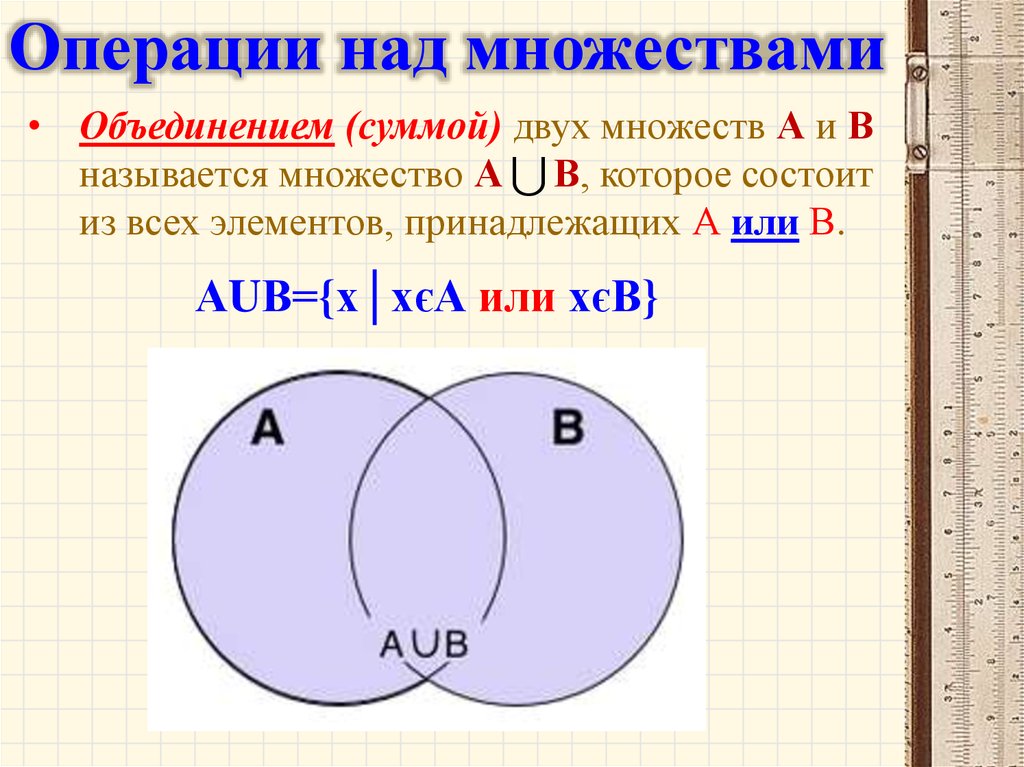
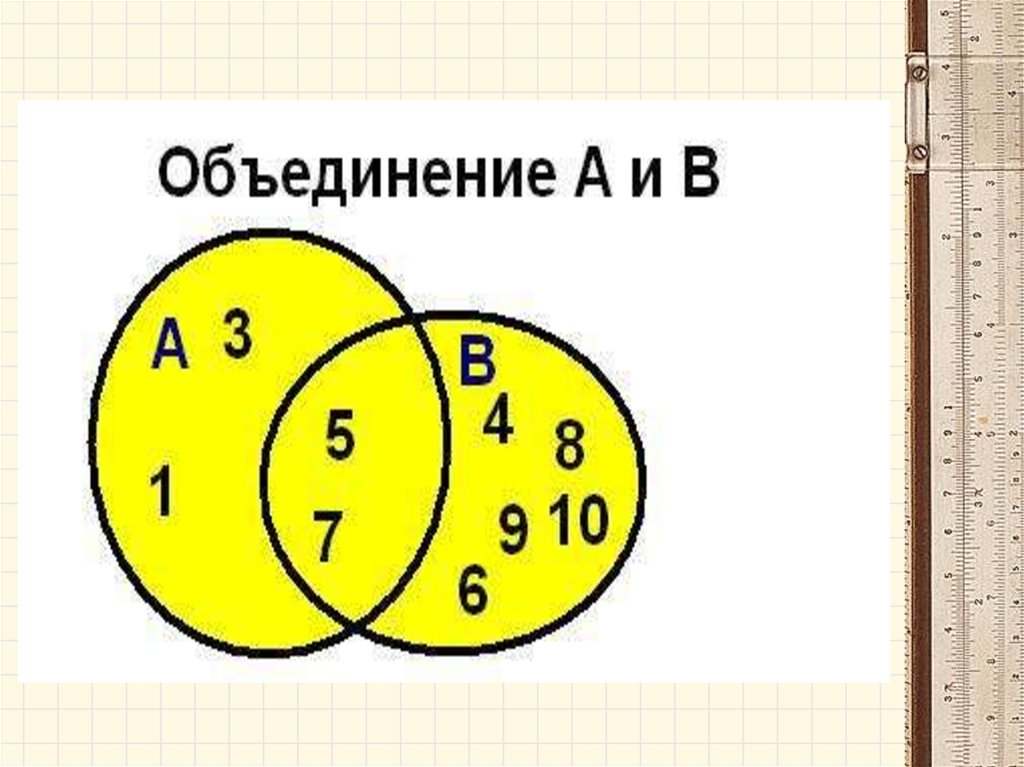
Операции над множествами
• Объединением (суммой) двух множеств А и В
называется множество А В, которое состоит
из всех элементов, принадлежащих А или В.
АUВ={х│хєА или хєВ}

32. объединение

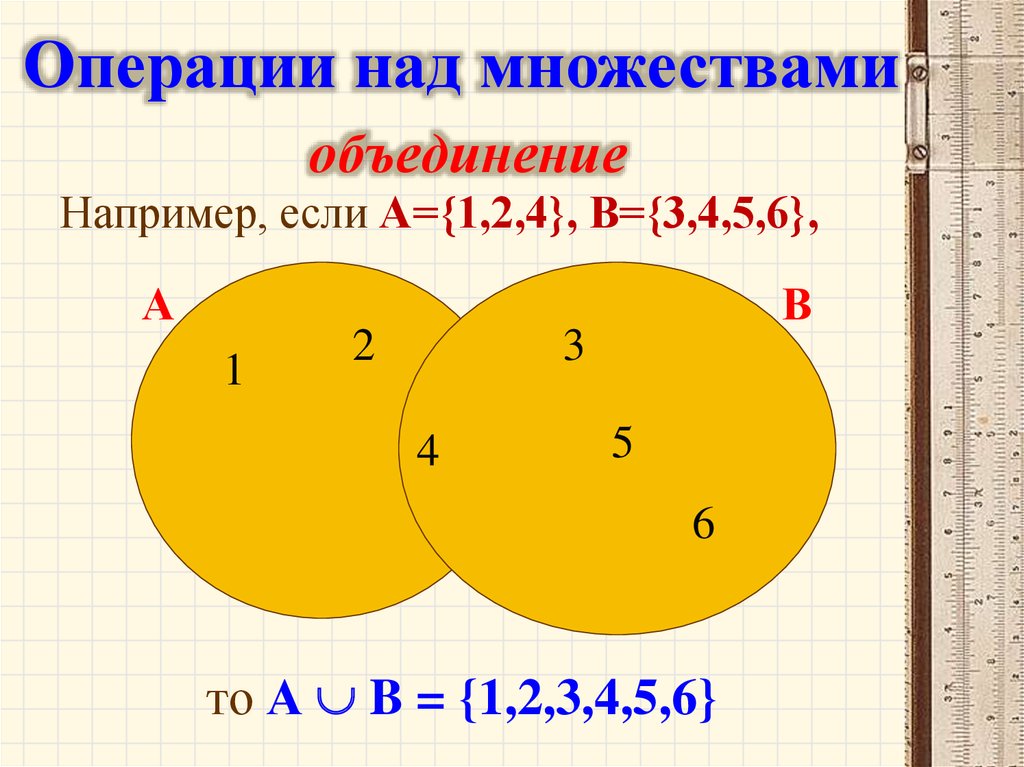
Операции над множествами
объединение
Например, если А={1,2,4}, B={3,4,5,6},
А
1
2
В
3
44
5
6
то А B = {1,2,3,4,5,6}

33. Операции над множествами

34. Операции над множествами

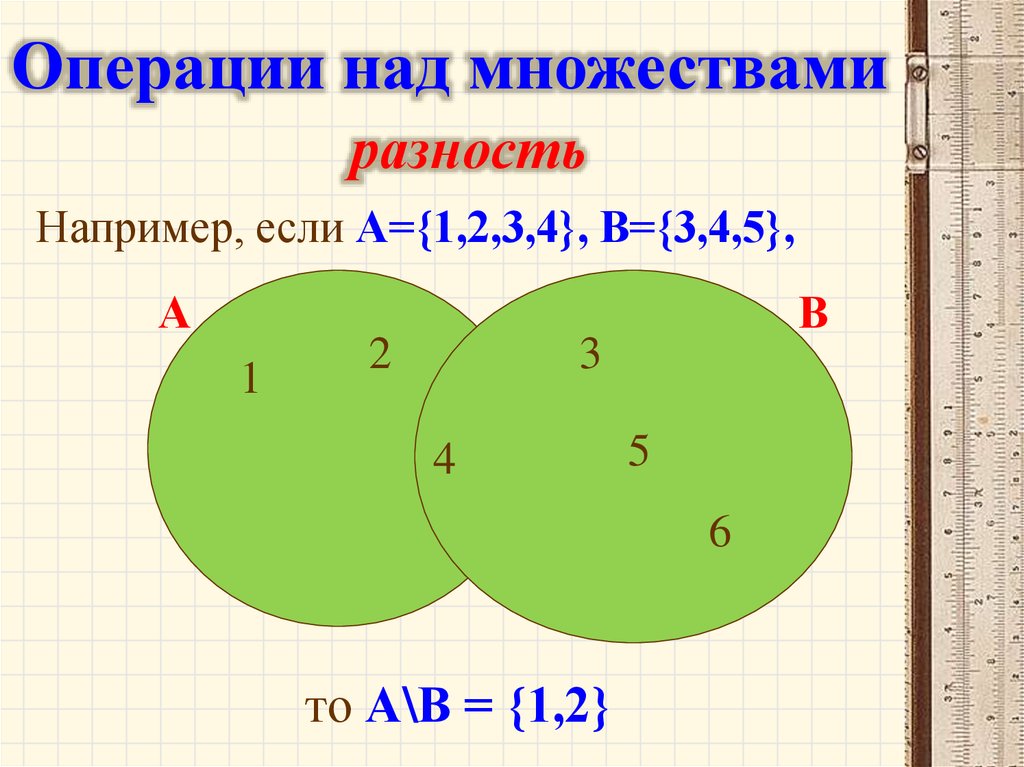
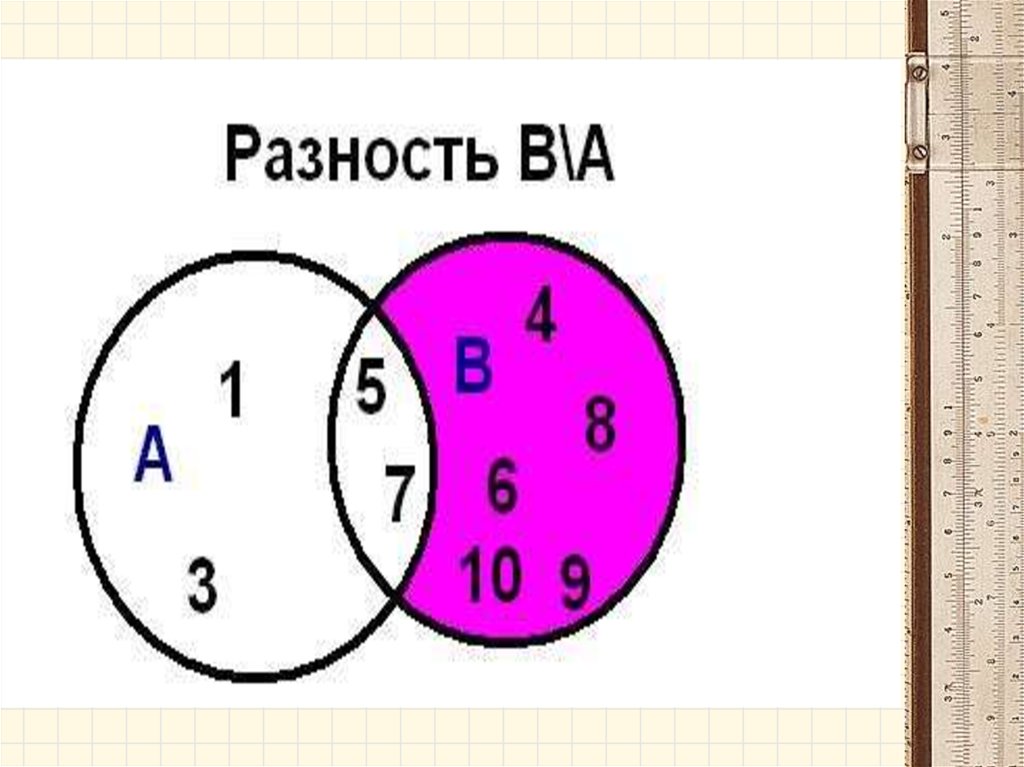
• Разностью множеств А и В называется
множество А- В, элементы которого
принадлежат множеству А, но не
принадлежат множеству В.
A B x | x A и x B

35. разность

Операции над множествами
разность
Например, если А={1,2,3,4}, B={3,4,5},
А
1
2
В
3
44
5
6
то А\В = {1,2}

36. Операции над множествами

37. Операции над множествами

Дополнение множества
Часто множества A,B,C … являются
подмножествами некоторого более широкого
множества U, принимаемого за универсальное.

38. Операции над множествами

ПРИМЕРЫ:
• Если А - множество параллелограммов, Вмножество трапеций, С - множество ромбов, D множество прямоугольников, E - множество
квадратов, то универсальным множеством U служит
множество всех четырехугольников.
• Если А - множество треугольников, В- множество
четырехугольников и так далее, то в качестве
универсального множества U можно выбрать
множество всех многоугольников.

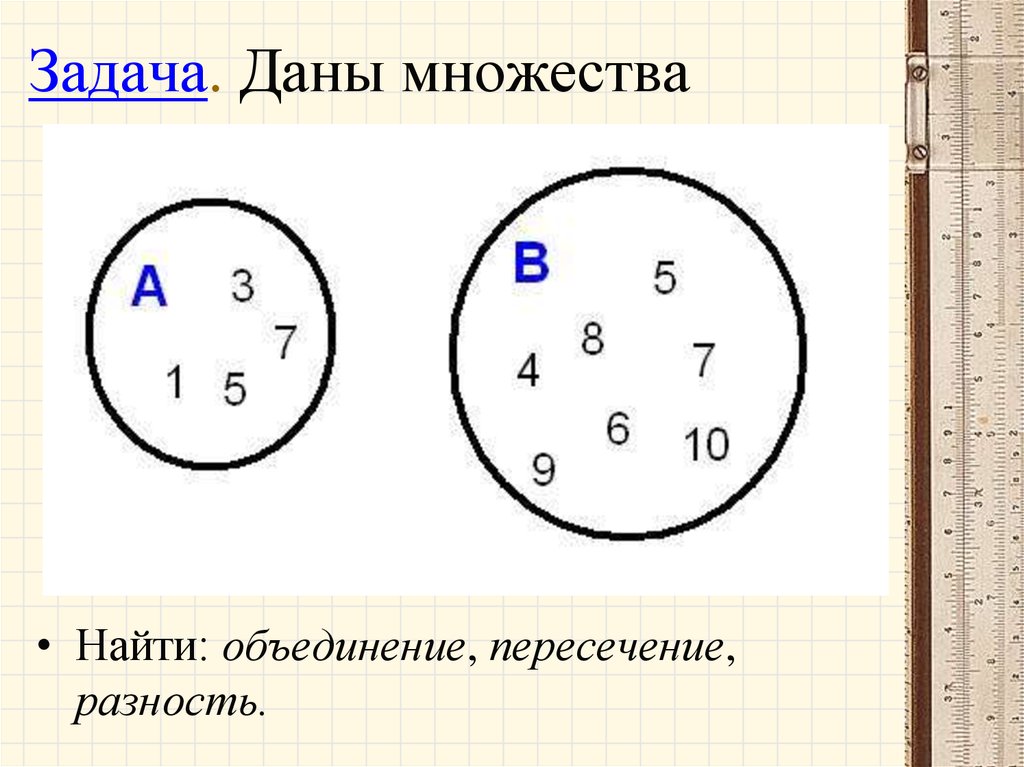
39. Задача. Даны множества

• Найти: объединение, пересечение,
разность.

40.

41.

42.

43.

44.

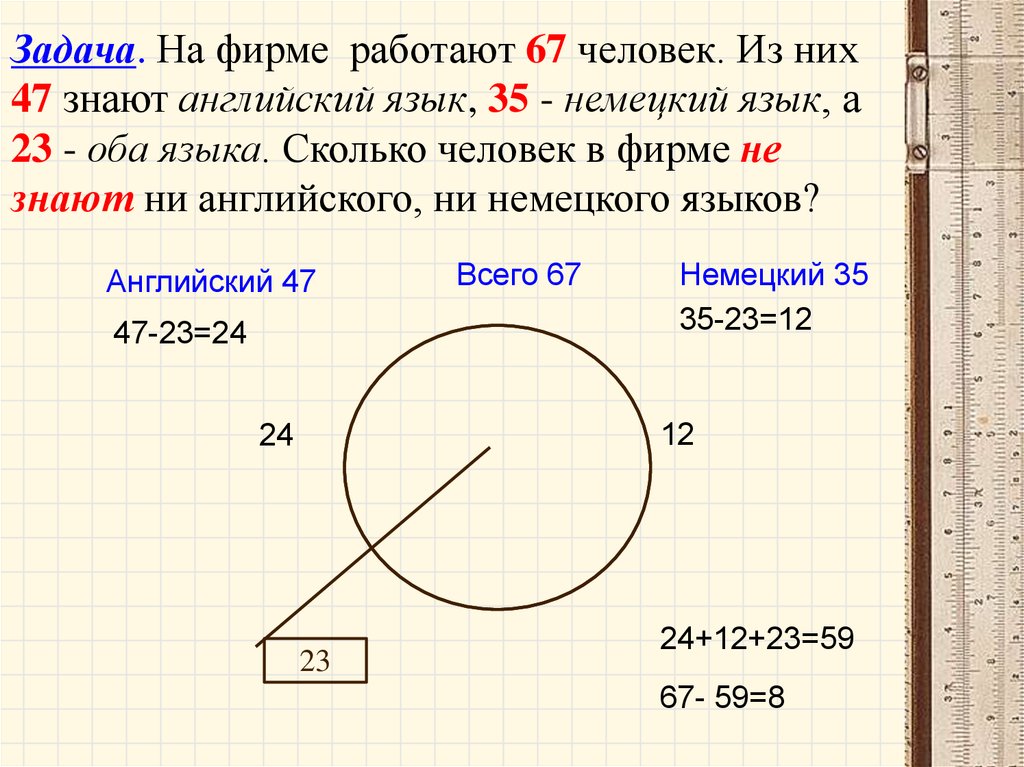
Задача. На фирме работают 67 человек. Из них
47 знают английский язык, 35 - немецкий язык, а
23 - оба языка. Сколько человек в фирме не
знают ни английского, ни немецкого языков?
Английский 47
47-23=24
Всего 67
Немецкий 35
35-23=12
12
24
23
24+12+23=59
67- 59=8

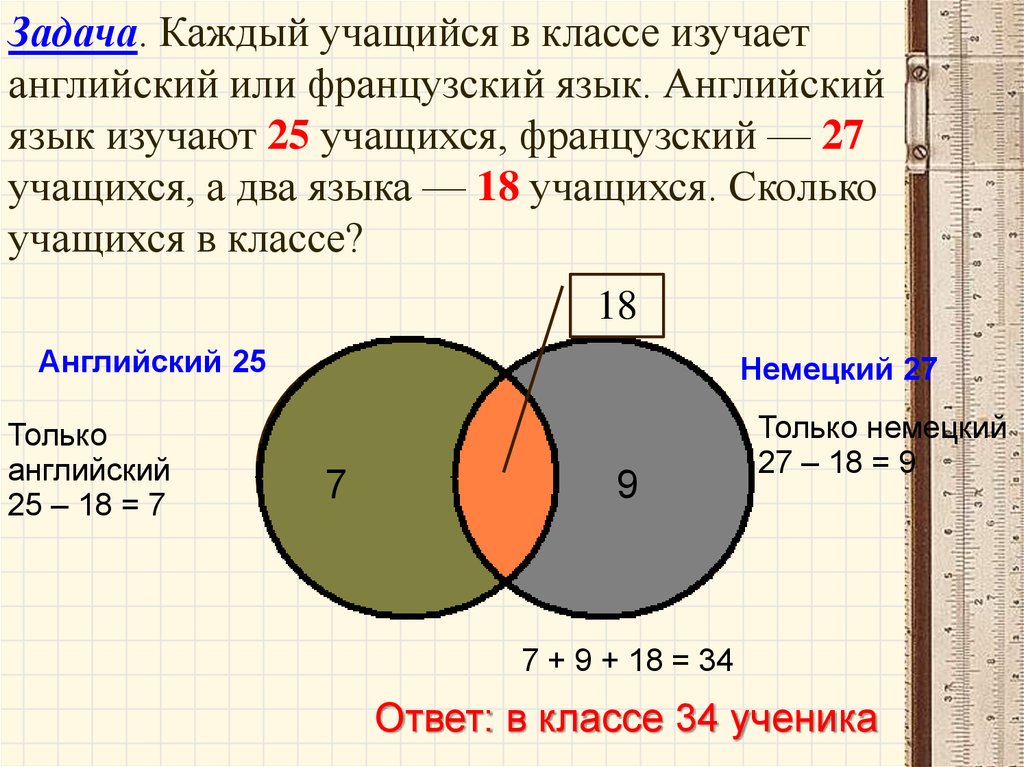
45. Задача. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27

учащихся, а два языка — 18 учащихся. Сколько
учащихся в классе?
18
Английский 25
Только
английский
25 – 18 = 7
Немецкий 27
7
9
Только немецкий
27 – 18 = 9
7 + 9 + 18 = 34
Ответ: в классе 34 ученика

46.

Задача. Каждая семья, живущая в нашем доме, выписывает
или газету, или журнал, или и то и другое вместе. 75 семей
выписывают газету, а 27 семей выписывают журнал и лишь
13 семей выписывают и журнал, и газету. Сколько семей
живет в нашем доме?
Всего: 14 + 13 + 62 =89
46

47. Графы. Элементы графов. Виды графов и операции над ними

48.

• Теория графов представляет
собой раздел математики,
имеющий широкие практические
приложения.
• Теория графов – область
дискретной математики,
особенностью которой является
геометрический подход к изучению
объектов.

49. История возникновения графов

Термин "граф" впервые появился в книге
венгерского математика Д. Кенига в 1936
г., хотя начальные важнейшие теоремы о
графах восходят к Л. Эйлеру.

50. В основе теории лежит понятие графа.

В основе теории лежит понятие
Граф - совокупность конечного числа
точек, называемых вершинами графа, и
попарно соединяющих некоторые из этих
вершин линий, называемых ребрами или
дугами графа. Иногда граф в целом
можно обозначать одной заглавной
буквой.
Графом G V , X
называется пара двух
конечных множеств: множество точек V и
множество линий X (ребер, дуг),
соединяющих некоторые пары точек.

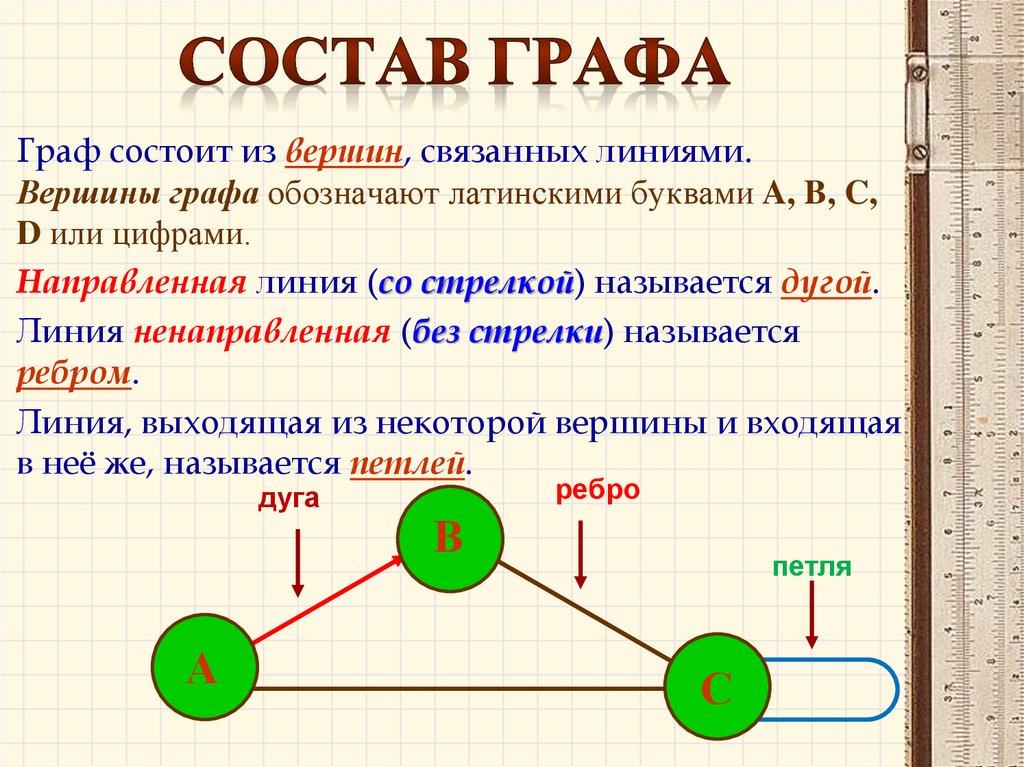
51. Состав графа

Граф состоит из вершин, связанных линиями.
Вершины графа обозначают латинскими буквами A, B, C,
D или цифрами.
Направленная линия (со стрелкой) называется дугой.
Линия ненаправленная (без стрелки) называется
ребром.
Линия, выходящая из некоторой вершины и входящая
в неё же, называется петлей.
дуга
А
ребро
В
петля
С

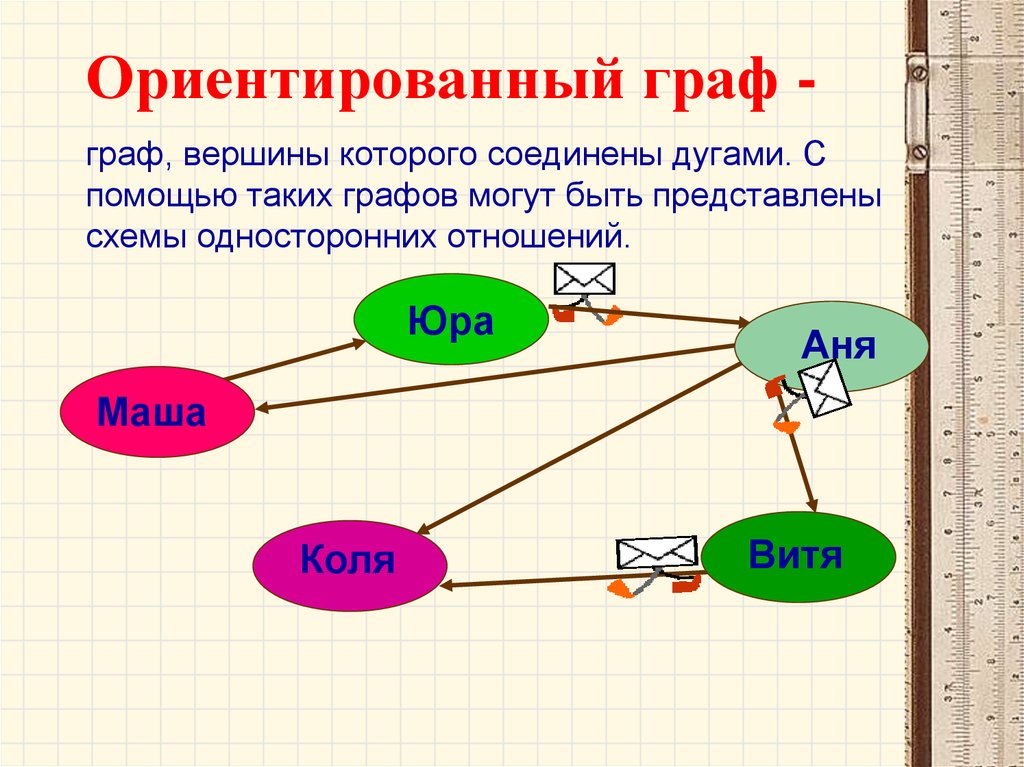
52. Ориентированный граф -

Ориентированный граф граф, вершины которого соединены дугами. С
помощью таких графов могут быть представлены
схемы односторонних отношений.
Юра
Аня
Маша
Коля
Витя

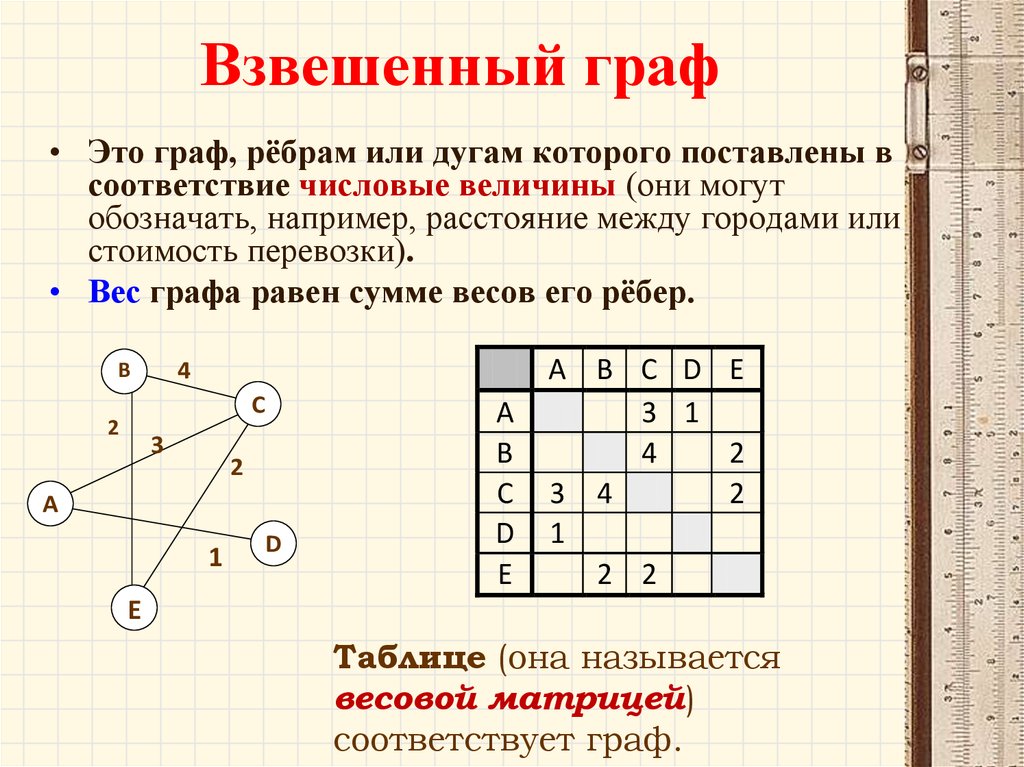
53. Взвешенный граф

• Это граф, рёбрам или дугам которого поставлены в
соответствие числовые величины (они могут
обозначать, например, расстояние между городами или
стоимость перевозки).
• Вес графа равен сумме весов его рёбер.
4
B
C
2
3
2
A
1
D
A
B
C
D
Е
A B C D Е
3 1
4
2
3 4
2
1
2 2
E
Таблице (она называется
весовой матрицей)
соответствует граф.

54.

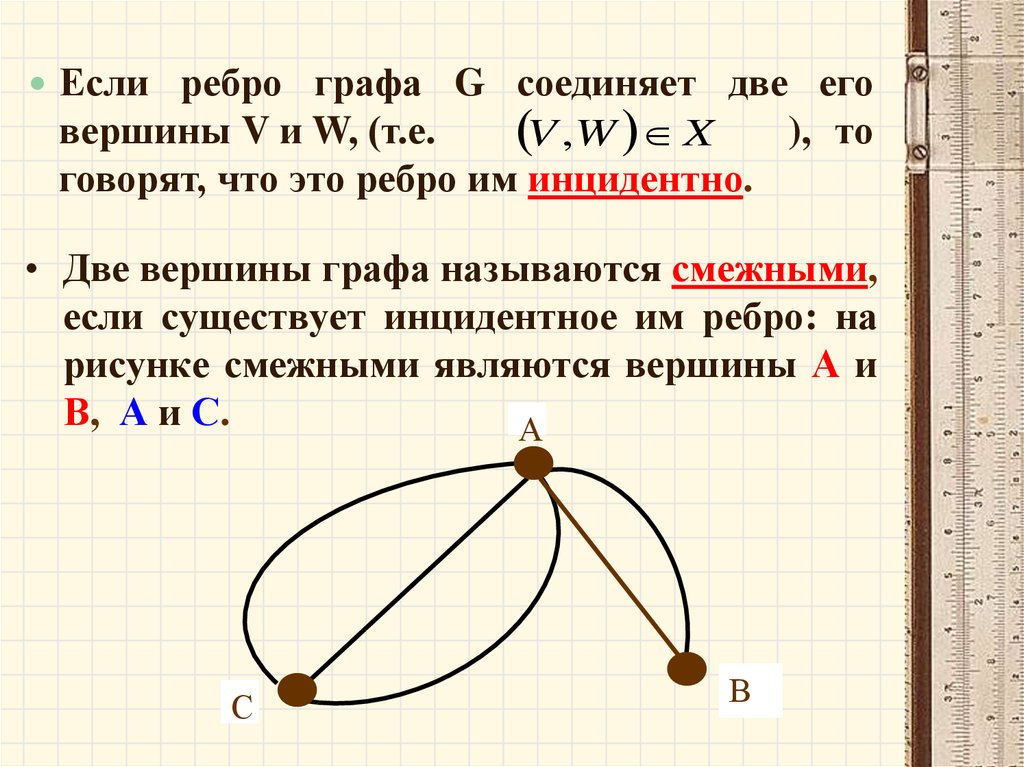
Если ребро графа G соединяет две его
вершины V и W, (т.е.
V ,W X ), то
говорят, что это ребро им инцидентно.
• Две вершины графа называются смежными,
если существует инцидентное им ребро: на
рисунке смежными являются вершины А и
В, А и С.
А
С
В

55.

Если граф G имеет ребро , у которого
начало и конец совпадают, то это ребро
называется петлёй. На рисунке ребро q(С, С)
– петля.
q
E
С
A
D
B

56.

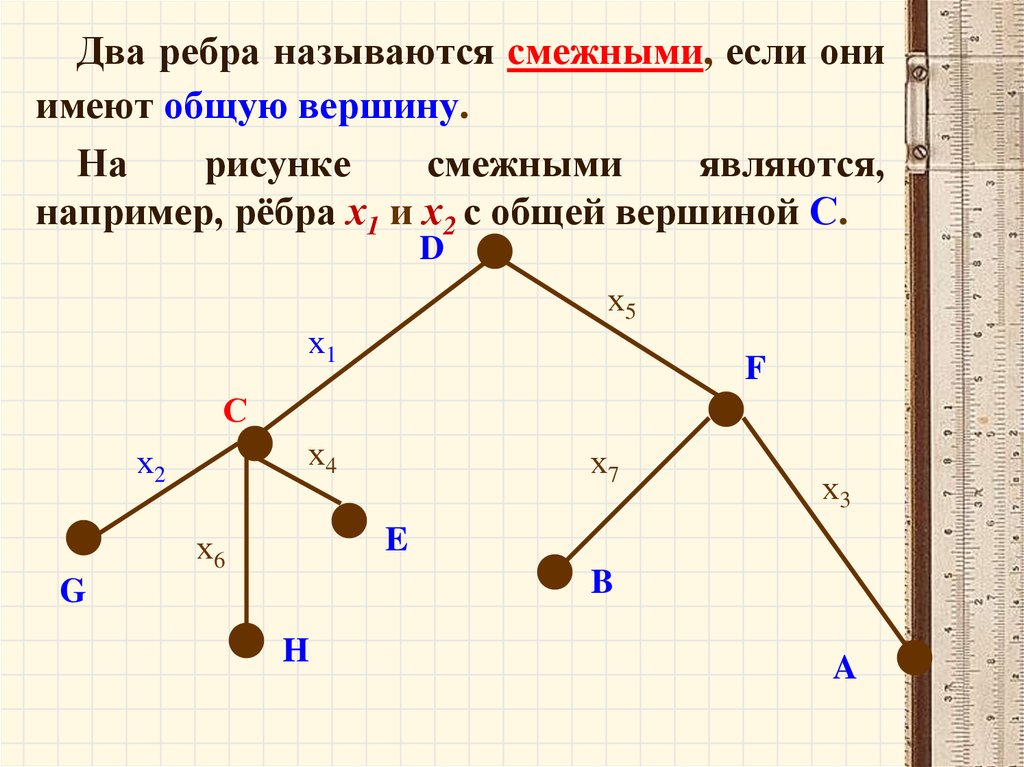
Два ребра называются смежными, если они
имеют общую вершину.
На
рисунке
смежными
являются,
например, рёбра х1 и х2 с общей вершиной С.
D
х5
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A

57.

• Рёбра, которые начинаются в одной и
той же вершине, заканчиваются также
в одной и той же вершине, называются
кратными, или параллельными.
• Количество одинаковых пар вида (V ,W )
называется кратностью ребра (V ,W )
• Число рёбер, инцидентных вершине А,
называется степенью этой вершины и
deg( A) (от англ. degree
обозначается
– степень).

58.

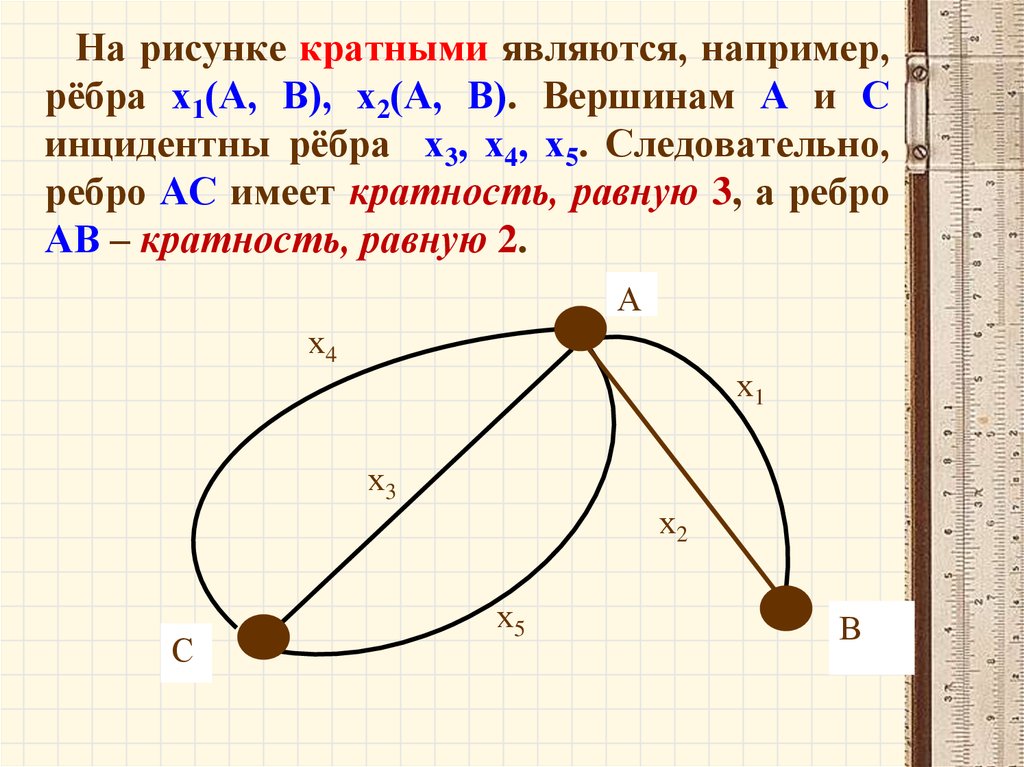
На рисунке кратными являются, например,
рёбра х1(А, В), х2(А, В). Вершинам А и С
инцидентны рёбра х3, х4, х5. Следовательно,
ребро АС имеет кратность, равную 3, а ребро
АВ – кратность, равную 2.
А
х4
х1
х3
С
х2
х5
В

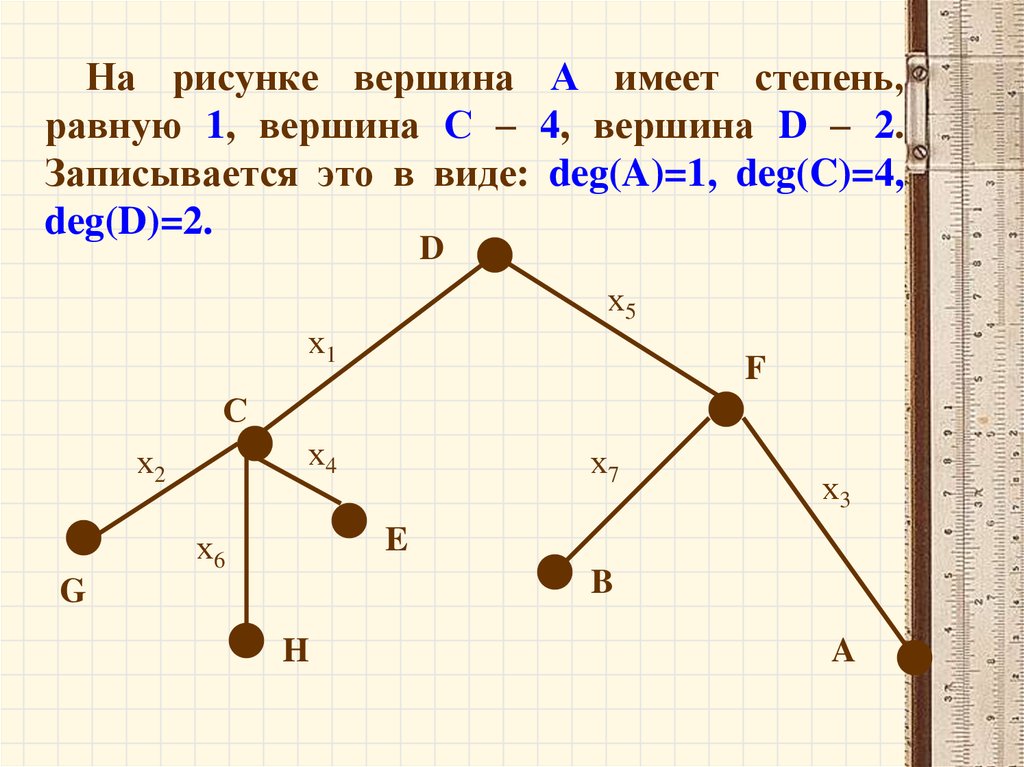
59.

На рисунке вершина А имеет степень,
равную 1, вершина С – 4, вершина D – 2.
Записывается это в виде: deg(A)=1, deg(C)=4,
deg(D)=2.
D
х5
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A

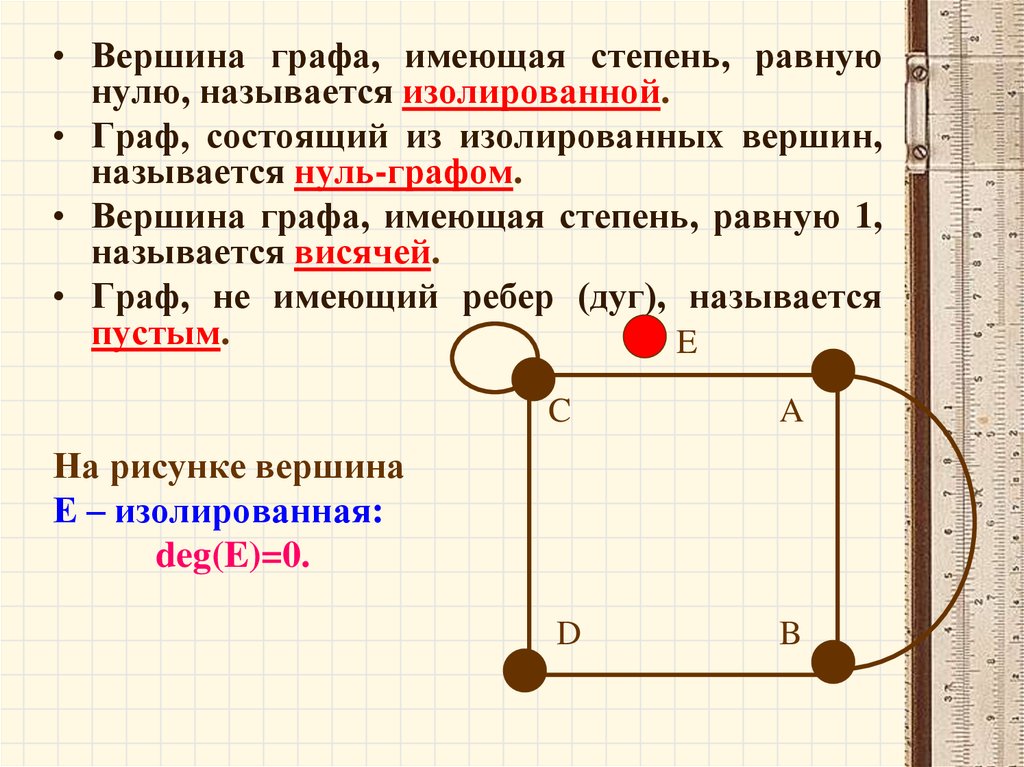
60.

• Вершина графа, имеющая степень, равную
нулю, называется изолированной.
• Граф, состоящий из изолированных вершин,
называется нуль-графом.
• Вершина графа, имеющая степень, равную 1,
называется висячей.
• Граф, не имеющий ребер (дуг), называется
пустым.
E
C
A
D
B
На рисунке вершина
Е – изолированная:
deg(E)=0.

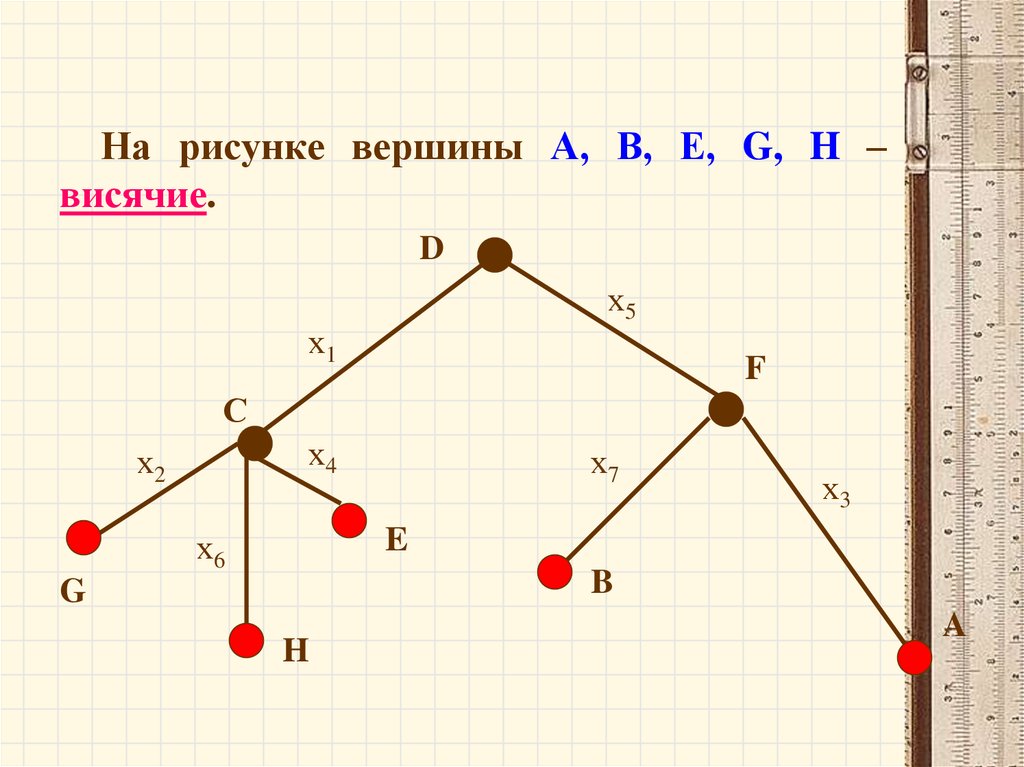
61.

На рисунке вершины А, В, Е, G, H –
висячие.
D
х5
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A

62.

Теорема 1. В графе G V , X
сумма
степеней всех его вершин – число чётное,
равное удвоенному числу рёбер графа:
n
deg(V ) 2m
i 1
где
n V
i
- число вершин;
m X - число рёбер графа.

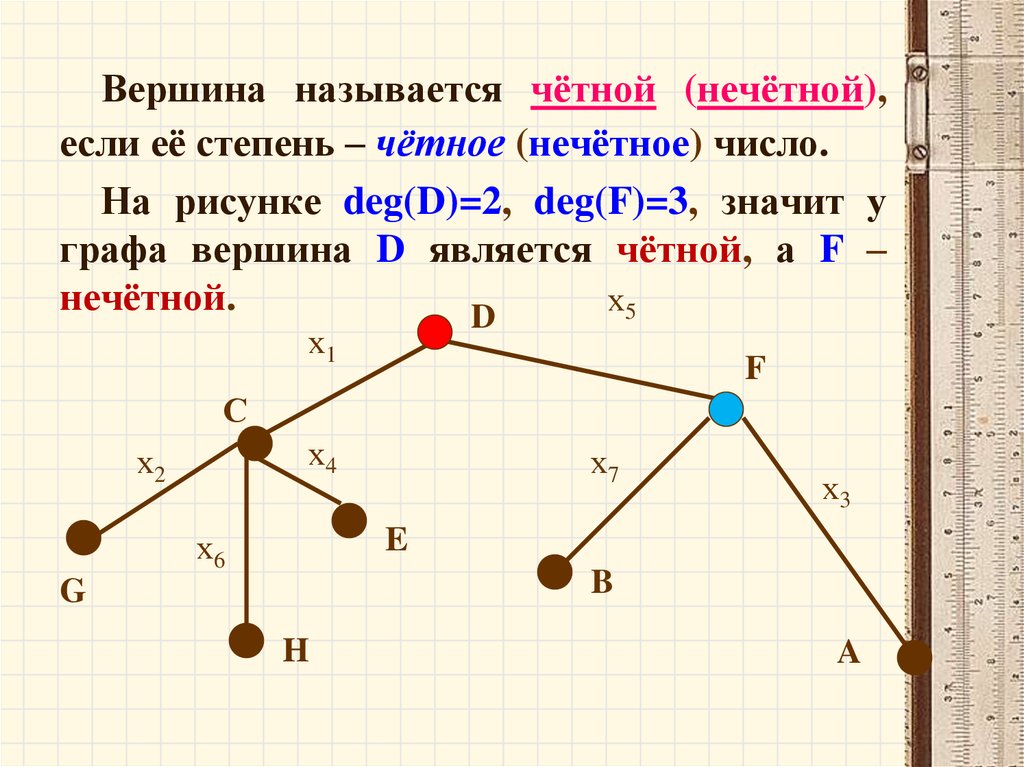
63.

Вершина называется чётной (нечётной),
если её степень – чётное (нечётное) число.
На рисунке deg(D)=2, deg(F)=3, значит у
графа вершина D является чётной, а F –
нечётной.
х5
D
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A

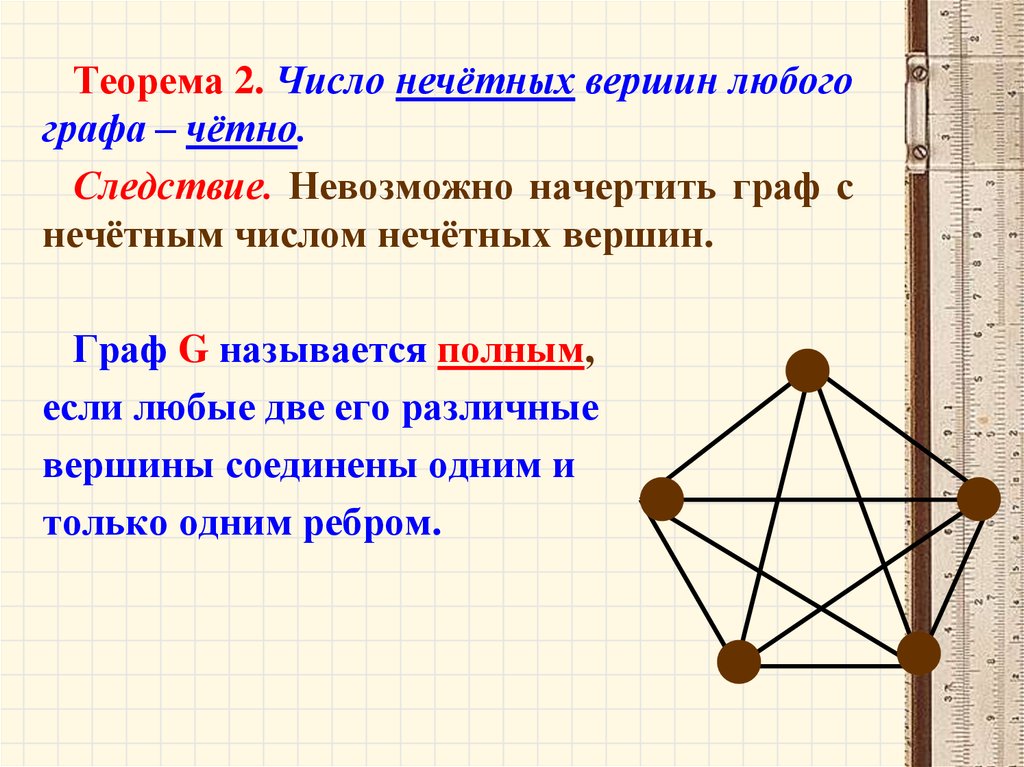
64.

Теорема 2. Число нечётных вершин любого
графа – чётно.
Следствие. Невозможно начертить граф с
нечётным числом нечётных вершин.
Граф G называется полным,
если любые две его различные
вершины соединены одним и
только одним ребром.

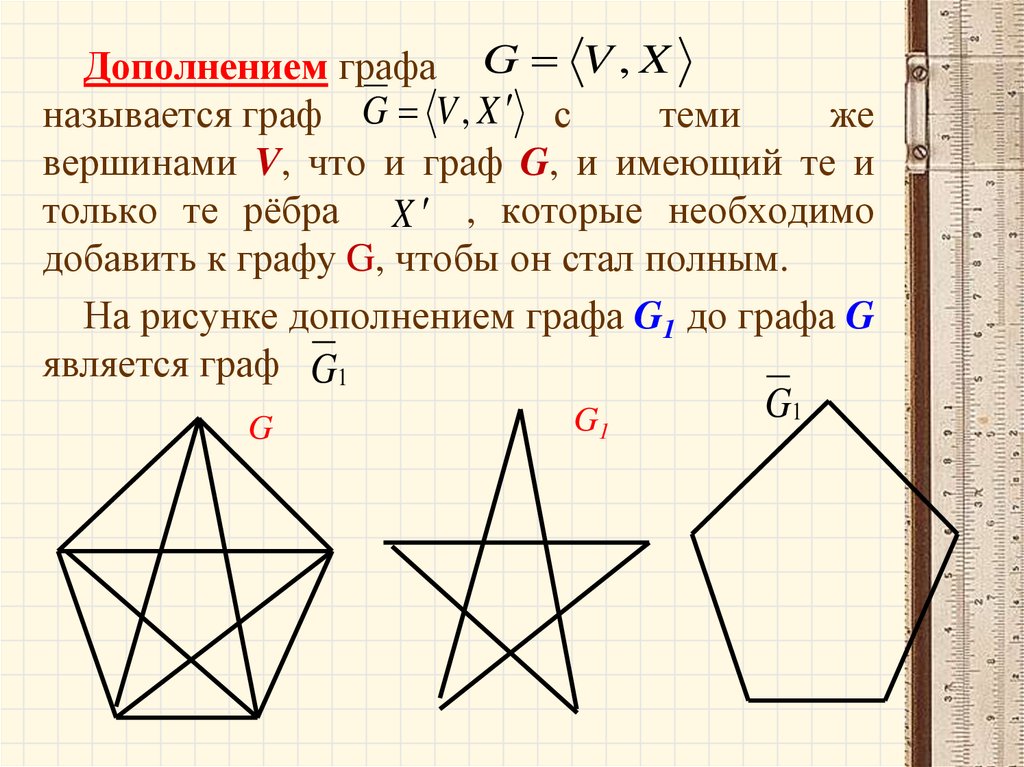
65.

Дополнением графа G V , X
называется граф G V , X с
теми
же
вершинами V, что и граф G, и имеющий те и
только те рёбра X , которые необходимо
добавить к графу G, чтобы он стал полным.
На рисунке дополнением графа G1 до графа G
является граф G1
G
G1
G1

66. Пути и маршруты в графах

• Путем в ориентированном графе называется
последовательность дуг, в которой конечная
вершина любой дуги, отличной от последней,
является начальной вершиной следующей
дуги.
• Вершина, от которой проложен маршрут,
называется началом пути, вершина в конце
маршрута — конец пути.
• Путь, в котором каждая вершина используется
не более одного раза, называется простым
путем.
• Длиной пути в графе называется количество
дуг (ребер), составляющих этот путь.

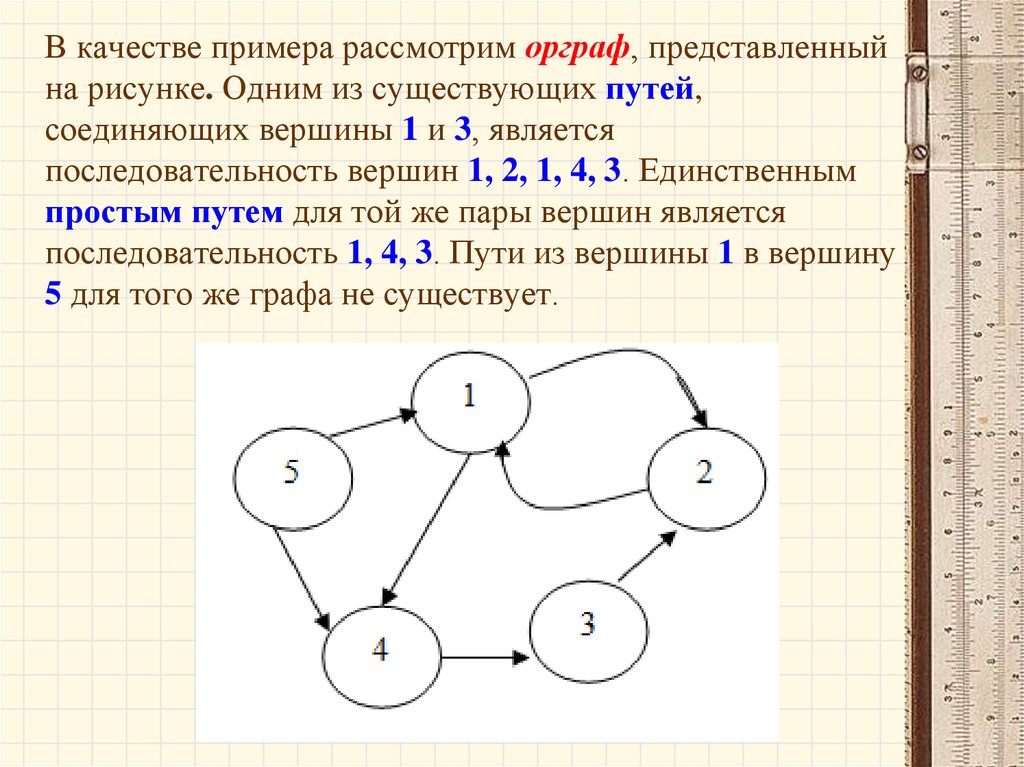
67.

В качестве примера рассмотрим орграф, представленный
на рисунке. Одним из существующих путей,
соединяющих вершины 1 и 3, является
последовательность вершин 1, 2, 1, 4, 3. Единственным
простым путем для той же пары вершин является
последовательность 1, 4, 3. Пути из вершины 1 в вершину
5 для того же графа не существует.

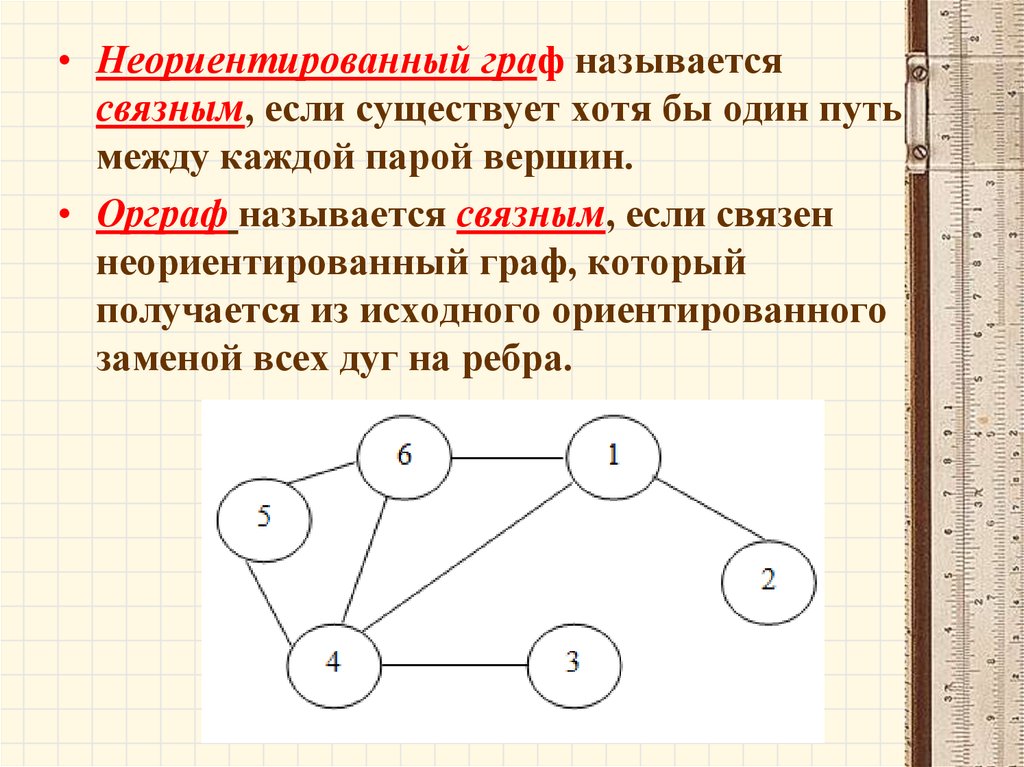
68.

• Неориентированный граф называется
связным, если существует хотя бы один путь
между каждой парой вершин.
• Орграф называется связным, если связен
неориентированный граф, который
получается из исходного ориентированного
заменой всех дуг на ребра.

69.

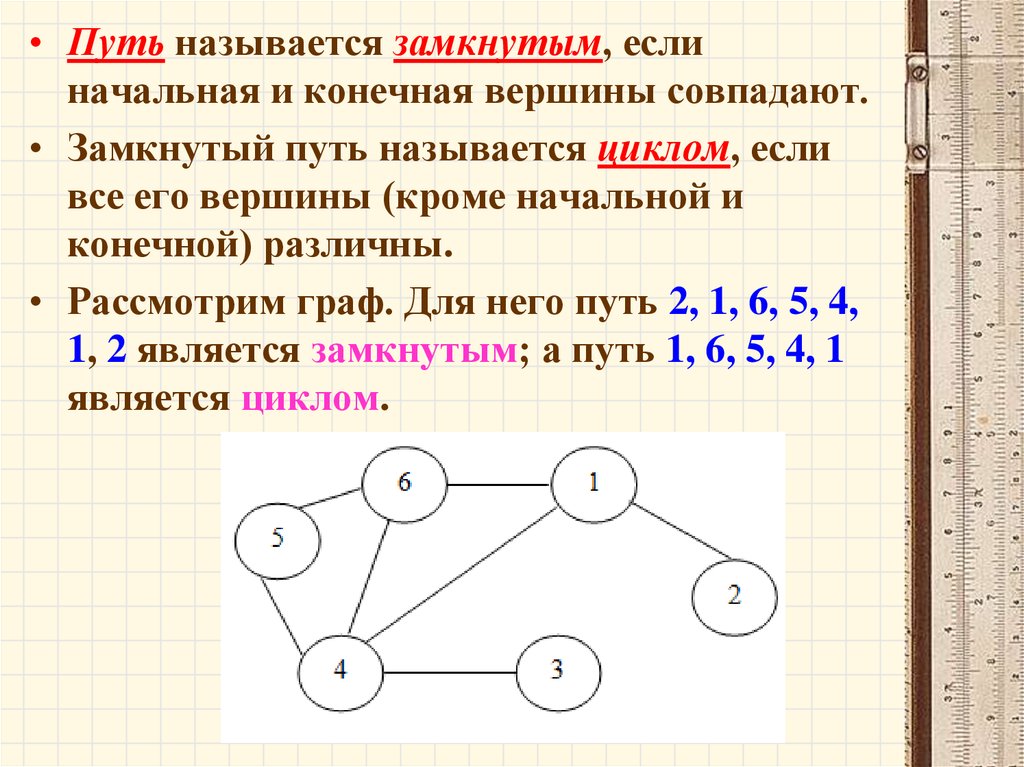
• Путь называется замкнутым, если
начальная и конечная вершины совпадают.
• Замкнутый путь называется циклом, если
все его вершины (кроме начальной и
конечной) различны.
• Рассмотрим граф. Для него путь 2, 1, 6, 5, 4,
1, 2 является замкнутым; а путь 1, 6, 5, 4, 1
является циклом.

70.

• Последовательность попарно смежных
вершин неориентированного графа, т.е.
последовательность рёбер
неориентированного графа, в которой
вторая вершина предыдущего ребра
совпадает с первой вершиной следующего,
называется маршрутом.
• Число рёбер маршрута называется длиной
маршрута.
• Если начальная вершина маршрута
совпадает с конечной, то такой маршрут
называется замкнутым или циклом.

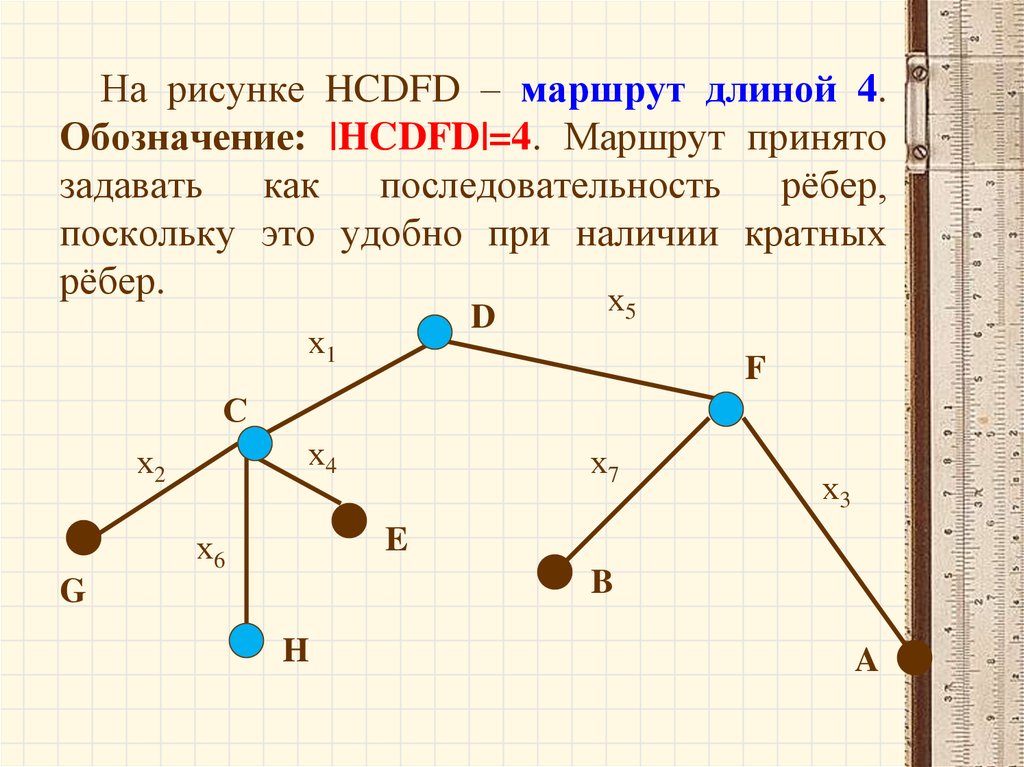
71.

На рисунке HCDFD – маршрут длиной 4.
Обозначение: |HCDFD|=4. Маршрут принято
задавать как
последовательность рёбер,
поскольку это удобно при наличии кратных
рёбер.
х
5
D
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A

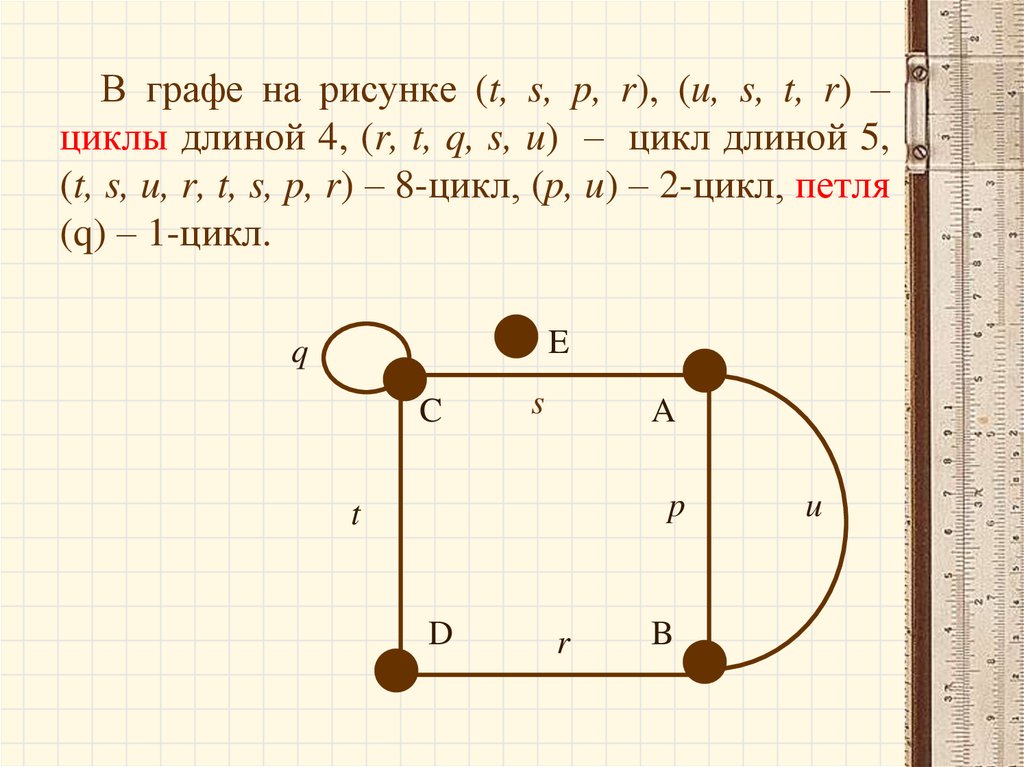
72.

В графе на рисунке (t, s, p, r), (u, s, t, r) –
циклы длиной 4, (r, t, q, s, u) – цикл длиной 5,
(t, s, u, r, t, s, p, r) – 8-цикл, (p, u) – 2-цикл, петля
(q) – 1-цикл.
E
q
C
s
A
p
t
D
r
B
u

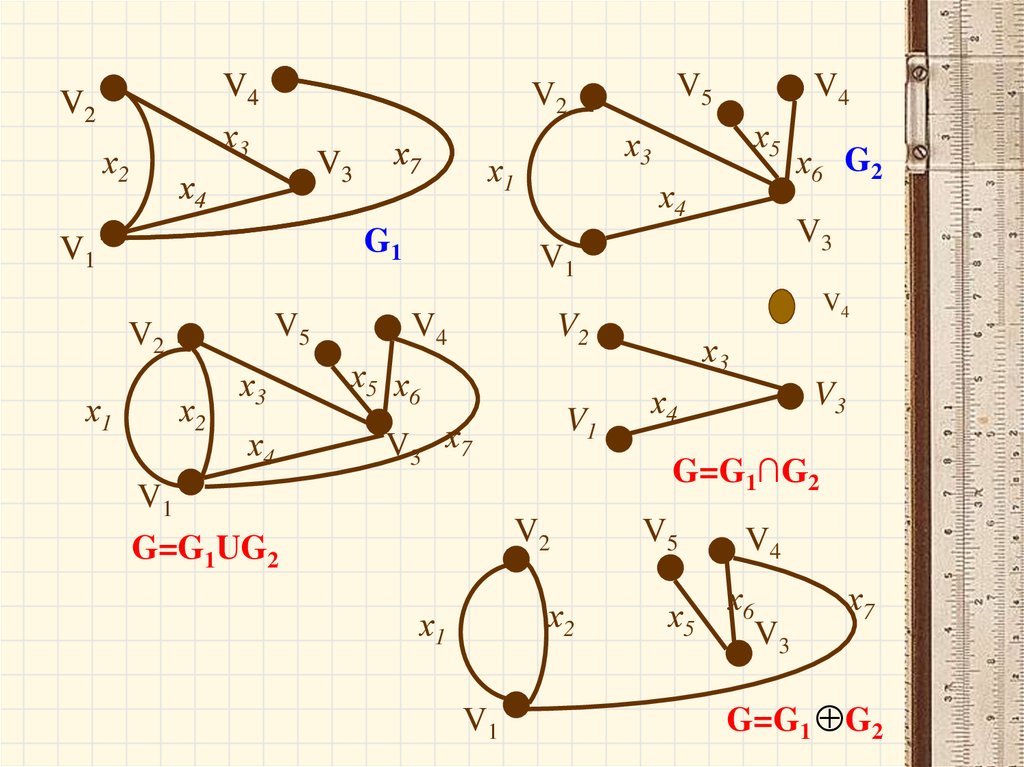
73. Операции над графами

Объединением графов G1 (V1 , X 1 ) и G2 (V2 , X 2 )
называется граф G G1 , G2 множество
вершин
которого V V1 V2 , а множество рёбер X X 1. X 2
Пересечением графов G1 и G2
называется граф G G1 G2 , для которого
X X 1 X 2 - множество рёбер, а V V1 V2 множество вершин.
Кольцевой суммой двух графов называется
граф G G1 G2 ,порождённый
множеством
вершин V V1 V2 и множеством рёбер ( X 1 X 2 ) \ ( X 1 X 2 )
, т.е. множеством рёбер, содержащихся либо в G1 ,
либо в G2 , но не в G1 G2
.

74.

V4
х3
V2
х2
V3
х4
х1
х7
V5
х2
х3
х4
V4
х5
х3
х1
G1
V1
V2
V5
V2
х4
V3
V1
V4
V3
V4
V2
х5 х6
V1
х7
V1
G=G1UG2
х2
V1
х3
V3
х4
G=G1∩G2
V2
х1
х6 G 2
V5
V4
х5 х6V
3
х7
G=G1 G2

75. Обоснование основных понятий комбинаторики: факториал, перестановки, размещения, сочетания.

76.

*Комбинаторикой называется раздел
математики, в котором исследуется,
сколько различных комбинаций
(всевозможных объединений элементов),
подчиненных тем или иным условиям,
можно составить из элементов,
принадлежащих данному множеству.
*Слово «комбинаторика» происходит от
латинского слова combinare, которое
означает «соединять, сочетать».

77.

В частности, одним из видов комбинаторных задач являются
задачи на соединения
Виды соединений
перестановки
размещения
сочетания
В задачах по комбинаторике часто применяется такое
понятие как факториал ( в переводе с английского «
factor» – множитель)
n! = 1· 2· 3· …· (n -1)n
Свойство: 0!=1

78. Перестановки

* Перестановки
Множество называется упорядоченным, если каждому элементу этого
множества поставлено в соответствие некоторое число (номер элемента) от 1
до n, где n – число элементов множества, так что различным элементам
соответствуют различные числа.
– различные упорядоченные множества,
которые отличаются лишь порядком элементов.
Формула (число размещений «из эн по эм»):
Pn n!
Термин “перестановка” употребил
впервые Якоб Бернулли в книге «Искусство
предположений».
Р – первая буква французского слова
permutation – перестановка.
(1654-1705)

79.

* Перестановки
Пример 1: В расписании сессии 3 экзамена (история,
геометрия, алгебра). Сколько может быть вариантов
расписаний?
Решение. (обратить внимание на его оформление!)
Основное множество: {история, геометрия, алгебра} n 3
Соединение – вариант расписания сессии
Проверим, важен ли порядок:
{история, геометрия, алгебра} и {геометрия, история, алгебра}
– варианты расписания сессии для разных групп порядок важен
это последовательность это перестановка из трех элементов.
Р3 3! 6
Ответ: 6 вариантов

80. Перестановки

* Перестановки
Пример 2
Перестановки множества А={a, b, c} из трёх элементов
имеют вид:
(a, b, c);
(b, c, a);
(c, a, b);
(a, c, b);
(b, a, c);
(c, b, a),
т. е. P3 = 3! = 1х2х3 = 6 перестановок.
Пример 3
Сколькими способами можно разместить на полке 4 книги?
P4 = 4! = 1х2х3х4 = 24 способа.

81. Перестановки с повторениями

* Перестановки с повторениями
Рассматривая перестановки ранее, мы предполагали, что n элементов
различны.
Если среди n элементов есть n1 элемент одного вида, n2 элементов другого
вида и т.д., nk элементов k-го вида, то имеем перестановки с повторениями,
их число:
n!
P n ( n1 ,.., nk )
, где
n1!.....nk !
n1 ... nk n
Пример 4.
Сколько различных «слов» можно составить из букв слова ДЕД?
n=3, k=2, n1=2, n2=1
3!
1 2 3
P 3 ( 2,1)
3
2! 1!
1 2 1

82.

* Перестановки с повторениями
Пример 5. Слова и фразы с переставленными буквами
называют анаграммами. Сколько анаграмм можно
составить из слова «макака»?
Решение.
Всего в слове «МАКАКА» 6 букв (m=6).
Определим сколько раз в слове используется каждая буква:
«М» - 1 раз (k1=1)
«А» - 3 раза (k2=3)
«К» - 2 раза (k3=2)
m!
Р=
k1! k2! …kn!
6!
4*5*6
Р1,3,2 =
= 2 = 60.
1! 3! 2!

83. Размещения

Размещением из n элементов по m ( m ≤ n)
называется последовательность, состоящая из m
различных элементов некоторого n элементного
множества.
Два размещения из n элементов считаются различными, если они
отличаются самими элементами или порядком их расположения.
Формула (число
размещений «из эн по эм»):
n!
A
( n m )!
m
n
Пример 6.
Сколькими способами можно рассадить 4 учащихся на 25
мест?
A 25 24 23 22 303600
4
25

84. Размещения

Пример 7. Сколькими способами из 40 учеников
класса можно выделить актив в следующем составе:
староста, физорг и редактор стенгазеты?
Решение:
Требуется выделить упорядоченные трехэлементные
подмножества множества, содержащего 40 элементов,
т.е. найти число размещений без повторений из 40
элементов по 3.
40!
A=
=38*39*40=59280
37!
3
40

85.

Пример 8. Сколько существует двузначных чисел, в которых
цифра десятков и цифра единиц различны и нечетны?
Решение (обратить внимание на его оформление!)
Основное множество: {1, 3, 5, 7, 9} – нечетные цифры
Соединение – двузначное число
n 5
m 2
Проверим, важен ли порядок: 13 31 -разные двузначные числа
-порядок важен это последовательность это размещение «из пяти по
два».
5!
A
4 5 20
( 5 2 )!
2
5
Ответ: 20 чисел.
двузначных чисел

86. Размещения с повторениями

*
– соединения,
содержащие n элементов, выбираемых из
элементов m различных видов ( n m ) и
отличающиеся одно от другого либо
составом, либо порядком элементов.
*Их количество в предположении
неограниченности количества элементов
каждого вида равно

87. Размещения с повторениями

Пример 9. В библиотеку, в которой есть много одинаковых учебников по
десяти предметам, пришло 5 школьников, каждый из которых хочет
взять учебник. Библиотекарь записывает в журнал по порядку названия
(без номера) взятых учебников без имен учеников, которые их взяли.
Сколько разных списков в журнале могло появиться?
Решение: Так как учебники по каждому предмету
одинаковые, и библиотекарь записывает лишь название (без
номера),то список – размещение с повторением, число
элементов исходного множества равно 10, а количество
позиций – 5.
Тогда количество разных списков равно
= 100000.
Ответ: 100000

88.

*
Сочетанием из n элементов по m ( m ≤ n)
называется m- элементное подмножество
некоторого n элементного множества.
Сочетания – конечные множества, в
которых порядок не имеет значения.
Формула (число размещений «из эн по эм»):
C
m
n
n!
( n m )! m!

89. Сочетания

*
Пример 10. Сколькими способами можно составить
букет из 3 цветов, если в вашем распоряжении 5 цветов:
мак, роза, тюльпан, лилия, гвоздика?
Решение. (обратить внимание на его оформление!)
Основное множество: {мак, роза, тюльпан, лилия, гвоздика}
Соединение – букет из трех цветков
Проверим, важен ли порядок:
m 3
n 5
{тюльпан, лилия, гвоздика} и {лилия, тюльпан, гвоздика} – один и тот же
букет порядок неважен это подмножество это сочетание «из пяти по
три».
C53
5!
4 5
10
( 5 3 )! 3!
2
Ответ: 10 букетов

90. Сочетания с повторениями

*
Сочетаниями с повторениями из m
по n называют соединения, состоящие
из n элементов, выбранных из
элементов m разных видов, и
отличающиеся одно от другого хотя бы
одним элементом.
Число сочетаний из m по n
обозначают

91. Сочетания с повторениями

*
*
Если из множества, содержащего n элементов,
выбирается поочередно m элементов, причём
выбранный элемент каждый раз возвращается обратно,
то количество способов произвести неупорядоченную
выборку – число сочетаний с повторениями –
составляет

92.

Пример 11. Сколько костей находится в
обычной игре "домино"?
Решение: Кости домино можно рассматривать как
сочетания с повторениями по две из семи цифр
множества (0,1,2,3,4,5,6).
Число всех таких
сочетаний равно