Хвильові рівняння

1. Розділ 6 ПОШИРЕННЯ ЕЛЕКТРОМАГНІТНИХ ХВИЛЬ У РІЗНИХ СЕРЕДОВИЩАХ

LOGO
1

2. Зміст

6.1
LOGO
Хвильові рівняння
6.2
Поняття про однорідні пласкі електромагнітні хвилі
6.3
Хвильові рівняння однорідних пласких хвиль
6.4 Особливості поширення однорідних пласких хвиль у різних
середовищах
2Напівпровідне середовище (діелектрик із
6.4.1 втратами)
6.4.2 Діелектрики та провідники
6.5
6
6.6
Поверхневий ефект у провідниках
Поляризація однорідних пласких хвиль
6.7
Висновки
6.8
Контрольні питання та завдання
2

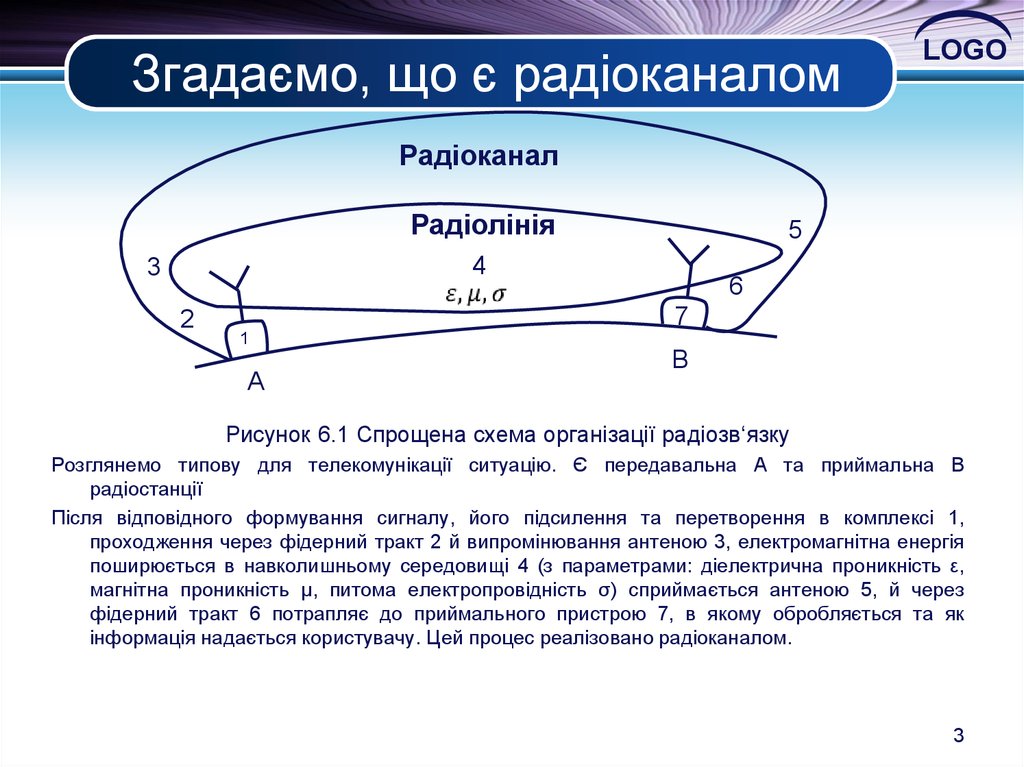
3. Згадаємо, що є радіоканалом

LOGO
Радіоканал
Радіолінія
5
4
3
2
6
7
1
A
B
Рисунок 6.1 Спрощена схема організації радіозв‘язку
Розглянемо типову для телекомунікації ситуацію. Є передавальна А та приймальна В
радіостанції
Після відповідного формування сигналу, його підсилення та перетворення в комплексі 1,
проходження через фідерний тракт 2 й випромінювання антеною 3, електромагнітна енергія
поширюється в навколишньому середовищі 4 (з параметрами: діелектрична проникність ε,
магнітна проникність μ, питома електропровідність σ) сприймається антеною 5, й через
фідерний тракт 6 потрапляє до приймального пристрою 7, в якому обробляється та як
інформація надається користувачу. Цей процес реалізовано радіоканалом.
3

4. 6.1 Хвильові рівняння

LOGO
6.1 Хвильові рівняння
Проаналізуємо електромагнітні процеси у навколишньому просторі із застосуванням
рівнянь Максвелла . Скористаємось першим та другим рівняннями:
E
rotH E
;
t
H
rotE
.
t
Здійснимо операцію rot стосовно другого рівняння Максвелла та підстановку із
першого, й отримаємо зі зміною порядку диференціювання:
H
E
rotrotE rot
E
.
t
t
t
(6.1)
Представимо ліву частину (6.1) за відомою тотожністю векторного аналізу:
rotrot E graddivE 2 E
отримаємо:
;
E
2 E
2 graddivE 2 E .
t
t
(6.2)
4

5.

LOGO
На основі третього та п’ятого рівнянь Максвелла маємо:
divE
після перегрупування доданків (6.2) отримаємо рівняння:
2 E
E
E 2 grad
t
t
2
;
(6.3)
відоме як рівняння Гельмгольца.
У цьому рівнянні є складники, які визначають процес у просторі й часі,
а також є добуток , який пов’язаний із швидкістю поширення
електромагнітних хвиль ( v 1 ),
тобто
рівняння
(6.3)
характеризує хвильовий процес.
Якщо аналогічно застосувати операцію rot до обох частин першого
рівняння Максвелла, отримаємо хвильове рівняння для вектора
напруженості магнітного поля:
2 H
H
H 2
t
t
2
(6.4)
5

6. Якщо аналогічно застосувати операцію rot до обох частин першого рівняння Максвелла, отримаємо хвильове рівняння для вектора

LOGO
Якщо аналогічно застосувати операцію rot до обох частин першого
рівняння Максвелла, отримаємо хвильове рівняння для вектора напруженості
магнітного поля:
2
H
H
2
H 2
.
t
t
(6.4)
Для гармонічних процесів наведемо хвильові рівняння в комплексній
формі. Отже, запишемо функцію, її першу та другу похідні:
j t
E (t ) Em e ,
j t
E
j E m e ,
t
j t
2E
2
Em e .
2
t
(6.5)
6

7. Підставимо (6.5) в (6.3) з урахуванням комплексного представлення функції й після скорочення отримаємо:

LOGO
Підставимо (6.5) в (6.3) з урахуванням комплексного представлення
функції t e j t й після скорочення e j t отримаємо:
m
m
Em j Em grad
2
2
(6.6)
Формула в дужках (6.6) – комплексна діелектрична проникність
З урахуванням цього, (6.6) матиме вигляд:
m
Em Em grad
2
2
.
(6.6а)
Аналогічним чином можна отримати комплексну форму хвильового
рівняння для вектора напруженості магнітного поля:
2 H m 2 H m 0
(6.7)
7

8. У загальній формі хвильові рівняння є складними. Але практичні розрахунки виконують за конкретних обставин, коли можна прийняти

LOGO
У загальній формі хвильові рівняння є складними. Але
практичні розрахунки виконують за конкретних
обставин, коли можна прийняти деякі умови, що
дозволяють спростити хвильові рівняння. Наприклад, в
однорідному середовищі, на великій відстані від
джерела електромагнітного поля кривизною фронту
хвилі можна знехтувати й вважати розподіл амплітуд
векторів напруженості електричного та магнітного
складників електромагнітного поля рівномірним. Така
хвиля має назву однорідна пласка, її застосовують
для виконання практичних розрахунків.
8

9. 6.2 Поняття про однорідні пласкі електромагнітні хвилі

LOGO
Припустимо, що джерело електромагнітного поля розташоване в
початку декартової системи координат, і хвиля поширюється в
додатному напрямі осі z. Звернемося до сферичного фронту хвилі,
фрагмент S , який можна вважати пласким, поширюється вздовж осі z
(на що вказує вектор Пойнтінга ) (рис. 6.2). Хвиля, яка може бути
представлена таким фронтом, має назву поперечна (плоска).
y
S
H
0
E
z
П
x
Рисунок 6.2 – Фрагмент фронту хвилі
та вектор Пойнтінга
9

10.

LOGO
Відомо, що вектори та в просторі взаємно перпендикулярні, кожен з них
має, в загальному випадку, три складники Еx, Ey, Ez та Hx, Hy, Hz,
відповідно.
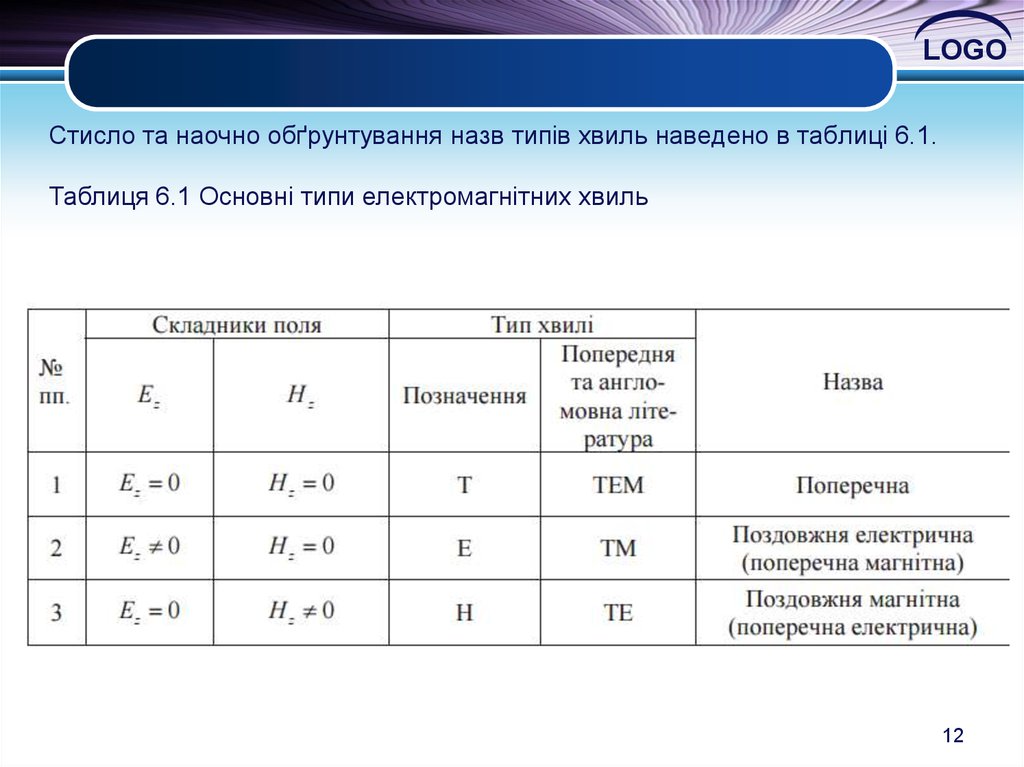
З’ясуємо три можливі ситуації:
1. Складники Ez та Hz відсутні, тобто Ez = 0 i Hz = 0. В цій ситуації є тільки
складникиі Еx, Ey та Hx, Hy й така хвиля має назву поперечна хвиля, або
хвиля типу Т (від transverse – поперечний); в англомовній літературі й
літературі попередніх років її називають хвиля типу ТЕМ – поперечна (Т)
електромагнітна (ЕМ);
2. Складник Ez є, складник Hz відсутній, тобто Ez 0, Hz = 0 й така хвиля
має назву поздовжня електрична хвиля типу Е; в англомовній літературі й
літературі попередніх років її називають хвиля типу ТМ – поперечна (Т)
магнітна (М);
3.Складник Нz є, складник Еz відсутній, тобто Ez = 0, Hz 0 й така хвиля
має назву поздовжня електрична хвиля типу Н; в англомовній літературі й
літературі попередніх років її називають хвиля типу ТЕ – поперечна (Т)
електрична (Е).
10

11. Таким чином, за умови великої відстані від джерела, ділянку фронту хвилі S можна вважати пласкою, для якої Ez = 0 і Hz = 0,

LOGO
Таким чином, за умови великої відстані від джерела, ділянку фронту
хвилі S можна вважати пласкою, для якої Ez = 0 і Hz = 0, тобто – це
хвиля типу Т, що має не шість, а тільки чотири проекції Еx, Ey та Hx, Hy.
Таке
припущення
суттєво
спрощує
опис
хвилі.
За умов однорідного й без втрат ( 0) середовища, тобто значення
незмінні: = const та = const, вектори напруженості електричного та
магнітного полів у всіх точках простору ділянки S не змінюють значення
та напрям. Тоді, відповідні частинні похідні дорівнюють нулю:
Ex
0,
x
Ex
0,
y
H x
0,
x
H x
0,
y
E y
x
H y
x
0,
0,
E y
0;
y
H y
0.
y
(6.8)
11

12. Стисло та наочно обґрунтування назв типів хвиль наведено в таблиці 6.1.

LOGO
Стисло та наочно обґрунтування назв типів хвиль наведено в таблиці 6.1.
Таблиця 6.1 Основні типи електромагнітних хвиль
Ez 0 H z 0
12

13.

LOGO
З урахуванням прийнятих припущень для пласкої однорідної хвилі
формули стають суттєво простішими, що полегшує розрахунки.
Пласка однорідна хвиля, за поширення якої напрям вектора –
незмінний, має назву лінійно-поляризована хвиля. Поляризація
електромагнітних хвиль має важливе практичне значення.
Наприклад, від виду поляризації електромагнітної хвилі залежить
взаємне розташування приймальної та передавальної антен, що є
важливим в організації зв’язку та забезпеченні електромагнітної
сумісності.
13

14. 6.3 Хвильові рівняння однорідних пласких хвиль

LOGO
Проаналізуємо ситуації, якщо в просторі заряд відсутній. Тоді хвильове рівняння
(6.6а) електричного поля матиме вигляд:
2 Em 2 Em 0
(6.9)
Вектор визначають трьома проекціями:
Em iEmx jEmy kEmz
(6.10)
Рівнянню (6.9) з урахуванням (6.10) задовольняє система трьох рівнянь
2 E mx 2 E mx 0,
2
2
E my E my 0,
2
2
E mz E mz 0.
(6.11)
14

15.

LOGO
Для однорідних пласких хвиль (див. умови (6.8)) з урахуванням того, що Ez = 0,
Hz=0 за визначенням пласкої (поперечної) хвилі, система (6.11) спрощується і має
вигляд:
2
Emx
2
Emx 0,
2
z
2
Emy
2
0.
E
my
z 2
(6.12)
Аналогічний вигляд має система для напруженості магнітного поля:
H mx
2
0,
H
mx
2
z
2
H my
2
H my 0.
2
z
2
(6.12а)
15

16.

LOGO
Рівняння (6.12) та (6.12а) мають однакову структуру й, відповідно, аналогічний
розв’язок. Це однорідні диференціальні рівняння другого порядку. Їх розв’язок
має два доданки із показовими функціями, якщо коефіцієнт другого доданка є
від’ємним, тобто:
k 2 2
(6.13)
k j
або
(6.13а)
Обґрунтування його назви - коефіцієнт поширення хвилі див. (6.19) та
(6.20).
Перепишемо системи (6.12) і (6.12а) з урахуванням коефіцієнта k:
Emx
2
k
Emx 0
2
z
2 Emy
z
2
k Emy 0
H mx
2
k
H mx 0
2
z
2
2
(6.14)
H my
(6.15)
2
2
(6.14а)
z 2
k 2 H my 0
(6.15а)
16

17.

LOGO
Розв’язок цих рівнянь визначає проекції векторів та у будь-який момент часу
t. В рівняннях (6.14) – (6.15а) є взаємно пов’язані пари, тому замість чотирьох
рівнянь можна розв’язувати лише два.
Скористаємось першим рівнянням Максвелла, яке встановлює зв’язок між
векторами напруженості електричного і магнітного полів:
rotH m j Em
Використаємо форму запису вектора через проекції та скористаємось визначенням
операції ротор. Тоді маємо:
rotH m i ( j E mx ) j ( j E my ) k ( j E mz )
H mz H my
i
y
z
H mx H mz
j
x
z
(6.16)
H my H mz
k
x
y
17

18.

LOGO
Із урахування ознак однорідних пласких хвиль (6.8) отримаємо з
(6.16):
H my
j E mx
z
H mx
j E my
z
(6.17)
(6.18)
Тобто проекція пов’язана з , а пов’язана - ці пари створюють поперечну
хвилю (типу Т).
З’ясуємо, яким чином описують процес поширення електромагнітних хвиль
в просторі та вплив на цей процес параметрів середовища.
18

19. 6.4.1. Напівпровідникове середовище (діелектрик з втратами)

LOGO
6.4. Особливості поширення однорідних
плоских хвиль у різних середовищах
6.4.1. Напівпровідникове середовище (діелектрик з втратами)
Задля отримання рівняння, що описує процес поширення електромагнітної хвилі,
визначимо розв’язок одного з рівнянь – (6.14), відомий з курсу математики:
Emx Emx1 e kx Emx2 ekx
(6.19)
Комплексний коефіцієнт , який має назву коефіцієнт поширення, запишемо у
формі:
k j ,
(6.20)
де – коефіцієнт згасання, – коефіцієнт фази. Із урахуванням (6.20) формула
(6.19) матиме вигляд:
(6.21)
z j z
z j z
Emx Emx1 e
e
Emx2 e e
Миттєві значення , тобто як функція часу:
Emx Emx 1 e az cos( t z 1 ) Emx 2 eaz cos( t z 2 )
(6.22)
19

20.

LOGO
У рівняннях (6.21) та (6.22) перші доданки характеризують хвилю, що
віддаляється від початку відліку (координат), тобто пряму хвилю або
хвилю, що падає. Її амплітуда зменшується за законом , тому параметр
має назву – коефіцієнт згасання. Параметр характеризує стан
відставання за фазою залежно від тому він має назву – коефіцієнт
фази. Таким чином, комплексний коефіцієнт має обґрунтовану назву –
коефіцієнт поширення електромагнітних хвиль.
У рівняннях (6.21) та (6.22) перші доданки характеризують хвилю, що
віддаляється від початку відліку (координат), тобто пряму хвилю або
αz
хвилю, що падає. Її амплітуда зменшується за законом e
, тому
параметр α має назву – коефіцієнт згасання. Параметр
характеризує стан відставання за фазою залежно від z тому він має
назву – коефіцієнт фази. Таким чином, комплексний коефіцієнт має
k
обґрунтовану назву – коефіцієнт поширення електромагнітних хвиль.
20

21.

LOGO
Другі доданки рівнянь (6.21) та (6.22) характеризують хвилю, що
наближається до початку відліку – тобто це зворотна, або відбита
хвиля. Обвідні таких хвиль наведено на рис. 6.3.
Для кращого сприйняття аргументу із двох змінних часу t і відстані z наведемо
функцію fм Fм cos( t z ) (за умови, що початкові фази та коефіцієнт
згасання дорівнюють нулю) і побудуємо відповідні залежності, з яких
випливає взаємозв’язок функції f від t (рис. 6.4).
На рис. 6.4а представлено залежність від t функції виду f 1 Fм cos (t z / )
із зсувом фази z / , а на рис. 6.4б представлено залежність від
. t/
z f 2 Fм cos ( t / z ) із зсувом фази
Ще раз звертаємо увагу на сутність фази хвильового процесу ( t z ) , яка
має два доданка t , де
, тобто характеризує відношення
T
2 періодів: на тригонометричному колі – 2 , та в часі – період ; й - z , де
, тобто характеризує відношення періодів: а тригонометричному колі – 2
та за відстанню – довжина хвилі .
21

22.

LOGO
f2
f1
t
z
z
t
(6.4a)
(6.4б)
Рисунок 6.4. Фрагменти залежностей хвильового процесу: а – як функції
часу, б – як функції відстані
22

23.

LOGO
Рисунок 6.2 – Фрагменти залежностей хвильового процесу: а – як функції часу,
б – як функції відстані
Аналогічно для (6.15а) маємо:
az
j
z
az
j
z
k
(6.23)
H my H my e e
H my e e H y e z H y e kz
1
2
1
2
H my H my 1 e az cos( t z 1 ) H my 2 eaz cos( t z 2 )
(6.24)
Встановимо зв’язок між складниками та . На підставі (6.17) після
диференціювання (6.23) з у рахуванням з (6.20) та перегрупування доданків
маємо:
k H my j E mx e kz k H my j E mx e kz 0. (6.25)
1
1
2
2
Рівняння (6.25) є правильним для будь яких значень , якщо обидві складника
(у дужках) тотожно дорівнюють нулю, тобто із (6.25) маємо два рівняння:
k H my 1 j E mx 1 0, (6.26)
k H my 2 j E mx 2 0. (6.26а)
23

24.

LOGO
Із формул (6.26) та (6.26а) випливає, що між та існує взаємозв’язок. Цей
взаємозв’язок визначають величиною:
E mx 1
k
(6.27)
Z w1
H my 1
j
Z w2
E mx 2
k
H my 2
j
(6.27а)
який має одиницю вимірювання [Ом] та відповідну назву – хвильовий опір, точніше –
імпеданс – внаслідок комплексного характеру. З урахуванням (6.13а), (4.41):
Zw
j
j
(6.28)
Хвильовий імпеданс можна представити в алгебраїчній формі:
j j j
Z w X w jYw
j
2 2
k
(6.29)
24

25.

LOGO
де дійсний складник:
(6.30)
уявний складник:
(6.31)
В полярній системі координат
E mx 1 e j 1
E mx 1 j ( 1 2 )
j
Zw
e
Z
e
w
H my 1 e j 2 H my
(6.32)
1
де модуль та фаза хвильового імпедансу, відповідно
Z w X w2 Yw2
2 2
(6.33)
Значення модуля характеризує співвідношення амплітуд напруженості електричного
та магнітного полів, – зсув за фазою між миттєвими значеннями складників Е та Н.
Yw
arctg
arctg
Xw
(6.33а)
25

26.

LOGO
Із (6.27) та (6.27а) маємо:
Z w1 Z w2
(6.34)
Таким чином, хвильові імпеданси для прямої та зворотної хвиль однакові за
модулем, але відрізняються за фазою на кут .
Тоді співвідношення (6.24) можна записати у вигляді:
H y (t , z )
Emx 1 e z
Zw
cos( t z 1 )
Emy 2 e z
Zw
cos( t z 2 ). (6.35)
Якщо вважати простір, в якому поширюється хвиля однорідним, то зворотної
(відбитої, вторинної) хвилі не буде, тобто другий складник (доданок) правої
частини (6.21), (6.22), (6.23), (6.24), (6.25), (6.35) відсутній.
26

27.

LOGO
Графіки миттєвих значень функцій Ex(t,z) та Hy(t,z) прямої хвилі представлено на рис. 6.5 в
момент , коли фаза хвилі в будь-якій точці простору відстає за фазою на значення ,
амплітуда менша в раз. В наступний момент фаза хвилі у всіх фіксованих точках буде
зміненою на значення , а амплітуда буде незмінною, тобто маємо рухому хвилю з
вектором Пойнтінга вздовж осі .
Рисунок 6.5 Хвильове рівняння визначає процес поширення у просторі та за часом електромагнітних
хвиль, тобто процес, який поширюється з певною швидкістю. Визначимо швидкість
поширення хвилі. Для цього наведемо приклад повної фазу у прямій хвилі в момент t1
на відстані z1 та визначимо момент t2 (t2>t1), для якого у точці z2 повна фаза також
дорівнює , тобто:
1
1
t z ,
t2 z2 .
(6.36)
27

28.

LOGO
Тоді
t2 t1
( z2 z1 )
(6.37)
Звідси швидкість поширення хвилі або фазова швидкість дорівнює:
v
z2 z1 2
,
t2 t1
T
2 2 j 2 2 .
(6.38)
де величину Т називають періодом хвилі.
Визначимо довжину хвилі, що поширюється. Нехай t2 - t1 =T період гармонічної
функції. Тоді довжина хвилі
z 2 z1 vT
T 2 fT 2
(6.39
Таким чином, досліджено закономірності, за які описують процес поширення
електромагнітних хвиль. Визначимо розрахункові формули для коефіцієнтів і .
Піднесемо до квадрату формули (6.13а) та (6.20) й отримаємо рівняння:
2 2 j 2 2 .
(6.40)
28

29.

LOGO
З урахуванням (4.41), де
Маємо
j
2 j 2 2 j 2
(6.40а)
Окремо для дійсної частини та уявної частини відповідно є:
2 2 2 ,
2 .
(6.41)
Розв’язок системи (6.41)з урахуванням того, що – додатна дійсна величина:
2
1
1
2
2
1
1
2
(6.42)
(6.43)
29

30.

LOGO
Із урахуванням тангенса кута втрат (4.39) маємо:
(6.42а)
(6.43а)
На практиці, зазвичай маємо середовища, в яких або Іпр>>Ізм (провідники),
або Іпр<<Ізм (діелектрики). Для цих випадків співвідношення можна
спростити.
30

31. 6.4.2. Діелектрики та провідники

LOGO
У пункті 6.4.1 наведено формули, які характеризують процес
поширення
електромагнітних
хвиль
в
напівпровідному
середовищі (діелектрик з втратами). Ознакою діелектрика або
провідника є співвідношення між густиною струму провідності та
зміщення, або значення тангенса кута втрат tg <<1 – діелектрик,
=0; tg >1 – провідник.
Величини, що характеризують процес поширення електромагнітних
хвиль в різних середовищах, для зручності застосування
зведено в таблицю 6.2.
31

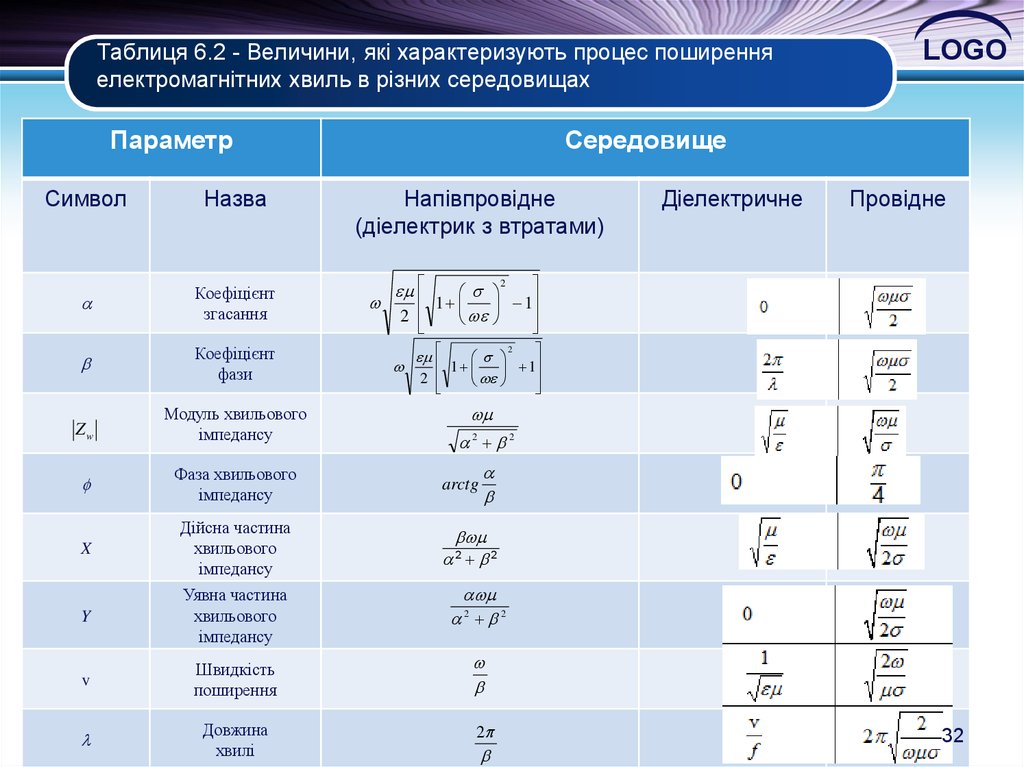
32. Таблиця 6.2 - Величини, які характеризують процес поширення електромагнітних хвиль в різних середовищах

Параметр
Символ
Назва
Коефіцієнт
згасання
Коефіцієнт
фази
Zw
Модуль хвильового
імпедансу
Фаза хвильового
імпедансу
X
Дійсна частина
хвильового
імпедансу
Y
Уявна частина
хвильового
імпедансу
v
Швидкість
поширення
Довжина
хвилі
LOGO
Середовище
Напівпровідне
(діелектрик з втратами)
Діелектричне
Провідне
2
1
1
2
2
1
1
2
2 2
arctg
2
2
2 2
2
32

33.

LOGO
На підставі співвідношень наведених в табл. 6.2 можна сформулювати такі
висновки:
- в діелектричному середовищі хвиля поширюється без втрат, фаза
хвильового опору дорівнює нулю;
- в провідному середовищі втрати пропорційні , фаза хвильового опору
незмінна, довжина хвилі залежить від параметрів середовища й
частоти.
Таким чином, найбільш сприятливим для поширення електромагнітних
хвиль є діелектричне середовище. В реальних провідниках
електромагнітне поле швидко згасає, що призвело до поширеного
поняття “витискання” (що не є коректним) поля змінного струму до його
поверхні, тобто в провіднику має місце, так званий, поверхневий
ефект (skin-effect).
33

34. 6.5. Поверхневий ефект у провідниках

LOGO
Рисунок 6.5. Процес проникнення
електромагнітного поля в провідник
34

35.

LOGO
35

36.

LOGO
36

37.

LOGO
37

38.

LOGO
38

39. 6.6. Поляризація однорідних пласких хвиль

LOGO
Поляризація – це явище, що характеризує орієнтацію векторів
напруженості електричного та/або магнітного поля.
Рисунок 6.5. Площина поляризації
однорідної пласкої хвилі
39

40.

LOGO
Така поляризація має назву – лінійна поляризація – вертикальна або
горизонтальна.
40

41.

LOGO
41

42.

LOGO
Тобто у цьому випадку довжина вектора незмінна, й він описує коло. Така
поляризація має назву – колова поляризація – лівостороння або правостороння
(стосовно приймача).
E
E
,
0
.
my
1
2
3. Нехай амплітуди мають різні значення mx
2
За цих умов модуль E та кут поляризації є величинами, що змінюються, край
вектора описує еліпс. Така поляризація має назву еліптична поляризація –
лівостороння або правостороння.
Таким чином, назву поляризації визначає геометрична фігура, яку описує за часом
вектор у відповідній площині.
Електромагнітні хвилі поширюються в конкретному середовищі. В підрозділі 4.6
показано, що характер середовища (провідне; напівпровідне, або діелектрик з
втратами; діелектричне) визначають не лише електродинамічними параметрами
(діелектрична проникність, магнітна проникність, питома електропровідність ), й
частота. Тобто одне й те саме середовище може бути провідником,
напівпровідником (діелектрик з втратами), діелектриком – з урахуванням
значення частоти електромагнітного поля.
42

43. 6.7. Висновки

LOGO
1. На підставі першого та другого рівнянь Максвелла отримано хвильові
рівняння, в яких вектори поля пов’язані з простором, часом та величиною,
яка визначає швидкість поширення хвилі.
2. З метою спрощення розв’язання хвильового рівняння та з урахуванням
практичної можливості – доцільно вважати на великій відстані від джерела
випромінювання в однорідному середовищі фронт хвилі пласким, тобто
аналізувати однорідні пласкі хвилі.
3. За класифікацією електромагнітних хвиль розрізняють: поперечні хвилі
типу Т (ТЕМ), поздовжні електричні хвилі типу Е (ТМ), поздовжні магнітні
хвилі типу Н (ТЕ).
4. Із розв’язання хвильового рівняння випливає, що існує два процеси –
прямий (хвиля, що падає) та зворотний (відбита, вторинна хвиля).
5. Параметр, який характеризує процес поширення хвилі – коефіцієнт
поширення де – коефіцієнт згасання, – коефіцієнт фази.
k j
43

44.

LOGO
6. Як випливає з розв’язання хвильового рівняння, між значеннями
напруженості електричного та магнітного полів існує взаємозв’язок,
визначений величиною, яка має одиницю вимірювання [ом], й тому має
назву – хвильовий імпеданс, яка є коректна для дальнього поля, бо
хвильовий процес є в дальньому полі (див. розд. 7) й залежить від
параметрів середовища.
E m
j
Zw
.
Hm
j
7. Електромагнітні хвилі поширюються в різних середовищах. Ознакою
діелектрика або провідника є співвідношення між густиною струму та
зміщення, або значення тангенса кута втрат tg
8. В діелектричному середовищі хвиля поширюється без втрат, фаза
хвильового опору дорівнює нулю.
9. В провідному середовищі втрати пропорційні , фаза хвильового опору
незмінна, довжина хвилі залежить від параметрів середовища й частоти.
10. Найбільш сприятливим для поширення електромагнітних хвиль є
діелектричне середовище.
44

45.

LOGO
11. У реальних провідниках в напрямі до центра електромагнітне поле
швидко згасає, що призвело до поширеного поняття, «витискання поля
змінного струму до його поверхні», яке не є коректним, тому його не
слід застосовувати.
12. Ефект згасання поля (й струму) в провіднику має назву
поверхневий (skin-effect), який полягає в тому, що струм протікає в
деякому поверхневому шарі на поверхні провідника, тобто значення
сили струму в напрямі до центру провідника стає меншим.
13. Із формули 2 / випливає, що глибина проникнення поля у
провідник стає меншою із зростанням питомої електропровідності,
магнітної проникності та частоти.
14. У зв’язку із зменшенням перерізу протікання струму на високих
частотах активний опір провідника стає більшим.
15. Значення частоти, за якого слід враховувати поверхневий ефект,
залежить зокрема від діаметра провідника, тому доцільно
застосовувати багатожильні провідники, в яких провідники мають
менший діаметр.
16. Поширення електромагнітних хвиль обумовлено процесом
поляризації: лінійна, колова й еліптична (правостороння та
лівостороння).
45

46. 6.8. Контрольні питання та завдання

LOGO
1. Обґрунтуйте підхід до виведення рівняння Гельмгольца та виведіть його.
2. Охарактеризуйте компоненти рівняння Гельмгольца.
3. Обґрунтуйте доцільність та наведіть рівняння Гельмгольца в комплексній формі.
4. Охарактеризуйте типи електромагнітних хвиль.
5. Охарактеризуйте пласкі однорідні хвилі.
6. Наведіть хвильові рівняння однорідних пласких хвиль.
7. Наведіть розв’язок хвильових рівнянь пласких хвиль. Поясніть сутність
коефіцієнтів: поширення, згасання та фази електромагнітних хвиль.
8. Обґрунтуйте виведення коефіцієнтів пропорційності між напруженостями
електричного та магнітного полів.
9. Визначте швидкість поширення фронту електромагнітної хвилі.
10. Виведіть формулу для коефіцієнта згасання.
11. Виведіть формулу для коефіцієнта фази.
12. Поясніть особливість визначення коефіцієнтів згасання та фази для ідеального
діелектрика.
13. Поясніть особливість визначення коефіцієнтів згасання та фази для ідеального
провідника.
14. Поясніть сутність поверхневого ефекту у провідниках.
15. Поясніть сутність величини глибина проникнення.
16. Поясніть залежність активного опору провідника від частоти.
17. Обґрунтуйте значення граничної частоти, від якої треба враховувати поверхневий
ефект.
18. Поясніть сутність та практичне значення поляризації електромагнітних хвиль. 46