Похожие презентации:
Комплексная форма гармонической функции
1.
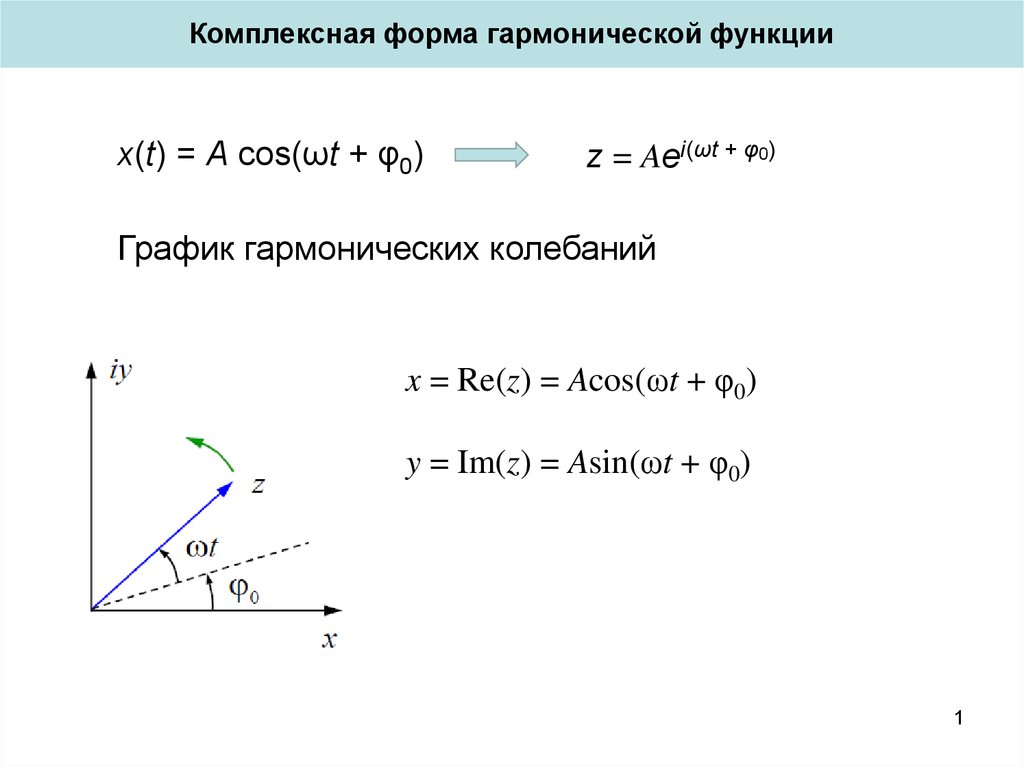
Комплексная форма гармонической функцииx(t) = A cos(ωt + φ0)
z = Aei(ωt + φ0)
График гармонических колебаний
x = Re(z) = Acos(ωt + φ0)
y = Im(z) = Asin(ωt + φ0)
1
2.
Сложение гармонических колебаний одинаковой частотыx = x1 + x2 = A1 cos(ωt + φ1) + A2 cos(ωt + φ2 )
z = z1+z2 = A1ei(ωt + φ1) + A2ei(ωt + φ2) = (A1eiφ1 + A2eiφ2)eiωt = A eiφeiωt
2
3.
Интерференция светаПринцип суперпозиции:
При наложении световых волн результирующий световой вектор
является суммой световых векторов отдельных волн.
Две гармонические волны:
a1 A1 cos t kx 1
a2 A2 cos t kx 2
a a1 a2 A cos t
A2 A12 A22 2 A1 A2 cos( 2 1 )
Интенсивность волны
I ~ A2
I I1 I 2 2 I1I 2 cos , 2 1
3
4.
Результат сложения зависит от разности фаз :I I1 I 2
cos 0
I I1 I 2
cos 0
Интерференция:
При наложении гармонических (в общем случае когерентных)
световых волн происходит перераспределение светового потока в
пространстве, в результате чего в одних местах возникают максимумы,
а в других – минимумы интенсивности.
Явление сложения световых пучков, ведущее к образованию светлых и
темных полос.
4
5.
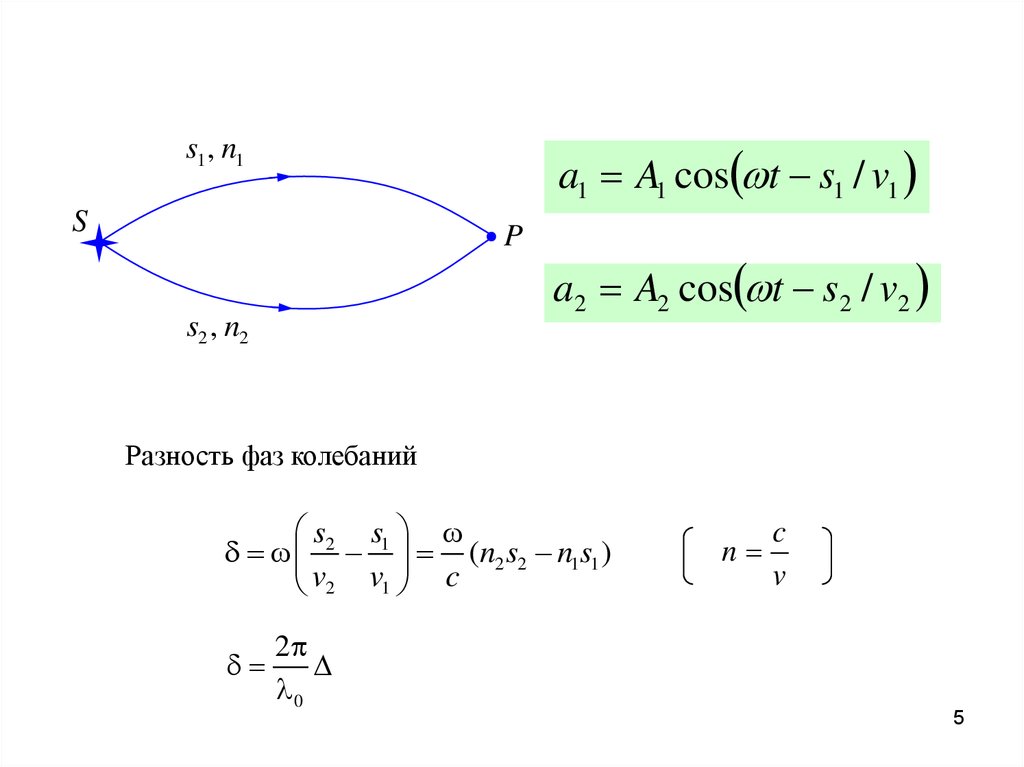
a1 A1 cos t s1 / v1s1 , n1
S
P
s2 , n2
a2 A2 cos t s2 / v2
Разность фаз колебаний
s2 s1
(n2 s2 n1s1 )
v2 v1 c
2
0
n
c
v
5
6.
n2 s2 n1s1 L2 L1 оптическая разность ходаL ns оптическая длина пути
Условие максимума: m 0 (m 0, 1, 2 ...)
Условие минимума:
m 1 2 0 (m 0, 1, 2 ...)
0 длина волны в вакууме
6
7.
Временная когерентностьКогерентность согласованное протекание колебательных
(волновых) процессов.
Временная когерентность когерентность колебаний,
совершаемых в одной и той же точке пространства, но в разные
моменты времени.
Излучение светящегося тела складывается из волн, испускаемых многими
атомами. Отдельные атомы излучают цуги волн длительностью ~10 8 с и
протяженностью около 3 м независимо друг от друга.
Начальные фазы этих волновых цугов никак не связаны между собой.
волновой цуг
l
S
длительность одного цуга, l = c длина цуга
7
8.
Временной подход к анализу интерференцииA
B
I I1 I 2 2 I1I 2 cos (t )
1.
l
cos (t ) 0
I I1 I 2 интерференция отсутствует
C
2.
l
cos (t ) 0
I I1 I 2 интерференция присутствует
tког
lког ct ког
время когерентности
длина когерентности (расстояние, при прохождении которого
волна утрачивает когерентность )
8
9.
Спектральный подход к анализу интерференцииинтервал длин волн
m
m
m 1
Интерференция не будет наблюдаться, если
( m 1) m( )
Максимумы промежуточных длин волн заполняют
промежуток между соседними максимумами для
, где m порядок интерференции
m
lког
m
2
9
10.
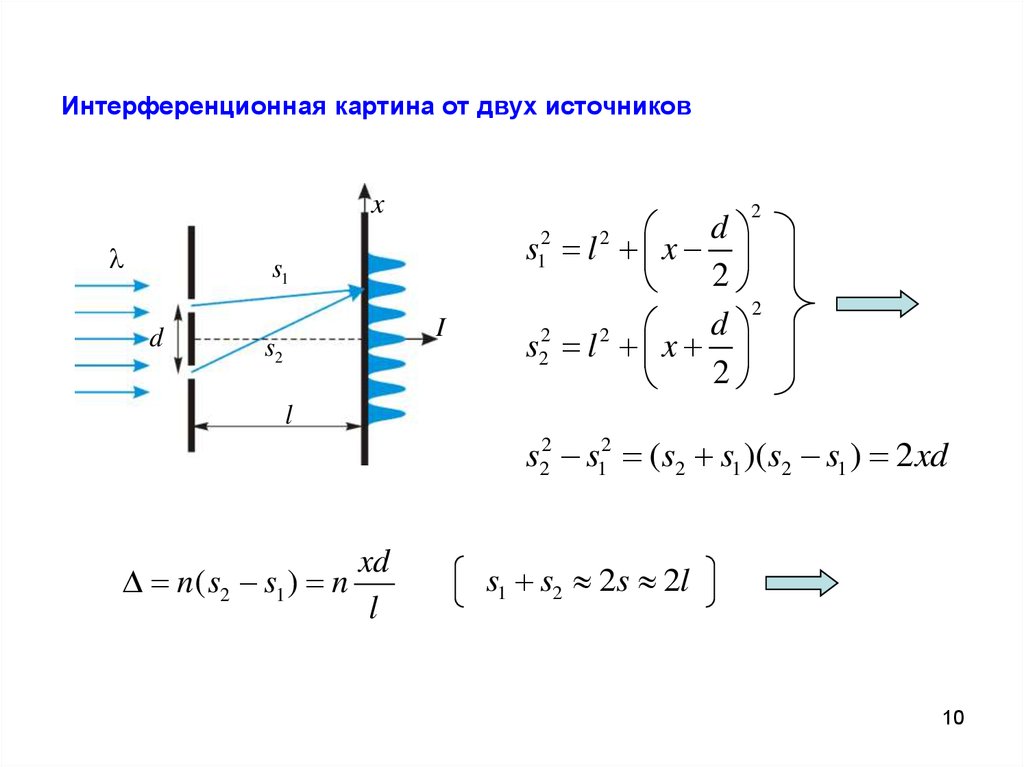
Интерференционная картина от двух источниковx
2
s1
d
I
s2
d
2
2
s1 l x
2
2
d
s22 l 2 x
2
l
s22 s12 (s2 s1 )(s2 s1 ) 2 xd
xd
n( s2 s1 ) n
l
s1 s2 2s 2l
10
11.
l(m 0, 1, 2, ...)
d
1 l
m (m 0, 1, 2, ...)
2 d
Максимумы:
xmax m
Минимумы:
xmin
0
n
– длина волны в среде
Ширина интерференционной полосы
расстояние между соседними минимумами
Расстояние между интерференционными полосами
расстояние между двумя соседними максимумами
x
l
d
11
12.
Пространственная когерентностьПространственная когерентность когерентность колебаний,
совершаемых в один и тот же момент времени, но в разных точках
пространства.
1
2
m
d
b
1
m
2
m 1
1
l
Интерференция не наблюдается (картина смазанная), если максимум (m 1)–го
порядка от точки 1 совпадает с максимумом m–го порядка от точки 2.
12
13.
1 2 0n
b
l
xd
l
bd
0
l
b
угловой размер источника
l
0
n
Интерференция возможна, если
d
n
d
условие когерентности колебания в области щелей
13
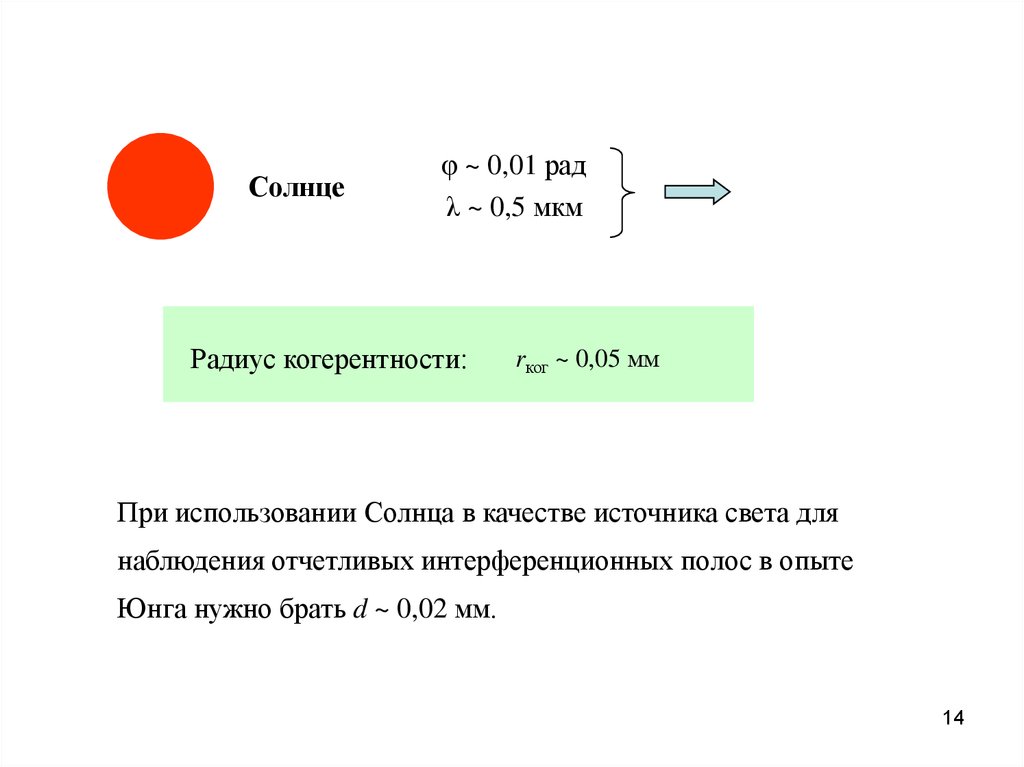
14.
Солнцеφ ~ 0,01 рад
λ ~ 0,5 мкм
Радиус когерентности:
rког ~ 0,05 мм
При использовании Солнца в качестве источника света для
наблюдения отчетливых интерференционных полос в опыте
Юнга нужно брать d ~ 0,02 мм.
14
15.
Методы наблюдения интерференции света1. Метод Юнга
S, S1, S2 щели,
Э экран.
15
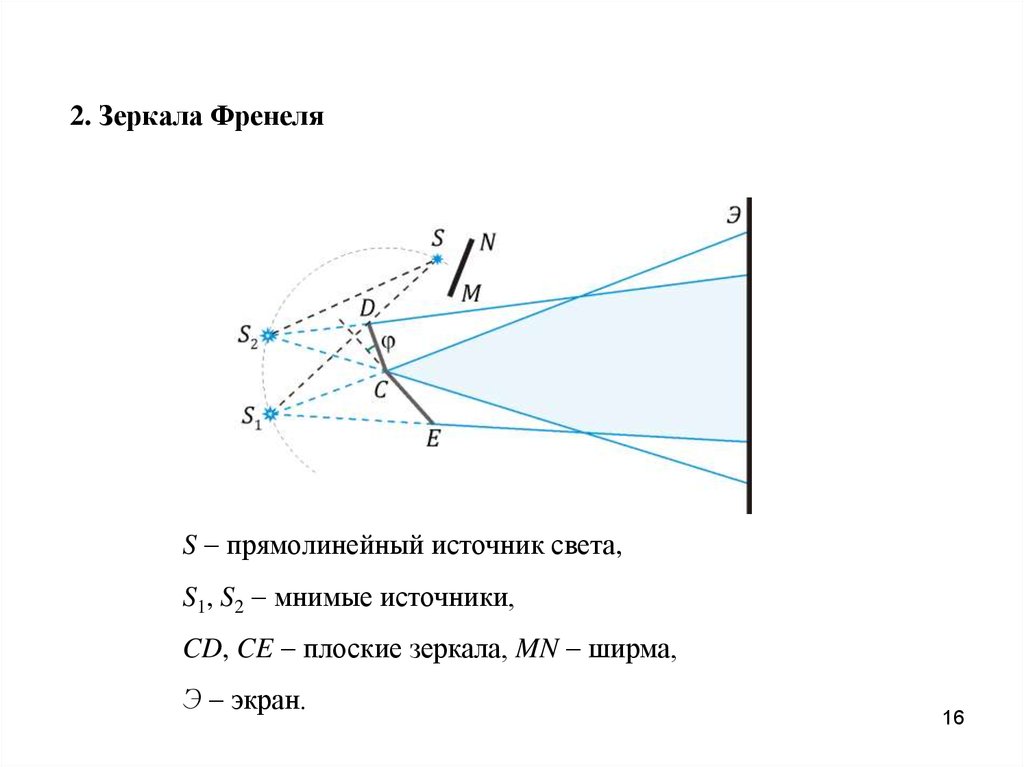
16.
2. Зеркала ФренеляS прямолинейный источник света,
S1, S2 мнимые источники,
CD, CE плоские зеркала, MN ширма,
Э экран.
16
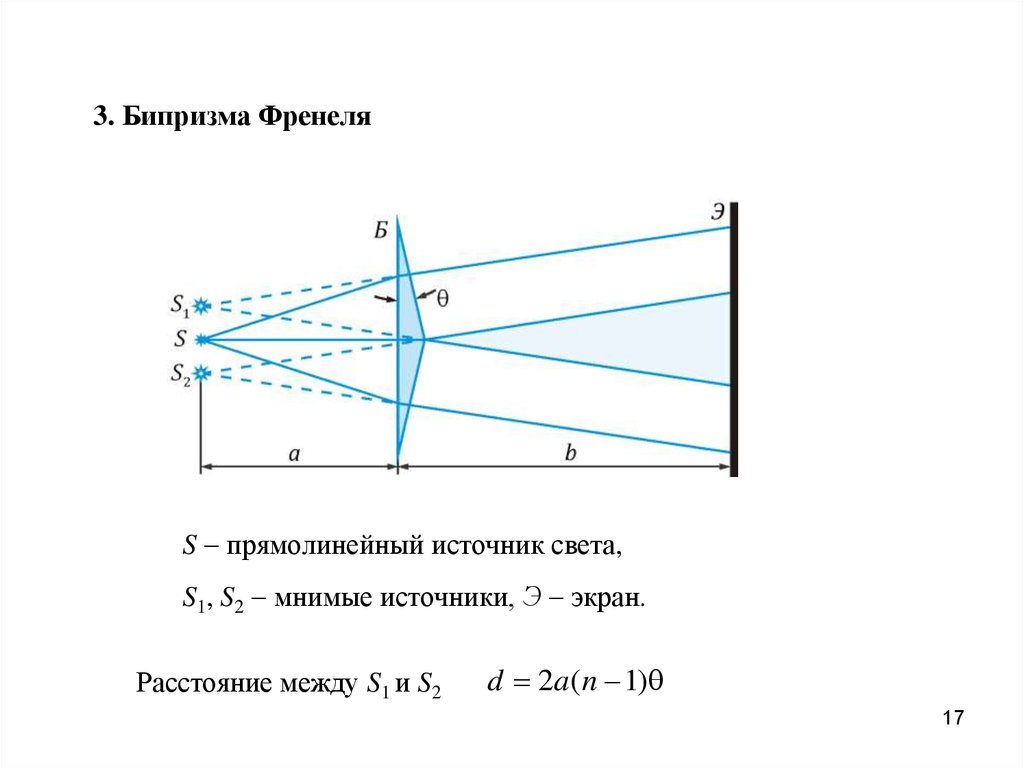
17.
3. Бипризма ФренеляS прямолинейный источник света,
S1, S2 мнимые источники, Э экран.
Расстояние между S1 и S2
d 2a (n 1)
17













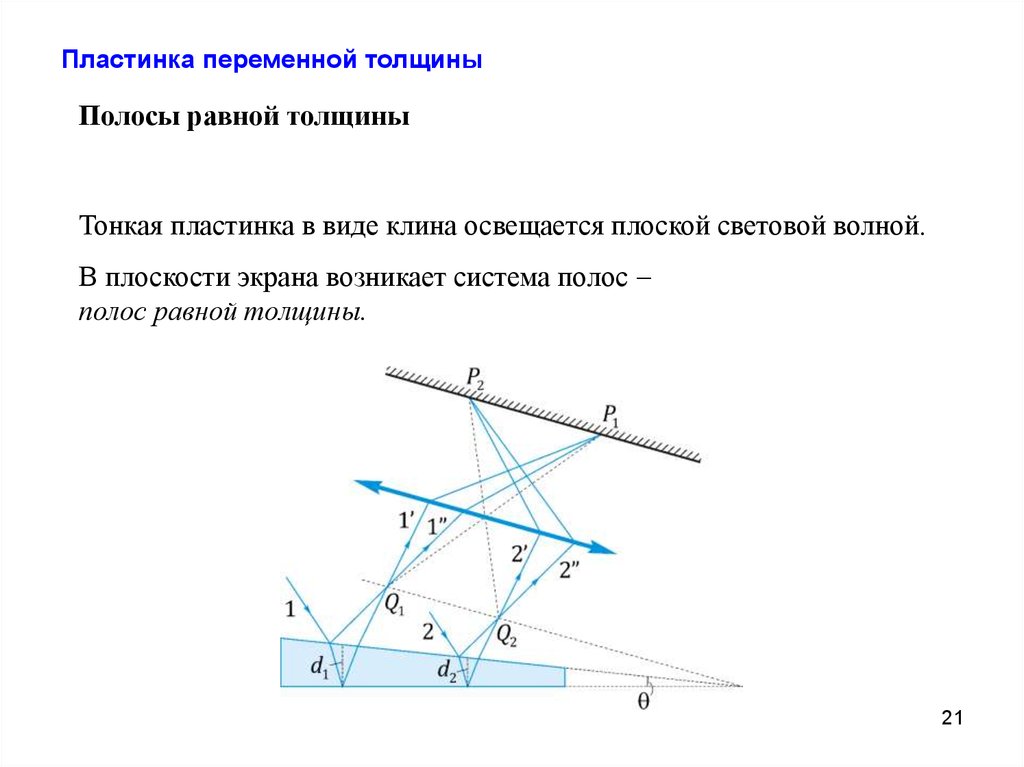
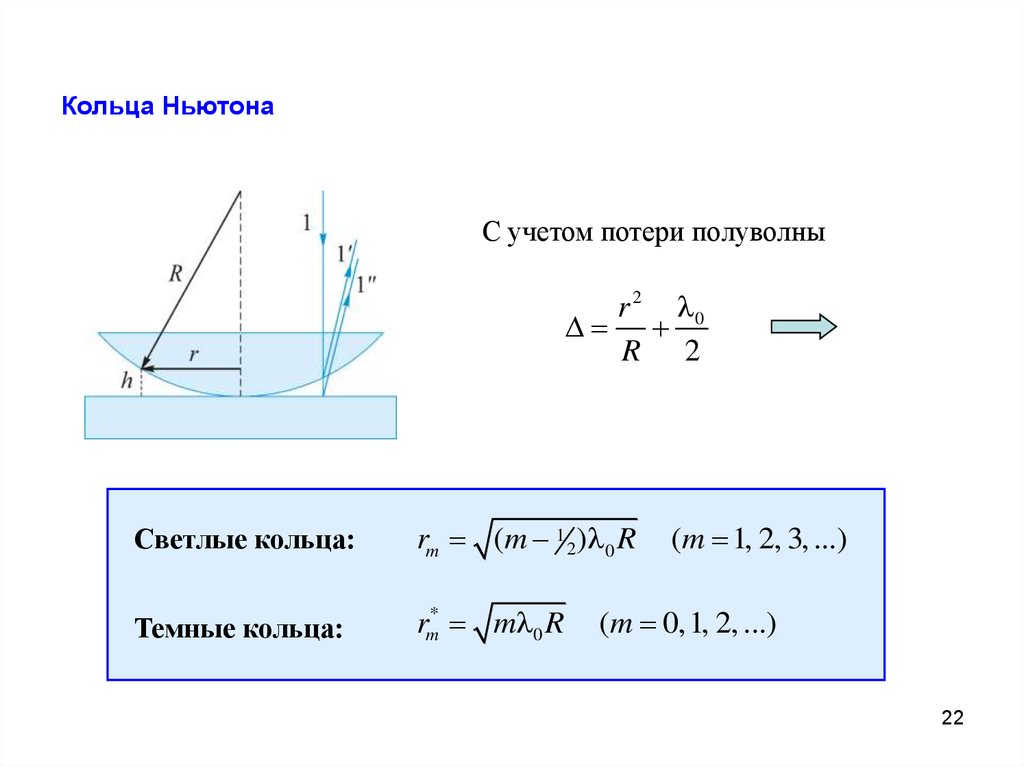

 Физика
Физика