Похожие презентации:
Физические методы исследования конструкционных наноматериалов
1. Государственный Технологический Университет «Московский институт стали и сплавов» Кафедра физического материаловедения
Демонстрационная презентация учебного курса«Физические методы исследования
конструкционных наноматериалов»
Автор: В.Ю. Введенский
2009
2. Лекция 1. Введение
Цель курса: Научить применению физических методовисследования конструкционных наноматериалов и
процессов.
Структура курса:
1. Введение. Классификация и описание методов
исследований.
2. Термический анализ.
3. Калориметрия.
4. Дилатометрия.
5. Методы измерения теплопроводности.
6. Электрические методы исследований.
7. Магнитные методы исследования.
Курс "Физические методы
исследования КНМ"
2
3. Классификации методов измерений
Критерий классификацииВиды методов
Электрические, магнитные,
механические,
По физическим принципам
акустические, оптические и
т.д.
По режиму
Статические и
взаимодействия средства
динамические
и объекта измерений
По виду измерительных
сигналов
Аналоговые и цифровые
Курс "Физические методы
исследования КНМ"
3
4. Классификация методов измерений по совокупности приёмов использования принципов и средств измерений
Методы измеренийМетод
непосредственной оценки
Дифференциальный
Нулевой
(компенсационный)
Методы сравнения с мерой
Метод
замещения
Курс "Физические методы
исследования КНМ"
Метод
отношения
4
5. Основные методы измерений
• метод непосредственной оценки – метод измерений, прикотором значение величины определяют непосредственно по
показывающему средству измерений.
• метод сравнения с мерой – метод измерений, в котором
измеряемую величину сравнивают с величиной,
воспроизводимой мерой.
• дифференциальный метод измерений – метод измерений,
при котором измеряемая величина сравнивается с однородной
величиной, имеющей известное значение, незначительно
отличающееся от значения измеряемой величины, и при
котором измеряется разность между этими двумя величинами.
• нулевой метод измерений – метод сравнения с мерой, в
котором результирующий эффект воздействия измеряемой
величины и меры на прибор сравнения доводят до нуля.
• метод дополнения – метод сравнения с мерой, в котором
значение измеряемой величины дополняется мерой этой же
величины с таким расчетом, чтобы на прибор сравнения
воздействовала их сумма, равная заранее заданному значению.
Курс "Физические методы
исследования КНМ"
5
6. Описание методов с помощью схем преобразования сигналов
Названиеx
Сигнал x
Линейный блок
преобразования
Преобразование
сигнала
Изображение
x
–
y
K
Узел
суммирования
x1
Узел
разветвления
x
x2
y
x3 –
y1
y2
y3
Курс "Физические методы
исследования КНМ"
y=Kx
(К – коэффициент
преобразования)
y = x1 + x2 – x3
x = y1 = y2 = y3
6
7. Схема преобразования сигнала для метода непосредственной оценки
В методе непосредственной оценки реализуется схемапрямого преобразования, состоящая из
последовательной цепи блоков.
K1
K2
…
Kn
Пример – термоэлектрический термометр:
Термопара
Усилитель
постоянного
тока
Курс "Физические методы
исследования КНМ"
Регистрирующее
устройство
7
8. Схема преобразования сигнала для дифференциального метода
В случае дифференциального метода должно быть двавходных сигнала: измеряемый х и сигнал сравнения
(эталонный) хср. Фактически измеряется разность
этих величин.
Величина
сравнения xср
Измеряемая
величина x
Первичный
преобразователь
–
Δy
Регистрирующее
устройство
Первичный
преобразователь
Курс "Физические методы
исследования КНМ"
8
9. Схема преобразования сигнала для нулевого метода
Для компенсационного (нулевого) метода характерно наличие контураотрицательной обратной связи и двух выходных сигналов: сигнала
рассогласования Δy, который необходимо довести до нуля, и
компенсирующего сигнала yк, значение которого в момент
компенсации является результатом измерений.
x
y
Первичный
преобразователь
–
Δy
–
yк
Δy = y – yк
Индикатор
yк
Блок
регулирования
Регистрирующее
устройство
Курс "Физические методы
исследования КНМ"
9
10. Характеристики схем преобразования сигналов
• Путь – связь на схеме между источником сигнала (входом) ипотребителем сигнала (выходом) с учётом направления
передачи этого сигнала. Число путей равно числу способов
переместиться от входа к выходу, двигаясь в направлении
стрелок. Значение пути p – произведение коэффициентов
преобразования блоков, через которые проходит путь.
• Контур (обратной связи) – замкнутая цепь по пути передачи
сигнала (в направлении стрелок), проходящая через каждый
элемент не более одного раза. Контур – однократно замкнутый
путь. Значение контура s – произведение коэффициентов
преобразования входящих в контур блоков.
• Контур второго порядка – произведение двух не касающихся
(не связанных, не имеющих общих блоков преобразования)
контуров: sij = si sj.
Курс "Физические методы
исследования КНМ"
10
11. Расчёт коэффициента преобразования
Формула Мэзонаn
K
p
k 1
k
r
q
i 1
( i , j ) 1
(1 * si * sij ...)
m
1 si
i 1
t
s
( i , j ) 1
ij
...
n – число путей, m – число контуров, t – число контуров второго
порядка, r – число контуров, не относящихся к данному пути, q –
число контуров второго порядка, не относящихся к данному пути.
Звёздочкой * помечены суммы не связанных на данном пути
контуров.
Курс "Физические методы
исследования КНМ"
11
12. Статическая характеристика преобразования средства измерения
Функция преобразования(статическая характеристика
преобразования) –
зависимость выходного
сигнала y от входного x:
y = f (x)
Входным сигналом является
измеряемая величина.
Выходным сигналом (в случае
аналогового СИ) является
отклонение указателя
(стрелки).
y
Курс "Физические методы
исследования КНМ"
x
12
13. Коэффициент преобразования и коэффициент передачи
Коэффициент преобразования – отношениевыходного сигнала к входному:
K = y/x.
Коэффициент преобразования называют
коэффициентом передачи в частном случае
одинаковой размерности y и x.
В наиболее распространенном случае
линейной функции преобразования
y=Kx
и коэффициент преобразования не зависит от
значения входного сигнала.
Курс "Физические методы
исследования КНМ"
13
14. Чувствительность средства измерений
Чувствительность средства измерений –свойство средства измерений, определяемое
отношением изменения выходного сигнала к
вызывающему его изменению измеряемой
величины (РМГ 29-99):
y
S
x
В случае линейной функции преобразования чувствительность
совпадает с коэффициентом преобразования:
S = K.
Курс "Физические методы
исследования КНМ"
14
15. Относительная чувствительность
Иногда используют различные видыотносительной чувствительности:
S отн, x
y
( x / x)
S отн, x / y
S отн, y
( y / y )
x
( y / y)
( x / x)
Курс "Физические методы
исследования КНМ"
15
16. Порог чувствительности
Порог чувствительности средстваизмерений – характеристика средства
измерений в виде наименьшего
значения изменения физической
величины, начиная с которого может
осуществляться ее измерение данным
средством (РМГ 29-99).
Курс "Физические методы
исследования КНМ"
16
17. Статическая характеристика преобразования средства измерения с ненулевым порогом чувствительности
Варианты статических характеристик для линейных средствизмерений:
y
а
y
б
–xпор
+xпор
x
x
xпор
Диапазон
измерений
Диапазон
показаний
Курс "Физические методы
исследования КНМ"
17
18. Точность (правильность и прецизионность) метода измерений
Точность: Степень близости результата измерений кпринятому опорному значению.
Правильность: Степень близости среднего значения,
полученного на основании большой серии
результатов измерений (или результатов испытаний),
к принятому опорному значению.
Прецизионность: Степень близости друг к другу
независимых результатов измерений, полученных в
конкретных регламентированных условиях.
(ГОСТ Р ИСО 5725-1–2002 Точность (правильность и
прецизионность) методов и результатов измерений. Часть 1.
Основные положения и определения)
Курс "Физические методы
исследования КНМ"
18
19. Сравнение правильности и прецизионности
Курс "Физические методыисследования КНМ"
19
20. Формы прецизионности
• Повторяемость (сходимость): Прецизионность в условияхповторяемости, при которых независимые результаты
измерений (или испытаний) получаются одним и тем же
методом на идентичных объектах испытаний, в одной и той же
лаборатории, одним и тем же оператором, с использованием
одного и того же оборудования, в пределах короткого
промежутка времени.
• воспроизводимость: Прецизионность в условиях
воспроизводимости, при которых результаты измерений (или
испытаний) получают одним и тем же методом, на идентичных
объектах испытаний, в разных лабораториях, разными
операторами, с использованием различного оборудования.
• промежуточная прецизионность – в условиях, отличающихся
от условий повторяемости и воспроизводимости.
Курс "Физические методы
исследования КНМ"
20
21. Классификация погрешностей по зависимости от значения входного сигнала
• Аддитивная составляющая абсолютнойпогрешности Δхадд – не зависящая от
входного сигнала х.
• Мультипликативная составляющая
погрешности Δхмульт – прямо
пропорциональная х.
• Нелинейная составляющая погрешности.
Δх = a + bx
Δхадд
Δхмульт
Курс "Физические методы
исследования КНМ"
21
22. Зависимости абсолютной и относительной погрешности от значения измеряемой величины
Абсолютная погрешностьОтносительная погрешность
δх
Δх
Δxмульт = bx
а
b
а
a/x
b
x
Курс "Физические методы
исследования КНМ"
x
22
23. Погрешность дрейфа нуля
yНСХ
ДСХ
0
Δx
0
x
xизм
xист
Смещение нуля –
показание средства
измерений,
отличное от нуля,
при входном
сигнале, равном
нулю (РМГ29-99).
-Δx
x
Курс "Физические методы
исследования КНМ"
Аддитивная погрешность
23
24. Погрешность чувствительности
yДействительная
статическая
характеристика (ДСХ):
ДСХ
y S x
НСХ
x
0
xист
Δx
0
Номинальная статическая
характеристика (НСХ):
y S ном x
xизм
Δx
Абсолютная погрешность
x
S ном
x x(1
)
S
– мультипликативная.
Курс "Физические методы
исследования КНМ"
24
25. Анализ погрешностей метода непосредственной оценки. Схема
Схема прямого преобразования сигнала из n последовательносоединённых линейных блоков:
x
K1
y1
K2
y2
…
Kn
yn = y
Учёт двух источников погрешности для каждого блока – аддитивного
дрейфа нуля zi и мультипликативной нестабильности
коэффициента преобразования ΔKi – эквивалентен включению в
схему дополнительно 2n входных сигналов:
ΔK1
x
K1
ΔKn
z1
y1±Δy1
…
Курс "Физические методы
исследования КНМ"
Kn
zn
y±Δy
25
26. Анализ погрешностей метода непосредственной оценки. Пример
Схема из двух блоков:ΔK1
x
K1
Сигнал без
искажений
ΔK2
z1
y1±Δy1
K2
Вклад нестабильности
коэффициентов
преобразования
zn
y±Δy
Вклад дрейфа
нуля
y K1 K 2 x ( K1 K 2 K 2 K1 ) x ( z1 K 2 z2 )
( K1 K 2 x z1 K 2 )
Взаимодействие погрешностей
(пренебрегаем)
Курс "Физические методы
исследования КНМ"
26
27. Анализ погрешностей метода непосредственной оценки. Разделение погрешности на вклады
Взаимодействием погрешностей пренебрегаюткак суммой произведений малых величин zi и
ΔKi. В этом случае вклады в погрешность изза нестабильности коэффициентов
преобразования (Δyнест) и дрейфа нуля (Δyдр)
можно рассчитывать раздельно, суммируя оба
вклада при определении полной погрешности.
y yнест yдр yвзаим yнест yдр
≈0
Курс "Физические методы
исследования КНМ"
27
28. Анализ погрешностей метода непосредственной оценки. Вклад нестабильности коэффициентов преобразования
Абсолютная погрешность из-за нестабильностикоэффициентов преобразования
yнест ( K1 K 2 K 3 ...K n K 2 K1 K 3 ...K n ...
K n K1 K 2 ...K n 1 ) x
– мультипликативная погрешность. Относительная погрешность
равна сумме относительных нестабильностей коэффициентов
преобразования:
n
нест
нест
i
y
y
x
x
K
i 1 K i
Курс "Физические методы
исследования КНМ"
28
29. Анализ погрешностей метода непосредственной оценки. Вклад дрейфа нуля
Абсолютная погрешность из-за дрейфа нуля(аддитивного шума, помех, наводок):
yдр z1 K 2 K 3 ...K n z2 K 3 K 4 ...K n ... zn
– аддитивная погрешность.
Абсолютная погрешность, приведённая ко входу:
zn
y z z1
z2
xдр
...
K
K1 K1 K 2
K1 K 2 ...K n
Курс "Физические методы
исследования КНМ"
29
30. Анализ погрешностей компенсационного метода. Схема
Цепь прямого преобразованияΔK1
x
–
…
K1
uk
ΔK2
z1
Δβk
βk
y
K2
u1
…
zn
Δβ1
β1
Цепь обратного преобразования
Коэффициент преобразования средства измерения:
K СИ
K1 K 2 ...K n
K
1 1 ... k K1 ...K n 1 K
Курс "Физические методы
исследования КНМ"
30
31. Анализ погрешностей компенсационного метода. Вклад нестабильности коэффициентов преобразования
Относительная погрешность из-за нестабильностикоэффициентов преобразования:
y нест x нест K
1
K
y
x
K 1 K 1 K
0при K 1
при K 1
– условие исключения влияния цепи прямого преобразования на
погрешность из-за нестабильности коэффициентов преобразования
Курс "Физические методы
исследования КНМ"
31
32. Анализ погрешностей компенсационного метода. Вклад дрейфа нуля
Аддитивная погрешность из-за дрейфануля:
xдр
zn
z1
z2
(
...
)
K1 K1 K 2
K 1 K 2 ...K n
(u1 2 3 ... k u 2 3 ... k ... u k )
Курс "Физические методы
исследования КНМ"
32
33. Динамические погрешности
Динамическая погрешность средства измерений –разность погрешности в динамическом режиме и
статической погрешности:
xдин x xстатич
Динамическая погрешность, приведённая к выходу, может быть
также определена как разность выходного сигнала и отклика на тот
же входной сигнал идеального безынерционного элемента:
yдин y(t ) yид (t )
Динамическая погрешность, приведённая ко входу, для
линейного средства измерений:
y(t ) yид (t )
xдин (t )
K0
Курс "Физические методы
исследования КНМ"
33
34. Уравнение преобразования идеального средства измерений
Идеальный (безынерционный) элемент:y(t ) K 0 x(t )
Нет ни запаздывания выходного сигнала
относительно входного, ни искажений сигнала:
значение коэффициента преобразования такое
же, как в статическом режиме,
K = K0,
(K0 – статический коэффициент преобразования)
Курс "Физические методы
исследования КНМ"
34
35. Преобразование сигнала в реальном средстве измерений
dmydy
bm m ... b1
y (t ) K 0 x(t )
dt
dt
слагаемые, описывающие
инерцию и искажения сигнала
как в идеальном элементе
(элементе 0-го порядка)
Дифференциальное уравнение наиболее полно описывает работу СИ
в динамическом режиме.
Наивысший порядок производной m – это порядок
динамического элемента.
Дифференциальное уравнение может быть представлено в виде
системы дифференциальных уравнений 0-го, 1-го и 2-го порядка,
т.е. сложное динамическое СИ может быть представлено в виде
совокупности динамических элементов 0-го, 1-го и 2-го порядка.
Курс "Физические методы
исследования КНМ"
35
36. Уравнения преобразования и параметры динамических элементов первого и второго порядка
• Динамический элемент 1-го порядка(инерционный элемент)
dy
T
y (t ) K 0 x(t )
dt
Т – постоянная времени
• Динамический элемент 2-го порядка
(колебательный элемент)
1 d 2 y 2 dy
2
y (t ) K 0 x(t )
2
0 dt
0 dt
ω0 – частота собственных колебаний, β – степень успокоения
Курс "Физические методы
исследования КНМ"
36
37. Ртутный термометр – пример инерционного элемента
Уравнение теплового баланса термометра с окружающей средой:Теплота, в единицу времени…
…поглощаемая термометром
…отдаваемая окружающей средой
dT
V0 c
Aк (Tсреды T )
dt
Закон термического расширения ртути:
A l V0 T
Дифференциальное уравнение преобразования:
V0 c d ( l )
V0
l
Tсреды
Aк
dt
A
Постоянная
времени
Курс "Физические методы
исследования КНМ"
K0
37
38. Реакция инерционного датчика на различные входные воздействия
x, y/K0x(t)
xm
y(t)/K0
Δx
0
x, y/K0
a
t
x = bt
Δx
б
y(t)/K0
0
x, y/K0
а – ступенчатый
режим
воздействия;
t
x(t)
Δxm
y(t)/K0
0
φ
в
б – линейный
режим;
в – гармонический
режим.
t
Курс "Физические методы
исследования КНМ"
38
39. Переходная функция
аx
xm
Ступенчатый
сигнал
0
t
y
б
Переходная функция
(переходная
характеристика) h(t) –
это временная
зависимость выходного
сигнала СИ, полученная
в результате подачи на
вход ступенчатого
сигнала.
K0 xm
0,9K0 xm
Переходная
функция
0
Динамический
режим
t
tуст
Для динамического
элемента 1-го порядка:
h(t ) K 0 x m (1 e t / T )
Статический
режим
Курс "Физические методы
исследования КНМ"
39
40. Время установления показаний
Время установления tуст – время, за которое выходнойсигнал достигнет определённого уровня (90 % от
установившегося значения).
Время установления определяет минимальное время
измерений в статическом режиме после подачи
сигнала на вход – время, через которое можно
производить считывание показаний.
Связь с постоянной времени Т (для элемента 1-го
порядка):
y(t уст ) 0,9 K 0 xm
y(t уст ) K 0 xm (1 e
t уст / T
)
t уст ln 10 T 2,3T
Курс "Физические методы
исследования КНМ"
40
41. Отклик динамического элемента второго порядка на ступенчатый сигнал
yТри режима работы
динамического
элемента 2-го порядка:
1 колебательный (β <1);
2 критический (β = 1);
3 апериодический (β >1).
β<1
K0 xm
Критический режим
характеризуется
минимальным
временем
установления.
β≥1
0
t
Курс "Физические методы
исследования КНМ"
41
42. Частотные характеристики средства измерений
Частотные характеристики используются для описания работы вгармоническом режиме (при подаче на вход синусоидального
сигнала).
X ( j ) xm ( ) exp( j t )
Y ( j ) y m ( ) exp{ j[ t ( )]}
Амплитудно-фазовая характеристика (комплексная частотная
характеристика, комплексный коэффициент преобразования):
K ( j ) K ( ) exp{ j ( )}
Амплитудночастотная
характеристика
y m ( )
K ( )
xm ( )
Курс "Физические методы
исследования КНМ"
Фазо-частотная
характеристика
42
43. Частотные характеристики динамического элемента первого порядка
K0K ( j )
1 j T
K(ω)
K0
0,9K0
K ( )
0
φ(ω)
ωгр
K0
1 T
2
2
ω
0
ω
( ) arctg ( T )
Курс "Физические методы
исследования КНМ"
43
44. Частотные характеристики динамического элемента второго порядка
KРезонанс
β<1
K0
β ≥1
0
φ
ω0
ω
0
ω
β ≥1
-π/2
β<1
Курс "Физические методы
исследования КНМ"
44
45. Лекция 2. Термический анализ
Термический анализ - способ изученияпревращений в материалах по
временны м зависимостям
температуры образца в процессе
непрерывного охлаждения или нагрева
(термограммам).
Курс "Физические методы
исследования КНМ"
45
46. Простой термический анализ
Термограммы при нагреве иохлаждении
для разных типов
превращений:
а – нонвариантное
превращение первого рода;
б – моновариантное
превращение первого рода;
в – фазовое превращение
второго рода.
Курс "Физические методы
исследования КНМ"
46
47. Дифференциальный термический анализ
Курс "Физические методыисследования КНМ"
47
48. Сравнение термограмм простого и дифференциального термического анализа
Курс "Физические методыисследования КНМ"
48
49. Теория термического анализа
Уравнение теплового баланса:m C (dT/dt) = q – qфп,
где m – масса образца, кг;
С – его удельная теплоемкость, Дж/кг·К;
T – температура образца, К;
dT/dt – скорость ее изменения, К/с;
q dQ/dt – возникающий в результате теплообмена
между образцом и окружающей средой тепловой
поток (количество теплоты Q, переносимое в единицу
времени), Вт;
qфп – количество теплоты, образующееся в образце в
единицу времени в результате фазового
превращения, Вт.
Курс "Физические методы
исследования КНМ"
49
50. Закон теплообмена Ньютона
q = S (Тср – T),где
– коэффициент теплообмена, Вт/м2·К;
S – площадь поверхности, через которую
осуществляется теплообмен, м2;
Т – температура образца, К;
Тср – температура среды, окружающей образец
(температура печи), К.
Тср = Т0 + v t,
где Т0 – начальная температура, К;
v dТср/dt = const – скорость нагрева (охлаждения), К/с.
Курс "Физические методы
исследования КНМ"
50
51. Тепловой поток, передаваемый образцу при нагреве в процессе термического анализа
q = mCv [1– exp (– t / )],где
= mC/( S)
– постоянная времени, характеризующая
термическую инерцию образца.
Курс "Физические методы
исследования КНМ"
51
52. Тепловой поток при фазовом превращении
qфп = – H m (ρ/ρ0) d /dt,где H – удельная теплота (энтальпия)
превращения,
(V/V0) – объёмная доля новой фазы,
m и V0 – масса и начальный объём образца,
ρ0 и ρ – исходная плотность и плотность новой
фазы.
Знак «–» введён для случая выделения тепла
при фазовом превращении (как, например, в
случае кристаллизации).
Курс "Физические методы
исследования КНМ"
52
53. Форма кривой охлаждения согласно теории термического анализа
а – зависимости от временитеплового потока, отводимого
от образца (q), и скорости
выделения тепла в образце
из-за фазового превращения
(qфп);
б – временная зависимость
скорости изменения
температуры образца;
в – кривая термического
анализа при охлаждении.
Курс "Физические методы
исследования КНМ"
53
54. Методика обработки кривых термического анализа
Интерпретация кривой термического анализа основана наизучении наклона кривой:
dT/dt = ( S / mC) (Т0 + v t – T) + ( H /C) (ρ/ρ0) d /dt
(dT/dt)баз = (q /mC)
(dT/dt)фп = – (qфп/mC)
Наклон базовой линии (при
температурах, где не
происходит превращение)
Составляющая наклона,
обусловленная фазовым
превращением
Поиск температур начала и конца превращения проводится путем
построения касательных к кривой термического анализа и
нахождения точки, где наклон касательных резко изменяется.
Курс "Физические методы
исследования КНМ"
54
55. Деривативный анализ
Деривативный анализ – разновидностьтермического анализа, в котором
регистрируется зависимость от времени
скорости изменения температуры образца
при непрерывном его нагреве или
охлаждении.
Деривативный анализ удобен тем, что именно
скорость изменения температуры прямо
пропорциональна тепловому потоку в
образце.
Курс "Физические методы
исследования КНМ"
55
56. Влияние скорости нагрева и кинетики превращения на температурный интервал его протекания
Температурныйинтервал
аустенитизации
эвтектоидной
углеродистой стали
при разных скоростях
нагрева (v2>v1):
М – массовая доля
аустенита.
Курс "Физические методы
исследования КНМ"
56
57. Влияние темпа фазового превращения на чувствительность термического анализа
Темпкристаллизации θ –
это производная массы
твердой фазы по
температуре dm /dT.
Для сплава X1 θ1 > θ2,
поэтому резкий излом
на термограмме – в
точке 1.
Для сплава X2 θ3 < θ4,
поэтому более
выраженный излом на
термограмме – в точке
4.
Курс "Физические методы
исследования КНМ"
57
58. Погрешность измерения температуры из-за отвода тепла термопарой
Уравнение теплового баланса для термопары:S T14 – S T4 = Sт (Т – Т0) / L
Тепловой поток от
образца
В окружающую
среду
От горячего спая к
холодному
Диаметр
термопары
Pt / Pt-Rh:
1 – 0,05 мм;
2 – 0,1 мм;
3 – 0,3 мм
Курс "Физические методы
исследования КНМ"
58
59. Динамическая погрешность измерения температуры при термическом анализе
ΔT = T – ( 0 + v t) = – v + (T0 – 0 + v ) exp(– t / )Т – температура
датчика,
θ – температура
окружающей среды
(измеряемая величина),
v – скорость охлаждения
(v = const < 0),
τ – время термической
инерции датчика
температуры.
Курс "Физические методы
исследования КНМ"
59
60. Лекция 3. Классификация и режимы калориметрических измерений
Калориметрия – раздел теплофизики, в которомизучаются методы и средства измерений физических
величин, характеризующих тепловые эффекты
физических, химических и биологических процессов,
а также тепловые свойства веществ.
Измеряемые тепловые величины:
• Количество теплоты Q, Дж;
• Тепловой поток q = dQ/dt, Вт;
• Теплоёмкость C = dQ/dT, Дж/К;
• Удельная теплоёмкость Cуд = (1/m) dQ/dT, Дж/кг·К.
Курс "Физические методы
исследования КНМ"
60
61. Методы калориметрических измерений
Методы калориметрииКомпенсационные
Методы измерения
разности температур
…временной
зависимости
Курс "Физические методы
исследования КНМ"
…локальной
(в разных точках)
61
62. Классификация методов калориметрии по способу ввода тепла в калориметрическую систему
Методы калориметрииМетод
смешения
Методы внутреннего
источника тепла
Метод периодического
нагрева
Метод
протока
Метод непрерывного
нагрева
Курс "Физические методы
исследования КНМ"
62
63. Компенсация теплового эффекта теплотой фазового перехода
Ледяной калориметрЛавуазье – Лапласа
Q = q. mл,
Сp = Q/(МТ),
где q – известная удельная
теплота фазового перехода,
mл – масса превращённого
калориметрического
вещества (льда),
M – масса образца, Т – его
начальная температура.
Курс "Физические методы
исследования КНМ"
63
64. Ледяной калориметр Бунзена
Принципиальная схемаледяного калориметра
Бунзена:
1 – сосуд с образцом; 2 –
калориметрический сосуд с
водой;
3 – капилляр со ртутью; 4 –
лед; 5 – термостат со
смесью
льда и воды; 6 – трубка со
ртутью
Курс "Физические методы
исследования КНМ"
64
65. Компенсация теплового эффекта теплотой химической реакции
Калориметр Ренос компенсацией теплового
эффекта теплотой
химической реакции:
1 – термометр; 2 – мешалка; 3 –
воронка для подачи реагента;
4 – внутренний сосуд с другим
реагентом;
5 – калориметрическая жидкость;
А – исследуемый образец
Курс "Физические методы
исследования КНМ"
65
66. Компенсация теплового эффекта термоэлектрическими эффектами
Калориметр Бренстедадля определения
теплоты растворения
соли:
1 – воронка для подачи
реагента; 2 – мешалка;
3 – термометр;
4 – электрический
нагреватель;
5 – калориметрическая
жидкость
Курс "Физические методы
исследования КНМ"
66
67. Составные части калориметра
Калориметр состоит из калориметрическойсистемы и оболочки.
Калориметрическая система (ядро) –
совокупность всех частей калориметра,
между которыми происходит распределение
измеряемой теплоты.
Оболочка – часть калориметра, окружающая
калориметрическую систему и
обеспечивающая определённые, строго
фиксированные условия теплообмена с
окружающей средой.
Курс "Физические методы
исследования КНМ"
67
68. Модели теплообмена в калориметрах
аб
Оболочка
q
q
Калориметрическая
система
Калориметрическое
вещество
а – с односоставным ядром, б – с двухсоставным ядром
Курс "Физические методы
исследования КНМ"
68
69. Режимы калориметрических измерений
Режимы:изотермический
Тоб = Тизм = const
изопериболический
Тоб = const, Тизм(t) Тоб
адиабатический
Тоб(t) = Тизм(t)
1 – окружающая среда, 2 –
оболочка, 3 – калориметрическая
система, 4 – теплопроводник.
Курс "Физические методы
исследования КНМ"
69
70. Сравнение условий теплообмена при разных режимах измерений
Режим измеренийТепловая характеристика
изотермический
Тоб = Тизм = const, Rт 0
Мгновенный обмен тепла между
калориметрической системой и
оболочкой
изопериболический
Тоб = const, Тизм(t) Тоб, Rт 0
Теплообмен между калориметрической
системой и оболочкой во времени
адиабатический
Тоб(t) = Тизм(t), Rт
Отсутствие теплообмена между
калориметрической средой и оболочкой
Курс "Физические методы
исследования КНМ"
70
71. Способы осуществления адиабатического режима
1) реакция проводится настолькобыстро, что за время измерений теплота
не успевает рассеяться (динамический
адиабатический режим );
2) Тепловая изоляция –
калориметрическая
система полностью
изолируется от оболочки;
3) Термическое
регулирование –
температура оболочки 2 с
помощью блока управления
3 и нагревательного
элемента 4 поддерживается
равной температуре
калориметрической системы
1, которая изменяется со
временем.
Курс "Физические методы
исследования КНМ"
71
72. Механизмы теплообмена
• Теплопроводностьq/A = – (T) grad T
• Конвекция
q = bA(Tср – T),
где b – коэффициент конвективного переноса тепла, который зависит от
свойств жидкости (газа), вида конвекции и скорости потока.
• Излучение
q/A2 = A1K1,2 (T14 – T24),
где = 5,67·10–8 Вт∙м–2 К–4 – постоянная Стефана–Больцмана;
К1,2 – эмпирический коэффициент, зависящий от коэффициентов
поглощения (степени черноты) тел 1 и 2.
Курс "Физические методы
исследования КНМ"
72
73. Закон охлаждения Ньютона в калориметре
q = αA(Tоб – T)α – коэффициент теплообмена,
Вт/м2·К.
Условия применимости на примере калориметра смешения:
1.Разность температур калориметрической системы и оболочки не
должна превышать 2–3 градуса: (Tоб – T) < 2…3 К.
2. Внешняя поверхность калориметра и внутренняя поверхность
оболочки должны обладать хорошей отражательной способностью.
3.Расстояние между стенками калориметрического сосуда и
оболочки должно составлять около 10 мм; при том конвекция
практически исключается, а тепловые потери из-за
теплопроводности воздуха невелики.
4. Подъём температуры в опыте не должен превышать 2 К.
Курс "Физические методы
исследования КНМ"
73
74. Лекция 4. Методы смешения и измерения локальной разности температур
В методах смешения нагретый образец вводят вкалориметр, температура которого
повышается. Количество теплоты, введённое в
калориметр:
Q = Cкал·(Tf – T0),
где Cкал – теплоёмкость калориметра (тепловой,
или энергетический, эквивалент),
Tf и T0 – конечная и начальная температуры
калориметрической системы
(калориметрического вещества – не путать с
температурой образца!).
Курс "Физические методы
исследования КНМ"
74
75. Жидкостный калориметр смешения
Принципиальная схемажидкостного калориметра,
основанного на измерении
разности температур во
времени:
1 – термометр; 2 – мешалка;
3 – калориметрическая
жидкость;
А – исследуемый образец
Q = T Св mв
Ср = Q / М (Тобр – Тк)
Курс "Физические методы
исследования КНМ"
75
76. Массивный калориметр смешения
Схема калориметрическойустановки для определения
энтальпии металлов в
расплавленном состоянии
методом смешения
1 – камера плавки,
2 – массивный блок калориметра,
3 – индуктор,
4 – водоохлаждаемый поворотный
диск,
5 – изложница для
непредусмотренного слива металла,
6 – образец.
Курс "Физические методы
исследования КНМ"
76
77. Кривая калориметрического опыта смешения
1 – начальный период,2 – главный период,
3 – конечный период.
T
Tf
Tк
T0
Tн
t0 – время введения
образца в калориметр
1
2
t0
3
tf
t
tf – время окончания
главного периода и
начала конечного
периода
Приведена кривая для часто используемого на практике случая,
когда температура оболочки выше Т0, но ниже Тf.
Курс "Физические методы
исследования КНМ"
77
78. Периоды калориметрического опыта смешения
• Начальный период (t < t0) – до введения образца вкалориметр.
• Главный период (t0 < t < tf) – в котором происходит
выделение теплоты и её распределение в
калориметрической системе.
• Конечный период (t > tf) – в котором температура
изменяется в результате теплообмена
калориметрической системы с оболочкой.
Время окончания главного периода и начала конечного
периода tf устанавливают по равномерному
изменению температуры калориметрической
системы (с постоянной скоростью).
Курс "Физические методы
исследования КНМ"
78
79. Расчёт поправки на теплообмен для калориметра смешения с изотермической оболочкой
Tиспр TdT T T
dt
1
Tdt T (t f t0 )
t0
tf
Курс "Физические методы
исследования КНМ"
tf
t0
T T
dt
Нахождение δ сводится к
двум операциям:
1. к определению τ и T∞;
2. Численному или
графическому
интегрированию Т(t).
79
80. Определение постоянной времени термической инерции калориметра и температуры оболочки
По кривой калориметрического опыта дополнительноопределяют методом наименьших квадратов
скорости изменения температуры в начальный и
конечный периоды v0 и vf.
T Tн
v0
Tк Tн
v0 v f
T Tк
vf
T Tн v f
Курс "Физические методы
исследования КНМ"
80
81. Формула Реньо-Пфаундлера
Используя метод трапеций для численногоинтегрирования и формулы для определения τ и Т∞,
получим:
v f v0
T0 T f n 1
t
Ti nTн (t f t 0 )v0
Tк Tн
i 1
2
Курс "Физические методы
исследования КНМ"
81
82. Графический учёт поправки на теплообмен в изопериболическом калориметре
TSAOB = SCOD
C
ΔTиспр
D
O
A B
t
Курс "Физические методы
исследования КНМ"
82
83. Коррекция экспериментальной кривой для адиабатического калориметра с утечкой теплоты
t1 и t2 – время началаи конца экзотермического процесса;
t3 – время при
равенстве площадей
F1 = F2;
T – скорректированное изменение
температуры
системы
Курс "Физические методы
исследования КНМ"
83
84. Пример экспериментальной кривой калориметрического опыта смешения
28T , oC
27
Определение теплоты
сгорания бензойной
кислоты C6H5COOH на
калориметре смешения с
изотермической
оболочкой.
tf
26
25
24
0
500
1000
1500
2000
t, c
Курс "Физические методы
исследования КНМ"
Время опыта – 32 мин (65
точек с интервалом 30 c).
v0 = 0,98147·10-4 оС/с
vf = 0,19372·10-4 оС/с
ΔT = 2,00021 оС
δ = 0,01819·10-4 oC
ΔTиспр = ΔT–δ =1,98202 оС
84
85. Проточный калориметр
Принципиальная схемапроточного
калориметра,
основанного на
измерении локальной
разности температур:
1, 2 – реагенты;
3
– продукты реакции.
qp = К T /m =
= К T / (V t ) ,
где qp – тепловой эффект реакции, Дж/кг, К – постоянная
калориметра, Дж/К; m – масса прореагировавших реагентов, кг; V –
объёмный расход продуктов реакции, м3/с, - плотность продуктов
реакции, кг/м3 .
Курс "Физические методы
исследования КНМ"
85
86. Калориметр теплового потока
Принципиальная схемакалориметра теплового
потока, основанного на
измерении локальной
разности температур:
1 – теплопроводник;
2 – контейнер с
образцом;
3 – термостат
Курс "Физические методы
исследования КНМ"
86
87. Метод Смита
Принципиальная схема метода Смита:1 – исследуемый образец; 2, 4, 5 –
термопары, 3 – калориметрический
стакан
В процессе эксперимента
поддерживается постоянный тепловой
поток через стенку
калориметрического стакана 3.
Неизменность теплового потока
контролируется дифференциальной
термопарой 5, измеряющей разность
температур между внутренней и
наружной стенками стакана.
Собр mобр / Сэ mэ = [( t/ T)обр – ( t/ T)с] / [( t/ T)э– ( t/ T)с].
Курс "Физические методы
исследования КНМ"
87
88. Микрокалориметр теплового потока Кальве
1 – термобатарея,подключённая к источнику
тока для компенсации
теплового потока с
помощью эффекта
Пельтье;
G
G
q
2 – детекторная
термобатарея,
3
3 – калориметрическая
ячейка с образцом;
1
2
4
Курс "Физические методы
исследования КНМ"
4 – оболочка в виде
массивного блока,
обладающего высокой
теплопроводностью.
88
89. Особенности калориметра Кальве
• Предназначен для измерения очень малыхколичеств энергии и для исследования очень
медленных процессов.
• Тепло отводится от калориметрической
ячейки к оболочке через термопары.
• Для повышения чувствительности измерений
используются термобатареи, состоящие из
многих десятков и даже сотен термопар.
• Измеряемый тепловой поток частично
компенсируется эффектом Пельтье.
Курс "Физические методы
исследования КНМ"
89
90. Уравнение Тиана
dTq P p(Tоб T ) c
dt
g (Tоб T )
g SU S Т
d
dT
g
dt
dt
при Tоб = const
q P
p
c d
g
g dt
q – тепловой поток в
калориметрической ячейке
(количество энергии, выделяемое
в калориметрической ячейке в
единицу времени), Вт;
Р – та часть теплового потока
(тепловой мощности), которая
скомпенсирована эффектом
Пельтье, Вт;
р = αS – количество энергии,
теряемое калориметрической
ячейкой в единицу времени при
разности температур (Тоб – Т),
равной 1 оС, Вт/К;
с – теплоёмкость (энергетический
эквивалент) калориметрической
ячейки, Дж/К,
Δ – отклонение гальванометра,
SU и Sт – чувствительности
гальванометра и термобатареи.
Курс "Физические методы
исследования КНМ"
90
91. Лекция 5. Сканирующая калориметрия
При сканирующем режиме предусматриваетсялинейное изменение температуры
калориметрической системы или оболочки
со временем. Сканирующий режим может
быть реализован различными способами:
1) режим сканирования оболочки
2) адиабатический сканирующий режим
3) изопериболический сканирующий режим
Курс "Физические методы
исследования КНМ"
91
92. Режим сканирования оболочки
1 – нагреватель оболочки; 2 –оболочка с температурой
Тоб (t);
3 – калориметрическая
система с температурой Тизм;
4 – термическое
сопротивление Rт конечной
величины;
5 – датчик температуры; 6 –
блок сравнения
Тоб(t) = Tоб(0) + t,
где Tоб(0) – начальная
температура оболочки;
– скорость нагрева;
t – продолжительность нагрева.
Курс "Физические методы
исследования КНМ"
92
93. Адиабатический сканирующий режим
1 – датчик температуры; 2 –оболочка с температурой Тоб (t);
3 – калориметрическая система
с температурой
Тизм (t) = Тоб (t);
4 – бесконечно большое
термическое сопротивление Rт;
5 – нагреватели; 6 – блок
управления
Адиабатический сканирующий режим также предусматривает
сканирование оболочки с постоянной скоростью нагрева, но при этом
сохраняются условия адиабатического режима:
Тизм = Тоб = Tоб(0) + t.
Курс "Физические методы
исследования КНМ"
93
94. Изопериболический сканирующий режим
1 – датчик температуры; 2 –оболочка; 3 –
калориметрическая система с
температурой Тизм (t); 4 –
сопротивление Rт конечной
величины;
5 – нагреватель; 6 – блок
управления.
Тизм(t) = Tизм(0) + t
Тоб = const
Курс "Физические методы
исследования КНМ"
94
95. Возможные сочетания разных методов и разных режимов
Режимы работы калориметраМетоды калориметрии
статические
динамические
ИТ ИП
А
АС ИПС СО
Компенсация теплового эффекта +
+
теплотой фазового перехода
Компенсация теплового эффекта +
+
+
+
+
термоэлектрическими эффектами
Измерение разности температур во
+
+
времени
Измерение локальной разности
+
+
температур
ИТ, ИП, А – изотермический, изопериболический и адиабатический
режимы; АС, ИПС и СО – сканирующие режимы адиабатический,
изопериболический и оболочки.
Курс "Физические методы
исследования КНМ"
95
96. Температурные сканирующие калориметры
Калориметрическая системасканирующего калориметра (в
разрезе) и соответствующее
температурное поле при
стационарном тепловом потоке
(Тн = t – температура
нагревателя; – скорость
нагрева; t – время; Тизм –
измеряемая температура; Тобр
– средняя температура
образца):
1 – нагреватель;
2 – теплопроводник;
3 – ячейка с образцом 4;
5 – датчик температуры
Курс "Физические методы
исследования КНМ"
96
97. Термограммы температурного сканирующего калориметра
Термограммы при нагреванииобразца без фазового перехода
(а), с экзотермическим (б) и
эндотермическим (в) фазовым
переходом при температуре Тф
( t1 и t2 – временные интервалы
восстановления стационарного
состояния; t3 – временной
интервал фазового перехода)
Курс "Физические методы
исследования КНМ"
97
98. Дифференциальные калориметры
Принципиальная схемадифференциального
калориметра:
1, 3 – калориметрические
системы; 2, 4 –
теплопроводники для
исследуемого образца и
эталона; 5 – блок сравнения
тепловых потоков (светлые
стрелки) калориметрических
систем и результирующий
дифференциальный тепловой
поток (заштрихованная
стрелка)
Курс "Физические методы
исследования КНМ"
98
99. Дифференциальные температурные сканирующие калориметры (ДТСК)
Принципиальнаясхема
дифференциального
сканирующего
калориметра
теплового потока
(ДТСК):
1 – оболочка; 2 –
теплопроводники; 3 –
калориметрическая
ячейка с исследуемым
образцом; 4 –
калориметрическая
ячейка с эталоном
Курс "Физические методы
исследования КНМ"
99
100. Обработка данных ДТСК
При идентичных калориметрических системах разностьтепловых потоков
q1 – q2 = (A/ x) (T) (Tизм1 – Tизм2),
или
q = f (T) T,
где
f (T) – градуировочный фактор, который
непостоянен в широком температурном интервале и
при различных скоростях нагрева.
Площадь между кривой T(t) и базовой линией
пропорциональна теплоте фазового перехода:
Qф = q dt = f (T) T dt,
где
T – разность температур с учетом базовой
линии.
Курс "Физические методы
исследования КНМ"
100
101. Коррекция базовой линии в ДТСК
Способы коррекции базовой линии по равенству площадей F1 и F2:ступенчатое (а), плавное (б) и линейное (в) изменение базовой
линии между точками начала (А) и конца (В) фазового перехода;
– температурный скачок изменения базовой линии
Курс "Физические методы
исследования КНМ"
101
102. Адиабатический мощностной сканирующий калориметр Сайкса
1 – оболочкакалориметра (термостат);
2 – нагреватель оболочки;
3 – нагреватель образца;
4 – калориметрическая
ячейка с образцом А; 5 –
блок управления; 6 – блок
программирования
режима нагрева
Cp = W / [m (dTобр/dt)]
Курс "Физические методы
исследования КНМ"
102
103. Метод Сайкса-Грузина
1 – исследуемыйобразец; 2 – нагреватель
образца; 3 – оболочка
калориметра; 4 – печь
для нагрева оболочки; 5
– термопара для
измерения температуры
оболочки; 6 –
дифференциальная
термопара
Cp = W / {m [ (dTоб/dt) + d(εобр – εоб)/dt. (dTоб/dεоб) ] }
Курс "Физические методы
исследования КНМ"
103
104. Пример использования метода Сайкса для исследования упорядочения латуни
Курс "Физические методыисследования КНМ"
104
105. Дифференциальные мощностные сканирующие калориметры (ДМСК)
Дифференциальныйадиабатический сканирующий
калориметр:
1, 2 – блоки управления
нагревом печи, 3 –
потенциометр, 6 – печь, 7 –
оболочка, 8 – нагреватель печи,
9 – термопара для измерения
температуры печи, 10 –
дифференциальная термопара
для контроля условия
адиабатичности, 11 – образец,
12 – дифференциальная
термопара для измерения
разности температур образца и
эталона, 13 – эталон.
Курс "Физические методы
исследования КНМ"
105
106. Кривые ДМСК
Экспериментальные кривые изменения теплового потока в ДМСК:а – температурная зависимость теплового потока для ячейки без
образца (q1) и с образцом (q2); б – температурная зависимость
разности тепловых потоков; Тф – температура фазового перехода;
Тизм – температура фазового перехода, полученная путем
экстраполяции; g1 – базовая линия до начала перехода
Курс "Физические методы
исследования КНМ"
106
107. Построение базовой линии ДМСК в интервале температур фазового превращения
g(T ) g1(T ) + [F1(T ) / F] gT – температура в интервале
АВ;
g1(T ) – базовая линия в
интервале АВ;
F1(T ) – площадь, ограниченная
пиком фазового перехода и
вертикальной прямой линией
между точками А и В в интервале
АТ ;
F – площадь, ограниченная пиком
фазового перехода и прямой АВ в
интервале АВ;
g g2(T) – g1(T) = const.
Курс "Физические методы
исследования КНМ"
107
108. Лекция 6. Модуляционная и импульсная калориметрия
Динамические методы калориметрическихизмерений определяются методом (режимом)
нагрева – законом изменения во времени
температуры одной из частей калориметра,
который задаёт экспериментатор:
1. Сканирующий – непрерывный нагрев с
постоянной скоростью
2. Модуляционный – метод периодического
нагрева
3. Импульсный – метод импульсного нагрева
Курс "Физические методы
исследования КНМ"
108
109. Модуляционный метод измерения теплоемкости
Осуществляется периодический нагрев образцаподводом к нему мощности, синусоидально
изменяющейся во времени.
m C dT/dt + α S (T – Tоб) = Р0 + Рm sin ωt
T = T0 + θ(t)
α S (T0 – Tоб) = Р0
dθ/dt + θ/τ = ωθ0 sin ωt
θ = θm sin (ωt – φ)
C = Рm sin φ / (ω θm m)
Курс "Физические методы
исследования КНМ"
109
110. Временные зависимости, регистрируемые в модуляционном методе измерений теплоёмкости
Четыре параметра,которые необходимо
определить по
временным
зависимостям
подводимой мощности
и температуры:
P
Pm
P0
2π/ω
0
T φ/ω
t
θm
T0
Pm, θm, ω и φ.
C = Рm sin φ / (ω θm m)
t
Курс "Физические методы
исследования КНМ"
110
111. Условие адиабатичности в модуляционном методе калориметрии
dθ/dt + θ/τ = ωθ0 sin ωtХарактеризует отвод тепла от образца к оболочке,
т.е. неадиабатичность измерений
Адиабатичность формально эквивалентна бесконечной
постоянной времени термической инерции образца τ = mC/(α S):
τ . В этом случае
dθ/dt = ω θ0 sin ωt, θ = – θ0 cos ωt = θ0 sin (ωt – 90o)
φ = 90о
Условие
адиабатичности
tg φ = ω τ = ω m C/( α S )
Курс "Физические методы
исследования КНМ"
Рост частоты ухудшает
теплообмен образца с
оболочкой
111
112. Достоинства модуляционного метода
• Помимо обычного способа достижения адиабатичности –улучшения теплоизоляции (например, путем создания вакуума
между образцом и оболочкой) – в модуляционном методе
измерения есть еще один способ – увеличение частоты
колебаний подводимой мощности. Именно это обстоятельство
создает существенные преимущества для использования
периодических колебаний температуры при измерениях
теплоемкости. При достаточно высокой частоте ω поправка на
теплообмен может быть сделана пренебрежимо малой даже
при высоких температурах.
• Колебания температуры регистрируются с помощью
избирательных усилителей, настроенных на частоту модуляции
ω. Это очень важно, когда необходима высокая разрешающая
способность по температуре, например при измерениях вблизи
температур фазовых переходов. В этом отношении
модуляционный метод создает уникальные возможности,
позволяя проводить измерения при колебаниях температуры
порядка 10–2… 10–3 К.
Курс "Физические методы
исследования КНМ"
112
113. Варианты реализации модуляционного метода
• По способу осуществления периодическогонагрева:
1) постоянным током с небольшой переменной
составляющей; 2) переменным током,
модулированным по амплитуде; 3) электронной
бомбардировкой; 4) индукцией; 5) модулированным
световым излучением.
• По регистрации колебаний температуры образца:
1) по электрическому сопротивлению;
2) термоэлектронной эмиссии; 3) светимости образца
(с помощью фотосопротивления или
фотоэлектронного умножителя); 4) с помощью
термопар.
Курс "Физические методы
исследования КНМ"
113
114. Создание колебаний мощности пропусканием через образец электрического тока
I = I0 + Im sin ωtP = (I0 + Im sin ωt)2 (R0 + R′ θ)
P P0 + Pm sin ωt + I02 R θ
вместо P = P0 + Pm sin ωt и
dθ/dt + θ/τ′ = ω θ0 sin ωt,
где τ′ = mC/(αS – I02 R ) вместо τ = mC/(α S)
τ′ > τ (теплообмен ухудшается)
tg φ = ω τ′ = ω m C/( α S – I02 R )
Курс "Физические методы
исследования КНМ"
114
115. Метод эквивалентного импеданса
1. Нагрев постоянным током спеременной составляющей
2. Измерение параметров полного
комплексного электрического
сопротивления (импеданса) образца
вместо измерений колебаний
температуры
Курс "Физические методы
исследования КНМ"
115
116. Импеданс образца при протекании постоянного тока с переменной составляющей
R = R0 + R θ = R0 + R θm cosφ sinωt – R θm sinφ cosωtZ = R0 + A – j B,
где j – мнимая единица;
A = R θmcosφ (I0/Im) = (2 I02 R0 R / ωmC) sinφ cosφ ;
B = R θmsinφ (I0/Im) = (2 I02 R0 R / ωmC) sin2φ .
Из этого выражения видно, что полное сопротивление
образца имеет как активную (R0 + A), так и реактивную
составляющую (–B). Отрицательный знак указывает на
емкостной характер реактивной составляющей
сопротивления.
Курс "Физические методы
исследования КНМ"
116
117. Установка для измерения теплоемкости методом эквивалентного импеданса
Схема установки дляизмерения теплоемкости
модуляционным методом
(метод эквивалентного
импеданса):
1 – образец; 2 –
усилитель; 3 –
осциллограф;
4 – генератор низких
частот
mC = (2 I02 R / ω2 R2 C2)
Курс "Физические методы
исследования КНМ"
117
118. Импульсный метод
На образец 1 подается импульстока от батареи 2. Сила тока и
падение напряжения с помощью
делителей 3 и 5 регистрируются
шлейфовыми (светолучевыми)
осциллографами 4.
Вращающийся цилиндр 8 с
зеркалом 6 и шкалой 7 позволяет
осуществлять временную
развёртку процесса.
Cp = U I / [m (dT/dt)]
Курс "Физические методы
исследования КНМ"
118
119. Особенности крепления образца в установке для определения теплоёмкости импульсным методом
Один конец образца закреплен вверхнем водоохлаждаемом
токоподводе 3 с помощью
графитового цангового крепления 8,
9. Нижний конец образца зажат в
подвижной медной втулке 4.
Необходимое свободное расширение
образца при высоких скоростях
нагрева обеспечивается системой
электропроводящих гибких элементов
6, соединяющих втулку 4 с
неподвижным стаканом 5 нижнего
токоподвода. Вес подвижной втулки и
гибких элементов компенсируется
пружиной 7.
Курс "Физические методы
исследования КНМ"
119
120. Лекция 7. Дилатометрия
По физическому эффекту, положенному воснову измерения удлинения, различают:
1) оптико-механические дилатометры,
2) емкостные дилатометры,
3) индуктивные дилатометры,
4) интерференционные дилатометры,
5) поляризационно-оптические дилатометры,
6) радиорезонансные дилатометры.
Курс "Физические методы
исследования КНМ"
120
121. Оптико-механический дилатометр Стрелкова
1 – исследуемый образец;2 – шток;
3 – зажим;
4 – зеркало; прикрепленное
к валику 5;
6 – магнит, притягивающий
зажим;
7 – источник света;
8 – зрительная труба
Курс "Физические методы
исследования КНМ"
121
122. Дифференциальный дилатометр Шевенара
Схема измерительной головки дифференциальногооптико-механического дилатометра Шевенара
Курс "Физические методы
исследования КНМ"
122
123. Способ повышения чувствительности дилатометра Шевенара
9 – подвижное зеркальце, 13 – осветитель, 14, 15 –вспомогательные неподвижные зеркала, 16 – экран из матового
стекла или фотопластинка
Курс "Физические методы
исследования КНМ"
123
124. Дифференциальная дилатограмма Шевенара
Схема дилатометрическойкривой (перемещения
световой точки на экране
дифференциального
дилатометра):
ОА – при расширении
только эталона,
ОВ – при расширении
только образца
y = Ky ( lобр – lэт)
x = Kx ( lэт – lкв)
обр = эт + (Кx /Кy) ( эт – кв) dy/dx
Курс "Физические методы
исследования КНМ"
124
125. Экспериментальное определение коэффициентов увеличения дилатометра Шевенара
yo
1 – линия расширения эталона,
получаемая при замене образца
кварцевым стержнем
a
x
φ
x = oa = Kx ( lэт – lкв)
1
y = – ас = Ky ( lкв – lэт)
c
oa
Kx
( эт кв ) l 0 T
ac
Ky
( эт кв ) l 0 T
Курс "Физические методы
исследования КНМ"
125
126. Измерительная головка дилатометра Шевенара для измерения абсолютным (недифференциальным) методом
Схема устройства абсолютныхизмерительных головок:
1, 3 – опоры, связанные
с образцом и эталоном
соответственно;
2 – неподвижная
опора;
4, 5 – направления
движения «зайчика» при
расширении эталона и образца
x = Kx ( lобр – lкв)
y = Ky ( lэт – lкв)
Курс "Физические методы
исследования КНМ"
126
127. Сравнение абсолютной и дифференциальной дилатограмм
Дилатограммы стали 40, записанные с помощью дифференциальнойголовки (a) и абсолютной (б). Коэффициенты увеличения головок : а)
Кх = 144,6; Кy = 318,8 и б) Кх = 335;Кy = 314,2.
Скорость нагрева ~1500 К/ч, охлаждения ~1000 K/ч.
Курс "Физические методы
исследования КНМ"
127
128. Оценка дилатометрического эффекта фазового превращения
Схема определениядилатометрического эффекта
превращения, протекающего
в интервале температур tн…tк
с уменьшением объема
Построения:
1. ab║hi → точка b
2. ae – продолжение оа →
точка e
3. bd = de → точка d
Длина отрезка dh = cg и равна
дилатометрическому эффекту
фазового превращения Δlпр –
уменьшению длины образца
из-за превращения.
Курс "Физические методы
исследования КНМ"
128
129. Дилатометрический эффект аустенитизации железа и сталей
Фрагменты дилатограмм нагрева железа и углеродистых сталей 20,40,У8 (а) и зависимость дилатометрического эффекта образования
аустенита от содержания углерода в стали (б)
Курс "Физические методы
исследования КНМ"
129
130. Влияние скорости нагрева на дилатограмму
Дилатограммы заэвтектоиднойуглеродистой стали:
а – медленный нагрев
(начальная температура печи
20 °С), охлаждение до 430 °C с
печью, далее на воздухе;
б – быстрый нагрев
(начальная температура печи
650 °C), охлаждение на
воздухе
Курс "Физические методы
исследования КНМ"
130
131. Оптико-механический дилатометр с призмой полного внутреннего отражения
1 – фотопластинка; 2 –кожух; 3 – луч света; 4 –
подвижное зеркало
гальванометра,
соединенного с термопарой;
5 – подвижная стеклянная
призма; 6 – подвижная
стальная игла; 7 – кварцевая
трубка; 8 – кварцевый
стержень; 9 – печь; 10 –
образец;
11 – осветитель; 12 –
неподвижные зеркала; 13 –
неподвижная стальная
игла;15 – полупрозрачное
зеркало; 16 – экран
Курс "Физические методы
исследования КНМ"
131
132. Ёмкостной дилатометр с дифференциальным ёмкостным преобразователем
l = d C/CКурс "Физические методы
исследования КНМ"
1 – генератор, 2 –
усилитель, 3 – вольтметр,
4 – синхронный детектор,
5 – самописец, 6 –
фазовращатель, С1 и С2 –
регулируемые
конденсаторы моста
переменного тока, Сизм –
дифференциальный
конденсатор с подвижной
средней пластиной,
соединённой с образцом,
Сэт – эталонный
конденсатор для
градуировки.
132
133. Индуктивный дилатометр с дифференциальным трансформаторным преобразователем
1 – первичная обмоткадифференциальнотрансформаторного
преобразователя (ДТП); 2а и
2б – вторичные обмотки ДТП;
3 – первичная обмотка
компенсационного
дифференциального
трансформатора (КДТ); 4а и
4б – вторичные обмотки КДТ;
5 – усилитель; 6 –
регистрирующее устройство
(самописец);
7 – регулировочный винт
Курс "Физические методы
исследования КНМ"
133
134. Интерференционный дилатометр
1 – образец, 2 – печь, 3 –подвижное зеркало, 4 – основание
корпуса, 5 – призма, 6 – объектив
микроскопа, 7 – объектив, 8 –
насадка на образец для крепления
зеркала 3, 9 – зеркало, 10 –
микроскоп, О – окуляр.
l = n /2
Курс "Физические методы
исследования КНМ"
134
135. Лекция 8. Методы измерения теплопроводности
Закон Фурье:q S T
Классификация методов измерения
теплопроводности
• По зависимости от времени теплового потока:
стационарные (q = const) и нестационарные
методы (температурной волны, импульсный).
• По направлению протекания теплового
потока: методы продольного потока тепла и
методы радиального потока тепла.
Курс "Физические методы
исследования КНМ"
135
136. Метод продольного потока тепла
= (q/S)L/ TВарианты
экспериментального
определения плотности
теплового потока q/S:
1. По тепловой мощности, отводимой
охладителем, – с измерением
скорости и перепада температур
охладителя на входе и выходе.
Курс "Физические методы
исследования КНМ"
2. По электрической
мощности нагревателя
136
137. Метод продольного потока тепла с измерением теплоотвода охладителем
1 – образец, 2 – медный блок сэлектронагревателем, 3 –
охлаждаемый медный блок, 4 –
устройство для впуска воды с
датчиками температуры и
скорости, 5 – датчик
температуры воды на выходе, 6,
7, 8 – термопары, 9 – трубчатый
защитный экран для уменьшения
радиационных потерь
q/S = Cв ρв v Tв
= Cв ρв v Tв L/ T
Курс "Физические методы
исследования КНМ"
137
138. Метод продольного потока тепла с измерением мощности нагревателя
1 – внутреннийэлектронагреватель
образца, 2 – образец, 3 –
термостатируемая ванна,
aa, bb – прорези для
размещения термопар
Курс "Физические методы
исследования КНМ"
138
139. Метод Кольрауша
1 – образец; 2 – печь; 3 –рубашка водяного
охлаждения;
4 – штатив; 5 – цанги
Осуществляется
стационарный метод
продольного потока тепла с
пропусканием тока через
образец. Концы образца
термостатируются.
= U2 / (8 ρ ΔT)
Курс "Физические методы
исследования КНМ"
139
140. Метод радиального потока тепла
Внутренний нагревательЦилиндрический полый образец,
собранный из плоских колец
2Т/ r2 + r–1 T/ r = 0
P/l = 2π λ [Т(r1) – Т(r2)] / ln(r2/r1)
Курс "Физические методы
исследования КНМ"
140
141. Метод Стакса – Чесмара
Метод Стакса – ЧесмараКурс "Физические методы
исследования КНМ"
141
142. Метод температурной волны (метод Ангстрема)
1,2 – термопары; 3 – образец;4 – слюда;
5 – нагреватель; 6 – медный штырек
T/ t = a 2Т/ x2, a = λ/Cρ
Т (x, t) = Тm ехр(–δx) sin(ωt – δx)
а = (1/2)ωx2/[lnΛ(х)]2, Λ(х) = ехр(δx)
а = (1/2) ωx2 / [ψ(х)]2
а = ωx2 / [2ψ(х) lnΛ(х)]
Курс "Физические методы
исследования КНМ"
142
143. Импульсный метод
Метод лазернойвспышки:
4
3
9
2
5
8
1
6
7
1 – образец в виде
пластины, 2 – печь, 3 –
инфракрасный датчик
температуры, 4 –
усилитель, 5 – источник
питания печи, 6 –
волоконно-оптический
кабель, 7 – импульсный
лазер, 8 – компьютер с
платой для сбора данных,
9 – программное
обеспечение
a = 1,37 d2 / (π2 τ1/2)
Курс "Физические методы
исследования КНМ"
a = 0,1388 d2 / τ1/2
143
144. Метод горячей проволоки
Курс "Физические методыисследования КНМ"
144
145. Лекция 9. Измерение электрического сопротивления методом амперметра–вольтметра
Лекция 9. Измерение электрическогосопротивления методом амперметра–
вольтметра
Определение удельного электрического сопротивления
для образца правильной формы
l
S
R
l
S
Курс "Физические методы
исследования КНМ"
145
146. Метод амперметра-вольтметра. Схема правильного подключения амперметра
Приближённая формула:a
Ix = IA
UV
R
IA
'
x
A
UV
V
Rx
(1)
Истинное значение:
U V I A RA
Rx
IA
Погрешность подсчёта по
приближённой формуле (1):
Схемой целесообразно
пользоваться при Rx>>RA,
т.е. для измерения больших
сопротивлений
U V U V I A RA
'
Rx Rx I A
RA
IA
1
Rx
Rx
Rx
Курс "Физические методы
исследования КНМ"
146
147. Метод амперметра-вольтметра. Схема правильного подключения вольтметра
UVUV
1
R
1
1
I A IV I x
RV Rx
'
x
б
A
UV
IA
Ix
IV
V
Rx
RV Rx
Rx
'
Rx Rx RV Rx
Rx
2
Rx
Rx
Rx RV
Схемой целесообразно
пользоваться при Rx<<RV,
т.е. для измерения малых
сопротивлений
Курс "Физические методы
исследования КНМ"
1
2
1 RV / Rx
147
148. Четырёхконтактная схема резистора низкого сопротивления
1, 2 – токовые контакты3, 4 – потенциальные
контакты
V
IV
Rx
1
3
4
2
Ток IV<<IA из-за различий
сопротивлений в цепи
вольтметра и цепи питания.
Rx R34
IA
A
Второй закон Кирхгофа для
цепи вольтметра:
IV Rк 3 IV Rпр IV RV IV Rпр IV Rк 4 ( I A IV ) Rx 0
Можно пренебречь
Курс "Физические методы
исследования КНМ"
148
149. Измерение удельного сопротивления методом Ван-дер-Пау
аV
1
2
Два измерения ( а, б ).
4
3
A
б
A
V
2
3
Образец в виде пластины
постоянной толщины d с
произвольным очертанием
контура.
U 12
R1
I 34
exp(
1
U 32
R2
I 41
dR1
dR2
) exp(
) 1
4
Курс "Физические методы
исследования КНМ"
149
150. Расчёт удельного сопротивления в методе Ван-дер-Пау
Курс "Физические методыисследования КНМ"
150
151. Метод Ван-дер-Пау в случае образцов симметричной формы
Достаточно одногоизмерения:
V
R1 R2 R
1
4
A
2
dR
2 exp(
) 1
3
Курс "Физические методы
исследования КНМ"
dR
ln 2
4,53dR
151
152. Лекция 10. Нулевой метод измерений сопротивления
Основные разновидности нулевого методаизмерения электрического сопротивления:
Нулевой метод
Мостовые методы
Одинарный мост
Потенциометрический
Двойной мост
Курс "Физические методы
исследования КНМ"
152
153. Одинарный мост постоянного тока (мост Уитстона)
ac, cb, bd, da – плечи моста,ab – диагональ питания,
cd – измерительная диагональ.
Условие равновесия
IГ = 0
выполняется при:
Rx R2 = RN R1.
Рабочая формула моста:
Е
Rx = RN R1 / R2
Курс "Физические методы
исследования КНМ"
153
154. Погрешность измерений сопротивления с помощью одинарного моста
Относительная погрешность измерения сопротивления= ΔRx/Rx складывается из трёх составляющих:
= 1 + 2 + 3
Из-за влияния сопротивлений
соединительных проводов и
переходных контактов
Из-за неточности
уравновешивания
моста
Погрешность сопротивлений
резисторов, включённых в плечи
моста
Курс "Физические методы
исследования КНМ"
154
155. Оценка погрешностей измерения с помощью одинарного моста
аRпр
Rx
Rпр
с
1 = 2 Rпр / Rx ≈ 0,01/ Rx
Следовательно, при помощи одинарного моста с
относительной погрешностью не больше 1 % можно
измерять лишь сопротивления Rx больше 1 Ом.
Rx = RN R1 / R2
2 = R1 + R2 + RN
Курс "Физические методы
исследования КНМ"
155
156. Оценка погрешности из-за неточности уравновешивания
100U cd
K(n)
U cd
10
RN
R2
E
RN Rx R1 R2
RN
E
Rx U
2
( RN Rx )
U ( RN Rx ) 2
RX
E
RN
1
0,01
0,1
1
10
n=R2/R1
n = R1/R2
100
Rx U (1 n) 2
3
Rx
E
n
K(n)
Курс "Физические методы
исследования КНМ"
n = R1/R2
Отношение
плеч моста
156
157. Чувствительность моста
Относительная чувствительность мостовой схемыпо напряжению и по току
S сх ,U
U
E / K ( n)
( Rx / Rx )
I
~ Sсх
( Rx / Rx )
Чувствительность моста:
I
S м оста
S Г S сх
( Rx / Rx ) I ( Rx / Rx )
Относительная погрешность
min
0,1дел
3
S сх S Г
S сх S Г
Курс "Физические методы
исследования КНМ"
157
158. Двойной мост Томсона
Реализованачетырёхконтактная схема
включения в
электрическую цепь
измеряемого
сопротивления Rx и
образцового
сопротивления RN.
Цель – исключить (в
максимальной степени
уменьшить) влияние на
результат соединительных
проводов и контактных
сопротивлений.
Курс "Физические методы
исследования КНМ"
158
159. Рабочая формула двойного моста постоянного тока
Rx = RN (R1/R2) + R4Rш (R1/R2 – R3 /R4)/(R3 +R4+Rш)Сопротивление шины
Rш – неизвестно.
Можно пренебречь при:
R1/R2 = R3 /R4
На практике это условие реализуют, выбирая одинаковыми
соответствующие пары сопротивлений (R1 = R3, R2 = R4) с общей
регулировкой.
Рабочая формула моста:
Rx = RN (R1/R2)
Курс "Физические методы
исследования КНМ"
159
160. Достоинства и недостатки мостовых методов
Измерения с мостовой схемой относятся к одним изнаиболее точных методов измерения сопротивления
с относительной погрешностью, достигающей 10–5.
Это объясняется тем, что в мостовой схеме
происходит непосредственное высокоточное
сравнение измеряемого сопротивления с
эталонными резисторами высокой точности и
стабильности.
К недостаткам метода можно отнести трудоемкость и
медленность измерений, что, однако, преодолено в
современных автоматических мостах, где подбор
баланса происходит автоматически под управлением
микропроцессора.
Курс "Физические методы
исследования КНМ"
160
161. Потенциометрический метод измерения сопротивления
Rx= RN (Ux / UN)Курс "Физические методы
исследования КНМ"
161
162. Устройство потенциометра
I – рабочая цепь,II – цепь установки рабочего
тока,
III – измерительная цепь.
Два положения переключателя
гальванометра ПГ:
1 – «Контроль рабочего тока»,
2 – «Измерение».
Рабочий ток (в цепи I)
I = EN / RN1
Измеряемое напряжение
потенциометр
Курс "Физические методы
исследования КНМ"
U = I·rк
162
163. Особенности применения потенциометрического метода для измерения малых сопротивлений
Измерения при двухнаправлениях тока для
исключения
паразитных термоЭДС
4-хконтактное включение
образца в цепь
Курс "Физические методы
исследования КНМ"
163
164. Измерение ЭДС и постоянной Холла
1 – образец, 2, 2’ –токовые контакты, 3, 5
– потенциальные
контакты, 4 –
дополнительный
контакт, 6 – реостат, 7
– переключатель
Н = EH b = RH ВI/d
Курс "Физические методы
исследования КНМ"
164
165. Поперечные эффекты переноса в магнитном поле
ЭффектВоздействия
Измеряемая
величина
Определяющее
соотношение
Холла
jx, Bz
Ey
Ey = RH jx Bz
Эттингсгаузена
jx, Bz
T/ y
T/ y = AE jx Bz
qx, Bz
Ey
Ey = ANE T/ x Bz
qx, Bz
T/ y
T/ y = ARL T/ x Bz
Нернста –
Эттингсгаузена
Риги – Ледюка
Курс "Физические методы
исследования КНМ"
165
166. Эффекты Эттингсгаузена, Нернста-Эттингсгаузена и Риги-Ледюка
Эффекты Эттингсгаузена, НернстаЭттингсгаузена и Риги-ЛедюкаЭффекты:
1. Эттингсгаузена,
2. Нернста-Эттингсгаузена,
3. Риги-Ледюка
Курс "Физические методы
исследования КНМ"
166
167. Исключение паразитных термоЭДС из результата измерений ЭДС Холла
• (+ H; + I) U1 = H + E + NE + RL + UIR,• (– H; + I) U2 = – H – E – NE – RL + UIR,
• (+ H; – I) U3 = – H – E + NE + RL – UIR,
• (– H; – I) U4 = H + E – NE – RL – UIR.
Отсюда
H + E = (U1 – U2 – U3 + U4) / 4.
Курс "Физические методы
исследования КНМ"
167
168. Измерение ЭДС Нернста – Эттингсгаузена
Ey = ANE T/ x BzКурс "Физические методы
исследования КНМ"
168
169. Лекция 11. Измерение электрических свойств на переменном токе
Параметры электрических цепей переменного тока:ёмкость С, индуктивность L, активное
сопротивление R,
ёмкостное сопротивление XC,
индуктивное сопротивление XL,
XC = 1/(ωC)
XL = ωL
реактивное сопротивление X,
полное комплексное сопротивление Z,
Z = R + j X = Z·exp(jφ)
модуль комплексного сопротивления Z,
Z = (R2 + X2)1/2
φ = arctg (X/R)
сдвиг фаз тока относительно
напряжения φ
δ = arctg (R/X)
угол потерь δ и др.
Курс "Физические методы
исследования КНМ"
169
170. Метод амперметра-вольтметра
бa
A
Hz
V
A
Z
Для Z >> ZA
Hz
V
Z
Для Z << ZV
Z = UV/I = (R2 + X2)1/2
Установить этим методом фазовый сдвиг φ = arctg (X/R)
невозможно.
Курс "Физические методы
исследования КНМ"
170
171. Применение метода амперметра-вольтметра для измерений малой ёмкости
Применение метода амперметравольтметра для измерений малойёмкости
Малая ёмкость С означает большое реактивное сопротивление
XC = 1/(ωC) и большое полное сопротивление, поэтому
выбираем схему правильного подключения амперметра.
I
I
C
U 2 fU
A
Hz
V
С
Необходим
частотомер!
Курс "Физические методы
исследования КНМ"
171
172. Метод двух вольтметров для измерения малых ёмкостей
U 2 IX C 0Cx
V1
С0
V2
I
C0
U1
U1
I
1
1
X Cx X C 0
C x C0
C0U 2
Cx
U1 U 2
Не нужно измерять частоту.
Курс "Физические методы
исследования КНМ"
172
173. Мостовой метод
Одинарный мостпеременного тока
Zi = Ri + j Xi = Zi·exp(jφi)
Условие равновесия
моста:
Z1 Z4 = Z2 Z3
Z1 Z4 = Z2 Z3
φ1 + φ4 = φ2 + φ3
Курс "Физические методы
исследования КНМ"
173
174. Мост Вина
Назначение: измерение ёмкостии активного сопротивления
Особенности схемы:
2 = 4 = 0, φ1 < 0, φ3 < 0
Условие равновесия в
комплексном виде:
(Rx – j/ωCx) R4 = (R3 – j/ωC3) R2
Рабочие формулы моста:
Rx = R3 R2 /R4
Cx = C3 R4 /R2
Курс "Физические методы
исследования КНМ"
174
175. Мост Максвелла – Вина
Мост Максвелла – ВинаНазначение: измерение индуктивности
и активного сопротивления
Особенности схемы:
2 = 3 = 0, φ1 > 0, φ4 < 0
Условие равновесия в
комплексном виде:
(Rx + j Lx)/ (1/R4 + j C4) = R2 R3
Рабочие формулы моста:
Rx = R3 R2 /R4
Lx = C4 R2 R3
Курс "Физические методы
исследования КНМ"
175
176. Резонансный мост
Назначение: измерение индуктивностии активного сопротивления
Особенности схемы:
2 = 3 = φ4 = 0, φx > 0,
регулируемый конденсатор в одном
плече с испытываемым образцом
Условие равновесия в комплексном виде:
(Rx + jωLx – j/ωC) R4 = R2 R3
Совпадение условий
резонанса и равновесия моста
приводит к повышению
чувствительности моста в
случае высоких частот.
Рабочие формулы моста:
Курс "Физические методы
исследования КНМ"
Rx = R3 R2 /R4
Lx = 1/(ω2 C)
176
177. Т-образный мост
Назначение: измерение индуктивности иактивного сопротивления при высоких
частотах
Преимущество схемы:
Возможность заземления входной и
выходной цепей, что облегчает
экранирование элементов схемы.
Рабочие формулы моста:
Rx = 1 /(R0 C02)
Lx = 2 / ( 2 C0)
Курс "Физические методы
исследования КНМ"
177
178. Трансформаторный мост
Назначение: для точных измеренийпараметров цепей переменного тока, а
также магнитных характеристик
ферромагнетиков
Условие равновесия:
Zx / Zобр = w1 / w2
δ = 0,001…0,1 %
Способ достижения равновесия:
изменением образцовой меры Zобр и
переключением витков индуктивносвязанных плечевых элементов
(изменением отношения числа
витков в обмотках трансформатора
w1 / w2)
Курс "Физические методы
исследования КНМ"
178
179. Лекция 12. Классификация магнитных методов исследования. Индукционные методы
Магнитные методы классифицируют:• По измеряемой магнитной величине (магнитной
индукции, магнитному моменту, магнитному потоку,
магнитной проницаемости)
• По первичному измерительному преобразователю
• По виду реализуемой в методе магнитной цепи
(замкнутой или разомкнутой)
• По режиму намагничивания (перемагничивания) –
статические и динамические
Курс "Физические методы
исследования КНМ"
179
180. Классификация методов измерений по виду первичного преобразователя
Величиныm
B
Ф
ИндукГальФерроционПервичные
Ядерно- вано- МагниИндукиндукные
преобразо- механические прецес- маг- то-оптиционционсверхватели
сионные нит- ческие
ные
ные
провоные
дящие
Уравнение
e=kB,
e=k·
преобра- =km F=km
=kB
=kB
e=kB
B=kФ
R=kB
·dФ/dt
зования
Интегратоугло- динары,
частото- вольт- угло- вольттесламе
Приборы мер- мометвольтмеры метры мерные метры
тры
ные
ры
метры,
компенсаторы
Курс "Физические методы
исследования КНМ"
180
181. Типовая схема установки для магнитных испытаний
(на примере определения магнитной индукции В вполе Н)
ИП Н
БП
НУ
СИ
Образец
ИП В
СИ
БП – блок питания, НУ – намагничивающее устройство,
ИП Н – измерительный преобразователь (ИП)
напряжённости магнитного поля Н, ИП В – ИП магнитной
индукции В, СИ – средство измерений.
Курс "Физические методы
исследования КНМ"
181
182. Измерительные преобразователи магнитного поля
ИПВыходной
сигнал
Диапазон
полей, Тл
Диапазон частот
δ, %
Вращающаяся
катушка
Напряжение
0 …11
Пост. поле
10–2
Катушка поля
Напряжение
0 … 10–3
5 Гц …400 кГц
2
Датчик Холла
Напряжение
0 … 10
0 … 1 кГц
0,5
Магниторезистивный
Сопротивление
0 … 2,5
Пост. поле
3
Феррозонд
Напряжение
0 … 2·10–3
Пост. поле
0,1
ЯМР
Частота
0,045 … 14
Курс "Физические методы
исследования КНМ"
Скорость
2·10–4
изменения 1 %/с
182
183. Датчики магнитного поля
a – датчик Холла,b – три датчика
Холла для
измерения
составляющих
вектора магнитной
индукции в трёх
перпендикулярных
направлениях,
с – неподвижная
катушка для
измерения
переменного поля,
d – вращающаяся
катушка.
Курс "Физические методы
исследования КНМ"
183
184. Образцы для магнитных испытаний
ав
б
г
д
е
ж
• Тороидальные (а)
• Кольцевые: цельные
(б), собранные из
плоских колец (шайб) и
ленточные витые
• Стержневые:
призматические (в) и
цилиндрические (г)
• Пластинчатые (прямые
ленточные)
• Рамочные: цельные (д)
и собранные из пластин
• Сферические (е)
• Дисковые (ж)
Курс "Физические методы
исследования КНМ"
184
185. Виды образцов, изготавливаемых из лент магнитомягких сплавов
а – прямойленточный образец,
б – витой кольцевой,
в – кольцевой.
1 – лента;
2 – измерительная
обмотка;
3 – компенсирующая
обмотка;
4 – намагничивающая
обмотка.
Курс "Физические методы
исследования КНМ"
185
186. Основные виды намагничивающих устройств
аа Намагничивающая
катушка
(соленоид)
б Кольца
Гельмгольца
в Намагничивающая
обмотка
г Электромагнит
б
r
r
i
в
г
i
Образец
i
Обмотка
Курс "Физические методы
исследования КНМ"
186
187. Намагничивание кольцевого образца
Пропускание тока через обмотку, намотанную наобразец, создаёт в нём циркулярное магнитное
поле (направленное по окружности).
Средняя магнитная линия
H
H
Образец
r1
lср 2 rср
r2
rср
Обмотка
w1i
H
lср
H1
H2
r1 r2
r
rср
r
w1i
1 2
H
H (r )dr
r2 r1 r1
2 rср.гарм
rср.гарм
Курс "Физические методы
исследования КНМ"
r1 r2
2
(r2 r1 )
ln( r2 / r1 )
187
188. Требования к размерам кольцевого образца
Кольцевой образец намагничиваетсянеоднородно:
w1i
H (r )
2 r
Для того чтобы исключить влияние неоднородности
намагничивания на результаты измерений, средний диаметр
образца должен значительно превышать радиальную толщину:
r2
1,3
r1
по ГОСТ 8.377-80
H 1 H 1 / r1 1 / rср r2 / r1 1
0,15
H
1 / rср
2
(ГОСТ 8.377-80 ГСИ Материалы магнитомягкие. Методика выполнения
измерений при определении статических магнитных характеристик.)
Курс "Физические методы
исследования КНМ"
188
189. Магнитное поле в образце
Напряжённость внутреннего магнитного поля в образцеHi меньше внешнего магнитного поля H,
создаваемого намагничивающим устройством, на
величину размагничивающего поля H0:
H i H H 0 H NI
H 0 NI
N – коэффициент размагничивания
(размагничивающий фактор), зависящий от формы и
размеров образца, а также от ориентации внешнего
магнитного поля по отношению к поверхности образца.
Курс "Физические методы
исследования КНМ"
189
190. Влияние размагничивающего магнитного поля на вид кривой намагничивания
Мφ
H0
N=0
N≠0
N tg
H0
Н
0
Курс "Физические методы
исследования КНМ"
190
191. Значения коэффициента размагничивания в образцах разной формы
• N = 0 в образцах замкнутой формы (тороидальных, кольцевых),если намагничивание осуществляется циркулярным полем,
направленным по окружности, и линии магнитного поля не
выходят за пределы образца. В этом случае говорят, что
магнитная цепь замкнута.
• N = 0 в бесконечно длинном прямом стержневом образце при
ориентации внешнего магнитного параллельно оси образца
• N = 0 для бесконечной пластины при ориентации внешнего поля
параллельно плоскости пластины
• N = 1 для бесконечной пластины при ориентации поля
перпендикулярно плоскости пластины
• N = 1/2 для бесконечного цилиндра в поле, перпендикулярном
оси цилиндра
• N = 1/3 для шара
Курс "Физические методы
исследования КНМ"
191
192. Коэффициент размагничивания цилиндрического образца
1,2H
N
1
0,8
d
0,6
l
0,4
0,2
0
0
5
10
15
20
25
l /d
Курс "Физические методы
исследования КНМ"
192
193. Проницаемость тела
BМагнитная проницаемость вещества:
0 H i
B
т
0 H
Магнитная проницаемость тела:
т
1 N ( 1)
Чем больше μ, тем сильнее зависимость
проницаемости тела от конструкции цепи,
в пределе приближаясь к проницаемости
формы μф.
1
ф
N
При испытаниях магнитомягких материалов следует использовать
замкнутую магнитную цепь с N = 0 (например, кольцевые образцы).
Курс "Физические методы
исследования КНМ"
193
194. Магнитная цепь
– совокупность находящихся в магнитном поле тел,внутри которых замыкаются линии магнитной
индукции.
Использование понятия «магнитная цепь» – способ
описания магнитопровода, аналогичный
электрической цепи
Магнитная цепь состоит из:
– Испытуемого образца;
– Источника магнитного поля;
– Устройств для проведения (замыкания) магнитного
потока
Курс "Физические методы
исследования КНМ"
194
195. Виды магнитных цепей
• Замкнутые магнитные цепи – это цепи, вкоторых отсутствуют участки с магнитной
проницаемостью, меньшей, чем
проницаемость материала образца
• Разомкнутые магнитные цепи – это цепи, в
которых магнитный поток через образец
замыкается через среду с магнитной
проницаемостью, значительно меньшей
проницаемости материала образца
(например, через воздух)
Курс "Физические методы
исследования КНМ"
195
196. Пермеаметр
Пермеаметр – этоустройство для
замыкания магнитного
потока (магнитной цепи).
Другими словами,
пермеаметр –
устройство,
дополняющее магнитную
цепь разомкнутого
образца до замкнутой.
Курс "Физические методы
исследования КНМ"
196
197. Определение напряжённости поля, создаваемого намагничивающим устройством
• Для намагничивающей катушки (соленоида), катушекГельмгольца – по силе тока и постоянной катушки k:
H k i
• Для намагничивающей обмотки, навитой на
кольцевой образец, – по силе тока и среднему
радиусу кольца:
wi
wi
H
1
lср
1
2 rср
• Измерением с помощью измерительных
преобразователей (датчиков) магнитного поля
Курс "Физические методы
исследования КНМ"
197
198. Индукционные методы
В индукционных методах измерений используется законэлектромагнитной индукции:
d
dФ
e
w2
dt
dt
Индукционный первичный измерительный преобразователь –
измерительная обмотка или катушка, в которой индуцируется ЭДС е
при изменении во времени магнитного потока Ф.
е – ЭДС индукции,
Ψ – потокосцепление,
t – время,
w2 – число витков в измерительной (вторичной) обмотке,
Ф – магнитный поток через один виток измерительной обмотки.
Курс "Физические методы
исследования КНМ"
198
199. Основные этапы формирования сигнала в индукционном методе измерений
Созданиепеременного
магнитного
потока
Ф(t)
Индукционный
преобразователь
е(t)
Курс "Физические методы
исследования КНМ"
Интегрирование
Измерение
199
200. Классификация индукционных методов по способу создания переменного магнитного потока
Изменение магнитногопотока
Изменение
магнитного поля
Непрерывное
Гистерезисграф
Скачком
Перемещение образца
или катушки
Выдёргивание
Индукционноимпульсный
метод
Курс "Физические методы
исследования КНМ"
Вибрация
Вибрационный
магнитометр
200
201. Интегрирующие приборы для измерения магнитного потока
• Баллистический гальванометр –магнитоэлектрический гальванометр
с увеличенным периодом свободных
колебаний указателя благодаря
утяжелённой подвижной рамке
гальванометра
• магнитоэлектрический веберметр
– магнитоэлектрический
гальванометр с нулевым
противодействующим моментом
подвеса подвижной рамки
• фотоэлектрический веберметр –
комбинация магнитоэлектрического
веберметра и фотоэлектрического
усилителя (для повышения
чувствительности)
Курс "Физические методы
исследования КНМ"
Ф CФ max
Ф CФ
201
202. Магнитоэлектрический гальванометр – пример динамического элемента второго порядка
1 – рамка с током2 – магнитомягкий
магнитопровод
3 – постоянный
магнит
4 – указатель
(стрелка)
4
Курс "Физические методы
исследования КНМ"
202
203. Фотоэлектрический веберметр
ГИК – измерительная катушка,
Г – магнитоэлектрический
зеркальный гальванометр, ФЭ
– фотоэлемент, УПТ –
усилитель постоянного тока,
ДЗ – дифференцирующее
звено, Uо.с – напряжение
обратной связи.
U о .с
di
k
dt
e U о .с
k i
w2
Движение рамки гальванометра и изменение фототока
будут происходить до тех пор, пока напряжение
обратной связи не уравновесит входной сигнал е.
Курс "Физические методы
исследования КНМ"
203
204. Индукционно-импульсный метод
Образецw1 – намагничивающая обмотка, w2 –
измерительная обмотка образца, wH –
катушка для измерения поля, БГ –
баллистический гальванометр, М –
образцовая катушка взаимной
индуктивности для градуировки БГ.
Курс "Физические методы
исследования КНМ"
204
205. Коммутационный режим измерений
Коммутация – изменениенаправления тока на
противоположное.
Осуществляется
переключателем П1 при
замкнутом ключе К.
B1
Ф1
B1
2
2 Sw2
Метод коммутации позволяет
определить точки основной
кривой намагничивания как
вершин симметричных
частных петель гистерезиса.
Курс "Физические методы
исследования КНМ"
205
206. Определение координат точек петли гистерезиса (метод переключений)
BBm
B1 ΔB1
ΔB1‘
-Hm -H1
H1
Hm
H
Замыкание ключа К
скачком уменьшает
сопротивление
намагничивающей цепи и
увеличивает ток (поле Н),
а размыкание – скачком
увеличивает
сопротивление и
уменьшает ток (поле Н).
K↑: (Нm, Bm) → (H1, B1)
измеряем ΔВ1 = Bm-B1
П1: (H1, B1) → (-H1, B1’)
ΔВ1’ = B1-B1’
-Bm
K↓: (-H1, B1’) → (-Нm, -Bm)
Курс "Физические методы
исследования КНМ"
206
207. Градуировка баллистического гальванометра
Вместо образца в измерительную цепь включают образцовуюкатушку взаимной индуктивности. При коммутировании
изменение магнитного потока равно
Ф 2Mi
Постоянная баллистического гальванометра по
магнитному потоку (условная баллистическая
постоянная)
2 Mi
CФ
Эта величина прямо пропорциональна сопротивлению цепи
гальванометра, которое часто меняют для изменения пределов
измерений. Поэтому при каждом изменении сопротивления
измерительной цепи необходима градуировка.
Курс "Физические методы
исследования КНМ"
207
208. Поправка на воздушный зазор между образцом и измерительной обмоткой
Измеренный магнитный потокФизм Ф Фвз
в образце
в воздушном зазоре
BизмS BS 0 H (Sобм S )
B Bизм
S обм
0 H (
1)
S
Поправка на воздушный зазор
Курс "Физические методы
исследования КНМ"
208
209. Определение коэрцитивной силы по индукции методом выдёргивания
1 – соленоид,2 – измерительная
катушка,
3 – образец,
БГ –
баллистический
гальванометр
Положения
образца:
I – до, II – после
выдёргивания.
Курс "Физические методы
исследования КНМ"
209
210. Сверхпроводящий квантовый интерферометр (СКВИД)
42
1
3
6
1 – ток смещения, 2 –
сверхпроводник, 3 –
переход Джозефсона
(тонкий слой диэлектрика
между сверхпроводниками),
4 – магнитное поле, 5 –
один период изменения
напряжения соответствует
увеличению магнитного
потока внутри кольца на
один квант магнитного
потока Ф0=h/2e, 6 –
изменение напряжения со
временем при непрерывно
увеличивающемся
магнитном потоке.
5
Курс "Физические методы
исследования КНМ"
210
211. СКВИД-магнитометр, работающий по методу непосредственной оценки
ΔФСКВИД
u(t)
Счётчик
импульсов
напряжения
n
Схема преобразования изменения магнитного потока в
импульсный электрический сигнал на выходе СКВИДа с
последующим подсчётом числа импульсов n:
ΔФ = nФ0.
Курс "Физические методы
исследования КНМ"
211
212. Связь СКВИДа с измерительной катушкой магнитометра
L1 – индуктивность первичнойкатушки, в которой изменяется
измеряемое магнитное поле, L2 –
индуктивность вторичной катушки,
индуктивно связанной со
сверхпроводящим квантовым
интерферометром (SQUID).
i ( L1 L2 ) 1 B w1 A1
B w1 A1
M i M
L1 L2
L1
0 w12 A1
l
Максимальная чувствительность достигается
при L1 = L2.
Курс "Физические методы
исследования КНМ"
212
213. Измерительная катушка СКВИД-магнитометра
s – образец, sh – держательобразца, cs –
измерительная катушка, в
которой формируется
входной сигнал для
СКВИДа
Для устранения влияния
внешних полей
измерительная катушка
выполнена в виде
градиометра второго
порядка.
Курс "Физические методы
исследования КНМ"
213
214. Сигнал СКВИД-магнитометра
С помощью линейногошагового мотора образец
движется относительно
измерительной катушки,
индуктивно связанной со
СКВИДом.
Магнитный момент
пропорционален амплитуде
выходного сигнала
сверхпроводящего
квантового
интерферометра (СКВИД).
Курс "Физические методы
исследования КНМ"
214
215. Вибрационный магнитометр
i xii 1 xi t
n
Электромагнит
Измерительные
катушки
m
xi xi 0 А sin ωt v A cos t
i Bi S i 0 S i H внешн H обр,i
H обр,i
i
0 Si
xi
xi
Образец
Уравнение
преобразования:
ε 0 K m A ω cos ωt
k i
K Si
xi
i 1
n
Коэффициент преобразования катушек
Курс "Физические методы
исследования КНМ"
215
216. Компенсационный вибромагнитометр
1 – исследуемыйобразец;
2 – стандартный
образец;
3 – шток-держатель;
4 – вибратор;
5 и 7 – измерительные
катушки;
6 – электромагнит;
8 – датчик Холла;
9 – калиброванный
делитель напряжения;
10 – вычитающее
устройство; 11–
усилитель; 12 – нульиндикатор
m
Курс "Физические методы
исследования КНМ"
216
217. Феррозондовый (ферроиндукционный) магнитометр
Дифференциальный феррозонд:1 – ферромагнитные сердечники, 2 –
первичные обмотки для создания
переменного поля возбуждения, 3 –
вторичная обмотка
Курс "Физические методы
исследования КНМ"
217
218. Лекция 13. Магнитомеханические методы
В магнитомеханических методах измерений используютвзаимодействие магнитного момента m образца и
индукции В внешнего магнитного поля. Это
взаимодействие приводит к угловому или линейному
перемещению образца или пробного тела.
Основные магнитомеханические методы:
• Магнитометрический (метод магнитной стрелки)
• Силометрический (измерение силы, действующей на
образец, в неоднородном магнитном поле)
• Метод крутящих (вращающих) механических моментов
(измерение механического момента, действующего на
образец во внешнем магнитном поле)
Курс "Физические методы
исследования КНМ"
218
219. Магнитометрический метод
m0φ
Hоб
L
mобр
р
r
Образец и магнитная стрелка
находятся в первом
гауссовом положении.
m0 – магнитный момент магнита
(магнитной стрелки),
mобр – магнитный момент образца,
Hобр – магнитное поле,
создаваемое образцом в точке
расположения магнитной стрелки,
r – расстояние между образцом и
магнитной стрелкой,
L – механический вращающий
момент, действующий на стрелку.
L m0 Bобр 0 m0 H обр 0
m0 mобр
2 r 3
0 m0
L
mобр sin
3
2 r
Курс "Физические методы
исследования КНМ"
219
220. Гауссовы положения двух магнитов в пространстве
am2
φ
m1
r
m1
φ
r
б
m2
Оси магнитов – в одной
плоскости.
а – первое гауссово
положение (ось
неподвижного магнита 1
проходит через центр
второго магнита),
б – второе гауссово
положение (ось
неподвижного магнита
перпендикулярна к оси,
соединяющей центры
магнитов).
Курс "Физические методы
исследования КНМ"
220
221. Астатический магнитометр
M1 – намагничивающаякатушка,
M2 – катушка для компенсации
действия катушки К1 в
отсутствие образца,
B – компенсационная катушка.
Курс "Физические методы
исследования КНМ"
221
222. Силометрический метод Фарадея
b – весы, s – образец, em –электромагнит, gp – скошенные
полюсные наконечники для
создания неоднородного поля
(HdH/dx = const)
B
H
Fx m
0V H
x
x
При измерении намагниченности
насыщения поле должно иметь
постоянный градиент (dH/dx = const):
H
Fx 0VI s
x
Курс "Физические методы
исследования КНМ"
222
223. Метод Фарадея – Сексмита
Схема весов Фарадея—Сексмита (а);профиль магнитных полюсов N и S и
распределение градиента магнитного
поля dH/dx (б).
ЭМ — электромагнит для поднятия груза
Курс "Физические методы
исследования КНМ"
223
224. Силометрический метод Гуи
b – весы, s – образец в видедлинного стержня, em –
электромагнит
B
H
1
2
2
Fx H dV 0 H
Sdx 0 S ( H1 H 2 )
x
x
2
V
x1
x2
Курс "Физические методы
исследования КНМ"
224
225. Маятниковые весы с тензометрическими преобразователями
1 – полюса электромагнита, 2 –образец, 3 – компенсационная
катушка, 4 – держатель образца в
виде изгибающейся пластины с
тензометрическими датчиками А и В
Курс "Физические методы
исследования КНМ"
225
226. Крутильные весы с дифференциальным емкостным преобразователем поворота
Используя методнеуравновешенного
моста, получим сигнал S:
Курс "Физические методы
исследования КНМ"
226
227. Крутильный магнитометр с механическими указателями угла закручивания подвеса
Курс "Физические методыисследования КНМ"
227
228. Крутильный магнитометр с оптическим преобразователем крутящего момента
51 – образец,
2 – вращаемый электромагнит,
6
3 – зеркало,
4
7
3
4 – источник света,
5 – компенсационная катушка,
2
6 – постоянный магнит,
7 – фотодетекторы.
1
Курс "Физические методы
исследования КНМ"
228
229. Магнитоэлектрическая компенсация малого крутящего момента
Роль компенсационнойкатушки играет отрезок
провода в форме
полукольца,
охватывающего
дискообразный образец.
Создаваемый током
крутящий механический
момент
T = BiLr·cosφ.
Курс "Физические методы
исследования КНМ"
Способ может быть
использован для
измерения констант
анизотропиии магнитномягких материалов.
229
230. Пример кривых вращающих моментов для одноосного ферромагнетика
Ýêñïåðèìåíòàëü-íûåóãëîâûå çàâèñèìîñòè
âðàùàþùåãî
ìîìåíòà L äëÿ
ìîíîêðèñòàëëà
YFe11Ti, èçìåðåííûå â
ïëîñêîñòè
(110) â ïîëå H = 13
kOe ïðè ðàçëè÷íûõ
òåìïåðàòóðàõ. T (K):
1 . 78, 2 . 200, 3 .
300, 4 . 400, 5 . 480.
Курс "Физические методы
исследования КНМ"
230
231. Сравнение кривых вращающих моментов для одноосного и трёхосного ферромагнетиков
Кривые вращающих моментовдля магнитоодноосного (1-3) и
магнитотрёхосного (4)
кристаллов. Поле H, в котором
измерены кривые, по сравнению
с полем анизотропии Ha:
1 – Н << Ha,
2 – H ~ Ha,
3,4 – H >> Ha.
Курс "Физические методы
исследования КНМ"
231
232. Принцип кантилеверной магнитометрии
Курс "Физические методыисследования КНМ"
232
233. Пьезорезистивная регистрация отклонения кантилевера
Курс "Физические методыисследования КНМ"
233
234. Микромеханический магнитометр с модуляцией сигнала
Курс "Физические методыисследования КНМ"
234
235. Четырёхквадрантный фотодиод для раздельного определения изгибных и крутильных деформаций кантилевера
Курс "Физические методыисследования КНМ"
235
236. Пример измерений магнитного момента с помощью микромеханического магнитометра
Измеренияпроводили
непосредственно
в процессе
осаждения
плёнки Fe.
Курс "Физические методы
исследования КНМ"
236
237. Кантилевер для резонансного магнитометра крутящего момента
Кантилеверизготовляли из
монокристаллического кремния.
Курс "Физические методы
исследования КНМ"
237
238. Резонансный микромеханический магнитометр с регистрацией отклика с помощью интерферометра
Колебания кантилевера смагнитным образцом в виде
напылённой плёнки
возбуждаются переменным
магнитным полем с
помощью модуляционной
катушки, через которую
пропускают переменный
ток. Для измерения
отклонений кантилевера
использовался
интерферометр с лазером и
оптоволоконным кабелем
диаметром 5 мкм.
Курс "Физические методы
исследования КНМ"
238
239. Лекция 14. Магнитооптические резонансные и методы Магнитооптический гистерезисграф на основе эффекта Фарадея
1 – источник света, 2 – конденсор,3 – поляризатор, 4 – образец, 5 –
объектив, 6 – анализатор, 7 –
зеркало, 8 – объектив, Тр –
трансформатор, Д – держатель
образца, К – катушка (соленоид),
П – переключатель, Ш – шторка,
Ф – фотоумножитель, БП – блок
питания фотоумножителя, В –
вольтметр, ИП – источник питания
намагничивающей катушки, R –
регулятор тока, З – заглушка.
Курс "Физические методы
исследования КНМ"
239
240. Эффект Керра
Эффекты Керра:а – полярный,
б – продольный
(меридиональный),
в – поперечный
(экваториальный).
Изменение
поляризации
падающего пучка
света (слева) и
отражённого
(справа).
Курс "Физические методы
исследования КНМ"
240
241. Пример петли гистерезиса, полученной с помощью эффекта Керра
Полученная спомощью
продольного
эффекта Керра
петля
гистерезиса
нанопроволоки
из пермаллоя
толщиной 5
мкм, шириной
200 нм и длиной
15 мкм.
Курс "Физические методы
исследования КНМ"
241
242. Виды магнитного резонанса
Ядерный
Электронный парамагнитный
Ферромагнитный
Резонанс границ доменов
Магнитострикционный
Размерный
Антиферромагнитный
Ферримагнитный
Курс "Физические методы
исследования КНМ"
242
243. Схема эксперимента по магнитному резонансу
Курс "Физические методыисследования КНМ"
243
244. Ферромагнитный резонанс
– избирательное поглощение ферромагнетиком энергииэлектромагнитного поля при определённых частотах и полях.
при ω = const
Статическое
поле
H0
ВЧ-поле
H1 H m e
j t
Курс "Физические методы
исследования КНМ"
244
245. Кривая ферромагнитного резонанса
Зависимость вязкойсоставляющей
восприимчивости χ’’ от
индукции статического
внешнего магнитного поля
В0 для сферического
образца иттриевого
феррита-граната Y3Fe5O12
при частоте 3,33 ГГц и
температуре 300 К.
Курс "Физические методы
исследования КНМ"
245
246. Резонанс границ доменов
mэф x x kx 2 0 I s HУравнение
Дёринга
mэф – эффективная масса доменной границы, кг/м2,
β – коэффициент вязкого трения, кг/(м2·с),
k = 2μ0Is(dHэф/dx) – квазиупругий коэффициент, Дж/м4.
H H me
j t
0
k
m эф
Курс "Физические методы
исследования КНМ"
246
247. Влияние вихревых токов на комплексную магнитную проницаемость
При малых частотахПри больших частотах
Курс "Физические методы
исследования КНМ"
247
248. Магнитный спектр, обусловленный вихревыми токами
Зависимости от частотысоставляющих
комплексной магнитной
проницаемости
нанокристаллического
сплава
Fe77(Nb,Cu,Mo,Si,B)23.
Толщина ленты 30 мкм,
амплитуда магнитной
индукции 0,01 Тл.
x kx 2 0 I s H
Курс "Физические методы
исследования КНМ"
248
249. Магнитный спектр, обусловленный магнитным последействием
Зависимости от частотысоставляющих
комплексной магнитной
проницаемости никельцинкового феррита
(Ni,Zn)Fe2O4
Курс "Физические методы
исследования КНМ"
249
250. Магнитострикционный резонанс
Магнитный спектрферрита MnFe2O4 в
области
магнитострикционного резонанса
Курс "Физические методы
исследования КНМ"
250
251. Размерный резонанс
n cfn
2l
fn – частота резонанса,
n – целое число,
l – размер образца,
ε и μ – диэлектрическая и
магнитная относительные
проницаемости.
Для ферритовых образцов размером 1 см
магнитострикционный резонанс
наступает при частотах ~ 104-105 Гц, а
размерный резонанс – при 106-107 Гц.
Курс "Физические методы
исследования КНМ"
251
252. Ядерный магнитный резонанс
Ядро со спином ½ вмагнитном поле.
а) схема уровней и перехода ядра при
резонансе;
b) типичная кривая резонансного
поглощения энергии
Курс "Физические методы
исследования КНМ"
252
253. Установка для изучения ядерного магнитного резонанса
1 – частотомер, 2 –генератор высоких
частот, 3 – детектор, 4 –
усилитель низкой
частоты, 5 –
осциллограф, 6 –
генератор звуковых
частот, 7 – образец в
стеклянной ампуле, 8 –
электромагнит, 9 –
катушка
колебательного
контура, 10 –
модулирующие катушки
Гельмгольца
Курс "Физические методы
исследования КНМ"
253
254. Лекция 15. Измерение динамических магнитных свойств
Основной динамический режимнамагничивания и
перемагничивания магнитных
материалов – периодический
синусоидальный.
Особенность этого режима: даже
если напряжённость магнитного
поля изменяется по
синусоидальному закону с
определённой частотой, то
магнитная индукция имеет
спектр частот (уже не одна
гармоника, а несколько).
Причина – нелинейная связь
между магнитной индукцией и
напряжённостью магнитного
поля.
n
H t H mk sin k t H k
k 1
n
B t Bmk sin k t Bk
k 1
ω – частота первой
(основной) гармоники,
Hmk и Bmk – амплитуды k-й
гармоники напряжённости
магнитного поля и магнитной
индукции, φ – сдвиг фаз.
Курс "Физические методы
исследования КНМ"
254
255. Основные динамические режимы магнитных испытаний
• Синусоидального изменения напряжённости магнитного поля:H t H m1 sin t H1
B t Bmk sin k t Bk
k
• Синусоидального изменения магнитной индукции:
B t Bm1 sin t B1
H t H mk sin k t H k
k
• Постоянной скорости изменения напряжённости магнитного поля
или индукции:
dH / dt const
или
dB / dt const
Курс "Физические методы
исследования КНМ"
255
256. Комплексная магнитная проницаемость
В малых полях связь между B и H линейная, поэтому обе величиныв зависимости от времени содержат только одну первую
гармонику:
H H me
j t
B Bm e
Комплексная магнитная
проницаемость
j ( t )
Bm j
B
e a e j
0 H 0 H m
a cos j a sin j
Упругая
проницаемость
Амплитудная
проницаемость
Вязкая
проницаемость
Курс "Физические методы
исследования КНМ"
256
257. Динамическая петля гистерезиса в малых полях
При малых индукциях форма петли гистерезиса имеетэллиптическую форму. Две функции, изменяющиеся по
синусоидальному закону с одинаковой частотой, совместно
являются параметрическими уравнениями эллипса.
Площадь петли равна
потерям энергии в единице
объёма за один цикл
перемагничивания:
B
Bm
Br
T
Hc
Hm
H m Bm
dB(t )
W HdB H (t )
dt
sin
dt
2
H
0
δ – угол потерь
Курс "Физические методы
исследования КНМ"
257
258. Метод амперметра-вольтметра
i (t ) l ср H (t ) w1im l ср H m w1
e3 (t ) w2 S
dB Используется для
dt
определения
динамической
кривой
намагничивания
Bm(Hm).
1 – образец, 2 –
катушка
взаимной
индуктивности.
T
1
u3 e3 (t ) dt 4 fw2 SBm
T0
u 2 im r0
di(t ) Ml ср dH (t )
eM (t ) M
dt
w1 dt
T
1
u1 eM (t ) dt 4Ml ср H m / w1
T 0
Курс "Физические методы
исследования КНМ"
258
259. Осциллографический метод
dBe2 (t ) w2 S
dt
Используется для
измерения координат
динамической петли
гистерезиса.
1 – образец,
2 – осциллограф,
r0 – образцовое
сопротивление,
rC-цепочка –
интегратор.
w2 S
1
u B (t ) e2 (t )dt
B(t )
u H (t ) i1 (t )r0 r0 l ср H (t ) / w1
Курс "Физические методы
исследования КНМ"
259
260. Метод феррометра
Основан на способноститак называемого
фазочувствительного
преобразователя
измерять мгновенные
значения электрического
сигнала путём измерения
среднего за часть
периода Т (чаще всего –
за полпериода).
e2ср
1
(T / 2)
t1 T / 2
e2 (t )dt
t1
Для симметричной
петли
2w2
( t1 t1 T / 2 )
T
Bt1 Bt1 T / 2
Курс "Физические методы
исследования КНМ"
e2ср
2w2 S
( Bt1 Bt1 T / 2 )
T
e2 ср 4 fw2 SBt1
260
261. Определение координат точек петли гистерезиса по методу феррометра
1 – образцовая катушкавзаимной индуктивности М,
V1 и V2 – вольтметры с
фазочувствительными
преобразователями,
ФВ – фазовращатель,
позволяющий изменять
время t1, к которому
относится измеряемое
значение сигнала.
di (t ) Ml ср dH (t )
eM (t ) M
dt
w1
dt
e2 (t ) w2 S
dB
dt
u1 4Mflср H (t1 ) / w1
u 2 4 fw2 B(t1 )
Курс "Физические методы
исследования КНМ"
261
262. Стробоскопический метод измерений координат точек петли гистерезиса
Стробоскопическийпреобразователь
преобразует
периодический входной
сигнал u(t) в напряжение
u(t/k) при k~105 и более.
Высокочастотный сигнал
преобразуется в
низкочастотный.
Форма сигнала при этом
не изменяется, в точности
повторяя форму входного
сигнала.
Курс "Физические методы
исследования КНМ"
262
263. Стробоскопический преобразователь
Во время открытия ключа под управлением генератора импульсовконденсатор заряжается, набирая заряд, пропорциональный
мгновенному значению измеряемого напряжения. На выходе
операционного усилителя – ступенчатый сигнал с высотой,
пропорциональной мгновенному значению измеряемого напряжения.
Курс "Физические методы
исследования КНМ"
263
264. Определение потерь на перемагничивание ваттметровым методом
T1
2
P i1 (t )e1 (t )dt I1 r
T0
T
1
Pмагн i1 (t )e1 (t )dt
T0
W
T
w1
Pмагн
i1 (t )e2 (t )dt
w2T 0
2
2
w1
U U
Pмагн
PW
w2
RV RW
Pмагн
Pуд
m
Курс "Физические методы
исследования КНМ"
264
265. Аппарат Эпштейна для испытаний образцов в виде пластин
Курс "Физические методыисследования КНМ"
265
266. Мостовой метод определения проницаемости
Нулевой индикатор (НИ)настраивается на первую
гармонику частоты
намагничивания.
l ср
0 Sw1
2
Lx
tg
Rx Rобм
tg
Lx
Курс "Физические методы
исследования КНМ"
266
267. Лекция 16. Определение температуры Кюри и термомагнитный анализ
Основные методы определения температуры Кюри:- Приближённые, по температурной зависимости
параметров петли гистерезиса
- По температурной зависимости начальной
проницаемости (восприимчивости) в
ферромагнитном состоянии
- То же в парамагнитном состоянии
- Метод термодинамических коэффициентов Белова
- По температурной зависимости немагнитных свойств
(теплоёмкости, электрического сопротивления и др.).
Курс "Физические методы
исследования КНМ"
267
268. Температурные зависимости статических магнитных параметров железа
Курс "Физические методыисследования КНМ"
268
269. Температурная зависимость констант магнитной анизотропии железа
Курс "Физические методыисследования КНМ"
269
270. Влияние напряжённости магнитного поля на температурную зависимость магнитной индукции железа
Курс "Физические методыисследования КНМ"
270
271. Метод термодинамических коэффициентов Белова
В соответствии с теорией фазовых переходов IIрода Ландау вблизи температуры Кюри
Ф = 0 + 1/2 2 + 1/4 4 + – H
В состоянии равновесия ∂Ф/∂σ = 0 и
+ 3 = H или + 2 = H/
Термодинамические коэффициенты и
можно найти, строя зависимости H/ = f( 2 ) и
спрямляя их.
~ (T – TС) вблизи ТС, поэтому
ТС – это температура, при которой = 0.
Курс "Физические методы
исследования КНМ"
271
272. График Аррота – Белова для Ni
2H
Величину определяют по
длине отрезка, отсекаемой
прямой на оси ординат.
β характеризует наклон
прямых.
Курс "Физические методы
исследования КНМ"
272
273. Сравнение результатов определения температуры Кюри никеля различными методами
Ms – намагниченностьнасыщения,
(1/R0)(ΔR/ΔT) –
температурный
коэффициент
электрического
сопротивления,
α – термодинамический
коэффициент, α ~ (Т – θ),
θ – температура Кюри,
(ΔR/R)п –
гальваномагнитный
эффект, обусловленный
парапроцессом.
Курс "Физические методы
исследования КНМ"
273
274. Особенности определения температуры Кюри сплава (на примере Fe – 38 %Ni)
Флуктуации концентрации размывают изломы и экстремумытемпературных зависимостей свойств.
Курс "Физические методы
исследования КНМ"
274
275. Метод Штеблейна вталкивания образца
УстановкаШтеблейна для
термомагнитного
анализа:
1 – канал
электромагнита,
2 – обмотка
электромагнита, 3
– измерительная
катушка, 4 – печь,
5 – толкатель, 6 –
упор, 7 – образец
перед
вталкиванием, 8 –
термопара, 9 –
милливольтметр,
10 – втулка.
Курс "Физические методы
исследования КНМ"
275
276. Баллистический магнитометр Штейнберга – Зюзина (метод выдёргивания)
1 – стержневой образец, 2 – осевой канал полюсных наконечников, 3– полюсные наконечники электромагнита, 4 – измерительная катушка
в межполюсном пространстве
Курс "Физические методы
исследования КНМ"
276
277. Дипольный магнитометр (анизометр)
Вместоболее
точного
Курс "Физические методы
исследования КНМ"
277
278. Дифференциальный магнитометр
а) схема дифференциального магнитометра (1 – цилиндрическийобразец, 2 – железный сердечник электромагнита из двух Шобразных половин, 3 – датчик напряжённости магнитного поля, 4 –
намагничивающие катушки), б) распределение магнитного потока
без образца, в) распределение магнитного потока с образцом
Курс "Физические методы
исследования КНМ"
278
279. Силометрический метод Зилова-Ренкина для определения Тс
Силометрический метод ЗиловаРенкина для определения ТсВ методе Фарадея измеряется сила,
действующая на исследуемый образец,
а в методе Зилова-Ренкина измеряется
сила, действующая на магнит.
Магнитные весы
Зилова-Ренкина.
1 – аналитические весы, 2
и 3 – постоянные магниты,
4 – образец, 5 –
нагреватель, 6 – катушка
компенсационного
устройства, 7 –
термопара, 8 – сосуд с
таящим льдом для
термостатирования
холодного спая
термопары.
Курс "Физические методы
исследования КНМ"
F =(M+mχудH)·dH/dx
279
280. Метод дифференциального трансформатора для определения температурной зависимости восприимчивости
Курс "Физические методыисследования КНМ"
280
281. Фазовый магнитный анализ методом экстраполяции кривых Мs(T) фаз
Приближённоеопределение
температур Кюри фаз по
точкам перегиба на
температурной
зависимости
намагниченности
Курс "Физические методы
исследования КНМ"
281
282. Термомагнитный анализ сплава Fe – Si с тремя ферромагнитными фазами и одной парамагнитной
Курс "Физические методыисследования КНМ"
282
283. Исследование мартенситного превращения в сталях с помощью термомагнитного анализа
Магнитометрические кривые охлаждения стали 40Н25:1 – закалка с 950оС; 2 – деформация 20% (950 оС); 3 – деформация
20% (560 оС)
Курс "Физические методы
исследования КНМ"
283
284. Лекция 17. Изучение доменной структуры
Основные методы изучения доменной структуры:• магнитопорошковый (метод Акулова – Биттера)
• магнитооптический (микроскопия Фарадея и Керра)
• методы просвечивающей электронной микроскопии
(Лоренцева микроскопия, интерференционная
электронная микроскопия, метод электронной
голографии)
• магнитно-силовая микроскопия
• рентгеновская топография магнитострикционных
материалов
• гальваномагнитный метод (с использованием
преобразователей Холла и на основе
магниторезистивного эффекта)
Курс "Физические методы
исследования КНМ"
284
285. Магнитопорошковый метод
Схема наблюдения доменной структурыметодом порошковых фигур Акулова –
Биттера (метод магнитной суспензии, или
порошковый метод)
Доменная
структура на
поверхности
(001) Fe-4 %Si.
Курс "Физические методы
исследования КНМ"
285
286. Определение направления вектора намагниченности
Магнитные поля рассеяния(силовые магнитные линии)
вблизи царапины:
а) перпендикулярной вектору
намагниченности,
б) параллельной вектору
намагниченности.
Определение знака
намагниченности с помощью
иглообразного магнита
Курс "Физические методы
исследования КНМ"
286
287. Размер частиц порошка в магнитопорошковом методе
Тепловоеразмытие
Образование
фигур
D1
D2
0 m H s 3kT
m
D 3
6
D
Условие скопления частиц
Взаимодействие частиц
порошка:
I s 1. С доменной границей
2. Друг с другом
18 3kT
D2 2
2
0 I s
D2 > D1 –
условие
образования
порошковых
фигур
Образование
хлопьев
D1
H s1
1/ 3
Курс "Физические методы
исследования КНМ"
H s 2
4I s
r (1 * )
2m
3
D
287
288. Наблюдение доменной структуры с помощью эффекта Фарадея
Курс "Физические методыисследования КНМ"
288
289. Наблюдение доменной структуры с помощью полярного эффекта Керра
Курс "Физические методыисследования КНМ"
289
290. Доменная структура сплава Mn-Bi, полученная методом эффекта Керра
aИзображения на рис. а
соответствуют наиболее
толстому,
на рис. с – наиболее тонкому
образцам.
b
c
Курс "Физические методы
исследования КНМ"
290
291. Метод лоренцевой просвечивающей электронной микроскопии
Схема метода лоренцевойпросвечивающей электронной
микроскопии (ЛПЭМ).
e Bd
e
2mU
Изменение направления вектора
индукции B приводит к изменению
направления силы Лоренца.
Электроны, проходящие через
пленку в соседних магнитных
доменах, отклоняются в разные
стороны, что приводит либо к
сгущению, либо к ослаблению
интенсивности на экране.
Курс "Физические методы
исследования КНМ"
291
292. Изображение доменной структуры, полученное с помощью ЛПЭМ
Изображение доменной границы ввиде параллельных чередующихся
темных и светлых
интерференционных линий.
Курс "Физические методы
исследования КНМ"
292
293. Интерференционная электронная микроскопия
Для получения голографическогоизображения используют пленку с
четким краем, например, краем
отверстия в пленке. Часть пучка
проходит через отверстие, не задевая
пленку («холостой пучок»).
Бипризма – два заземленных электрода
с положительно заряженной тонкой
золотой проволочкой между ними.
Электроны пучка отклоняются в сторону
проволочки и благодаря сдвигу фаз
между эталонным и рабочим пучками
возникает интерференция,
наблюдаемая в плоскости изображения
ПЭМ.
Курс "Физические методы
исследования КНМ"
293
294. Лоренцевское и интерференционное изображение микромагнитной структуры
Аморфная магнитномягкая плёнка(Сo0.94Fe0.06)79Si10B11.
Расстояние между
двумя линиями
интерференции
равно
l = h/(edBs),
где h – постоянная
Планка, е – заряд
электрона, d –
толщина плёнки, Bs –
индукция насыщения.
Курс "Физические методы
исследования КНМ"
294
295. Магнитно-силовая микроскопия (МСМ)
Курс "Физические методыисследования КНМ"
295
296. Сканирование зонда и регистрация отклика в МСМ
Курс "Физические методыисследования КНМ"
296
297. Зонды для МСМ
Изображения, полученные спомощью сканирующей электронной
микроскопии до и после нанесения
магнитного покрытия на зонд
Варианты зондов:
1. Кремниевые или нитридкремниевые зонды с
кобальтовым или другим
магнитным покрытием (Fe, Ni
и т.д.).
2. Кремниевые зонды
вискерного типа с покрытием
только на острие.
Для изучения магнитномягких материалов магнитное
покрытие зонда может
выбираться из материала с
небольшой намагниченностью
насыщения или с доменной
структурой для снижения
воздействия зонда на
изучаемый объект.
Курс "Физические методы
исследования КНМ"
297
298. Силы, действующие между зондом МСМ и поверхностью
Курс "Физические методыисследования КНМ"
298
299. Режим постоянной высоты при регистрации отклика МСМ
Режим постояннойвысоты – это
неконтактный метод
а – расположение зонда
относительно
поверхности образца,
б – пространственное
изменение полей
рассеяния над
образцом,
в – пространственное
изменение силы,
действующей на зонд
Курс "Физические методы
исследования КНМ"
299
300. Двухпроходная методика регистрации отклика МСМ
Курс "Физические методыисследования КНМ"
300
301. Изображение доменной структуры, полученное с помощью МСМ
Полосовая доменнаяструктура (с периодом
около 250 нм) плёнки
железа, нанесённой на
лавсан электроннолучевым осаждением.
Использовалась
двухпроходная
методика и зонд с
кобальтовым
покрытием.
Размер изображения
3х3 мкм.
Курс "Физические методы
исследования КНМ"
301
302. Пример изображения МСМ
Изображение МСМповерхности жёсткого
диска (80 Гб) с размером
бита ~100 нм.
Размер изображения
2,5х2,5 мкм.
Курс "Физические методы
исследования КНМ"
302



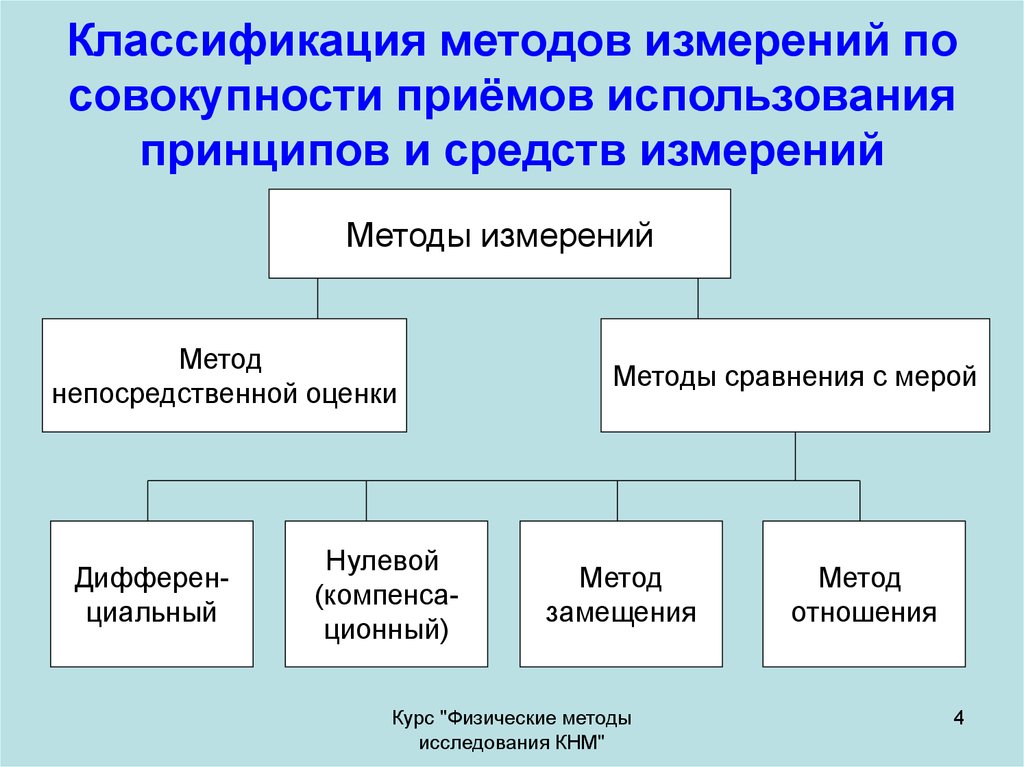

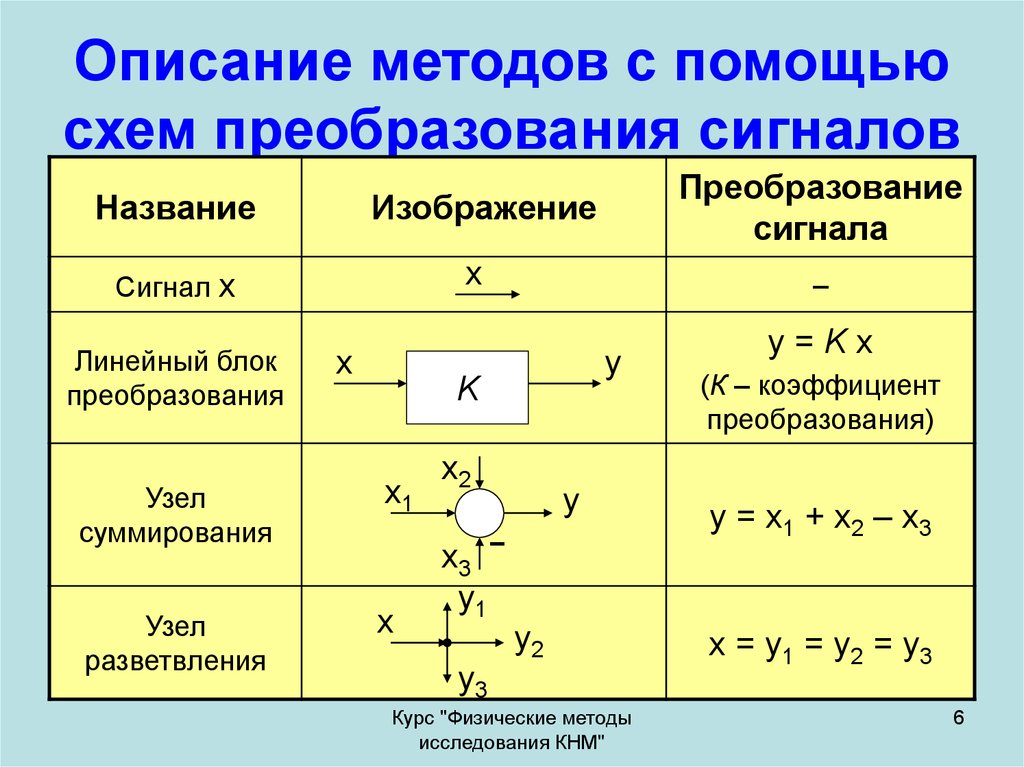
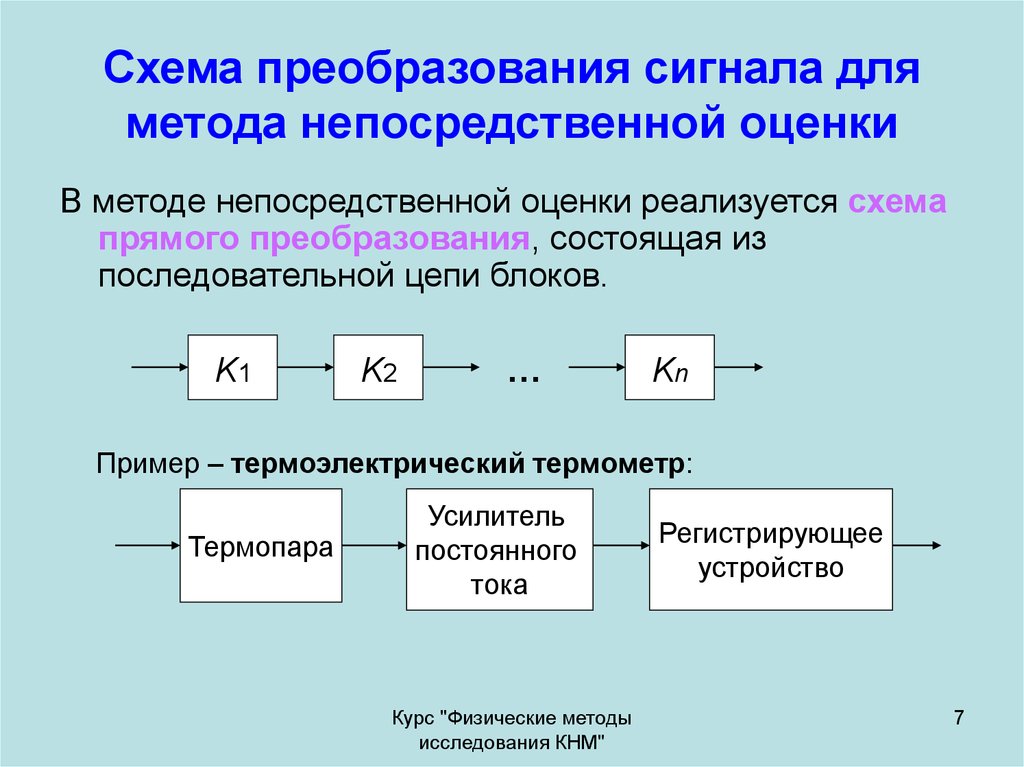
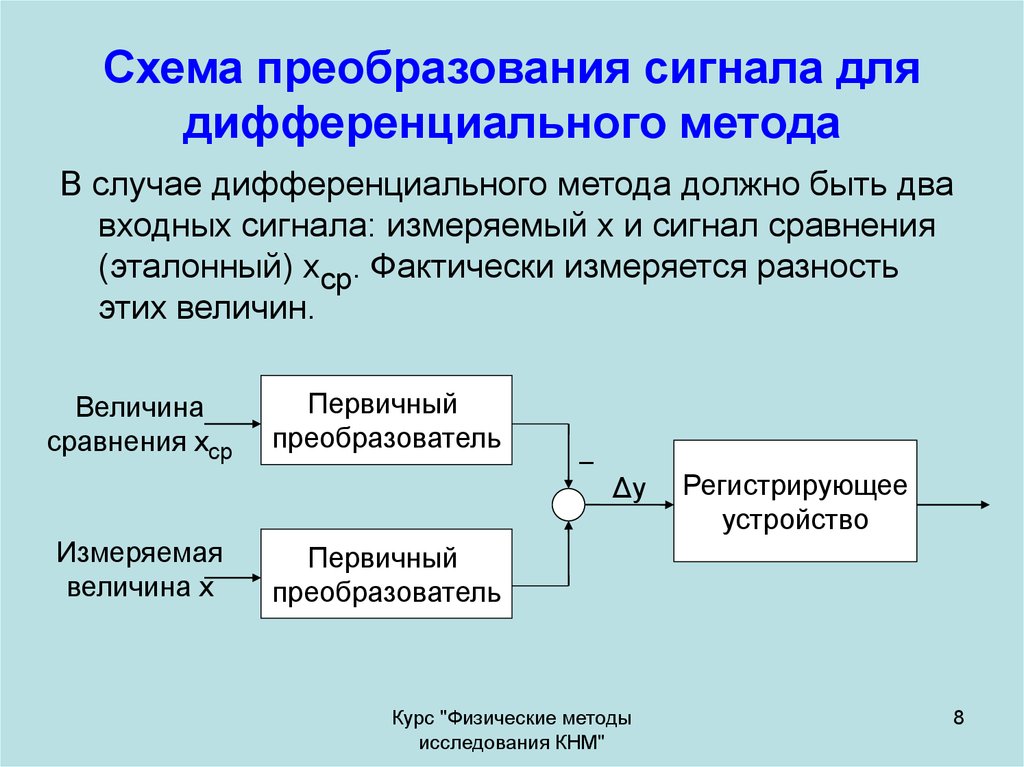
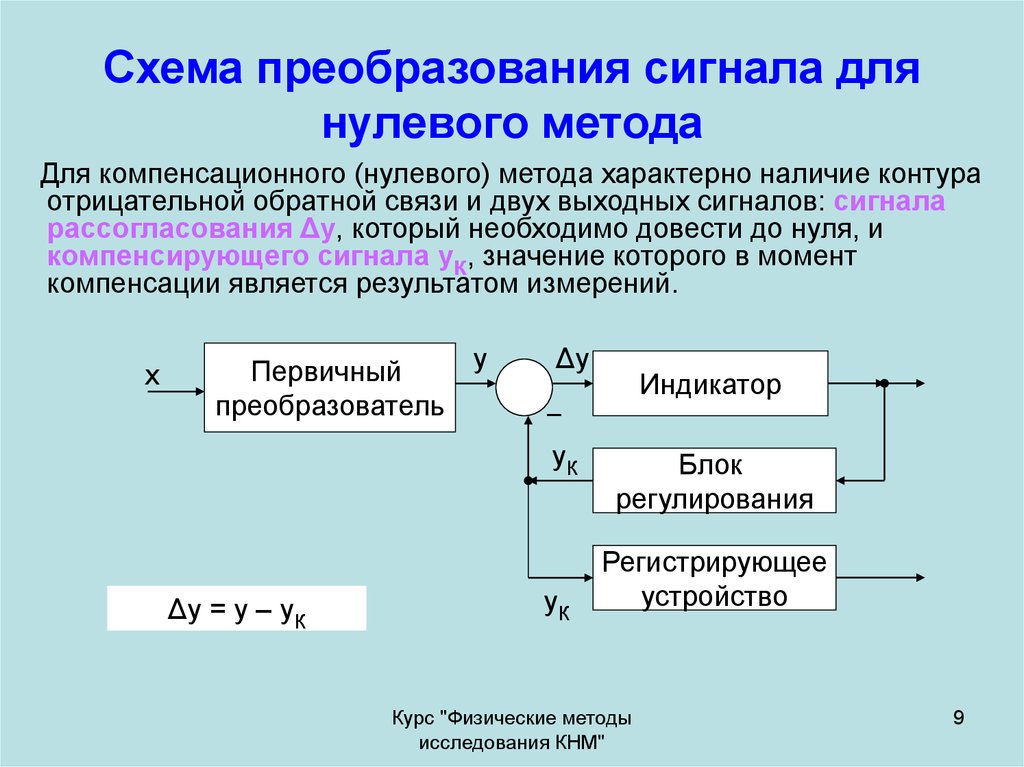


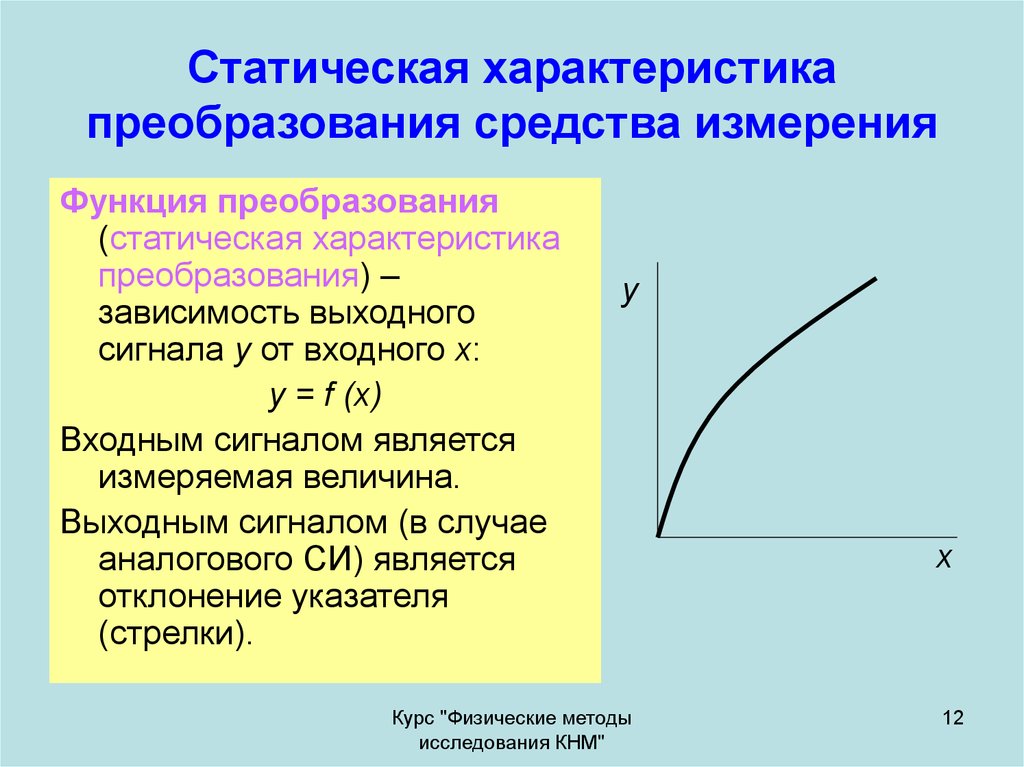




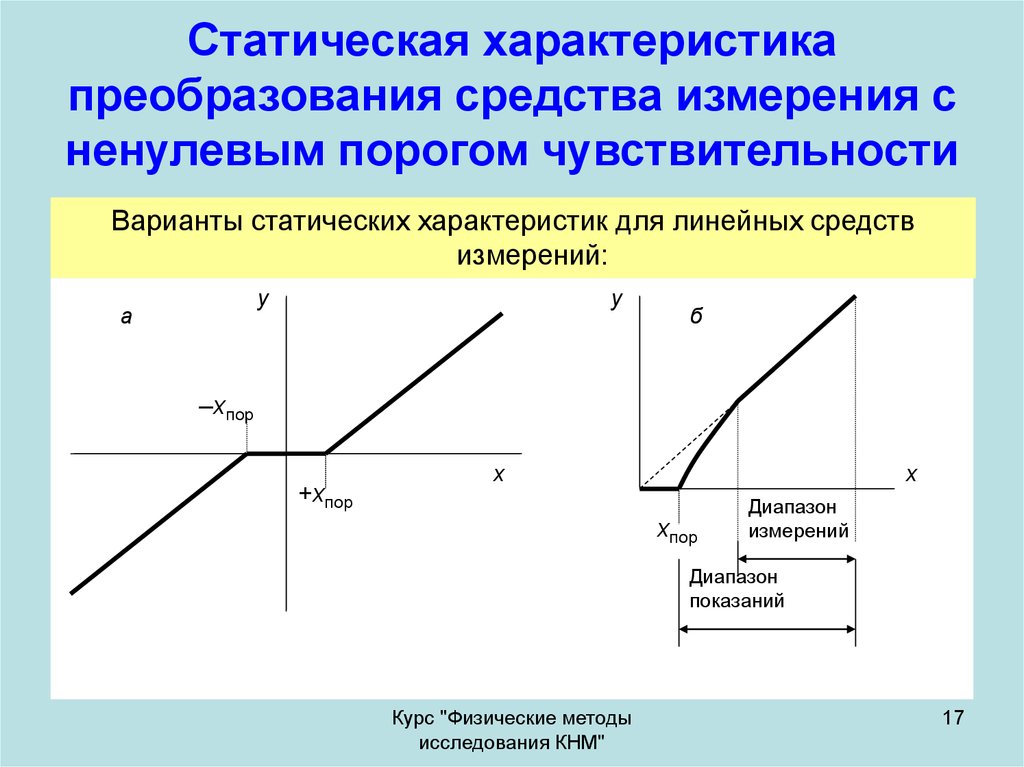

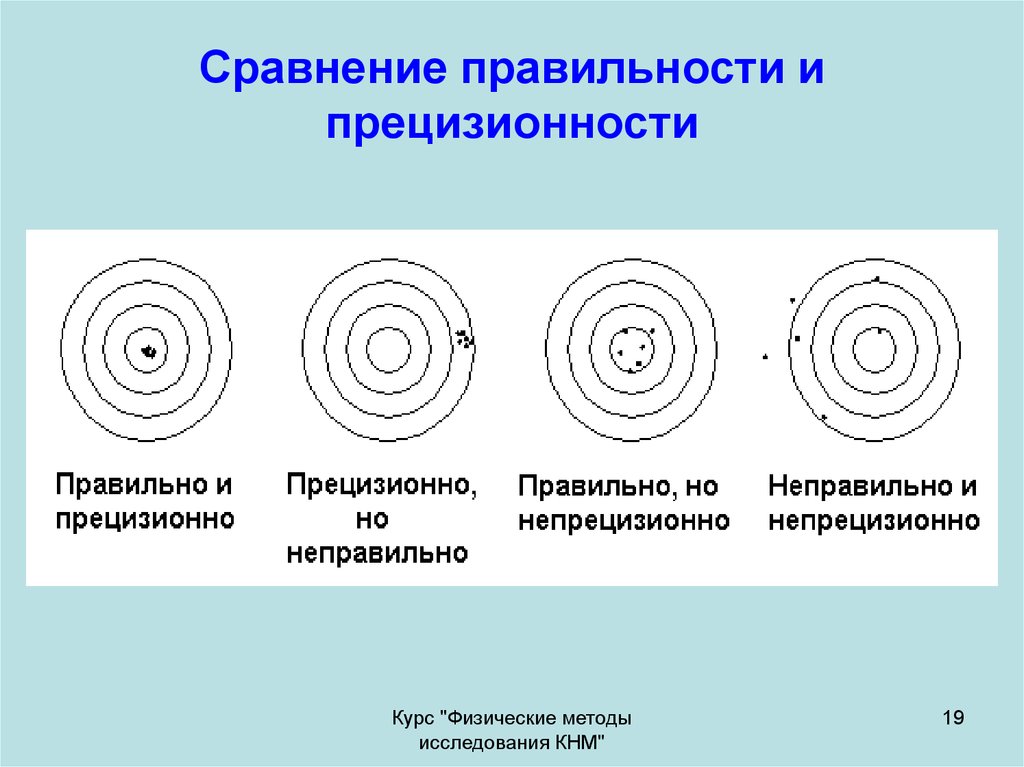

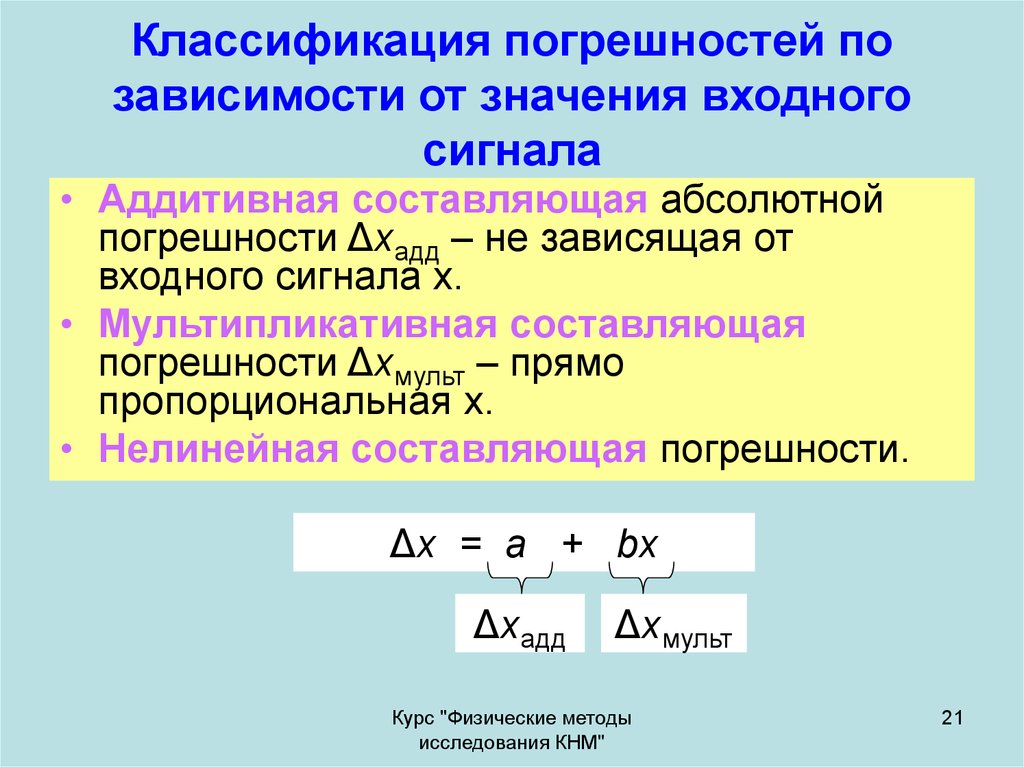
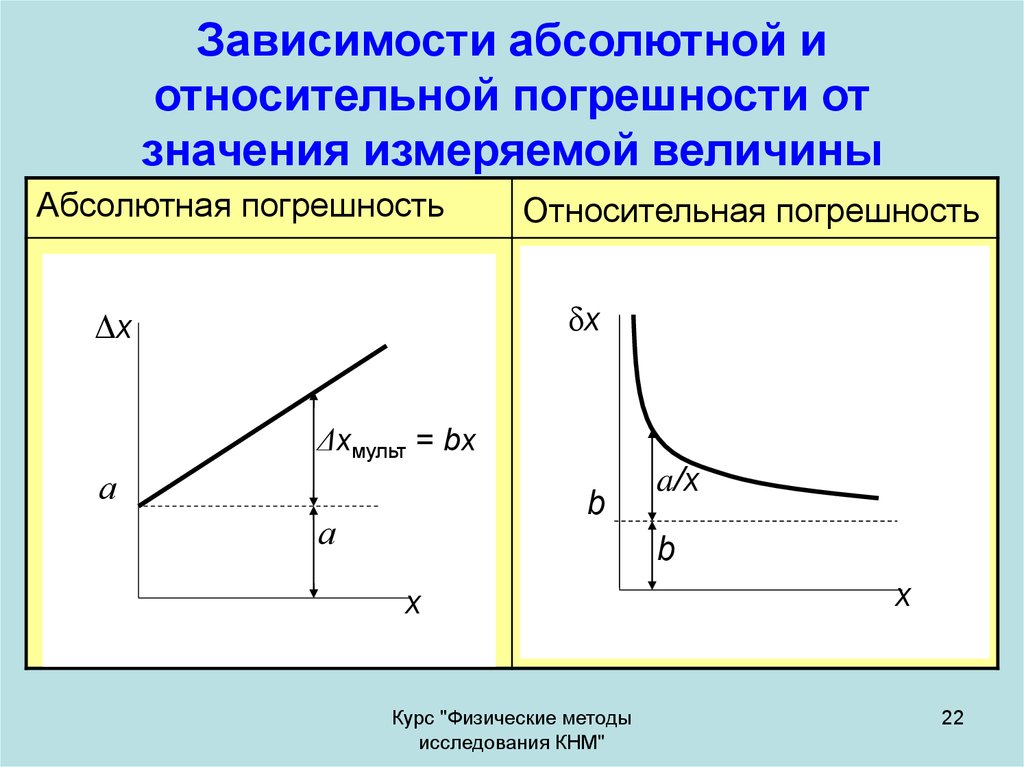
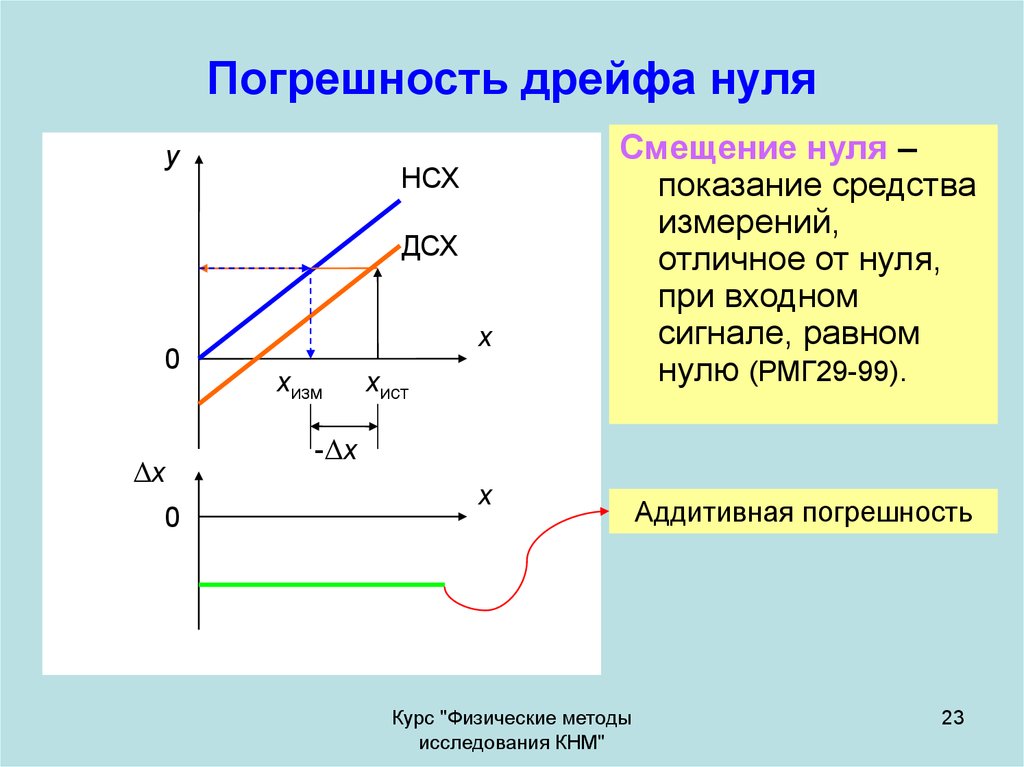
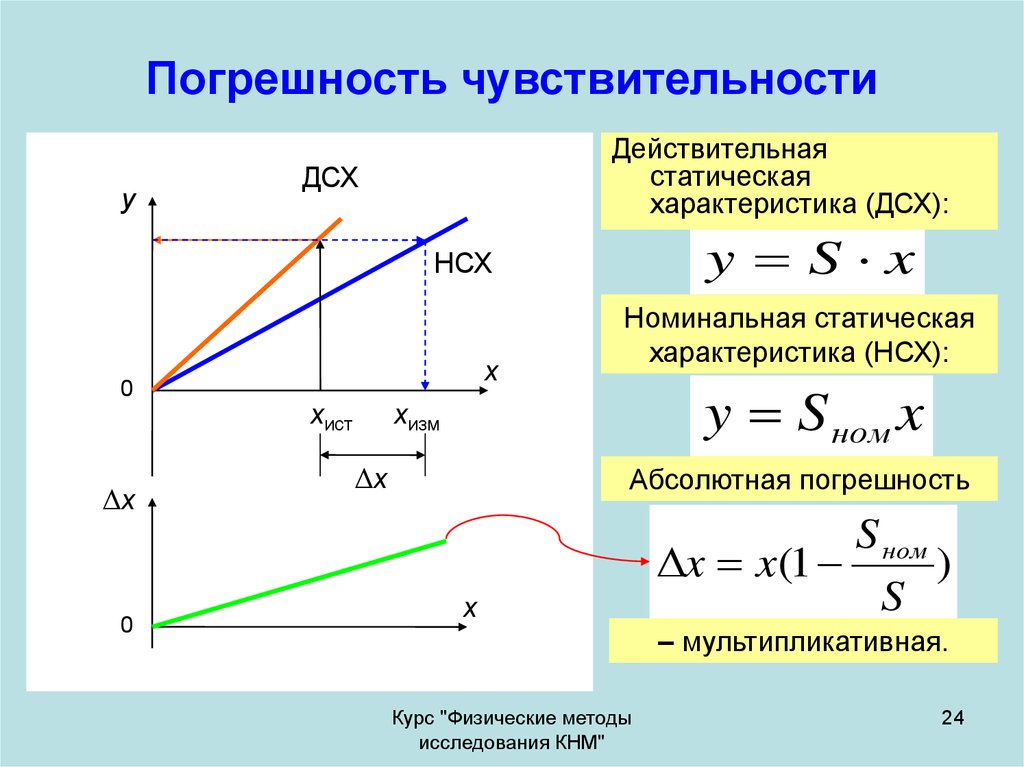
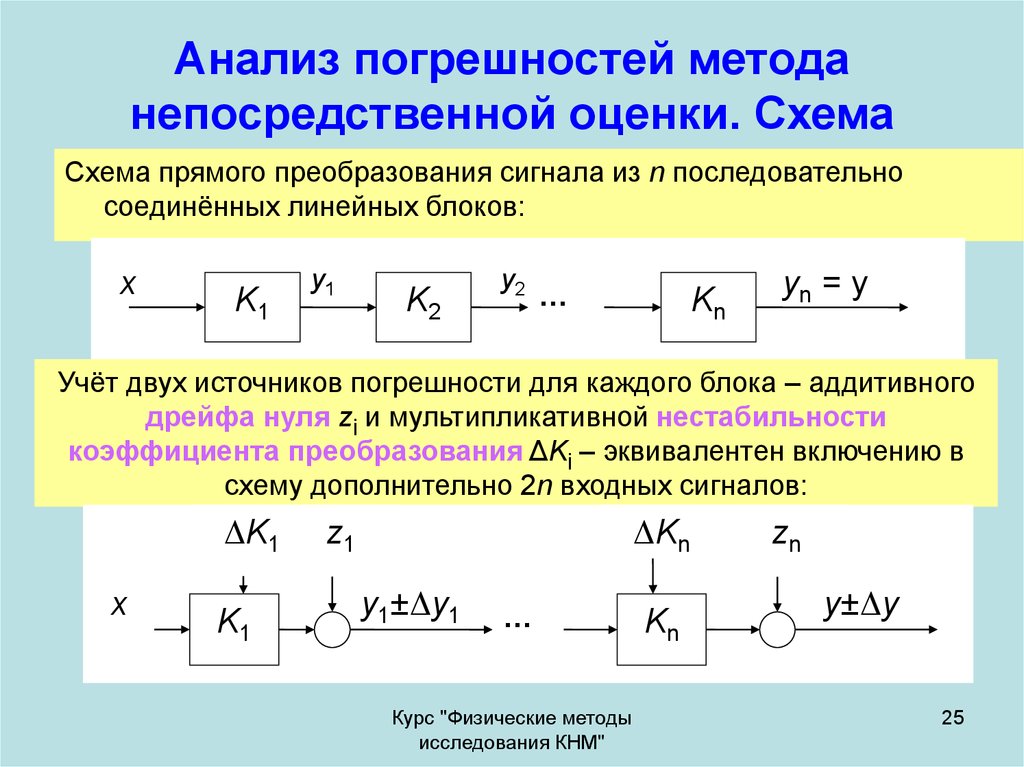
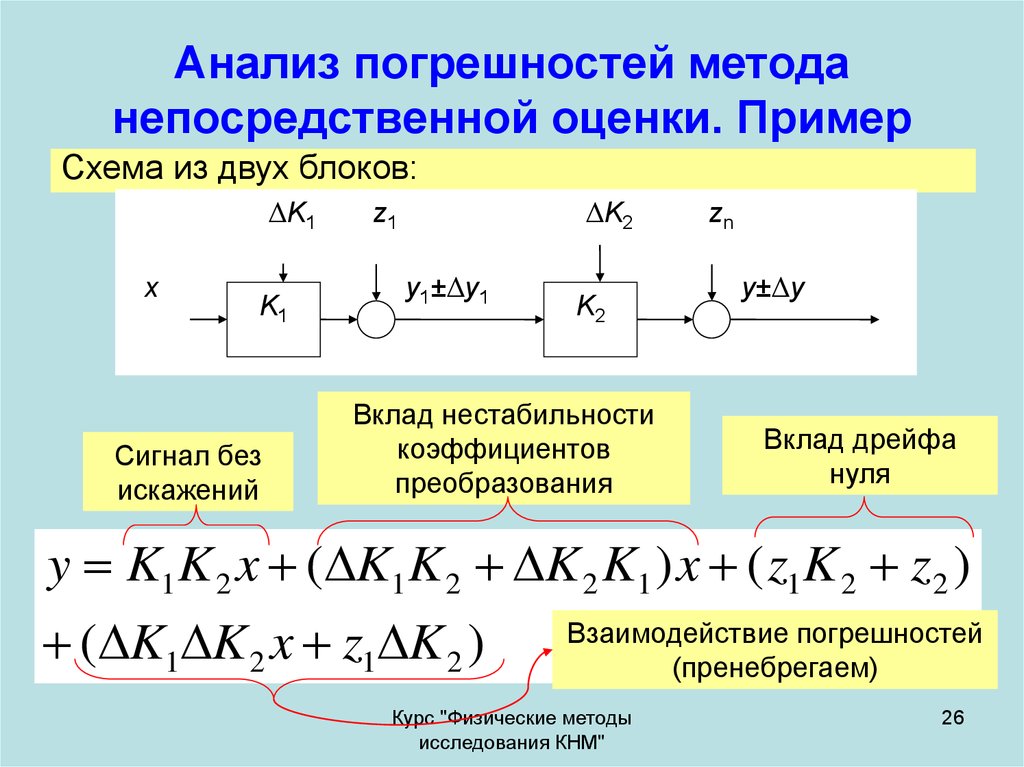

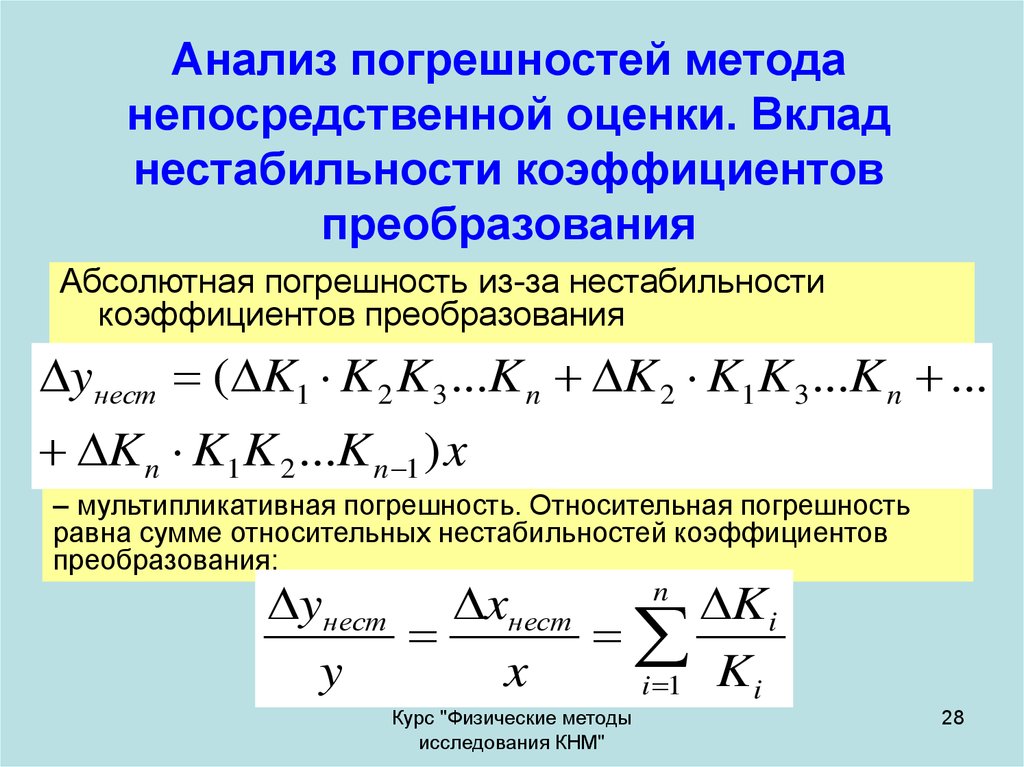

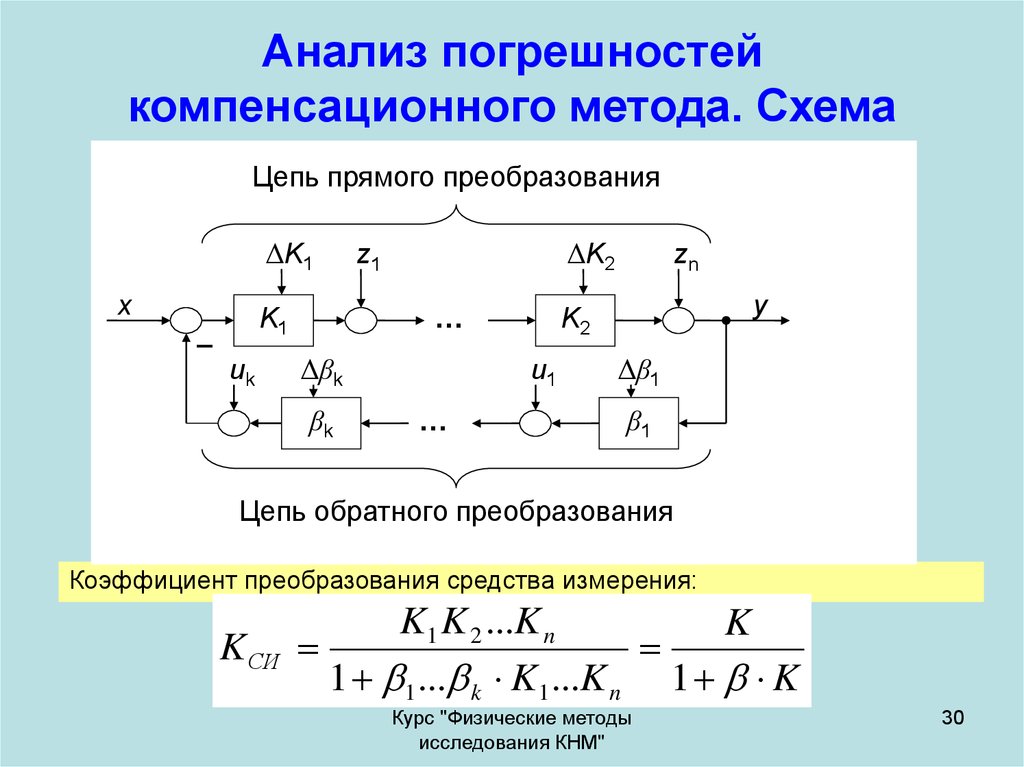
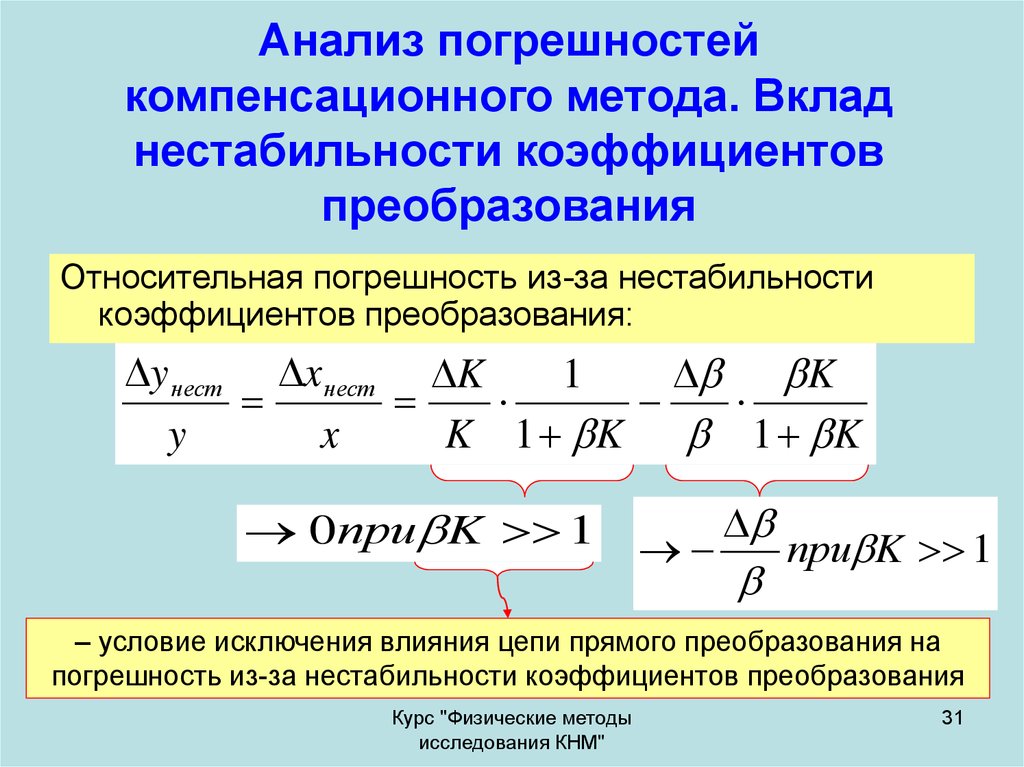

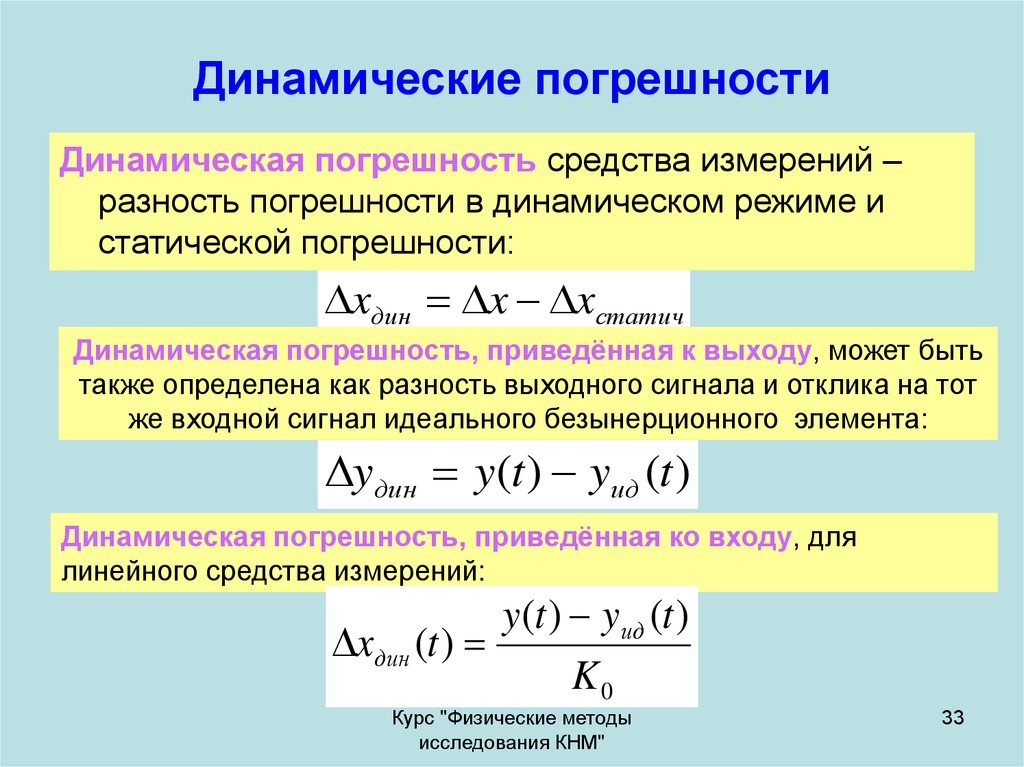



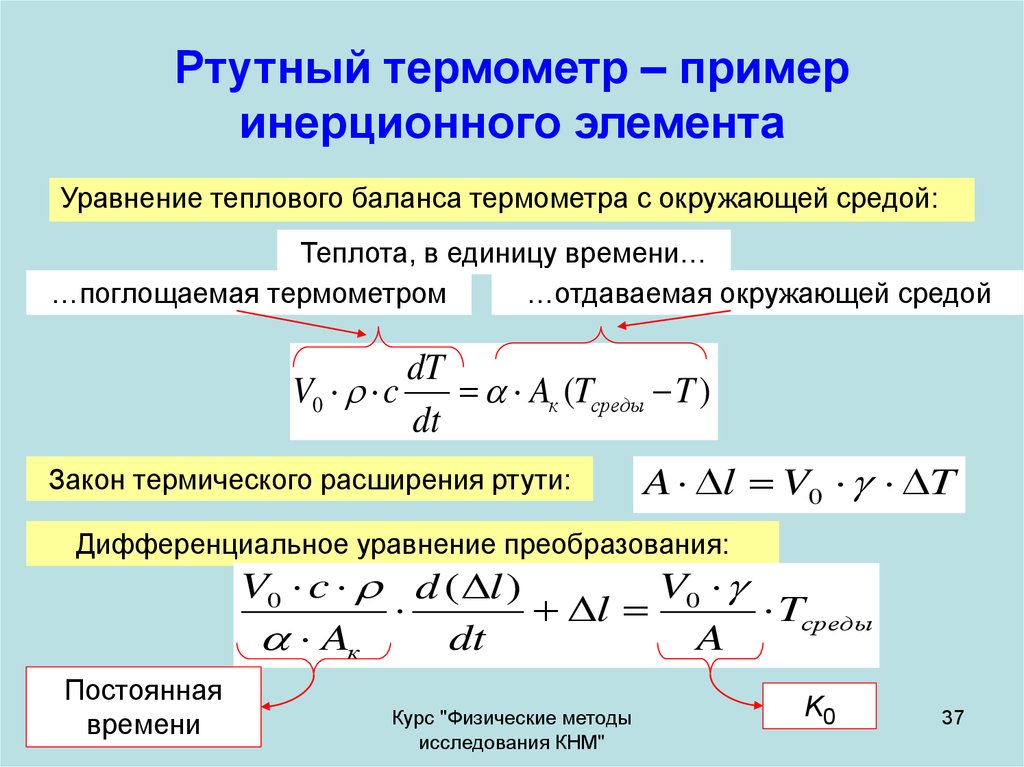
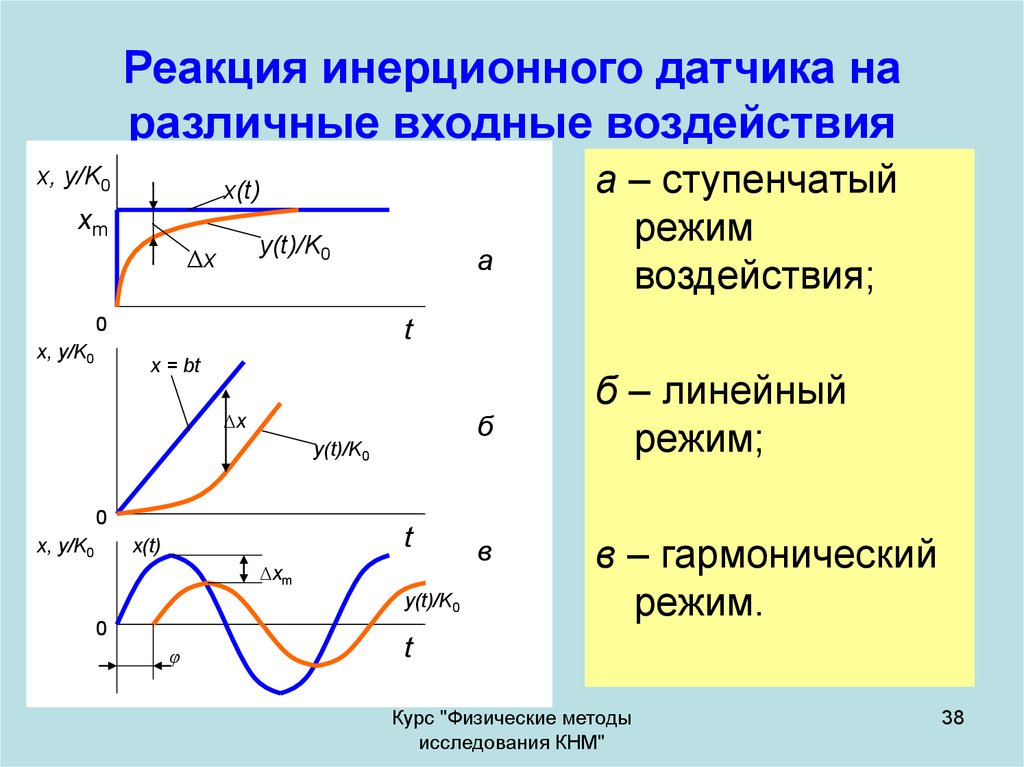


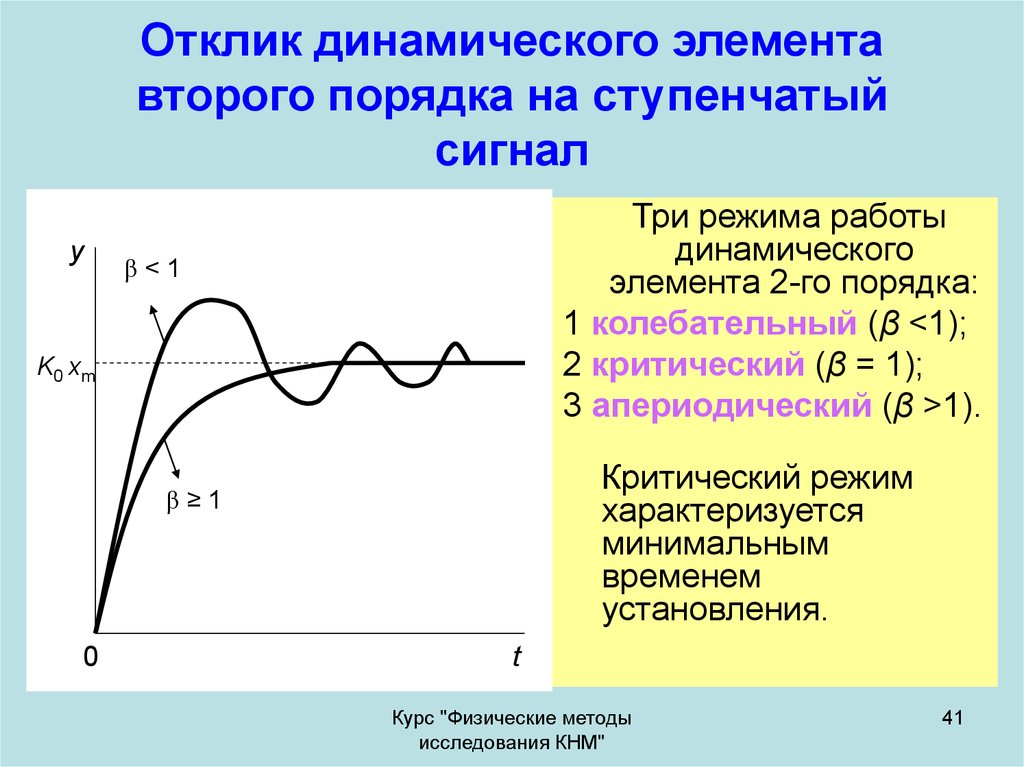

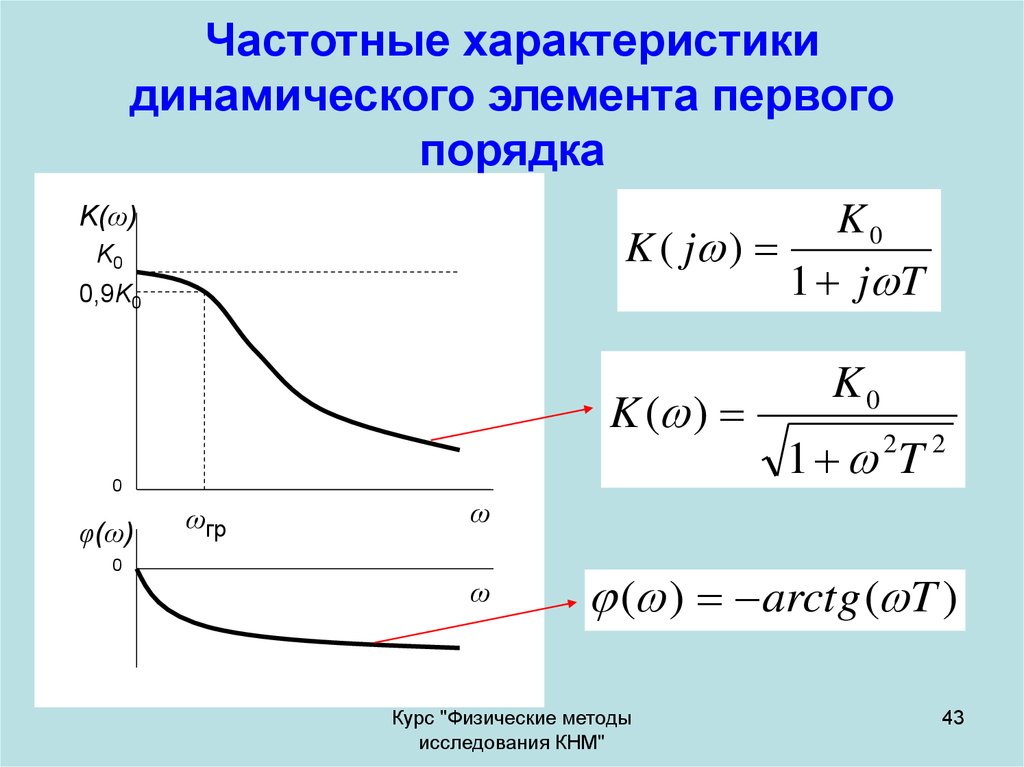
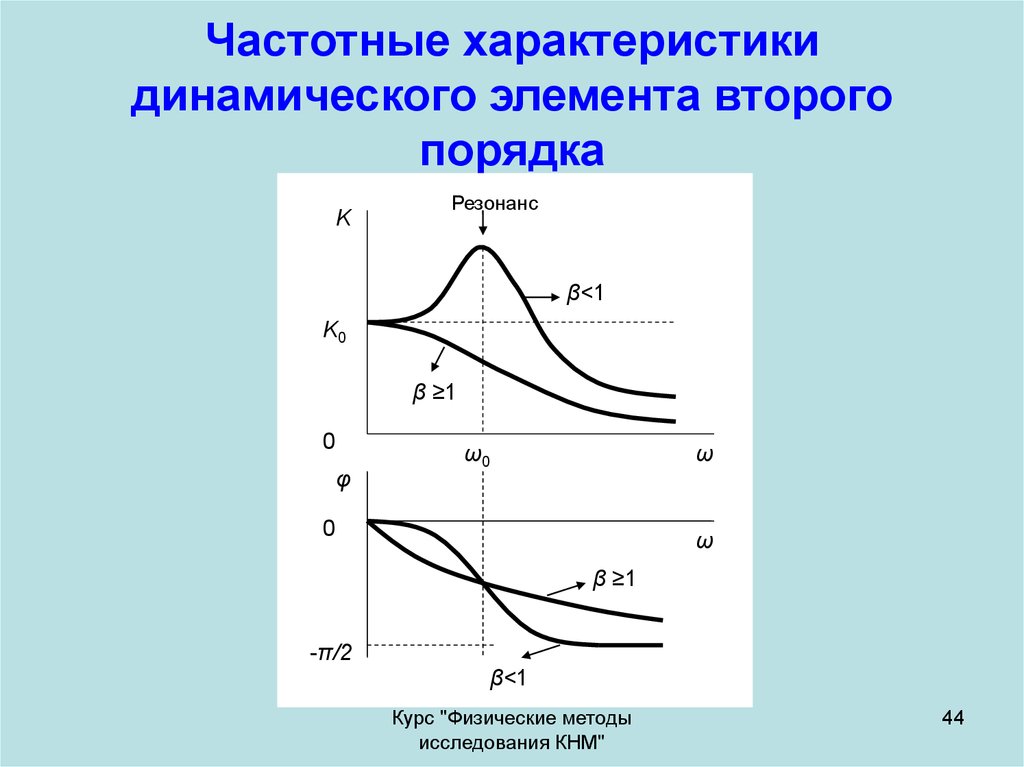

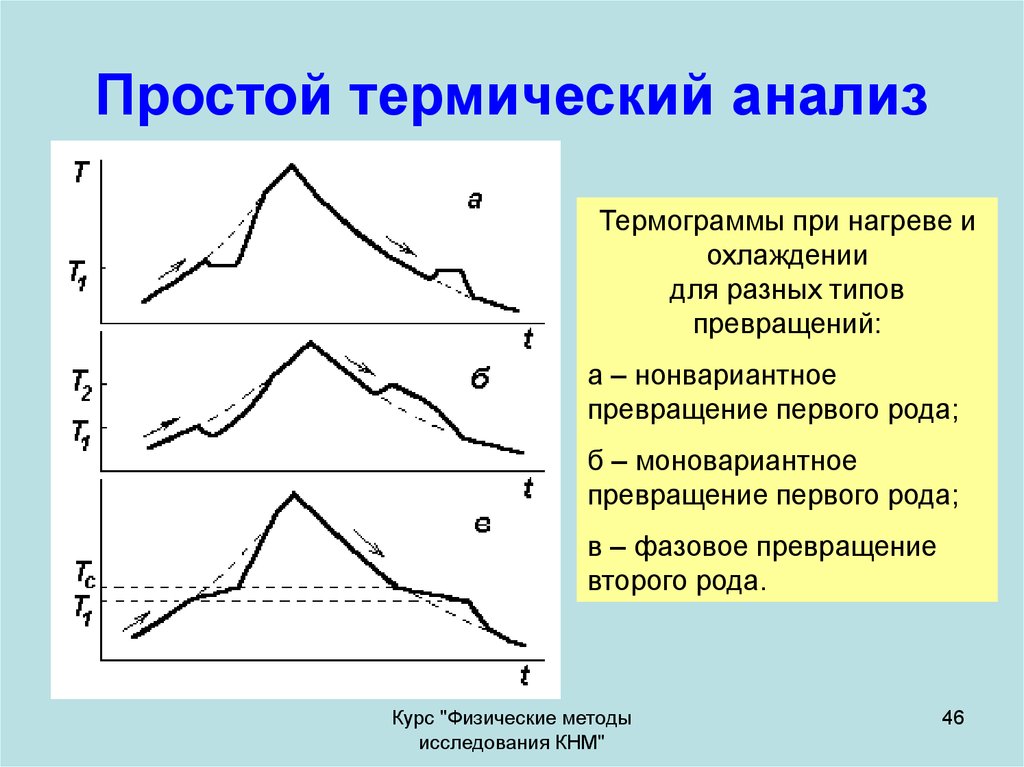
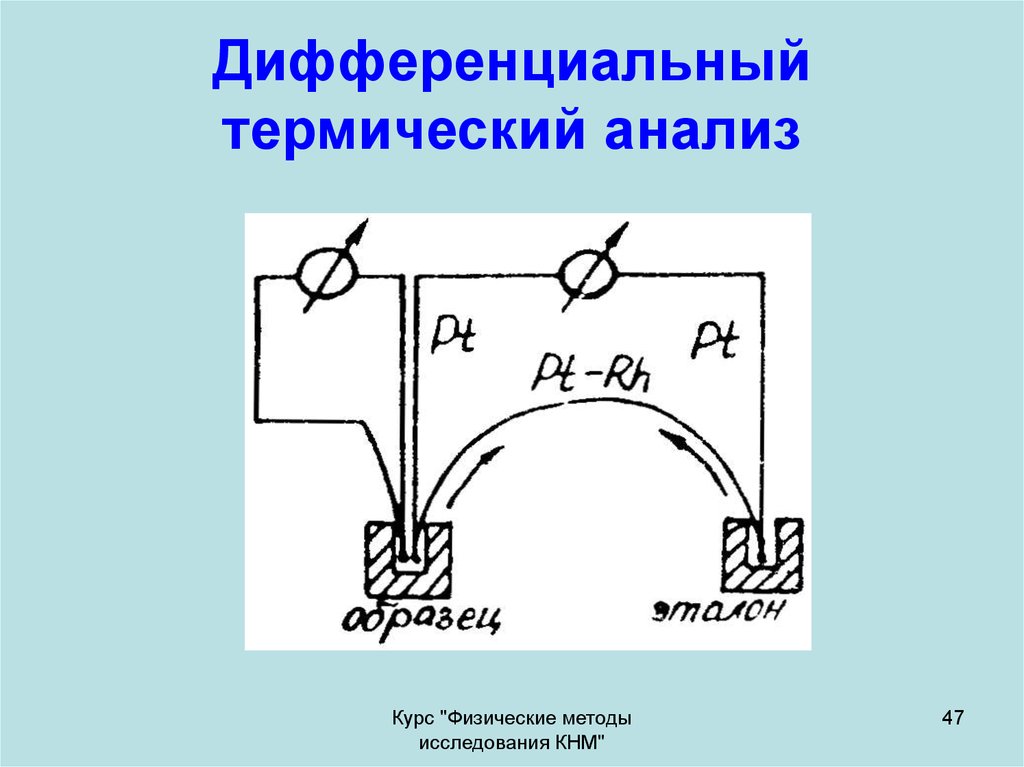
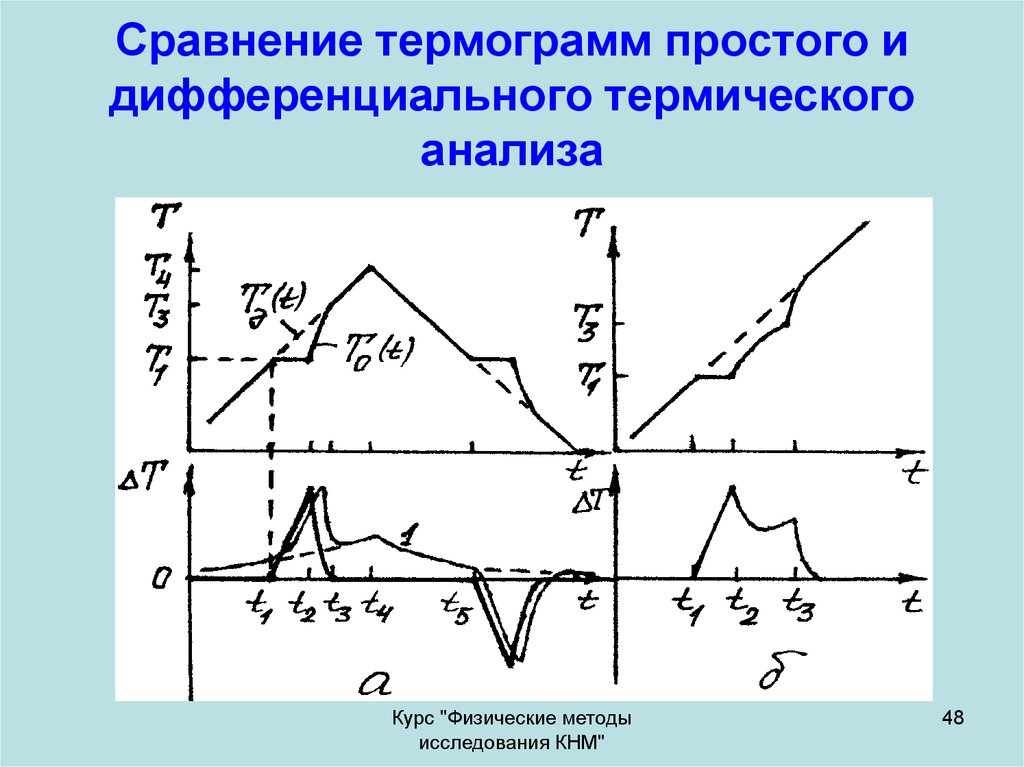




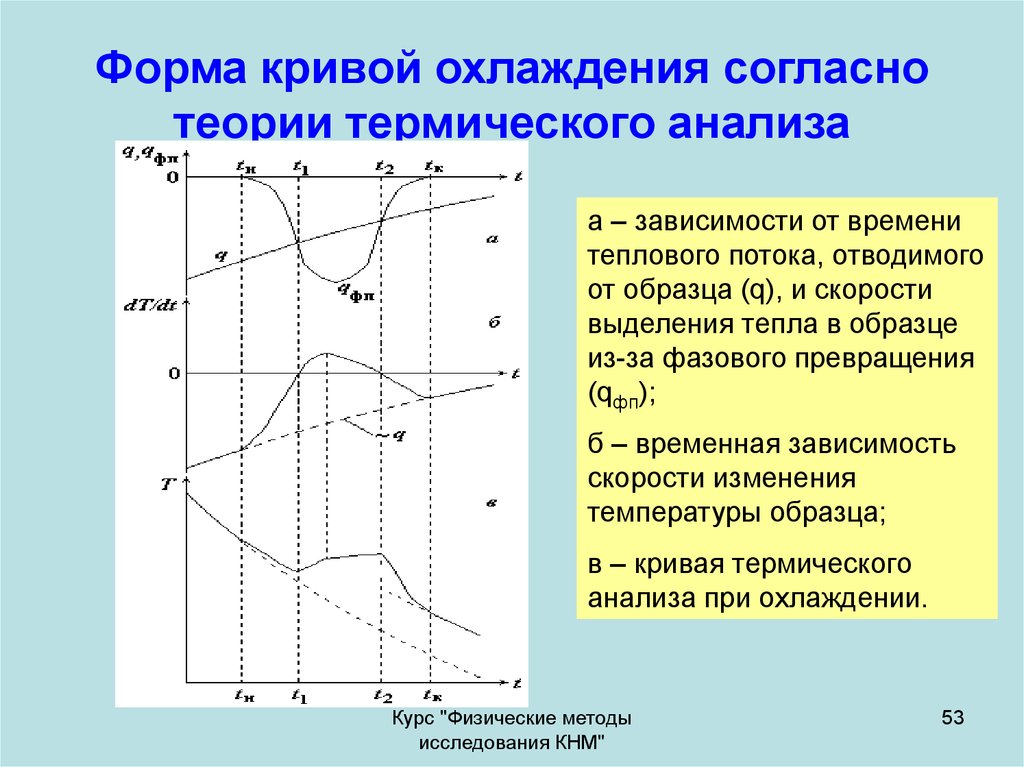
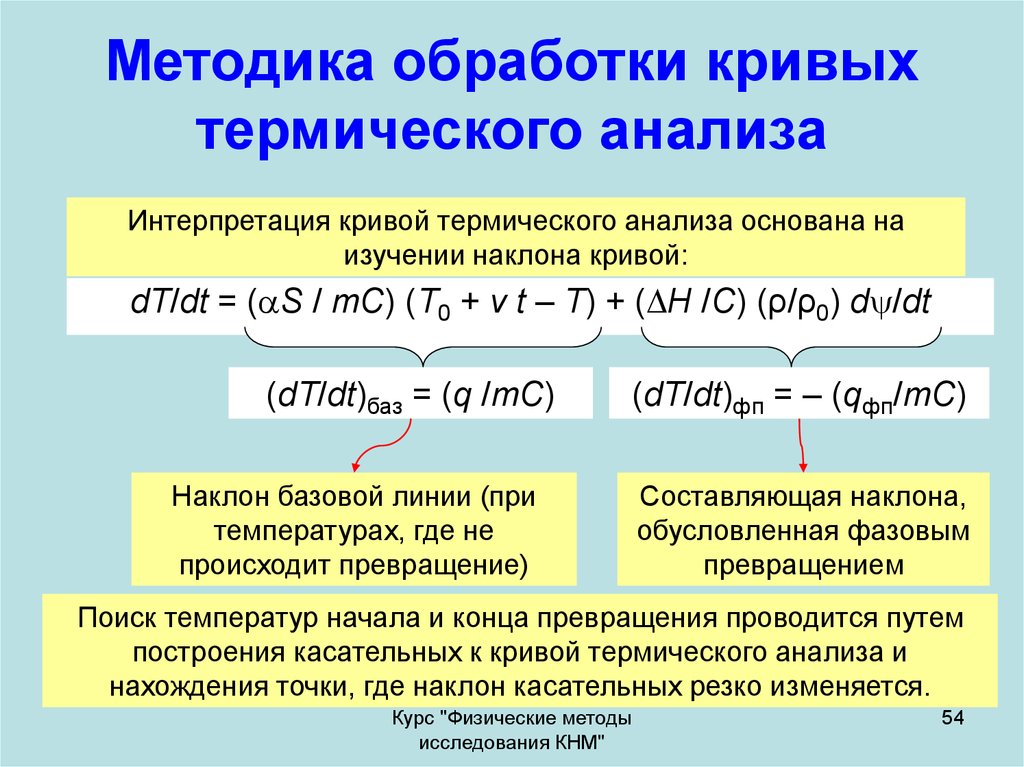

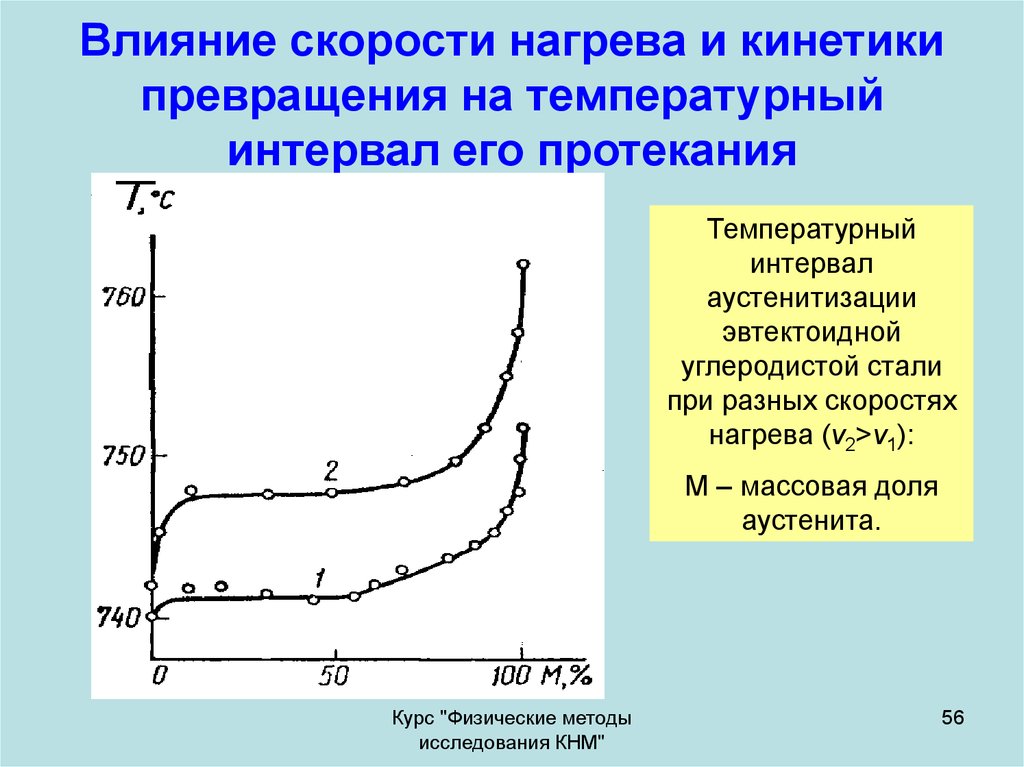
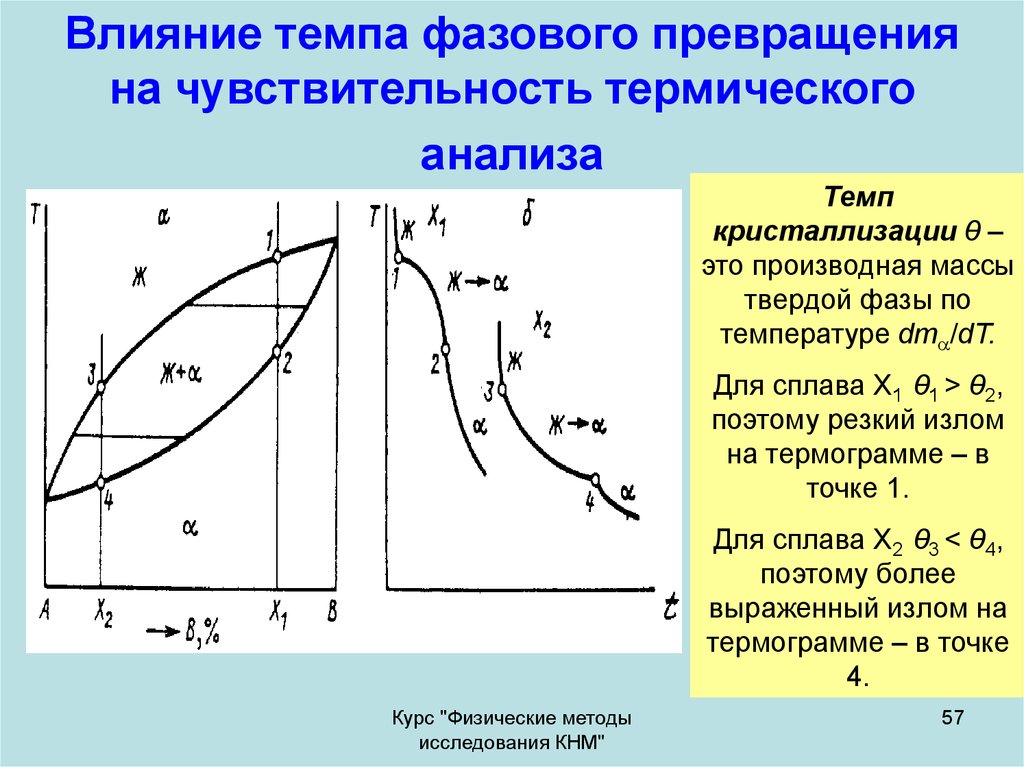
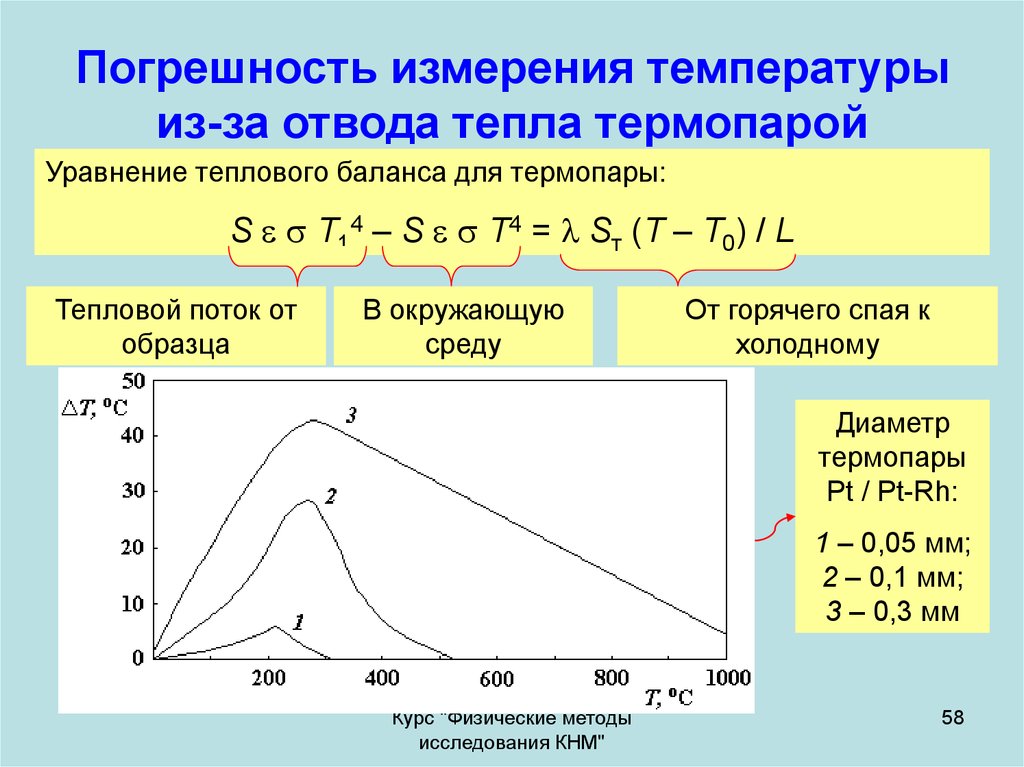
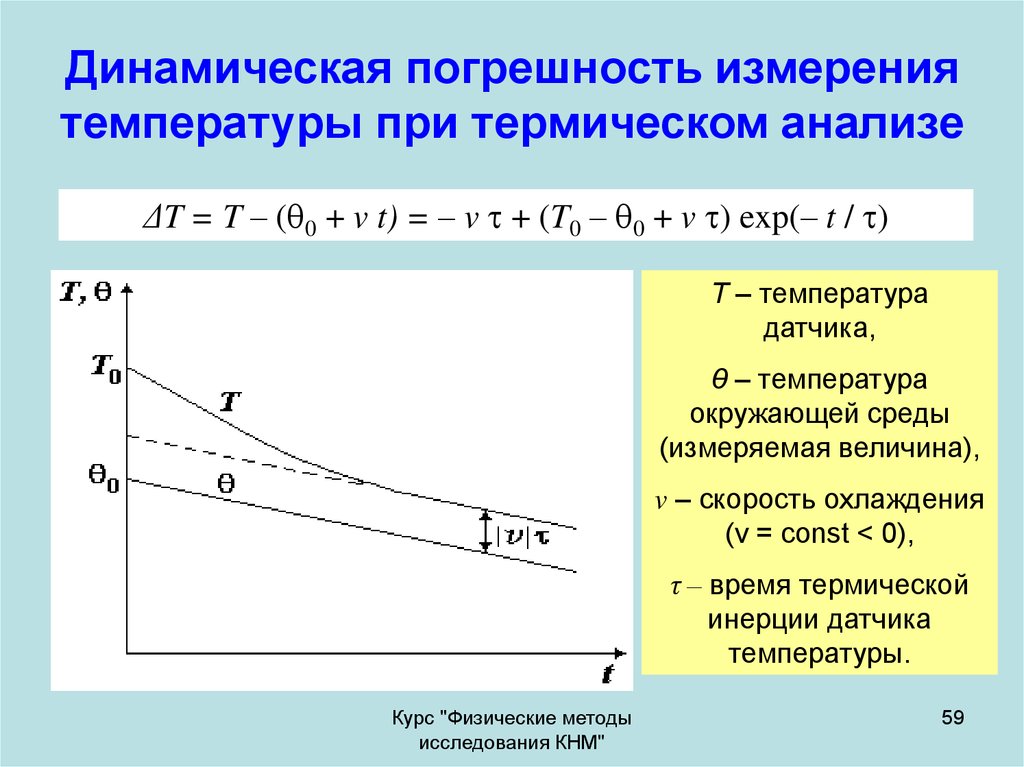

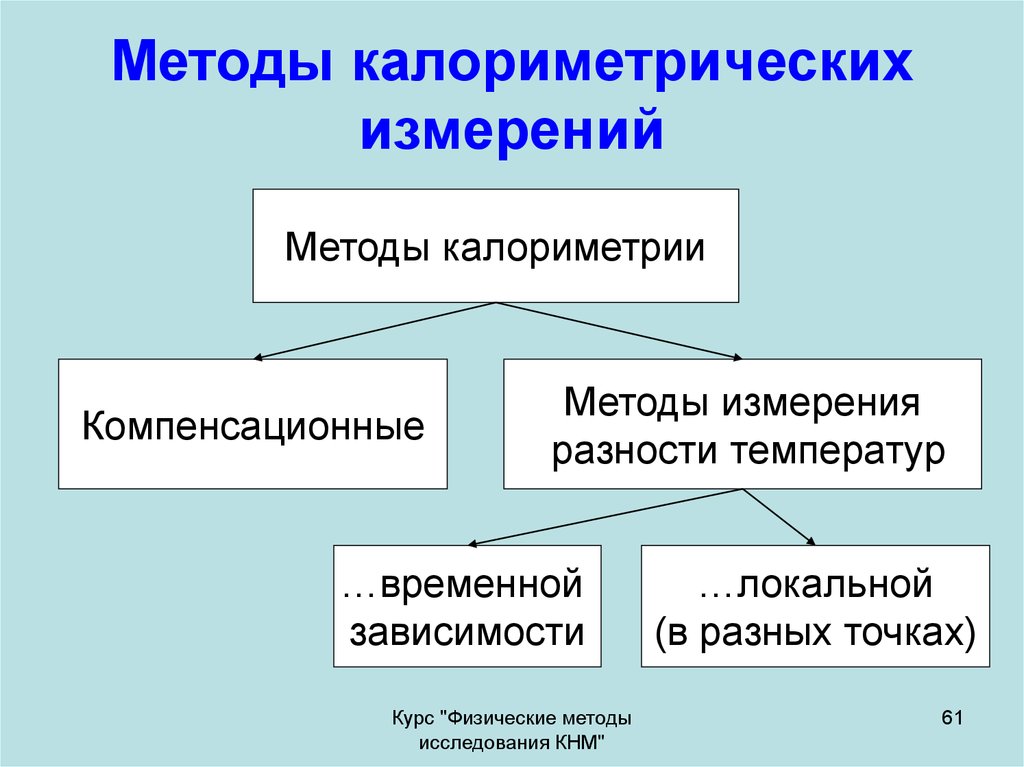
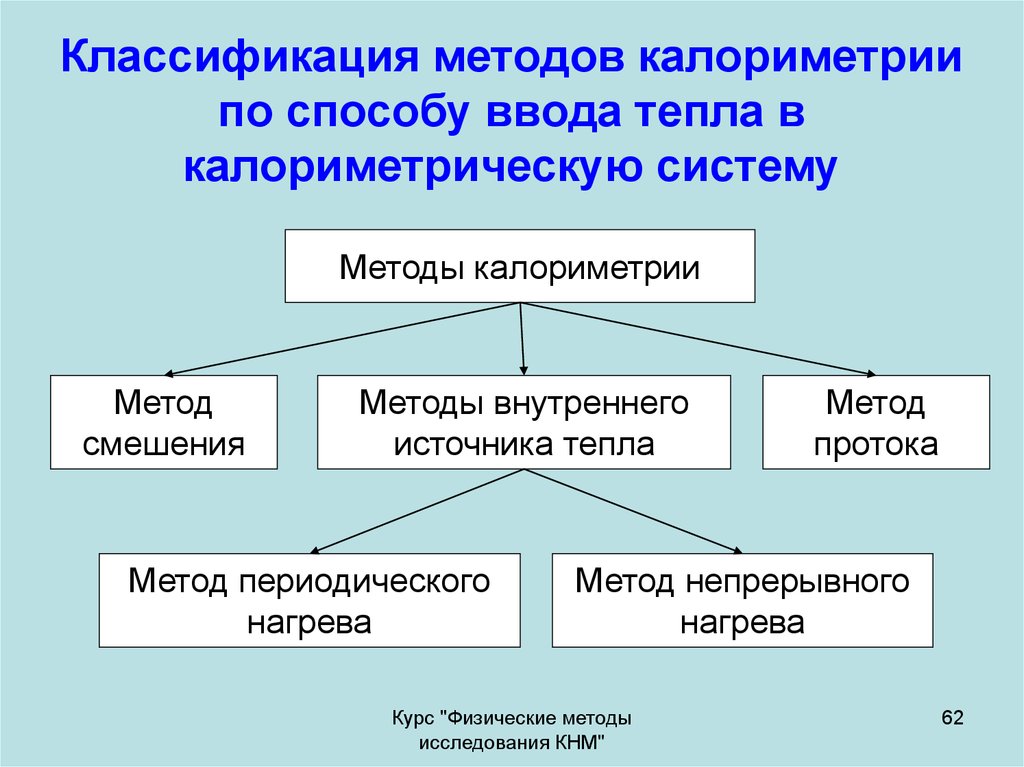
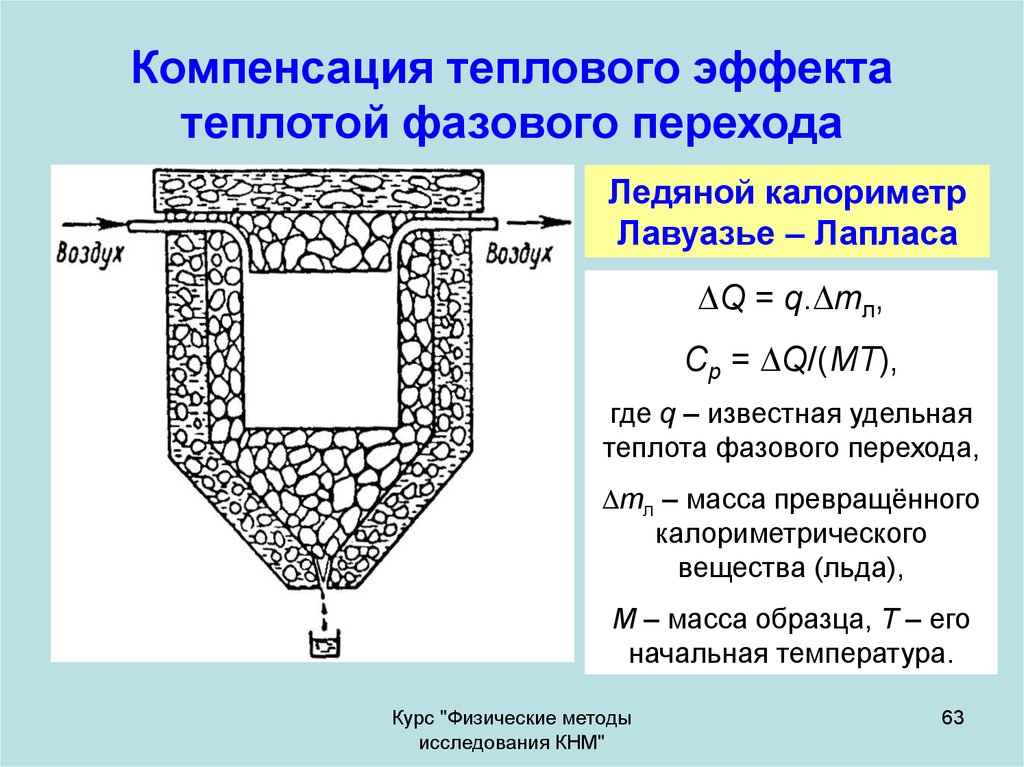
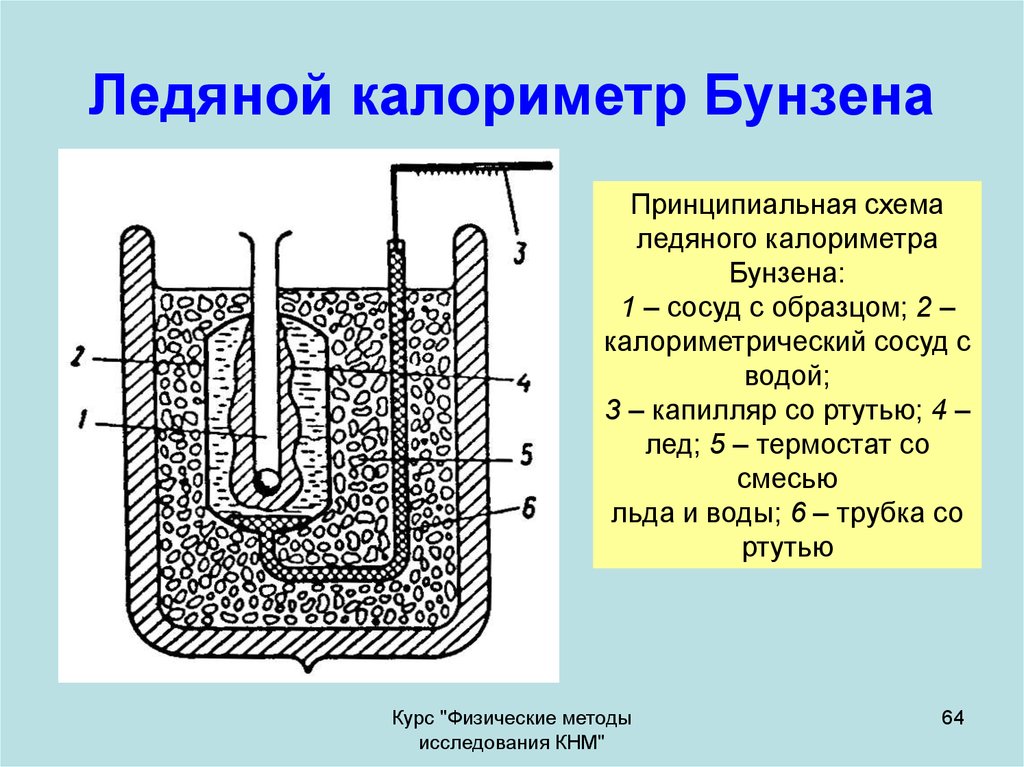
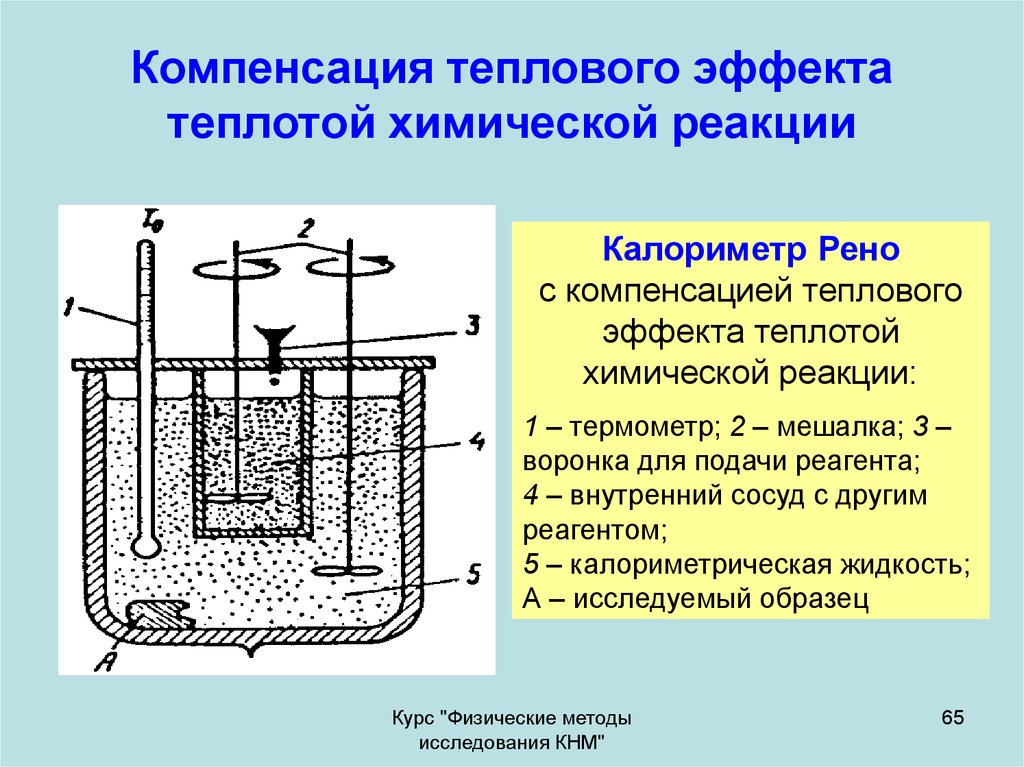
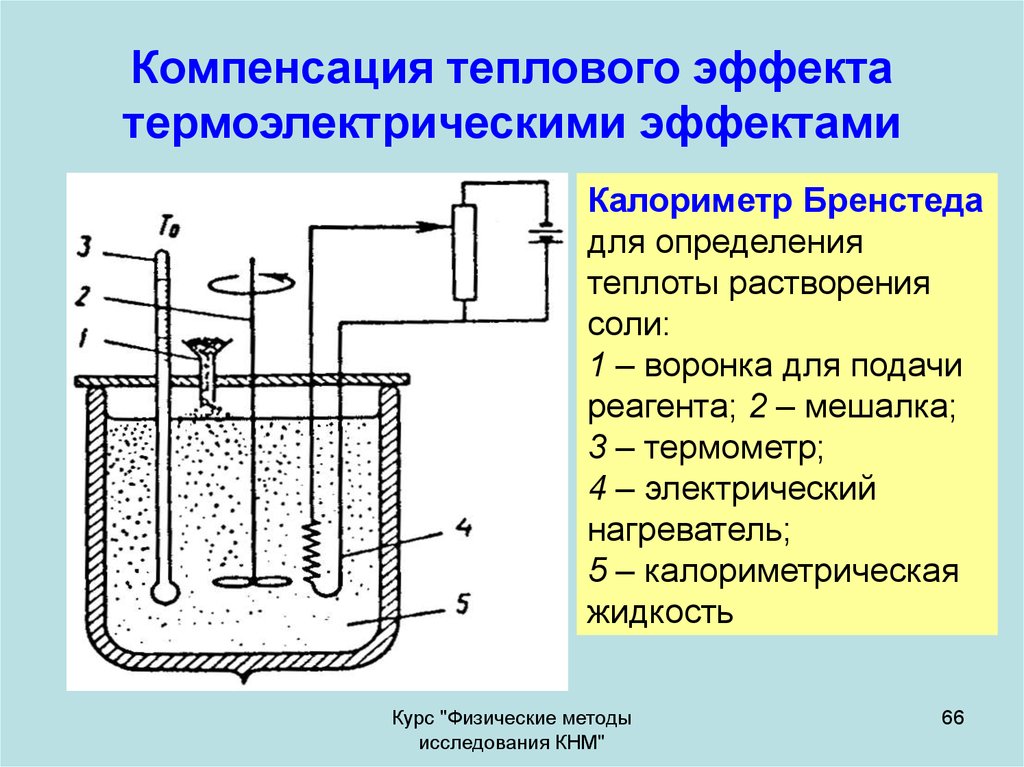

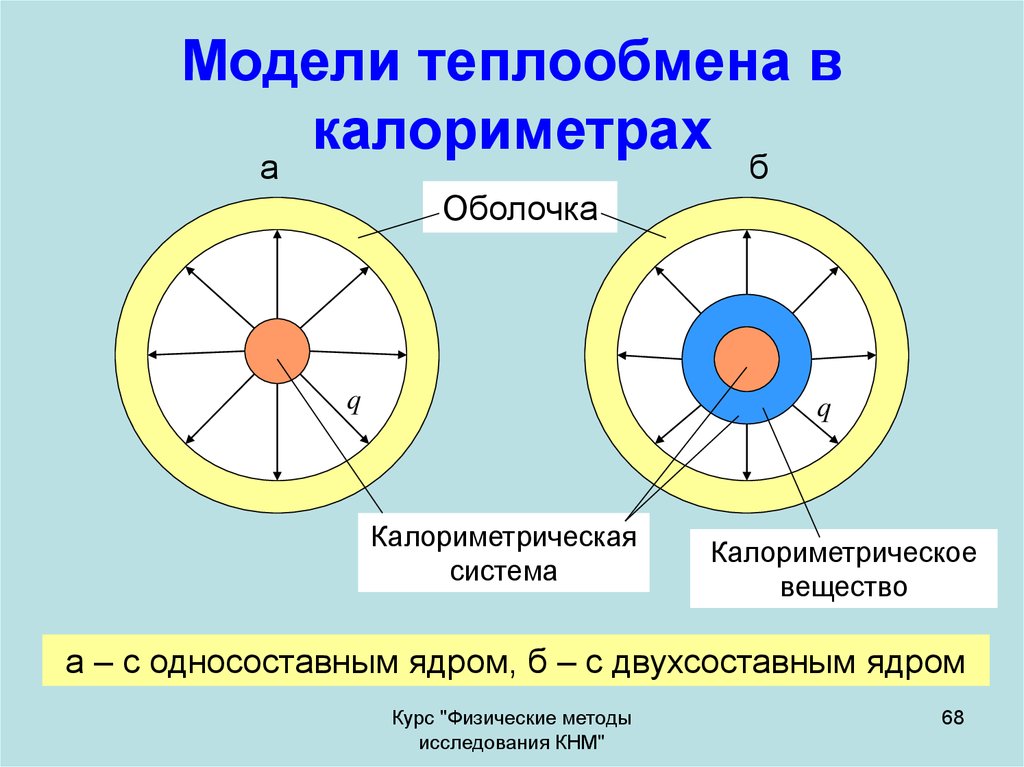
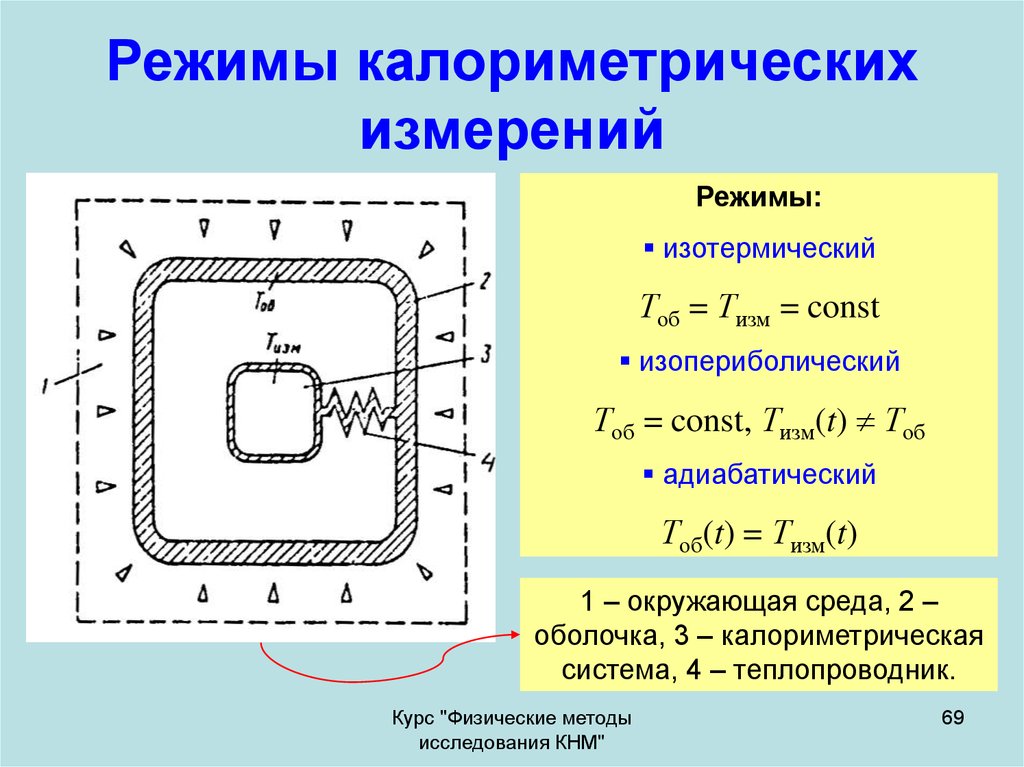





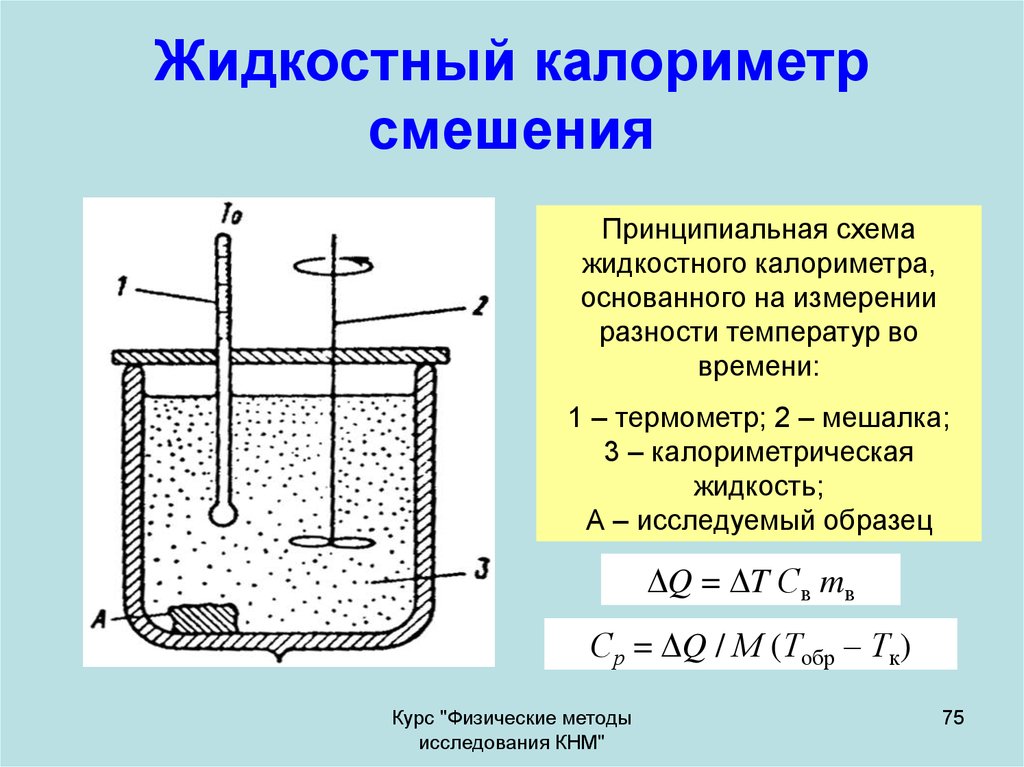
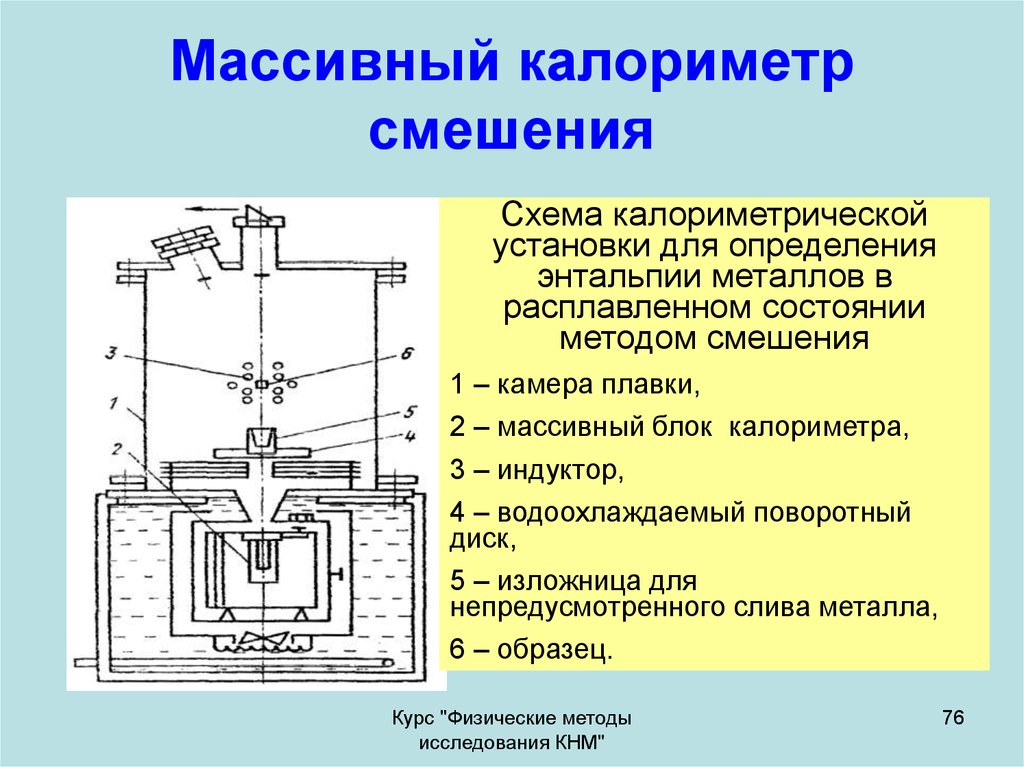
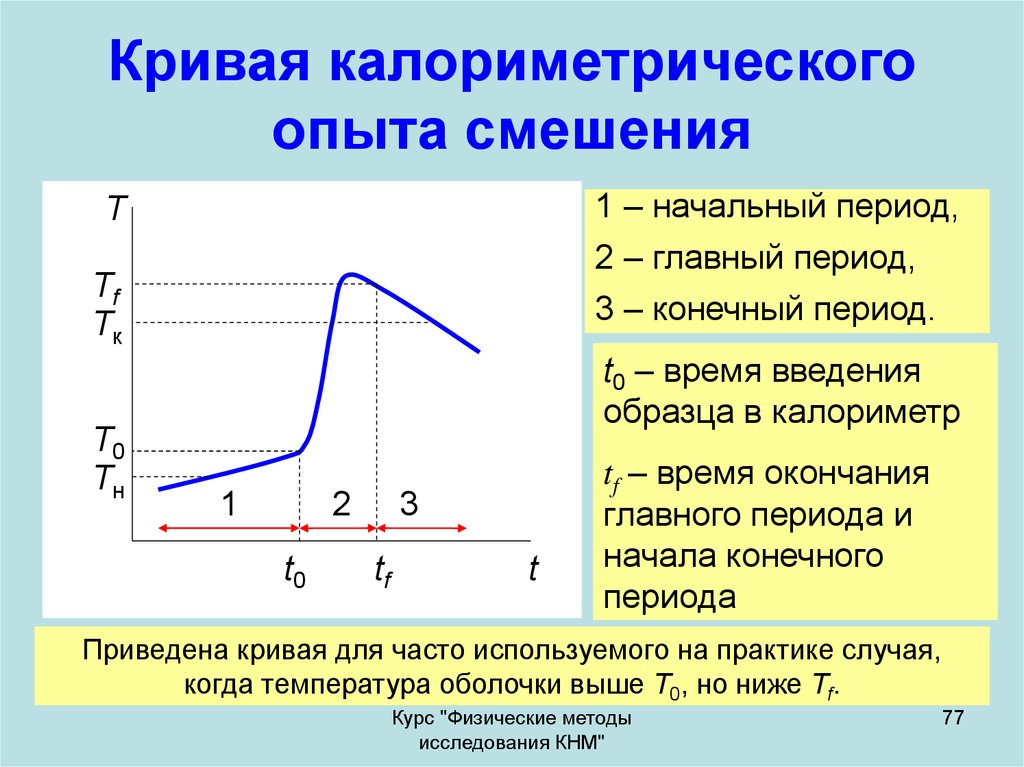

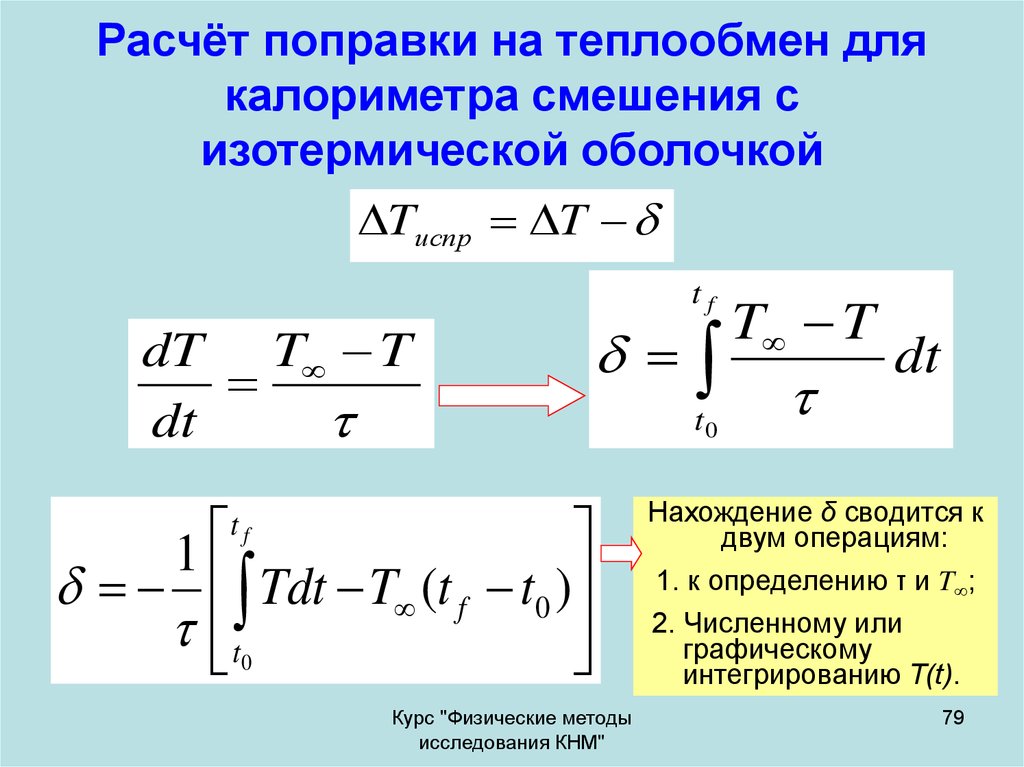
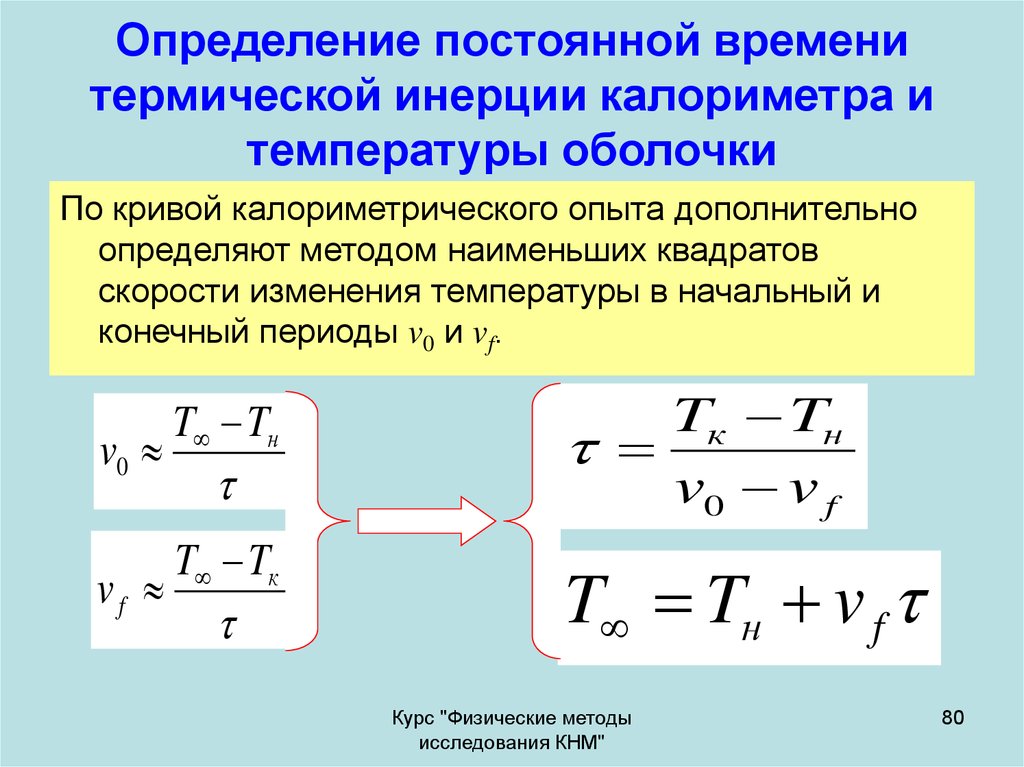

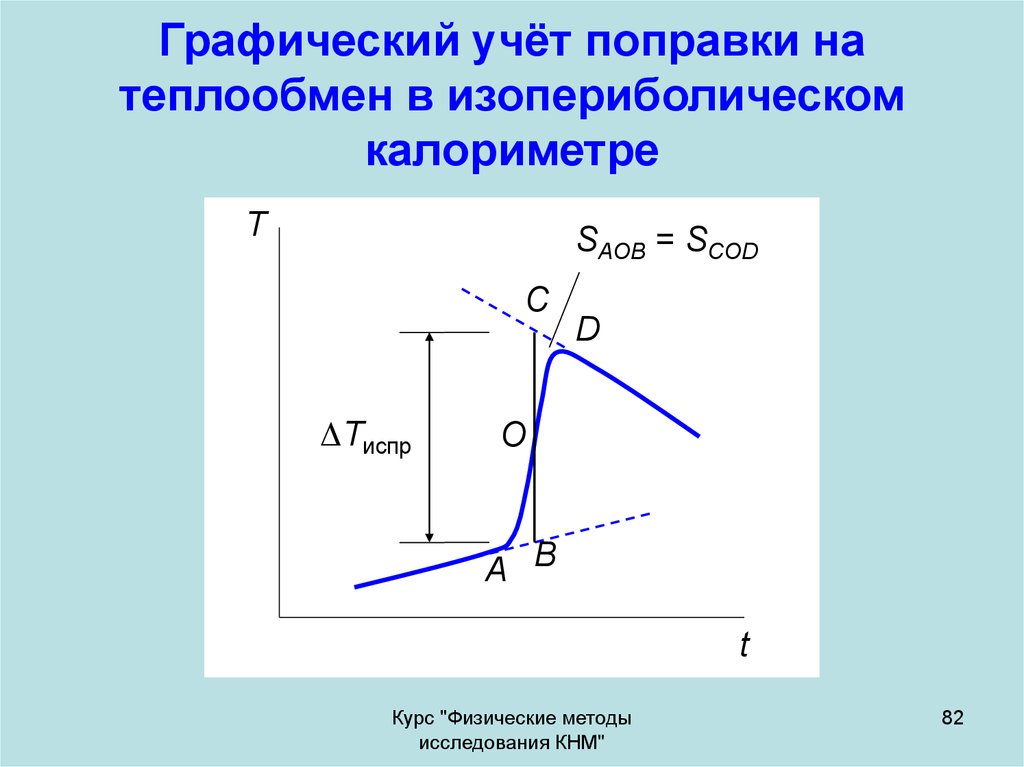
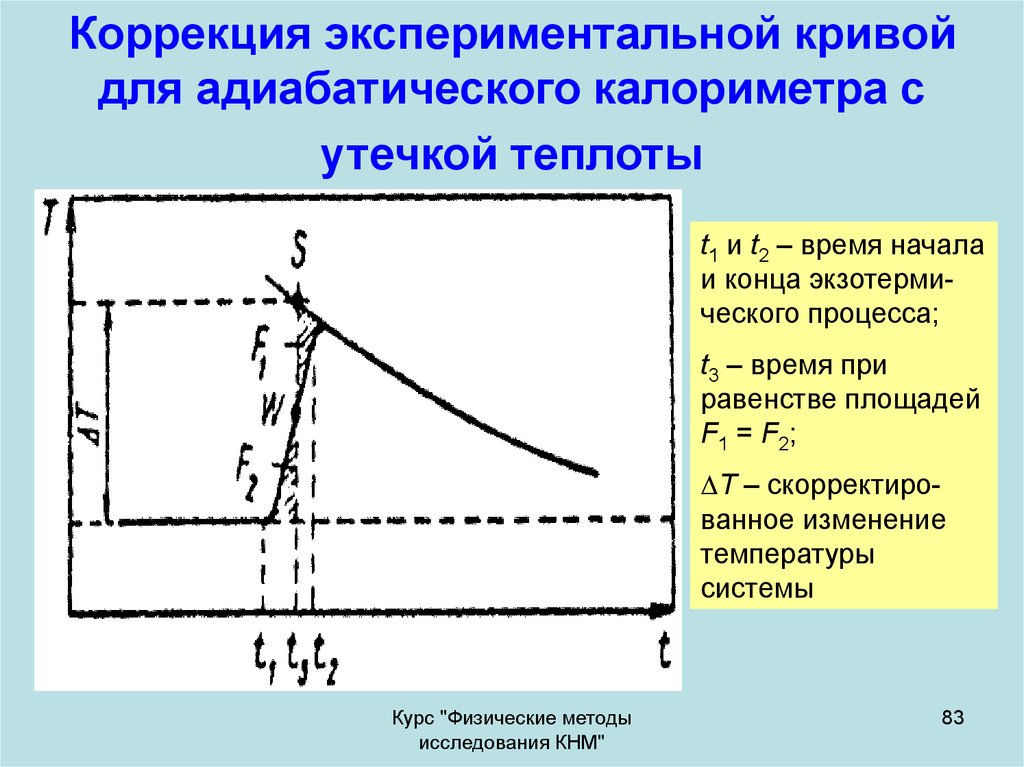

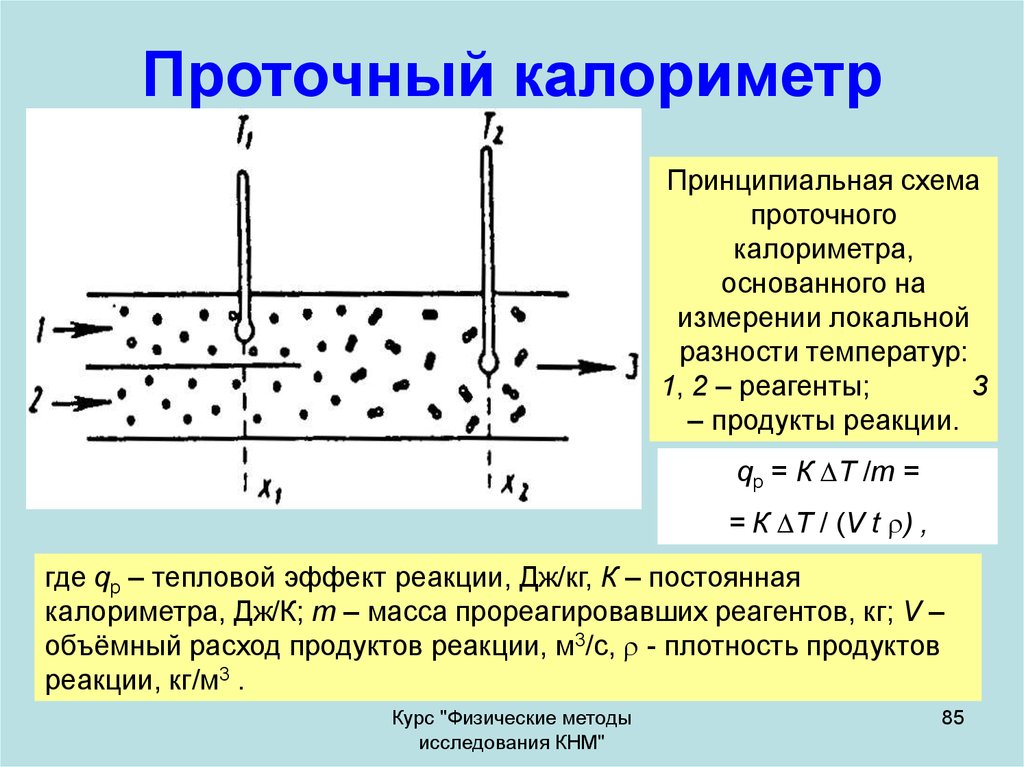
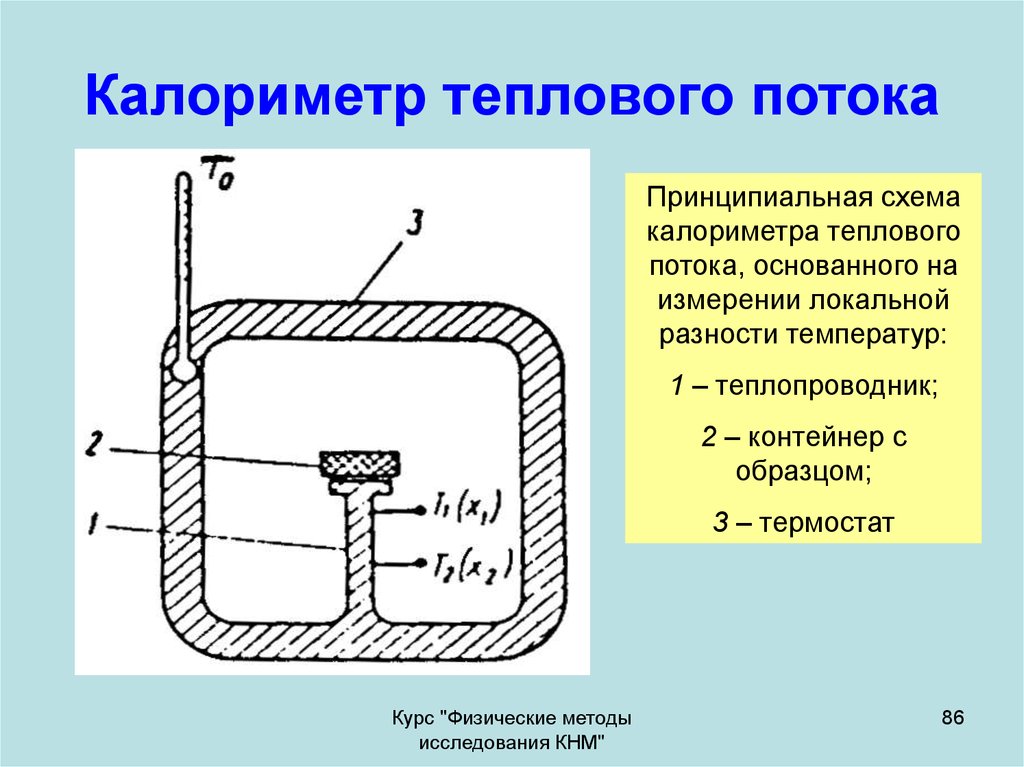
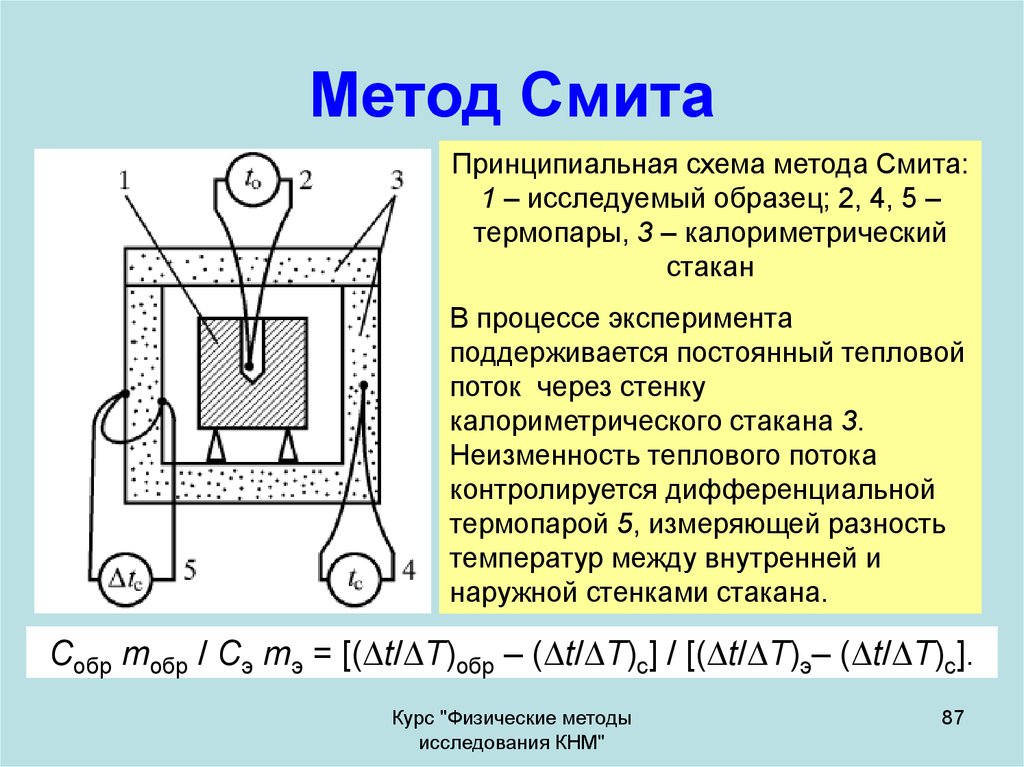
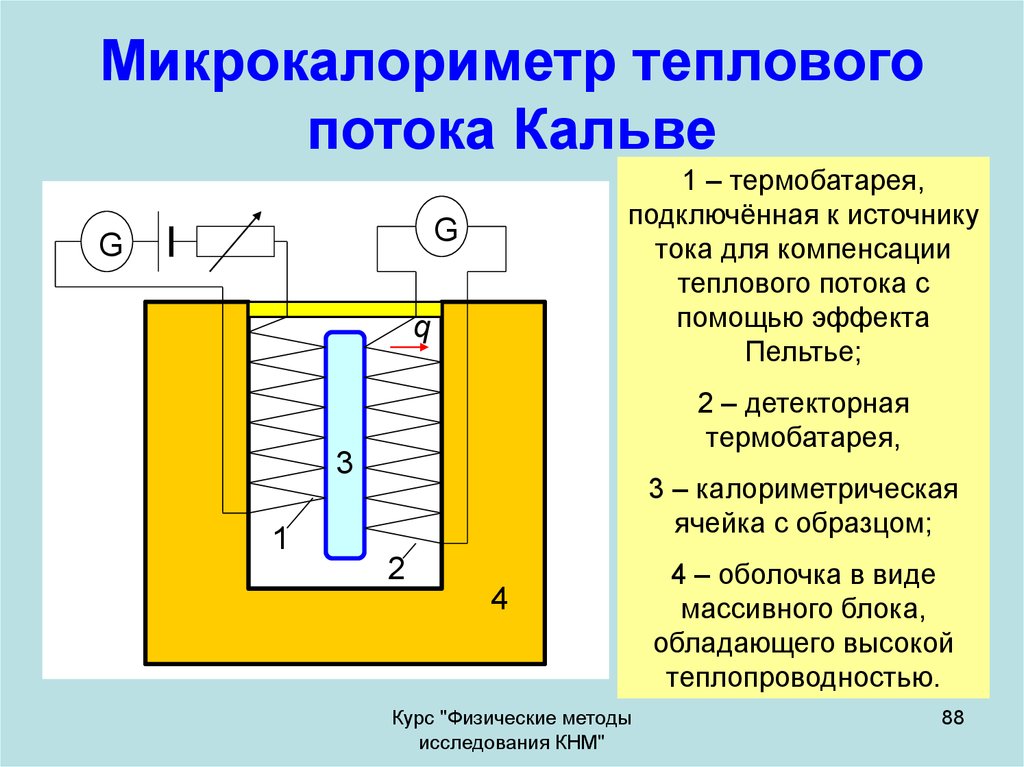



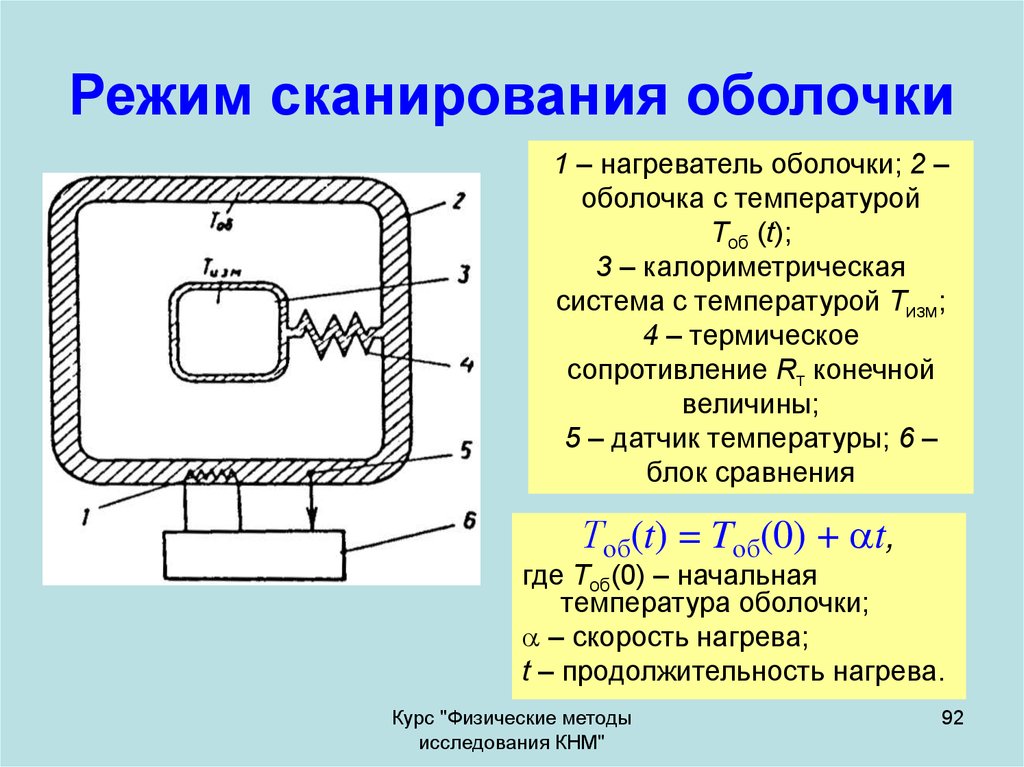
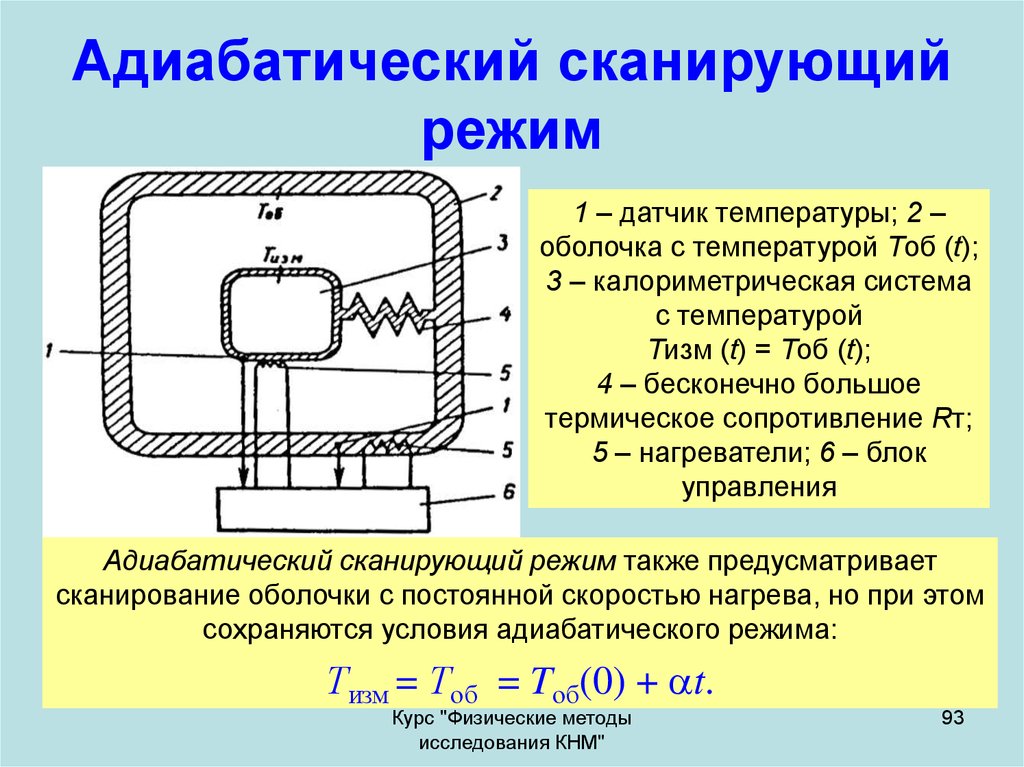
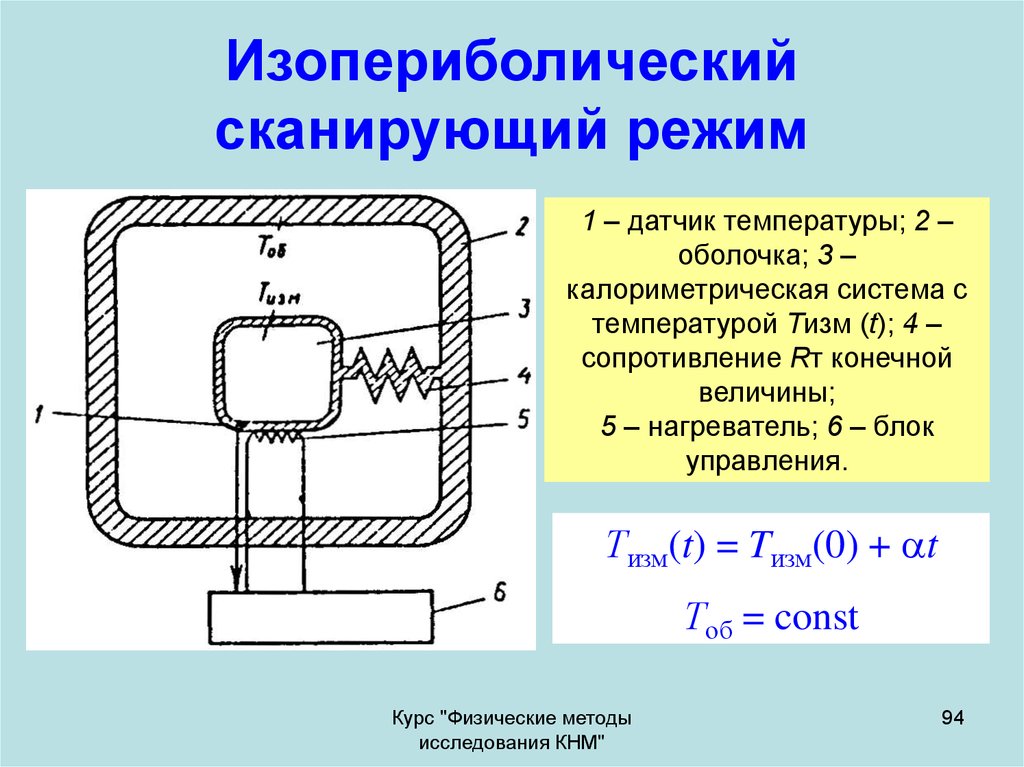
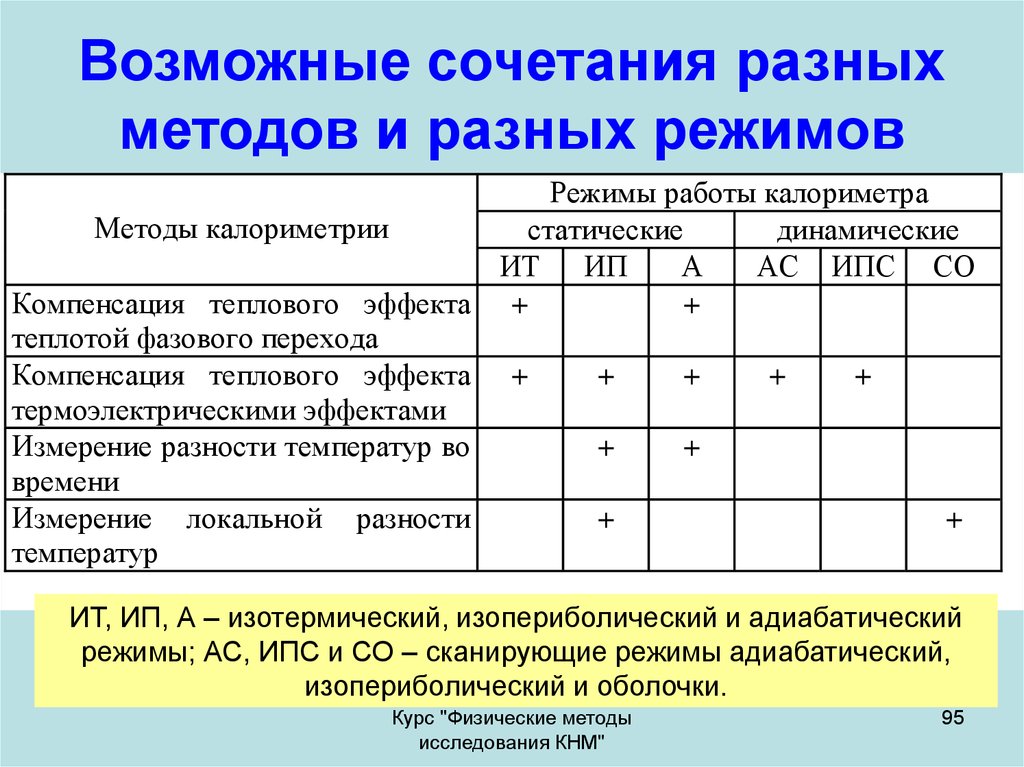
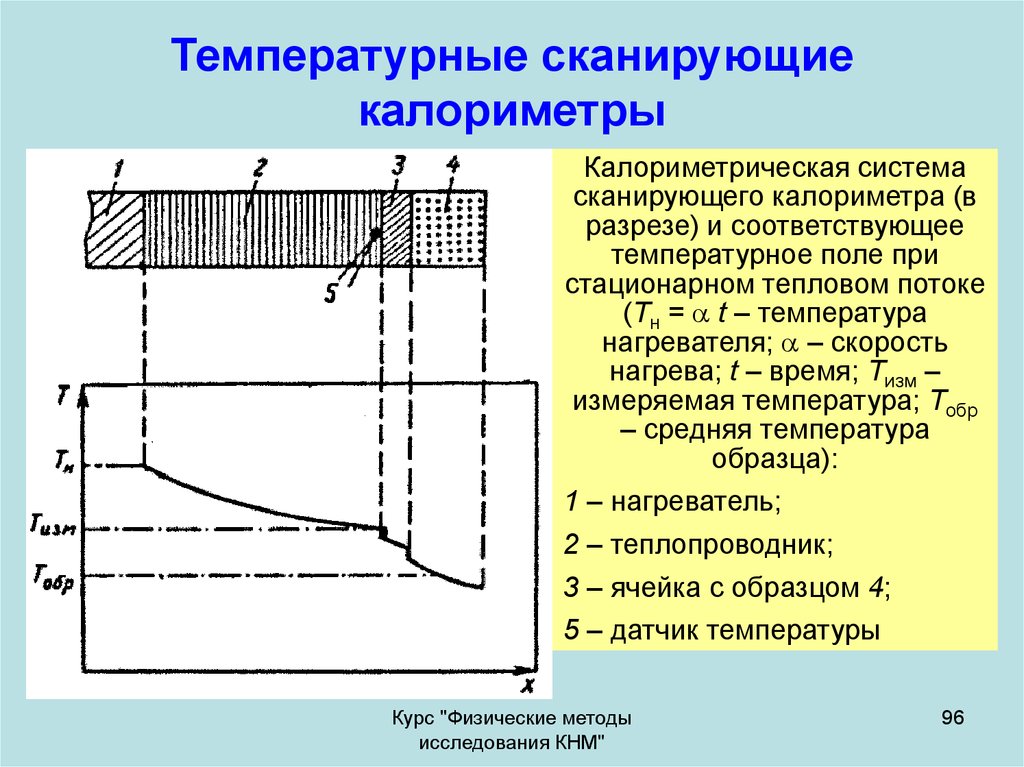
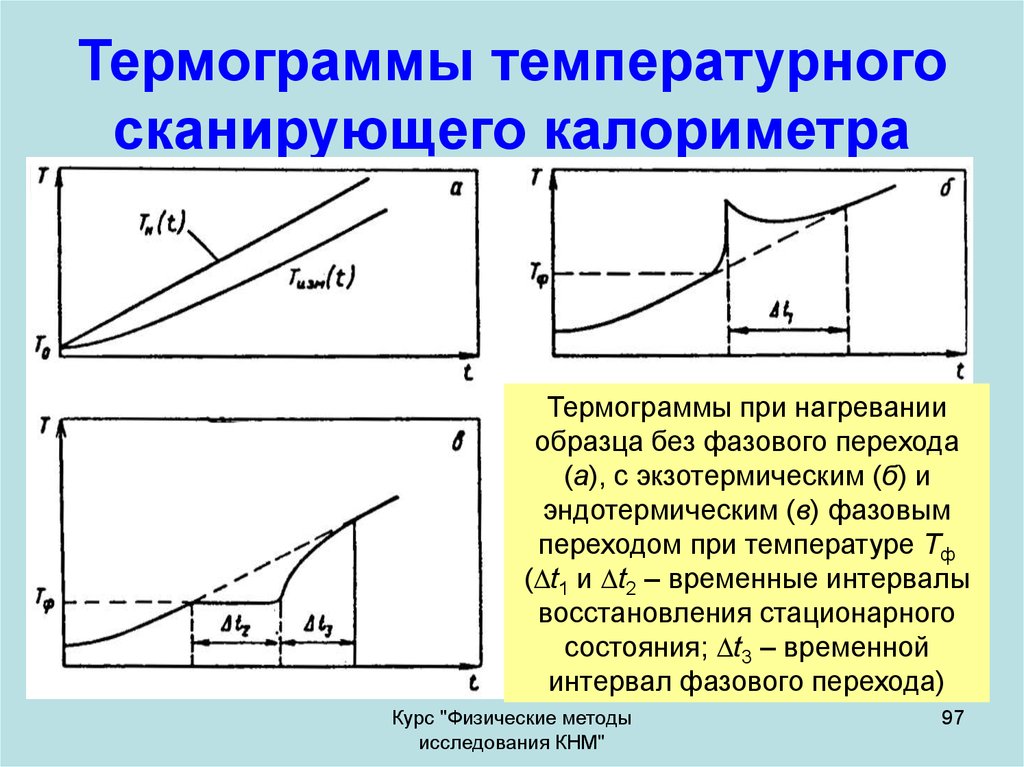
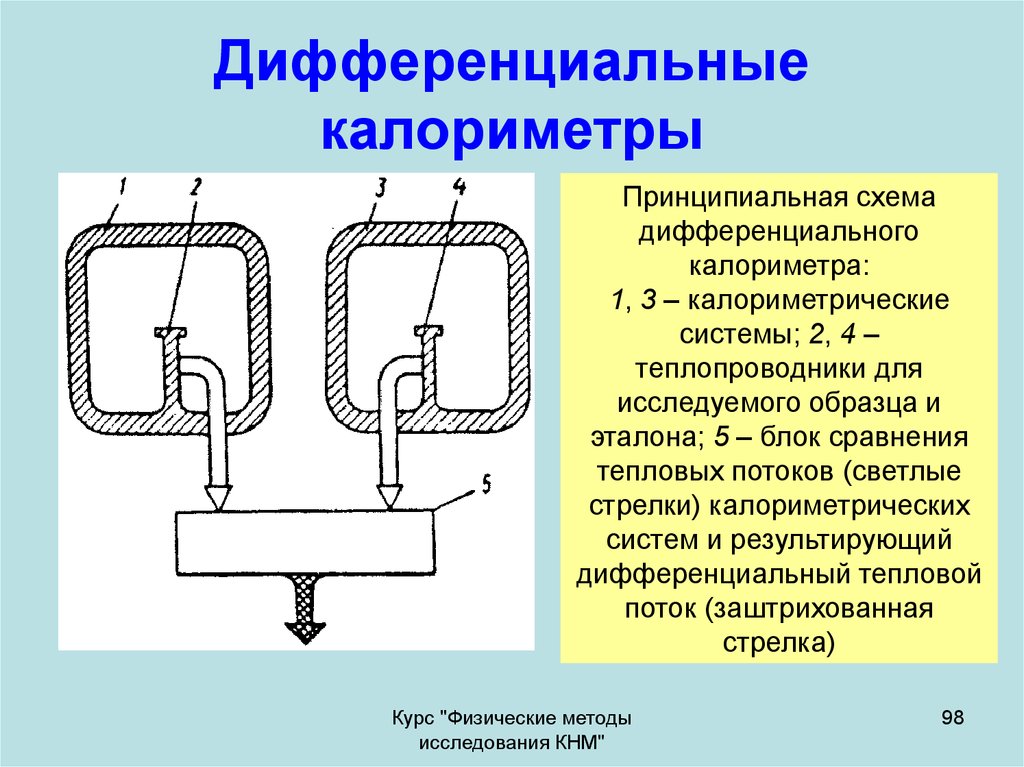
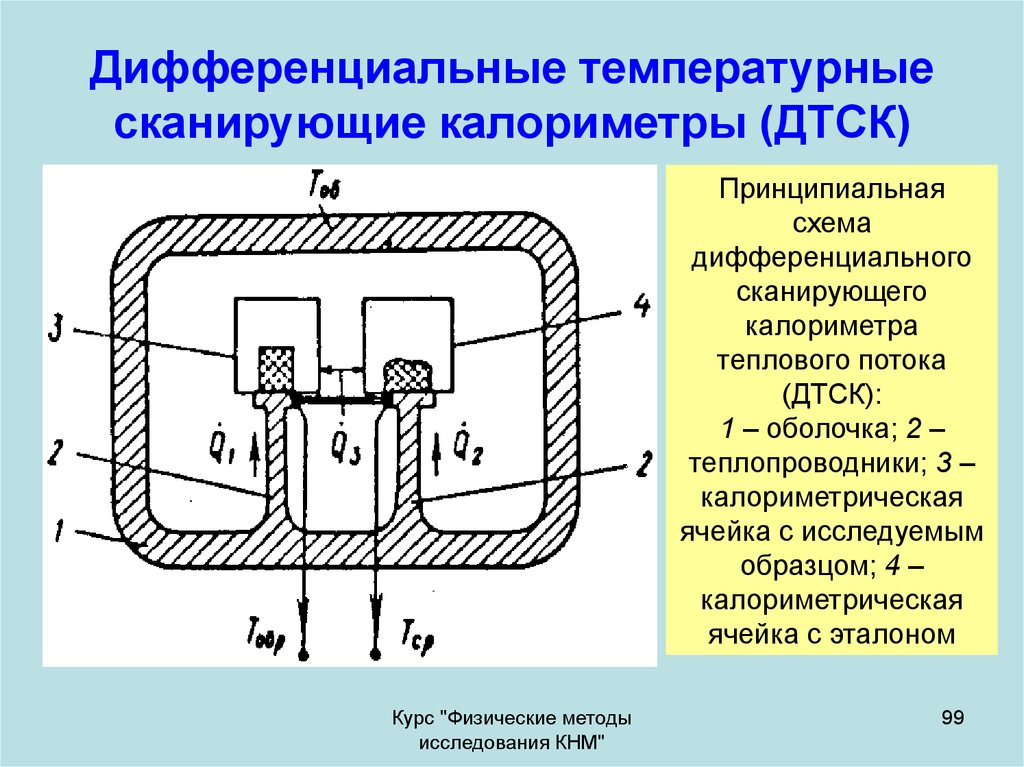


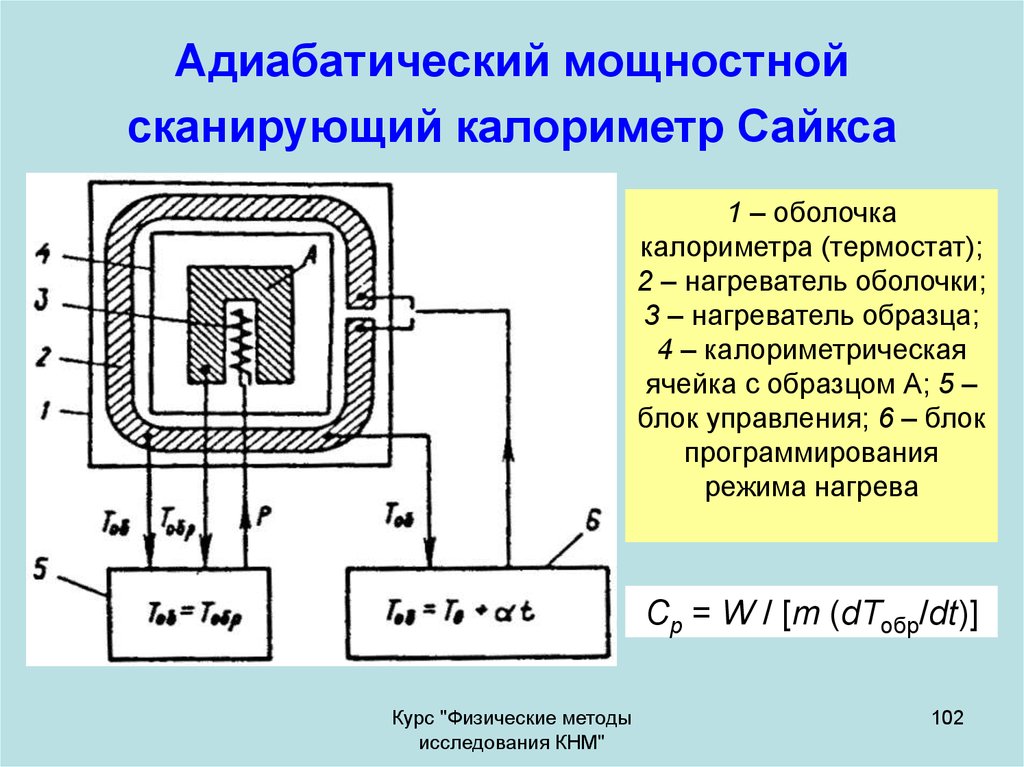
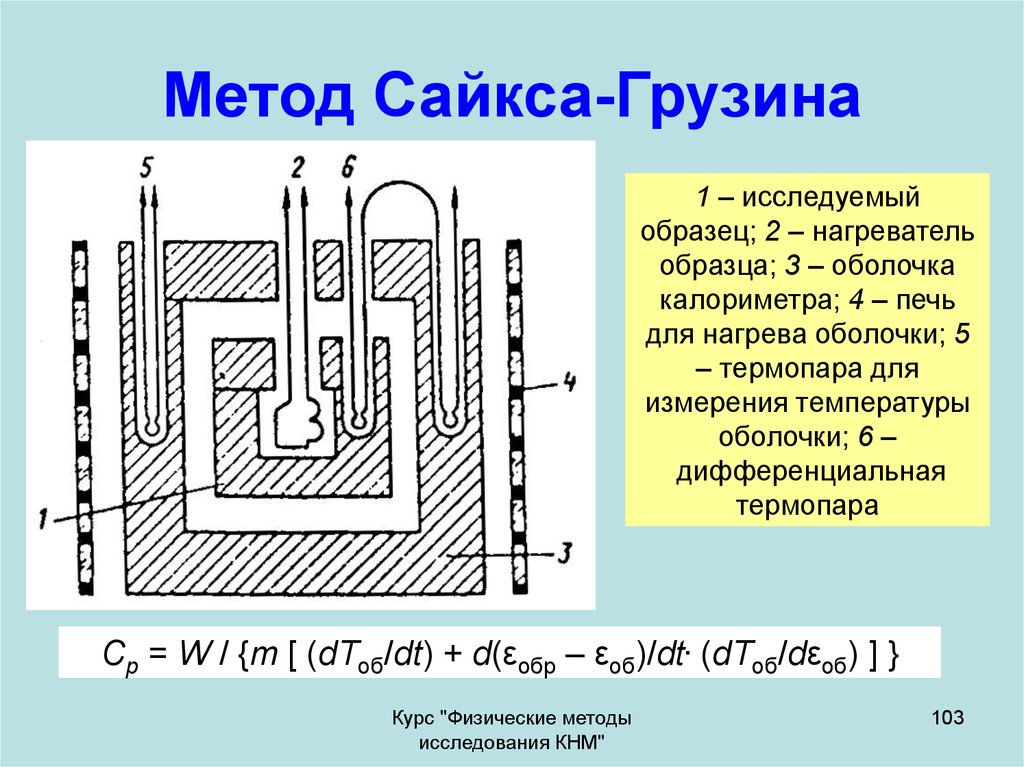
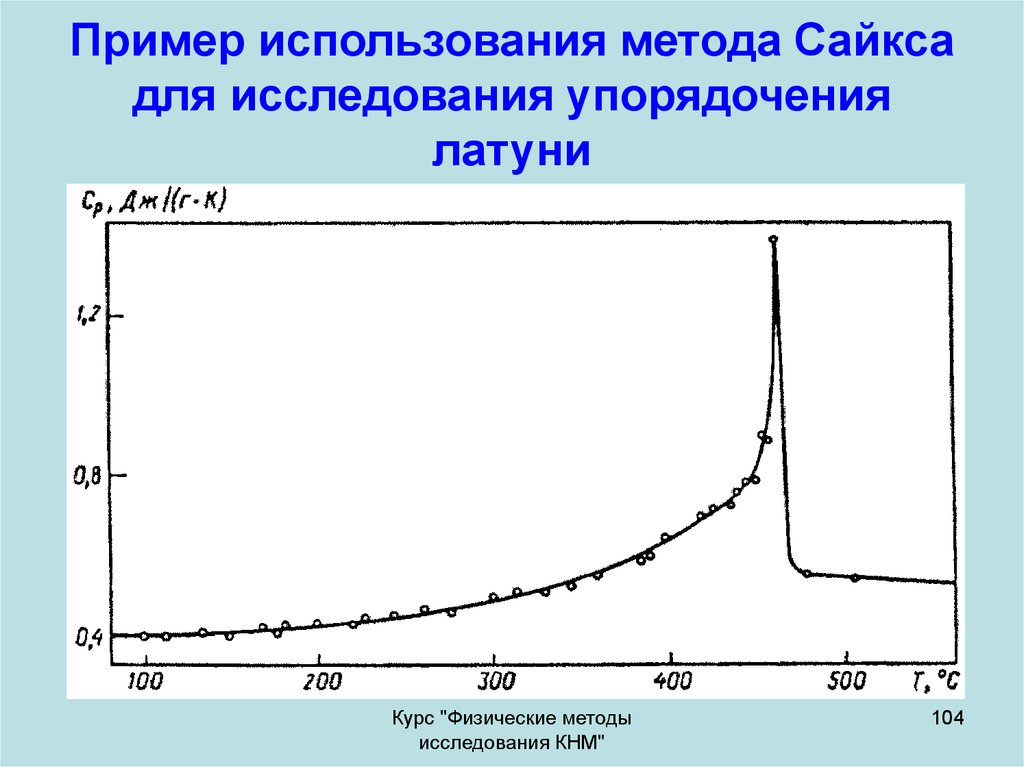
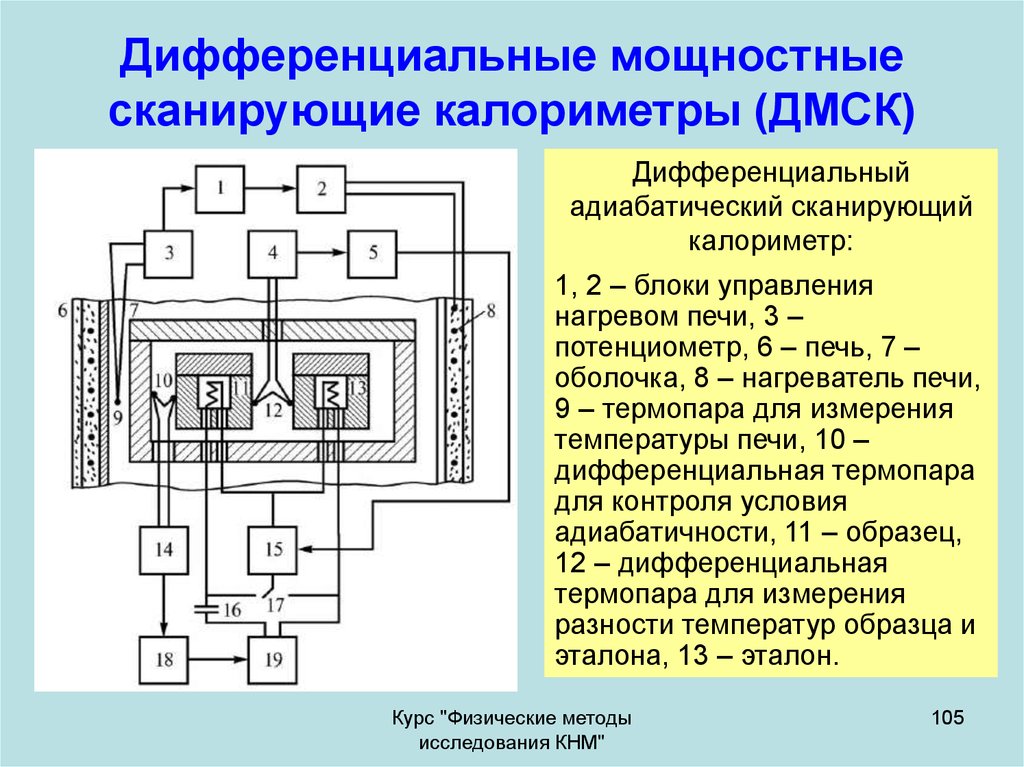
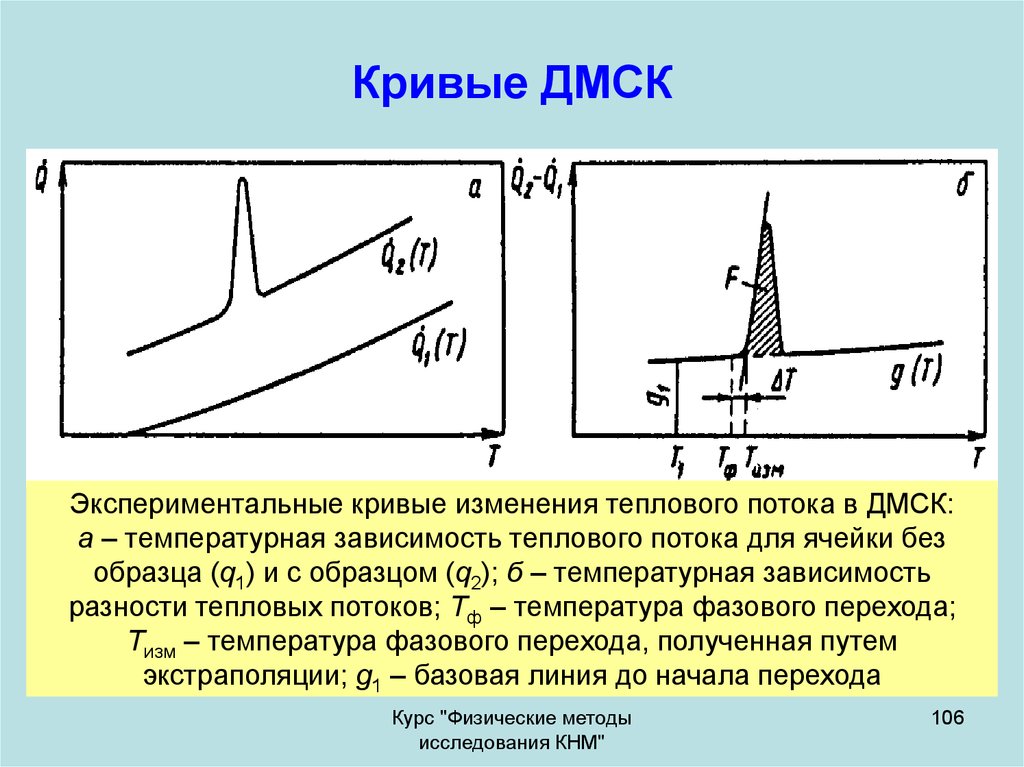
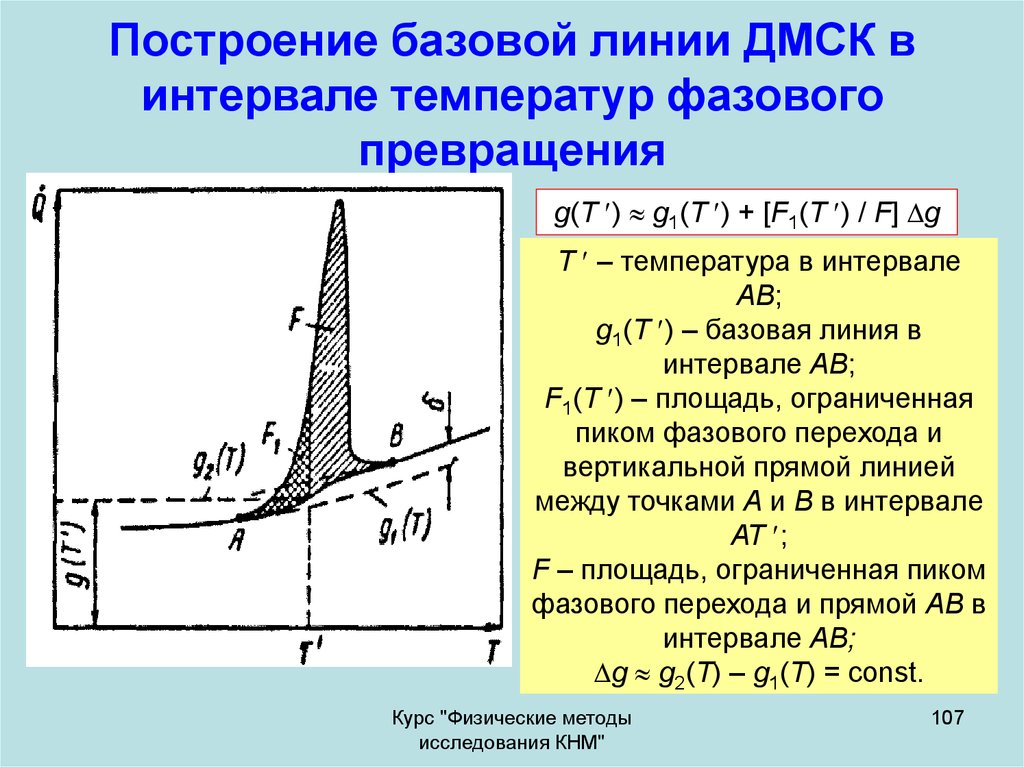


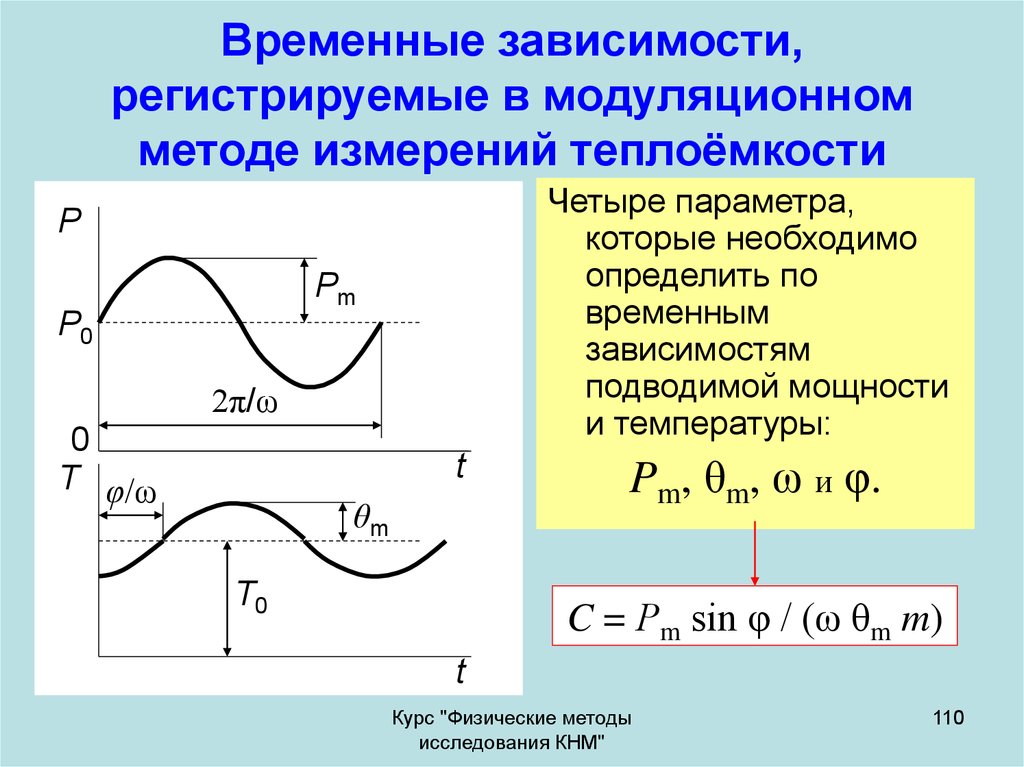






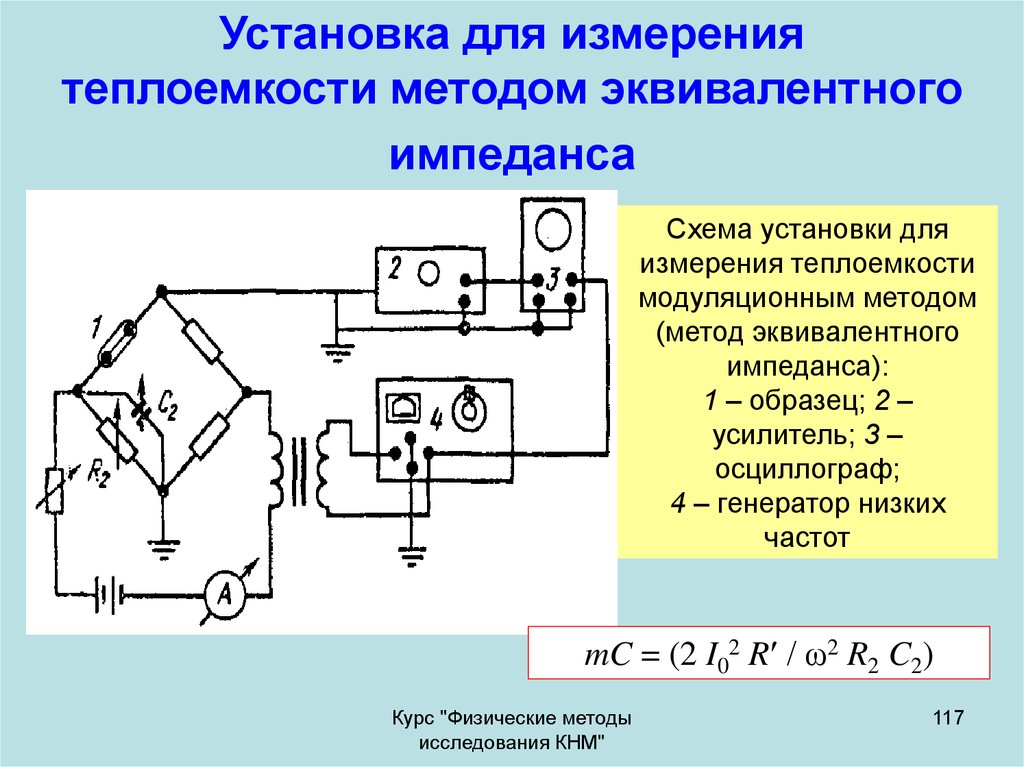
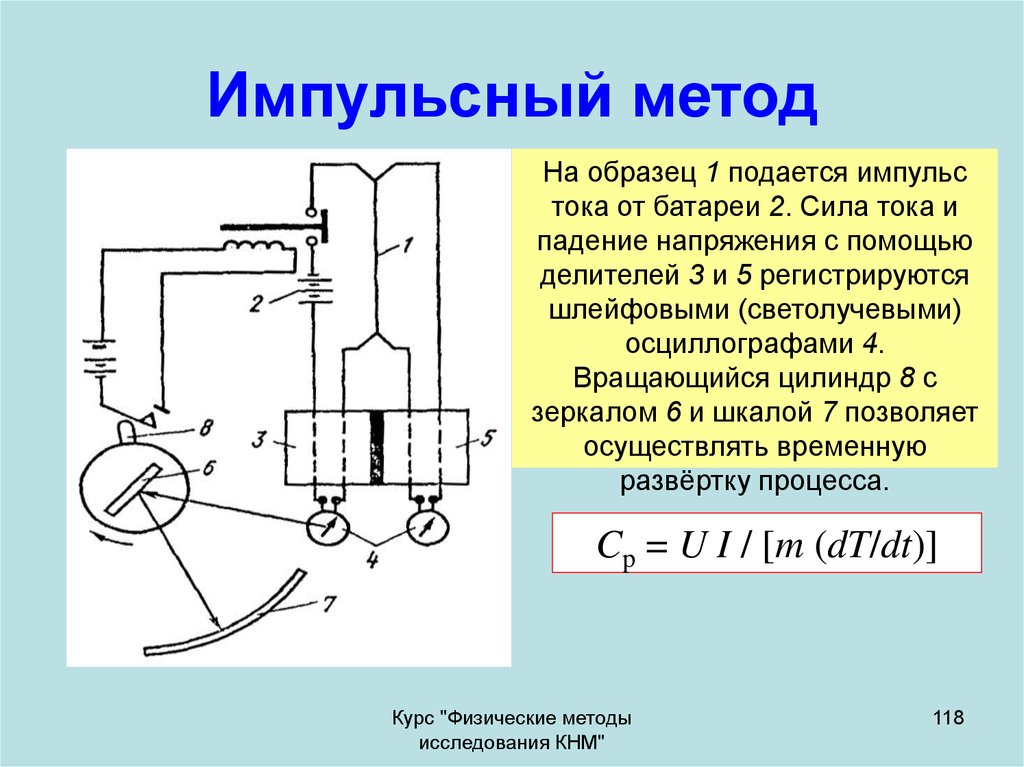


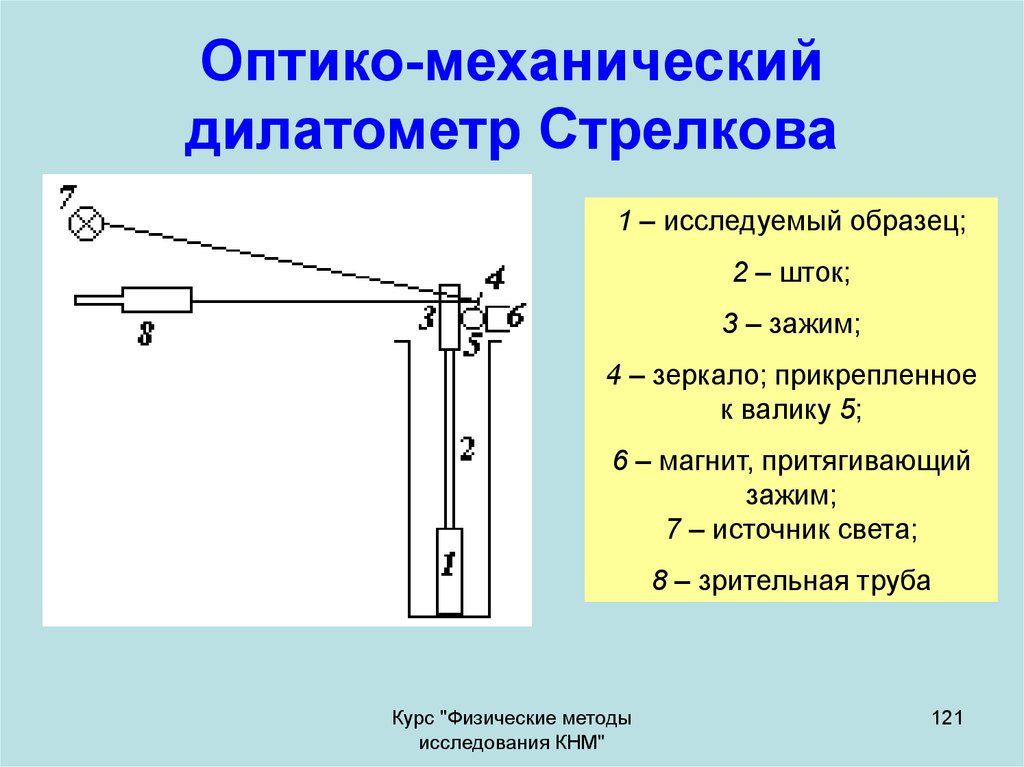
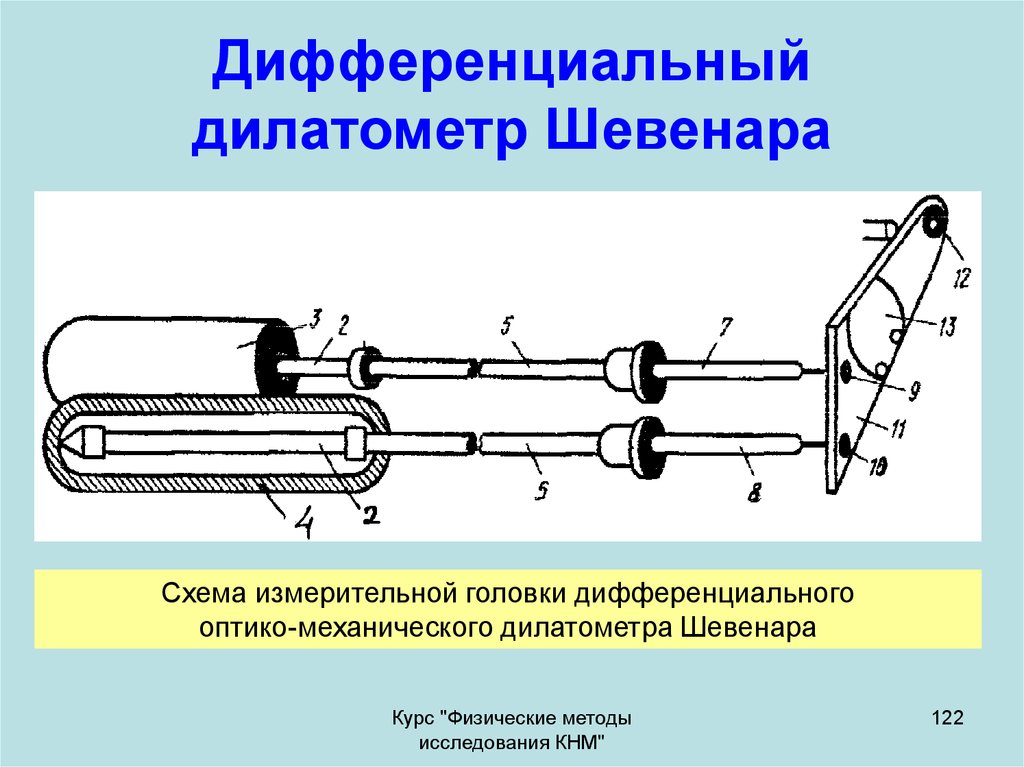
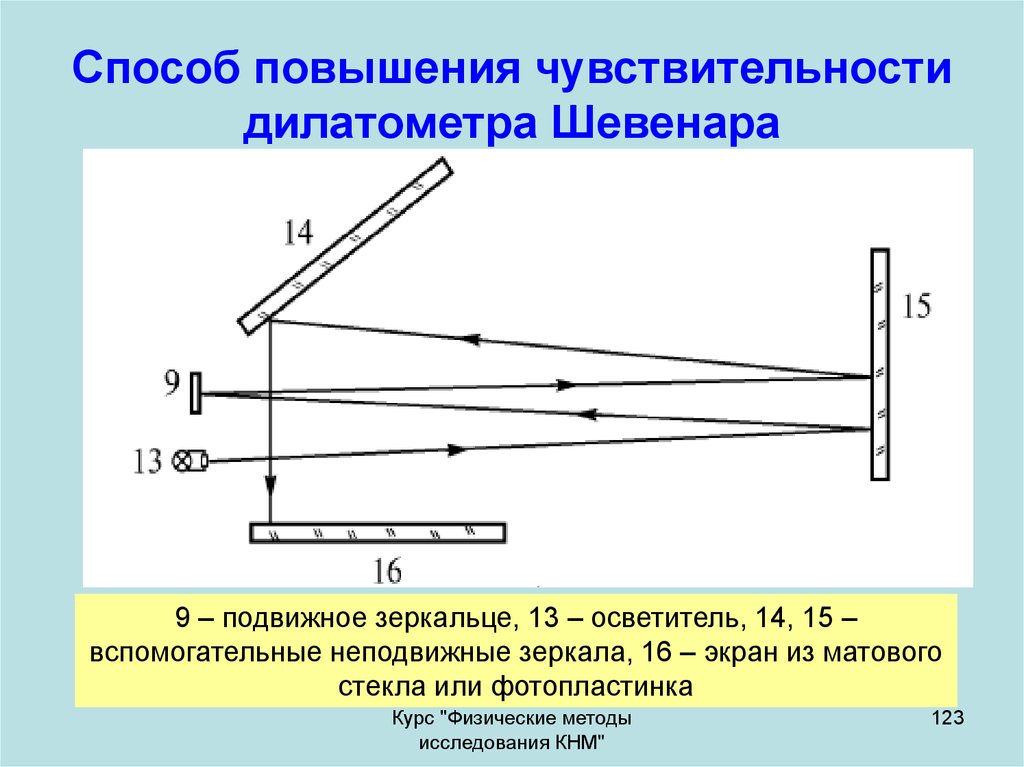
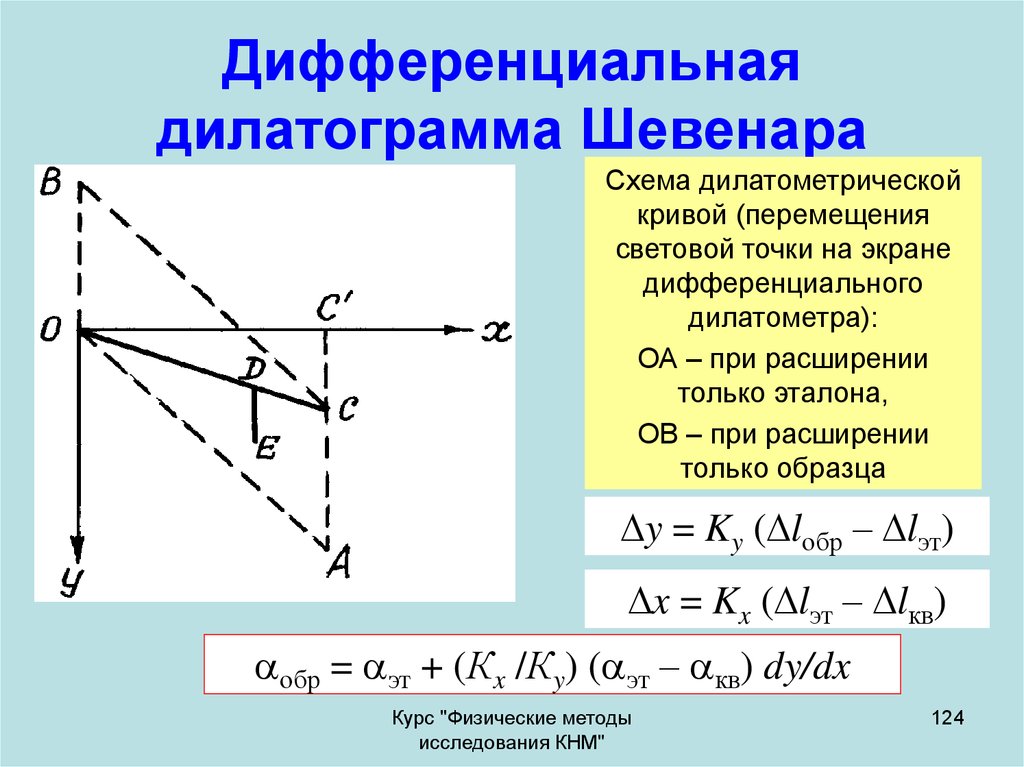


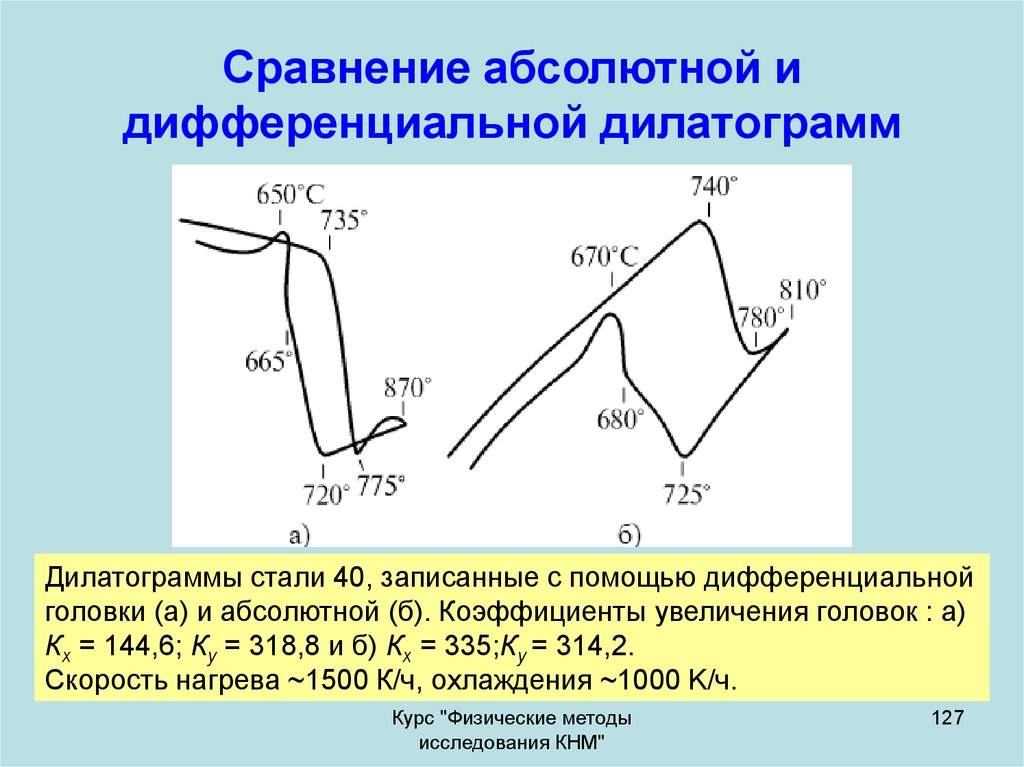
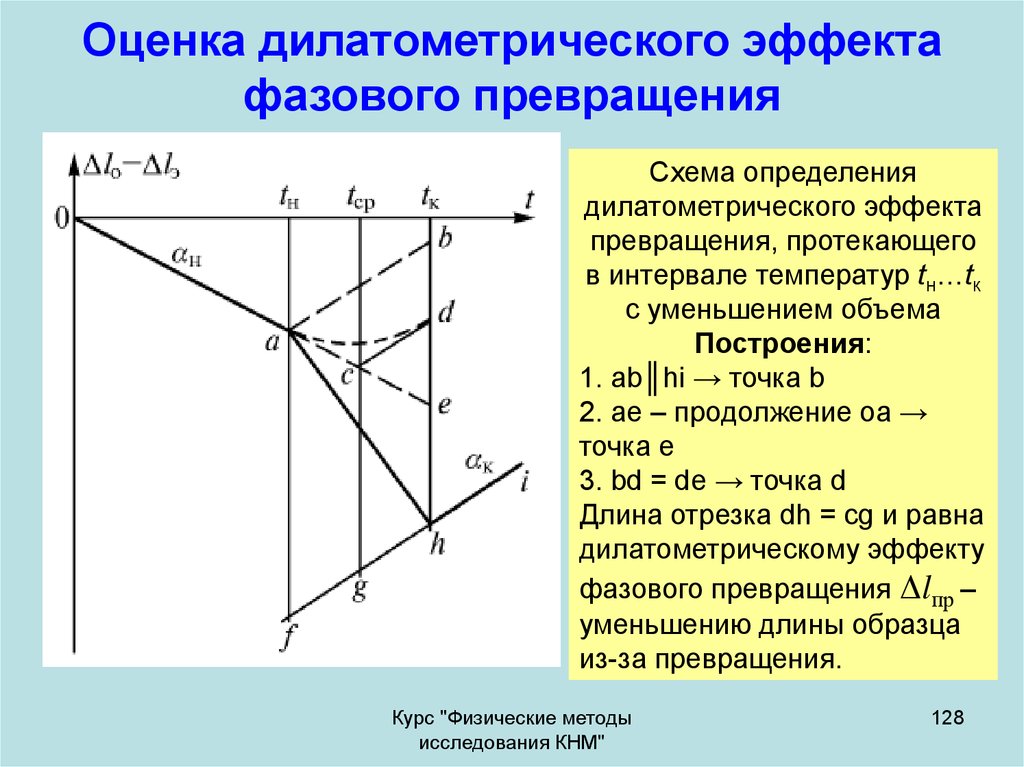
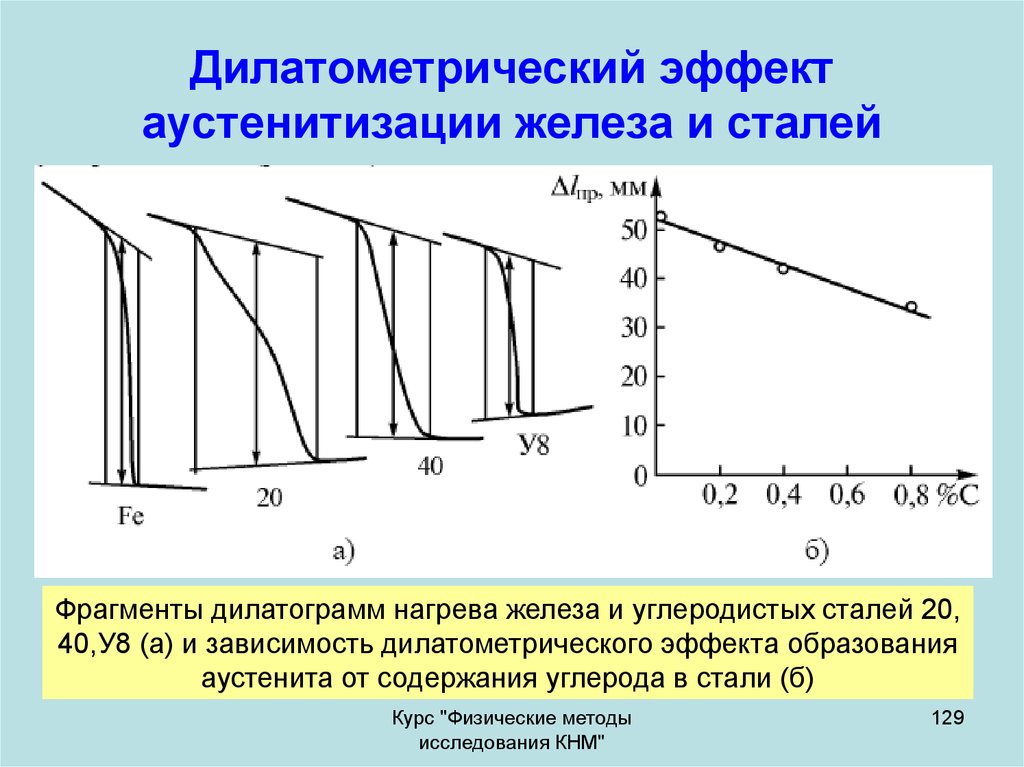
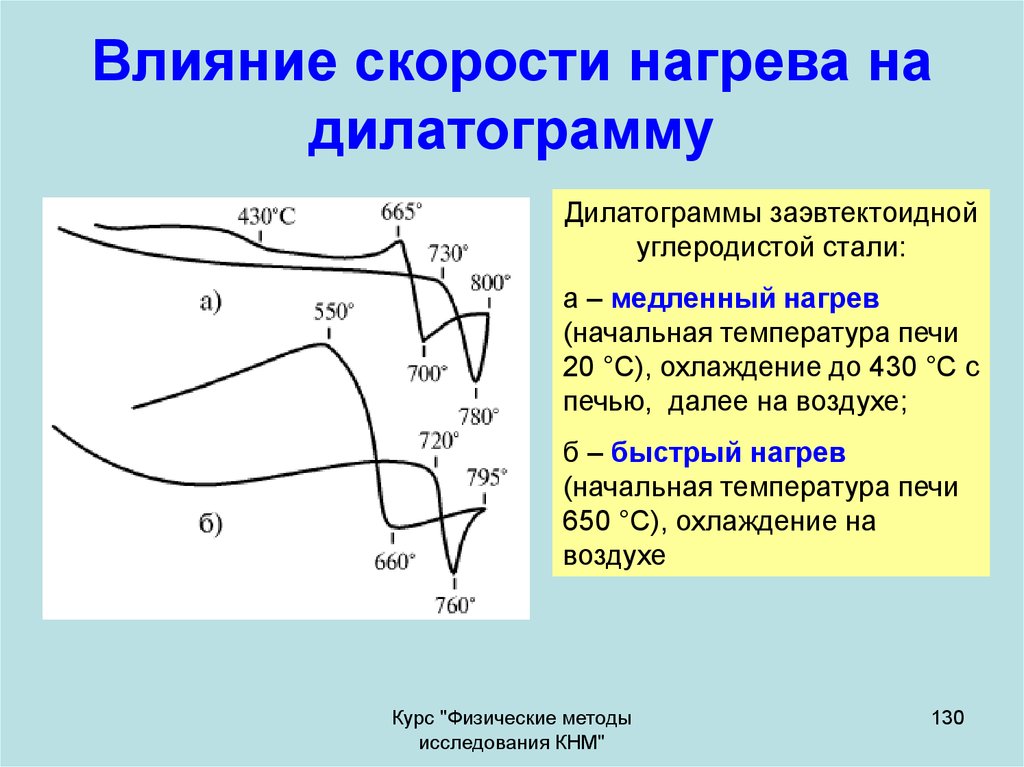
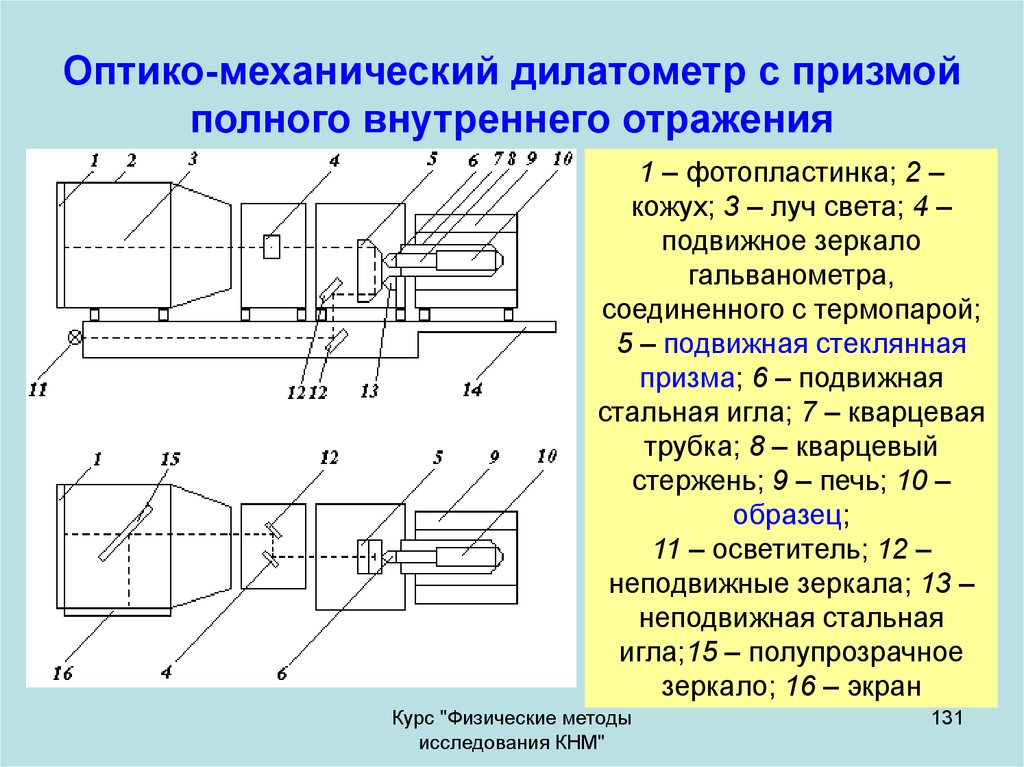
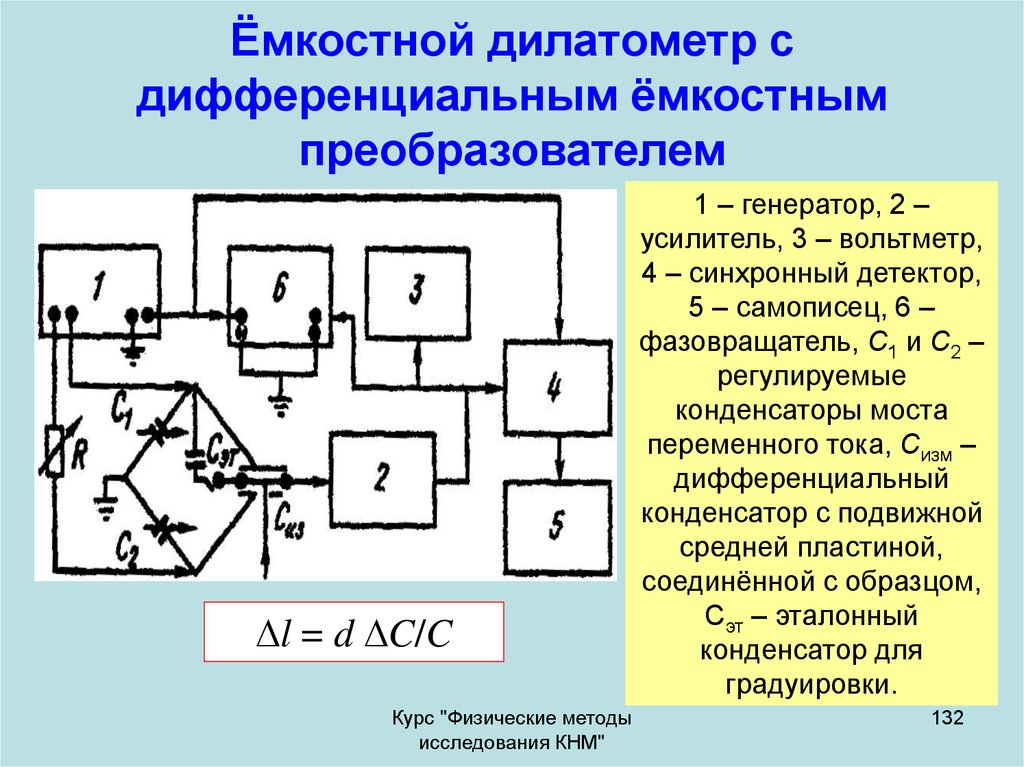
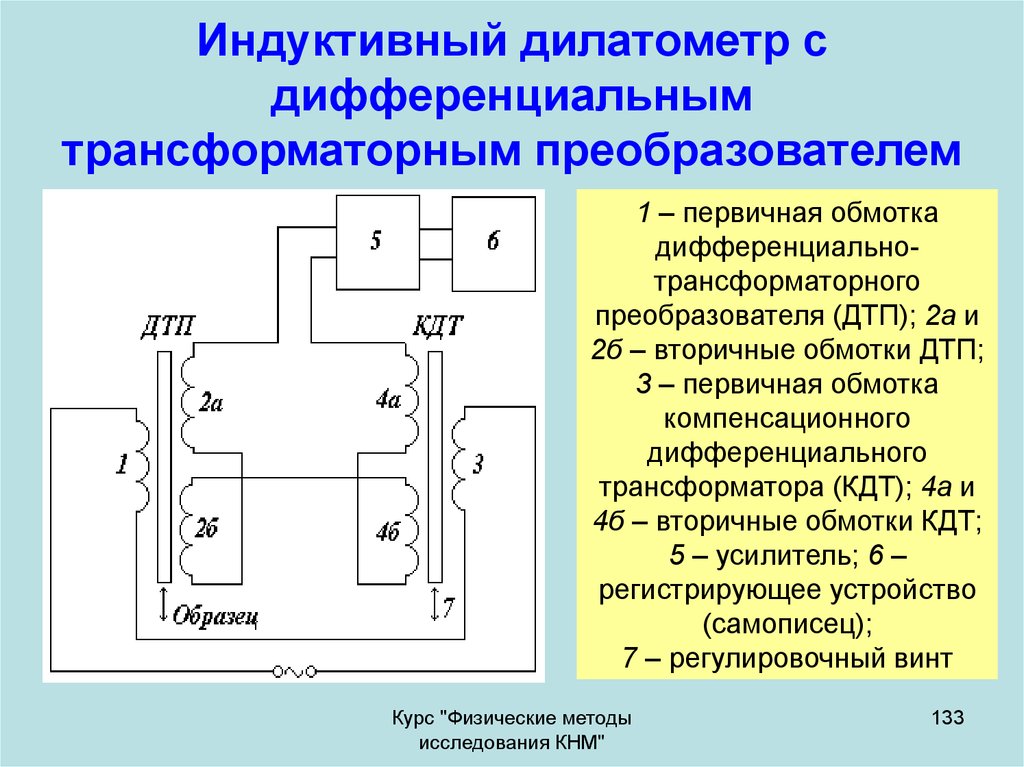
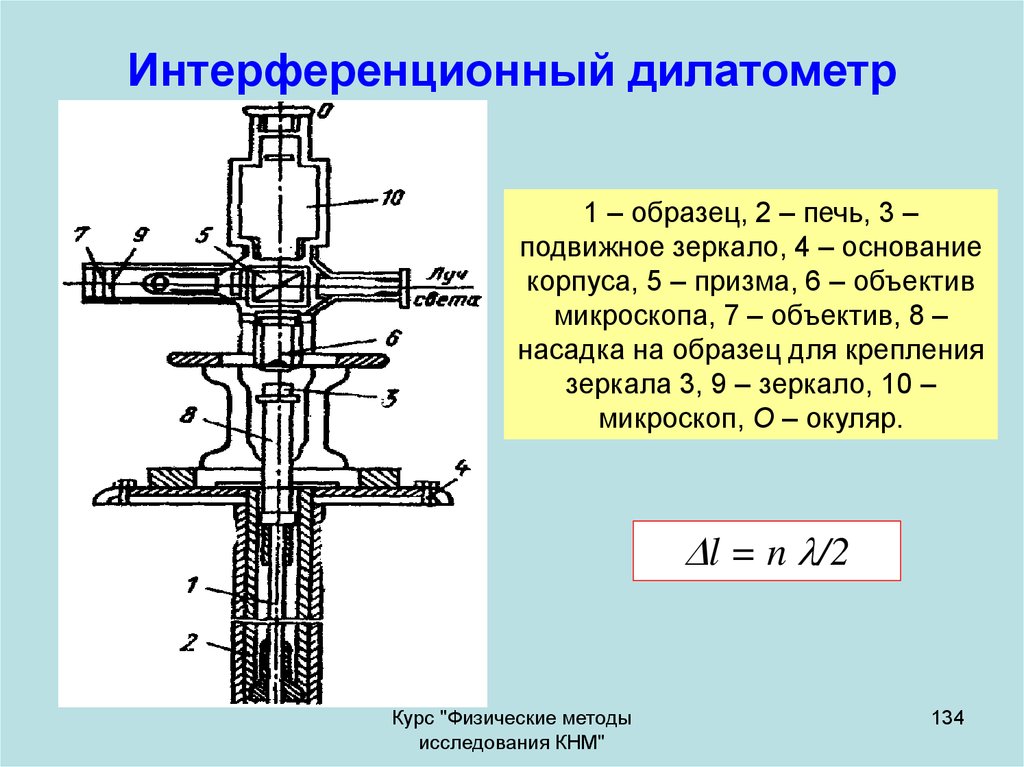

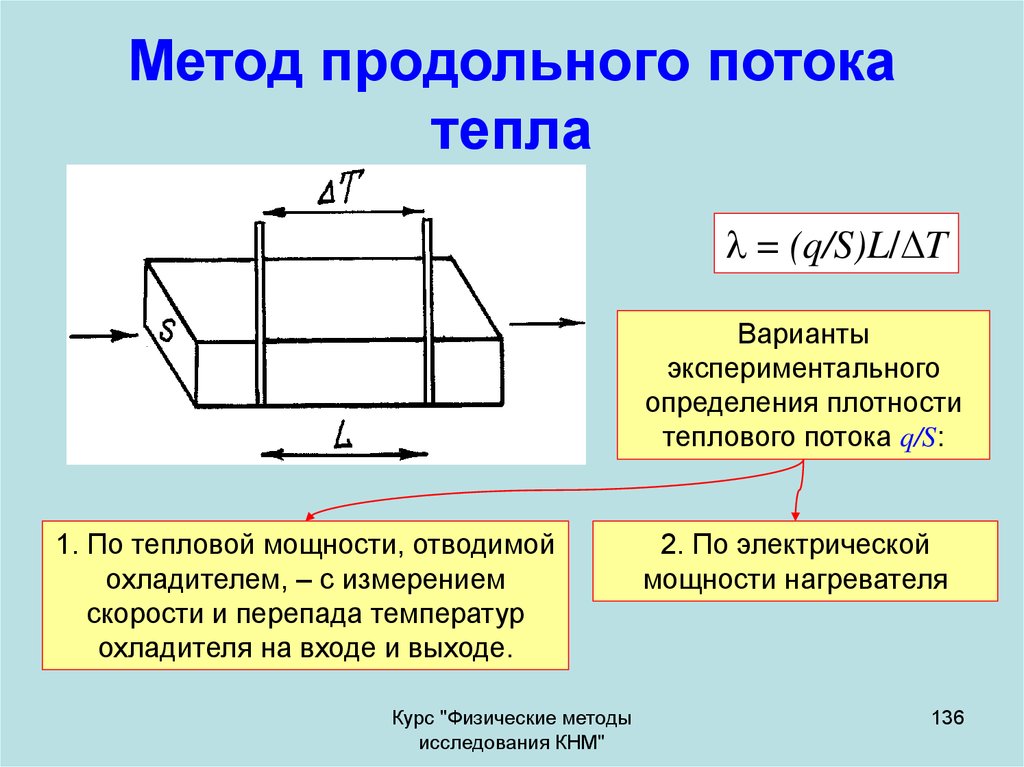
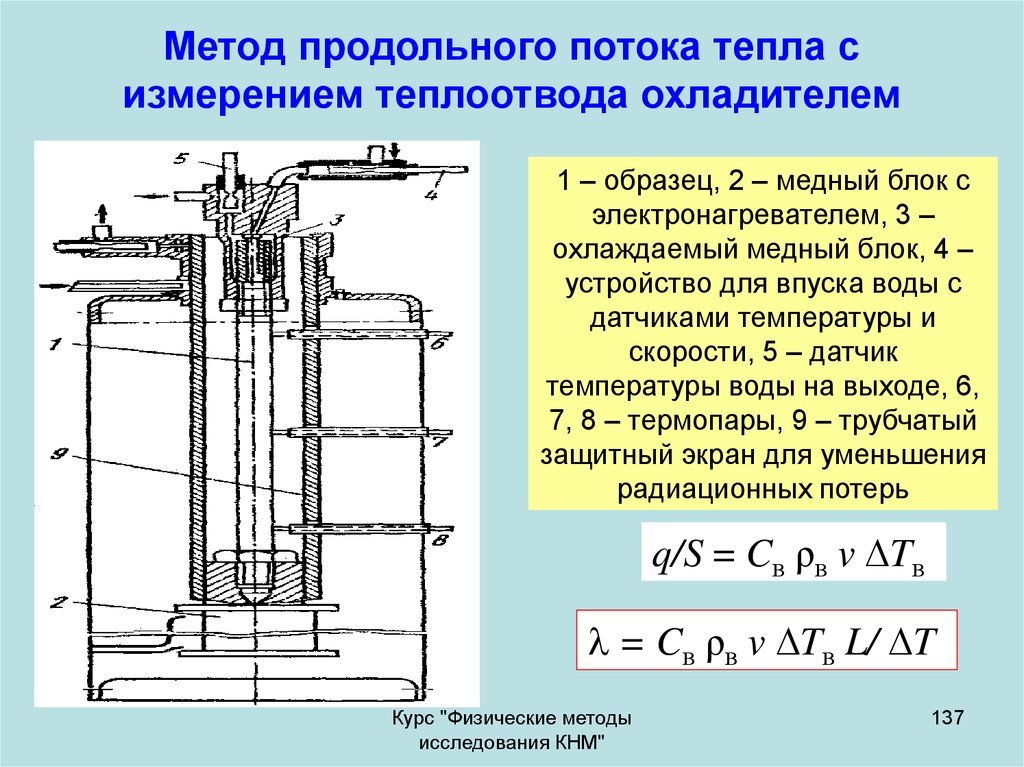
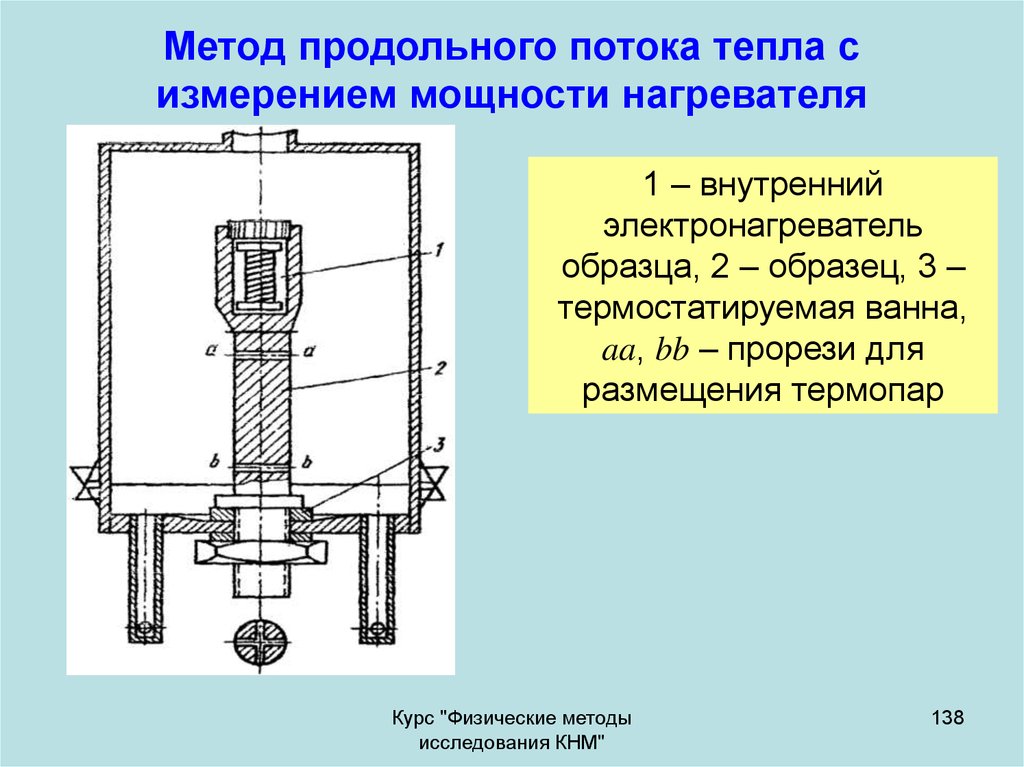
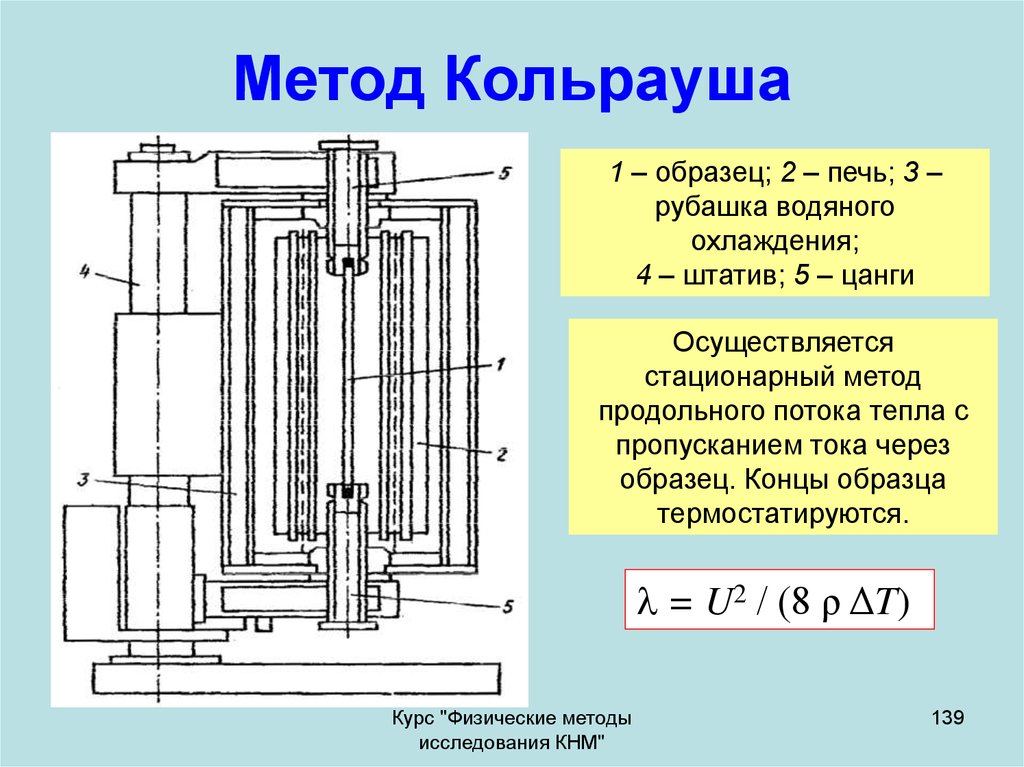
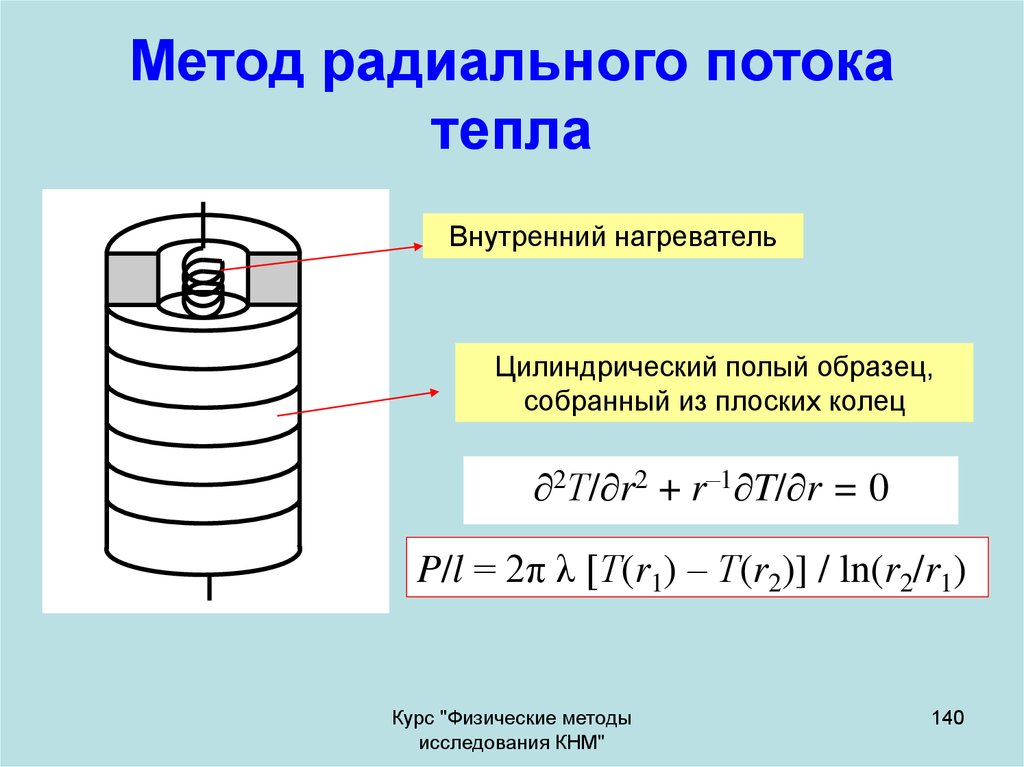
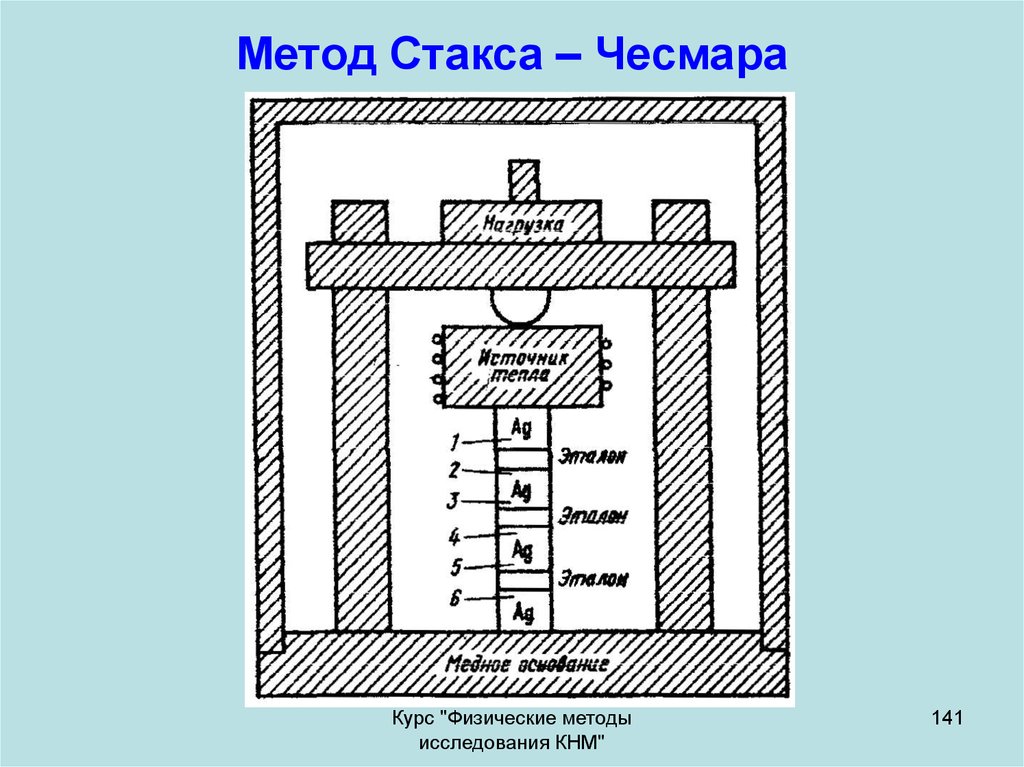
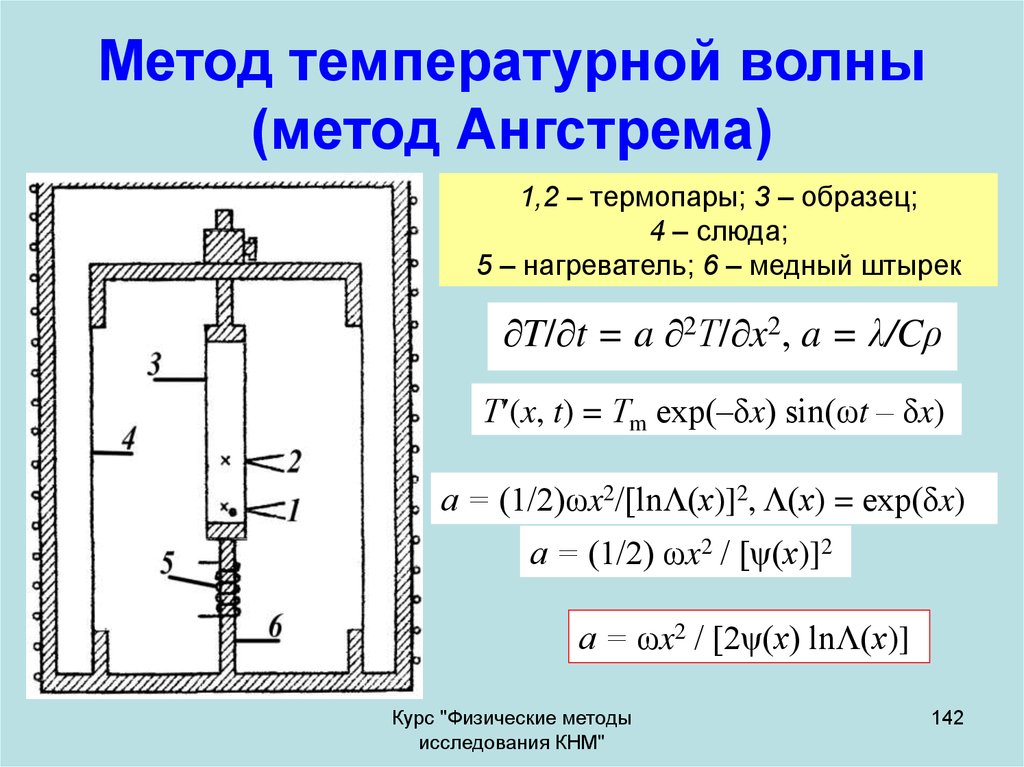
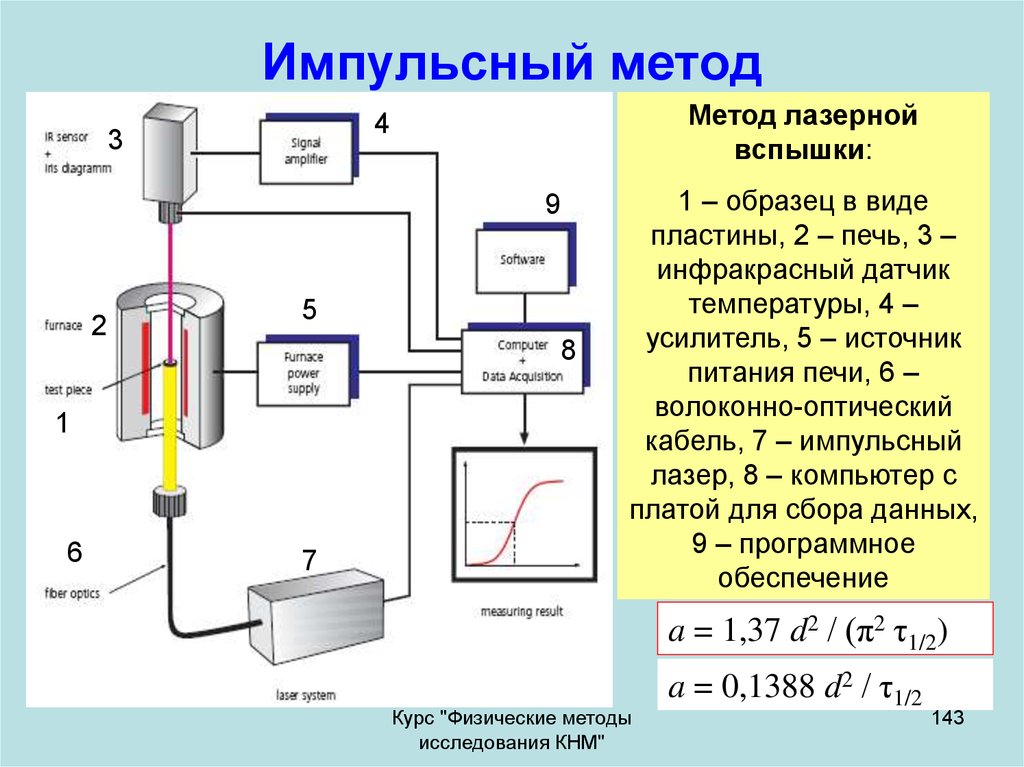
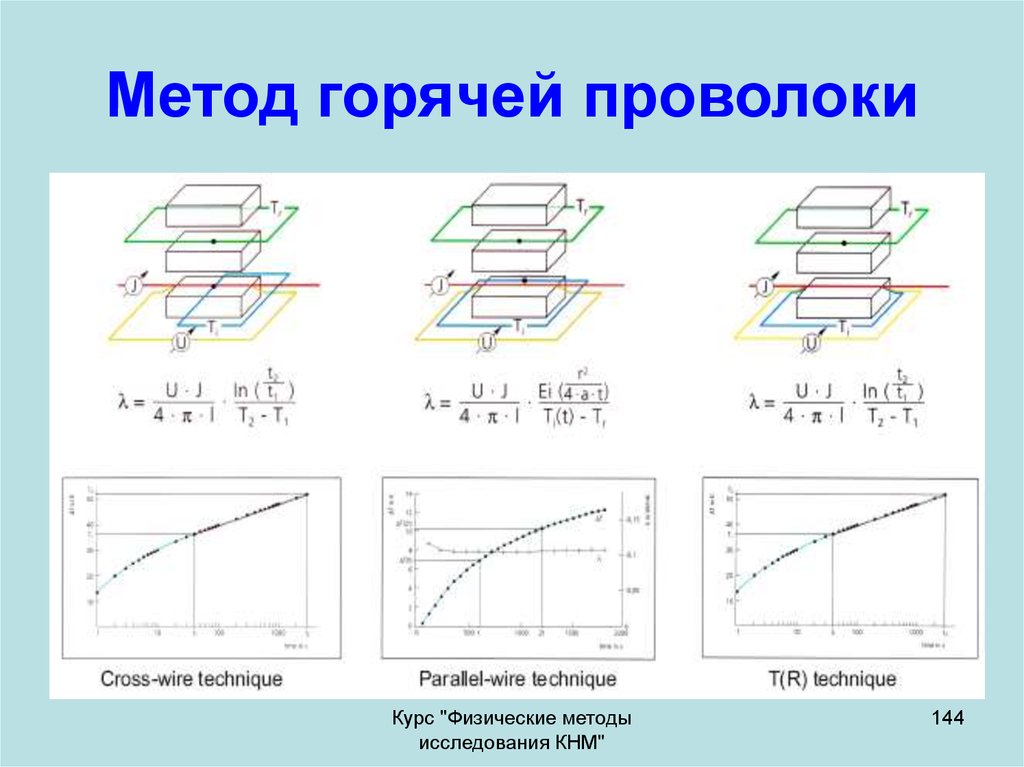
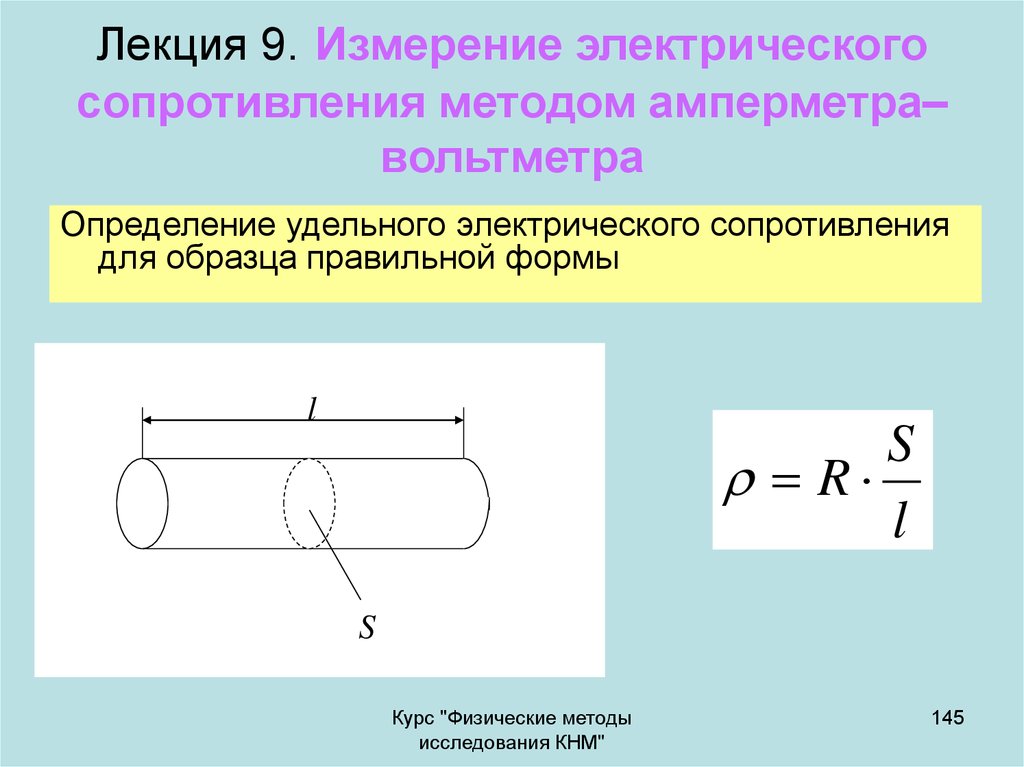

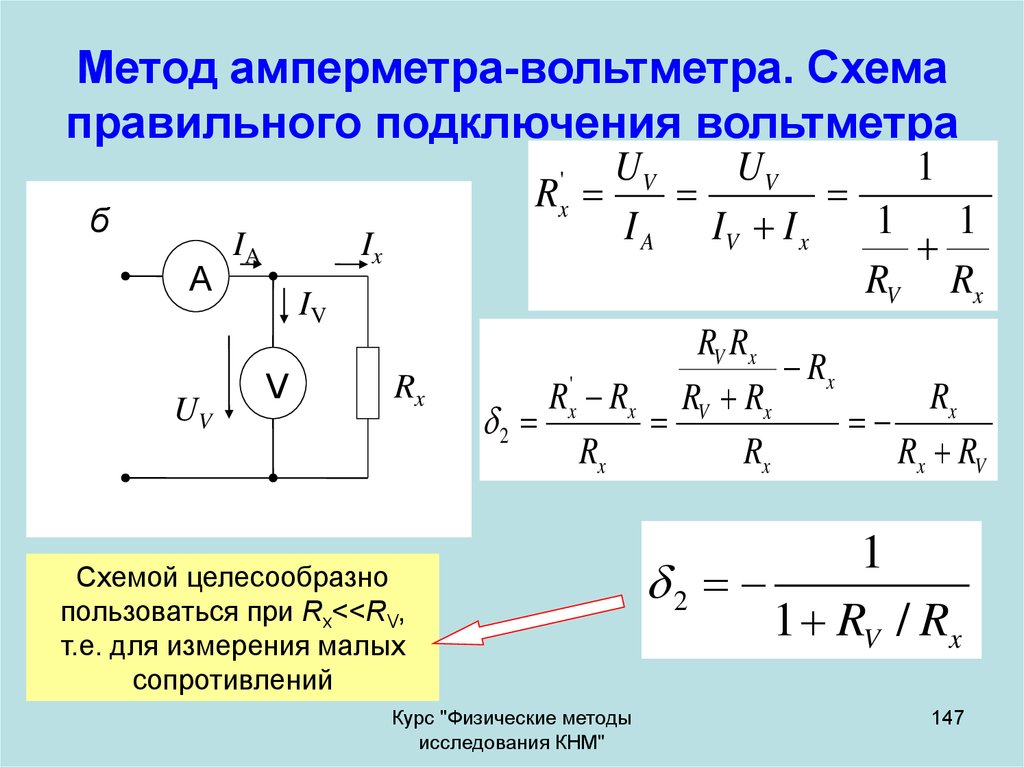
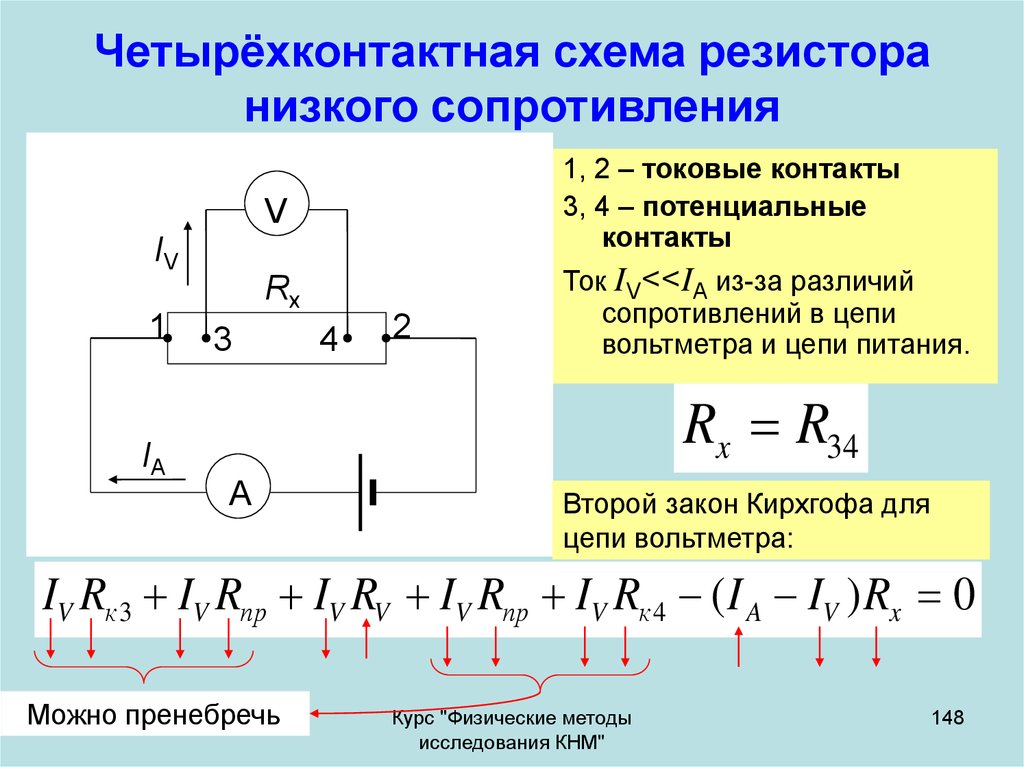
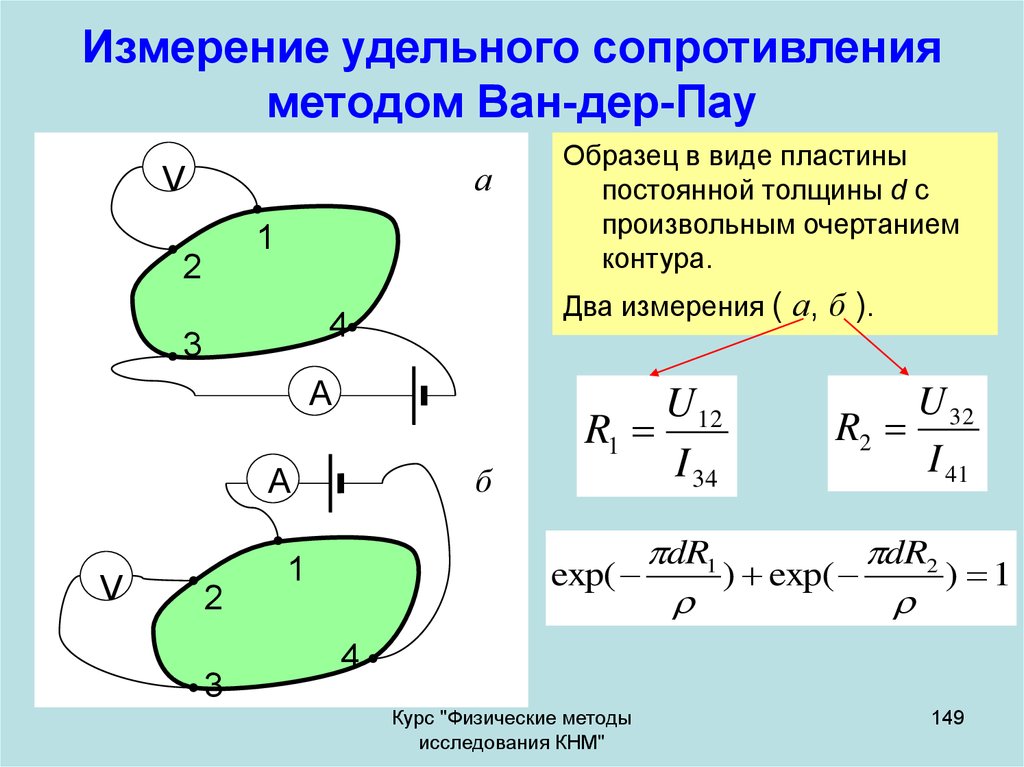
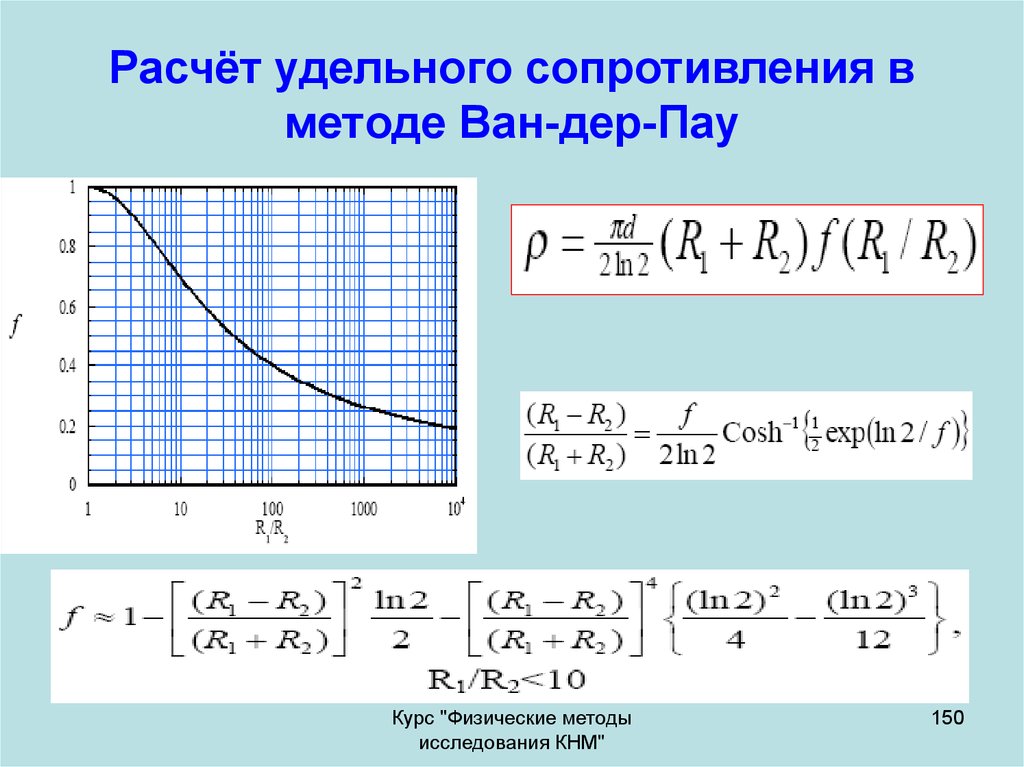
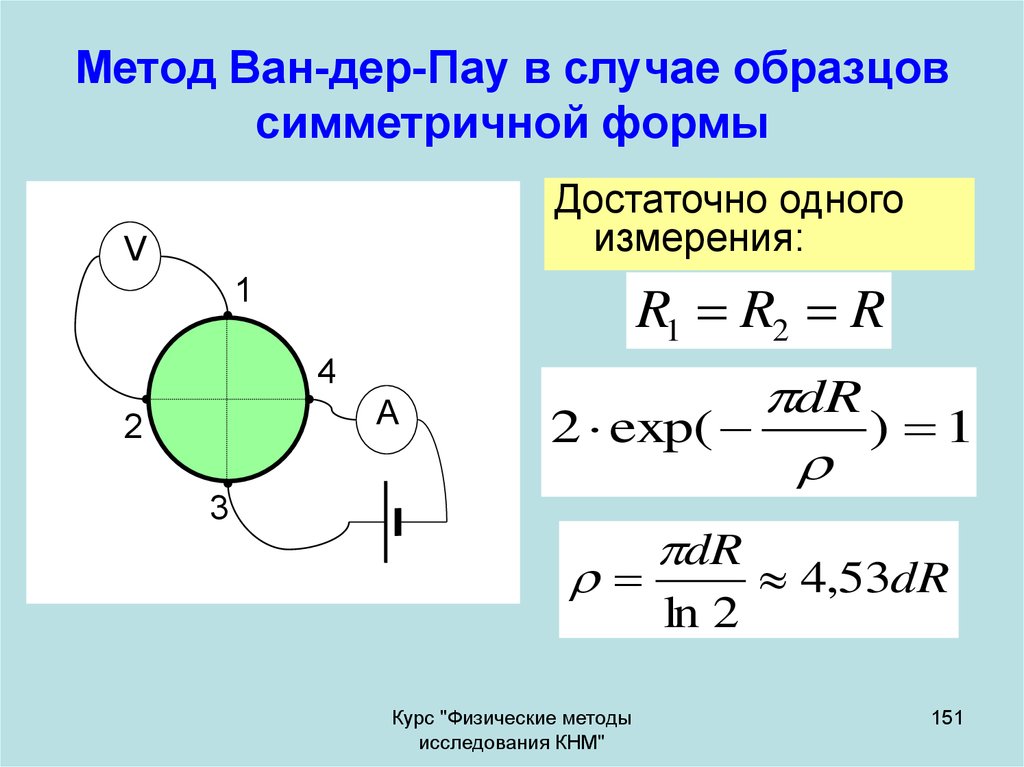
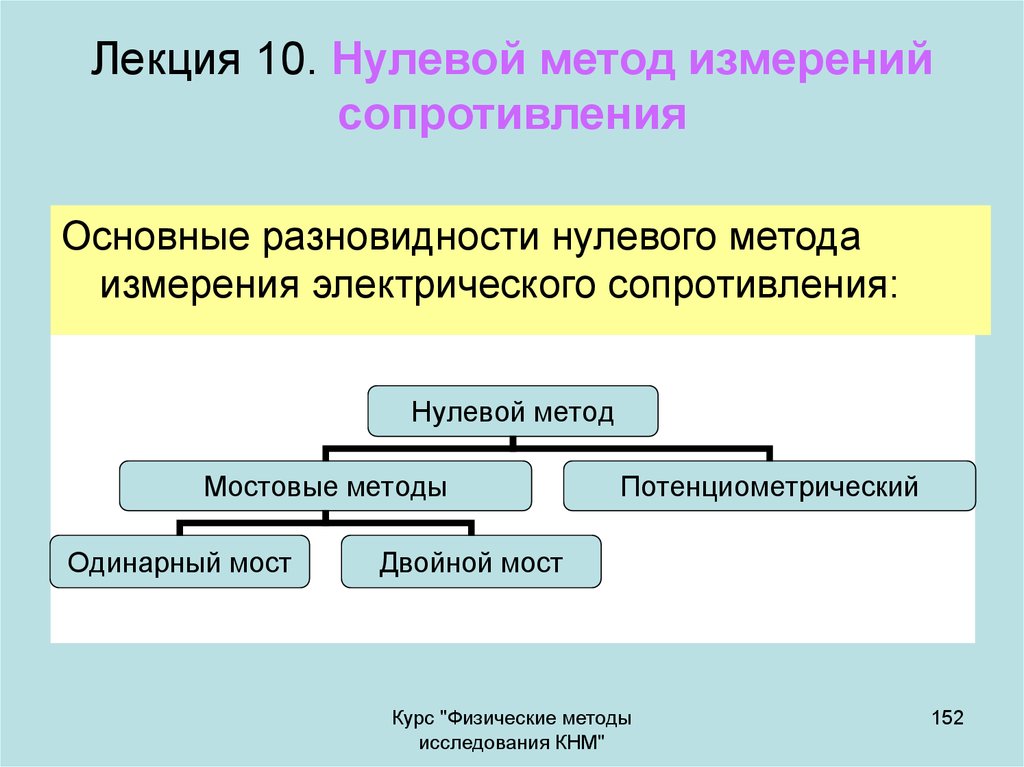
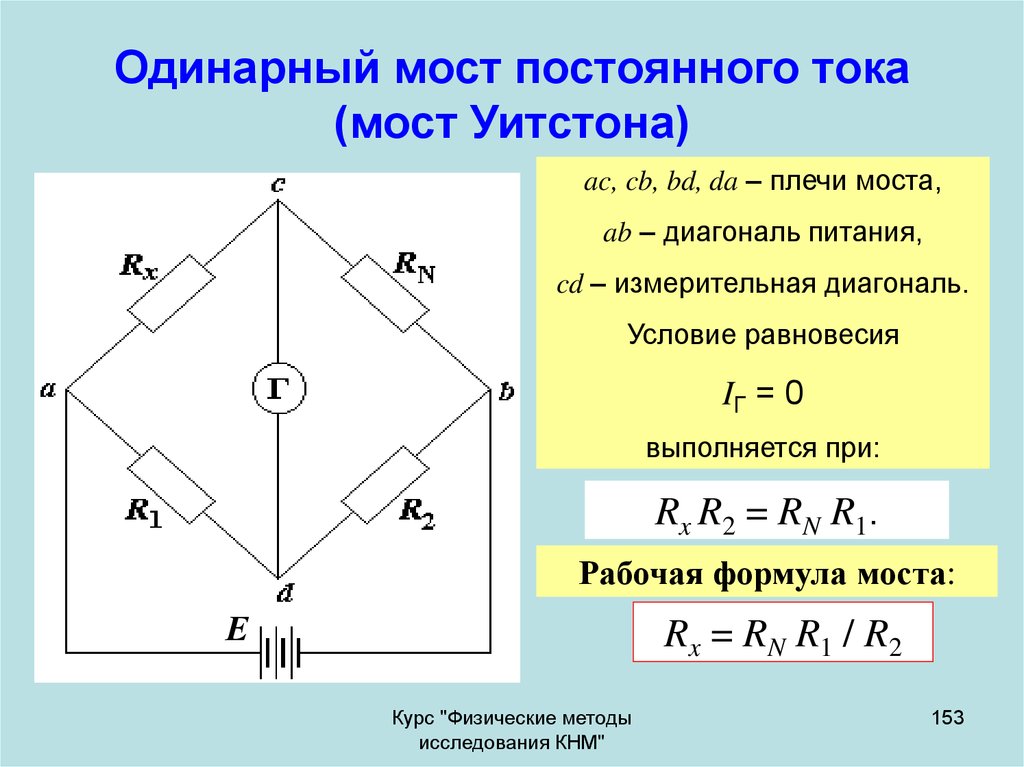
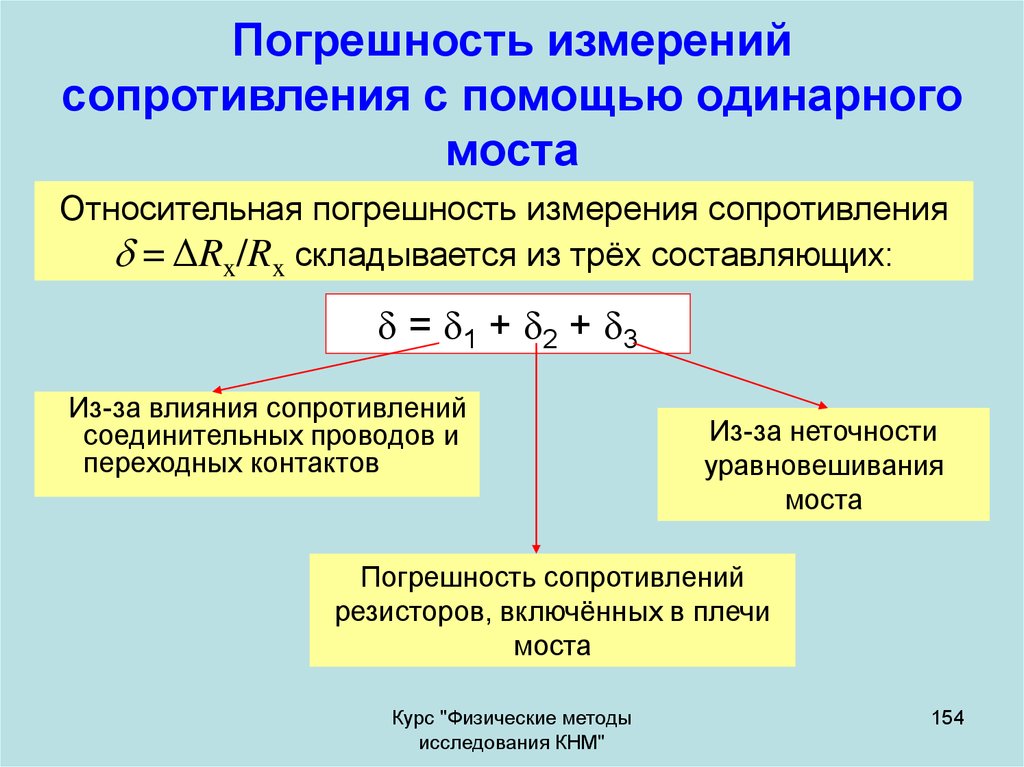
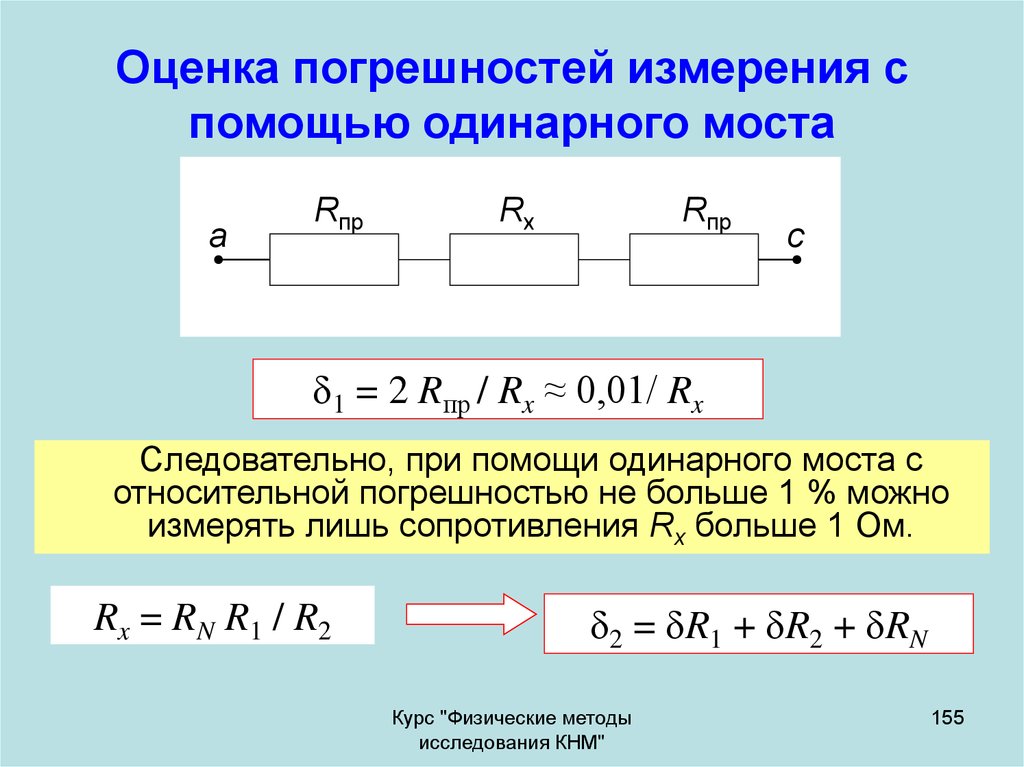
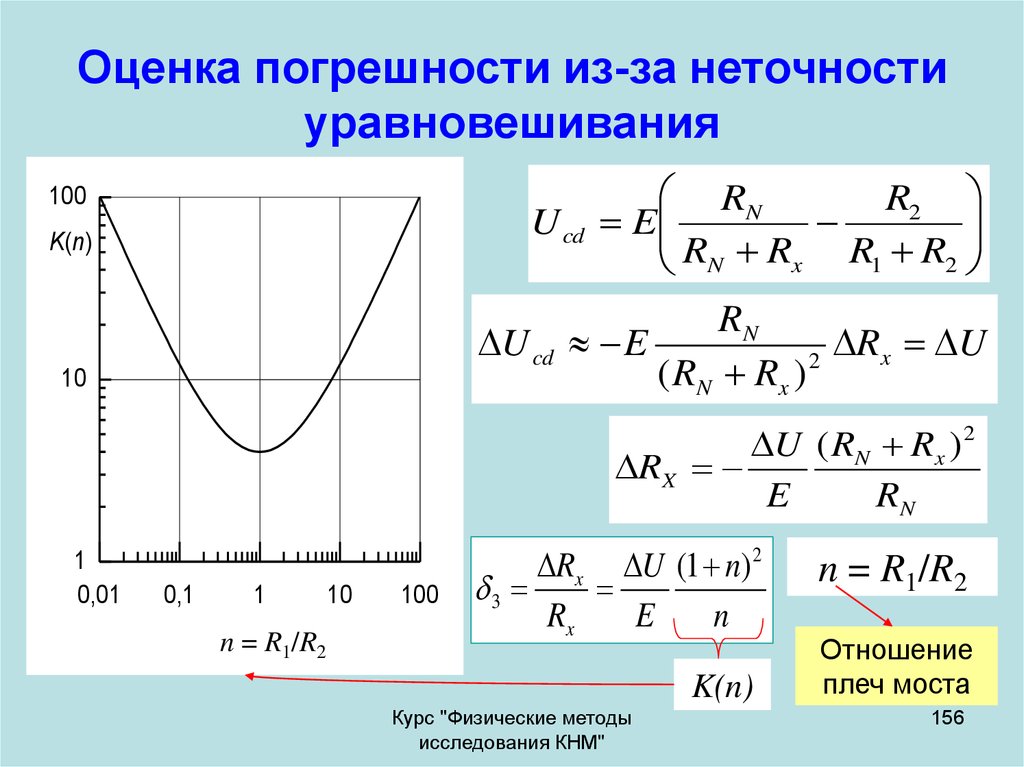
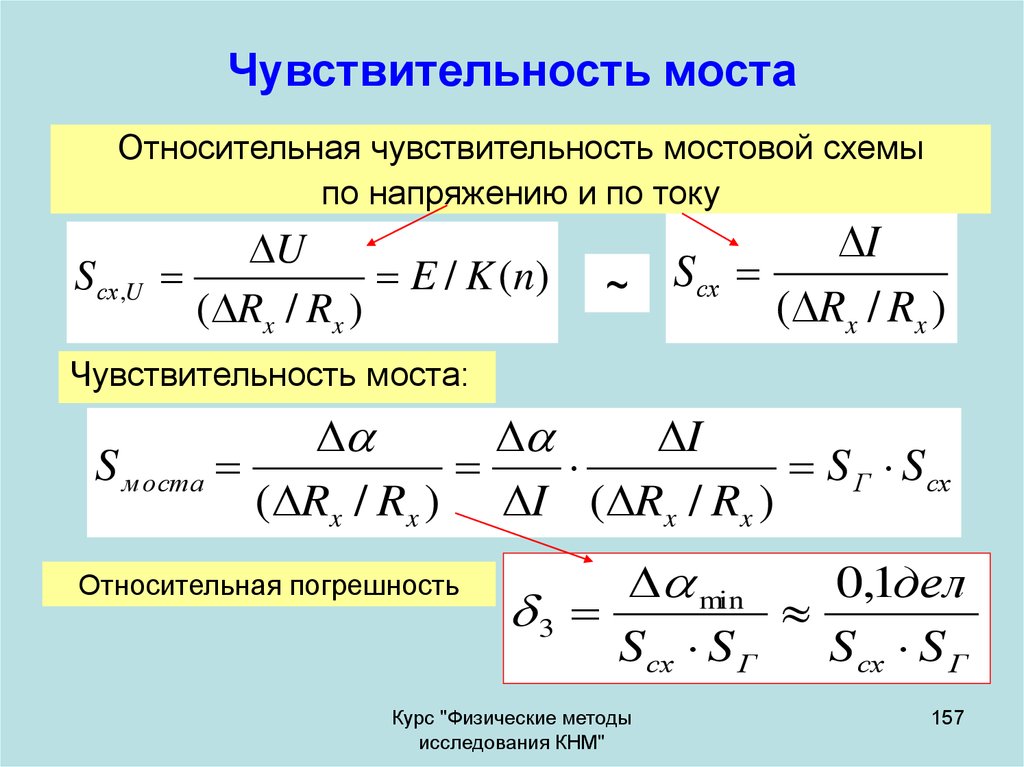
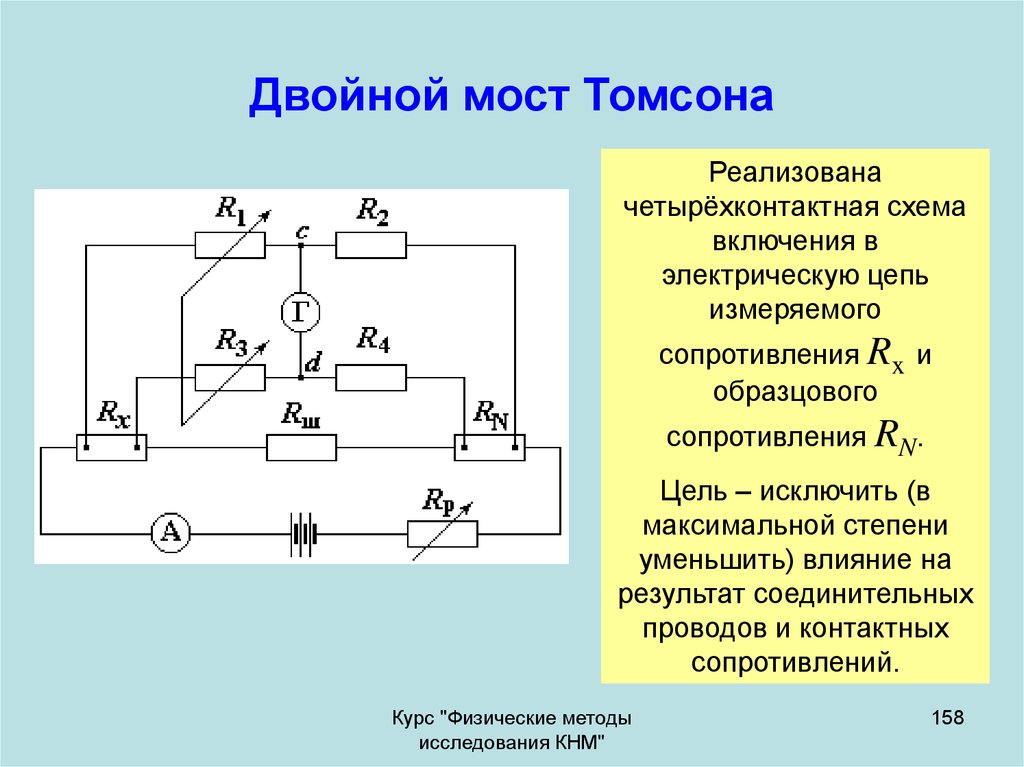
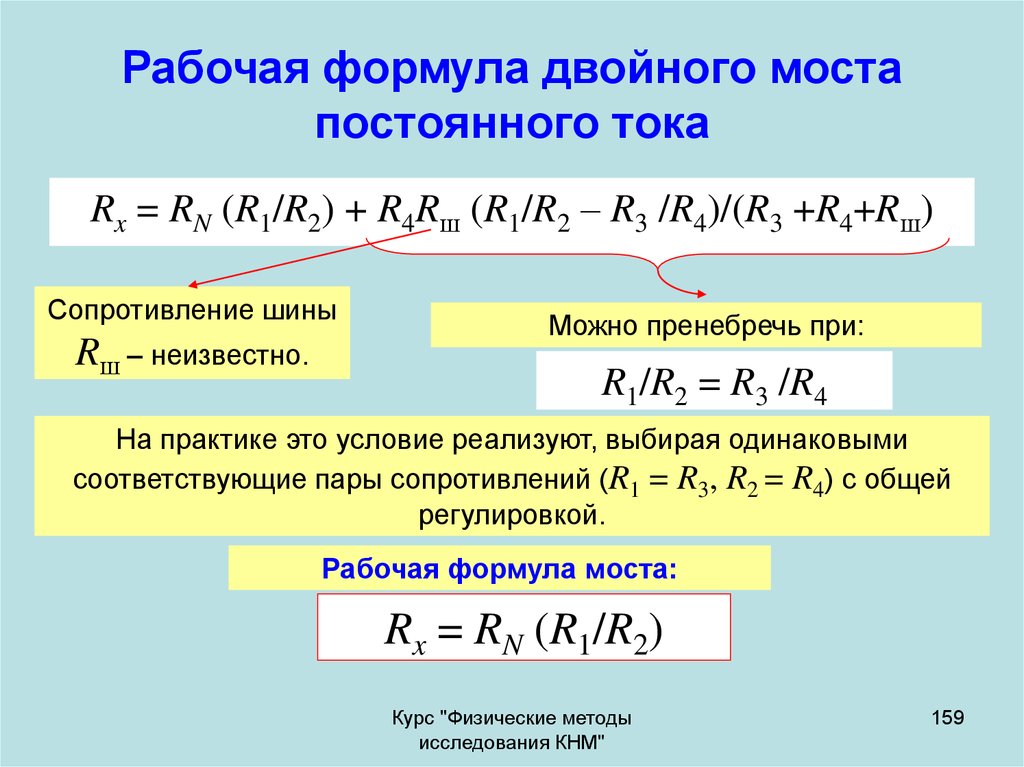

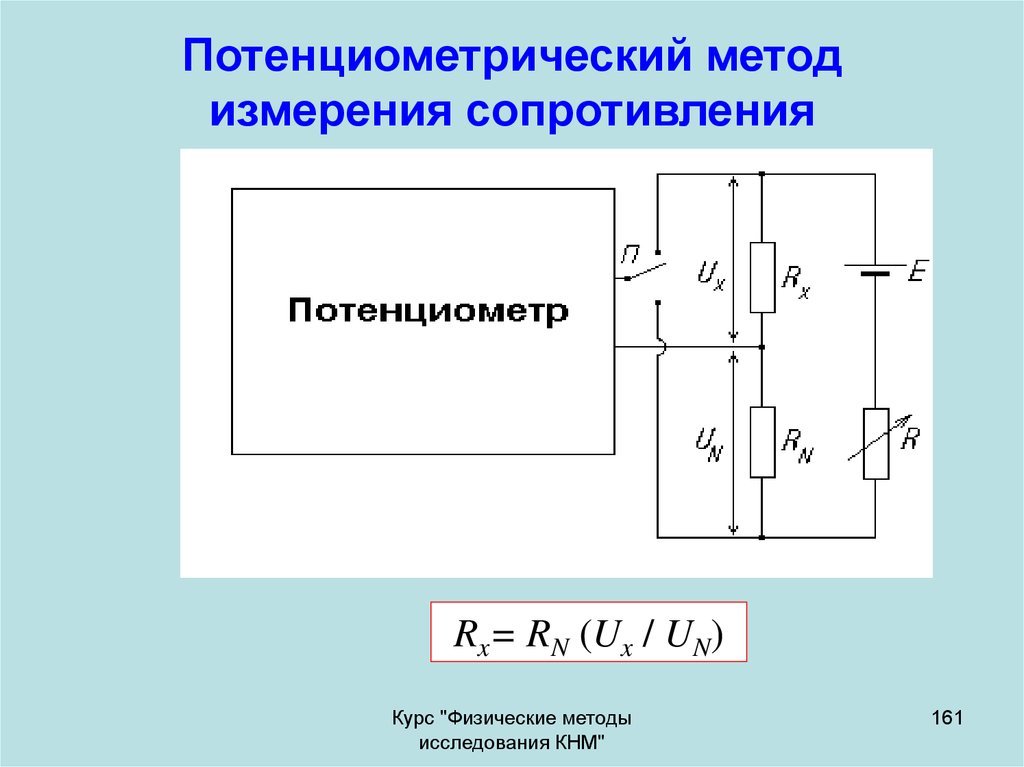
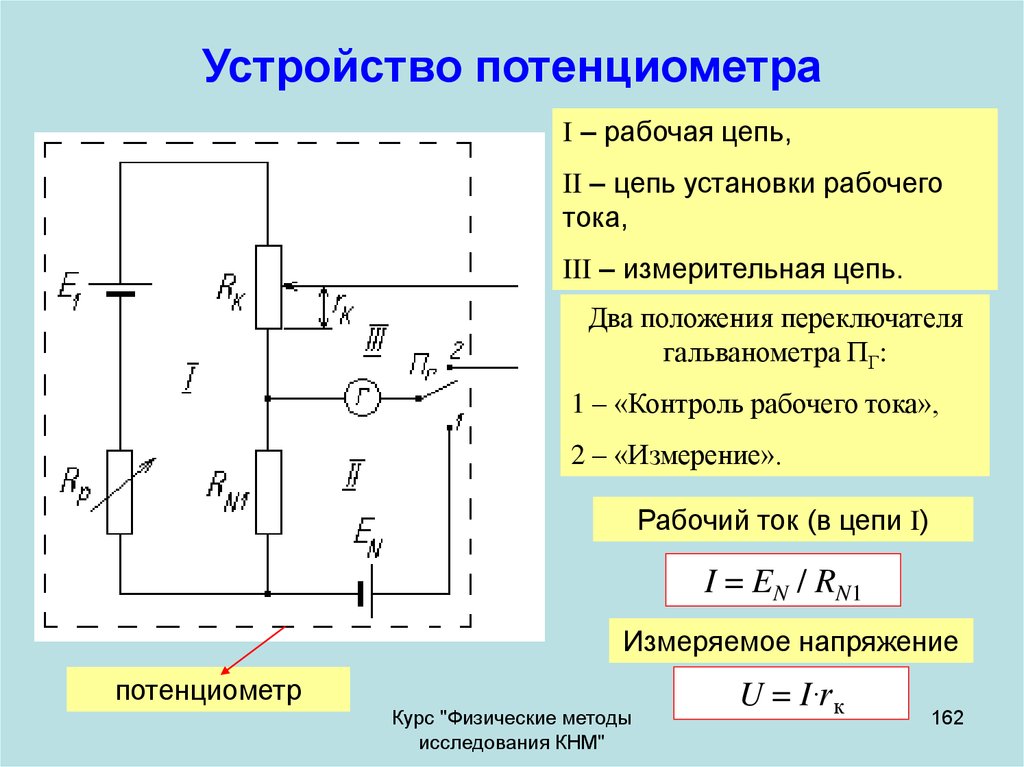
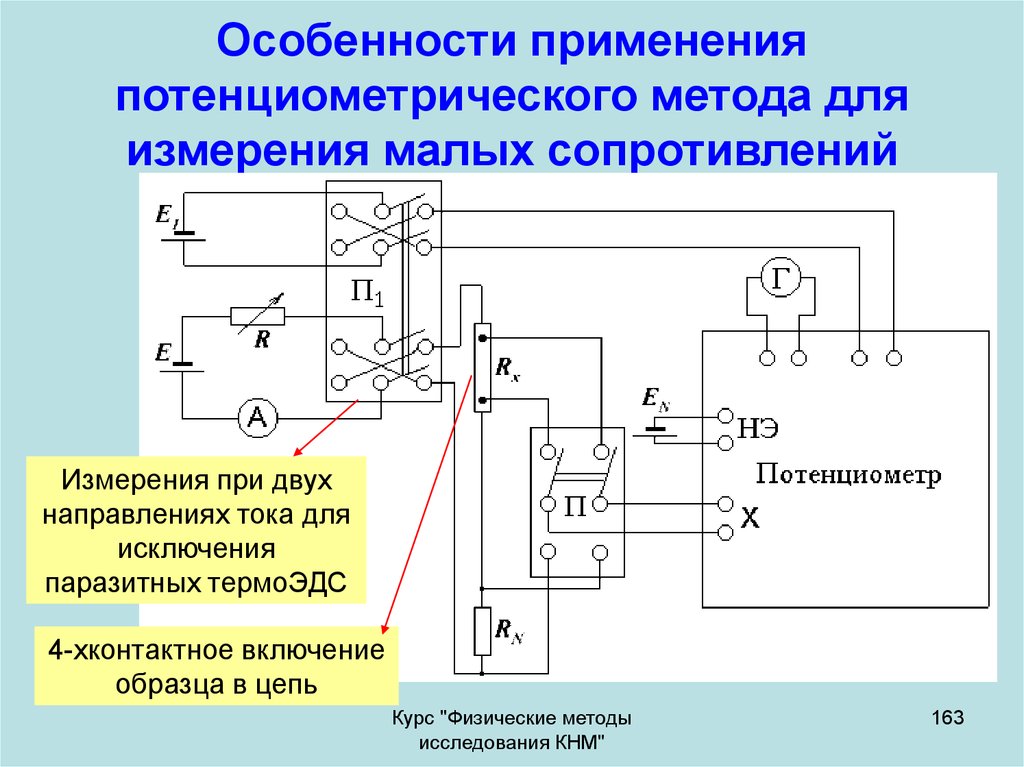
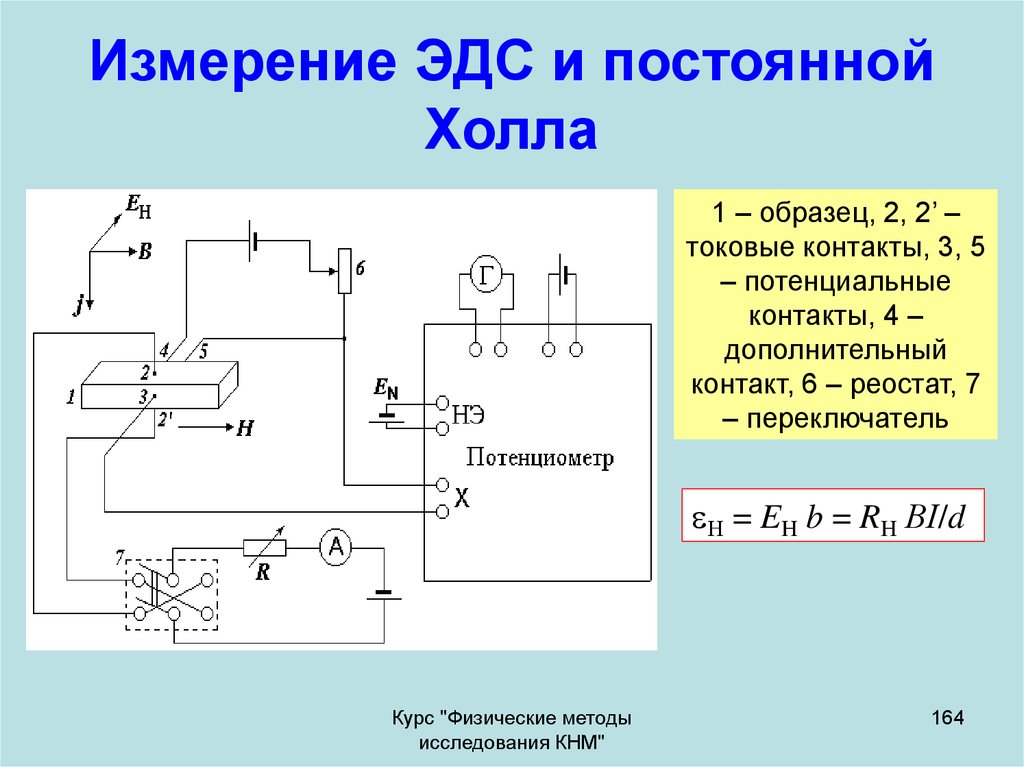

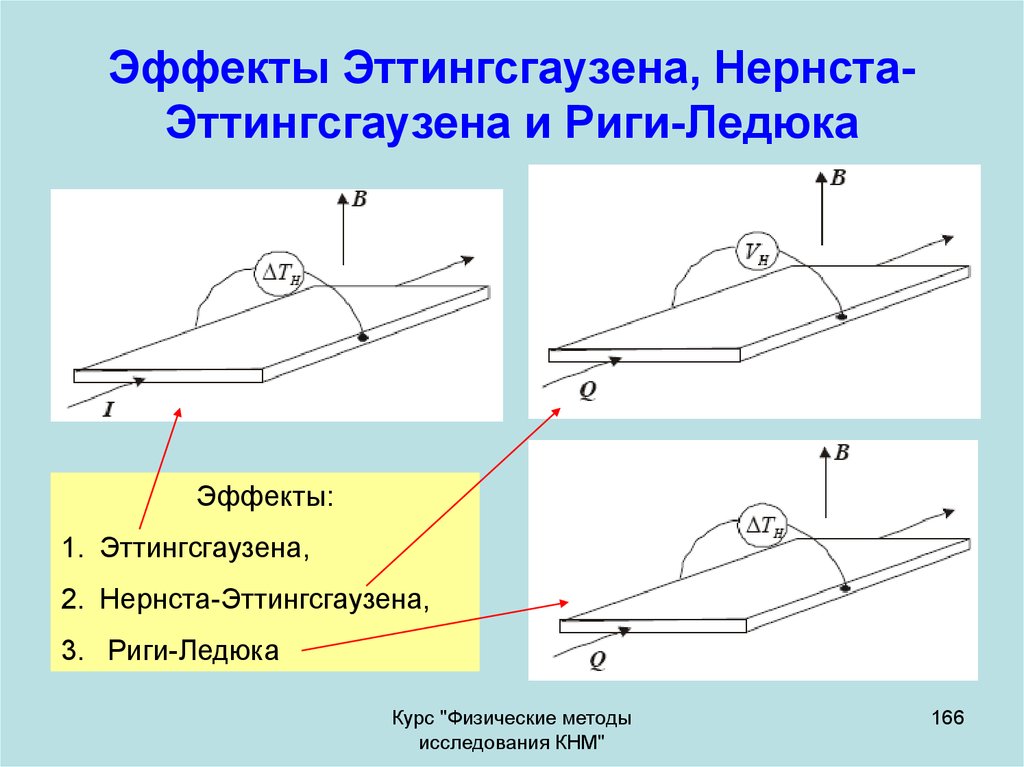

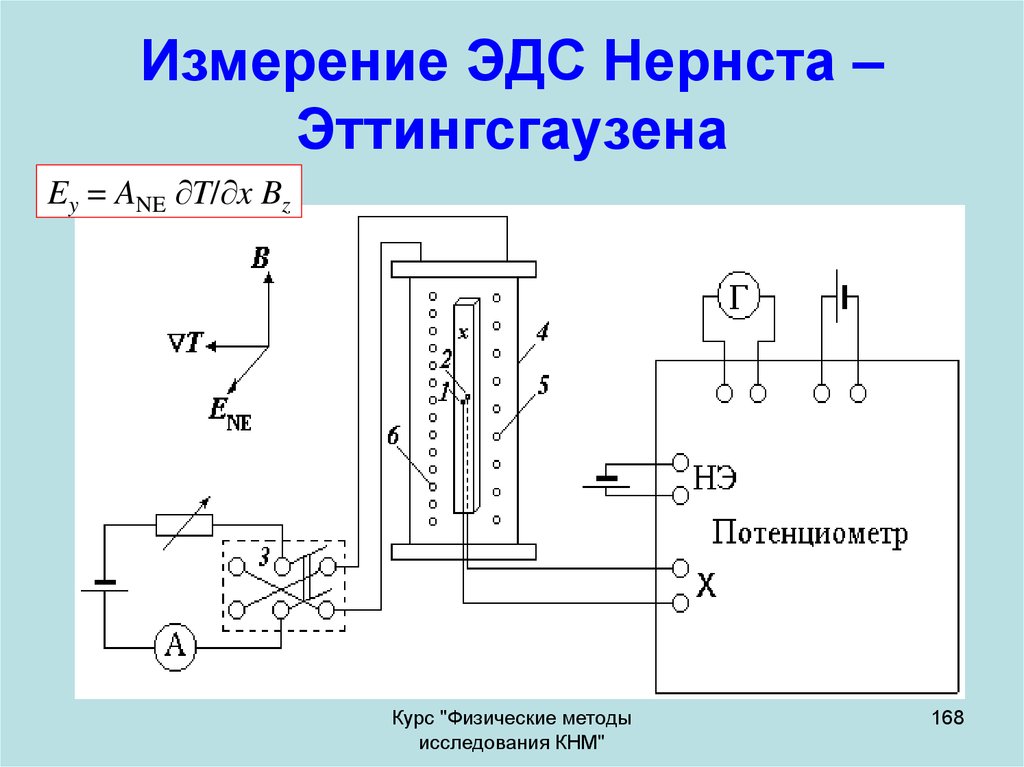


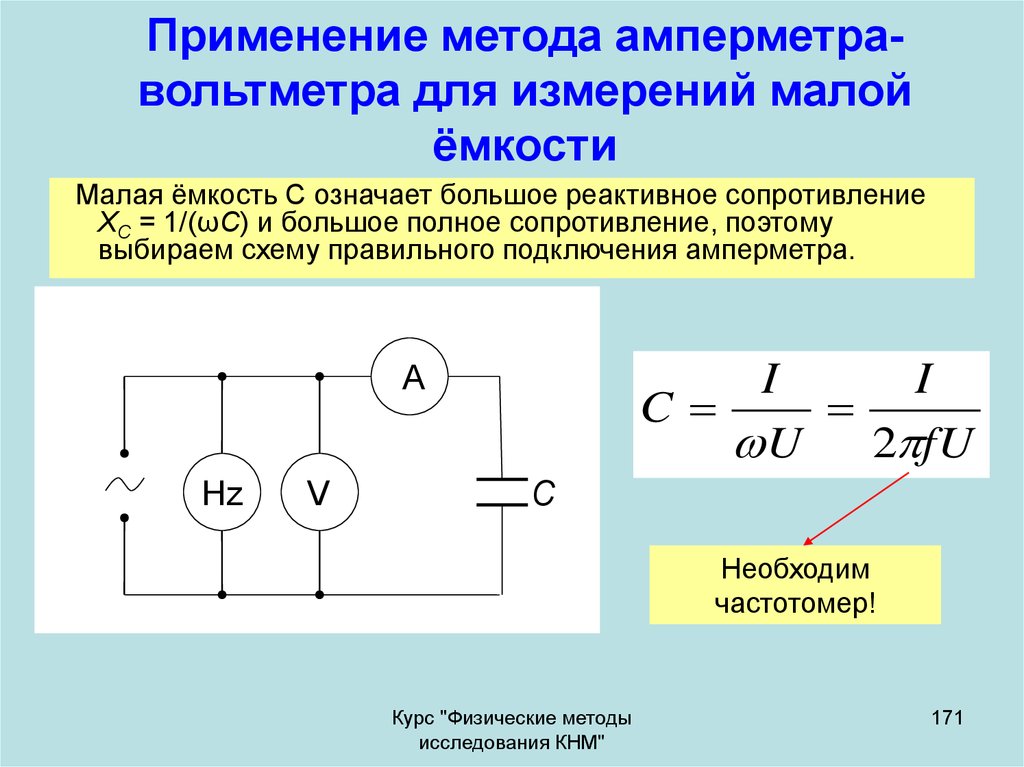
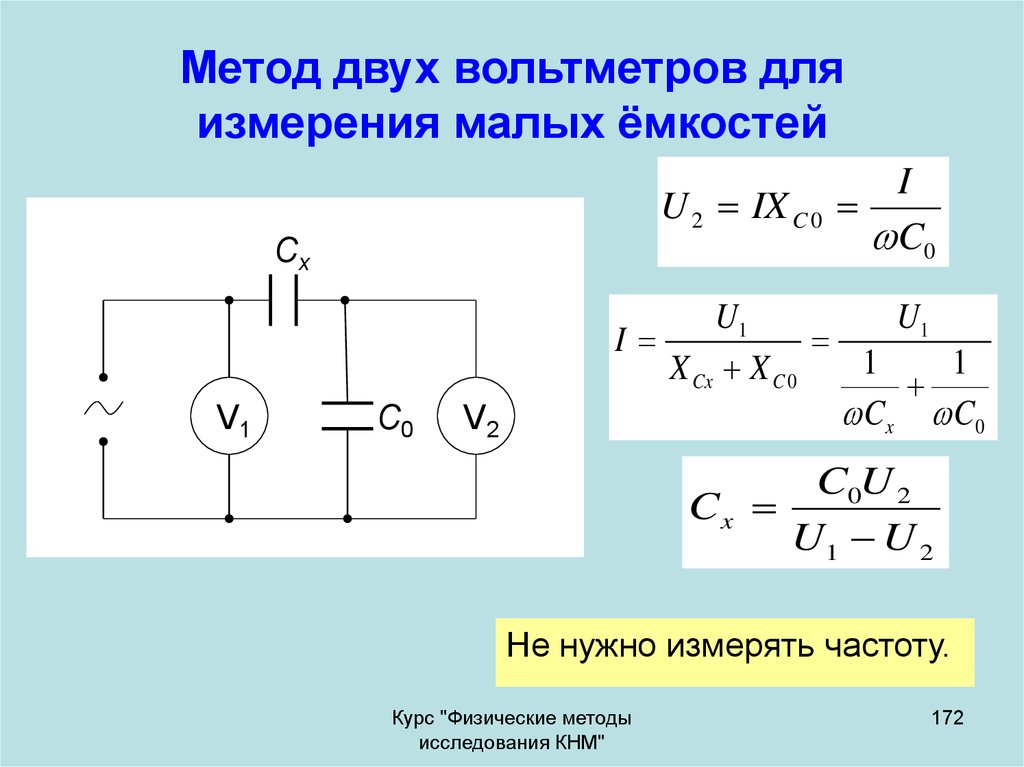
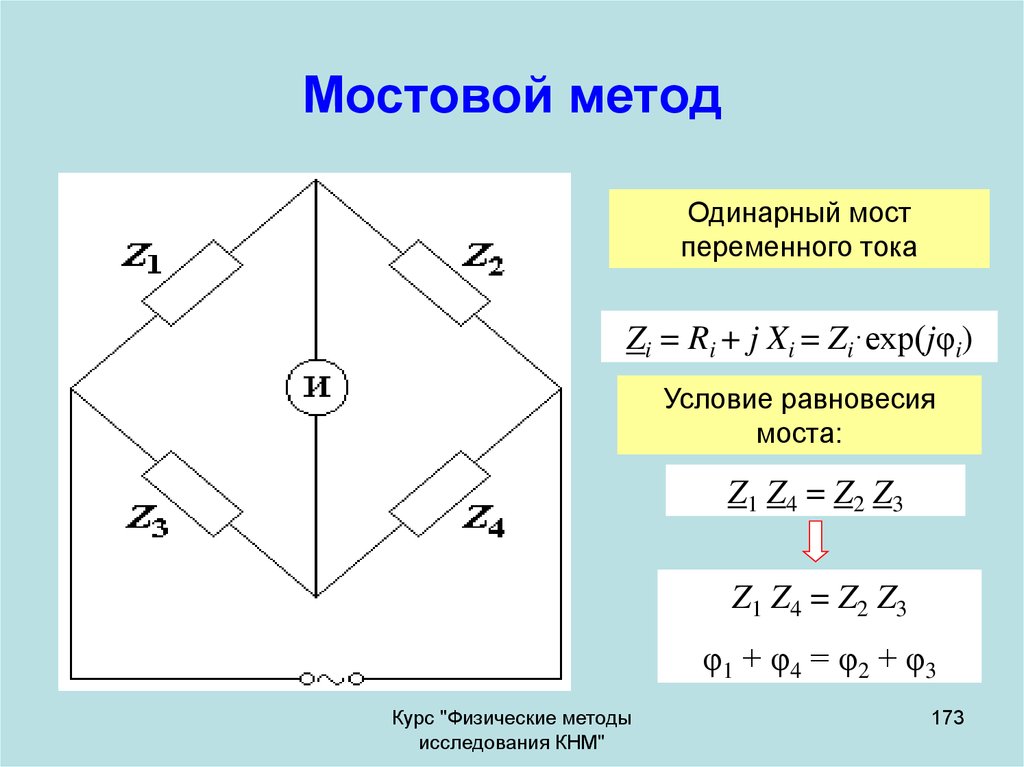
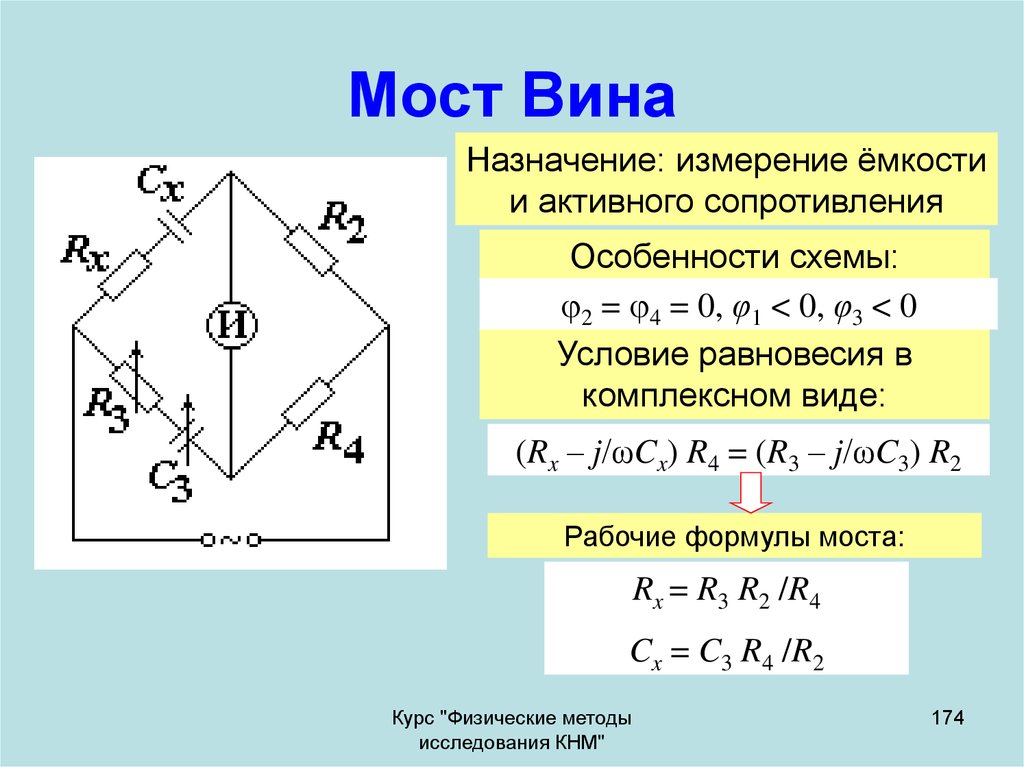
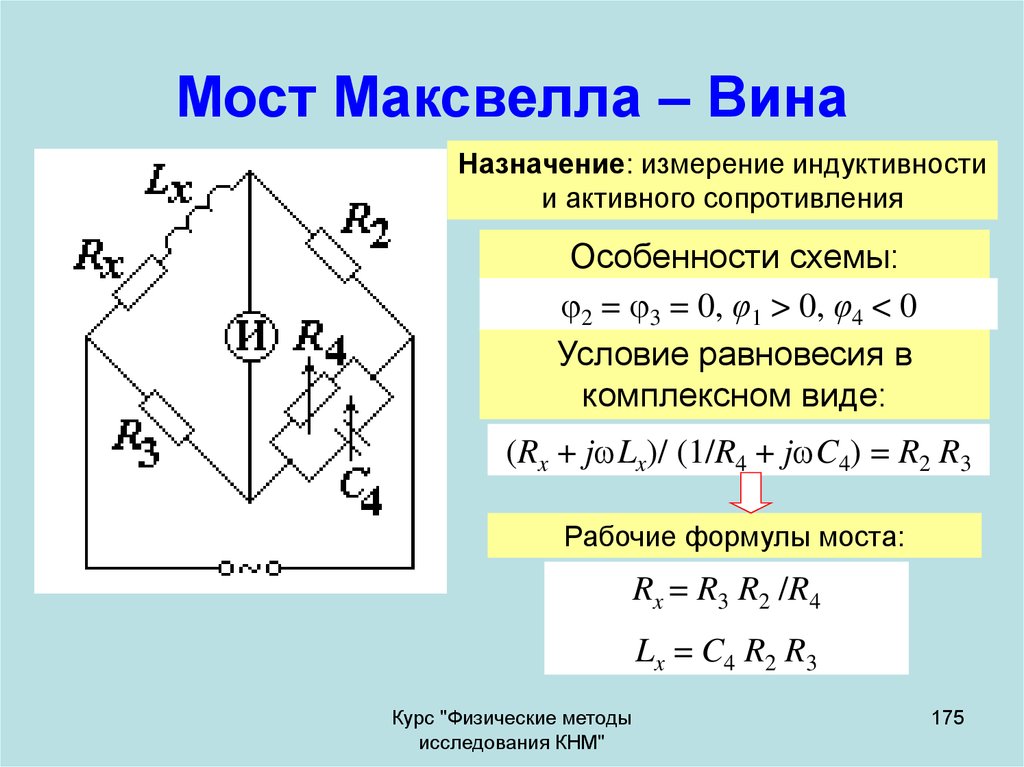
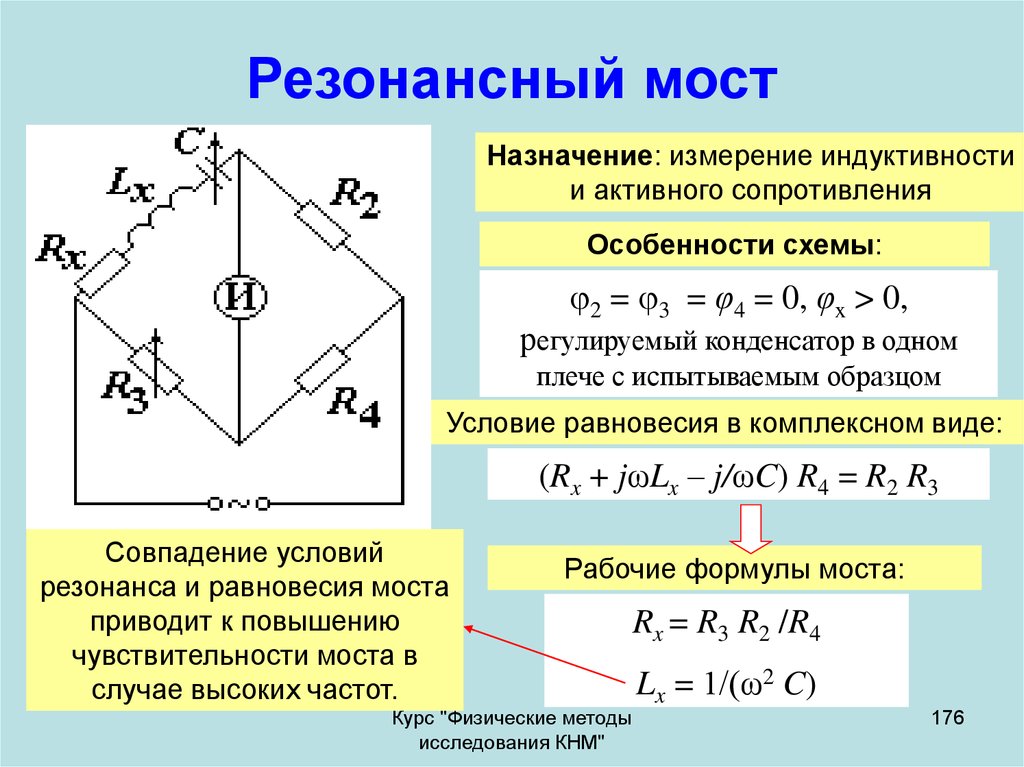
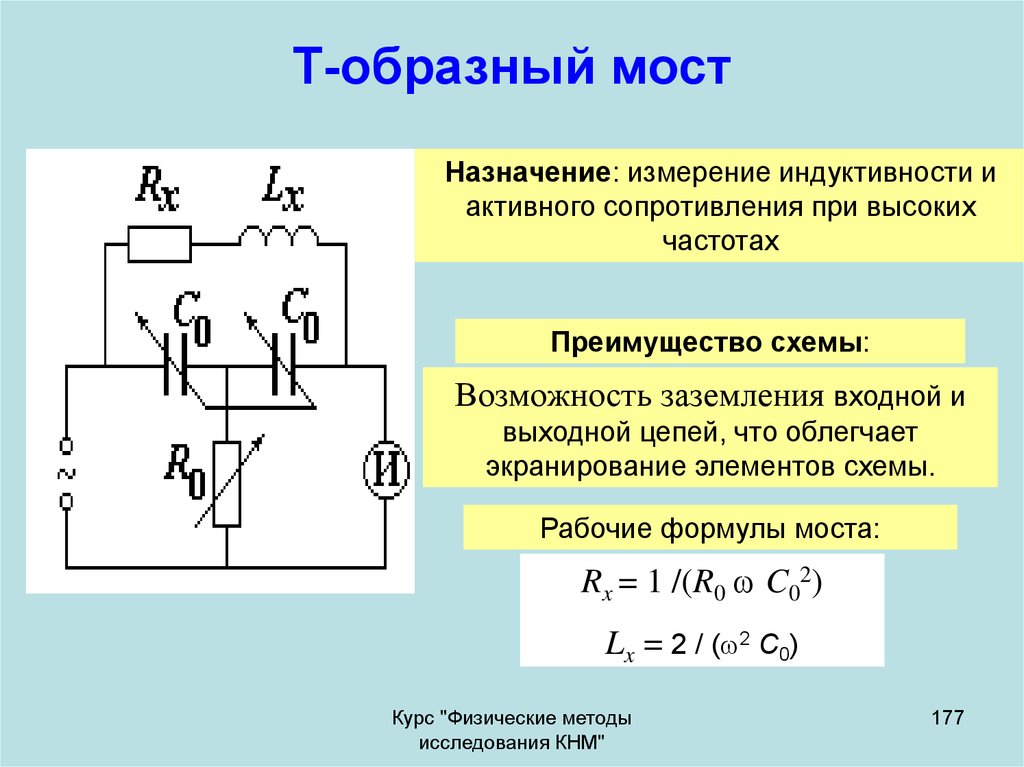

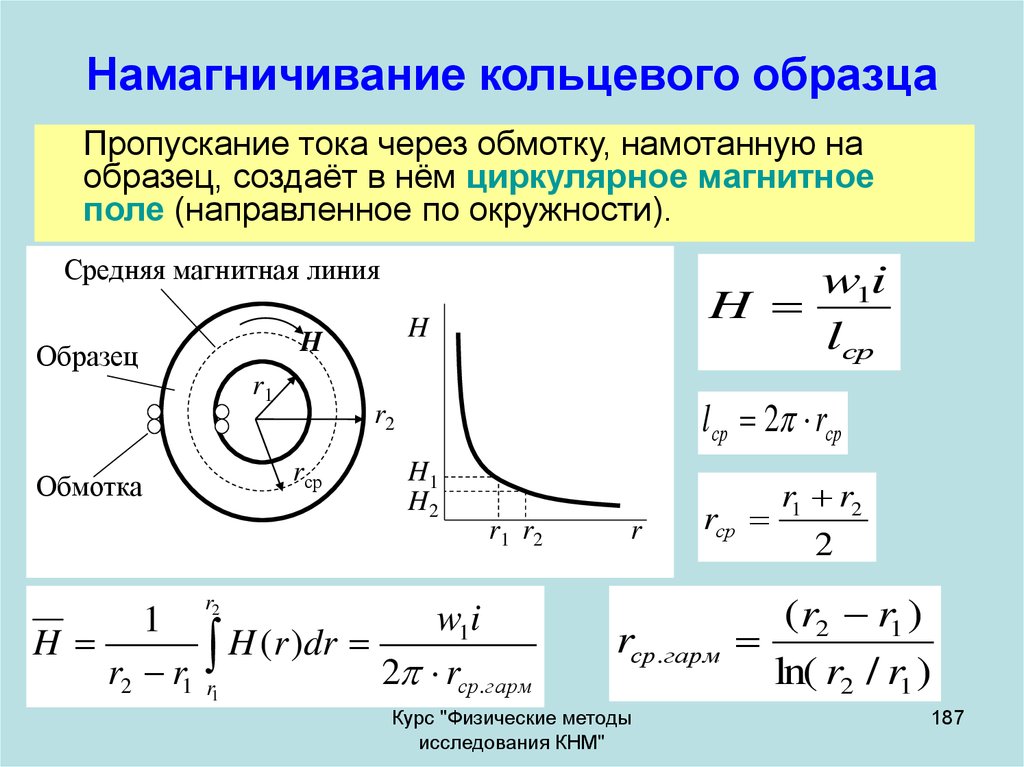


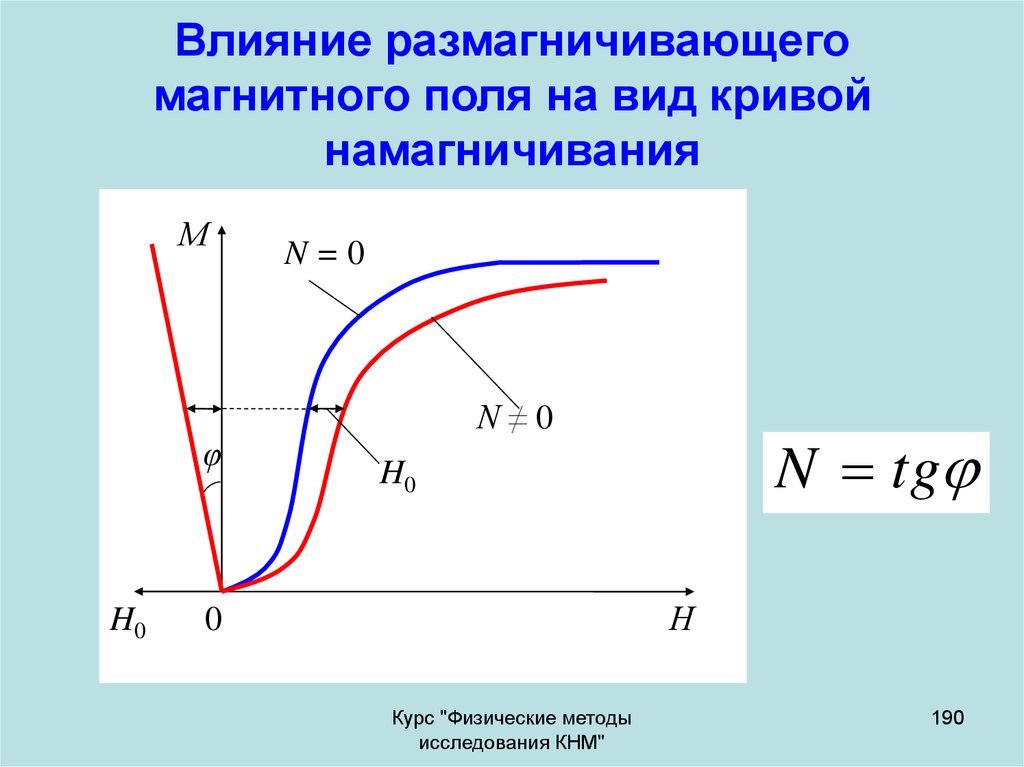

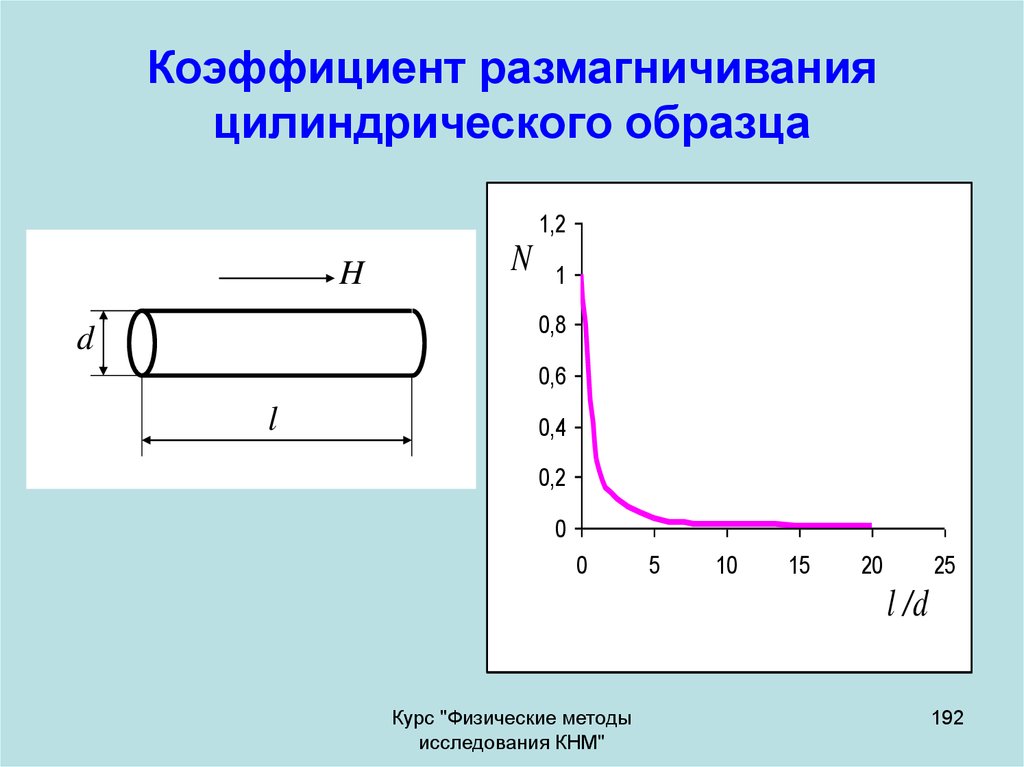



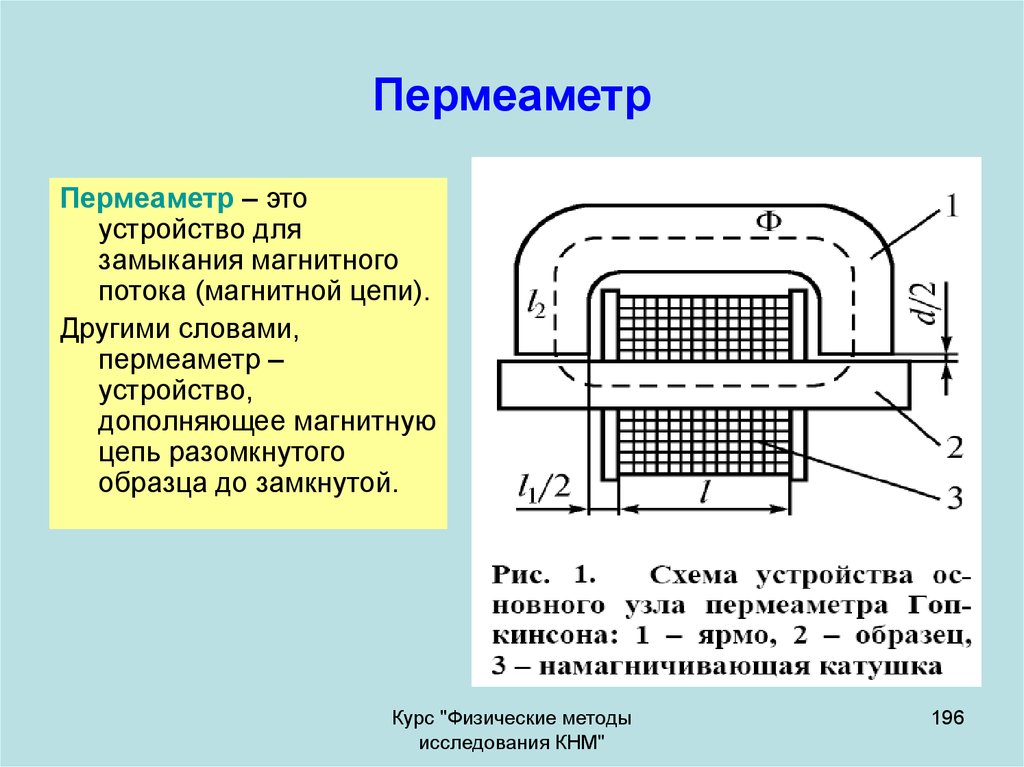


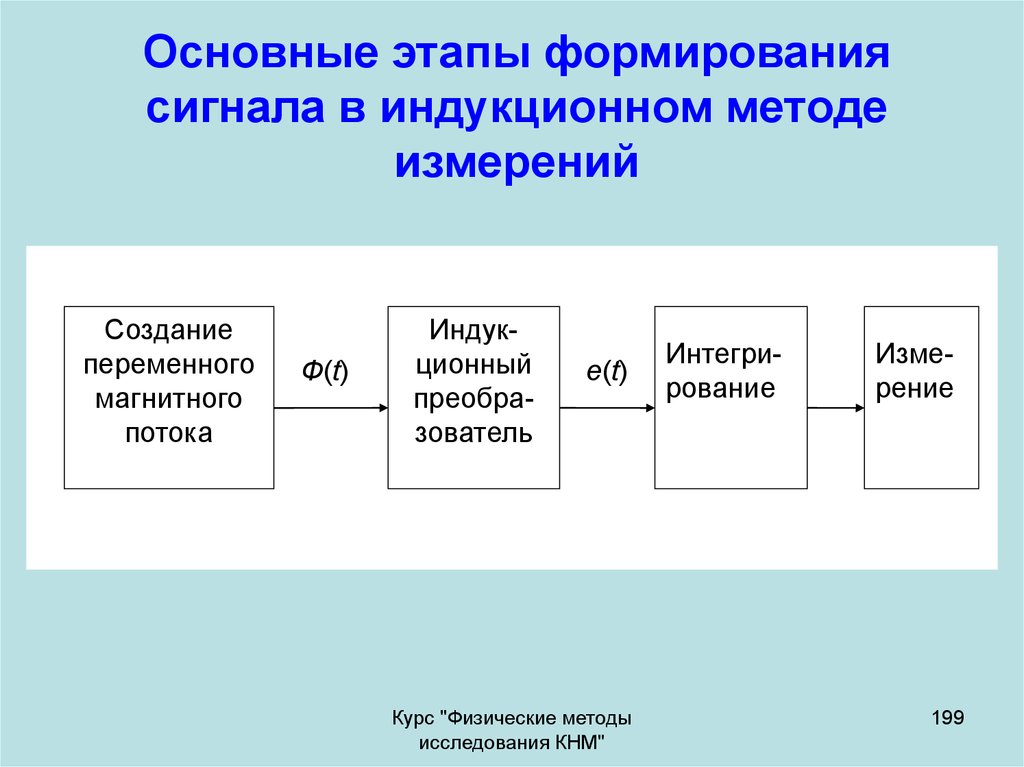
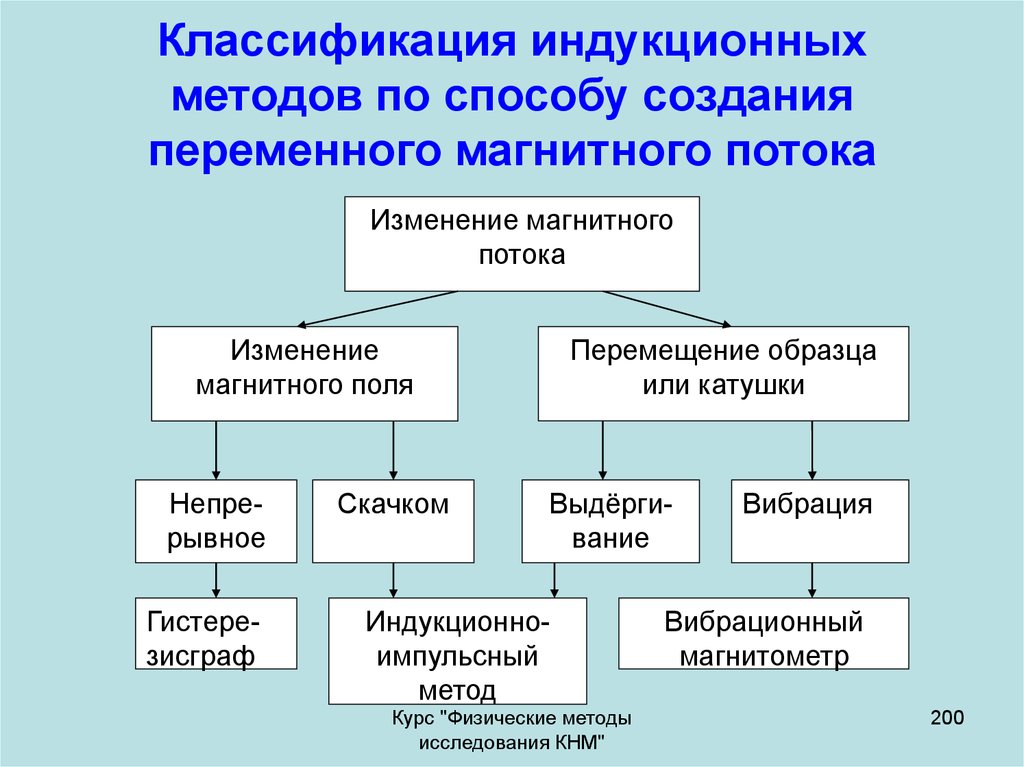
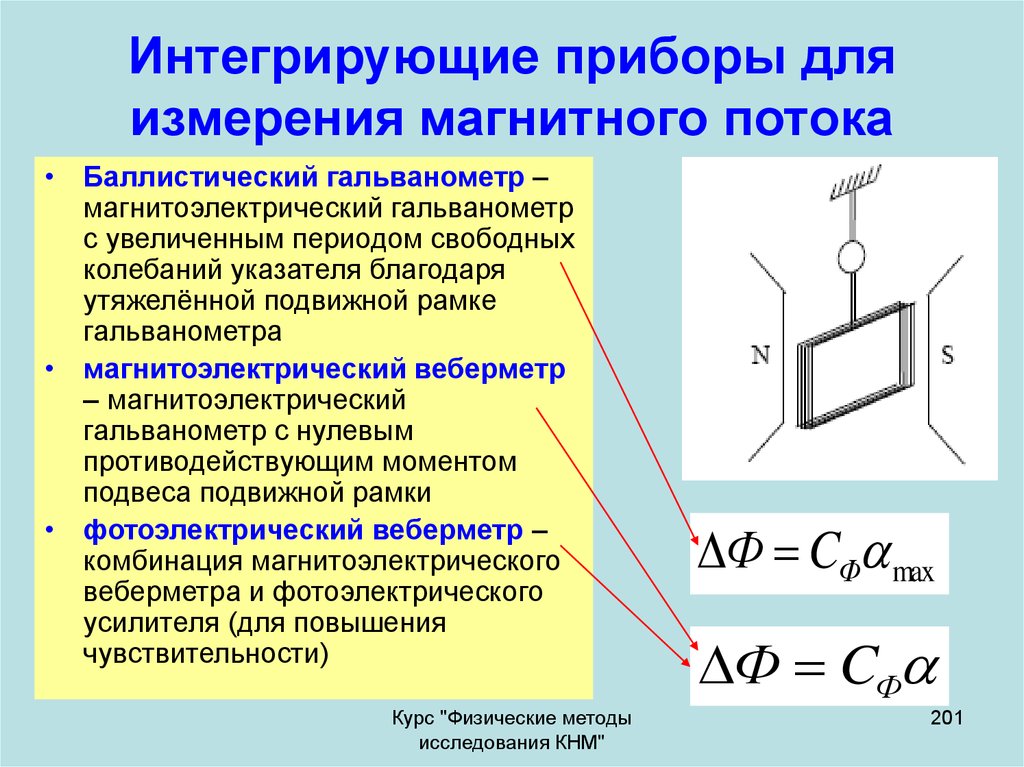
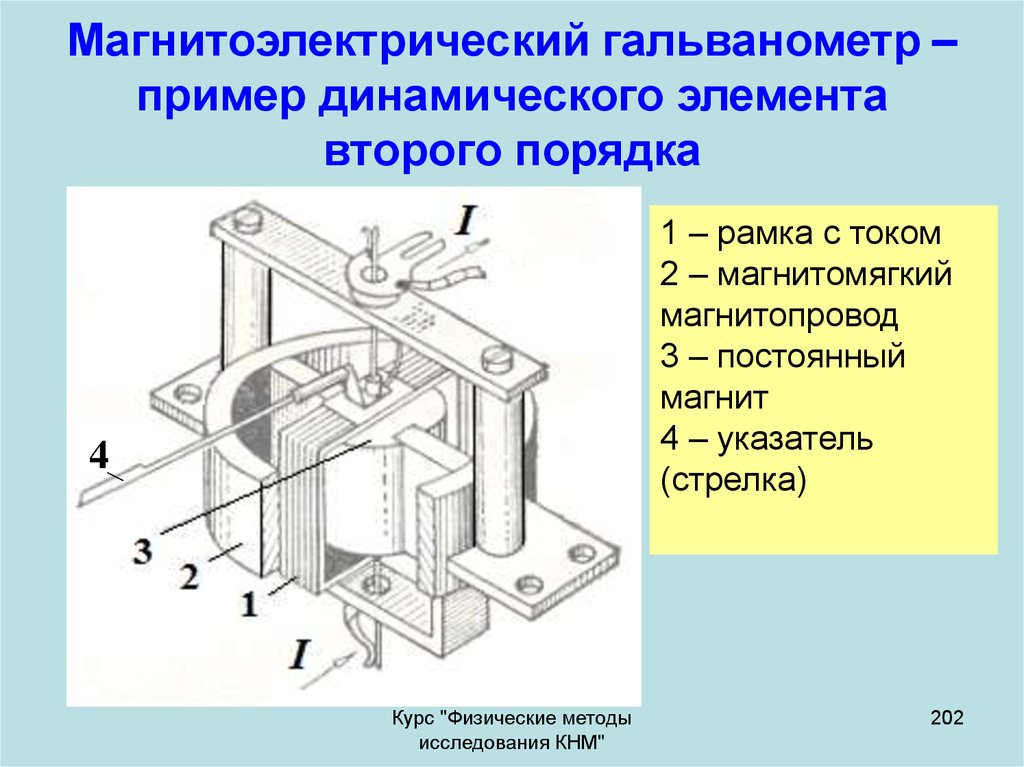




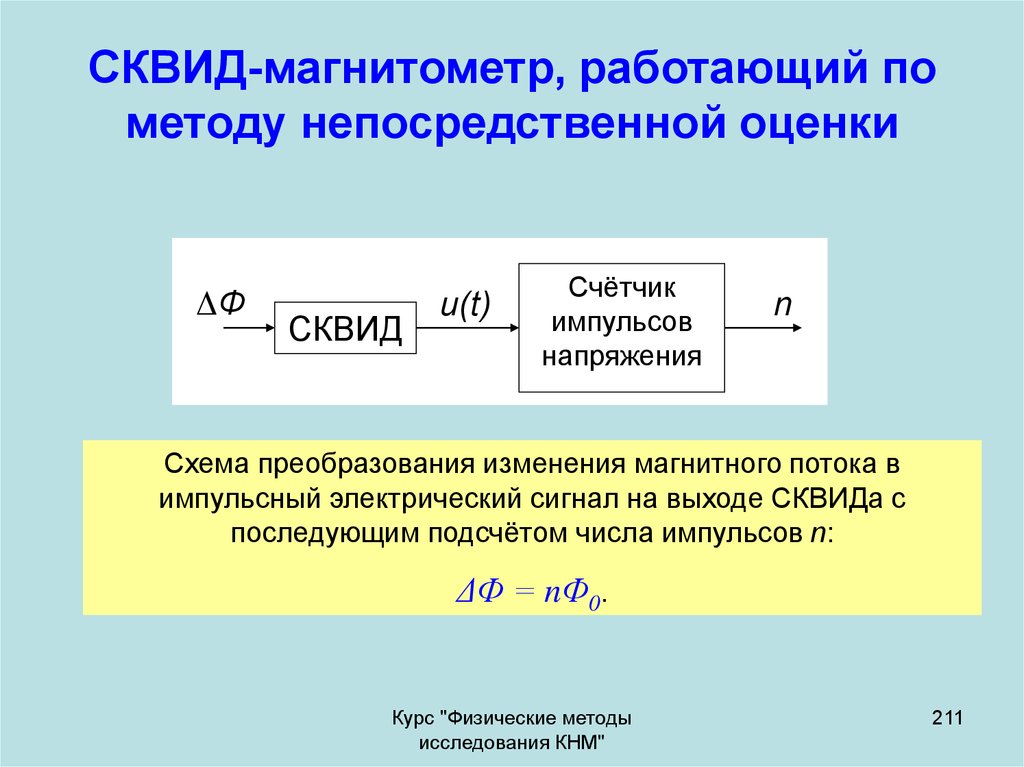
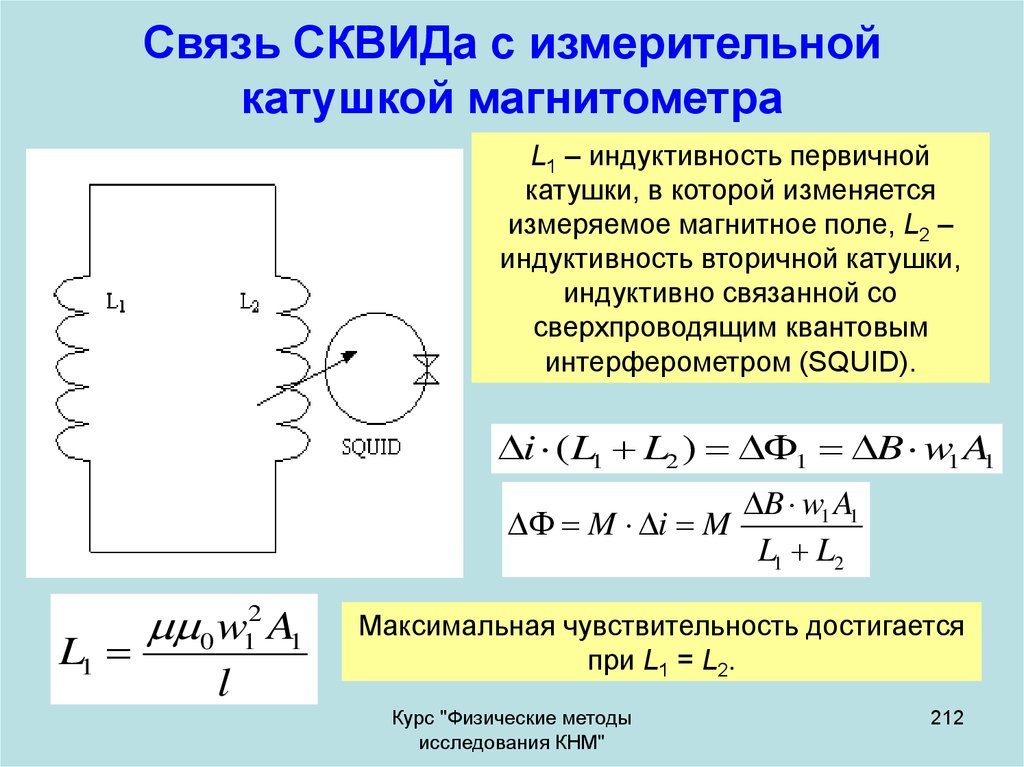
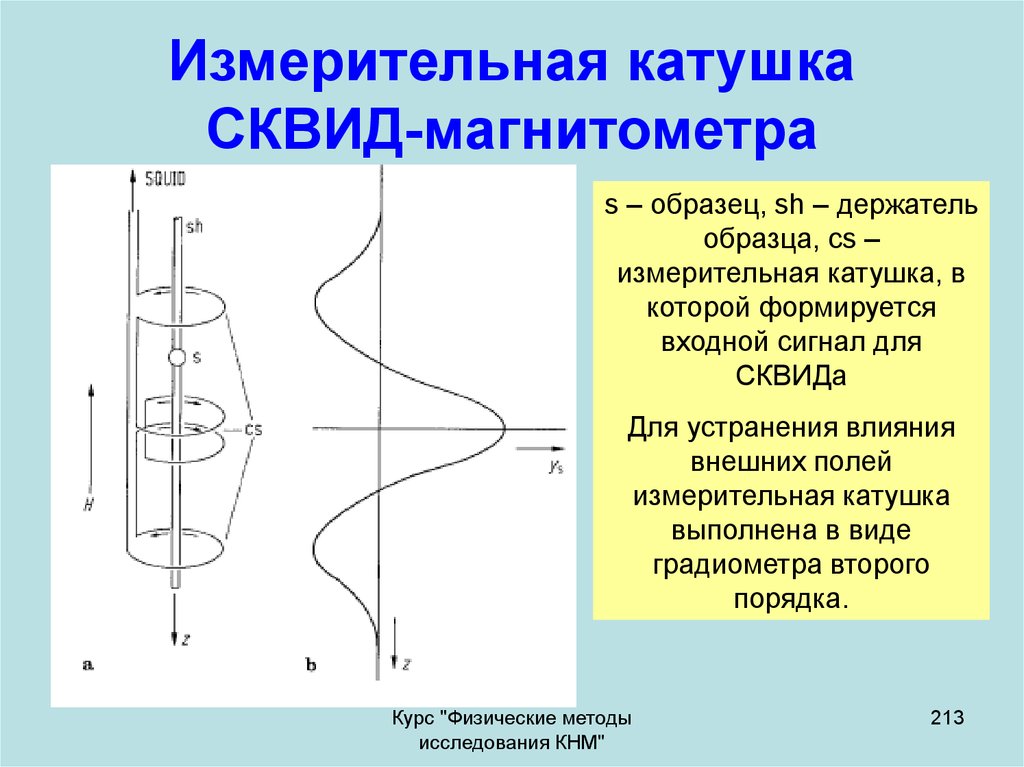
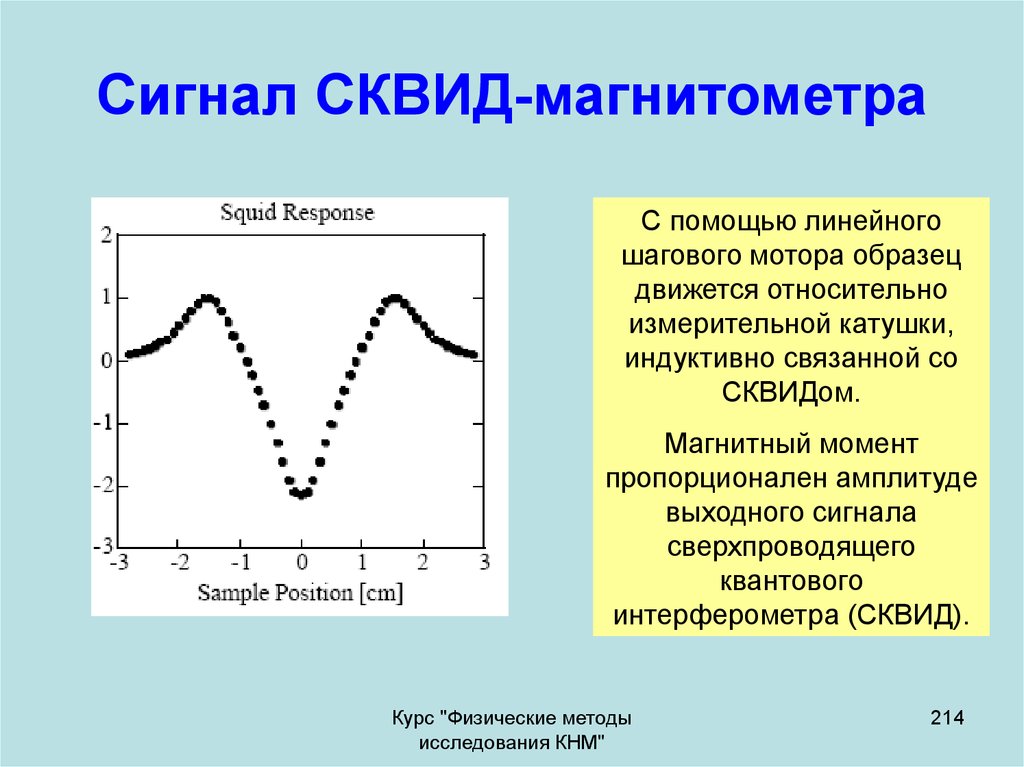
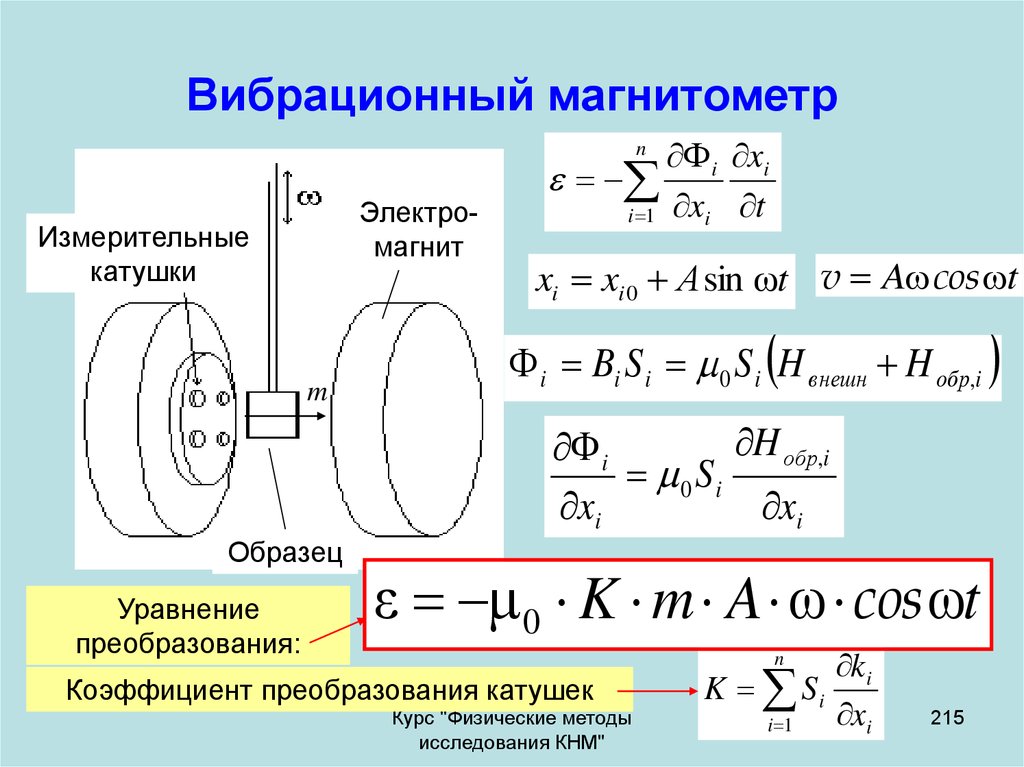
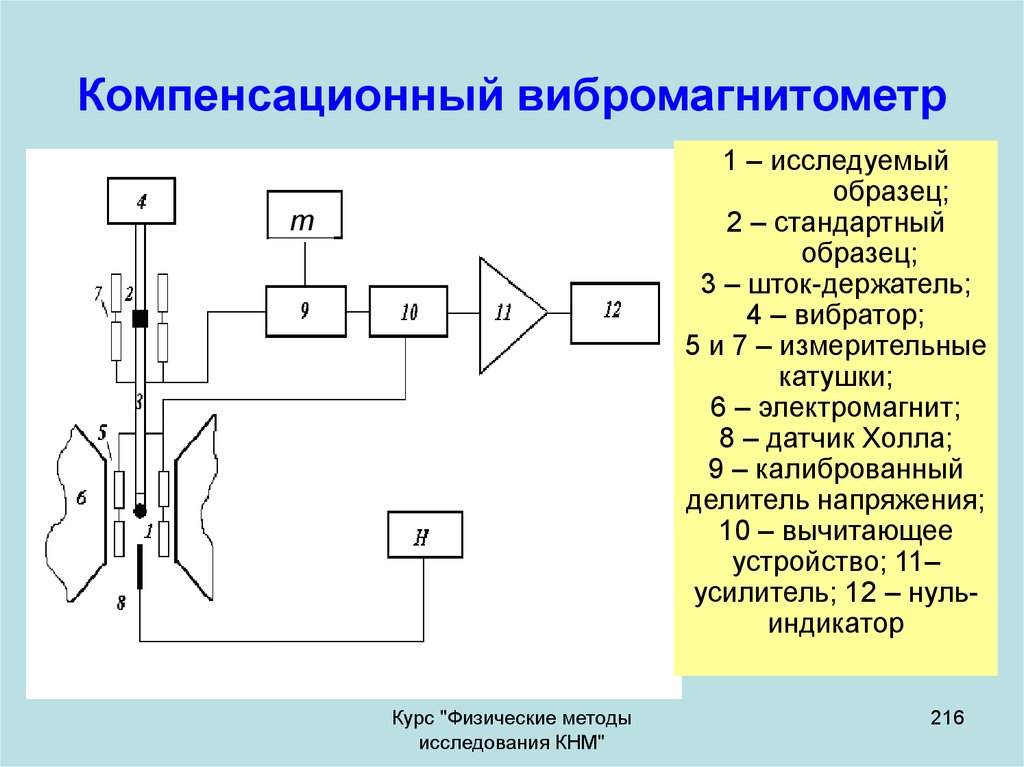
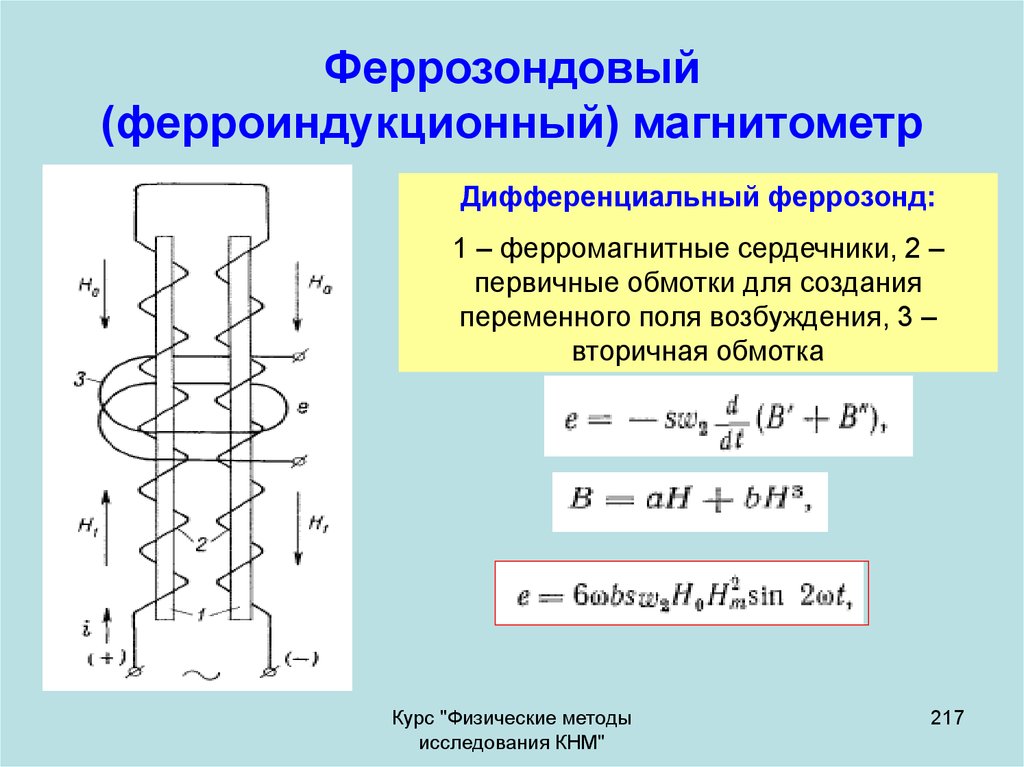

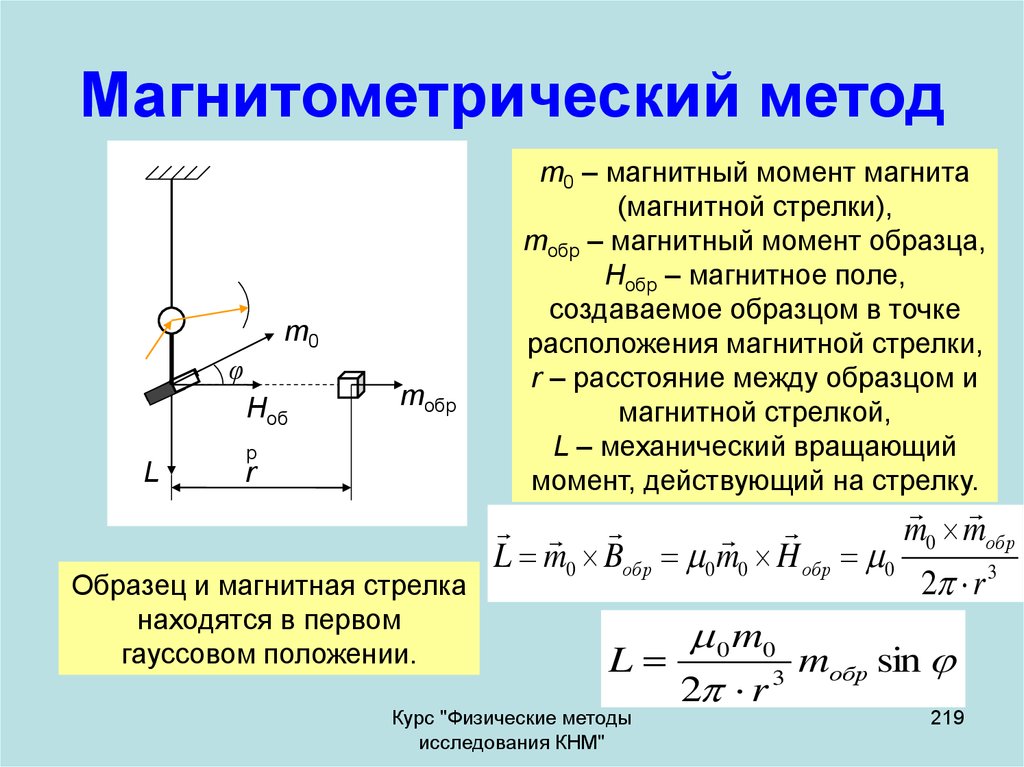

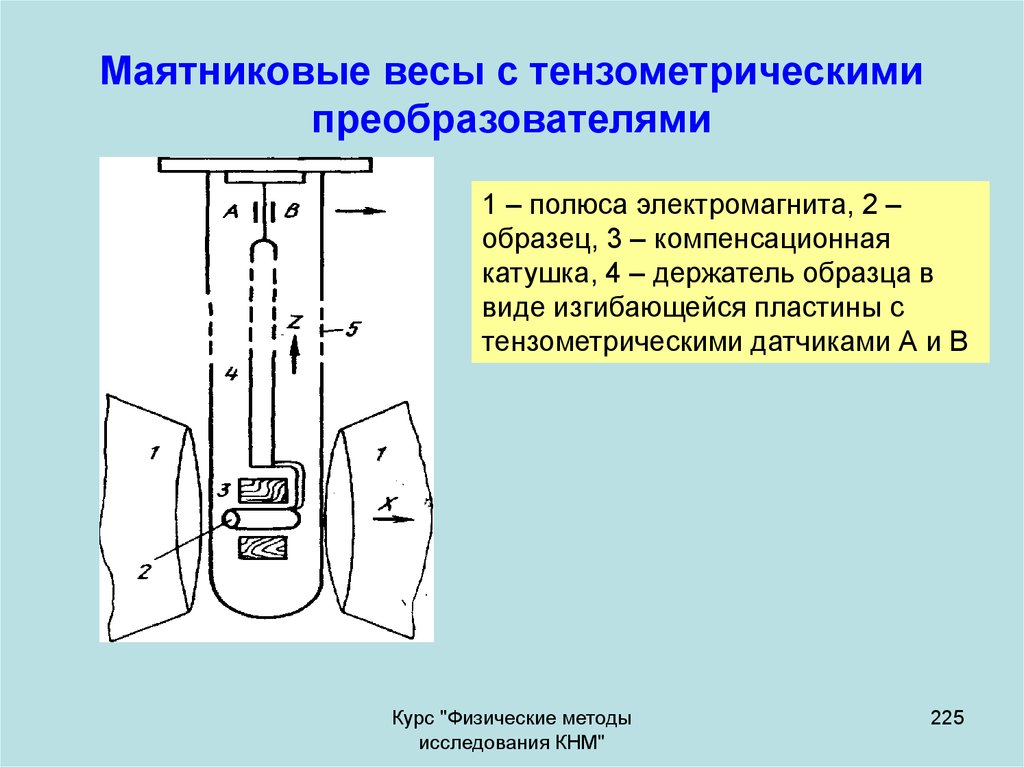
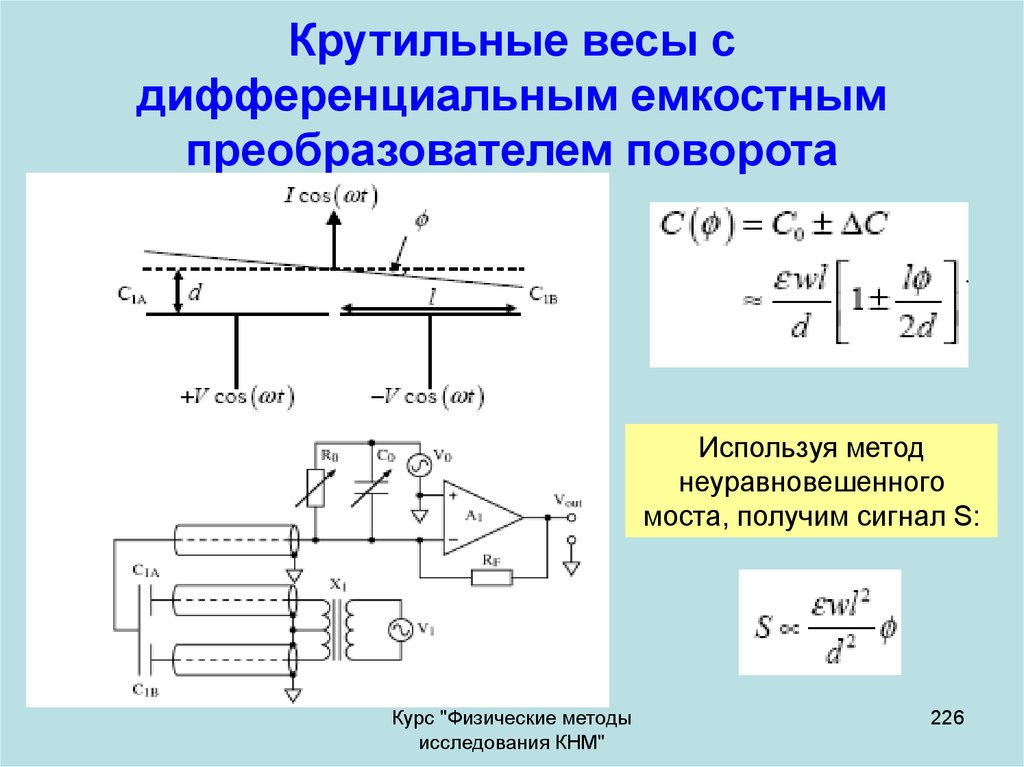
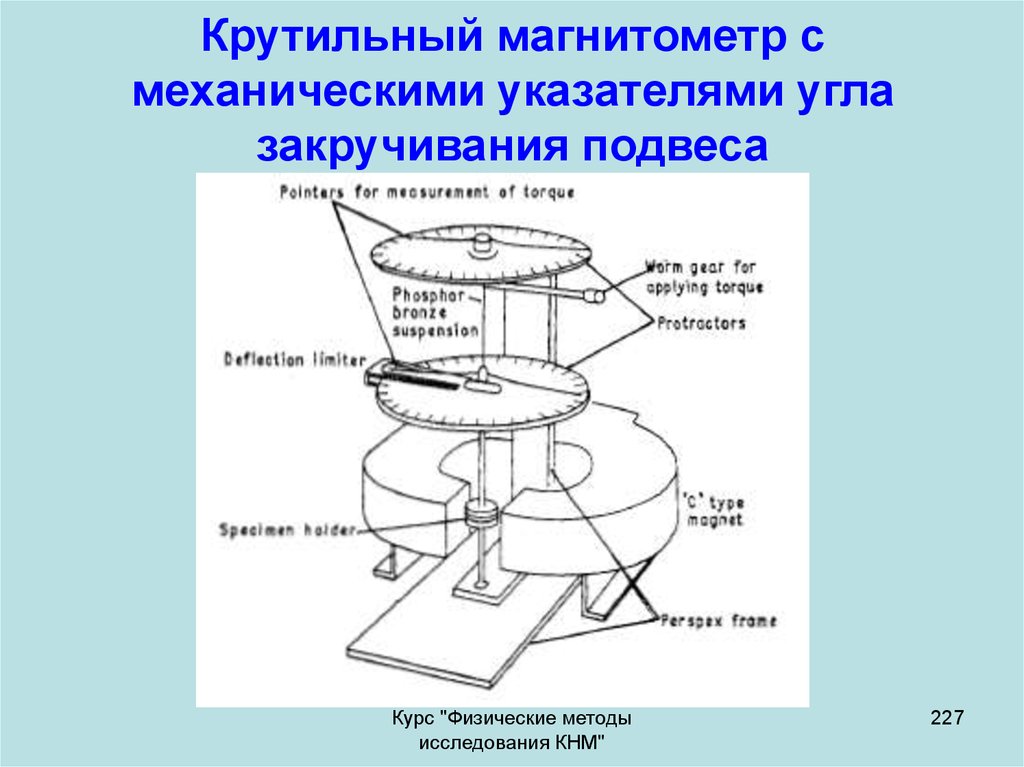
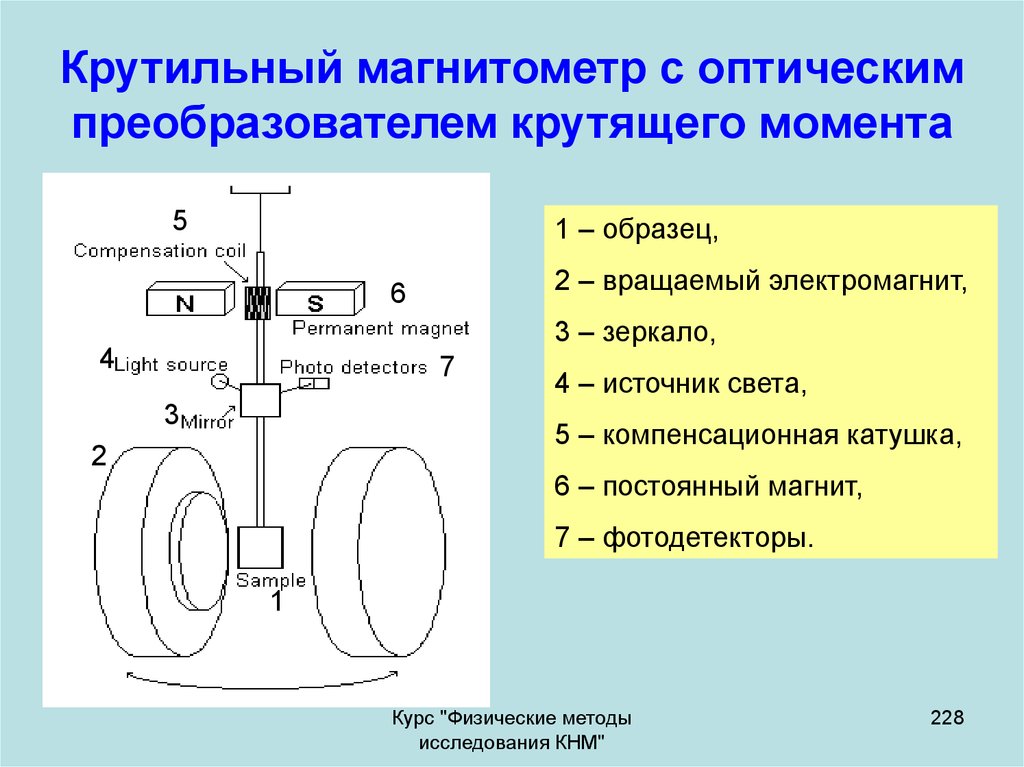
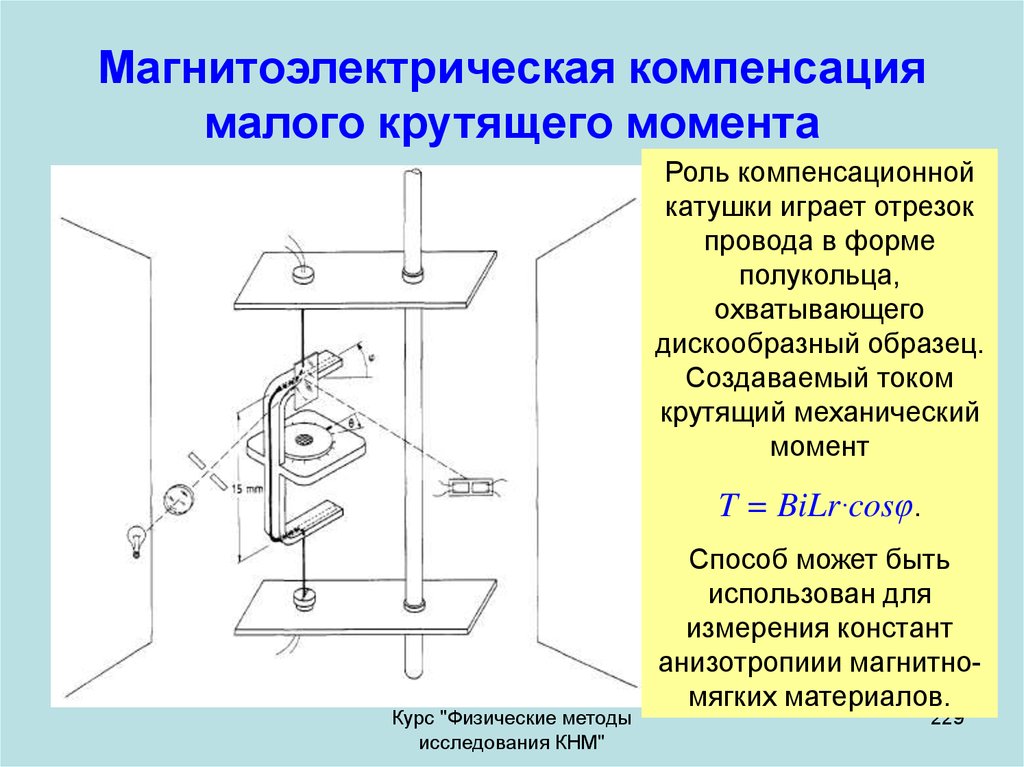
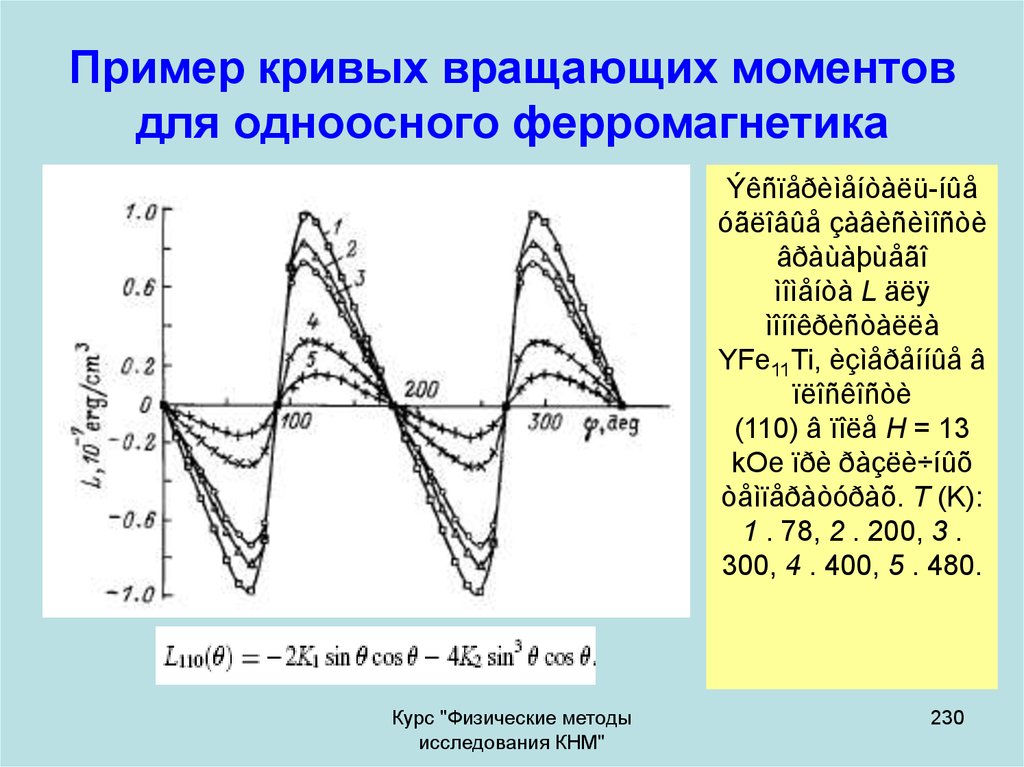
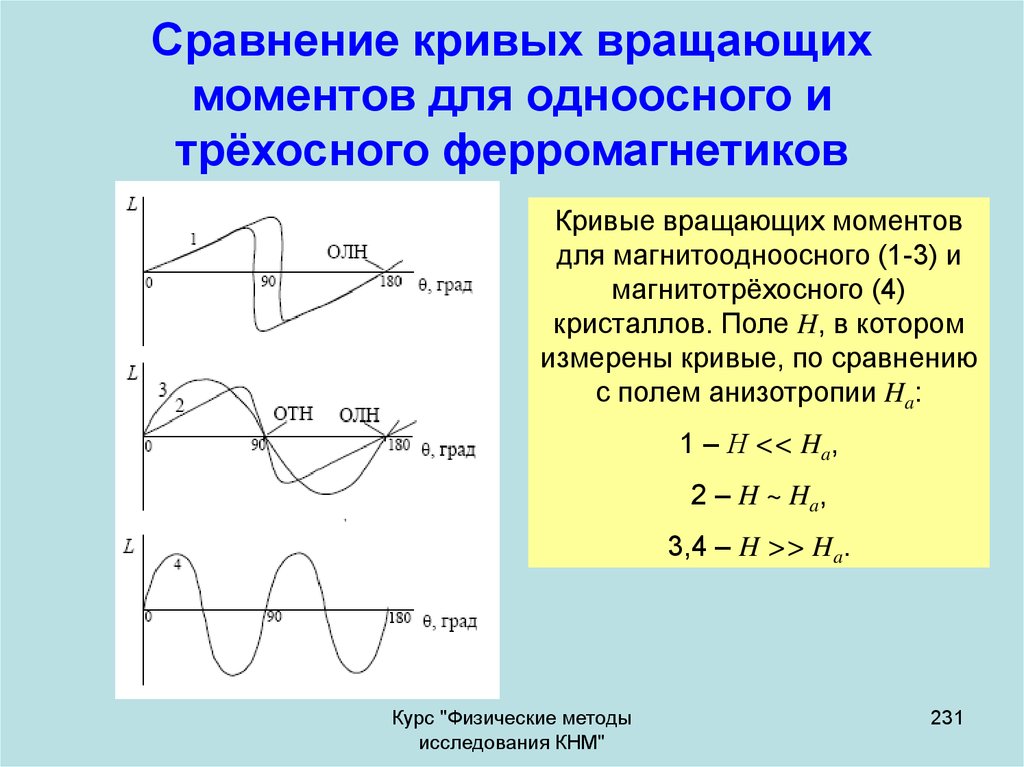
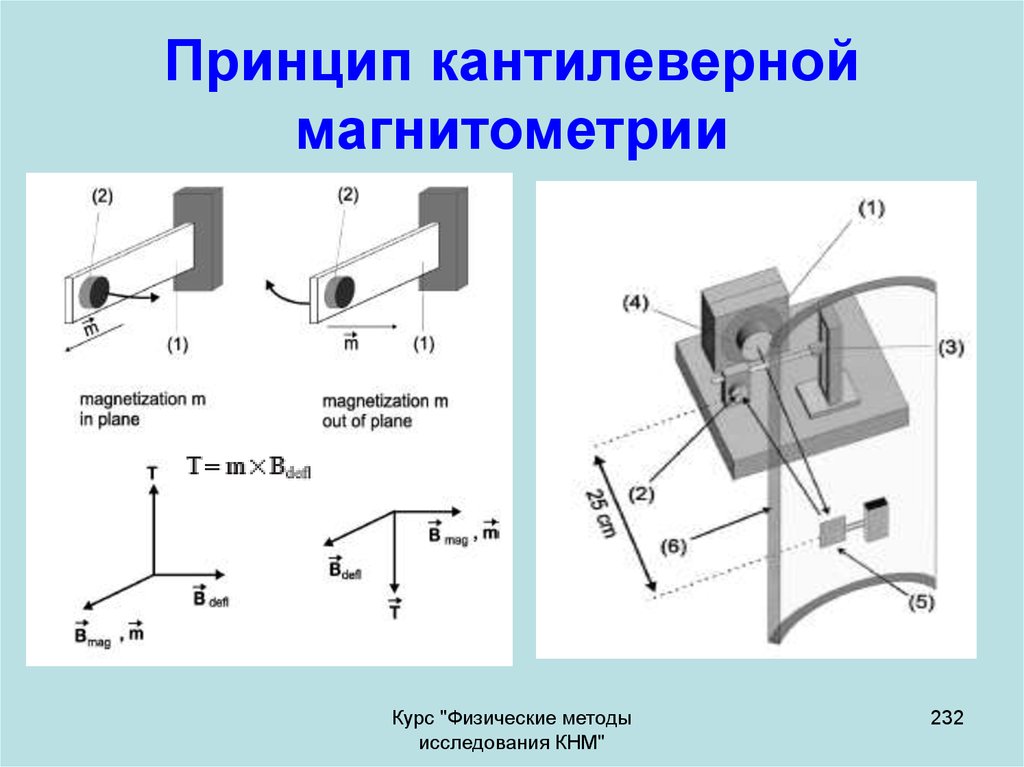
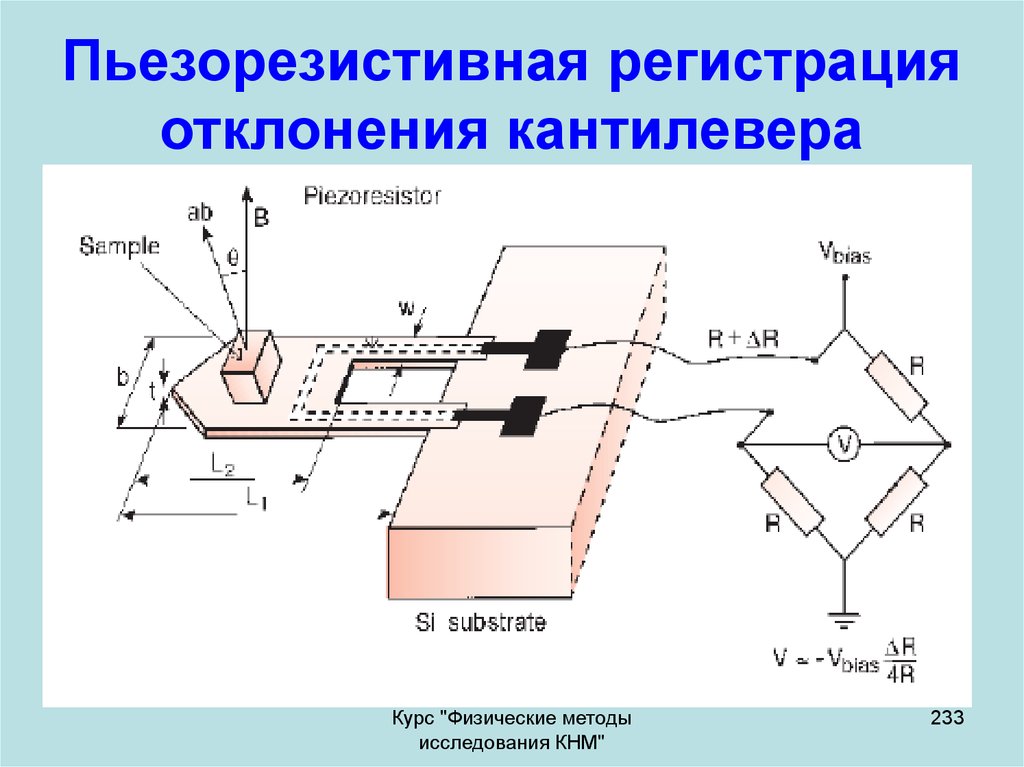
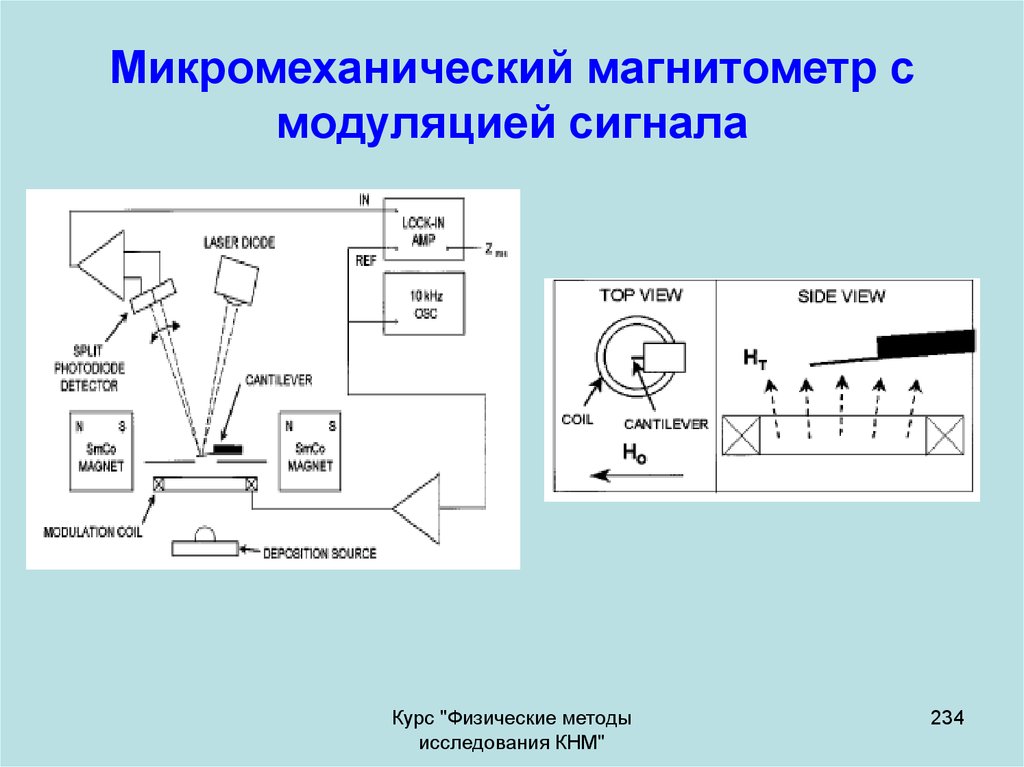
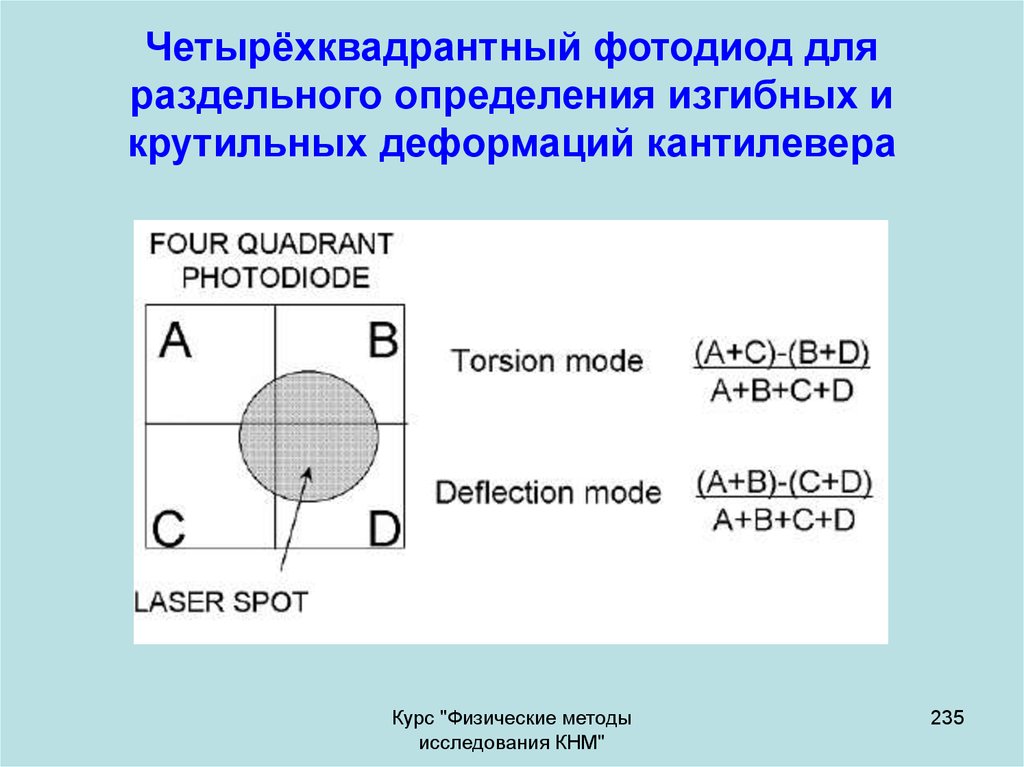
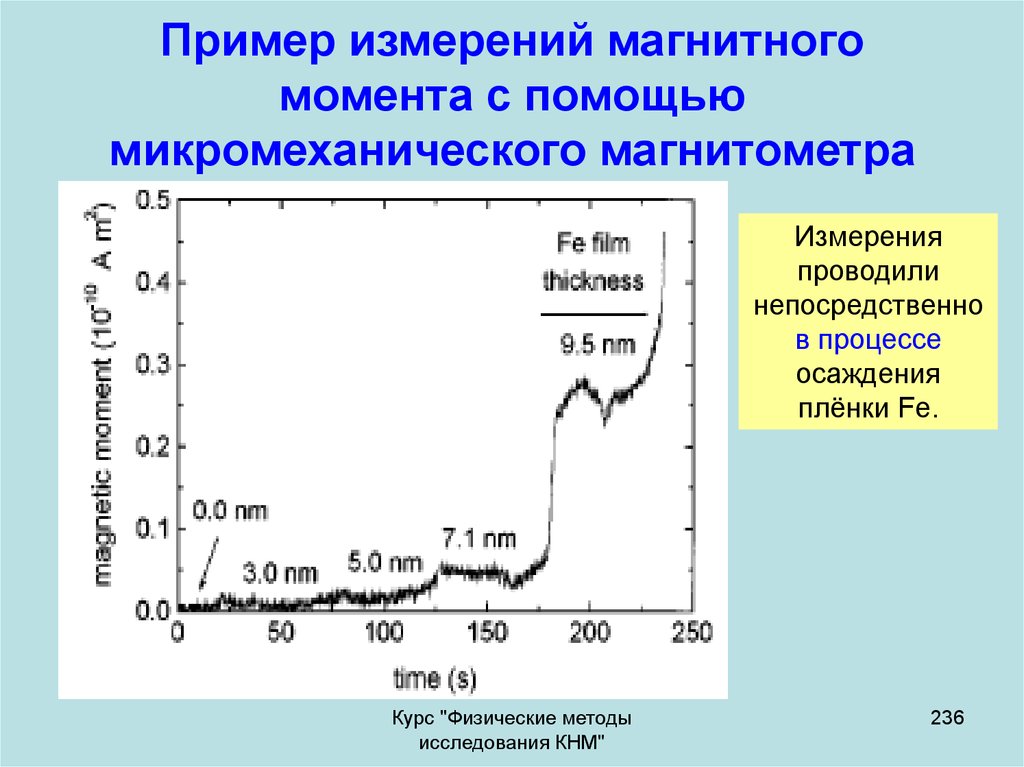


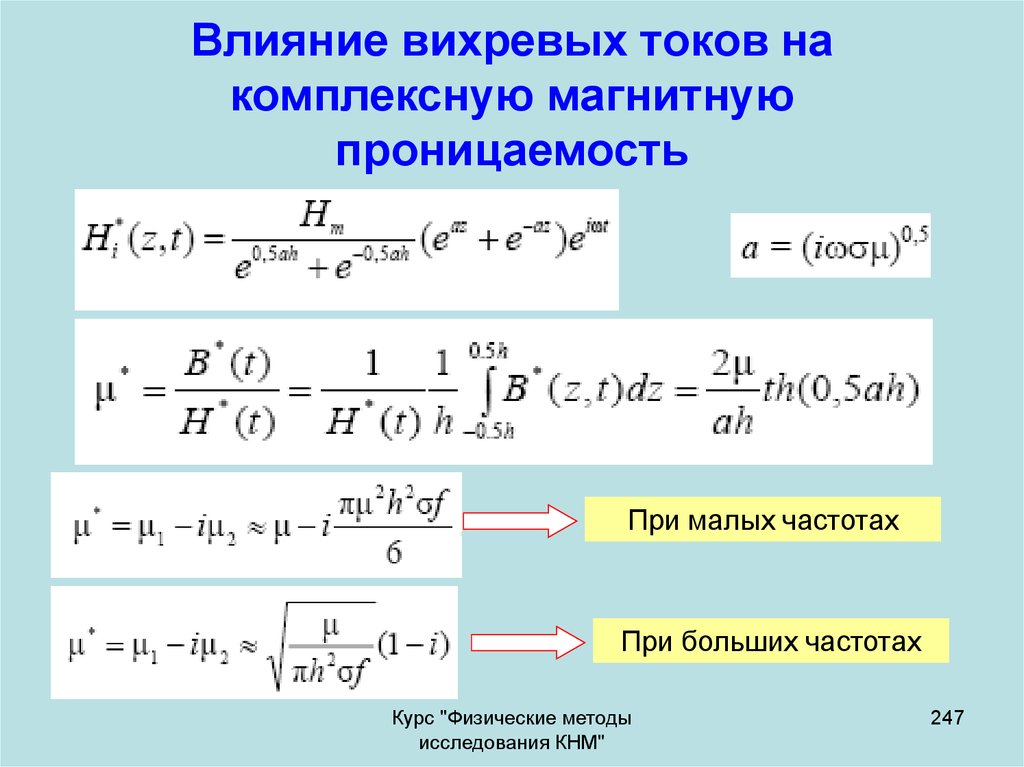
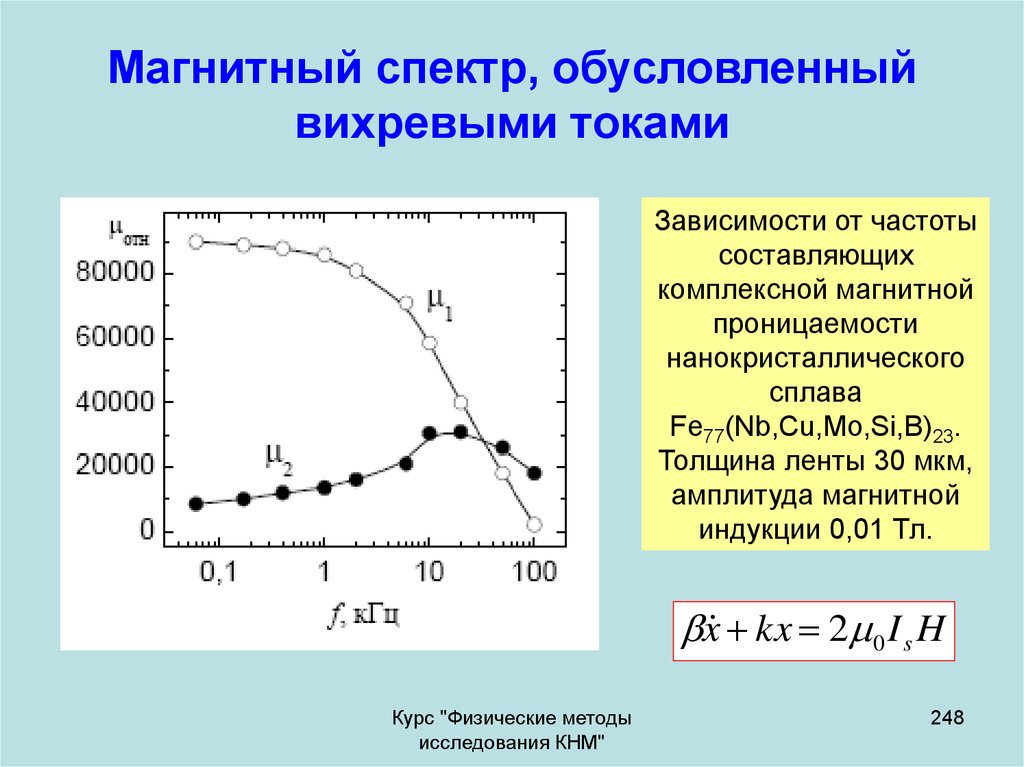



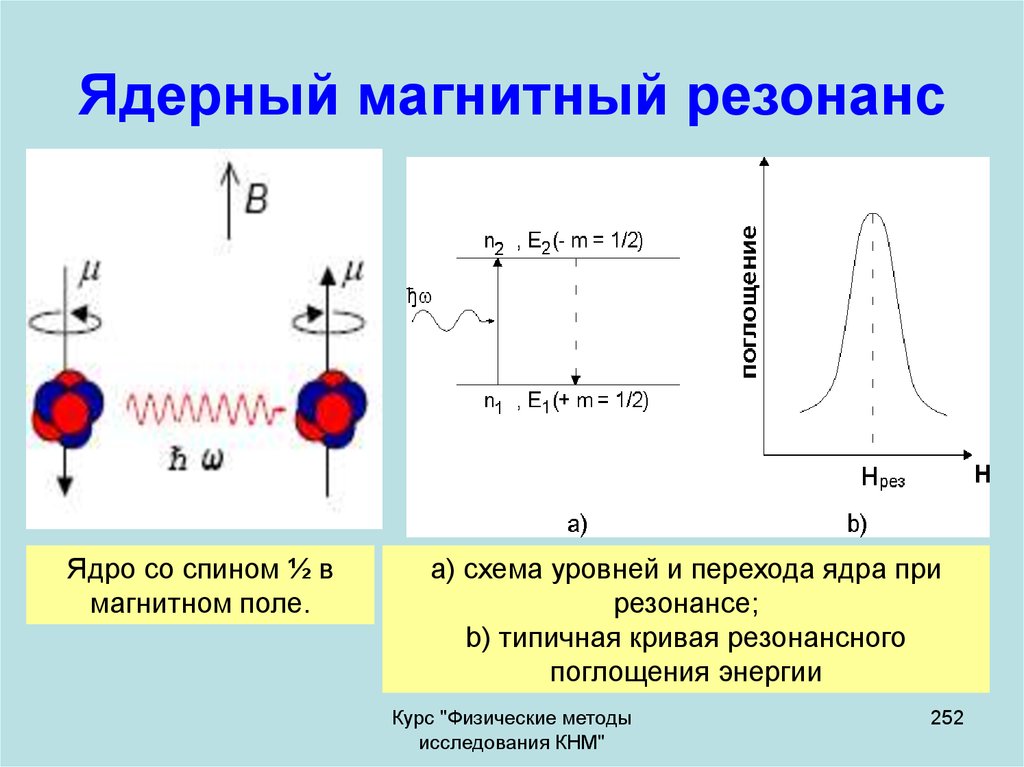
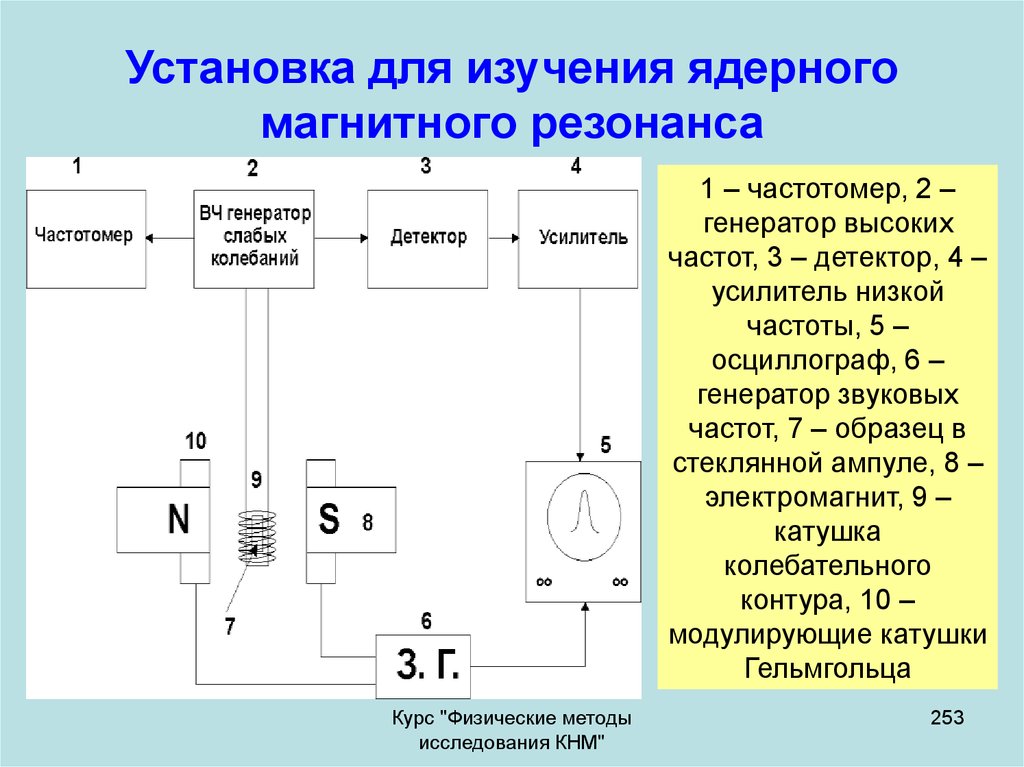


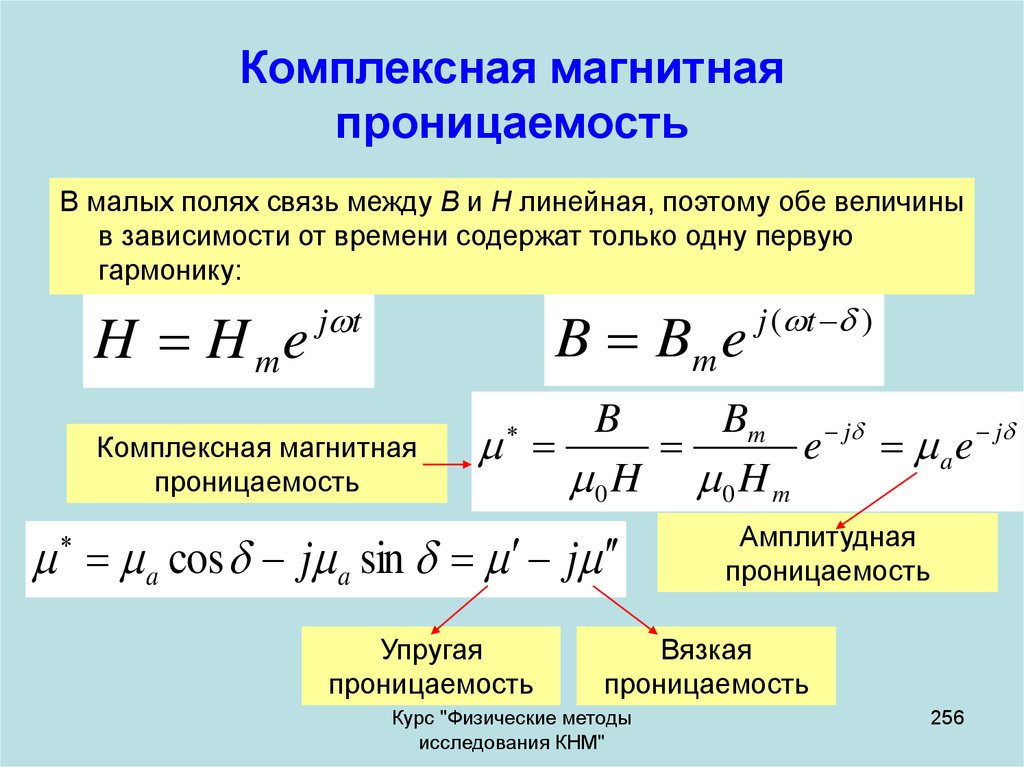

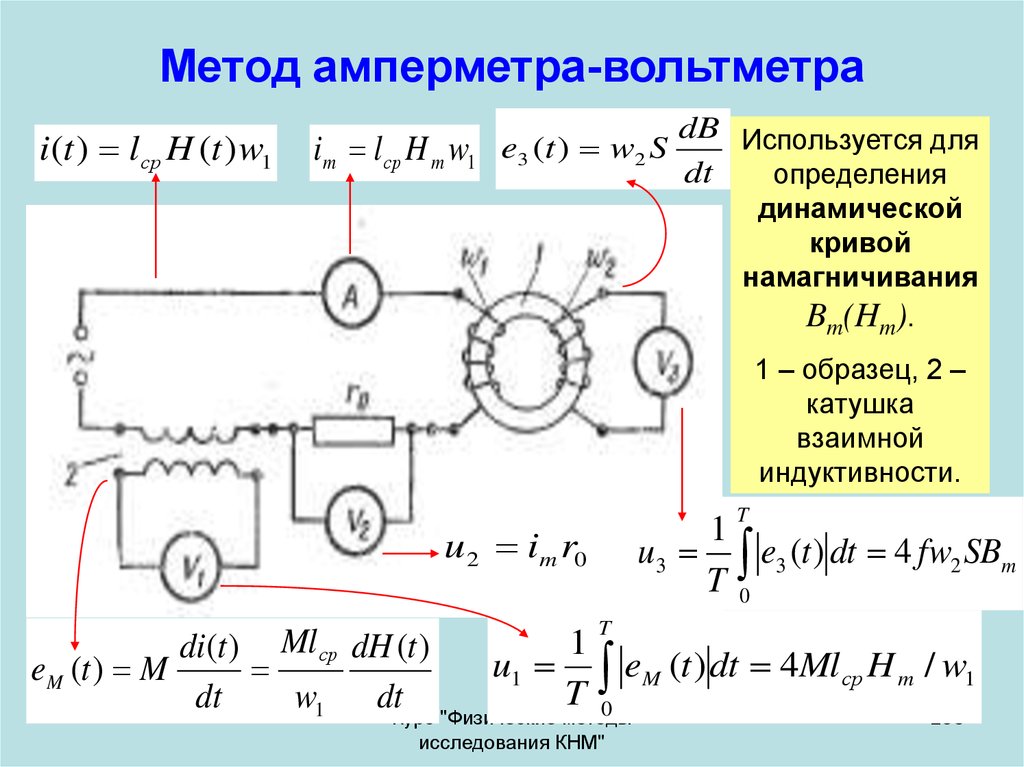
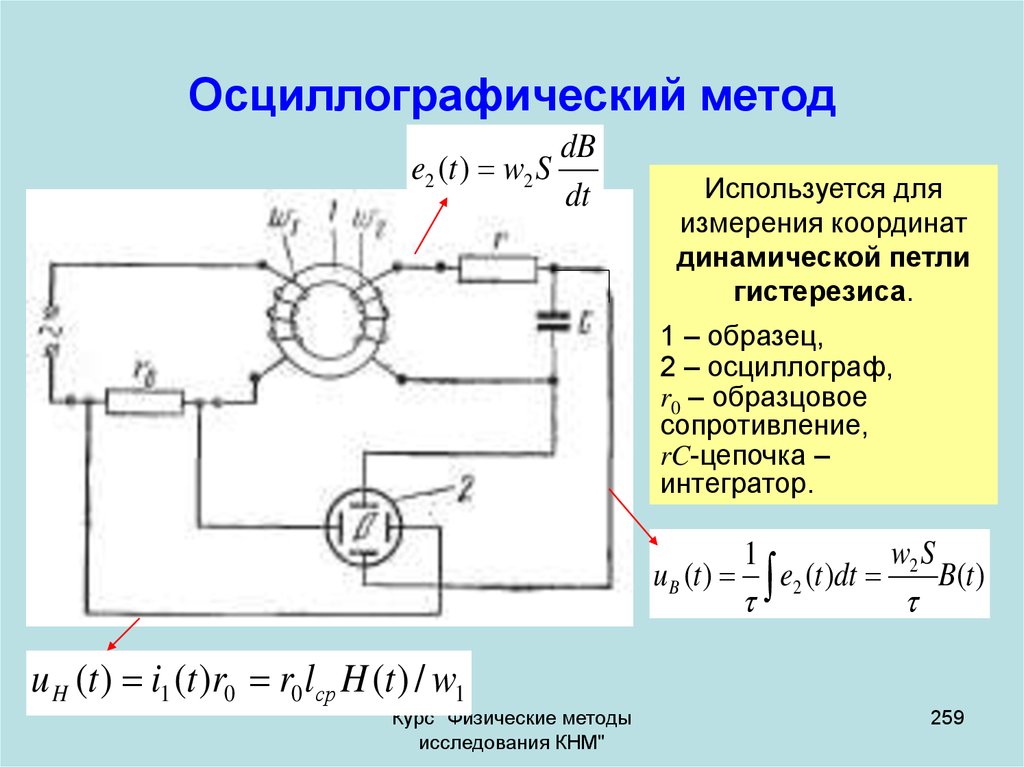
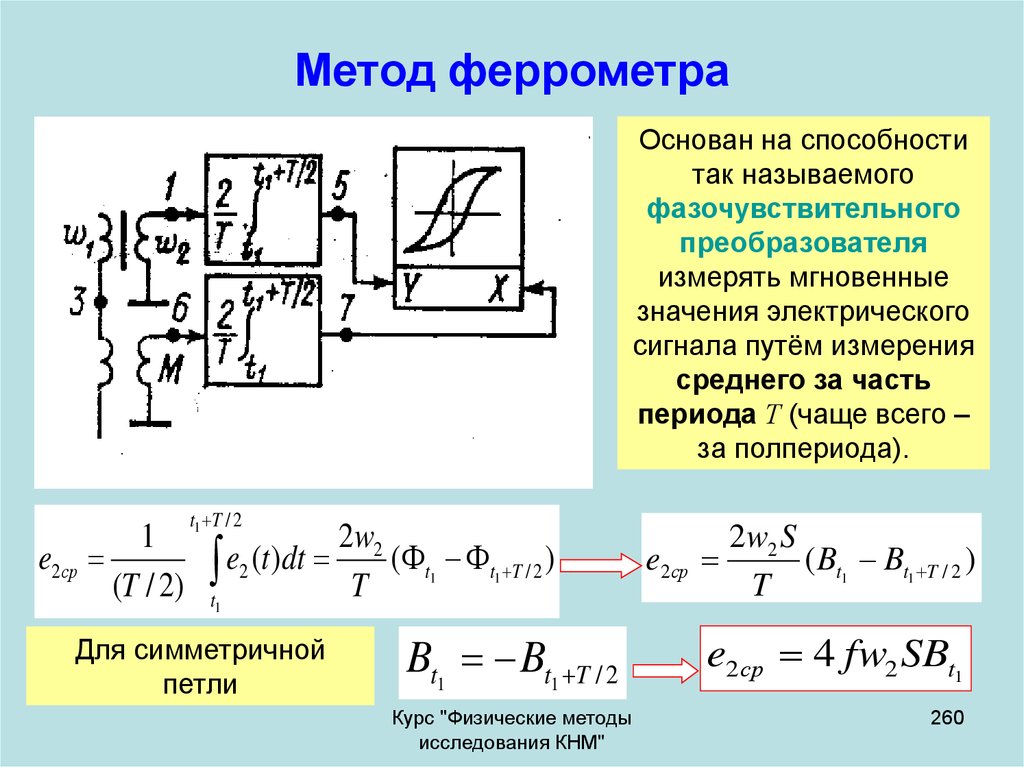
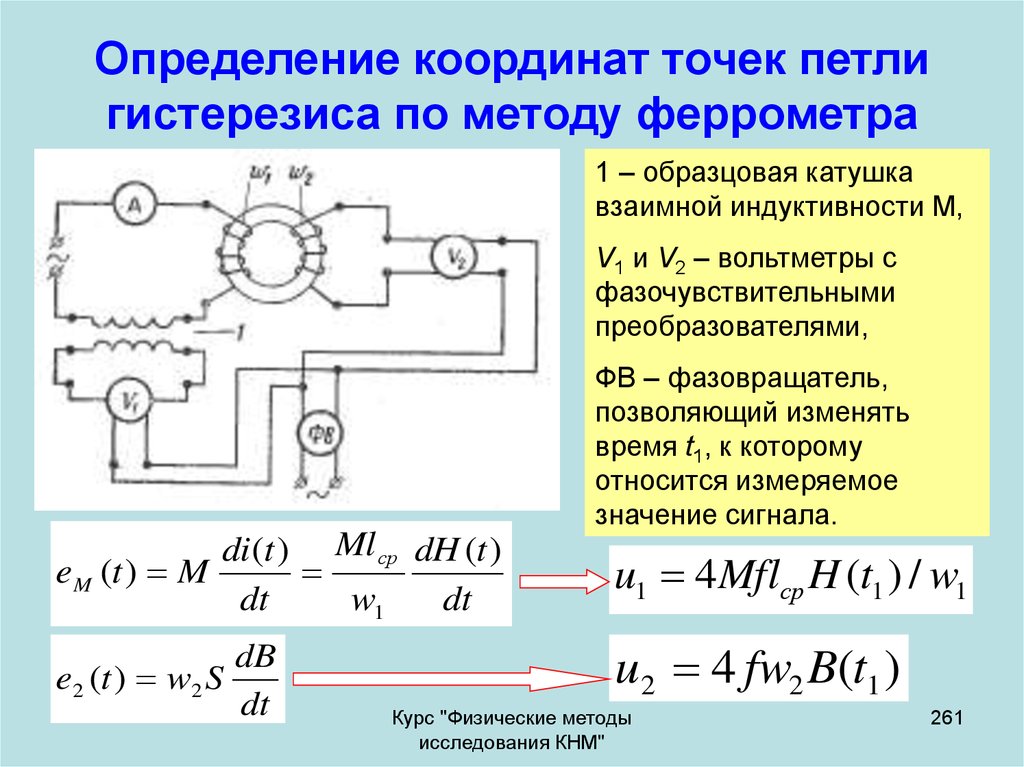
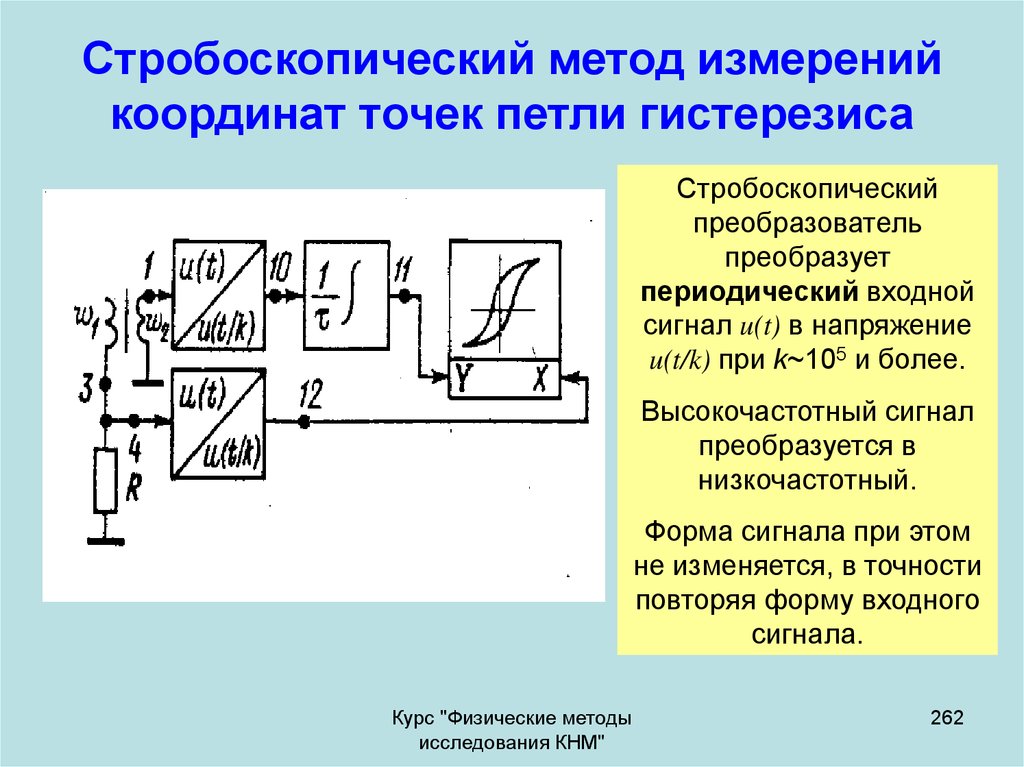
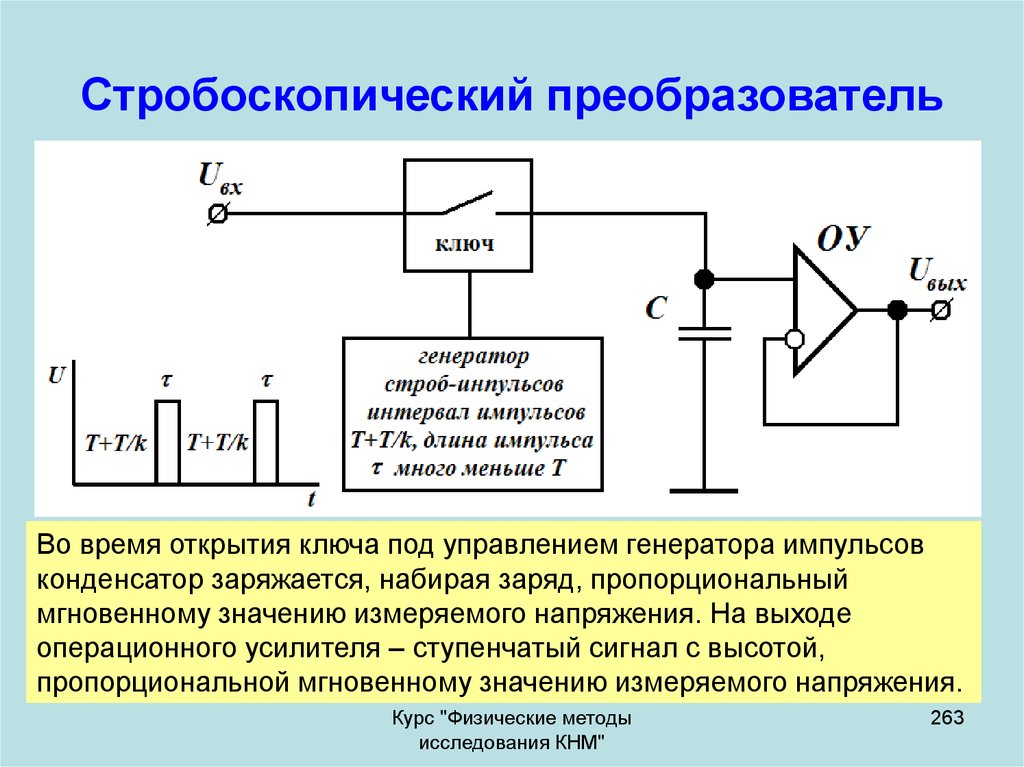
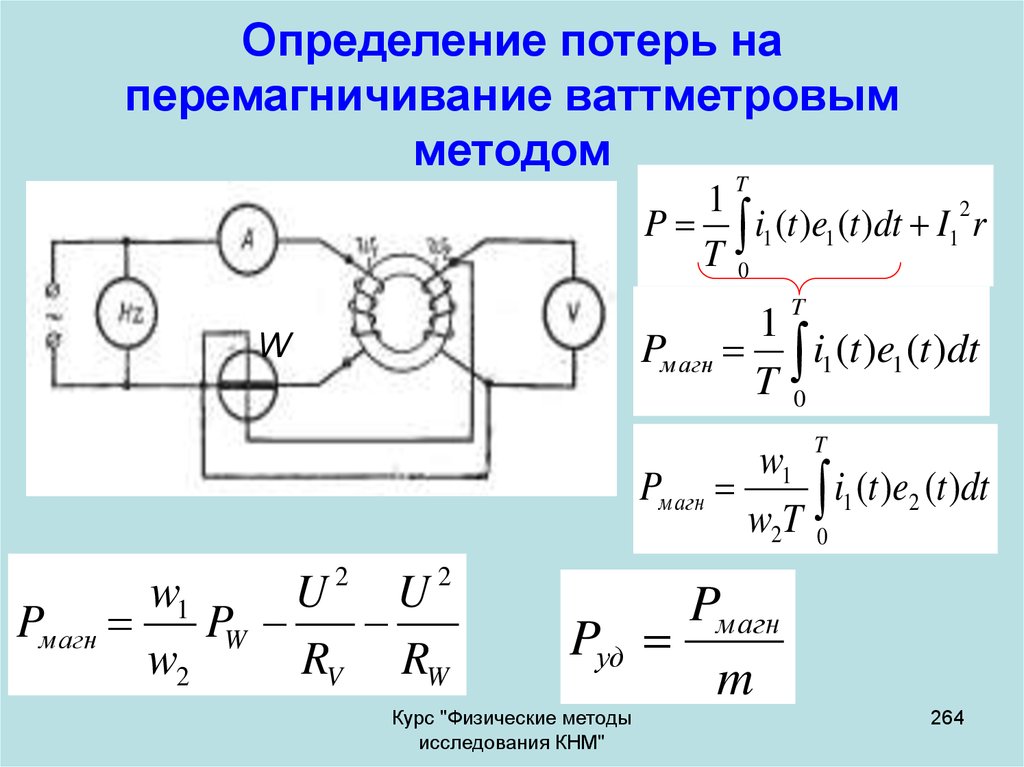
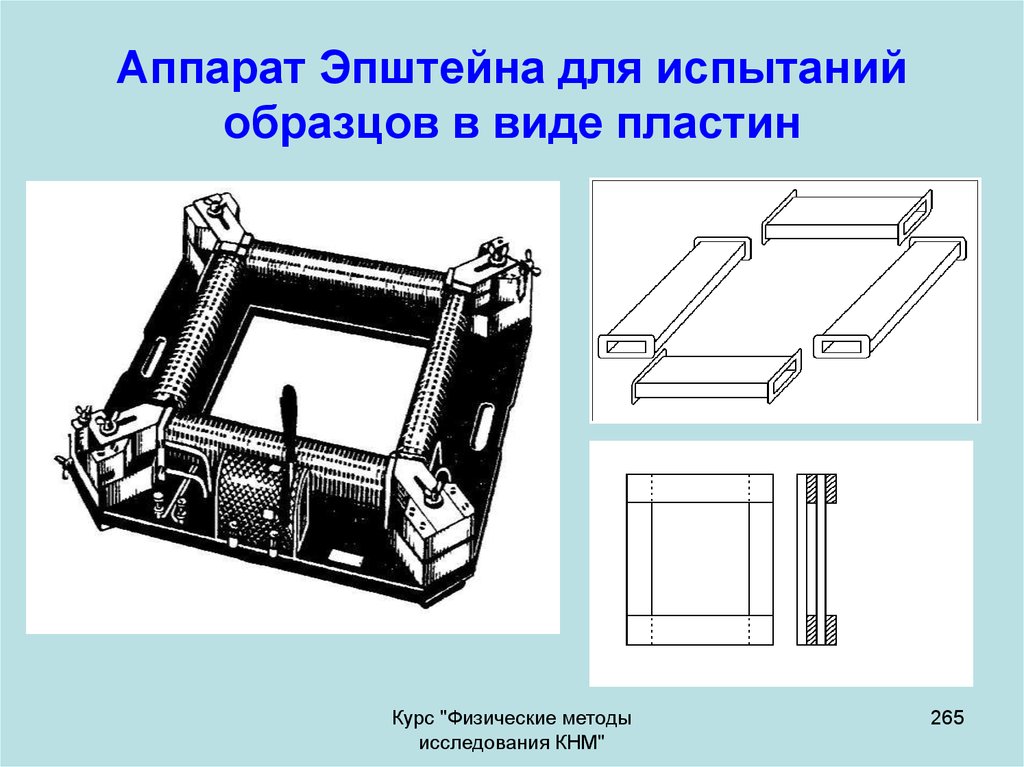
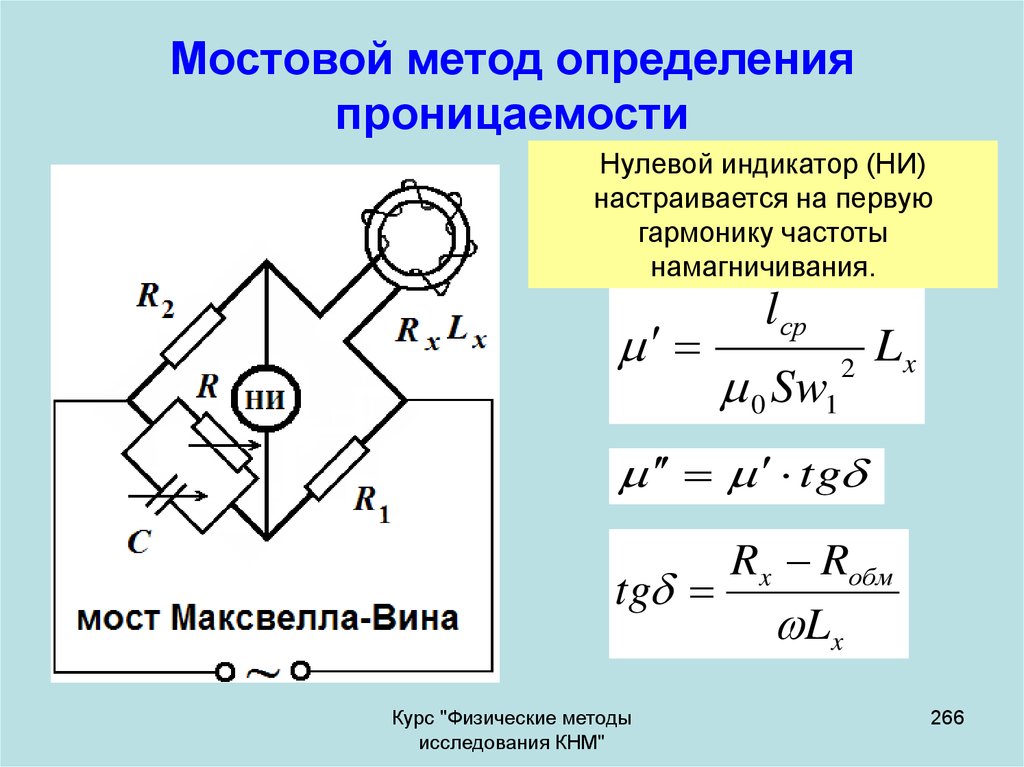

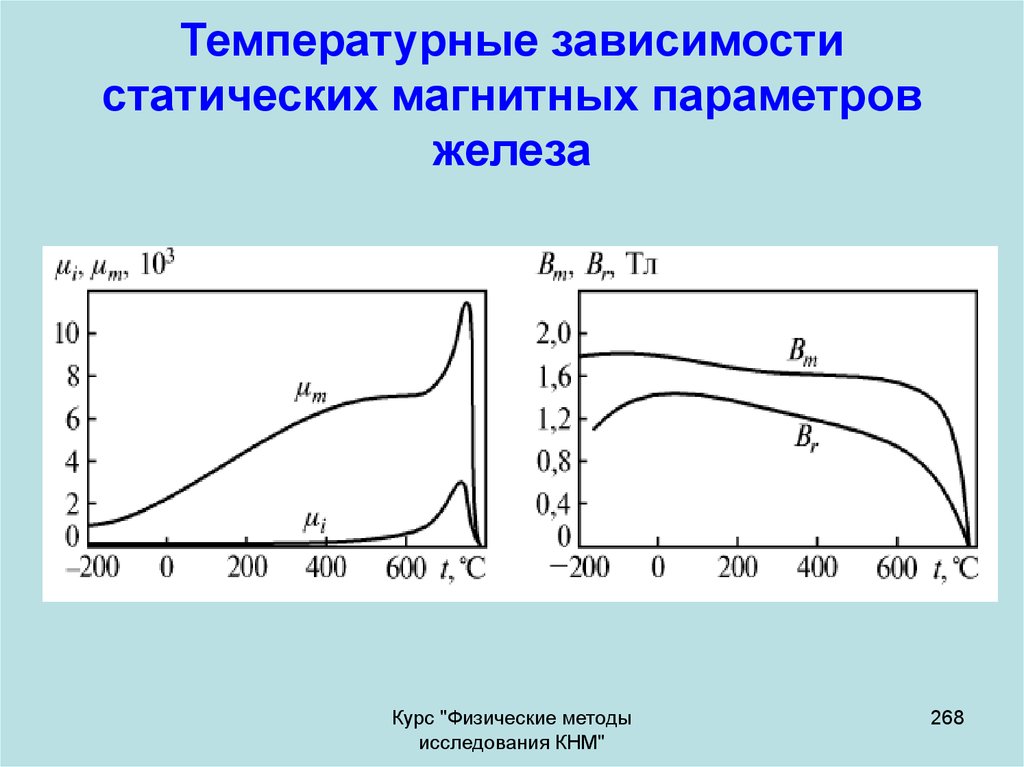
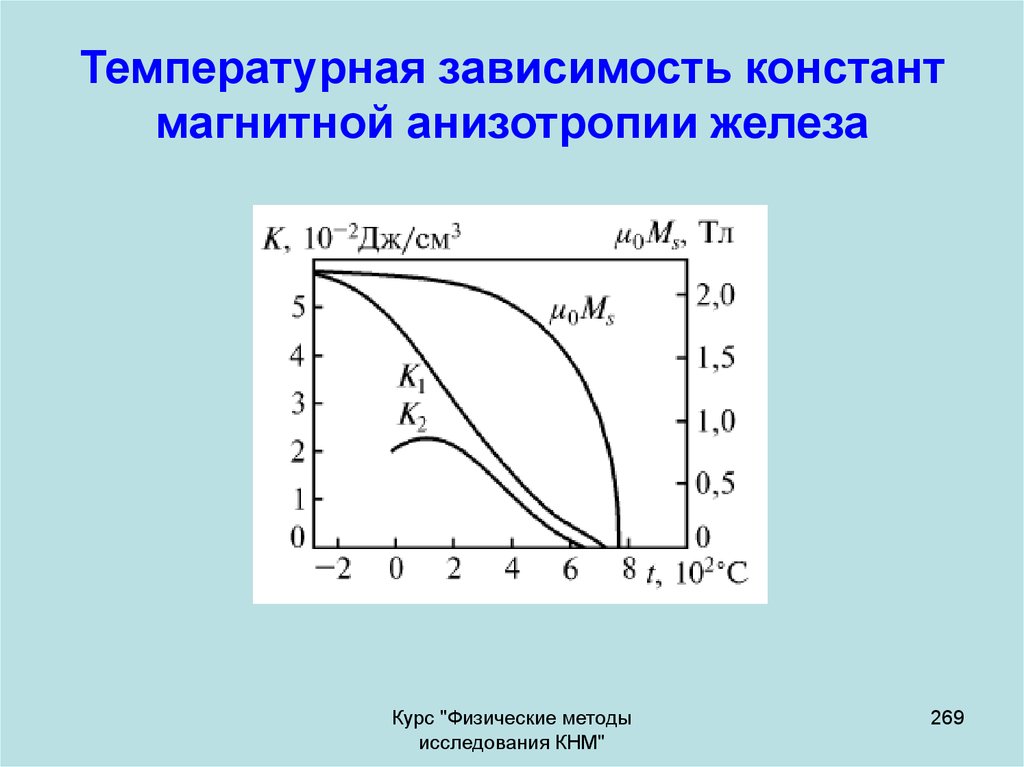
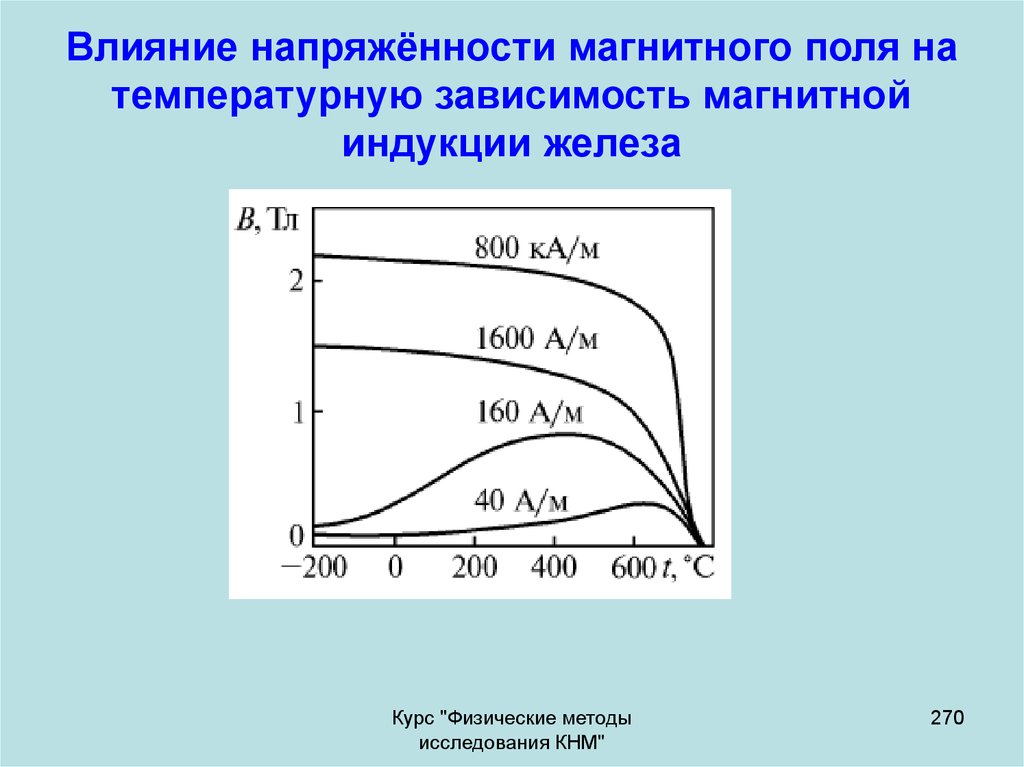


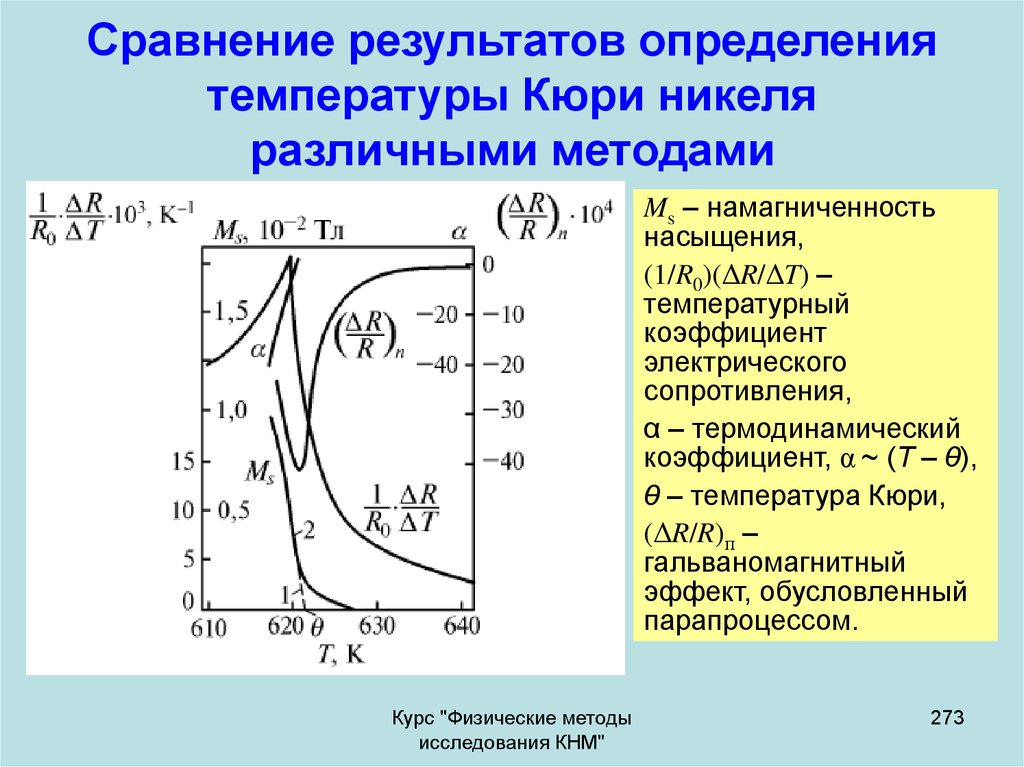

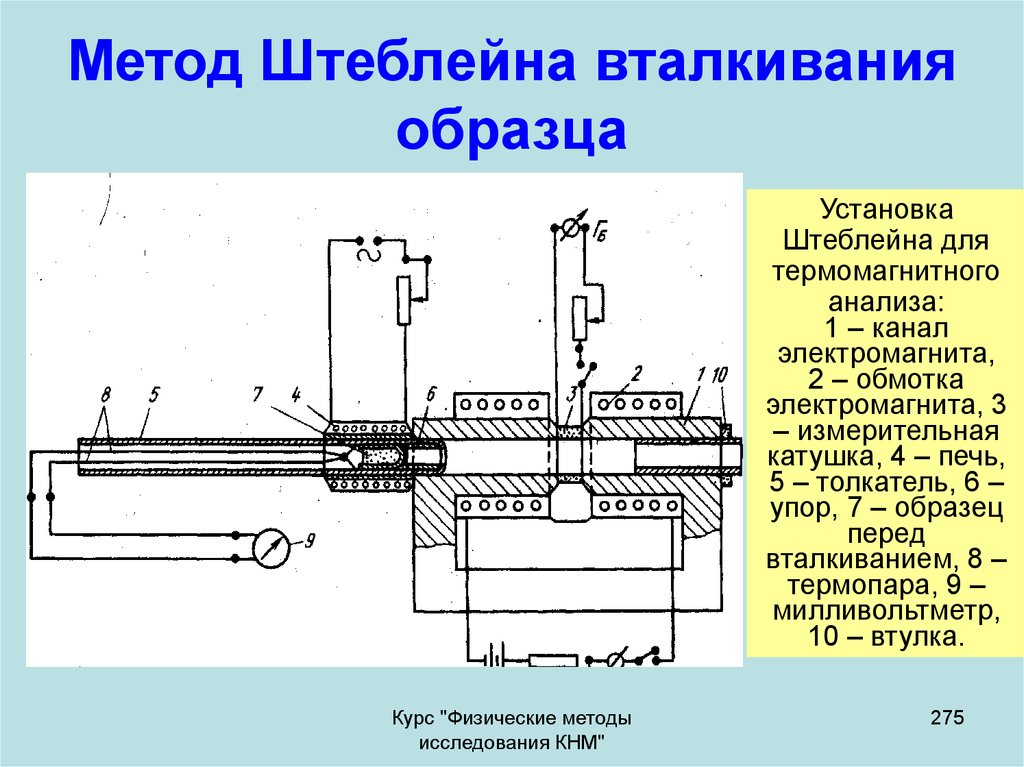
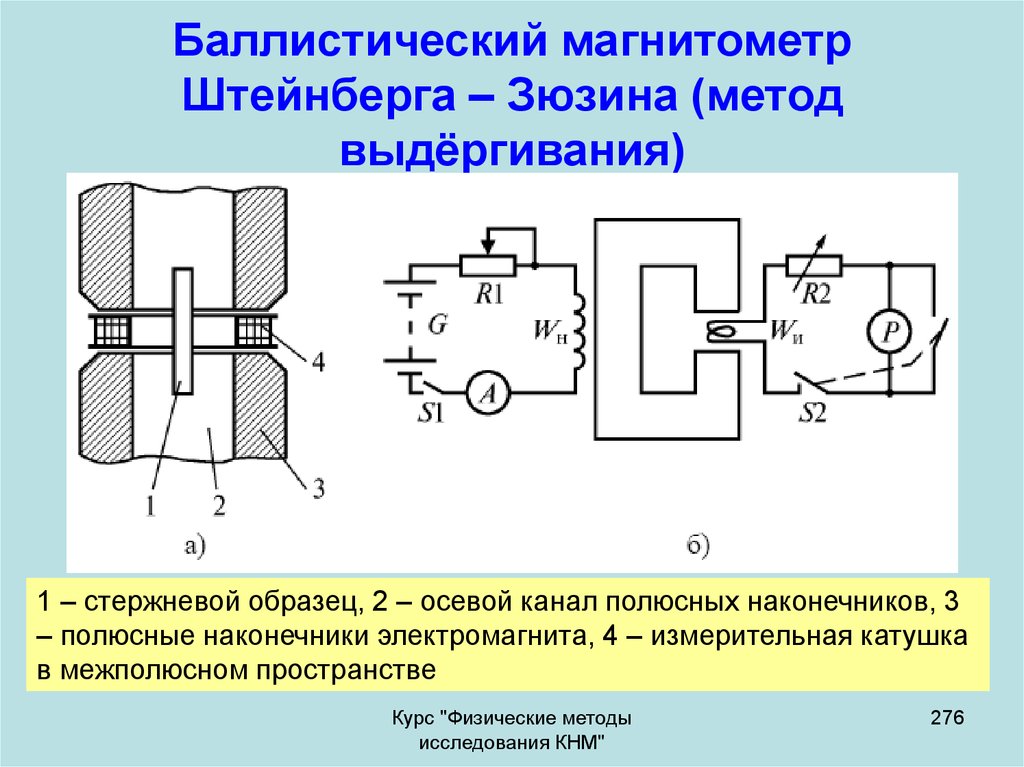
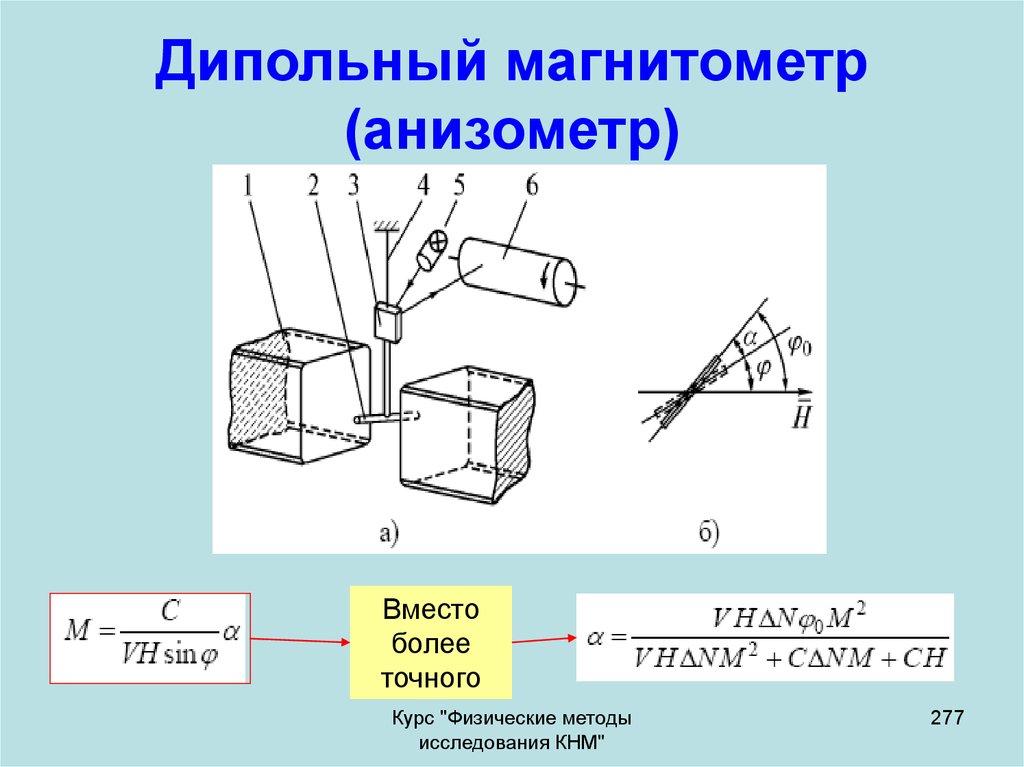
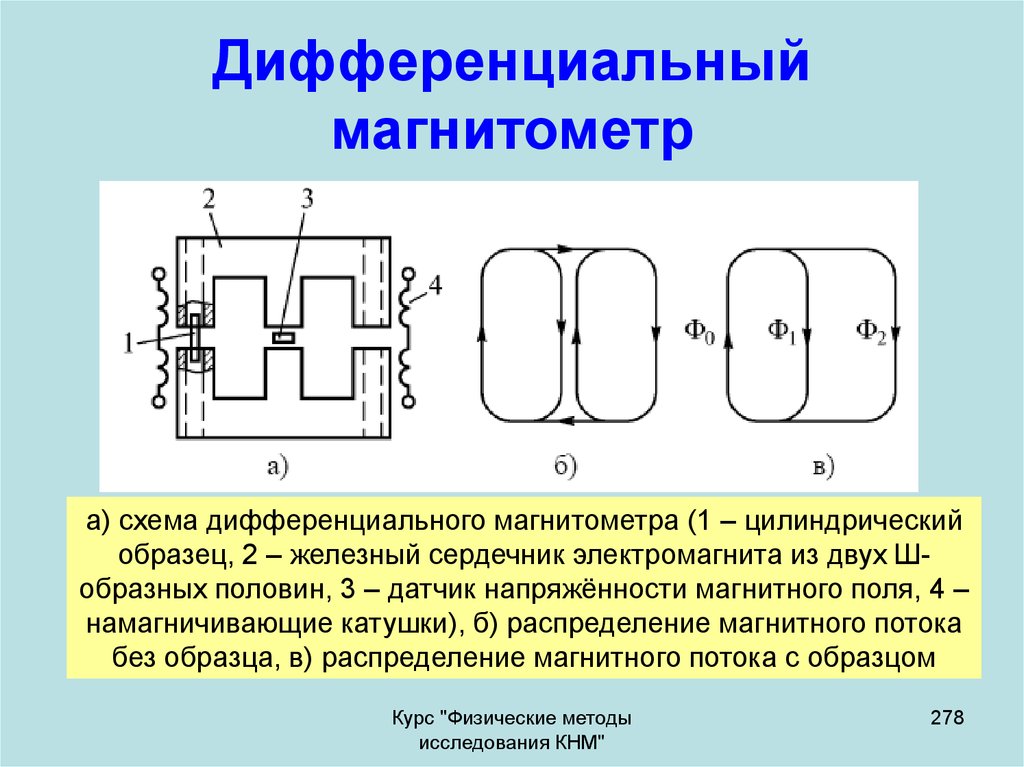
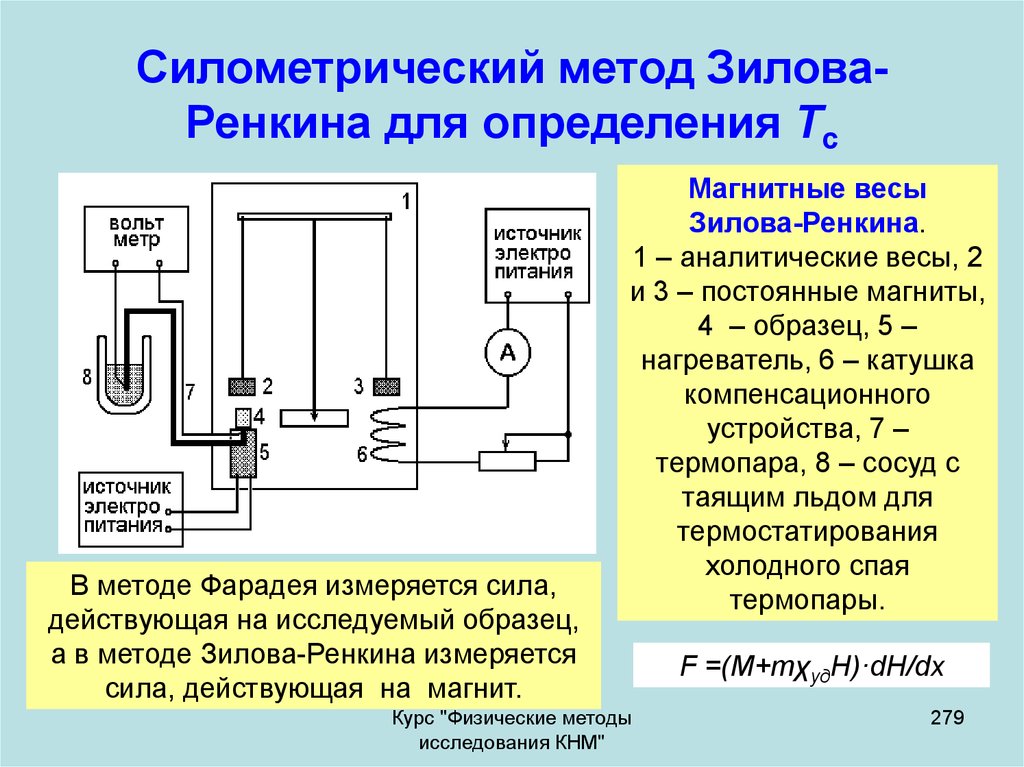
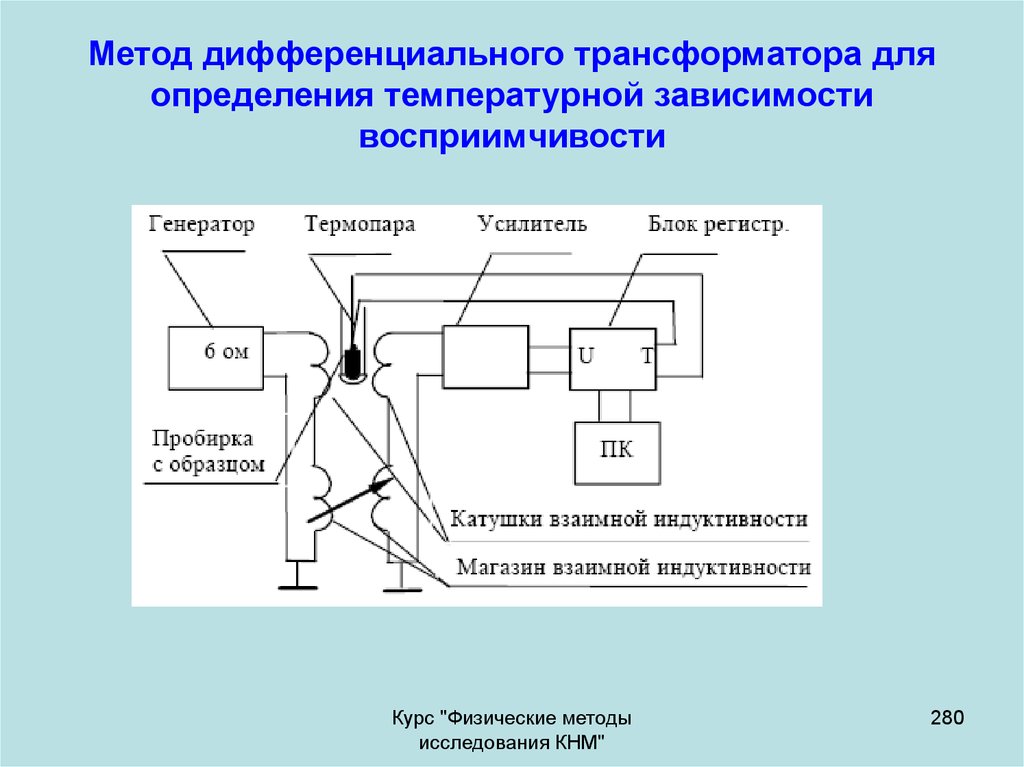
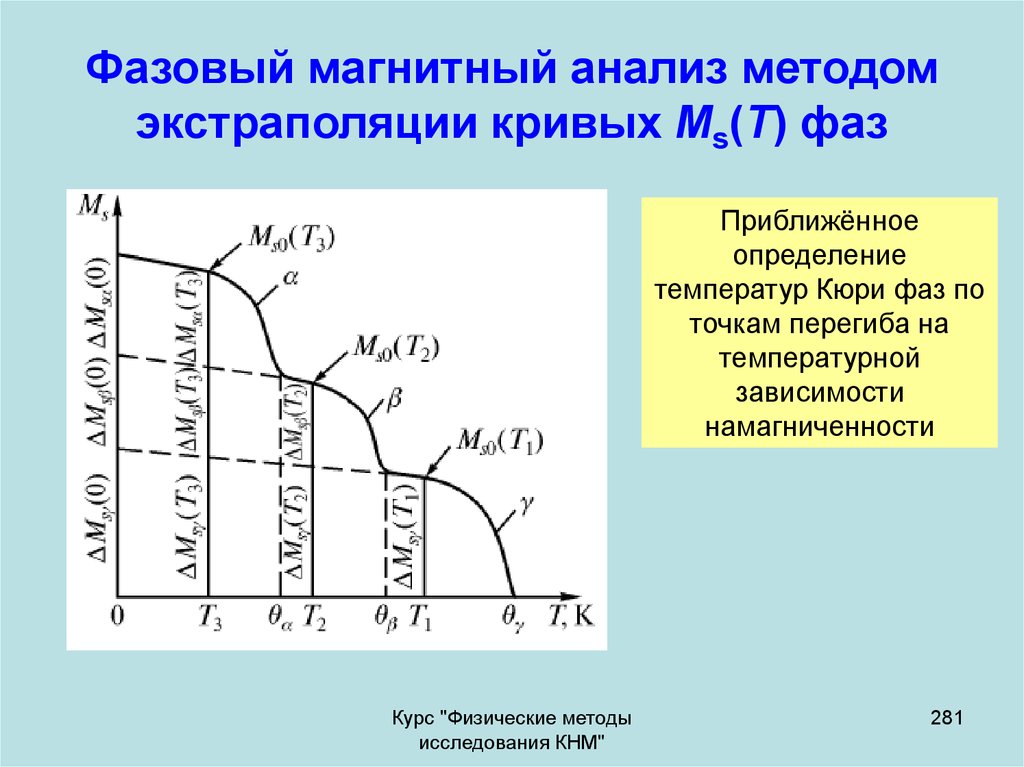
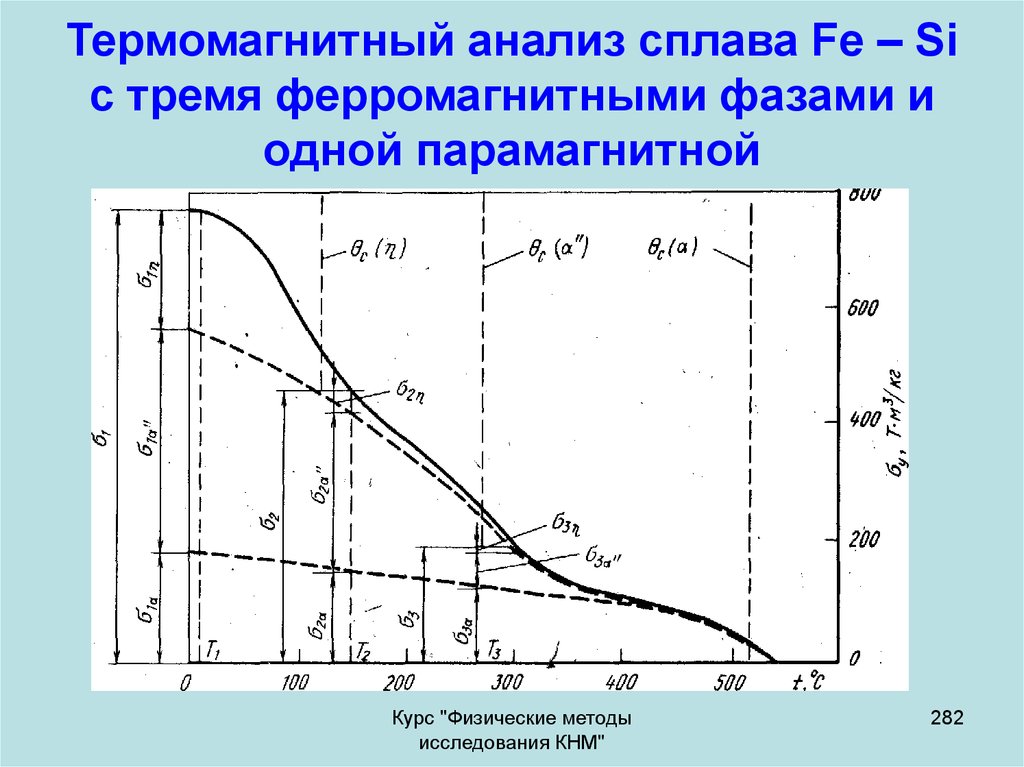
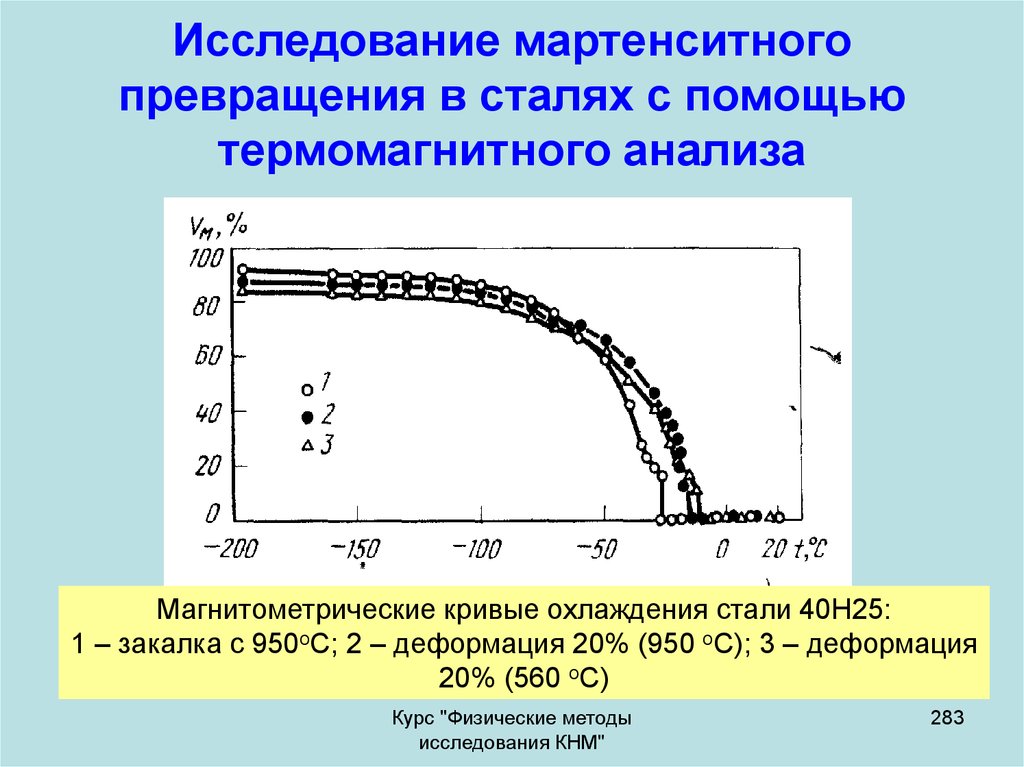

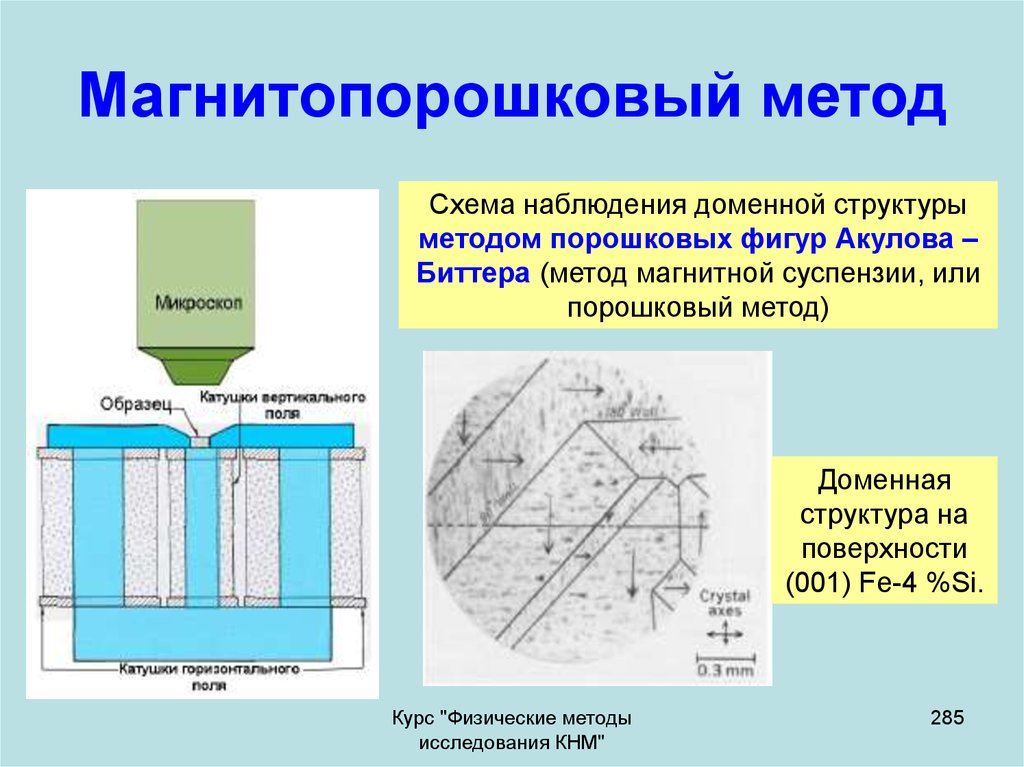
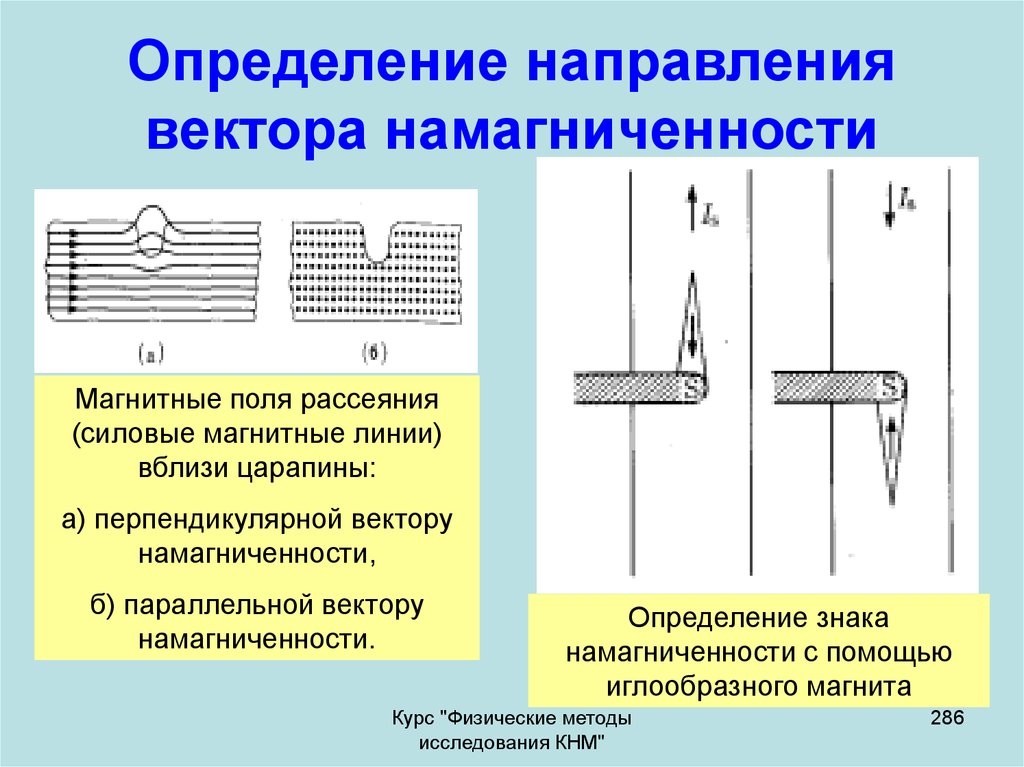
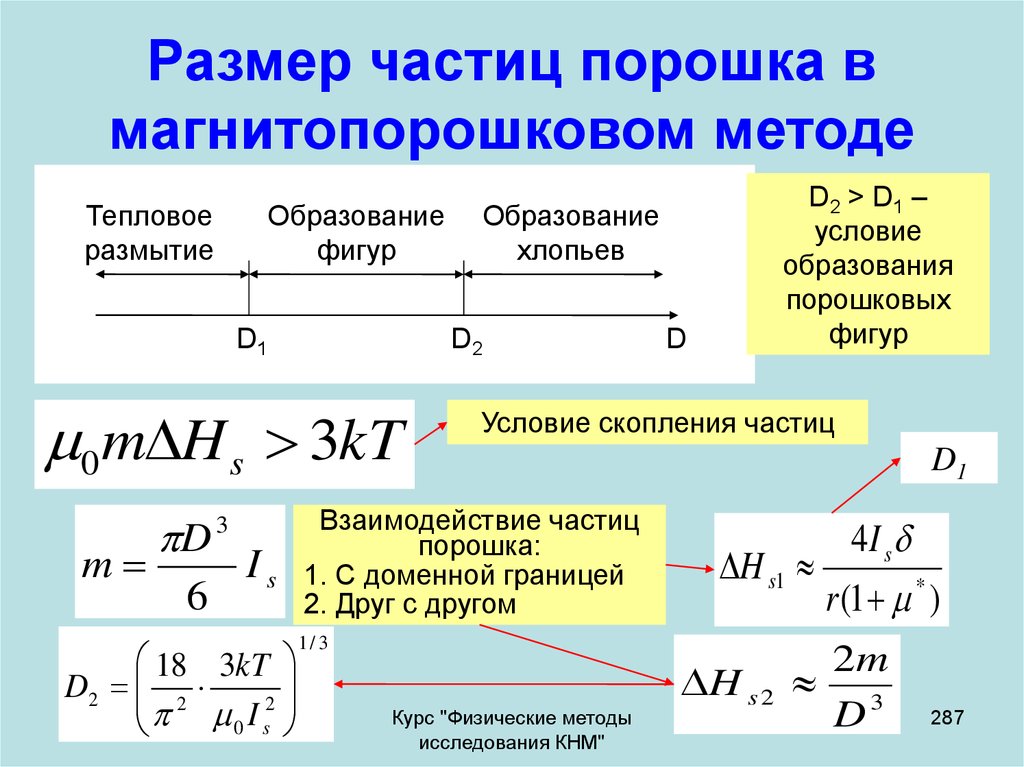
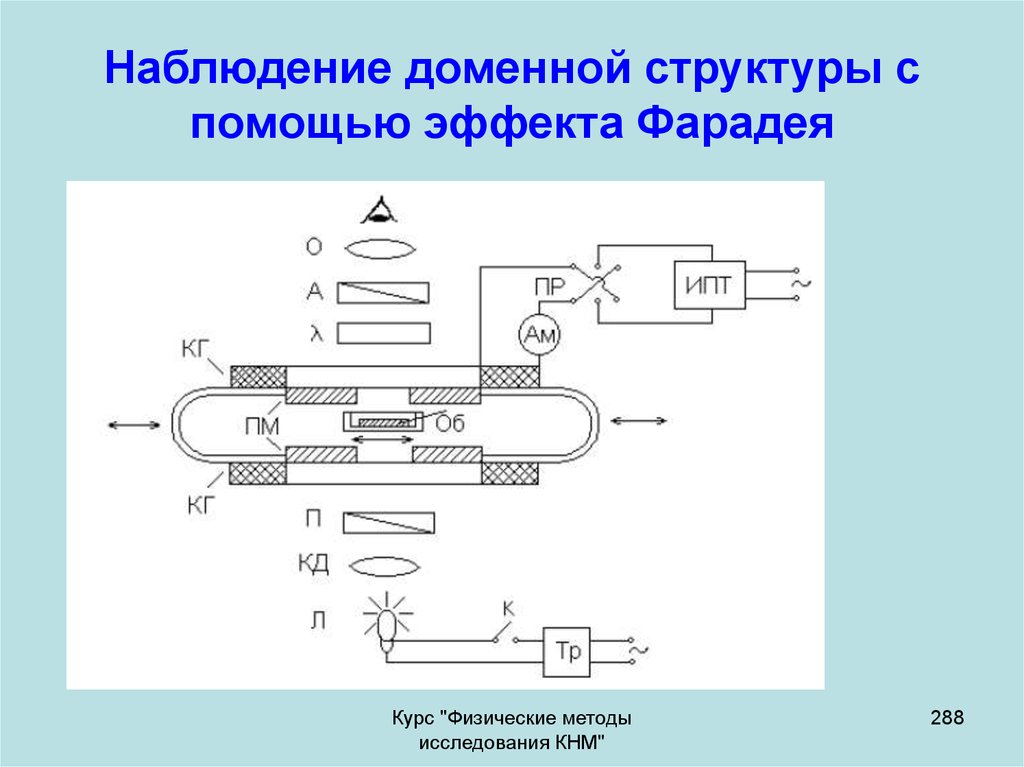
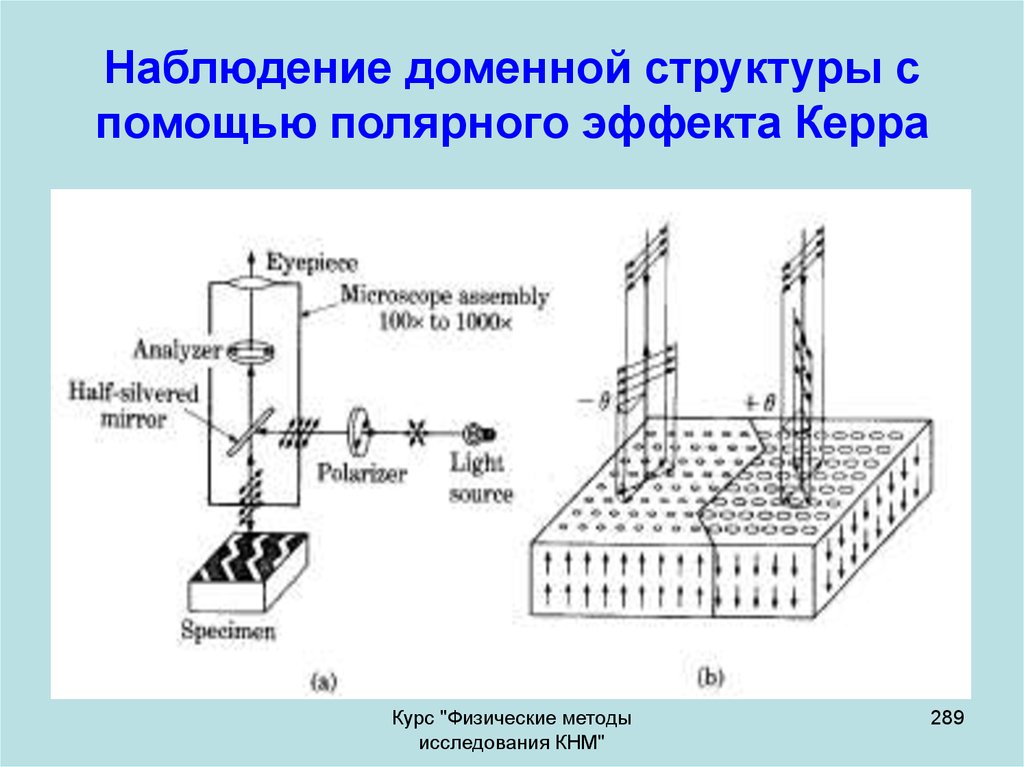

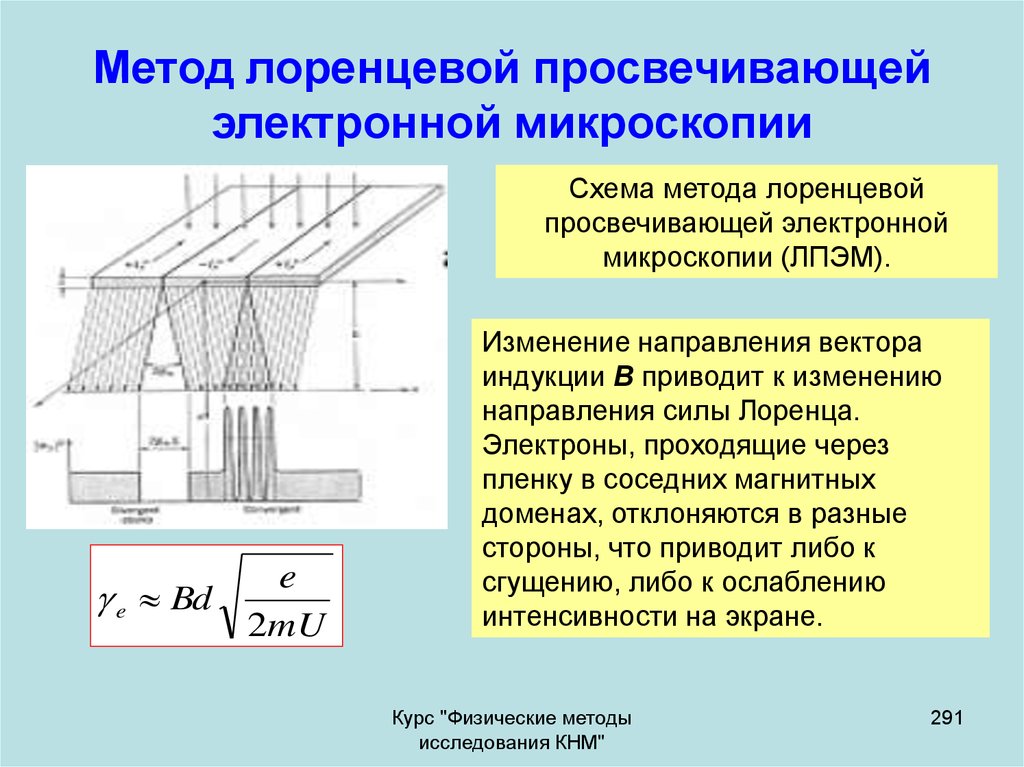

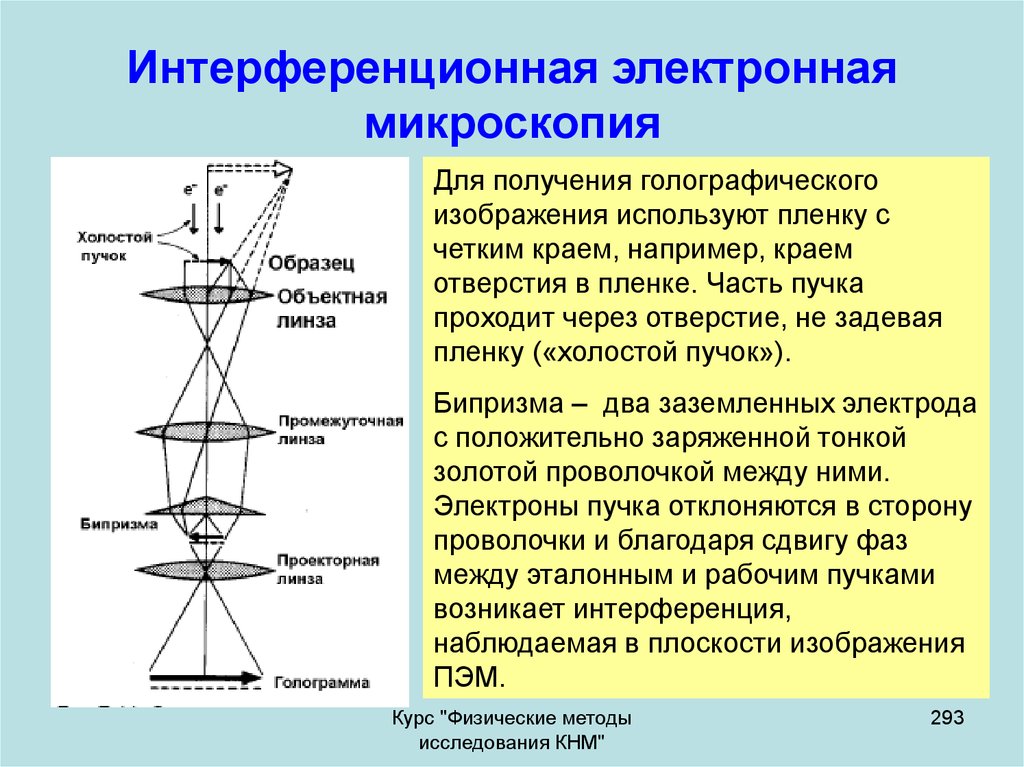
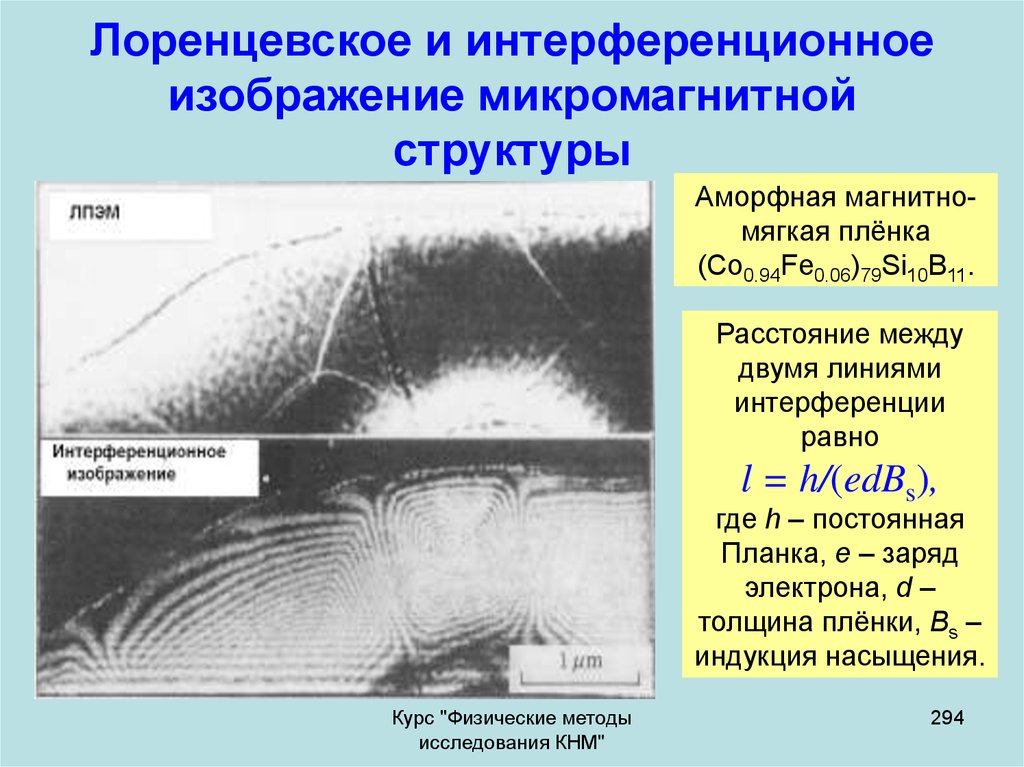
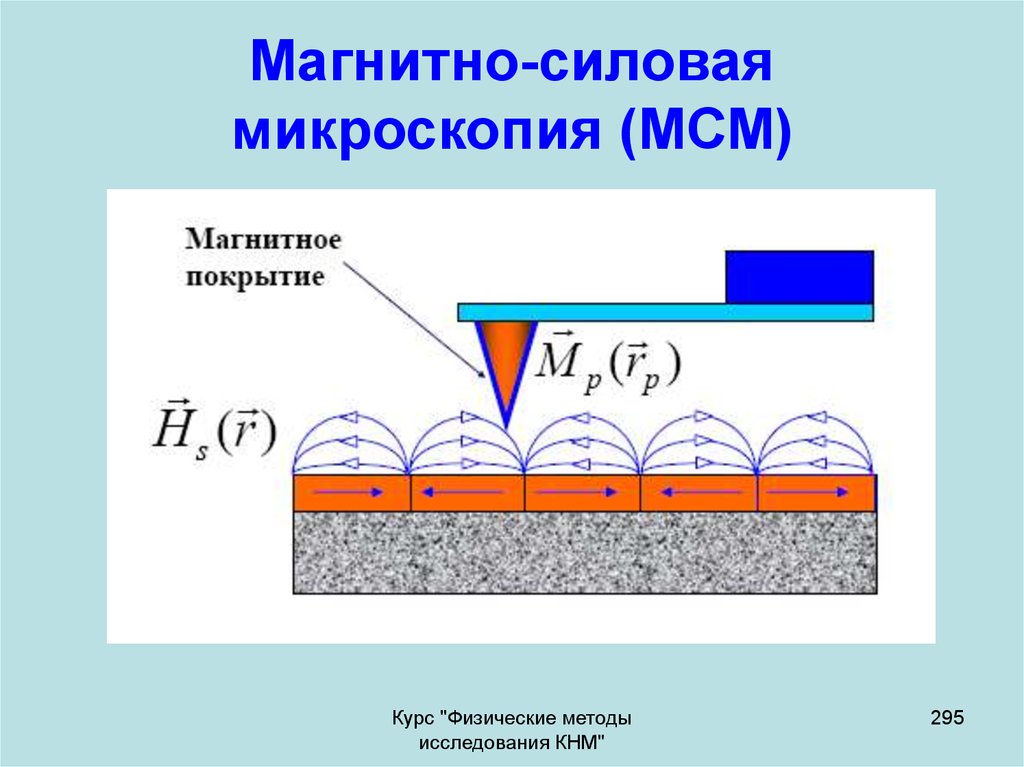
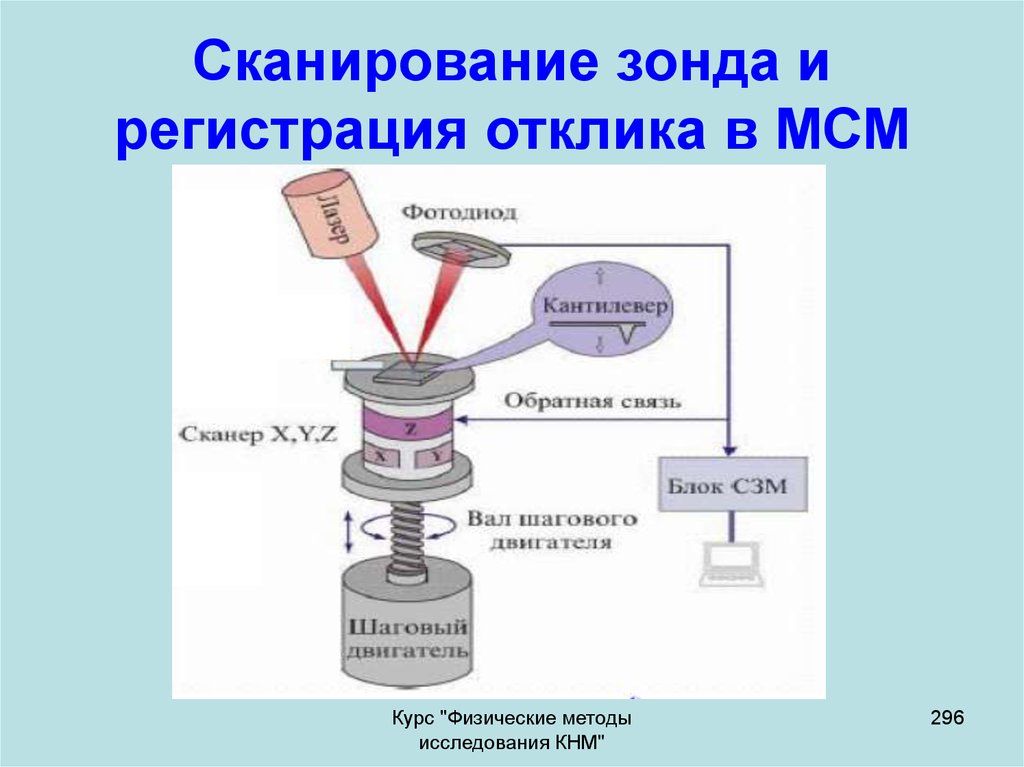

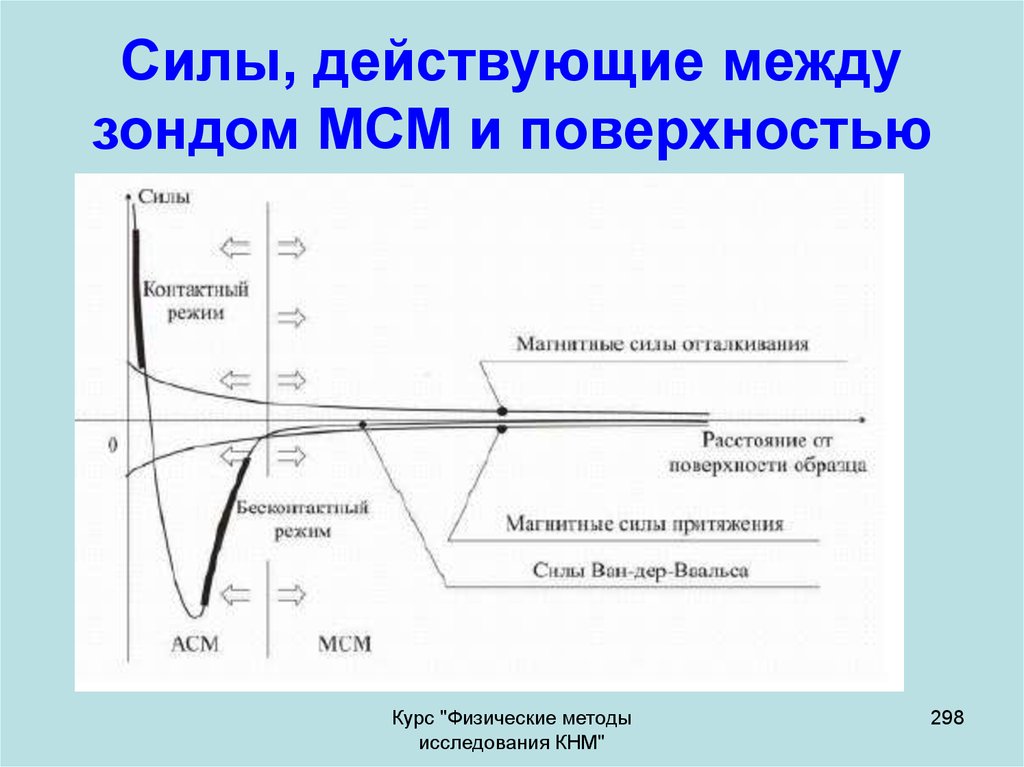
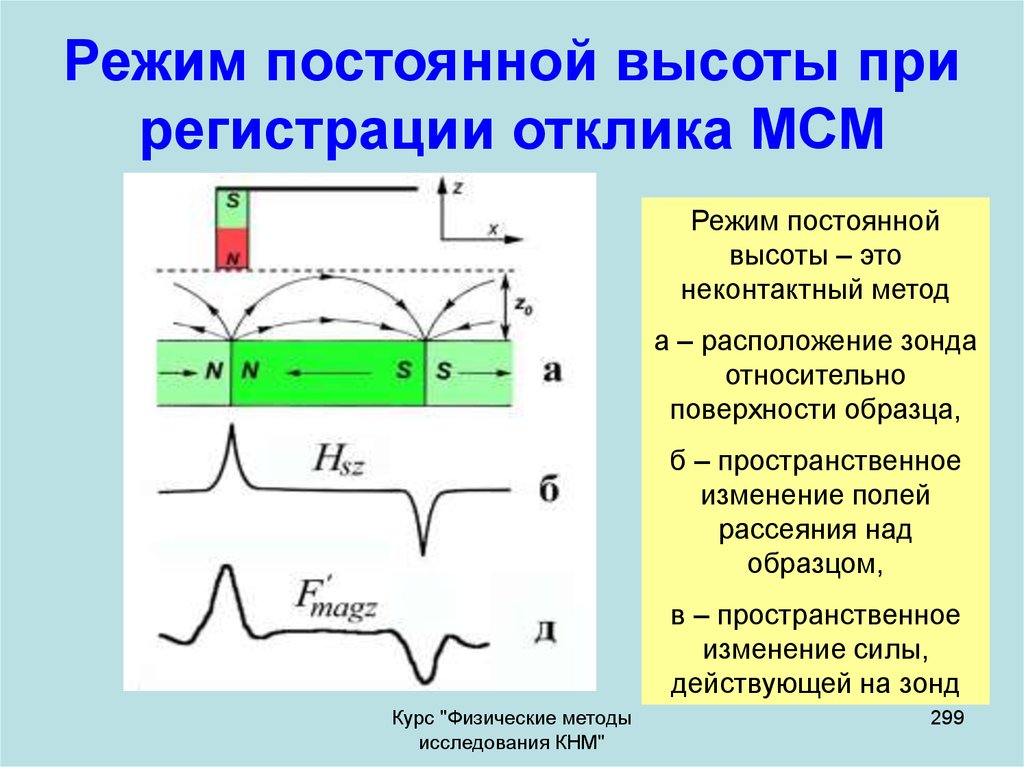



 Физика
Физика








