Похожие презентации:
Понятие о кривой распределения в психологии. (Лекция 3)
1. ТЕМА N 3 Понятие о кривой распределения
2. Вопросы:
1. Вводные понятияматематической статистики.
2. Кривая распределения и ее виды.
3. Математическая статистика
– это раздел математики,посвященный методам сбора,
анализа и обработки
статистических данных для
научных и практических
целей.
4. Структура математической статистики
Структура математическойстатистики
Математическая
статистика
Описательная
статистика
Аналитическая
статистика
5.
Описательная статистика охватываетметоды описания статистических
данных, представления их в форме
таблиц, распределений и пр.
Аналитическая статистика называется
также теорией статистических выводов.
Ее предметом является обработка
данных, полученных в ходе
эксперимента, и формулировка
выводов, имеющих прикладное
значение для самых различных областей
человеческой деятельности
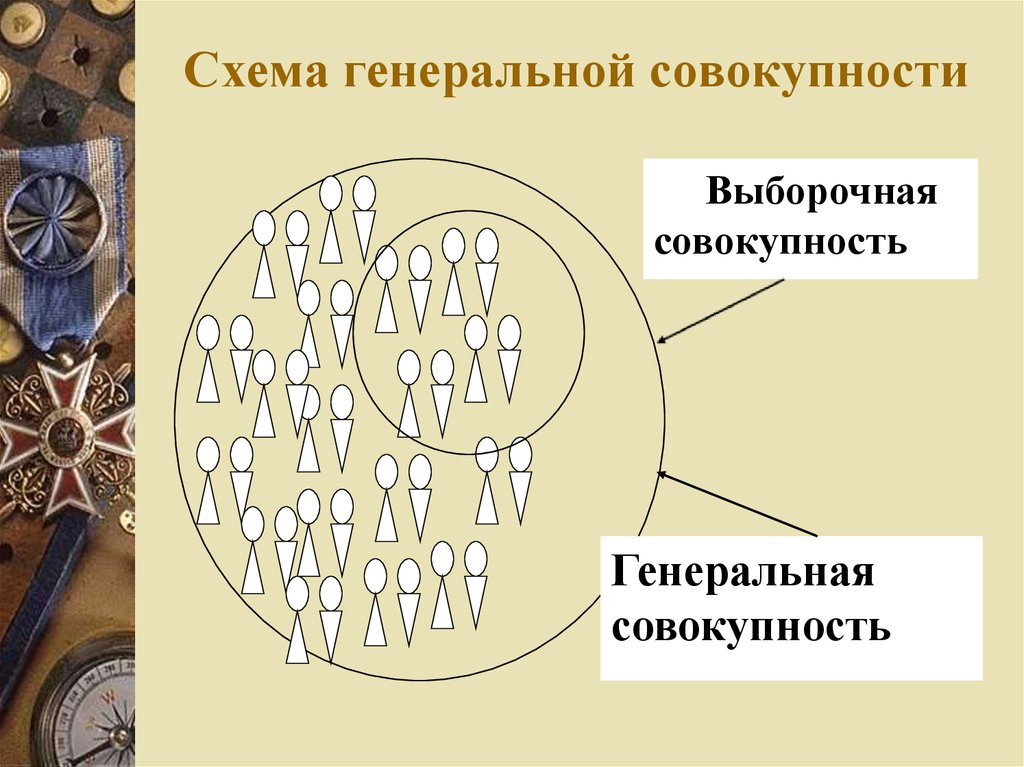
6. Генеральная совокупность и выборка
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ ИВЫБОРКА
Часть объектов исследования,
определенным
образом
выбранная из более обширной
совокупности,
называется
выборкой,
Исходная совокупность, из
которой взята выборка –
генеральной совокупностью.
7. Схема генеральной совокупности
Выборочнаясовокупность
Генеральная
совокупность
8. Основа образования статистической совокупности
наличие общего признакапозволяющего
классифицировать объекты,
сравнивать их друг с другом
(пол, возраст и т.п.).
9. Виды признаков
Качественные признаки - это признаки,которыми объект обладает либо не
обладает. Они не поддаются
непосредственному измерению
(например, чувство юмора,
коммуникативные способности,
национальность и т.п.).
Количественные признаки
представляют собой результаты подсчета
или измерения. В соответствии с этим
они делятся на дискретные и
непрерывные.
10.
Дискретные признаки могутпринимать лишь отдельные значения
из некоторого ряда чисел, например,
число правильно выполненных
заданий, число попаданий и
промахов при стрельбе и т. п.
Непрерывные признаки могут
принимать любые значения в
определенном интервале. Например,
время выполнения тестового
задания.
11. Эмпирические распределения
ЭМПИРИЧЕСКИЕ РАСПРЕДЕЛЕНИЯЧастота интервалов - числа, показывающие,
сколько раз варианты, относящиеся к каждому
интервалу группировки, встречаются в
выборке.
Накопленная частота интервала – это число,
полученное последовательным суммированием
частот в направлении от первого интервала к
последнему, до того интервала включительно,
для которого определяется накопленная
частота.
Частость (относительная частота) называется
отношение частоты к объему выборки.
12. Эмпирические распределения
ЭМПИРИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ№ Границы
Накопл
Распределение Частот
Частост
интер интервал
енные
данных
ы
и
вала
ов
частоты
i
пi
Fi
I
Хнi-Хвi
пхi
1
0-3
IIII
4
4
0,09
2
4-7
IIIII
5
9
0,11
3
8-11
12
21
0,28
4
12-15
IIIIIIIIIII
I
IIIIIIIIIII
11
32
0,26
5
16-19
IIIIIIIII
9
41
0,21
6
20-23
II
2
43
0,05
13. Частость
fini
n
ni – частота интервала, n – общее
число наблюдений.
Сумма всех
всегда равна 1.
частостей
14. Графическое представление экспериментальных данных
Гистограмма используется дляграфического представления
распределений непрерывно
варьирующих признаков и состоит
из примыкающих друг к другу
прямоугольников.
15. Гистограмма
У12
10
8
6
4
2
0 0-3 4-7
8-11
12-15
6-19
20-23
16. Графическое представление экспериментальных данных
Полигон частот образуетсяломаной линией, соединяющей
точки, соответствующие
срединным значениям интервалов
группировки и частотам этих
интервалов.
17. Полигон частот
У12
10
8
6
4
2
0 0-3 4-7
8-11
12-15
6-19
20-23
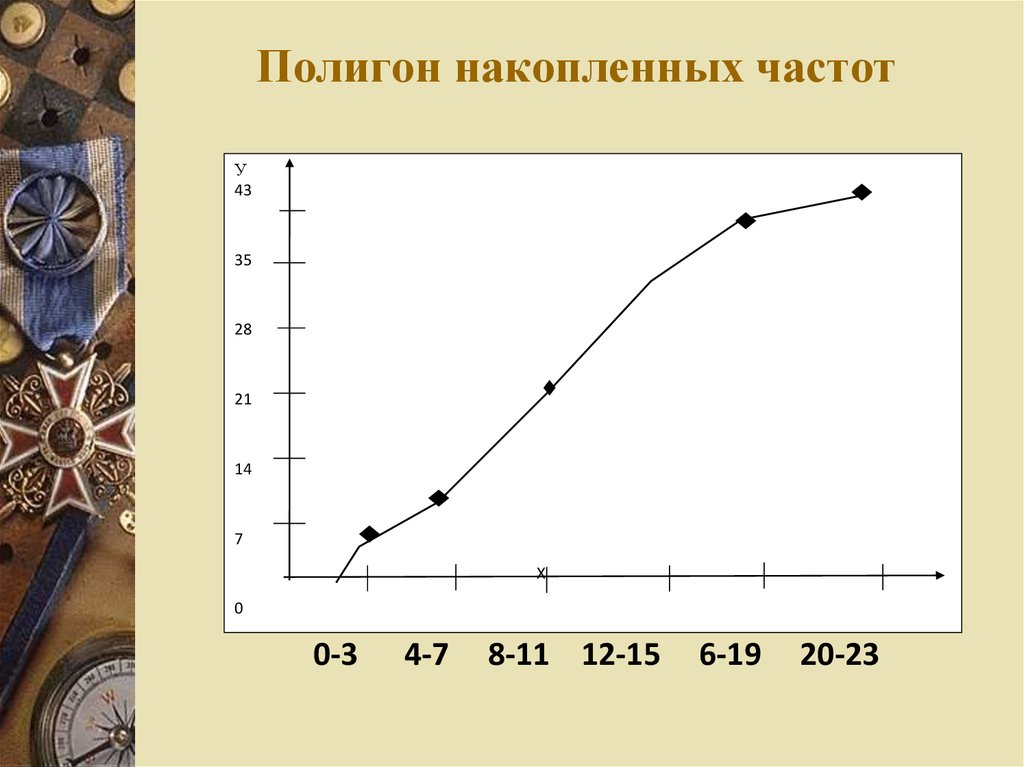
18. Графическое представление экспериментальных данных
Полигон накопленных частот(кумулята) получается при
соединении отрезками прямых
точек, координаты которых
соответствуют верхним границам
интервалов группировки и
накопленным частотам
19. Полигон накопленных частот
У43
35
28
21
14
7
Х
0
0-3
4-7
8-11 12-15
6-19
20-23
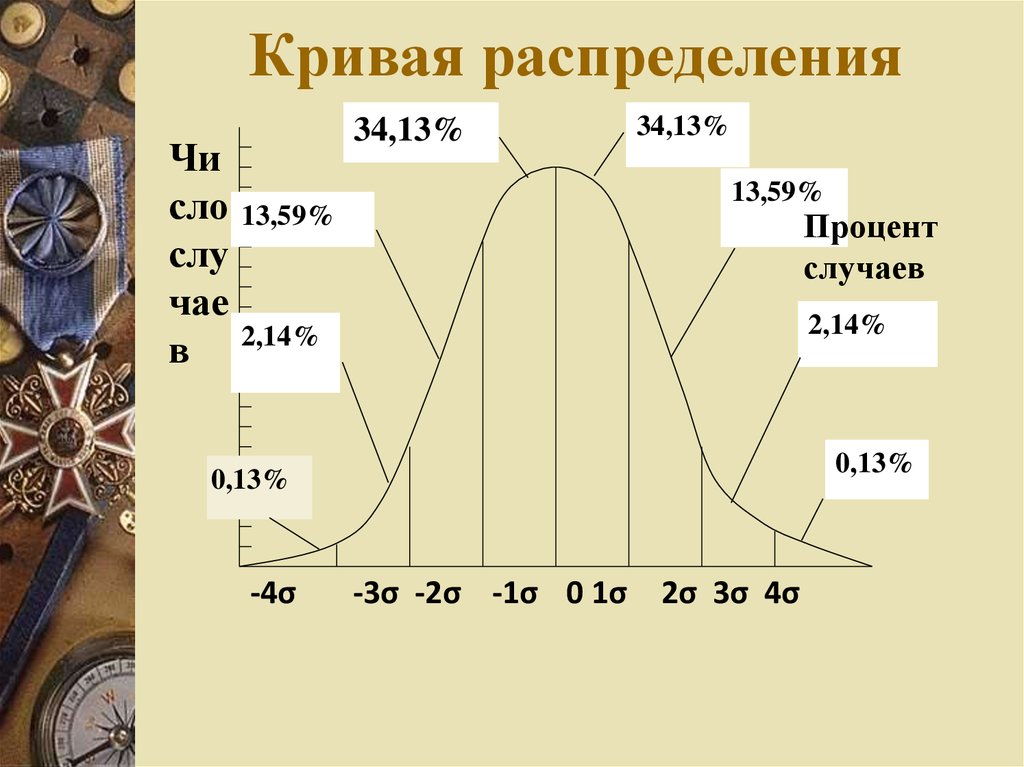
20. Кривая распределения
Число
слу
чае
в
34,13%
13,59%
34,13%
13,59%
Процент
случаев
2,14%
2,14%
0,13%
0,13%
-4σ
-3σ -2σ -1σ 0 1σ 2σ 3σ 4σ

















 Математика
Математика Психология
Психология








