Bioorganic chemistry

1. BIOORGANIC CHEMISTRY

2. Bio-organic chemistry studies organization and features of substances taking part in the processes of life, in connection to

study of their biological functions.
• The main objects of its study are biological polymers
(bio-polymers) and bio-regulators.
• Bio-polymers are high molecular natural compounds,
which are structural basis of all living beings, which play
a certain role in the processes of life. Bio-polymers
include peptides and proteins, polysaccharides
(carbohydrates), nucleic acids. This group includes lipids,
which are not high molecular combinations by themselves
but in the organism they are usually bonded to other biopolymers.
• Bio-regulators are compounds, which chemically
regulate the exchange of substances. They comprise
vitamins, hormones, many synthetic biologically active
compounds, including medicines.

3. The unity of chemical reactions, going on in the organism, is called the exchange of substances or metabolism. Substances,

formed in
cells, muscles and organs of plants and animals in the process of
metabolism, are called metabolites.
• Metabolism comprises two directions: catabolism and
anabolism.
• Catabolism includes reactions of substances decomposition,
which come into the organism with food. As a rule, they go
hand-in-hand with oxidation of organic compounds and go with
the discharge of energy.
• Anabolism is a synthesis of complex molecules from more
simple, as a result of which formation and renovation of
structural elements of a living organism is realized.
• Metabolic processes come with participation of enzymes, i.e.
specific proteins, which are in the organism cells, and play the
role of catalysts for bio-chemical processes (bio-catalysts).

4. HOMOLOGOUS SERIES

Rank of similar structured compounds, having similar chemical
properties, in which separate members of the rank differ from each
other only by the number of -CH2- groups, are called homologues
rank (homologous series), and –CH2- group is called homologous
diversity.
Reactions with the majority of members of homologous rank go in
the same way (the exceptions are only the first members of the rank).
Thus, if you know chemical reactions of only one member of the
rank, you can state with a high degree of possibility, that the similar
transformations take place with the rest members of the homologous
rank.
A general formula can be defined for any homologous rank, which
reflects the relation between carbon and hydrogen atoms at members
of this rank. Such formula is called general formula of the
homologous rank. Thus, CnH2n+2 – formula of alkanes, CnH2n+1OH –
is a formula of aliphatic single atom alcohols.

5. Isomerism of organic compounds

• If two or more individual substances have the same quantity
structure (molecular formula) but are different from each other by the
succession of atom bonds or their place in the space, then they are
called isomers.
• If their structure differs, then their chemical and physical
properties are also different.
• Types of isomery are structural (isomers of organization,
structure) and stereo-isomery (space).
• Structural isomery could be of the following types:
• isomery of the hydrocarbon skeleton (chain isomers), for example,
butane and 2-methy-l-propane;
• isomery of the place of functional groups (or multiple bonds), for
example, 1-butanol and 2-butanol;
• isomers of functional group (interclass), for example, 1-buta-nol
and di-ethyl ether.
• Stereo-isomery is divided into conformation and configuration.

6. Structural isomerism of organic compounds

propanal
acetone or
2-propanone

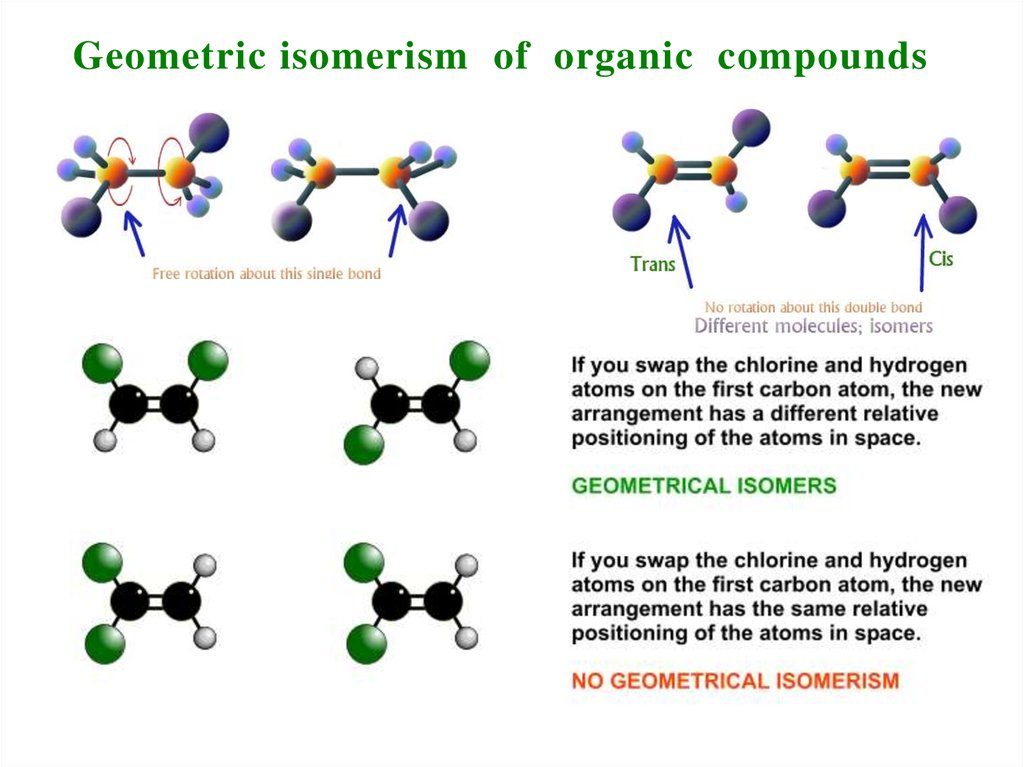
7. Geometric isomerism of organic compounds

8. Enantiomerism (optical or mirror reflection isomerism)

Optically active compounds
form two special isomers
which are each other’s
mirror reflections
(enantiomers).

9.

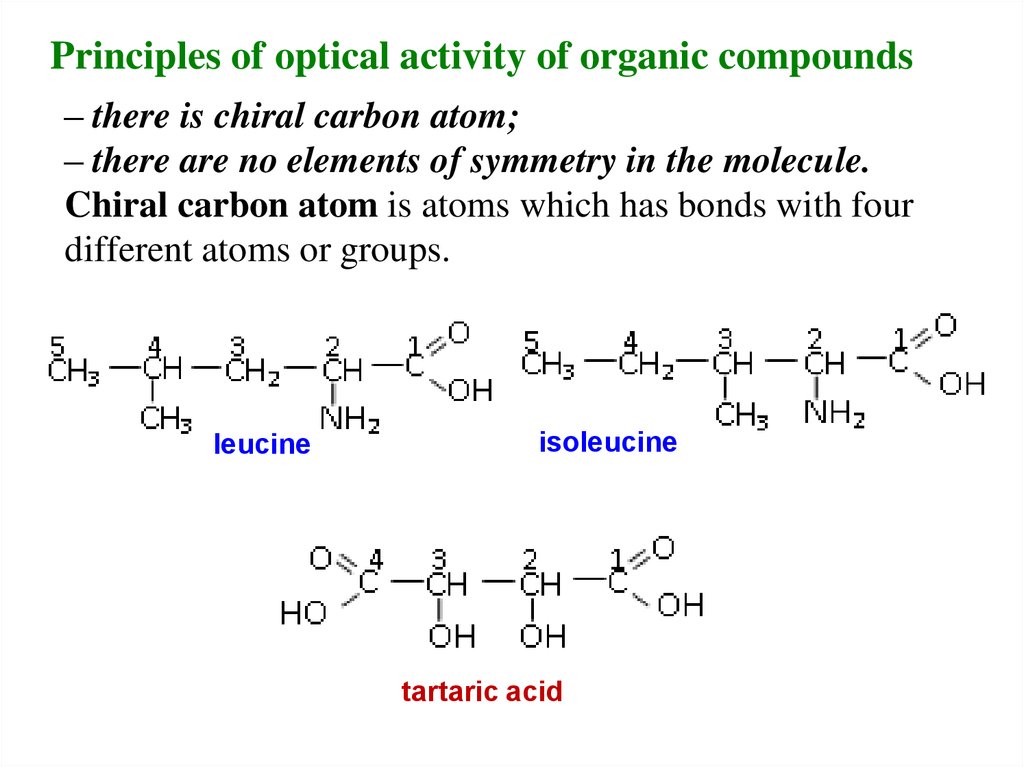
Principles of optical activity of organic compounds
– there is chiral carbon atom;
– there are no elements of symmetry in the molecule.
Chiral carbon atom is atoms which has bonds with four
different atoms or groups.
leucine
isoleucine
tartaric acid

10.

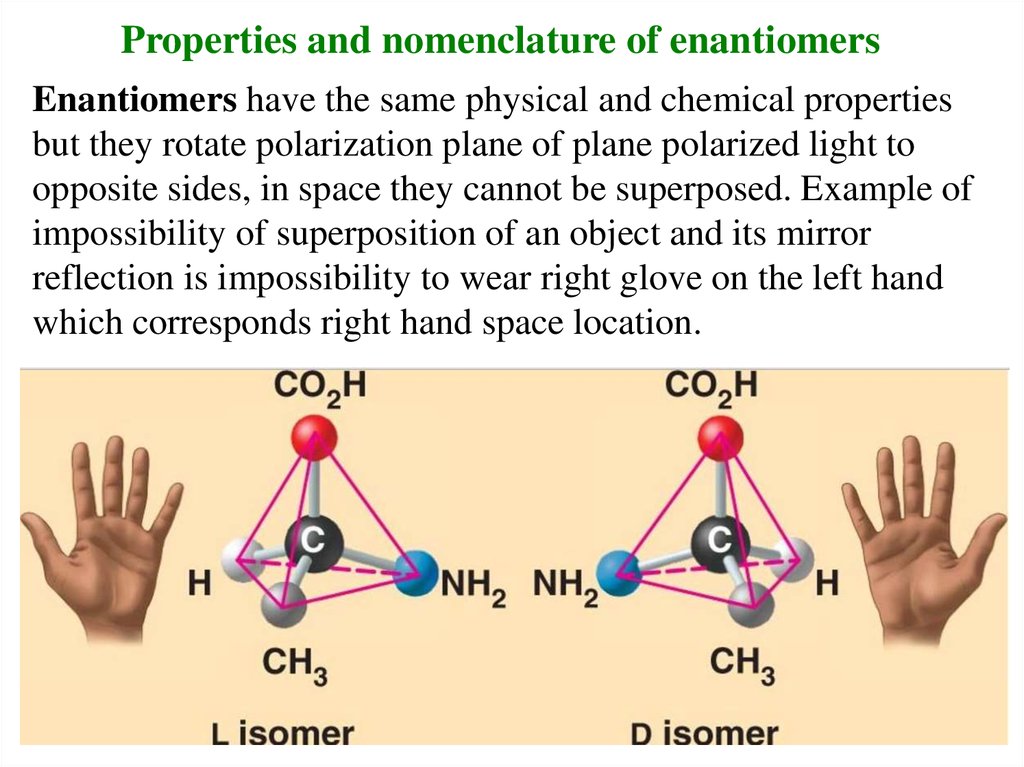
Properties and nomenclature of enantiomers
Enantiomers have the same physical and chemical properties
but they rotate polarization plane of plane polarized light to
opposite sides, in space they cannot be superposed. Example of
impossibility of superposition of an object and its mirror
reflection is impossibility to wear right glove on the left hand
which corresponds right hand space location.

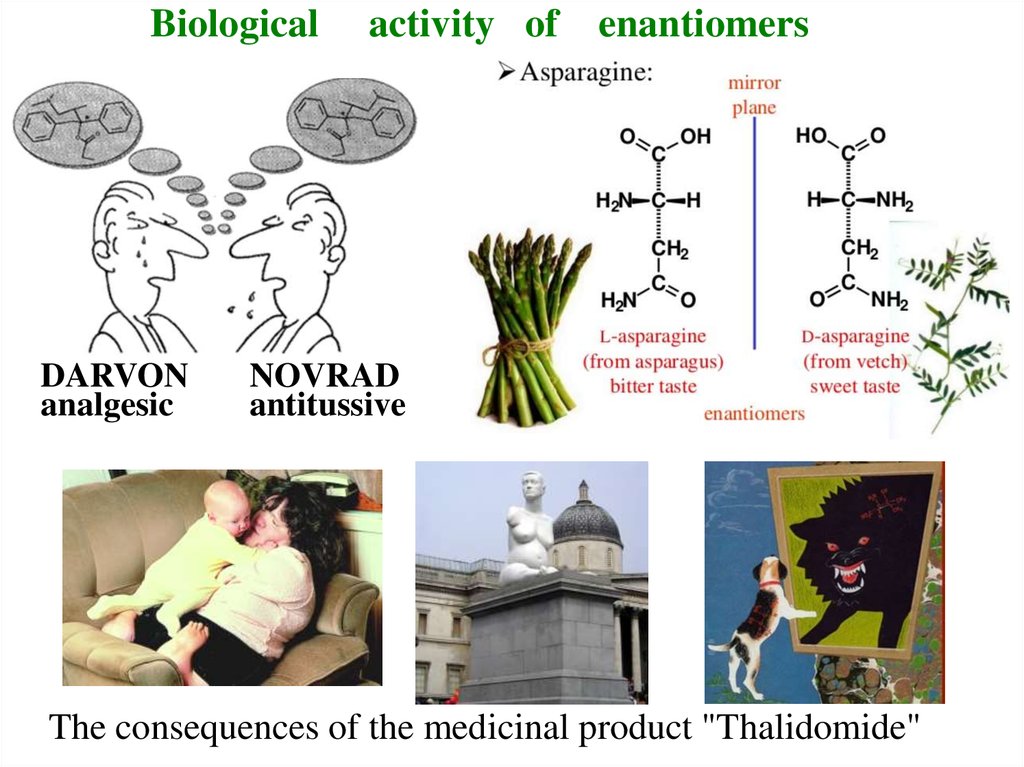
11. Biological activity of enantiomers

12. Biological activity of enantiomers

Biological
DARVON
analgesic
activity of enantiomers
NOVRAD
antitussive
The consequences of the medicinal product "Thalidomide"

13. Acidity and basicity of organic compounds

• Bronsted’s acids (proton acids) are neutral molecules
or ions, which are able to donate proton (proton donors).
• Bronsted’s bases are neutral molecules or ions, which
are able to accept proton (proton acceptors).
• Acid and base features are not absolute but relative
features of compounds: acid features appear only in the
presence of base; and base features appear only in the
presence of acid. As a solvent at studying acid-base
balance water is usually used.

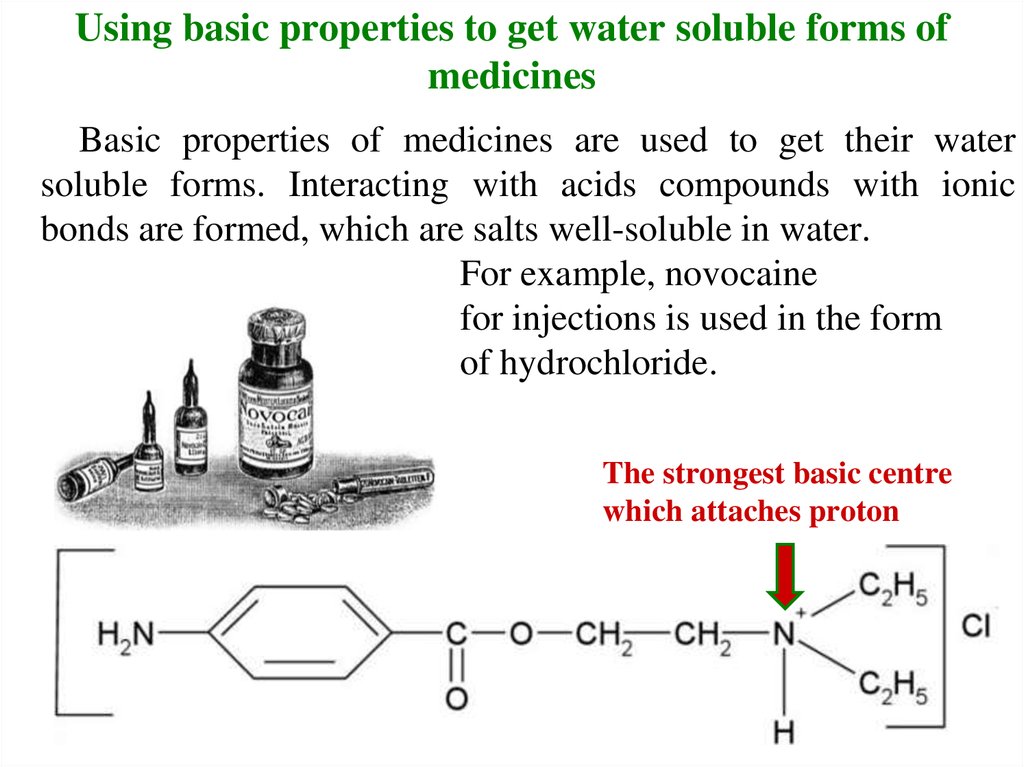
14. Using basic properties to get water soluble forms of medicines

Basic properties of medicines are used to get their water
soluble forms. Interacting with acids compounds with ionic
bonds are formed, which are salts well-soluble in water.
For example, novocaine
for injections is used in the form
of hydrochloride.
The strongest basic centre
which attaches proton

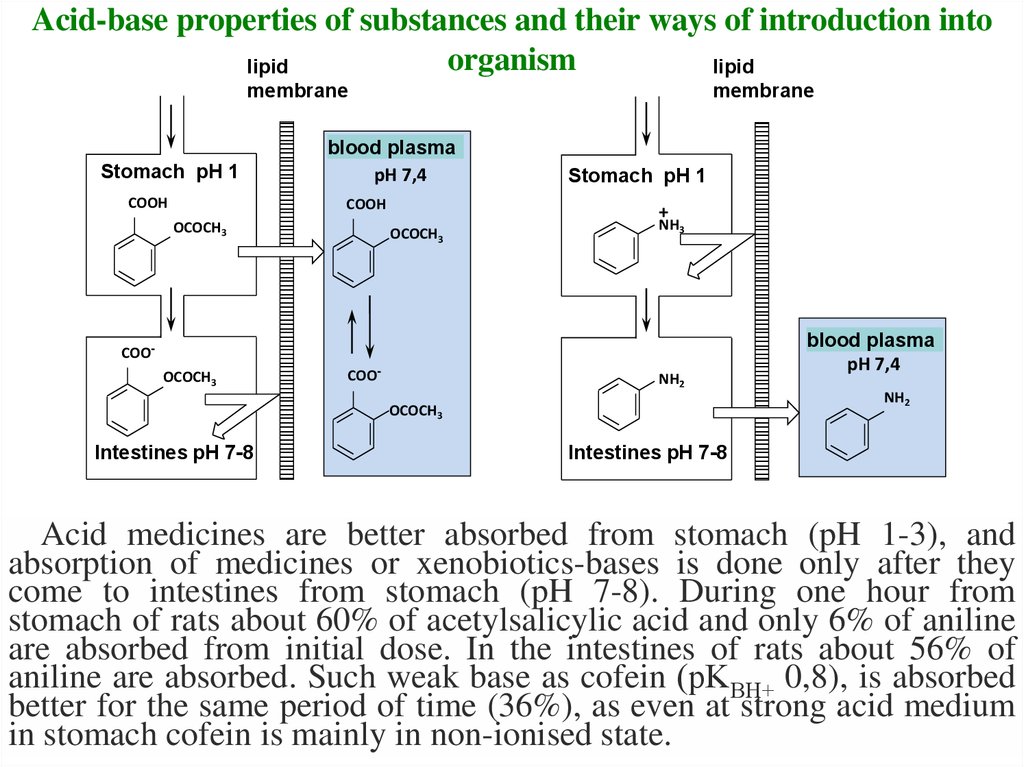
15. Acid-base properties of substances and their ways of introduction into organism

lipid
lipid
липидная
липидная
мембрана
membrane
Желудок рН 1рН
Stomach
1
СООН
мембрана
membrane
blood plasma
рН 7,4
СООН
ОСОСН3
Желудок рНрН
1 1
Stomach
+
ОСОСН3
NH3
СОООСОСН3
СОО-
NH2
NH2
ОСОСН3
Кишечник рН 7-8
Intestines
рН 7-8
blood plasma
рН 7,4
Кишечник рН 7-8
Intestines
рН 7-8
Acid medicines are better absorbed from stomach (pH 1-3), and
absorption of medicines or xenobiotics-bases is done only after they
come to intestines from stomach (pH 7-8). During one hour from
stomach of rats about 60% of acetylsalicylic acid and only 6% of aniline
are absorbed from initial dose. In the intestines of rats about 56% of
aniline are absorbed. Such weak base as cofein (рKВH+ 0,8), is absorbed
better for the same period of time (36%), as even at strong acid medium
in stomach cofein is mainly in non-ionised state.

16. Types of reactions in Organic chemistry

Organic reactions are classified according to the
following principles:
1. Electron nature of reagents.
2. Number of particle change due to reaction.
3. Panial (additional) principles.
4. Mechanism of elementary
reaction stage.

17. According to electron nature of reagents reactions are subdivided into: nucleophilic, electrophilic and free radical

• Free radicals are electroneutral particles which have non-shared
electron, for example, Cl , NO2. Free radical reactions are typical
of alkanes.
• Electrophilic reagents are cations or molecules which in itself or
in the presence of catalyst have high affinity to electron pair or
negatively charged molecule centres. They include cations H+, Cl+,
+NO2, +SO3H, R+ and molecules with free orbitals AlCl3, ZnCl2 и
т.п.
Electrophilic reactions are typical of alkenes, alkanynes, aromatic
compounds (addition on the place of the double bond, proton
substitution).
• Nucleophilic reagents are anions or molecules which have
centres of higher electron density. They include anions and moleculs
as
HO-, RO-, Cl-, Br-, RCOO-, CN-, R-, NH3, C2H5OH, etc.

18.

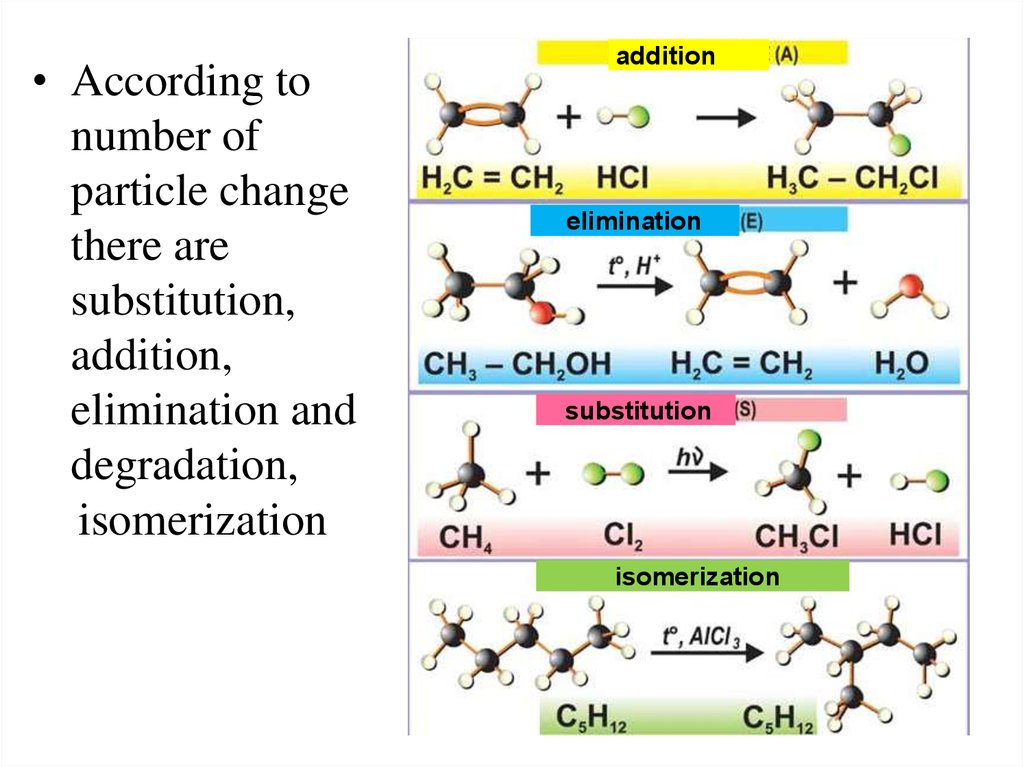
• According to
number of
particle change
there are
substitution,
addition,
elimination and
degradation,
isomerization
addition
elimination
substitution
isomerization

19.

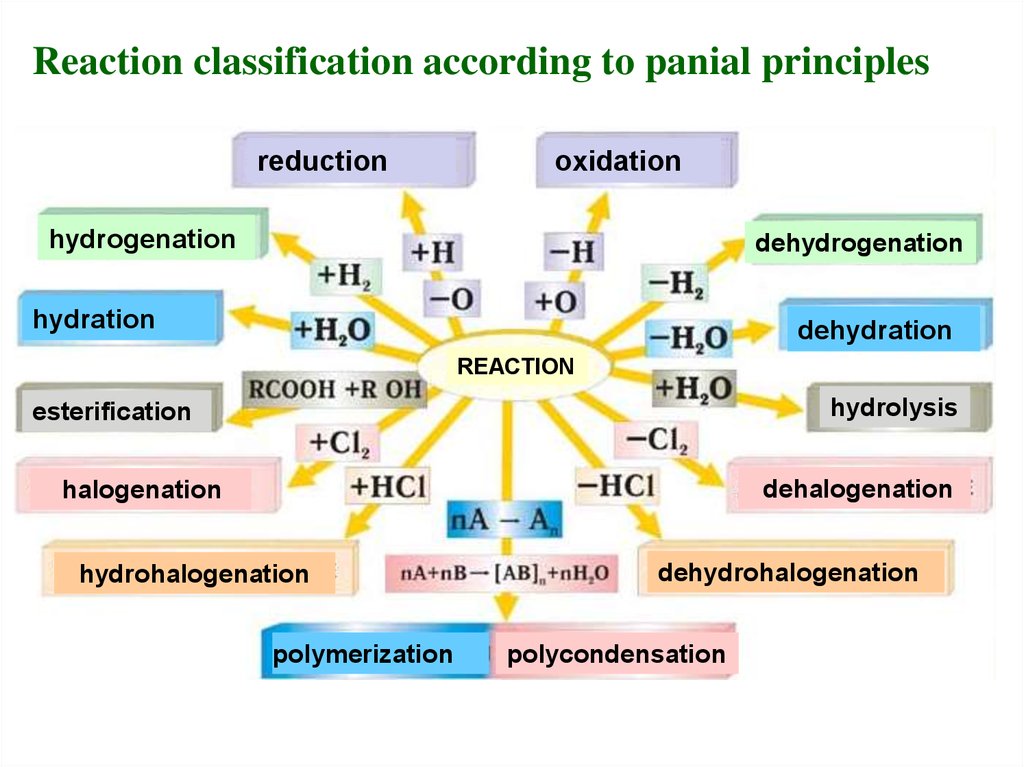
Reaction classification according to panial principles
reduction
oxidation
hydrogenation
dehydrogenation
hydration
dehydration
REACTION
hydrolysis
esterification
dehalogenation
halogenation
hydrohalogenation
polymerization
dehydrohalogenation
polycondensation

20.

• Poly-functional compounds contain several same
functional groups.
• Hetero-functional compounds contain several
different functional groups.
• Hetero-poly-functional compoundsные
contain same and
different functional groups.
glucose
fructose

21.

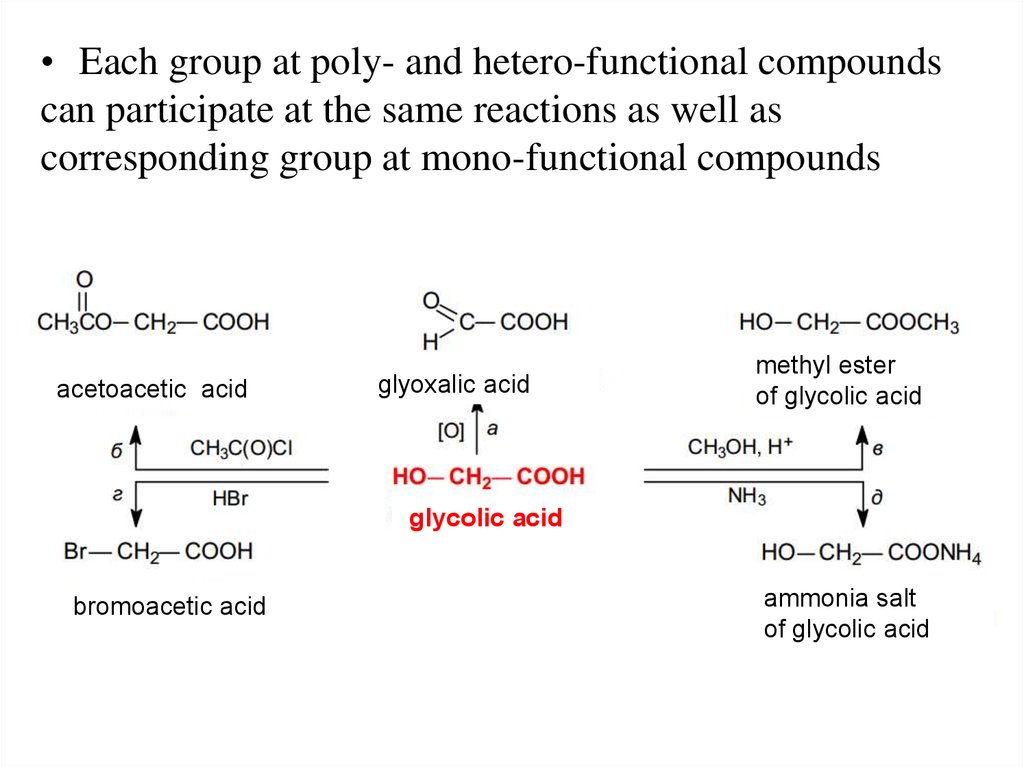
• Each group at poly- and hetero-functional compounds
can participate at the same reactions as well as
corresponding group at mono-functional compounds
acetoacetic acid
glyoxalic acid
methyl ester
of glycolic acid
glycolic acid
bromoacetic acid
ammonia salt
of glycolic acid

22. Characteristic properties of poly- and hetero-functional compounds

• A lot of properties (amphoteric character)
• Increase or decrease of some properties in comparison to
mono-functional compounds (if ОН, SH, СООН groups are at the
structure of the molecule then it leads to acidic property increase, if
amino groups are at the molecule NH2, NH, it leads
to basic property increase.
acetic acid
If there is additional electron acceptor group near
acid centre then acid property is increased;
If there is electron acceptor substitute then
oxalic acid
nucleophilic reactions are facilitated and electrophilic reaction rate is
slower
• New specific properties appear

23. Specific properties of poly- and hetero-functional compounds

Specific properties of poly- and heterofunctional compounds
• Cycle formation reaction
• Chelate complex formation

24. Polyfunctional compounds as an antidotes

protein
unitiol
protein

25.

Bioorganic chemistry