Похожие презентации:
Point defects and diffusion
1.
2.
Point DefectsCrystal defects
Crystalline solids have a very regular atomic structure: that is, the local positions of
atoms with respect to each other are repeated at the atomic scale. These
arrangements are called perfect crystal structures. However, above 0°C all crystalline
materials are not perfect: the regular pattern of atomic arrangement is interrupted by
crystal defects. The defect types are classified according to their dimension:
- Point defects
- Line defects
- Planar defects
- Bulk defects
Importance of defects: Defects determine many properties of materials (those
properties that we call "structure sensitive properties"). Even properties like the
specific resistance of semiconductors, conductance in ionic crystals or diffusion
properties in general which may appear as intrinsic properties of a material are
defect dominated - in case of doubt by the intrinsic defects. Few properties - e.g.
the melting point or the elastic modulus - are not, or only weakly influenced by
defects.
3.
Point DefectsPoint defects in ionic solids I
Missing atoms within a structure, atoms at "wrong" sites, "wrong" atoms (impurities) are
considered 0-dimensional irregularities and are called point defects.
Frenkel defect: anion
vacancy-interstitial
cation pair.
Yanagida et al.: p. 59
Schottky defect: anion
-cation vacancy pair.
Anti-Schottky defect:
anion-cation vacancy
pair plus interstial pair.
http://www.tf.uni-kiel.de/matwis/amat/def_en/index.html
4.
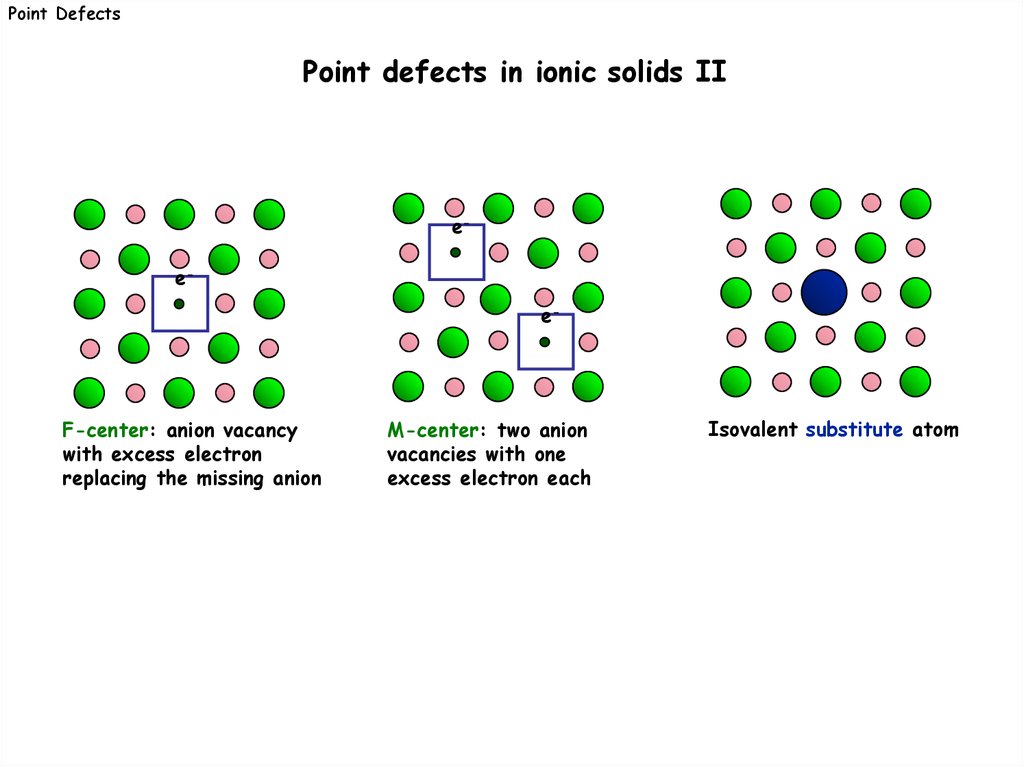
Point DefectsPoint defects in ionic solids II
ee-
e-
F-center: anion vacancy
with excess electron
replacing the missing anion
M-center: two anion
vacancies with one
excess electron each
Isovalent substitute atom
5.
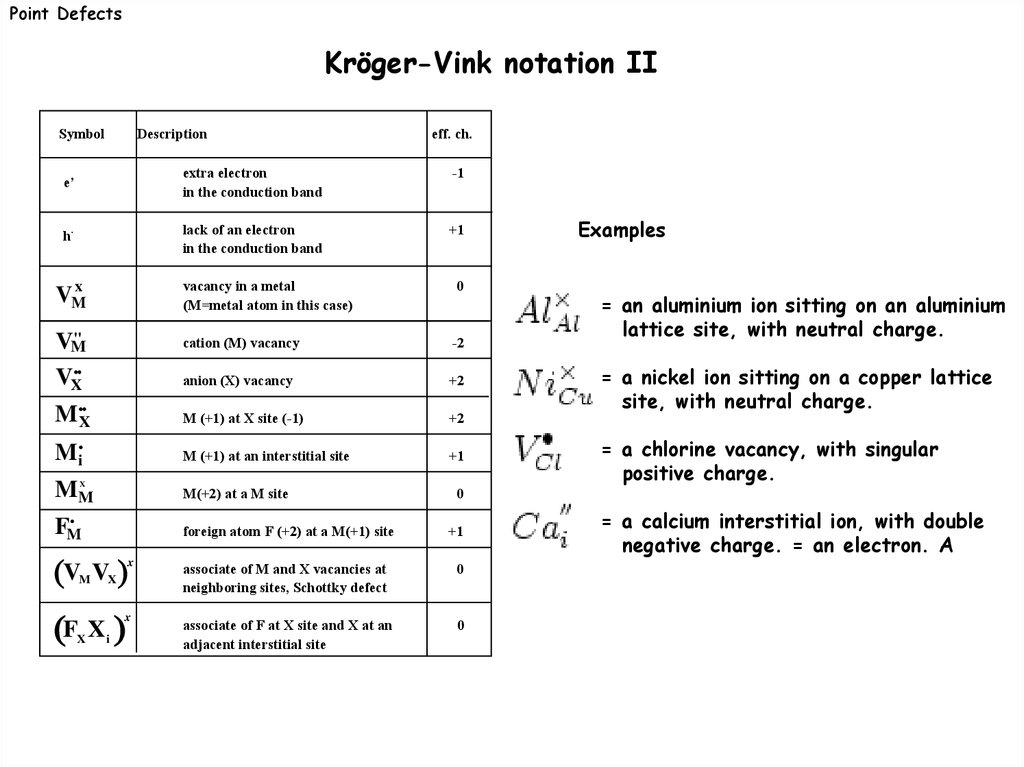
Point DefectsKröger-Vink notation I
Point defects can be treated like chemical species. The Kröger-Vink notation is a set of
conventions used to describe defect species e.g their electical charge and their lattice
position.
C
MS
General form:
M corresonds to the species. These include:
atoms - e.g. Si, Ni, O, Cl,
vacancies - V
interstitials - i
electrons - e
holes - h
(missing electrons)
S indicates the lattice site that the species occupies. For instance, Ni might occupy a Cu site.
In this case, M in the general formula would be Ni and S would be replaced by Cu.
Interstitial sites are also used here.
C corresponds to the electric charge of the species relative to site that it occupies. To
continue the previous example, Ni often has the same valency as Cu, so the relative charge is
zero. To indicate null charge, the sign " " is used. A single " " indicates a single positive
charge, while two would represent two positive charges. Finally," ' "signifies a single negative
charge, so two, would indicate a double negative charge.
6.
Point DefectsKröger-Vink notation II
Symbol
Description
eff. ch.
e’
extra electron
in the conduction band
-1
h·
lack of an electron
in the conduction band
+1
VMx
vacancy in a metal
(M=metal atom in this case)
0
''
VM
cation (M) vacancy
-2
anion (X) vacancy
+2
M (+1) at X site (-1)
+2
Mi
M (+1) at an interstitial site
+1
MM
M(+2) at a M site
VX
MX
X
FM
V
M
+1
x
associate of M and X vacancies at
neighboring sites, Schottky defect
0
x
associate of F at X site and X at an
adjacent interstitial site
0
F X
X
i
= an aluminium ion sitting on an aluminium
lattice site, with neutral charge.
= a nickel ion sitting on a copper lattice
site, with neutral charge.
= a chlorine vacancy, with singular
positive charge.
0
foreign atom F (+2) at a M(+1) site
VX
Examples
= a calcium interstitial ion, with double
negative charge. = an electron. A
7.
Point DefectsDefect chemical reaction
Reaction involving defects must be:
- mass balanced
- charge balanced: the effective charge must
be balanced.
- site balanced: the ratio between
anion and cation must remain constant
Example:
Formation of a Schottky defect in periclase:
''
MgMg + OO = VMg
+ VO + MgO (sf)
X
X
8.
Point DefectsThermodynamics of point defects I
- Free energy of a perfect crystal
G perf H perf TS perf
(1)
- The entropy has configurational, Sconf, and vibrational contributions Svib
S perf Sconfig Svib
(2)
- In a perfect crystal the configurational contribution is zero
- Free energy of a real crystal containing n Frenkel defect
Gdef G perf nhdef nTsdvib TSconf
gdef hdef Tsdvib
(4)
gdef: free energy of one defect
- Change of the free energy due to the
formation of n defects:
G G perf Gdef ngdef TSconf
(3)
Gperf: free energy of the perfect crystal
hdef: enthalpy of formation of one defect
sdvib: vibrational entropy of one defect
Sconf: configurational entropy due to the
arrangement of n defects
(5)
-Configurational entropy
Sconf k ln
(6)
Yanagida et al.: p. 60-61
s. Exercice 2.1-4 in http://www.tf.uni-kiel.de/matwis/amat/def_en/index.html
9.
Point DefectsThermodynamics of point defects II
-Number of ways to arrange nv vacancies within a crystal with N lattice sites
and to distribute ni interstitial sites :
v
N!
(N nv )!nv !
N! N ln N N
i
N!
(N ni )!ni !
v i
(7)
(8, Stirling approximation)
-Configurational entropy (assuming number of interstial sites = number of lattice sites):
(9)
Sconf 2k N ln N N n ln N n n ln n
-Change of the free energy due to the formation of n defects:
N
N n
G ngdef N ln
n
ln
n
N n
(10)
- Concentration of defects at equilibrium
gdef
G
n
0 exp
n
N
2kT
(11)
Yanagida et al.: p. 60-61
s. Exercice 2.1-4 in http://www.tf.uni-kiel.de/matwis/amat/def_en/index.html
10.
Point DefectsThermodynamics of point defects III
Entropy
Configurational Entropy
Entropy originating from the many possibilities of arranging many vacancies
Formation ("vibrational") Entropy
It can be seen as the additional entropy or disorder added to the crystal with every
additional vacancy. There is disorder associated with every single vacancy because the
vibration modes of the atoms are disturbed by defects.Atoms with a vacancy as a
neighbour tend to vibrate with lower frequencies because some bonds, acting as
"springs", are missing. These atoms are therefore less well localized than the others
and thus more "unorderly" than regular atoms.
11.
Point DefectsThermodynamics of point defects IV
hf
T=const.
G
G
G0
Gmin
-T Sc
neq
n
The stippled lines are for a higher temperature than for
the solid lines. The equilibrium defect concentration
increases thus with increasing temperature.
12.
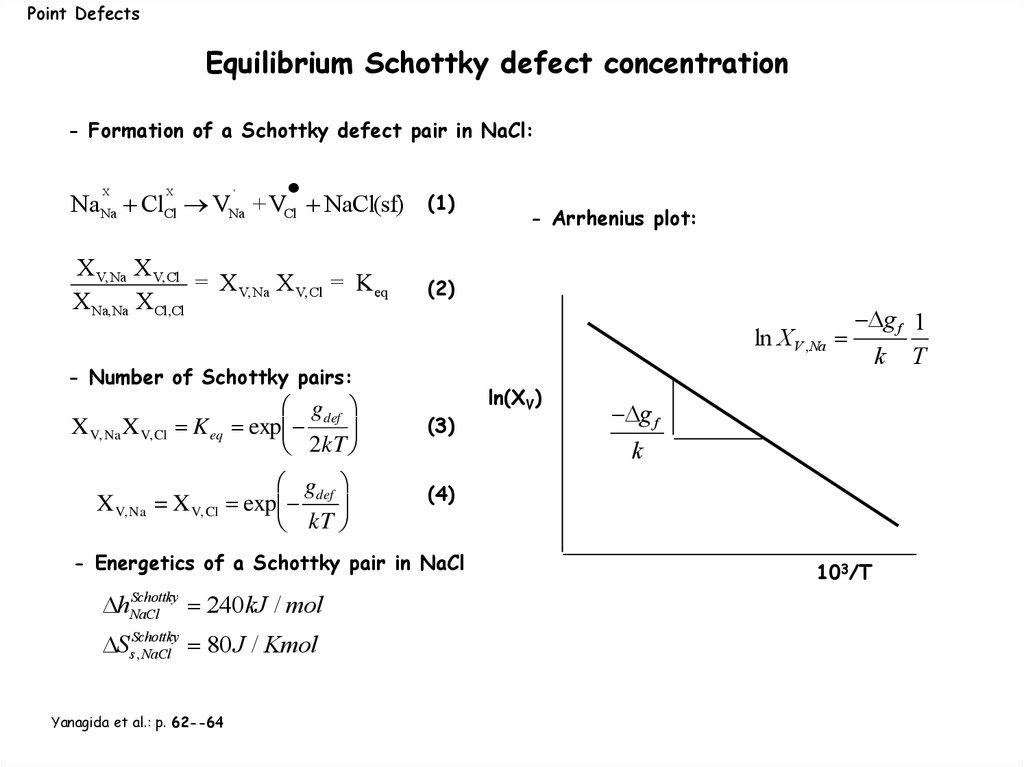
Point DefectsEquilibrium Schottky defect concentration
- Formation of a Schottky defect pair in NaCl:
X
,
X
NaNa ClCl VNa +VCl NaCl(sf)
(1)
X V,Na X V,Cl
= X V,Na X V, Cl = K eq
X Na,Na X Cl,Cl
(2)
- Arrhenius plot:
ln XV ,Na
- Number of Schottky pairs:
X V, Na X V, Cl
gdef
K eq exp
2kT
g
X V, Na = X V, Cl exp def
kT
(3)
Ss,Schottky
NaCl 80J / Kmol
Yanagida et al.: p. 62--64
g f
k
(4)
- Energetics of a Schottky pair in NaCl
Schottky
hNaCl
240kJ / mol
ln(XV)
g f 1
k T
103/T
13.
Point DefectsExtrinsic defect concentration I
- Substitution of a divalent cation (Ca) for
Na in NaCl and formation of extrinsic
vacancies:
2NaNa Ca CaNa +VNa Na(sf) (1)
X V,Na = X Ca,Na (2)
XV ,Cl XCa,Na XV ,Cl Keq
- Formation of intrinsic vacancies:
X
X
,
NaNa ClCl VNa +VCl NaCl(sf) (3)
- Total number of cation vacancies:
tot
XV ,Na XV ,Cl Keq (5)
X
'
tot
X V, Na = X V, Cl + X Ca,Na (4)
- Number of anion vacancies:
XV ,Cl
2
XV ,Cl
(6)
XV ,Cl XCa,Na Keq 0 (7)
XCa,Na
XCa,Na
2
2K eq
4K eq
(8)
14.
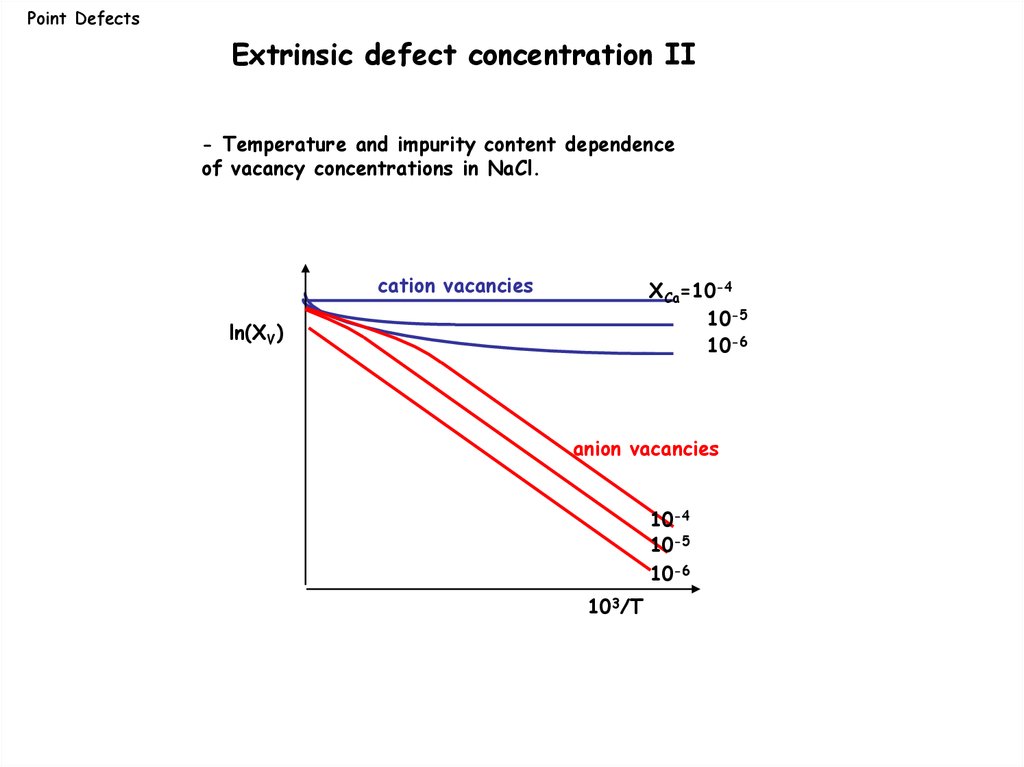
Point DefectsExtrinsic defect concentration II
- Temperature and impurity content dependence
of vacancy concentrations in NaCl.
cation vacancies
XCa=10-4
10-5
10-6
ln(XV)
anion vacancies
10-4
10-5
10-6
103/T
15.
Point DefectsNonstoichiometric defects
In nonstoichiometric defect reactions the composition of the cystal changes as a result
of the reaction. One of the more common nonstoichiometric reactions that occurs at low
oxygen partial pressure is
X
OO =
1
O 2 + VO + 2e 2
The two electrons remain localized at the vacant site to guarantee charge neutrality.
oxigen partial pressure addition of oxygen may lead to nonstoichiometry:
At higher
1
O 2 = O i + 2h
2
The label h means "electron hole" e.g. the oxygen atom "steels" the electrons from a
cation leaving holes behind. The above reaction in the case of iron would be written
1
+ 2h
O 2 = O xO + VFe
2
2Fe 2+ + 2h = 2Fe 3
The vacancy in the left side of the first reaction is necessary to maintain site neutrality.
The overall reaction for the oxidation of magnetite is given by
1
O 2 + 2Fe 2+ = O xO + 2Fe 3 + VFe
2
16.
Point DefectsDiffusion
Atomic diffusion is a process whereby the random thermally-activated hopping of
atoms in a solid results in the net transport of atoms. For example, helium atoms
inside a balloon can diffuse through the wall of the balloon and escape, resulting in
the balloon slowly deflating. Other air molecules (e.g. oxygen, nitrogen) have lower
mobilities and thus diffuse more slowly through the balloon wall. There is a
concentration gradient in the balloon wall, because the balloon was initially filled with
helium, and thus there is plenty of helium on the inside, but there is relatively little
helium on the outside (helium is not a major component of air).
17.
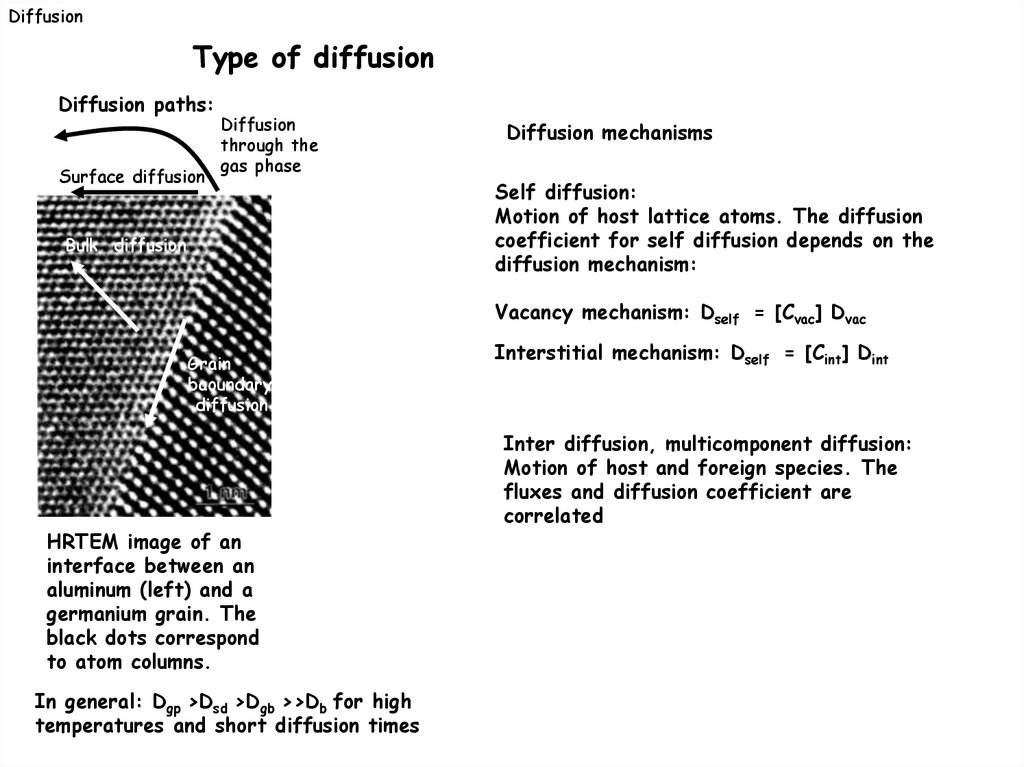
DiffusionType of diffusion
Diffusion paths:
Surface diffusion
Diffusion
through the
gas phase
Bulk diffusion
Diffusion mechanisms
Self diffusion:
Motion of host lattice atoms. The diffusion
coefficient for self diffusion depends on the
diffusion mechanism:
Vacancy mechanism: Dself = [Cvac] Dvac
Grain
baoundary
diffusion
HRTEM image of an
interface between an
aluminum (left) and a
germanium grain. The
black dots correspond
to atom columns.
In general: Dgp >Dsd >Dgb >>Db for high
temperatures and short diffusion times
Interstitial mechanism: Dself = [Cint] Dint
Inter diffusion, multicomponent diffusion:
Motion of host and foreign species. The
fluxes and diffusion coefficient are
correlated
18.
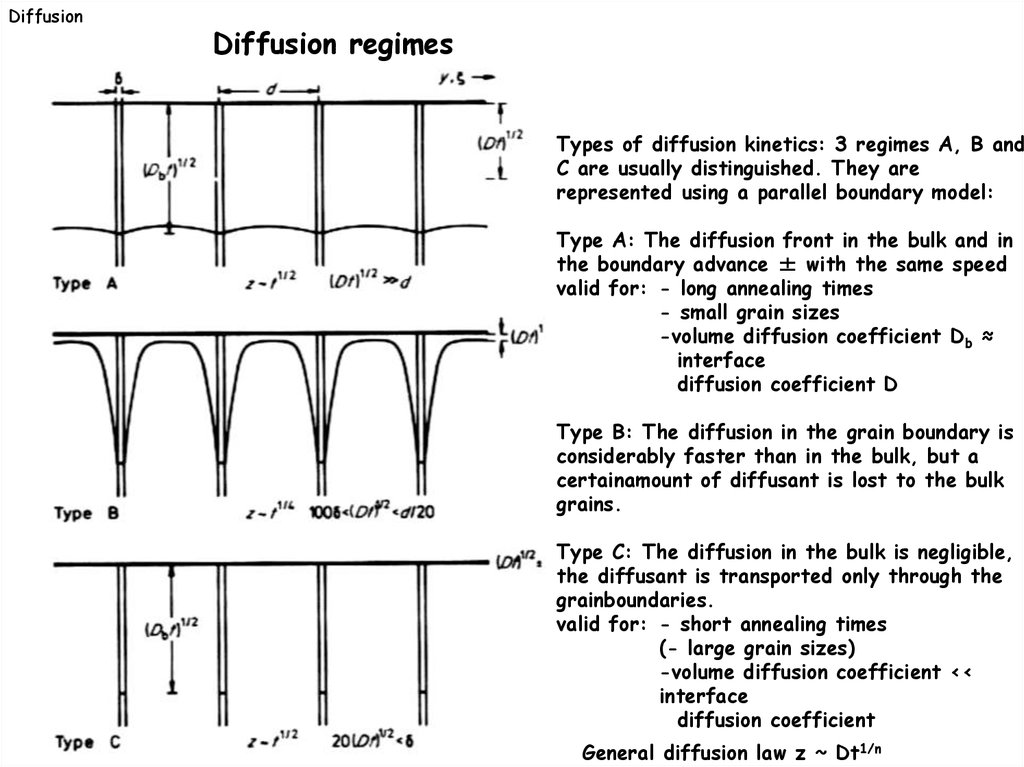
DiffusionDiffusion regimes
Types of diffusion kinetics: 3 regimes A, B and
C are usually distinguished. They are
represented using a parallel boundary model:
Type A: The diffusion front in the bulk and in
the boundary advance ± with the same speed
valid for: - long annealing times
- small grain sizes
-volume diffusion coefficient Db ≈
interface
diffusion coefficient D
Type B: The diffusion in the grain boundary is
considerably faster than in the bulk, but a
certainamount of diffusant is lost to the bulk
grains.
Type C: The diffusion in the bulk is negligible,
the diffusant is transported only through the
grainboundaries.
valid for: - short annealing times
(- large grain sizes)
-volume diffusion coefficient <<
interface
diffusion coefficient
General diffusion law z ~ Dt1/n
19.
DiffusionAtomistic diffusion mechanisms
Exchange mechanism
Ring rotation mechanicsm
Vacancy mechanism
Interstitial mechanism
Diffusion couple
t0
t1
t2
A diffusion couple is an assembly of two materials in such intimate contact that the
atoms of each material can diffuse into the other.
Yanagida et al.: p. 58 - 68
20.
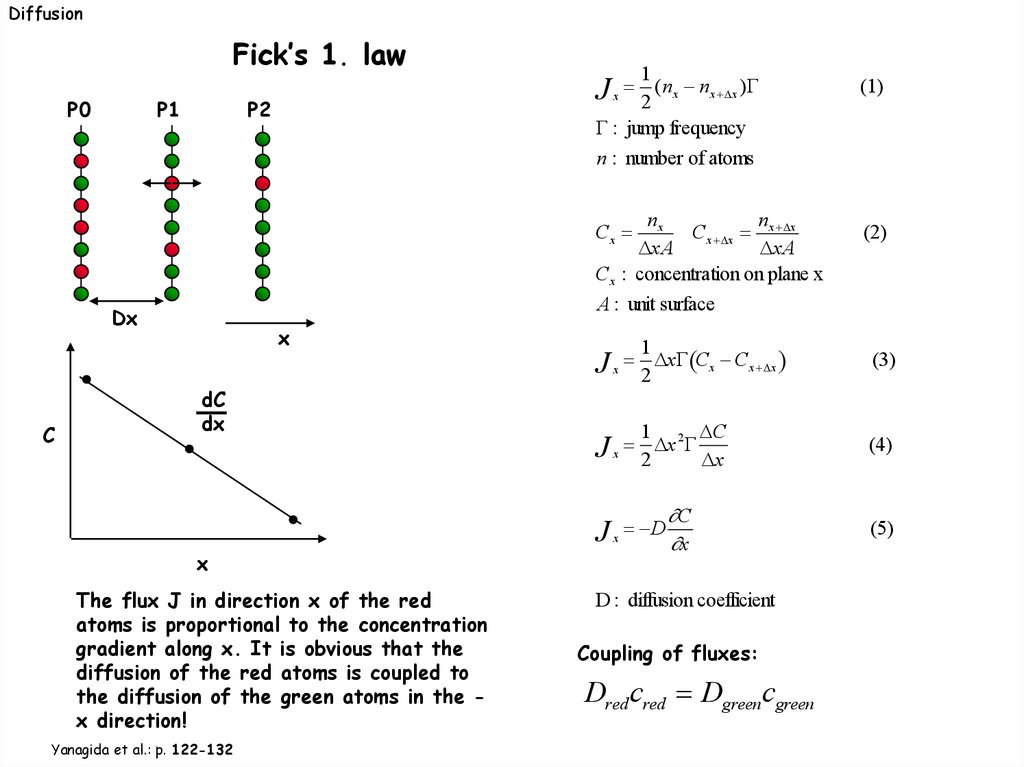
DiffusionFick’s 1. law
P0
P1
1
(n x n x x )
2
: jump frequency
J
P2
x
(1)
n : number of atoms
nx
n
Cx x x x
xA
xA
Cx : concentration on plane x
Cx
A : unit surface
Dx
C
(2)
x
dC
dx
J
x
J
x
1
x Cx Cx x
2
(3)
1
C
x 2
2
x
(4)
C
x
(5)
J x D
x
The flux J in direction x of the red
atoms is proportional to the concentration
gradient along x. It is obvious that the
diffusion of the red atoms is coupled to
the diffusion of the green atoms in the x direction!
Yanagida et al.: p. 122-132
D : diffusion coefficient
Coupling of fluxes:
Dred cred Dgreen cgreen
21.
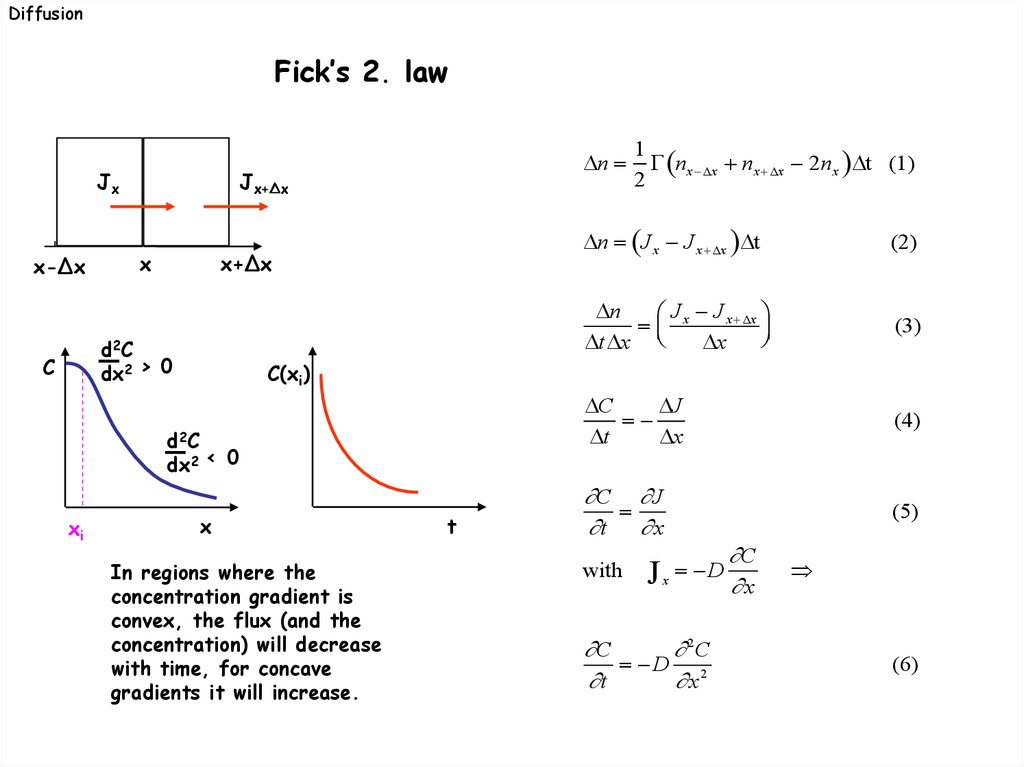
DiffusionFick’s 2. law
Jx
Jx+∆x
x
x-∆x
x+∆x
d2 C
dx2 > 0
C
n
n J x J x x t
(2)
n
J J x x
x
t x
x
(3)
C
J
t
x
(4)
C J
t x
(5)
C(xi)
d2 C
dx2 < 0
xi
1
nx x nx x 2nx t (1)
2
x
In regions where the
concentration gradient is
convex, the flux (and the
concentration) will decrease
with time, for concave
gradients it will increase.
t
with
J x D
C
2C
D 2
t
x
C
x
(6)
22.
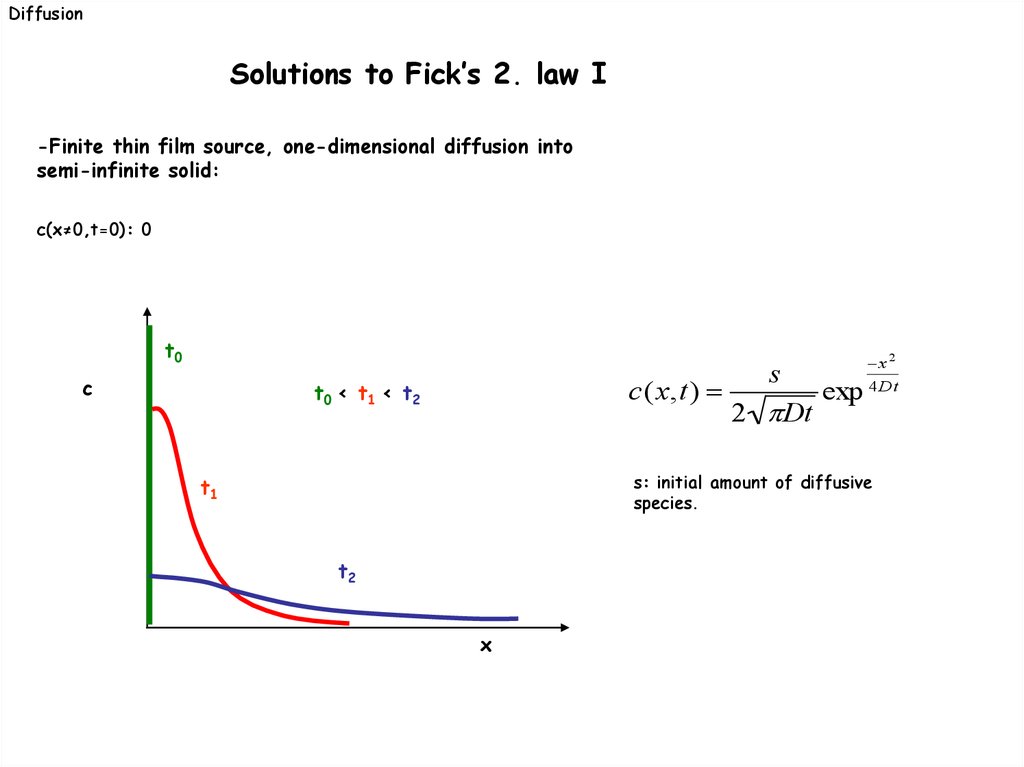
DiffusionSolutions to Fick’s 2. law I
-Finite thin film source, one-dimensional diffusion into
semi-infinite solid:
c(x≠0,t=0): 0
t0
c
c(x,t)
t0 < t1 < t2
t1
t2
x
s
2 Dt
exp
x 2
4 Dt
s: initial amount of diffusive
species.
23.
Diffusion1-D diffusion
1-D diffusion from a finite point source
24.
DiffusionSolutions to Fick’s 2. law II
-Finite thin film source of constant concentration, onedimensional diffusion into semi-infinite solid:
c(x≠0,t=0): 0
c(x=0,t): const.
t0 < t1 < t2
t0
c
x
c(x,t) c 0 1 erf
2 Dt
t1
t2
x
c0: initial concentration
erf: error function
25.
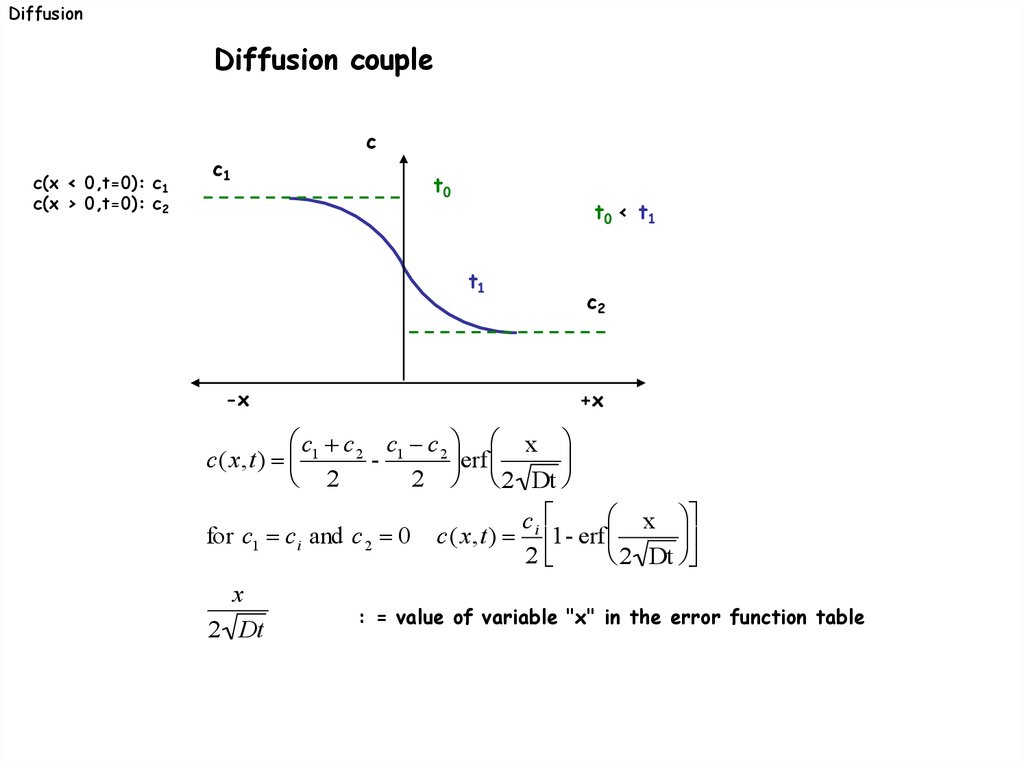
DiffusionDiffusion couple
c(x < 0,t=0): c1
c(x > 0,t=0): c2
c1
c
t0
t0 < t1
t1
-x
c2
+x
c1 c 2 c1 c 2 x
c(x,t)
erf
2
2 2 Dt
x
c
for c1 c i and c 2 0 c(x,t) i 1- erf
2
2 Dt
x
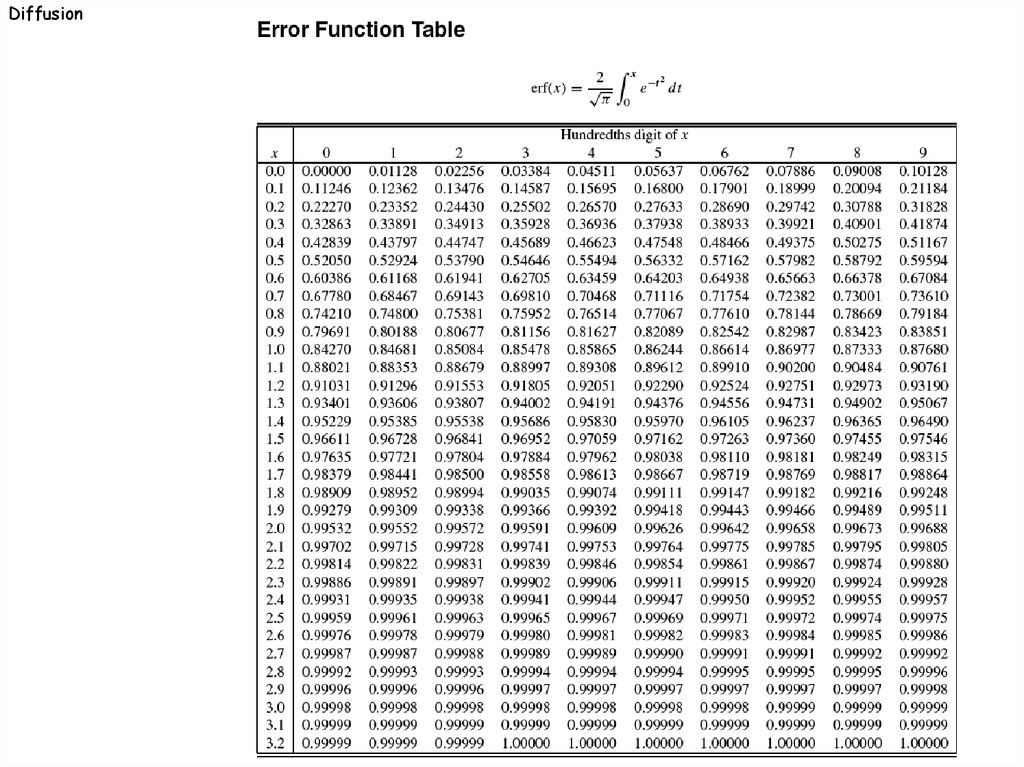
: = value of variable "x" in the error function table
2 Dt
26.
Diffusion1-D diffusion couple
1.00
1
0.5 0.1
2
3
C/C 0
0.750
5
10
0.500
2(Dt)
1/2
=
0.250
0.00
-4
-3
-2
-1
0
1
Distance, x [units of 2(Dt)
2
1/2
3
]
Diffusion profiles for 1-D diffusion couple for different
diffusion times
4
27.
Diffusion28.
DiffusionDiffusion front
- Distance x’ from a source with finite concentration where a certain small amount of the
initial concentration has passed f.ex. < 10-3 c0 :
c
Diffusion profile after time t:
co
c0
exp
x 2
4 Dt
dt
0
Material that diffused beyond the point x'
at which the concentration is 10-3 c0 :
10-3co
10 3
exp
x'
exp
x 2
x 2
10 c 0
4 Dt
4 Dt
dt
exp
x 2
x'
x
x’
3
solving for x’:
dt
0
x' 4 Dt Dt
4 Dt
dt
29.
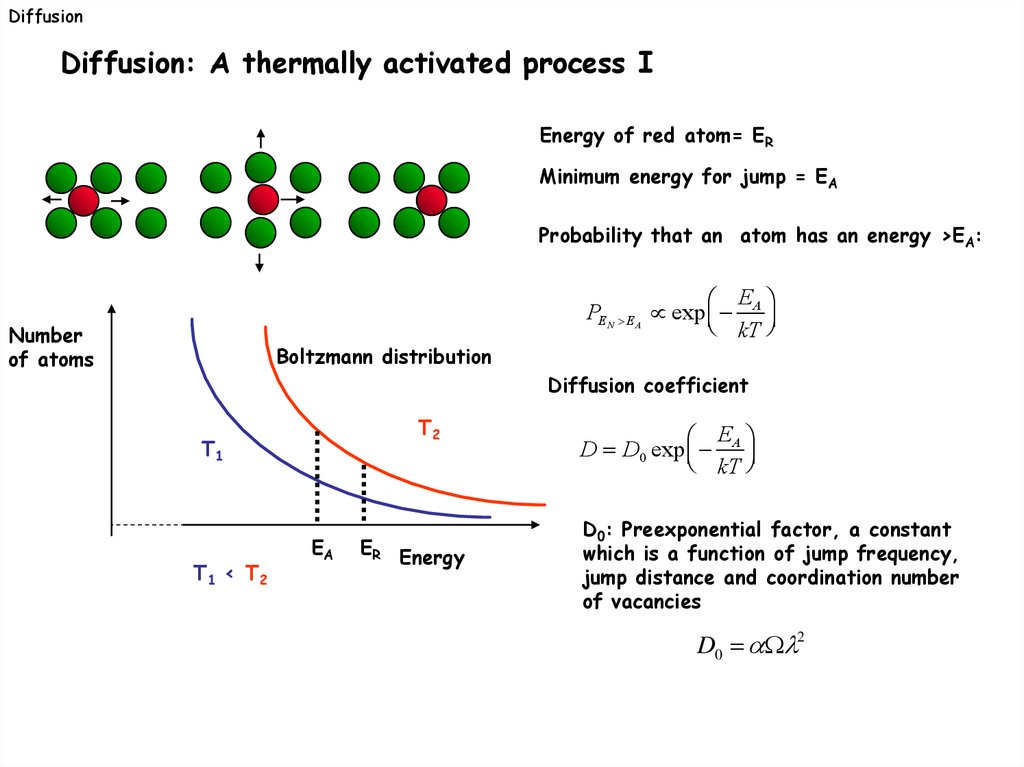
DiffusionDiffusion: A thermally activated process I
Energy of red atom= ER
Minimum energy for jump = EA
Probability that an atom has an energy >EA:
Number
of atoms
Boltzmann distribution
E
PEN EA exp A
kT
Diffusion coefficient
T2
T1
T1 < T2
EA
ER Energy
E
D D0 exp A
kT
D0: Preexponential factor, a constant
which is a function of jump frequency,
jump distance and coordination number
of vacancies
D0 2
30.
DiffusionDiffusion: A thermally activated process II
The preexponential factor and the activation energy for a diffusion process can be
determined from diffuson experiments done at different temperatures. The result are
presented in an Arrhenius diagram.
E
D D0 exp A
kT
ln D0
E
A
k
lnD
1/T
ln D ln D0
EA 1
k T
In the Arrhenius diagram the slope
is proportional to the activation
energy and the intercept gives the
preexponential factor.
31.
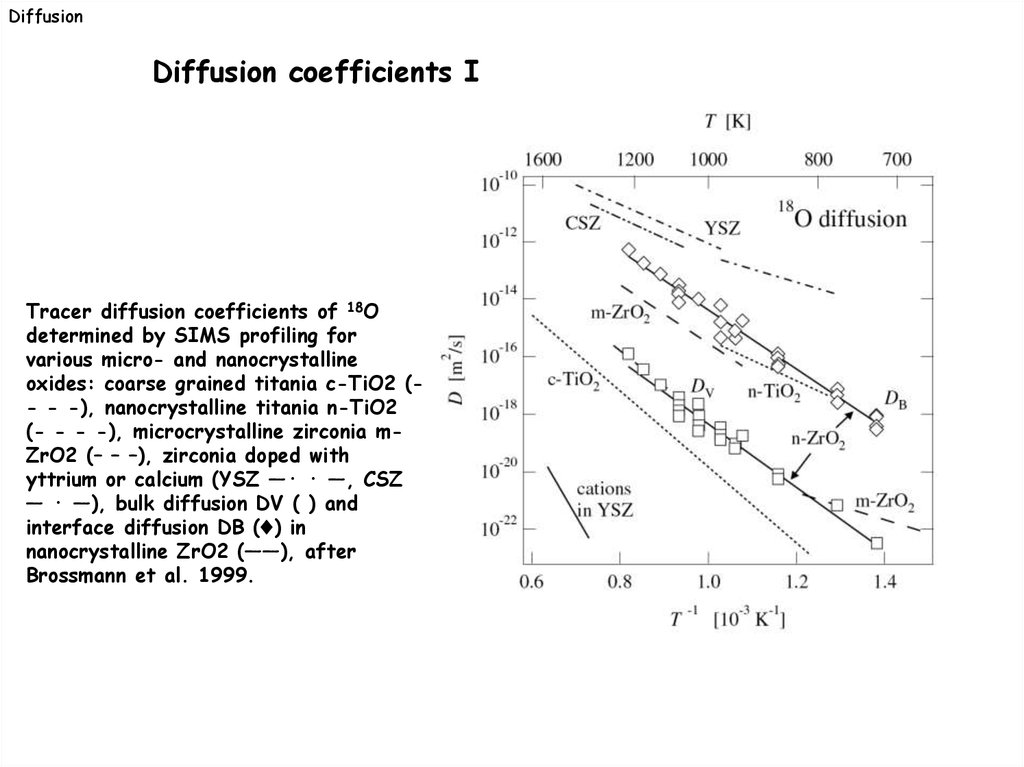
DiffusionDiffusion coefficients I
Tracer diffusion coefficients of 18O
determined by SIMS profiling for
various micro- and nanocrystalline
oxides: coarse grained titania c-TiO2 (- - -), nanocrystalline titania n-TiO2
(- - - -), microcrystalline zirconia mZrO2 (– – –), zirconia doped with
yttrium or calcium (YSZ —· · —, CSZ
— · —), bulk diffusion DV ( ) and
interface diffusion DB (♦) in
nanocrystalline ZrO2 (——), after
Brossmann et al. 1999.
32.
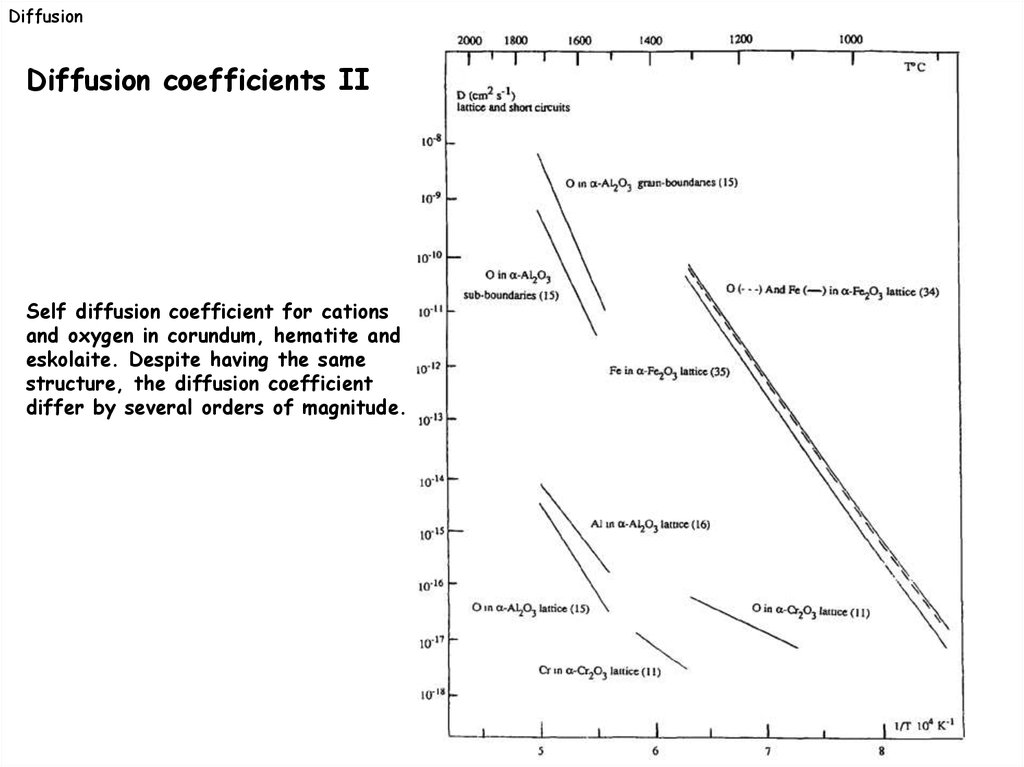
DiffusionDiffusion coefficients II
Self diffusion coefficient for cations
and oxygen in corundum, hematite and
eskolaite. Despite having the same
structure, the diffusion coefficient
differ by several orders of magnitude.

















 Химия
Химия








