Похожие презентации:
Кинематика материальной точки
1. Литература
1. Трофимова Т.И. курс физики: учебное пособие для вузов.М.: Издательский центр «Академия», 2007.
2. Савельев И.В. Курс общей физики (в 5 кн). Кн.1.
Механика. М.: Наука.1998
3. С.М. Новиков. Сборник заданий по общей физике. –
М.: Оникс, Мир и образование, 2007.
2. Предмет физики
Физика - наука, изучающая простейшиеи вместе с тем наиболее общие
закономерности явлений природы,
свойства и строение материи и законы
ее движения.
3.
Материя объективная реальность, которую мыпознаем с помощью органов чувств и
приборов
Движение–
всякое изменение вообще
4. Структура курса в семестре
Часть1. Физические основы механики.Часть 2.Молекулярная физика, основы
термодинамики.
Часть 3. Квантовая физика микрочастиц,
статистическая физика.
5. Физические основы механики
Кинематика материальной точкиКинематика вращательного дфижения
Динамика материальной точки и
поступательного движения
Динамика вращательного движения
Механическа работа. Мощность
Энергия . Закон сохранения энергии
Элементы специальной теории
относительности
6. Тема 1. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
7.
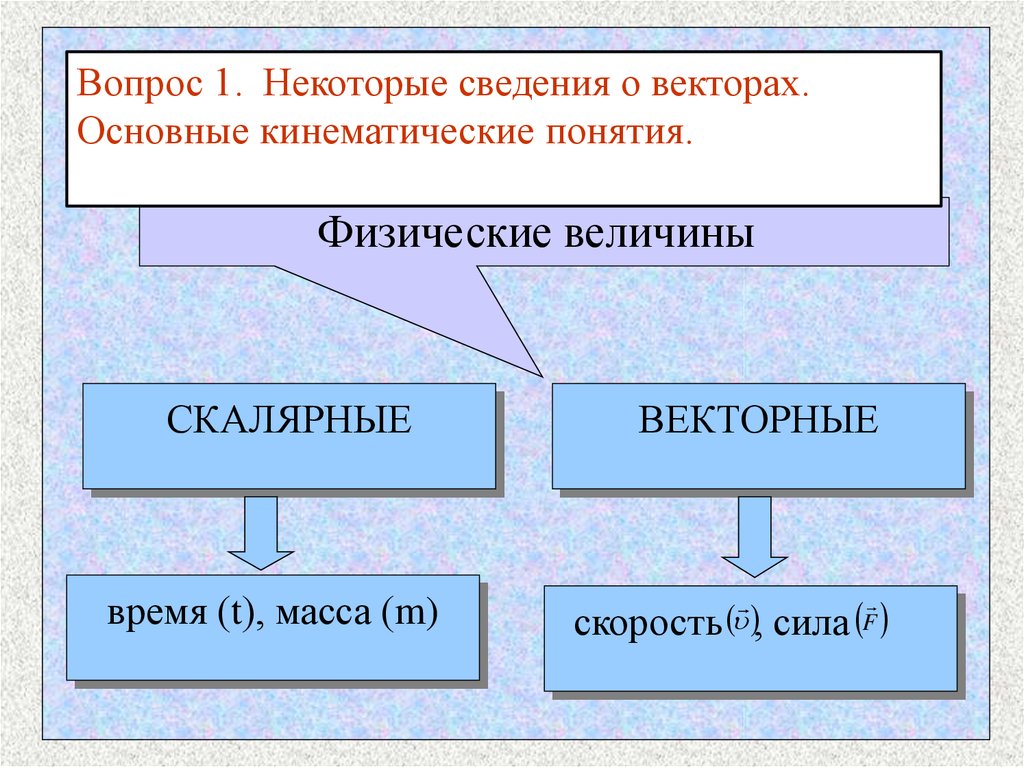
Вопрос 1. Некоторые сведения о векторах.Основные кинематические понятия.
Физические величины
СКАЛЯРНЫЕ
время (t), масса (m)
ВЕКТОРНЫЕ
скорость , сила F
8.
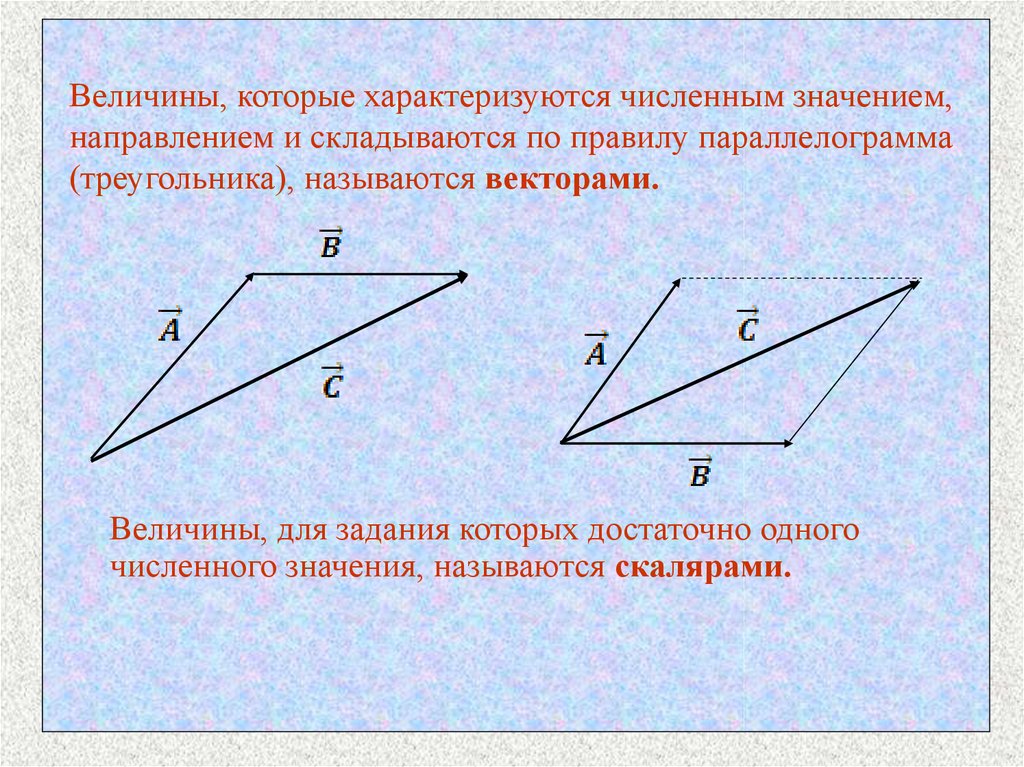
Величины, которые характеризуются численным значением,направлением и складываются по правилу параллелограмма
(треугольника), называются векторами.
Величины, для задания которых достаточно одного
численного значения, называются скалярами.
9.
В литературе вектора принято обозначать буквамижирного шрифта (A).
Числовое значение вектора или его модуль обозначается
тем же символом |A| = A
Обозначение при записях в конспектах A
1. Сложение векторов
Ñ
À Â
Ñ À2 Â 2 2 ÀÂños
2. Вычитание векторов
C A B A B
10.
Основные кинематические понятияМеханика подразделяется на три раздела:
1) кинематику; 2) динамику; 3) статику.
Кинематика рассматривает движение тел,
не рассматривая причин, обуславливающих
это движение.
ФИЗИЧЕСКАЯ МОДЕЛЬ
Материальная точка - это тело, обладающее
массой, размерами которого в условиях
рассматриваемой задачи можно пренебречь.
11. Основные понятия кинематики
Абсолютно твердое тело − тело, деформацией которогов условиях данной задачи можно пренебречь.
Абсолютно упругое тело − тело, которое после
прекращения внешнего силового воздействия полностью
восстанавливает свои первоначальные размеры и форму.
Абсолютно неупругое тело − тело, которое после
прекращения внешнего силового воздействия полностью
сохраняет деформированное состояние, вызванное этим
воздействием.
12. СИСТЕМА КООРДИНАТ
yМасштаб 1 м
0
z
x
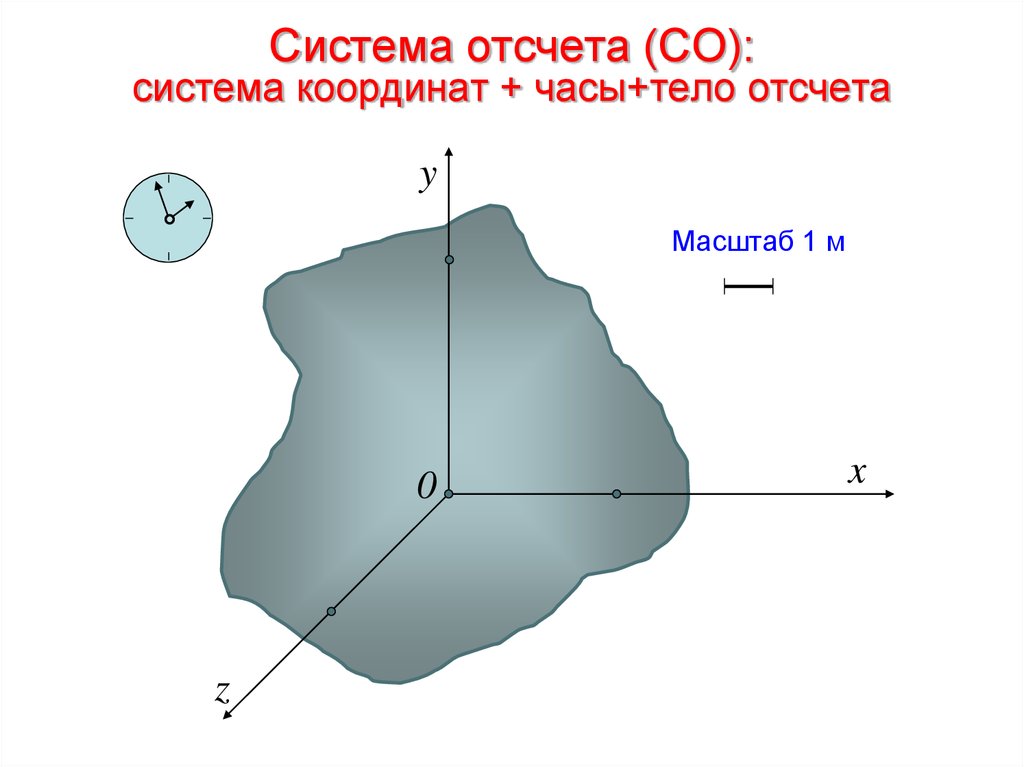
13. Система отсчета (СО): система координат + часы+тело отсчета
yМасштаб 1 м
0
z
x
14.
Тело отсчета – произвольно выбранное тело,относительно которого определяется положение
других (движущихся )тел.
Система отсчета – тело отсчета, связанная с ним
система координат и часы.
В декартовой системе координат положение точки
определяется тремя координатами x, y, z или
радиус- вектором r0 , проведенным из начала отсчета в
данную точку А.
Движение м.т. можно описать тремя
скалярными уравнениями
x x t ; y y t ; z z t
или векторным уравнением
r r t
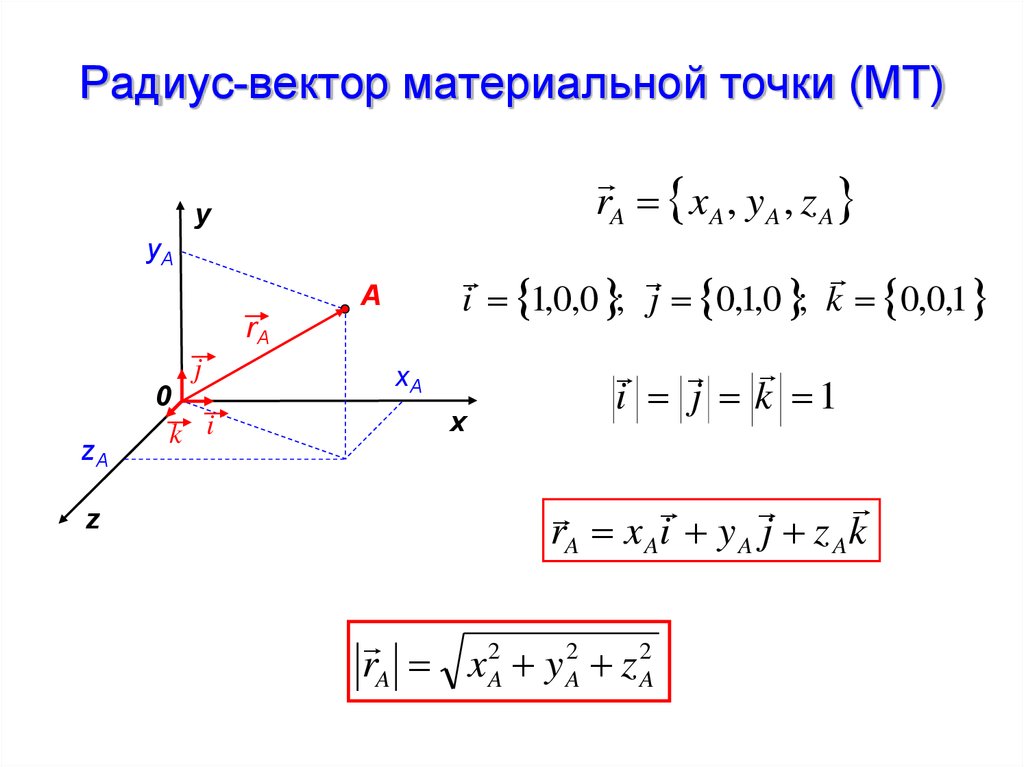
15. Радиус-вектор материальной точки (МТ)
rA xA , y A , z Ay
yА
i 1,0,0 ; j 0,1,0 ; k 0,0,1
A
rA
j
zА
z
0
k i
xА
x
i j k 1
rA x Ai y A j z Ak
rA xA2 y A2 z A2
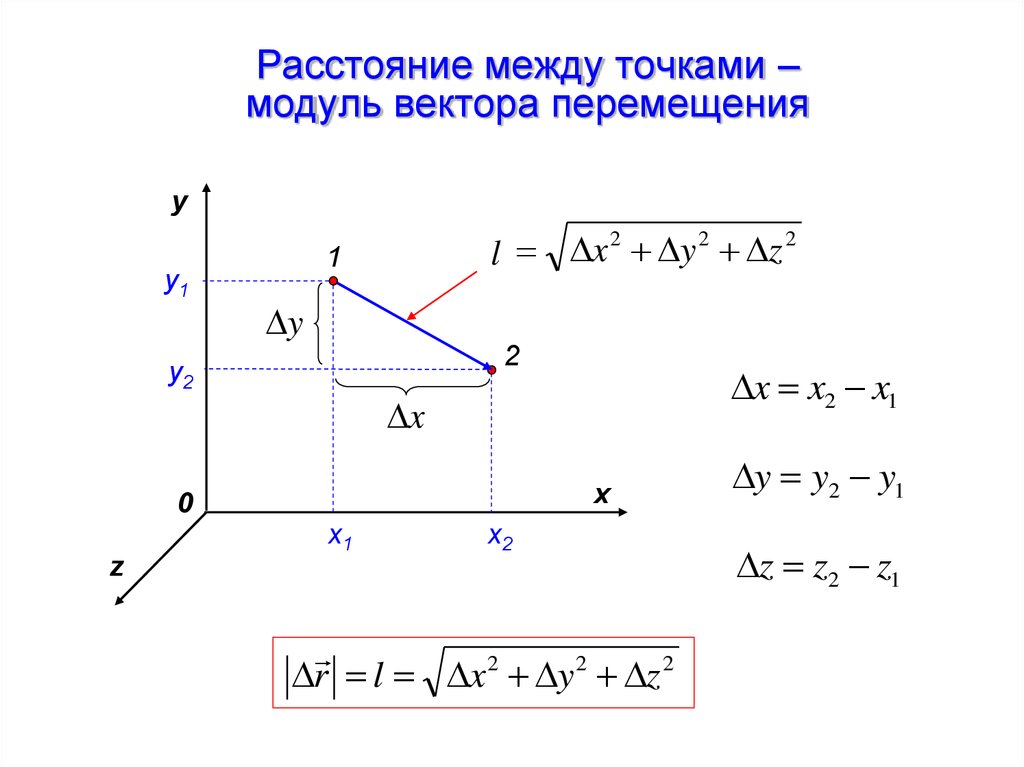
16. Расстояние между точками – модуль вектора перемещения
yy1
2
2
2
l x y z
1
y
2
y2
x x2 x1
x
x
0
x1
x2
z
r l x 2 y 2 z 2
y y2 y1
z z2 z1
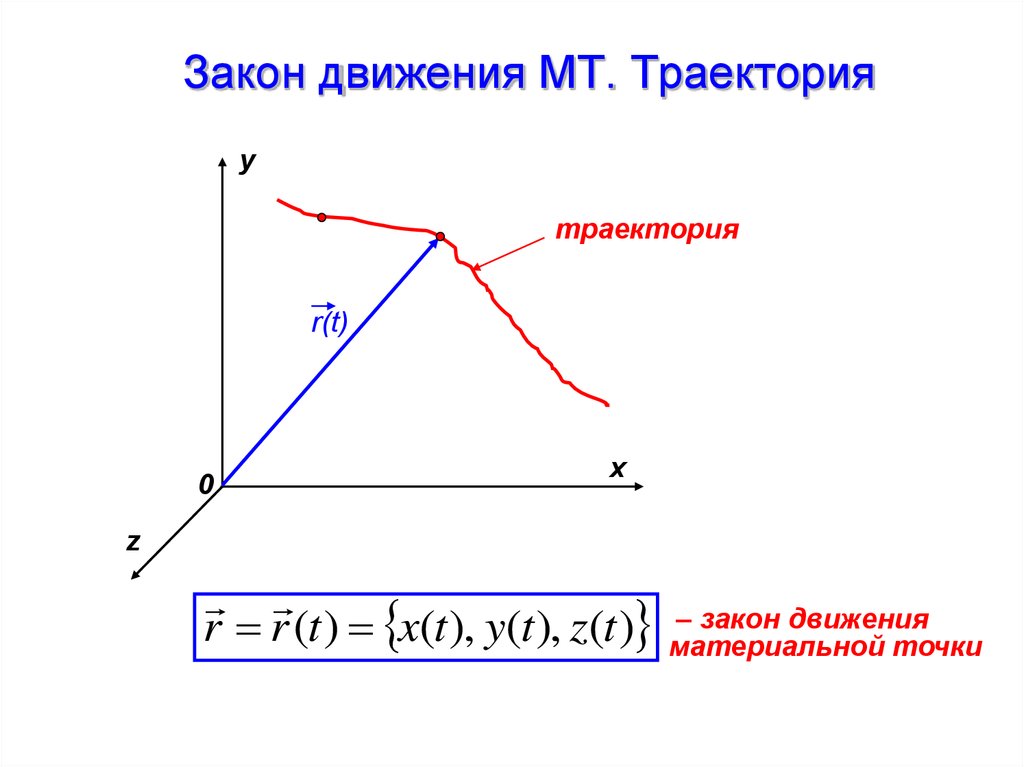
17. Закон движения МТ. Траектория
yтраектория
r(t)
0
x
z
– закон движения
r r (t ) x(t ), y(t ), z(t ) материальной
точки
18.
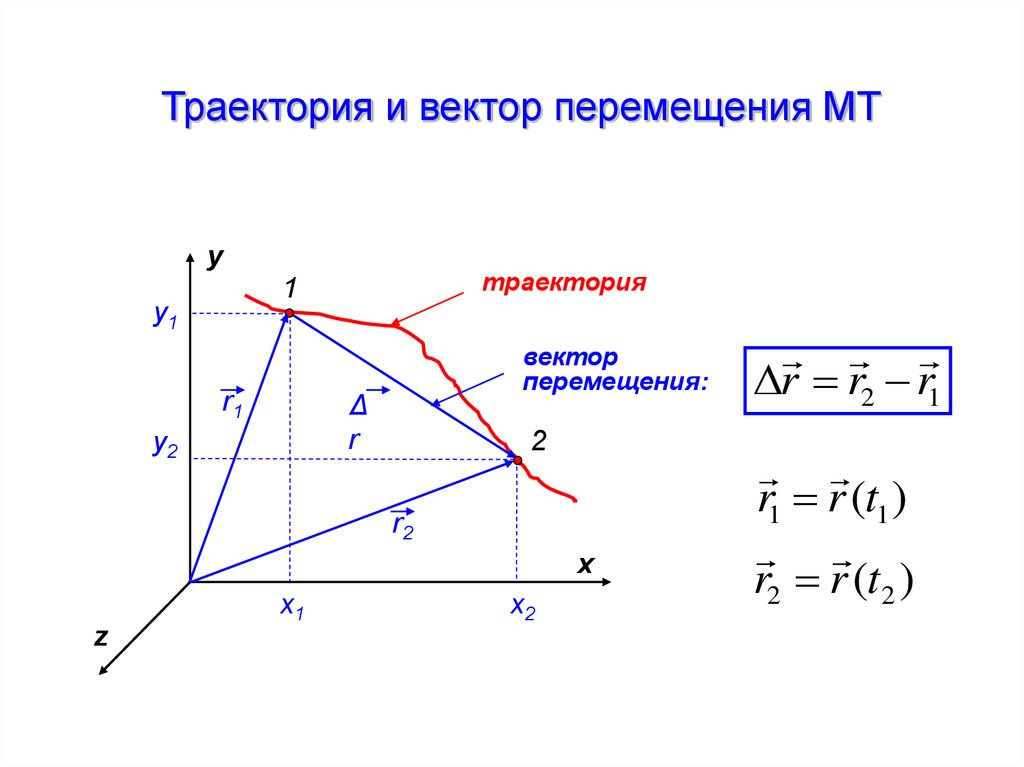
Траектория и вектор перемещения МТy
траектория
1
y1
вектор
перемещения:
Δ
r
r1
y2
2
r2
x
x1
z
x2
r r2 r1
r1 r (t1 )
r2 r (t2 )
19.
sÀ
Z
r
r0
Линия, описываемая в
пространстве движущейся
точкой, называется
траекторией.
Â
r
Î
Y
X
Длина участка траектории АВ,
пройденного материальной
точкой (м.т.) за время Δt,
называется длиной пути Δs
Δs = Δs(t) – скалярная функция
времени
Вектор, проведенный из начального положения точки в положение
ее в данный момент времени, называется перемещением. r
r r r0
В зависимости от формы траектории движение может быть
прямолинейным или криволинейным.
r s в случае прямолинейного движения
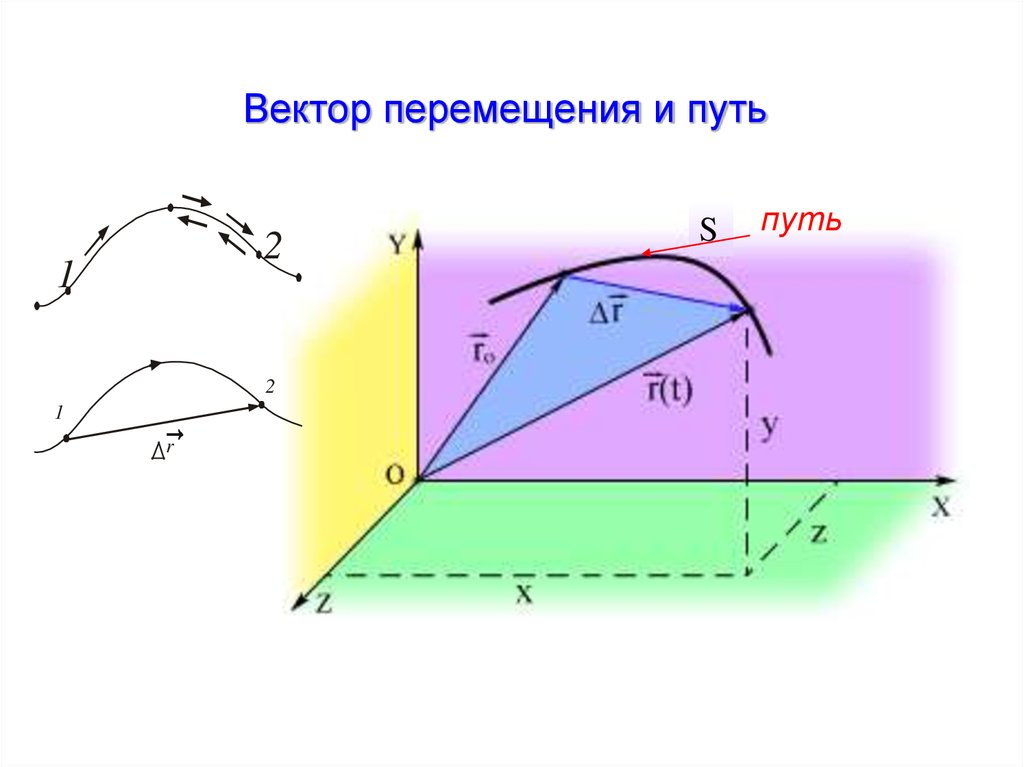
20. Вектор перемещения и путь
21
2
1
r
S
путь
21.
Вопрос 2. Скорость. Ускорение и егосоставляющие.
Скорость - векторная величина определяющая как
быстроту движения, так и его направление в данный
момент времени.
B
A
r
r0
0
r
22.
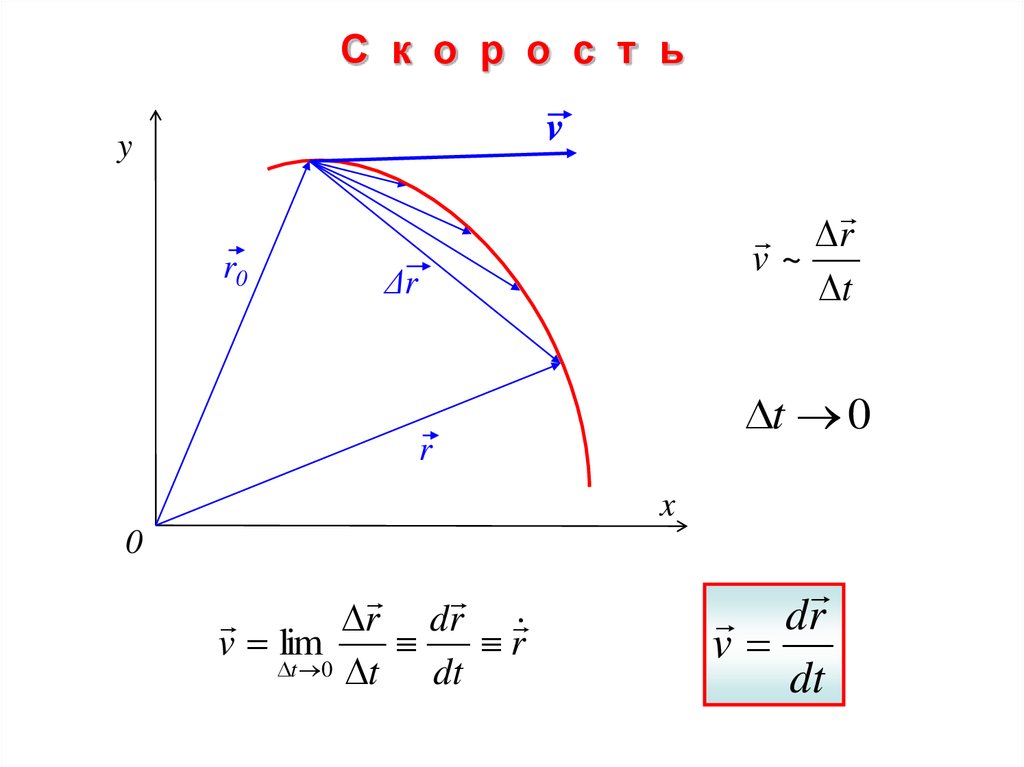
С к о р о с т ьv
y
r0
r
v~
t
Δr
t 0
r
x
0
r dr
r
v lim
t 0 t
dt
dr
v
dt
23.
Средняя скорость движения за время ∆tr
t
Мгновенная скорость
lim
t 0
r dr
lim
dt
t 0 t
ì
ñ
Мгновенная скорость есть векторная величина, равная
первой производной радиуса - вектора движущейся
точки по времени.
lim lim
t 0
t 0
r
s ds
lim
t t 0 t dt
Числовое значение мгновенной скорости равно первой производной
пути по времени.
Вектор скорости направлен по касательной к траектории в сторону
движения.
24.
В случае неравномерного движения, пользуютсяскалярной величиной - средней скоростью
неравномерного движения на данном участке:
s
t
Длина пути, пройденного точкой за время ∆t
s
t t
t dt
t
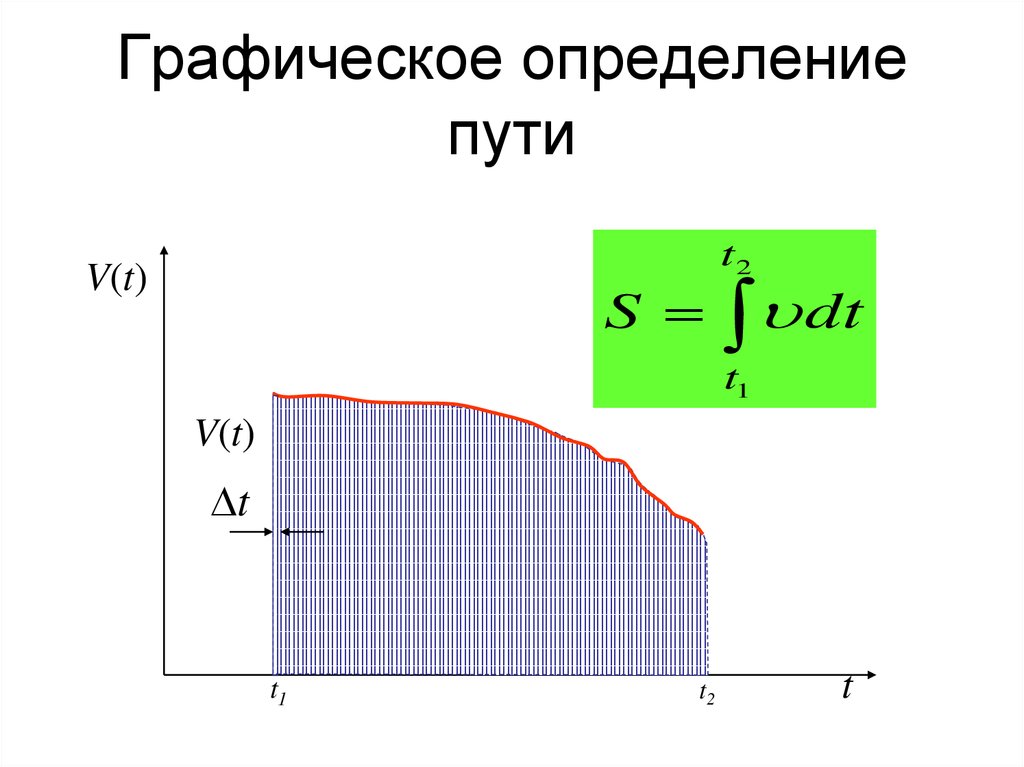
Путь, пройденный за промежуток времени от t1 до t2, дается интегралом
t2
s t dt
t1
25. Графическое определение пути
V(t)S
t2
dt
t1
V(t)
t
t1
t2
t
26.
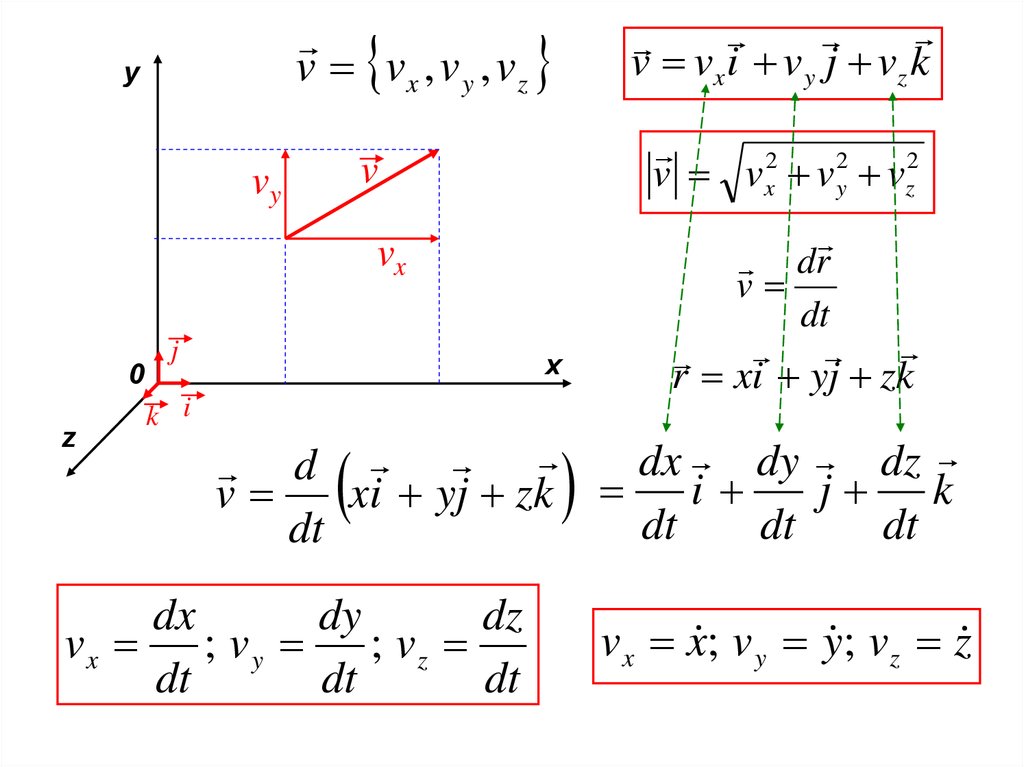
v vx i v y j vz kv v x , v y , v z
y
v vx2 v y2 vz2
v
vy
dr
v
dt
vx
0
z
j
k i
r xi yj zk
x
dx dy dz
d
j k
v
xi yj zk i
dt
dt
dt
dt
dx
dy
dz
vx ; v y ; vz
dt
dt
dt
vx x ; v y y ; vz z
27.
Ускорение2
v dv d r
a lim
2 v r
t 0 t
dt dt
v
1
2
dv d r
a
2
dt dt
v
a ax i a y j az k
a a x , a y , a z
28.
Ускорение1
v
1
r1
2
v
v
1
2
v
r2
v
a
a
29.
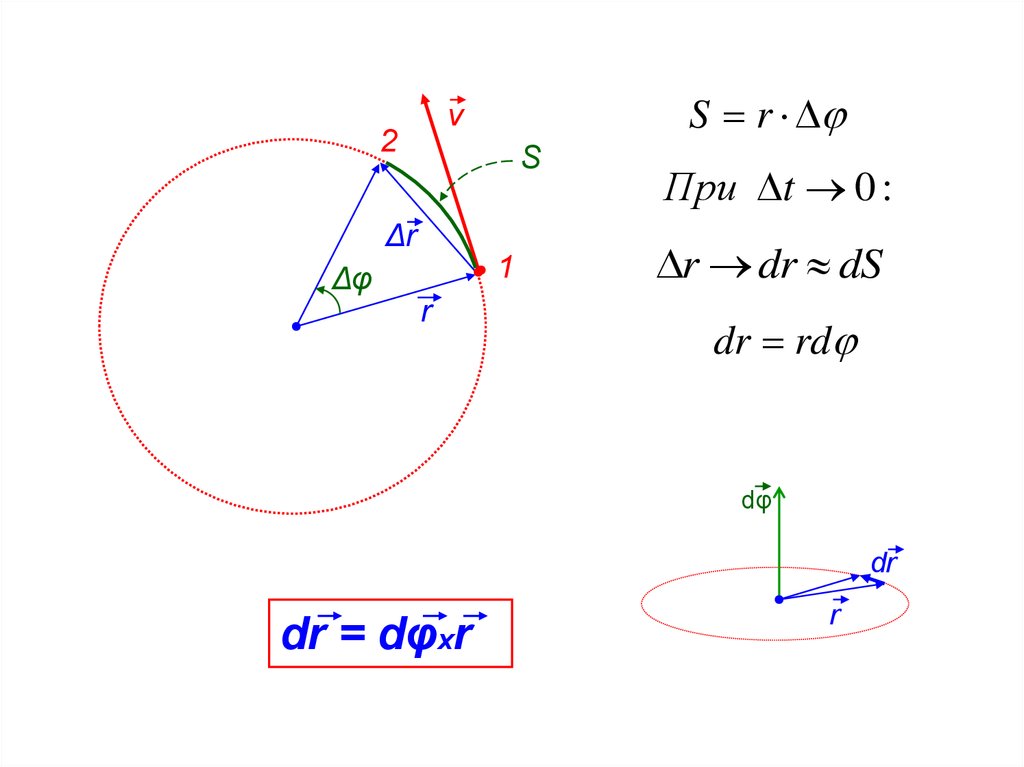
S rv
2
S
Δr
1
Δφ
r
При t 0 :
r dr dS
dr rd
dφ
dr
dr = dφxr
r
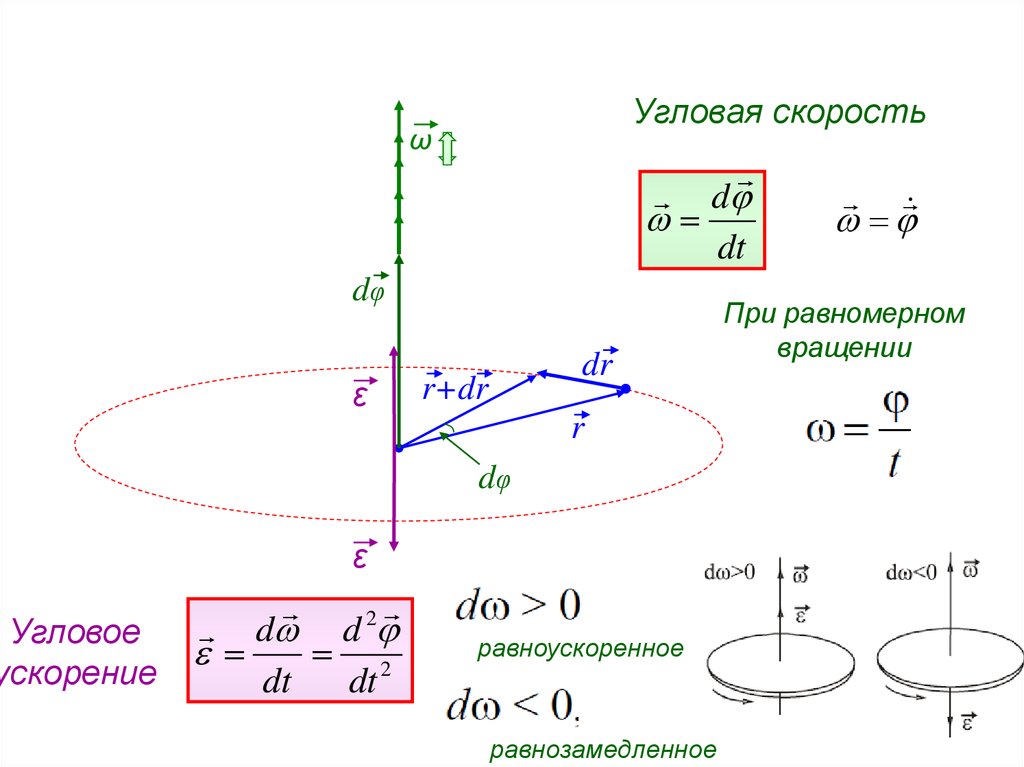
30.
Угловоеускорение
Угловая скорость
ω
d
dt
dφ
ε
dr
r+dr
r
dφ
ε
d d
2
dt
dt
2
равноускоренное
равнозамедленное
При равномерном
вращении
31.
Период вращения Т время в течение которого совершается один оборотЧастота вращения число оборотов за единицу времени
При равнопеременном движении
32. Линейная и угловая скорости
drv
dt
ω
v
r
dr rd
rd
v
r
dt
v r
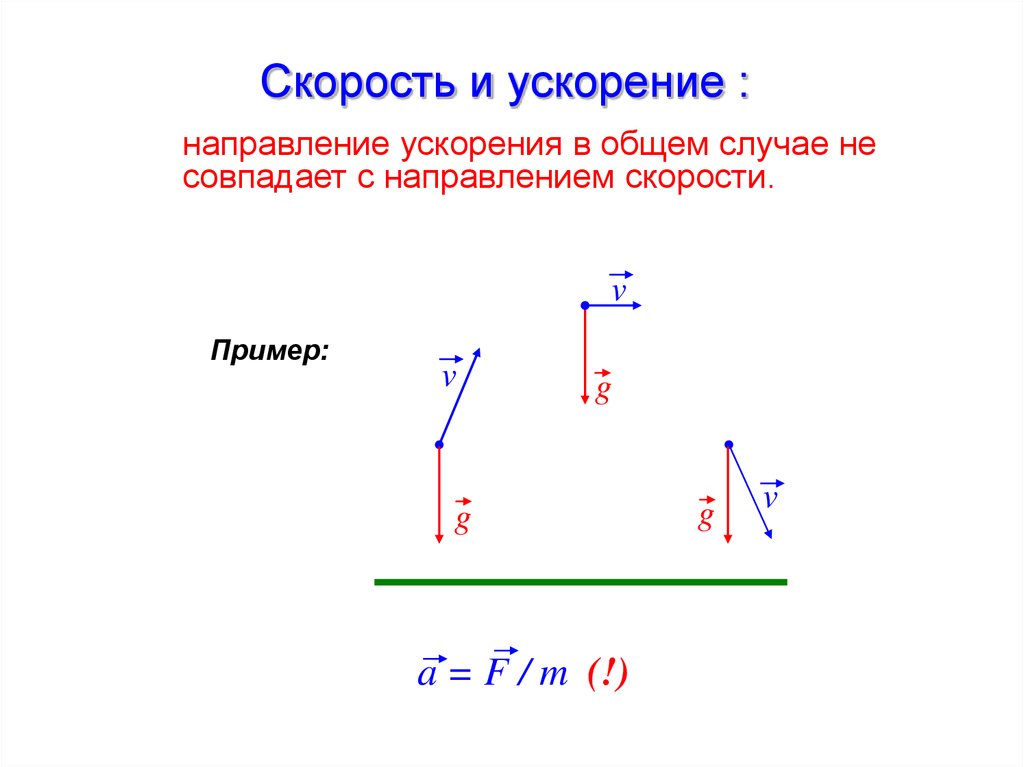
33. Скорость и ускорение :
направление ускорения в общем случае несовпадает с направлением скорости.
v
Пример:
v
g
g
a = F / m (!)
g
v
34.
aτan
a a an
v
a
a a a
2
R
2
n
0
dv
a
dt
2
v
2
an
R v
R
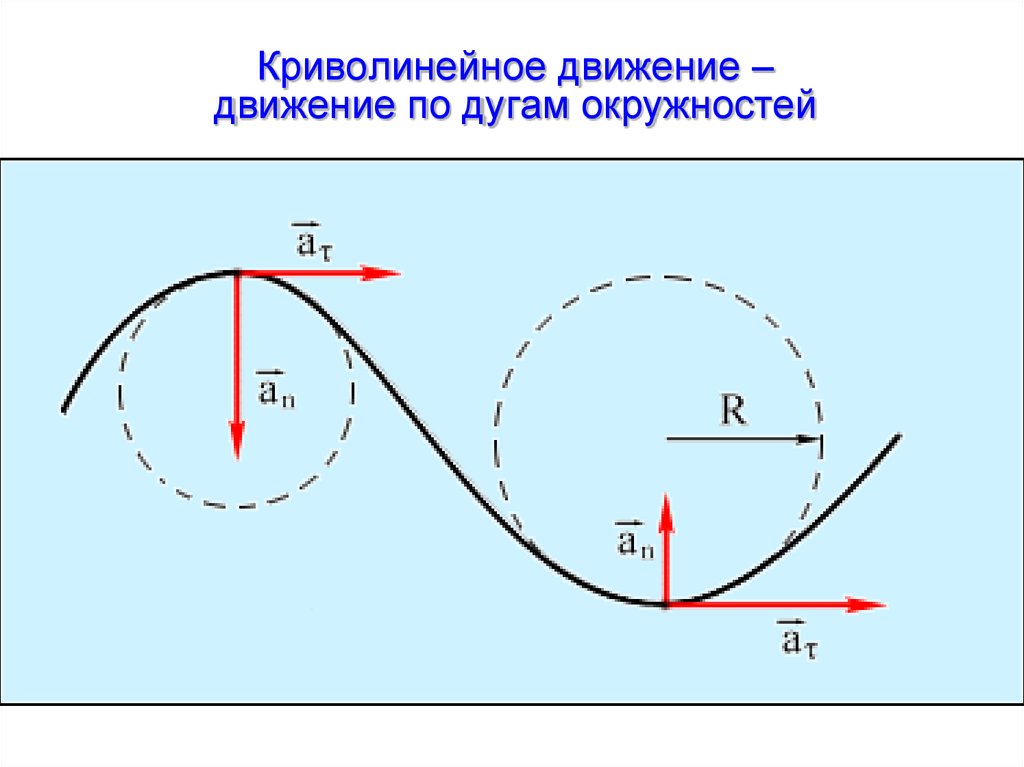
35. Криволинейное движение – движение по дугам окружностей
36. ВЫВОДЫ: СКОРОСТЬ
drv
dt
37. УСКОРЕНИЕ
da
dt
38. Прямые и обратные задачи кинематики
d xax
dt
dx
x
dt
x(t)
υx(t)
x x t d t C1
ax(t)
x a x t d t C2





















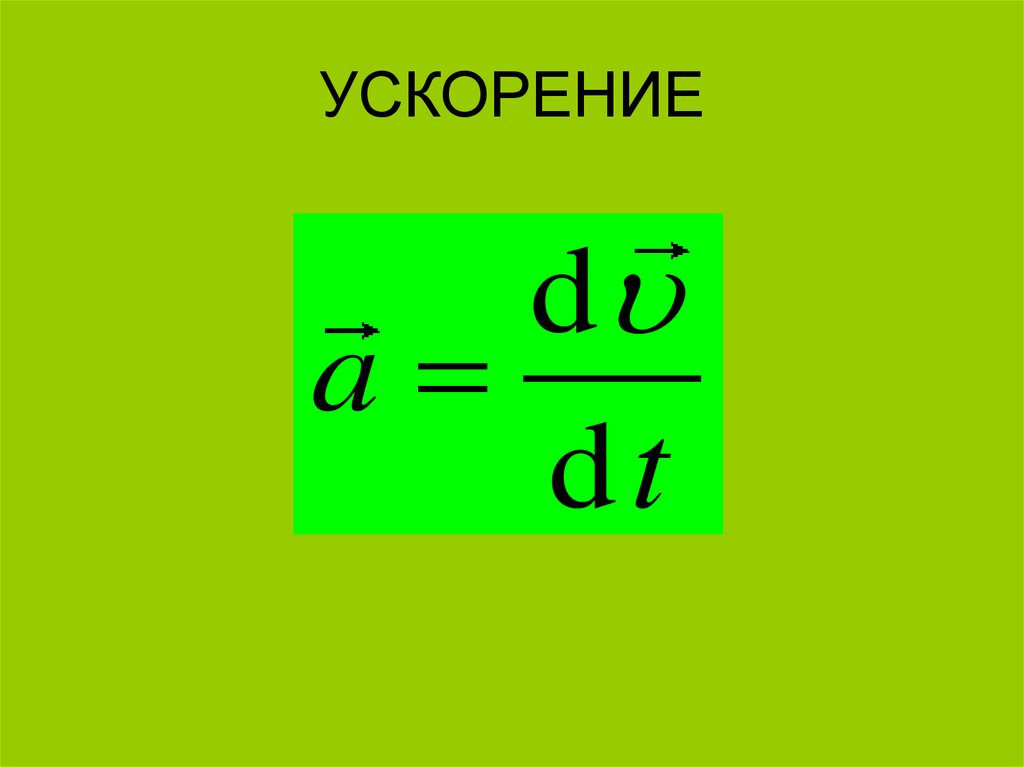

 Физика
Физика








