Похожие презентации:
Алгоритмы. Понятия. Свойства алгоритмов
1. Математическая логика Теория алгоритмов
2. Теория алгоритмов
Тема 1. Алгоритмы. Понятия.Свойства алгоритмов.
3.
3Определения
Родоначальник термина «алгоритм»
Великий ученый средневекового Востока
Мухаммед ибн Мусса ал-Хорезми
(Мухаммед сын Муссы из Хорезма)
783 – 850 гг.
Единого
определения
алгоритма
не существует, есть только разные подходы,
описания этого понятия, причем, в полном
соответствии с той областью знаний, где он
применяется.
Известен как математик, астроном и географ.
В девятом веке он переселился в Багдад, где с 815 года возглавлял
«Дом мудрости» – хранилище рукописей, созданное арабскими
халифами.
Автор двух знаменитых трактатов: по арифметике и алгебре.
«Dixit algorizmi» – «Сказал Алгоризми».
4.
4Определения
Алгоритм - это строгая, четкая последовательность математических
и логических операций, приводящая к решению задачи.
В Толковом словаре по информатике (1991г.) дано общепринятое
понятие: Алгоритм - точное предписание, определяющее
вычислительный процесс, ведущий от варьируемых начальных
данных к искомому результату.
Алгоритм
– система четких однозначных указаний, которые
определяют последовательность действий над некоторыми
объектами и после конечного числа шагов приводят к желаемому
результату.
Запись алгоритма
программой.
на
языке
программирования
называется
5.
5Определения
Математические определения:
«В математике принято понимать под «алгоритмом» точное предписание, определяющее вычислительный процесс, ведущих от
варьируемых исходных данных к исходному результату».
Алгоритм – это детерминированная процедура, которую можно
применить к любому элементу некоторого класса символических
входов, которая для каждого такого входа дает, в конце концов,
соответствующий символический выход.
Алгоритм – точное предписание о выполнении в определенном
порядке некоторой системы операций, позволяющее решать
совокупность задач определенного класса.
6.
6Свойства алгоритмов
Описание основных свойств помогает углубить само понятие
алгоритма.
Каждый алгоритм должен обладать следующими свойствами:
Дискретность — алгоритм должен представлять процесс решения
задачи как последовательное выполнение некоторых простых шагов.
При этом для выполнения каждого шага алгоритма требуется
конечный отрезок времени, то есть преобразование исходных
данных в результат осуществляется во времени дискретно.
Детерминированность (определённость). В каждый момент
времени следующий шаг работы однозначно определяется
состоянием системы. Таким образом, алгоритм выдаёт один и тот же
результат (ответ) для одних и тех же исходных данных.
С другой стороны, существуют вероятностные алгоритмы, в
которых следующий шаг работы зависит от текущего состояния
системы и генерируемого случайного числа. Однако, при включении
метода генерации случайных чисел в список «исходных данных»
вероятностный алгоритм становится подвидом обычного.
7.
7Свойства алгоритмов
Понятность — алгоритм должен включать только те команды,
которые доступны исполнителю и входят в его систему команд.
Завершаемость (конечность) — в более узком понимании
алгоритма как математической функции, при корректно заданных
исходных данных алгоритм должен завершать работу и выдавать
результат за конечное число шагов. С другой стороны,
вероятностный алгоритм может и никогда не выдать результат, но
вероятность этого равна 0.
Массовость (универсальность). Алгоритм должен быть применим к
разным наборам исходных данных.
Результативность — завершение алгоритма определёнными
результатами.
Алгоритм содержит ошибки, если приводит к получению
неправильных результатов либо не даёт результатов вовсе.
Алгоритм не содержит ошибок, если он даёт правильные
результаты для любых допустимых исходных данных.
8.
8Способы задания алгоритмов
На практике наиболее распространены следующие формы
представления алгоритмов:
1. Словесная
(запись на естественном языке);
Например.
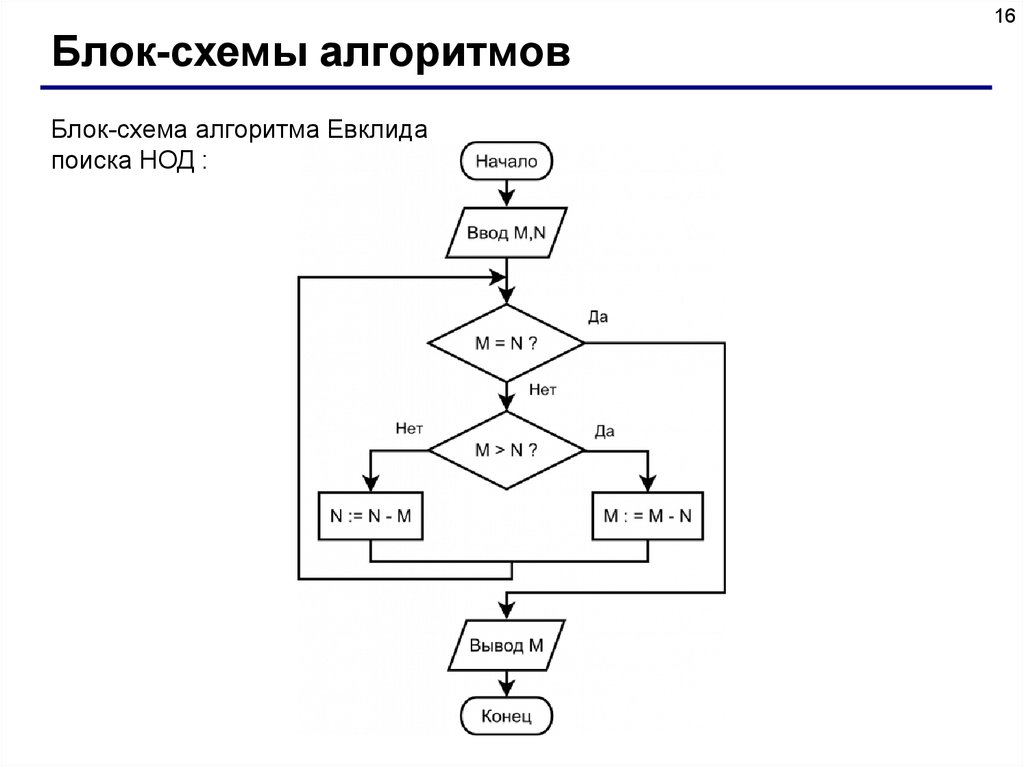
Записать алгоритм нахождения наибольшего общего делителя (НОД)
двух натуральных чисел (алгоритм Эвклида).
Алгоритм может быть записан следующим образом:
1. задать два числа;
2. если числа равны, то взять любое из них в качестве ответа и
остановиться, в противном случае продолжить выполнение
алгоритма;
3. определить большее из чисел;
4. заменить большее из чисел разностью большего и меньшего из
чисел;
5. повторить алгоритм с шага 2.
9.
9Способы задания алгоритмов
2. Псевдокоды
(полуформализованные описания алгоритмов на условном
алгоритмическом языке, включающие в себя как элементы языка
программирования,
так
и
фразы
естественного
языка,
общепринятые математические обозначения и др.);
Пример записи алгоритма на школьном АЯ :
алг Сумма квадратов (арг цел n, рез цел S)
дано | n > 0
надо | S = 1*1 + 2*2 + 3*3 + ... + n*n
нач цел i
ввод n; S:=0
нц для i от 1 до n
S:=S+i*i
кц
вывод "S = ", S
кон
3. Программный (тексты на языках программирования).
10.
10Блок-схемы алгоритмов
4. Графическая (изображения из графических символов);
На территории Российской Федерации действует единая система
программной документации (ЕСПД), частью которой является
Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов
программ, данных и систем» [1].
Не смотря на то, что описанные в стандарте обозначения могут
использоваться для изображения схем ресурсов системы, схем
взаимодействия программ и т.п., в настоящей статье описана лишь
разработка схем алгоритмов программ.
Рассматриваемый ГОСТ практически полностью
международному стандарту ISO 5807:1985.
соответствует
Блок-схема представляет собой совокупность символов,
соответствующих этапам работы алгоритма и соединяющих их
линий. Пунктирная линия используется для соединения символа с
комментарием. Сплошная линия отражает зависимости по
управлению между символами и может снабжаться стрелкой.
11.
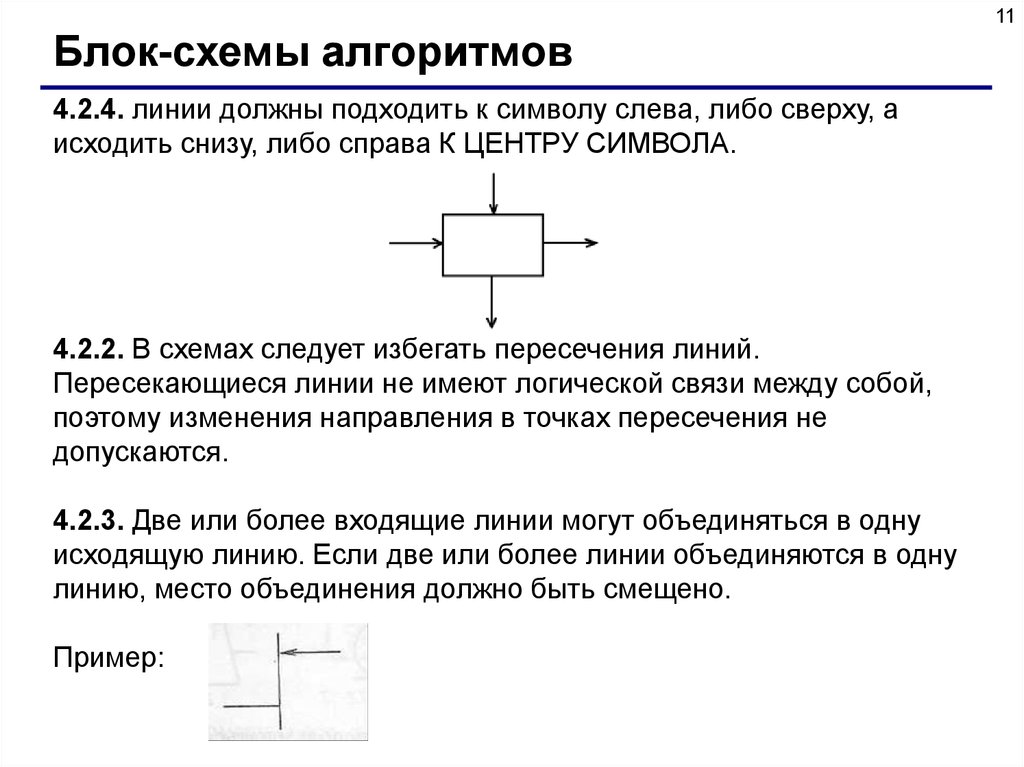
11Блок-схемы алгоритмов
4.2.4. линии должны подходить к символу слева, либо сверху, а
исходить снизу, либо справа К ЦЕНТРУ СИМВОЛА.
4.2.2. В схемах следует избегать пересечения линий.
Пересекающиеся линии не имеют логической связи между собой,
поэтому изменения направления в точках пересечения не
допускаются.
4.2.3. Две или более входящие линии могут объединяться в одну
исходящую линию. Если две или более линии объединяются в одну
линию, место объединения должно быть смещено.
Пример:
12.
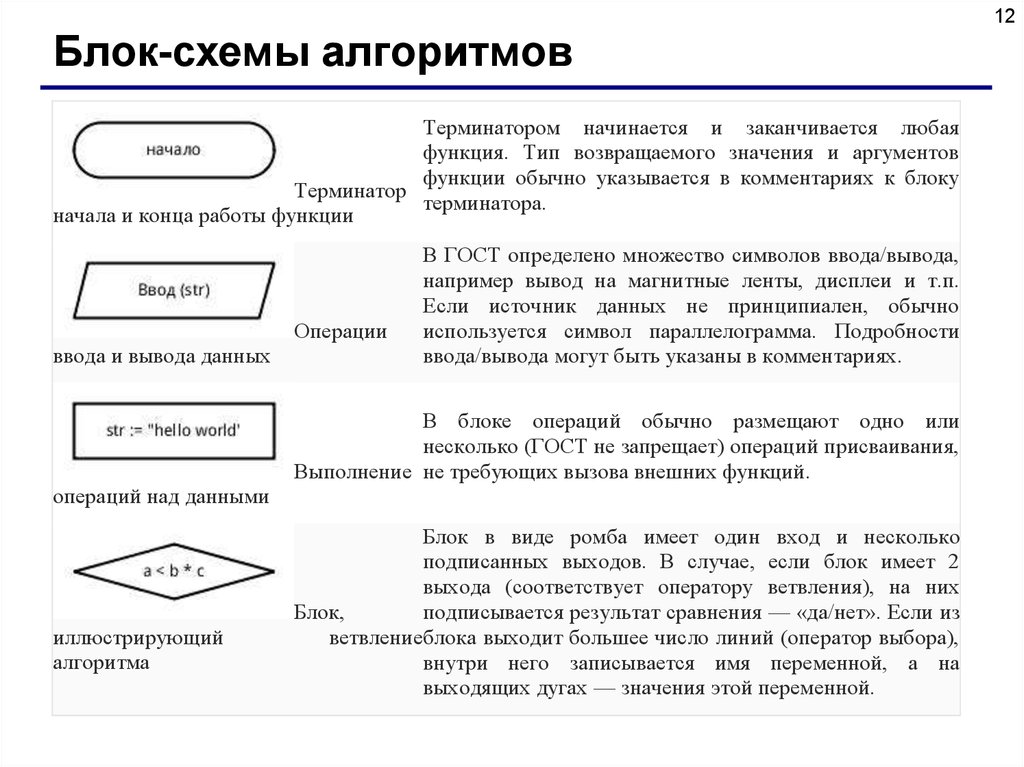
12Блок-схемы алгоритмов
Терминатором начинается и заканчивается любая
функция. Тип возвращаемого значения и аргументов
функции обычно указывается в комментариях к блоку
Терминатор
терминатора.
начала и конца работы функции
Операции
ввода и вывода данных
В ГОСТ определено множество символов ввода/вывода,
например вывод на магнитные ленты, дисплеи и т.п.
Если источник данных не принципиален, обычно
используется символ параллелограмма. Подробности
ввода/вывода могут быть указаны в комментариях.
В блоке операций обычно размещают одно или
несколько (ГОСТ не запрещает) операций присваивания,
Выполнение не требующих вызова внешних функций.
операций над данными
иллюстрирующий
алгоритма
Блок в виде ромба имеет один вход и несколько
подписанных выходов. В случае, если блок имеет 2
выхода (соответствует оператору ветвления), на них
Блок,
подписывается результат сравнения — «да/нет». Если из
ветвлениеблока выходит большее число линий (оператор выбора),
внутри него записывается имя переменной, а на
выходящих дугах — значения этой переменной.
13.
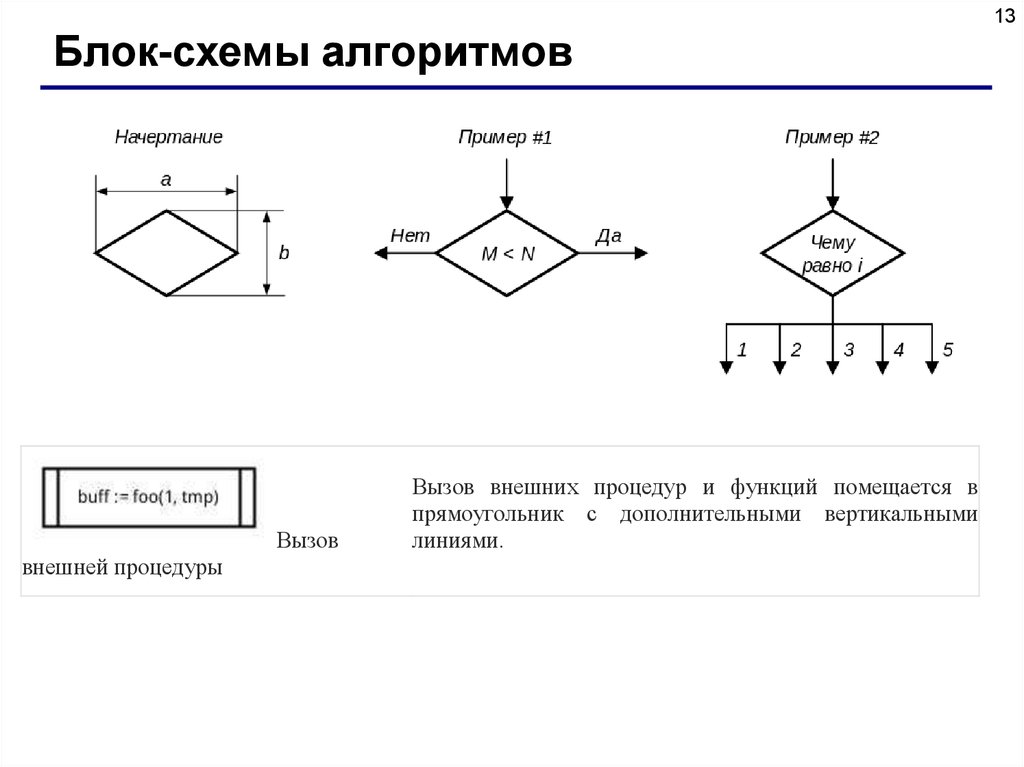
13Блок-схемы алгоритмов
Вызов
внешней процедуры
Вызов внешних процедур и функций помещается в
прямоугольник с дополнительными вертикальными
линиями.
14.
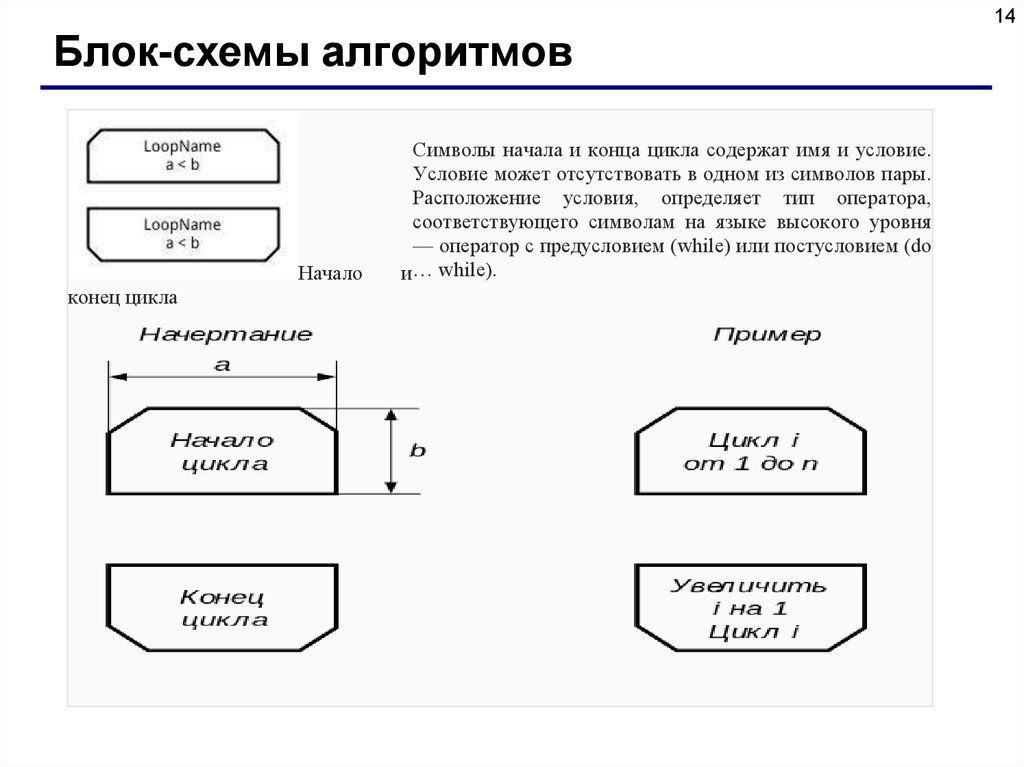
14Блок-схемы алгоритмов
Начало
конец цикла
Символы начала и конца цикла содержат имя и условие.
Условие может отсутствовать в одном из символов пары.
Расположение условия, определяет тип оператора,
соответствующего символам на языке высокого уровня
— оператор с предусловием (while) или постусловием (do
и… while).
15.
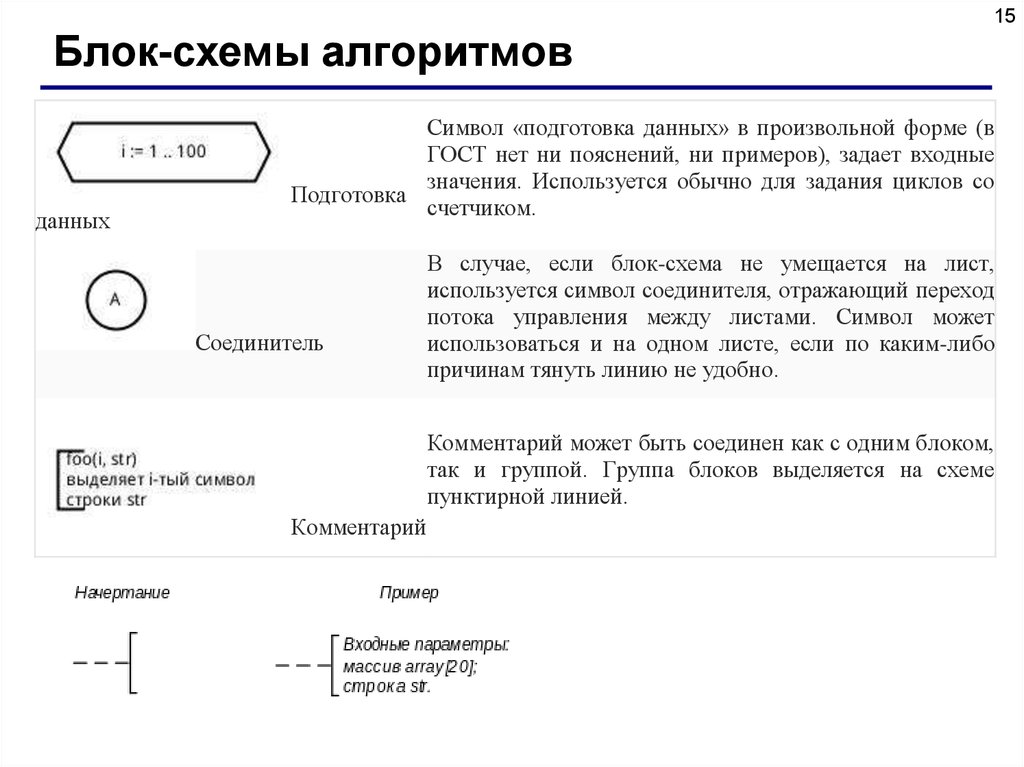
15Блок-схемы алгоритмов
данных
Символ «подготовка данных» в произвольной форме (в
ГОСТ нет ни пояснений, ни примеров), задает входные
значения. Используется обычно для задания циклов со
Подготовка
счетчиком.
Соединитель
В случае, если блок-схема не умещается на лист,
используется символ соединителя, отражающий переход
потока управления между листами. Символ может
использоваться и на одном листе, если по каким-либо
причинам тянуть линию не удобно.
Комментарий может быть соединен как с одним блоком,
так и группой. Группа блоков выделяется на схеме
пунктирной линией.
Комментарий
16.
16Блок-схемы алгоритмов
Блок-схема алгоритма Евклида
поиска НОД :
17.
17Проблема уточнения понятия алгоритма
30 гг. XX века
количество исследований перешло на качественно новый уровень
Попытки дать строгое определение понятию «алгоритм» были сделаны в
разное время, разными способами, разными учеными, но в конечном итоге
все они описали один и тот же класс функций.
Свести алгоритм к функции можно так:
Говорят, что функция f(x) вычислима, если существует алгоритм,
вычисляющий ее значения f, по каждому аргументу x из области
определения.
Основные направления по уточнению понятия «алгоритма» и их авторы:
1) Общерекурсивные функции (К. Гёделя, С. Клини, Ю. Эрбран)
2) - рекурсивные функции (Л. Гёделя, С. Клини)
3) - определение функции (А. Чёрч, С. Клини)
4) Машины Тьюринга-Поста (А. Тьюринг, Е. Пост)
5) Марковские алгоритмы (А. А. Марков)
6) Графические схемы (Р. Петер)
18. Теория алгоритмов
Тема 2. Машины Тьюринга –Поста.
19.
19Машины Тьюринга - Поста
английский математик
Алан Мэтисон Тьюринг
Американский математик
Польского (русского) происхождения
Эмиль Леон Пост
А.М. Тьюринг опубликовал первую свою работу в журнале Лондонского
матема-тического сообщества (London Mathematical Society (LMS)), том. 58,
за 1936 г. (рукопись подана в редакцию – 19.04.1935 г.) под названием «О
вычислимых чис-лах, с применением к проблеме невычислимости».
Статья Поста вышла в свет в журнале символической логики (Jornal of Symbolic Logic) в третьем номере, за сентябрь 1936 г. Она насчитывает 3
страницы и носит более общий характер.
20.
20Машины Тьюринга - Поста
Определение алгоритма через понятие вычислительной машины основано
на понимании эффективной процедуры, представляющей собой множество
сообщаемых исполнителю время от времени правил, которые точно
определяют его поведение.
Чтобы решить проблему интерпретации (понимания) правил необходимо
установить:
• язык, на котором описывается множество правил поведения,
• конструкцию интерпретирующего устройства, которое может «понимать»
утверждения, сделанные на этом языке, и, таким образом, выполнять шаг за
шагом каждый точно определенный процесс.
Следовательно, задача описания алгоритма может быть сведена к
построению машины некоторого типа, которая способна воспринимать
набор правил, выраженных на некотором языке, и делать то, что предписано
этими правилами.
21.
21Машины Тьюринга - Поста
Определение алгоритма через понятие вычислительной машины основано
на понимании эффективной процедуры, представляющей собой множество
сообщаемых исполнителю время от времени правил, которые точно
определяют его поведение.
Чтобы решить проблему интерпретации (понимания) правил необходимо
установить:
• язык, на котором описывается множество правил поведения,
• конструкцию интерпретирующего устройства, которое может «понимать»
утверждения, сделанные на этом языке, и, таким образом, выполнять шаг за
шагом каждый точно определенный процесс.
Следовательно, задача описания алгоритма может быть сведена к
построению машины некоторого типа, которая способна воспринимать
набор правил, выраженных на некотором языке, и делать то, что предписано
этими правилами.
22.
22Машины Тьюринга - Поста
Машина Тьюринга - абстрактная (воображаемая) "вычислительная
машина" некоторого точно охарактеризованного типа, дающая
пригодное для целей математического рассмотрения уточнение общего
интуитивного представления об алгоритме.
С помощью машины Тьюринга можно доказать существование или не
существование алгоритмов решения различных задач.
Так как машина выполняет определенный алгоритм, то к машине
предъявляются требования, вытекающие из свойств алгоритмов.
Во-первых, машина должна быть полностью детерминированной
(вычисления должны быть точные и общепонятные) и действовать в
соответствии с заданной системой правил.
Во-вторых, она должна допускать ввод различных “начальных данных”
(соответствующих различным задачам из данного класса задач).
В-третьих, заданная система правил работы машины и класс решаемых
задач должны быть согласованы так, чтобы всегда можно было “прочитать”
результат работы машины.
23.
23Одноленточная Машина Тьюринга
Классической моделью считается одноленточная машина Тьюринга.
Под одноленточной машиной Тьюринга понимают кибернетическое
устройство, состоящее из следующих элементов:
• бесконечной ленты, разделенной на ячейки,
• управляющей головки, способной читать символы, содержащиеся в
ячейках ленты, и записывать символы в эти ячейки,
• выделенной ячейки памяти, содержащей символ внутреннего алфавита,
задающий состояние машины Тьюринга,
• механического устройства управления, обеспечивающего перемещение
головки относительно ленты,
• функциональной схемы — области памяти, содержащей команды
(программу) машины Тьюринга (эта область доступна только для чтения).
Обычно машина Тьюринга схематично изображается в виде ленты с
отмеченной указателем ячейкой.
24.
24Одноленточная Машина Тьюринга
Лента
Поскольку бесконечную ленту физически смоделировать затруднительно,
обычно предполагается что она конечная. В процессе работы к
существующим ячейкам машина может пристраивать новые ячейки, так что
лента может считаться потенциально неограниченной в обе стороны.
Каждая ячейка ленты может находиться в одном из конечного множества
состояний. Эти состояния будем обозначать символами a0, a1, …, am или
другими символами. Совокупность таких символов называется внешним
алфавитом машины, а сама лента часто называется внешней памятью
машины. Если ячейка пустая, будем считать, что в ней
записан условный символ λ.
Без ограничения общности ленту можно считать бесконечной лишь с одной
стороны. В этом случае для удобства введем специальный символ ∂,
обозначающий начало ленты. Этот символ имеет строго определенное
место, его нельзя ни стирать, ни сдвигать. Тогда ленту можно считать
однонаправленной (бесконечной вправо) и ее ячейки удобно просматривать
слева направо.
25.
25Одноленточная Машина Тьюринга
Управляющая головка
Управляющая головка – это некоторое устройство, которое может
перемещаться вдоль ленты так, что в каждый рассматриваемый
момент времени оно находится напротив определенной ячейки ленты.
Иногда, наоборот, считают управляющую головку неподвижной, а
движущейся частью становится лента. В таком случае предполагается, что в
управляющую головку вводится то одна, то другая ячейка ленты. Если
какая-нибудь ячейка находится в управляющей головке, то говорят также,
что машина в данный момент «воспринимает» или «обозревает» эту ячейку.
Внутренняя память
Внутренняя память машины – это выделенная ячейка памяти, которая
в каждый рассматриваемый момент находится в некотором «состоянии».
Предполагается, что число возможных состояний внутренней памяти
конечное и для каждой машины фиксированное. Состояние внутренней
памяти мы будем обозначать символами S0, S1, …, Sn или любыми другими
символами, не входящими во внешний алфавит машины. Совокупность
символов, обозначающих состояния внутренней памяти, называется
внутренним алфавитом машины или внутренними состояниями
машины.
26.
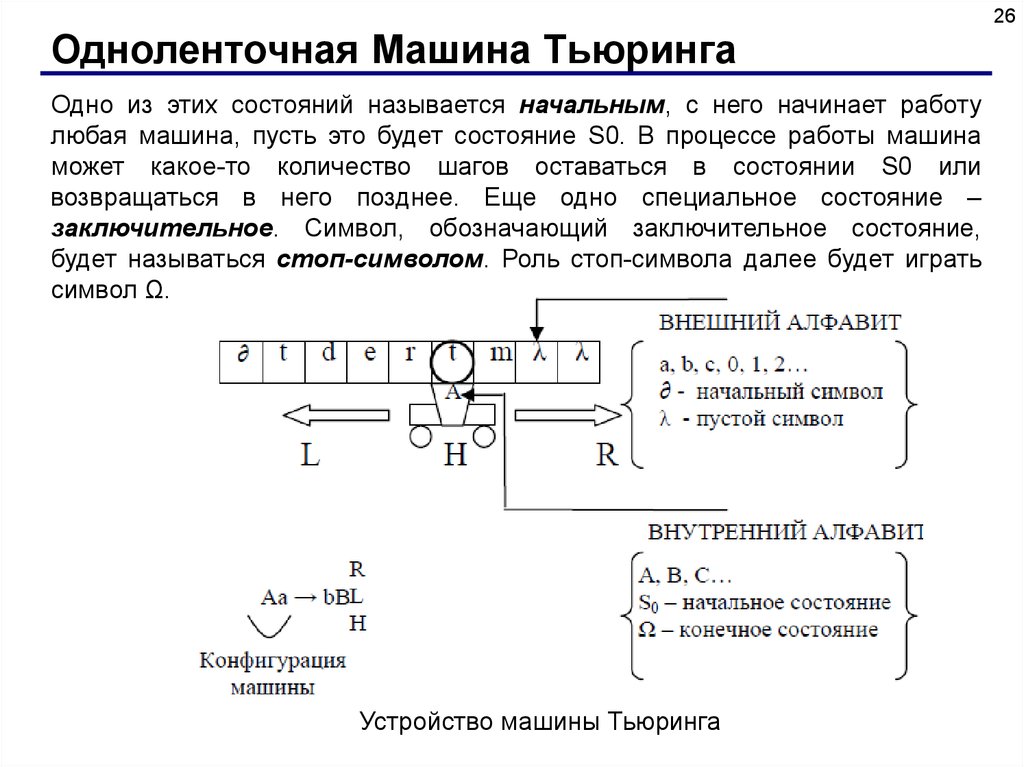
26Одноленточная Машина Тьюринга
Одно из этих состояний называется начальным, с него начинает работу
любая машина, пусть это будет состояние S0. В процессе работы машина
может какое-то количество шагов оставаться в состоянии S0 или
возвращаться в него позднее. Еще одно специальное состояние –
заключительное. Символ, обозначающий заключительное состояние,
будет называться стоп-символом. Роль стоп-символа далее будет играть
символ Ω.
Устройство машины Тьюринга
27.
27Работа Машины Тьюринга
Конфигурация машины Тьюринга – совокупность, образованная
содержимым текущей обозреваемой ячейки aj и состоянием внутренней
памяти Si.
Работа машины состоит в том, что она из данного «состояния» по истечении
одного такта работы механического устройства переходит в следующее
«состояние», затем из этого состояния по истечении такта работы переходит
в новое состояние и так далее.
Таким образом, если машина, имея внутреннее состояние Si и воспринимая
ячейку ленты с символом aj, изменяет свое внутреннее состояние на Sq и
одновременно содержимое воспринимаемой ячейки заменяет символом ar,
а управляющая головка сдвинется на одну ячейку вправо (R), то говорят, что
машина выполняет команду соответственно Si aj→ak R Sl.
Если управляющая головка сдвинется влево (L) или останется
неподвижной (Н), то команды записываются соответственно: Si aj→ak L Sl
Si aj→ak H Sl
28.
28Работа Машины Тьюринга
Программа машины Тьюринга – совокупность команд установленного
формата.
Программа машины с символами {a0, a1, …, an } и состояниями {S0, S1, …,
Sm } содержит максимум n·m команд.
При этом некоторые команды являются «мертвыми», в том случае, если ни
при каких входных словах в данном алфавите невозможно наступление этой
конфигурации. В грамотной, с точки зрения реализации, программе таких
строк быть не должно, хотя формально их наличие ошибкой не является.
Тезис Тьюринга – любой алгоритм можно преобразовать в машину
Тьюринга.
Эту гипотезу невозможно доказать, потому что она оперирует
неформальным понятием алгоритма. Однако обоснование гипотезы есть:
все алгоритмы, придуманные в течение столетий, могут быть реализованы
на машине Тьюринга. Чтобы опровергнуть основную гипотезу, необходимо
придумать такой алгоритм, который невозможно было бы реализовать на
машине Тьюринга, но пока такого алгоритма нет.
29.
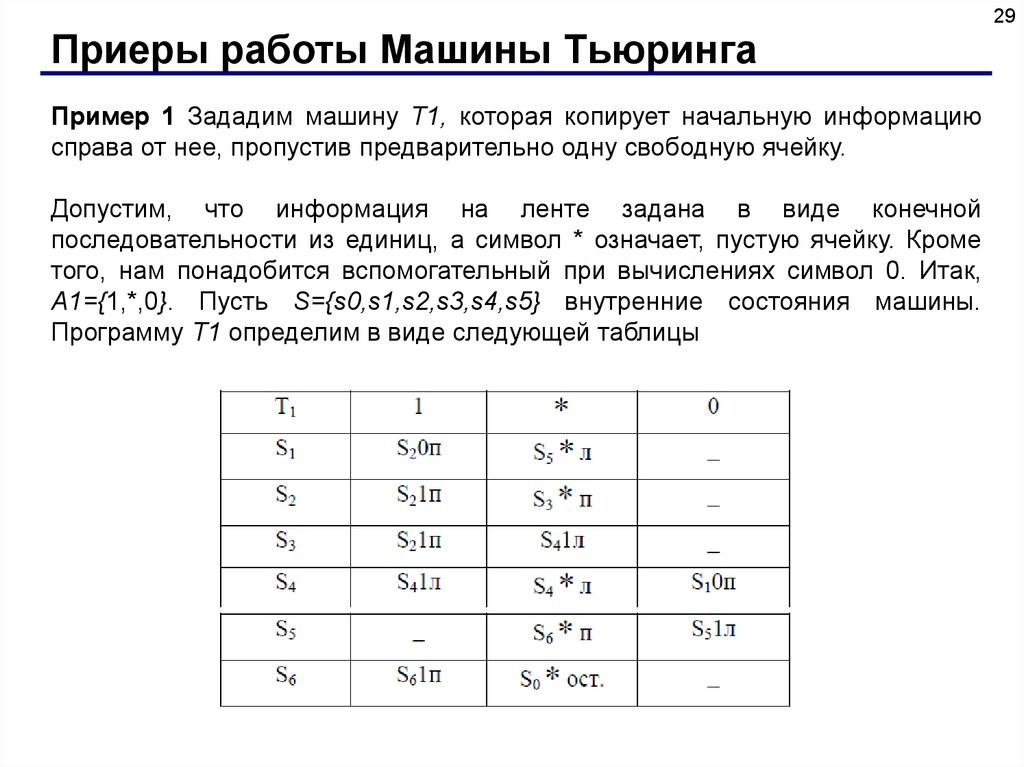
29Приеры работы Машины Тьюринга
Пример 1 Зададим машину Т1, которая копирует начальную информацию
справа от нее, пропустив предварительно одну свободную ячейку.
Допустим, что информация на ленте задана в виде конечной
последовательности из единиц, а символ * означает, пустую ячейку. Кроме
того, нам понадобится вспомогательный при вычислениях символ 0. Итак,
А1={1,*,0}. Пусть S={s0,s1,s2,s3,s4,s5} внутренние состояния машины.
Программу Т1 определим в виде следующей таблицы
30.
30Приеры работы Машины Тьюринга
Пример 3.1.1
В таблице машины имеются незаполненные клетки (прочерк). Это потому,
что в работе машины не возникнут такие ситуации. Тем не менее, во
избежание недоразумений, договоримся, что в таких ситуациях Т1
останавливается, не изменяя при этом своего внутреннего состояния и
обозреваемого на ленте символа.
Отдельные такты работы машины Т1 приведем в следующих таблицах:
31.
31Приеры работы Машины Тьюринга
Пример 3.1.1
В описаниях ситуаций на ленте положение считывающей головки отмечено
над обозреваемым символом в виде внутреннего состояния машины.
Так, в первом такте машина Т1 обозревает в ячейке ленты символ 1 в
состоянии s2 . При этом она идет вправо, не меняя своего внутреннего
состояния и символа в ячейке.
В такте шесть она имеет состояние s3 и обозревает пустую ячейку. В этой
ситуации, согласно программе, она печатает 1, переходит в состояние s4 и
передвигает головку на одну ячейку влево.
32.
32Приеры работы Машины Тьюринга
Пример 2 Рассмотрим машину Т2 с внутренними состояниями s0, s1, s2, s3
и с внешним алфавитом {1,*} , программа которой задана следующей
таблицей:
Машина Т2 к заданной группе единиц добавляет справа одну единицу, возвращается в исходное положение и останавливается.
33.
33Приеры работы Машины Тьюринга
Пример 3 Пусть А3={1, *}, S={s0,s1,s2,s3,s4}.
Машина Т3 отыскивает на ленте группу единиц (справа от головки), стирает
одну крайнюю правую единицу и останавливается. При этом результат
работы Т3 остается справа от головки машины. Если лента в начале работы
Т3 была пустой, то головка бесконечно передвигается вправо.
34.
34Универсальная Машина Тьюринга (УМТ)
Универсальные машины
Тьюринг показал возможность построения определённой вычислительной
машины U, универсальной в том смысле, что на U можно выполнить любое
вычисление.
Универсальная машина – машина Тьюринга, обладающая способностью
путём подходящего кодирования выполнить любое вычисление.
Однако к этому, несомненно, надо присоединить то условие, что кодирование
должно быть в некотором смысле простым.
Пусть машина А имеет m символов aj и n внутренних состояний Si .
Закодируем знаки, используемые при написании программы работы такой
машины следующим образом:
aj = 1…1 (a1=1, a2=11, a3=111 и т.д.)
R=3
Si = 2…2 (S1=2, S2=22, S3=222 и т.д.)
L = 33
H = 333
В этом случае всю программу работы машины можно записать неким числом,
причем возможны два варианта записи:
1. С разделителем команд, допустим Х, которые можно закодировать числом
4. В этом случае классическая запись S old a old→a new R S new,
2. Без разделителя команд. В этом случае команды следует писать в формате
a old S old a new R S new, тогда две команды, записанные непосредственно
друг за другом, будут явно различаться элементарным анализатором.
35.
34Универсальная Машина Тьюринга (УМТ)
Пример машины Тьюринга, которая на пустой ленте бесконечно много раз
печатает последовательность 001.
Из соображений удобства формат записи будет следующим aSi → a'{R,L,H}Sj.
При такой записи обозначение символа указывается ранее обозначения
состояния. Цель данной перестановки довольно банальная: избежать наличия
лишнего разделителя.
Программа такой машины выглядит следующим образом (λ-пустой знак):
λA0RB
Закодируем символы и состояния:
λ=1
A=2
λB0RC
0=11
B=22
λC1RA
1=111 C=222
Тогда запись программы машины будет выглядеть так (пробелы поставлены
для повышения читаемости, в реальности их нет):
1 2 11 3 22 1 22 11 3 222 1 222 111 3 2
В итоге каждая МТ представлена числом – это дескриптивное (описательное)
число машины. Вместе с тем оно является кодом для входного слова.
Таким образом решается проблема унификации записи программы машины
Тьюринга и входного слова на её ленте.
Несмотря на это, построение реально работающей универсальной машины
Тьюринга представляет собой довольно сложный процесс.
36. Теория алгоритмов
Тема 3. Нормальные алгоритмыМаркова.
37.
36Андрей Андреевич Марков
Выдающийся советский математик и логик,
член-корреспондент АН СССР, заведующий
кафедрой
математической
логики
Московского государственного университета.
Научная
деятельность
А.
А.
Маркова
чрезвычайно плодотворна и многогранна. Она
распространяется
на
многие
области
математики и смежных с ней наук. Почти в
каждой из тех областей науки, которые
привлекли внимание А. А. Маркова, с его
Андрей Андреевич Марков
именем
связаны
научные
достижения
(22.09.1903 - 11.10.1979 гг.)
первостепенного значения.
Основные циклы опубликованных работ А. А. Маркова относятся к
следующим наукам разделам:
теоретическая физика, небесная механика, общая теория динамических
систем, комбинаторная топология (теория кос и зацеплений), теория
полиномов, теория топологических групп, алгоритмические проблемы
алгебры, общая теория алгоритмов, конструктивная математическая логика
и основания математики, конструктивный математический анализ,
алгоритмические проблемы топологии, теория булевых функций.
38.
37Идея нормальный алгорифмов Маркова
Если попытаться уйти от наличия самого управляющего механизма
машины Тьюринга со своим собственным регистром для записи внутреннего
состояния и перенести информацию о состоянии некоторого агрегата
непосредственно на ленту, можно получить новую нотацию для записи
алгоритмов.
Проблемы движения управляющего механизма в этом случае не
существует:
для
выполнения
предписания
необходимо
будет
проанализировать заданное слово и найти первое попавшееся соответствие
между левой частью инструкции и каким-либо фрагментом содержимого
ленты.
Для удобства допустим, что анализ производится укрупненно, не по одному
символу, а сразу по нескольким.
Кроме того, лента является «растяжимой», т.е. вместо одного символа
можно вписывать произвольное их количество и наоборот, без процедуры
сдвигания части слова.
Таким образом, формируется идея нормального алгоритма переработки
входного слова, называемого в литературе алгоритмом Маркова.
39.
38Определение
Нормальный алгоритм Маркова – математическое построение,
предназначенное для уточнения понятия алгоритм, которое задается
алфавитом и нормальной схемой подстановок, выполняемых по заранее
определенной схеме.
Нормальные алгоритмы можно рассматривать как обобщение машины
Тьюринга. В свою очередь работу машин Тьюринга можно рассматривать как
переработку начального слова некоторого нормального алгоритма. Этот
алгоритм получается сразу же из таблицы машины.
По своей сути основная операция при работе алгоритмов Маркова – это
переработка слов в некотором алфавите. Эта переработка заключается в
производстве
некоторого
количества
замен
определенных
последовательностей символов. Эти замены совершаются в СТРОГО
определенном порядке, а именно: после каждой замены алгоритм
читается с самого начала, а слово анализируется с самого первого
(левого) символа. В отличие от машин Тьюринга, алгоритмы Маркова
выполняются без какого-либо устройства, осуществляющего движения и
имеющего внутреннюю память. В данном случае мы можем оперировать
только ленточными знаками.
40.
39Формат команды
Формат команды (строки) следующий: {ai} {bj} [•],
где
•{ai} - последовательность символов, которая ищется в слове,
• - знак перехода к операции записи,
•{bj} - последовательность символов, которая записывается вместо
найденной последовательности,
•[•] - знак принудительного окончания алгоритма (необязательный параметр).
•Λ – служебный знак, обозначающий пустой символ, присутствует везде:
изначально на ленте (если она пустая), справа и слева от каждого символа
(если на ленте записано слово).
Программа (алгоритм) представляет собой совокупность строк указанного
вида, причем порядок строк имеет важнейшее значение.
Окончание работы алгоритма происходит в тот момент, когда
1.выполняется строка, содержащая знак принудительной остановки,
2.когда более ни одна строка не может быть выполнена (в слове нет ни
одной из искомых последовательностей символов).
Тезис Маркова: любой вычислительный процесс можно преобразовать в
нормальный алгоритм.
41.
40Примеры
Пример 1 Пусть в алфавите A2={a,b,c} задана система ориентированных
подстановок:
1. cb → cc
2. cca → ab
3. ab → bca
4. ca →Λ
Этот алгоритм, будучи применен к слову cabc, никогда не обрывается:
cabc → cbcac→ cccab→ cabc (3,1,2 правила) – получилось первоначальное
слово, т.е.
Если же брать слово baaacca, то после нескольких шагов процесс оборвется
на слове bb:
baaacca → baaabca → baabcaca → babcacaca → bbcacacaca → …→ bb.
2
3
3
3
4
Два нормальных алгоритма отличаются друг от друга алфавитом и системой
ориентированных подстановок или даже только порядком подстановок.
42.
41Примеры
Пример 2 Пусть в одном и том же алфавите заданы два нормальных
алгоритма I1 и I2 , отличающиеся друг от друга только порядком
подстановок:
I1:
I2:
1. ab→bac
1. bc→bb
2. ac→ca
2. ab→bac
3. aa→Λ
3. ac→ca
4. bc →bb
4. aa→Λ
5. bb→Λ
5. bb→Λ
Покажем, что I1(abbc)≠I2(abbc):
I1(abbc) 1 → bacbc 2 → bcabc 1 → bcbacc 2 → bcbcac 2 → bcbcca 4 → bbbcca
4 → bbbbca 4 → 4 → bbbbba 5 → …5 → ba.
I2(abbc)1 → abbb 2 → bacbb 3 → bcabb 1 → bbabb 2 → bbbacb 3 → bbbcab 1
→ bbbab 2 → bbbbbac 3 → bbbbbca 1 → bb bb bba → 5 ... → a.
Этот пример показывает, что в нормальных алгоритмах имеет значение
не только сами подстановки, но и их порядок.
43.
42Вычисление арифметических функций
Определение
Функция y=F(x1,x2,…,xn) называется арифметической функцией, если
аргументы xi и значение y принимают только натуральные значения из
N*={0, 1, 2, 3,…}.
Положительные натуральные числа зададим как слова в однобуквенном
алфавите А={1}: пусть число n задается в виде слова из n «палочек».
Далее примеры на доске…
44. Теория графов
44Теория графов
Тема 1. Основные определения
45.
45История возникновения теории графов
Леона́рд Э́йлер (4 апреля 1707, Базель, Швейцария —
7 сентября 1783, Санкт-Петербург, Российская империя)
— швейцарский, немецкий и
российский математик, внёсший
значительный вклад
в развитие математики, а также
механики, физики, астрономии
и ряда прикладных наук.
Почти полжизни провёл в
России, где внёс существенный
вклад в становление российской
науки.
Считается родоначальником теории графов.
46.
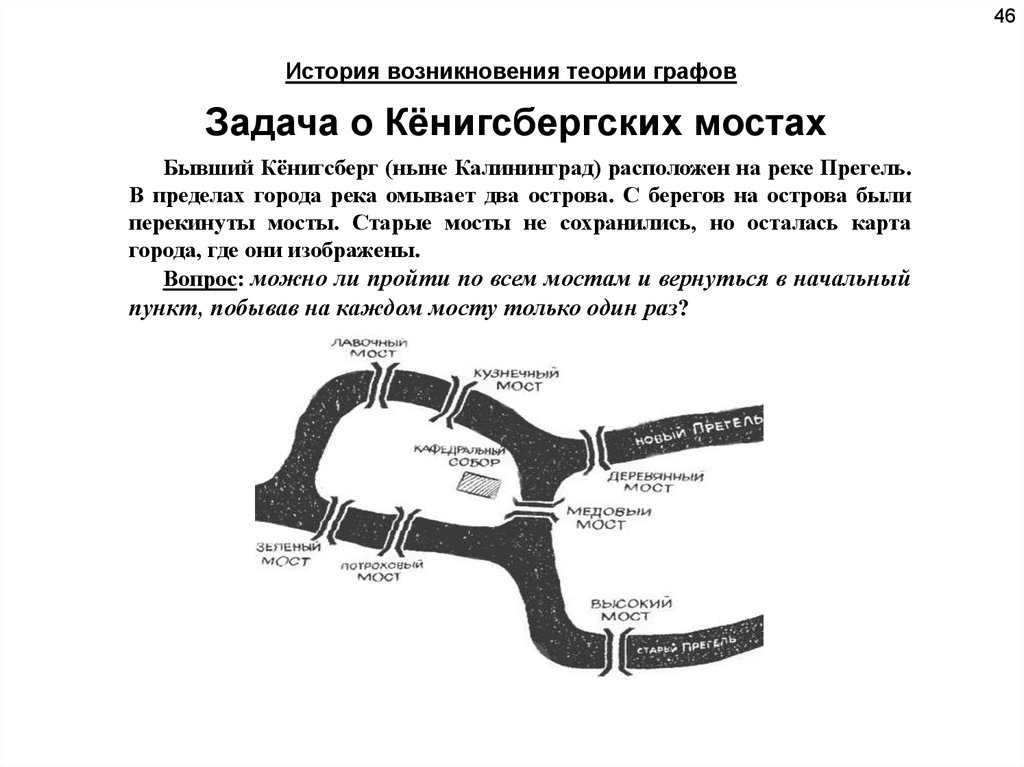
46История возникновения теории графов
Задача о Кёнигсбергских мостах
Бывший Кёнигсберг (ныне Калининград) расположен на реке Прегель.
В пределах города река омывает два острова. С берегов на острова были
перекинуты мосты. Старые мосты не сохранились, но осталась карта
города, где они изображены.
Вопрос: можно ли пройти по всем мостам и вернуться в начальный
пункт, побывав на каждом мосту только один раз?
47.
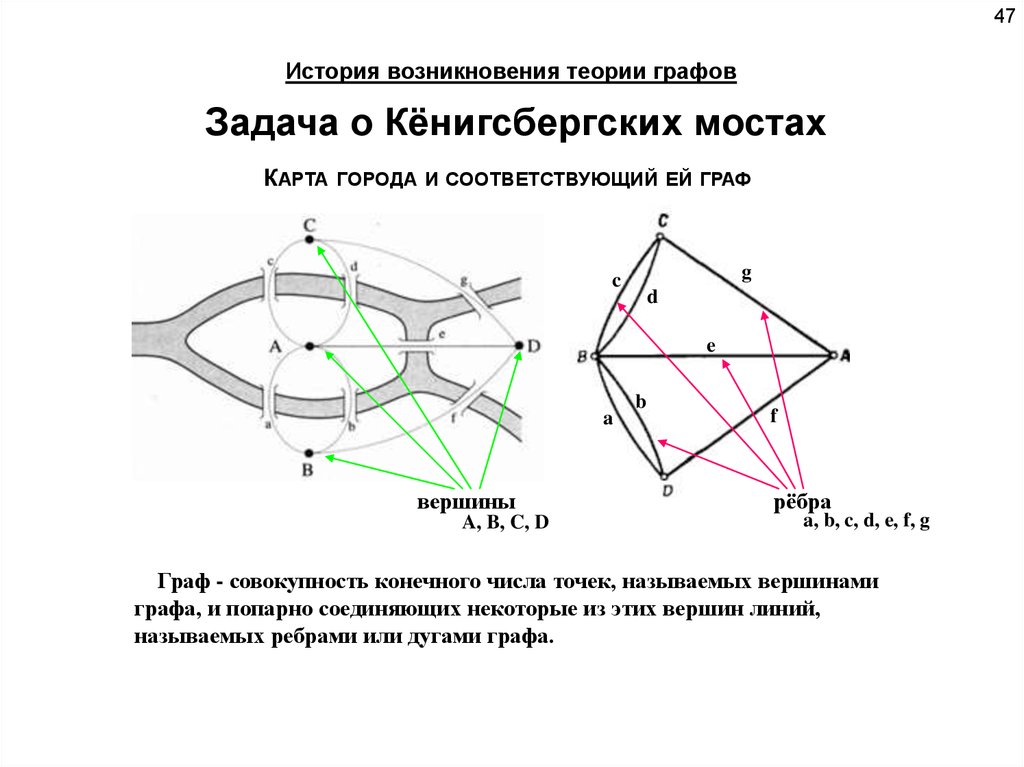
47История возникновения теории графов
Задача о Кёнигсбергских мостах
КАРТА
ГОРОДА И СООТВЕТСТВУЮЩИЙ ЕЙ ГРАФ
g
c
d
e
a
вершины
A, B, C, D
b
f
рёбра
a, b, c, d, e, f, g
Граф - совокупность конечного числа точек, называемых вершинами
графа, и попарно соединяющих некоторые из этих вершин линий,
называемых ребрами или дугами графа.
48.
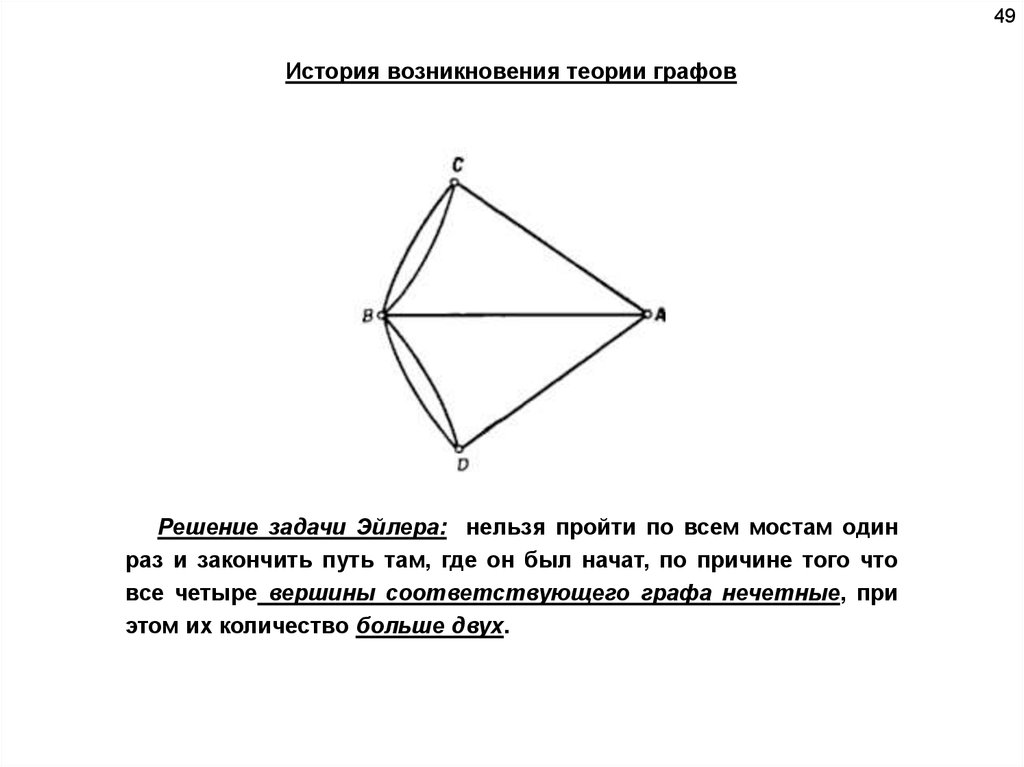
48История возникновения теории графов
Решая задачу про кенигсбергские мосты, Эйлер установил
следующие свойства графа:
если все вершины графа четные, то можно одним росчерком (т.е. не
отрывая карандаша от бумаги и не проводя дважды по одной и той же
линии) начертить граф. При этом движение можно начать с любой
вершины и окончить в той же вершине.
граф с двумя нечетными вершинами тоже можно начертить одним
росчерком. Движение надо начинать от любой нечетной вершины, а
заканчивать на другой нечетной вершине.
граф с более чем двумя нечетными вершинами невозможно начертить
одним росчерком.
49.
49История возникновения теории графов
Решение задачи Эйлера: нельзя пройти по всем мостам один
раз и закончить путь там, где он был начат, по причине того что
все четыре вершины соответствующего графа нечетные, при
этом их количество больше двух.
50.
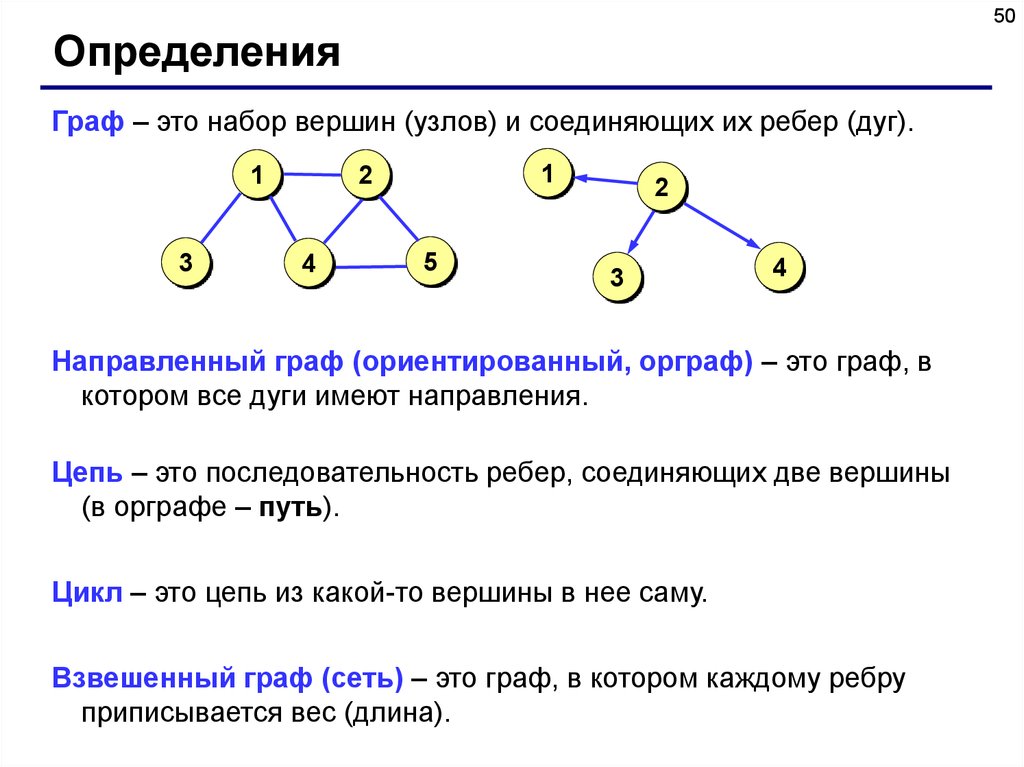
50Определения
Граф – это набор вершин (узлов) и соединяющих их ребер (дуг).
1
3
1
2
4
5
2
3
4
Направленный граф (ориентированный, орграф) – это граф, в
котором все дуги имеют направления.
Цепь – это последовательность ребер, соединяющих две вершины
(в орграфе – путь).
Цикл – это цепь из какой-то вершины в нее саму.
Взвешенный граф (сеть) – это граф, в котором каждому ребру
приписывается вес (длина).
51.
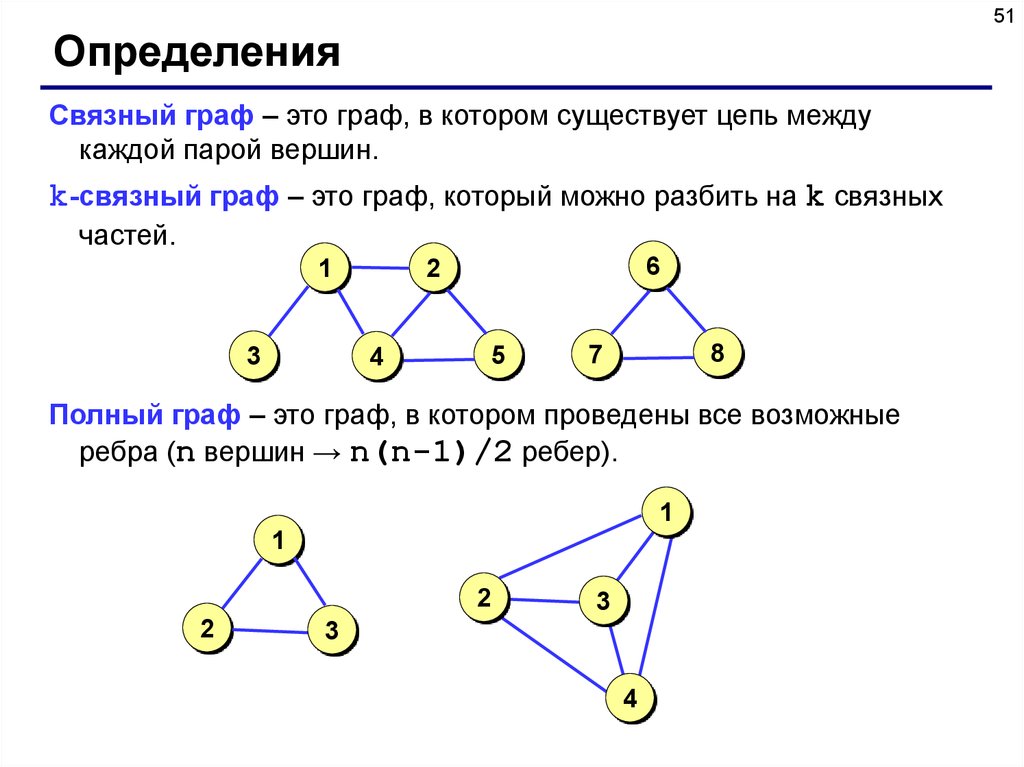
51Определения
Связный граф – это граф, в котором существует цепь между
каждой парой вершин.
k-cвязный граф – это граф, который можно разбить на k связных
частей.
1
3
6
2
5
4
8
7
Полный граф – это граф, в котором проведены все возможные
ребра (n вершин → n(n-1)/2 ребер).
1
1
2
2
3
3
4
52.
52Основные понятия теории графов
__________________________________________________________________
______
Плоский граф
– который можно представить на
плоскости в таком виде, когда его ребра пересекаются
только в вершинах.
плоский граф, изоморфный (равный) графу,
изображённому на рисунке а)
Не каждый граф является плоским, однако любой
плоский граф можно представить в обычном виде.
53.
53Основные понятия теории графов
__________________________________________________________________
______
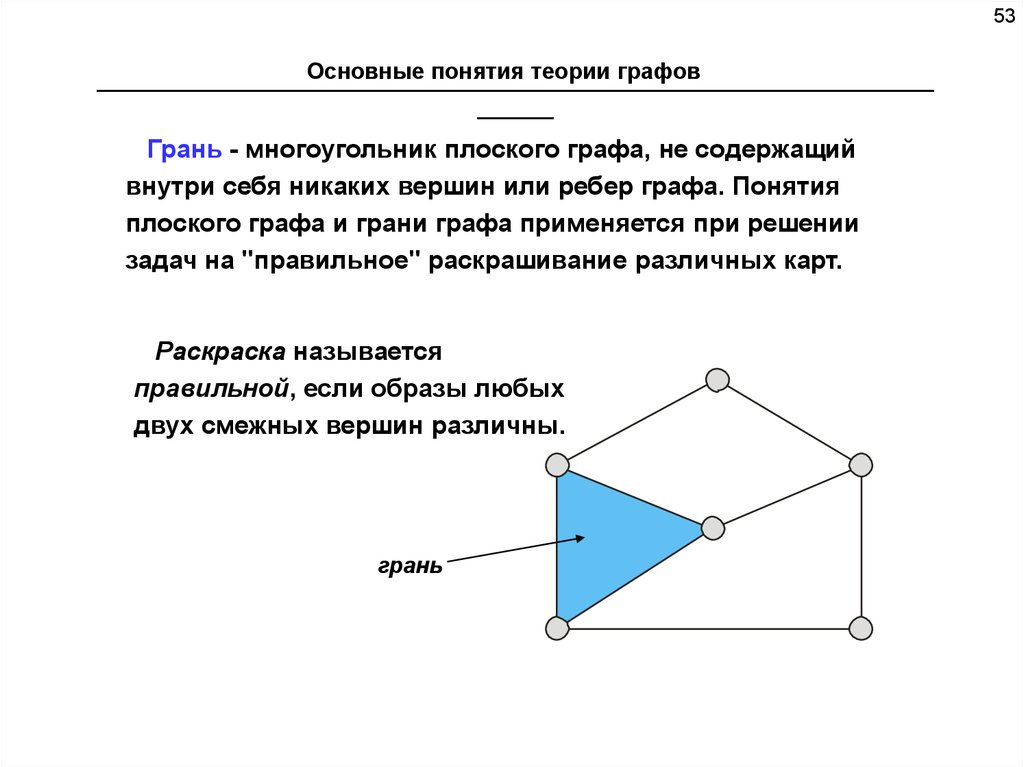
Грань - многоугольник плоского графа, не содержащий
внутри себя никаких вершин или ребер графа. Понятия
плоского графа и грани графа применяется при решении
задач на "правильное" раскрашивание различных карт.
Раскраска называется
правильной, если образы любых
двух смежных вершин различны.
грань
54.
54Основные понятия теории графов
__________________________________________________________________
______
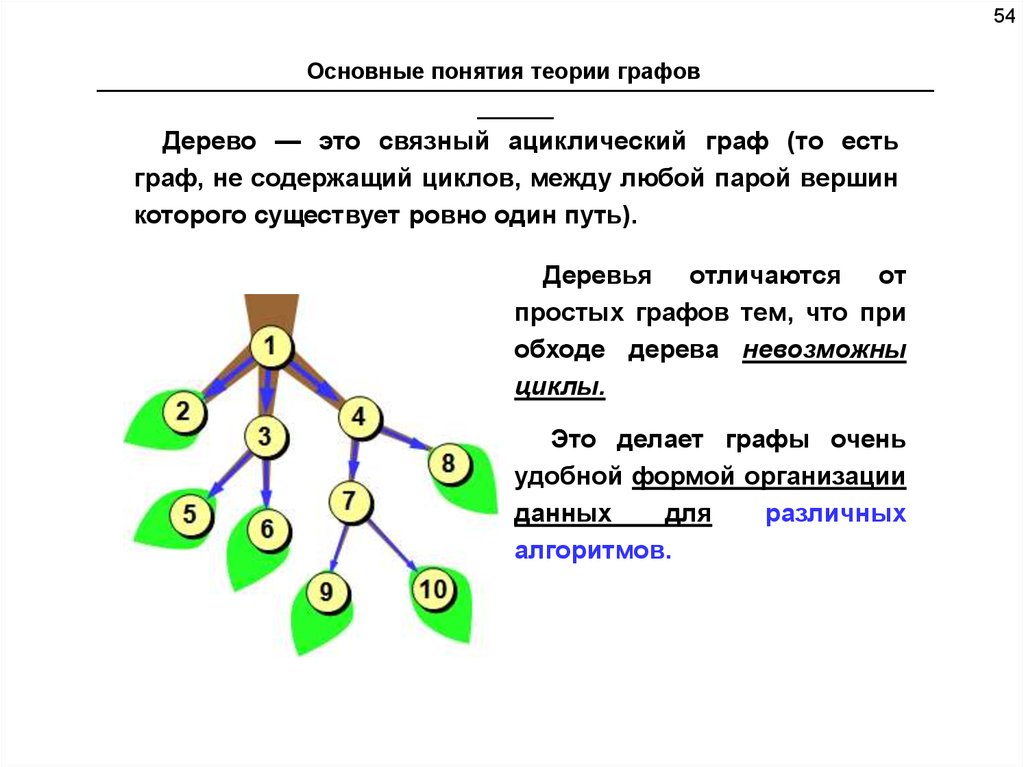
Дерево — это связный ациклический граф (то есть
граф, не содержащий циклов, между любой парой вершин
которого существует ровно один путь).
Деревья отличаются от
простых графов тем, что при
обходе дерева невозможны
циклы.
Это делает графы очень
удобной формой организации
данных
для
различных
алгоритмов.
55.
55Основные понятия теории графов
__________________________________________________________________
______
При изображении графов на рисунках или схемах отрезки
могут быть прямолинейными или криволинейными, длины
отрезков и расположение точек произвольны.
=
=
Все три фигуры на рисунке изображают один и тот же
граф.
56. Операции над графами
56Операции над графами
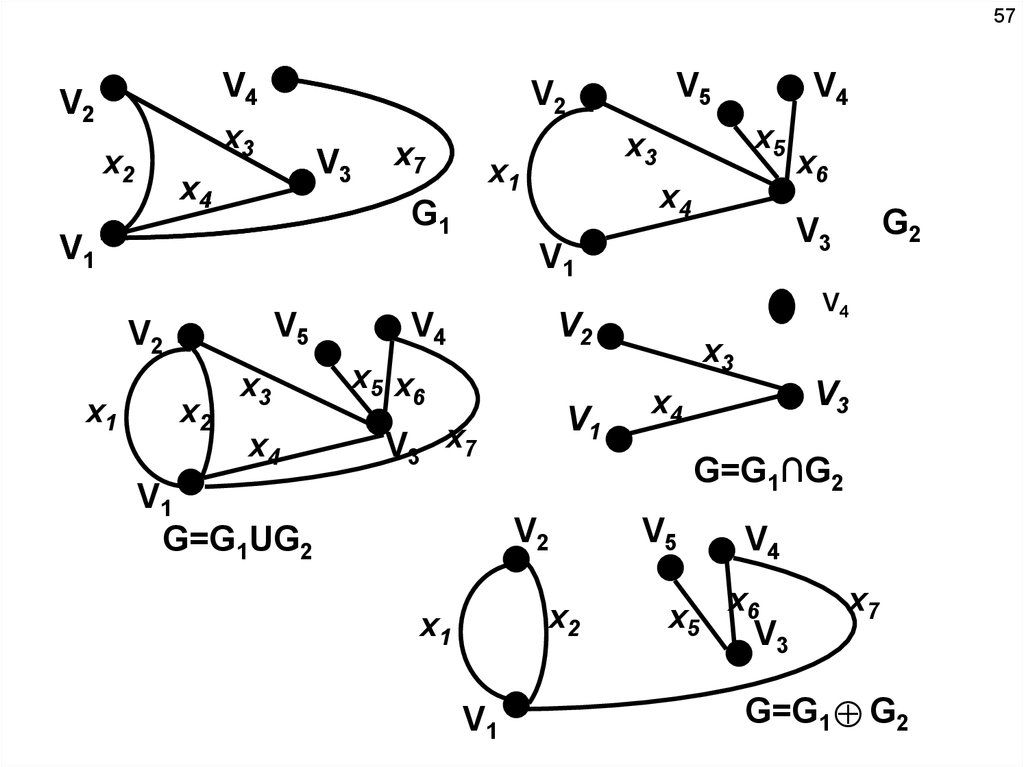
Объединением графов G1 (V1 , X 1 ) и G2 (V2 , X 2 )
называется граф G G1 G2, множество вершин
которого V V1 V2 , а множество рёбер X X 1 X 2 .
Пересечением графов G1 и G2 называется
граф G G1 G2 , для которого X X 1 X 2 множество рёбер, а V V1 V2 - множество вершин.
Кольцевой суммой двух графов называется
граф G G1 G2 ,
порождённый
множеством
вершин V V1 V2 и множеством рёбер ( X1 X 2 ) \ ( X1 X 2 )
, т.е. множеством рёбер, содержащихся либо в G1 ,
либо в G2 , но не в G1 G2 .
57.
57V4
х3
V2
х2
V3
х4
х7
х1
V4
х5
х3
х4
G1
V1
V5
х2
х3
х4
V4
V3
V1
х7
V1
G=G1UG2
х2
V1
х3
V3
х4
G=G1∩G2
V2
х1
G2
V4
V2
х5 х6
х6
V3
V1
V2
х1
V5
V2
V5
V4
х5 х6V
3
х7
G=G1 G2
58.
58Подграфом графа G (V , X ) называется граф
G1 (V1 , X 1 ) , все вершины и рёбра которого
являются подмножествами множества вершин
и рёбер графа G.
Графы G’ и G’’ называются изоморфными ,
если
существует
взаимно-однозначное
соответствие между их ребрами и вершинами,
причем соответствующие ребра соединяют
соответствующие вершины.
59. Цикломатическое число графа
Цикломатическимчислом
неориентированного графа G называется число
,
(G ) m(G ) c(G ) n(G )
где m(G ) - число его рёбер;
c (G ) - число связных компонент графа;
n(G ) - число вершин.
Цикломатическое число показывает, сколько
рёбер нужно удалить из графа, чтобы в нём не
стало циклов.
60.
60Задачи на графы. Идея чётности. Раскраска.
__________________________________________________________________
______
Задача №1.
Аркадий, Борис, Владимир, Григорий и Дмитрий при встрече
обменялись рукопожатиями (каждый пожал руку каждому по
одному разу). Сколько всего рукопожатий было сделано?
Решение.
Пусть каждому из пяти молодых людей соответствует
определенная точка на плоскости, названная первой буквой его
имени, а — отрезок – производимое рукопожатие.
В
В
Б
Б
Г
А
Г
А
Д
Д
61.
61Задачи на графы. Идея чётности. Раскраска.
__________________________________________________________________
______
Задача №1.
Аркадий, Борис, Владимир, Григорий и Дмитрий при встрече
обменялись рукопожатиями (каждый пожал руку каждому по
одному разу). Сколько всего рукопожатий было сделано?
Решение.
В
Б
Если полный граф
имеет n вершин, то количество
ребер будет равно
n(n-1)/2.
Г
А
Д
Ответ: было совершено 10 рукопожатий.
62.
62Задачи на графы. Идея чётности. Раскраска.
__________________________________________________________________
______
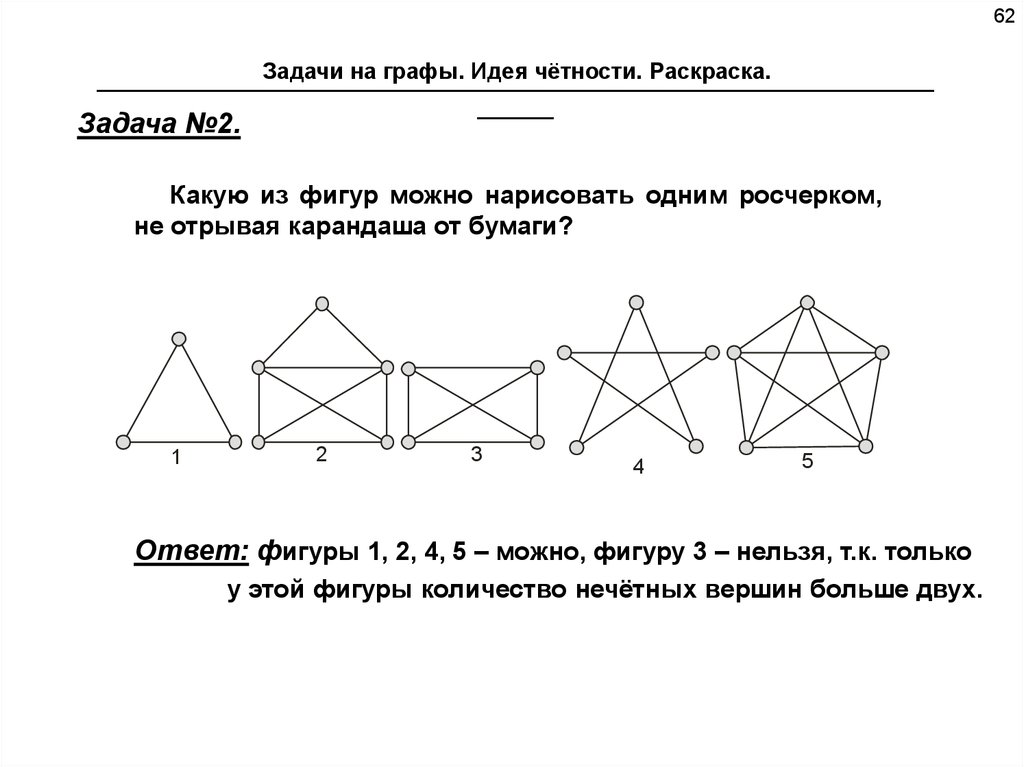
Задача №2.
Какую из фигур можно нарисовать одним росчерком,
не отрывая карандаша от бумаги?
1
2
3
4
5
Ответ: фигуры 1, 2, 4, 5 – можно, фигуру 3 – нельзя, т.к. только
у этой фигуры количество нечётных вершин больше двух.
63.
63Задачи на графы. Идея чётности. Раскраска.
__________________________________________________________________
______
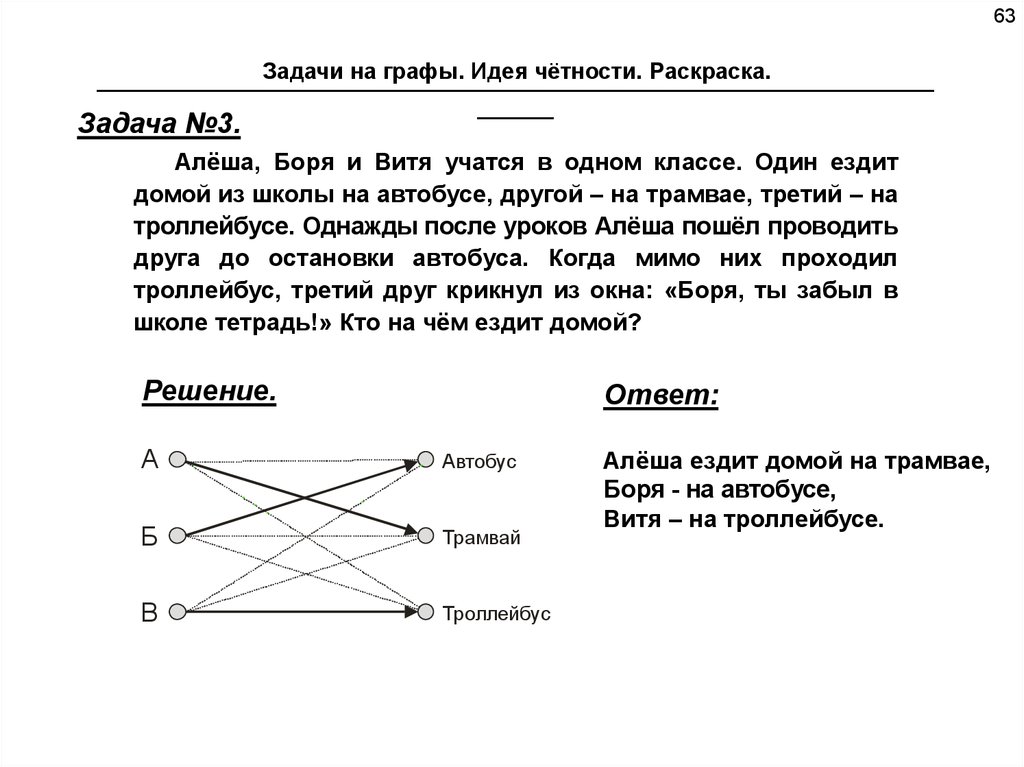
Задача №3.
Алёша, Боря и Витя учатся в одном классе. Один ездит
домой из школы на автобусе, другой – на трамвае, третий – на
троллейбусе. Однажды после уроков Алёша пошёл проводить
друга до остановки автобуса. Когда мимо них проходил
троллейбус, третий друг крикнул из окна: «Боря, ты забыл в
школе тетрадь!» Кто на чём ездит домой?
Решение.
Ответ:
А
Автобус
Б
Трамвай
В
Троллейбус
Алёша ездит домой на трамвае,
Боря - на автобусе,
Витя – на троллейбусе.
64.
64Задачи на графы. Идея чётности. Раскраска.
__________________________________________________________________
______
Задача №4.
Между девятью планетами солнечной системы установлено
космическое сообщение. Рейсовые ракеты летают по
следующим маршрутам: Земля – Меркурий; Плутон – Венера;
Земля – Плутон; Плутон – Меркурий; Меркурий – Венера; Уран –
Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и
Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли
до Марса?
Решение.
Земля
Меркурий
Нептун
Сатурн
Юпитер
Плутон
Венера
Уран
Марс
Ответ: очевидно, что долететь с Земли до Марса нельзя.
65.
65Задачи на графы. Идея чётности. Раскраска.
__________________________________________________________________
______
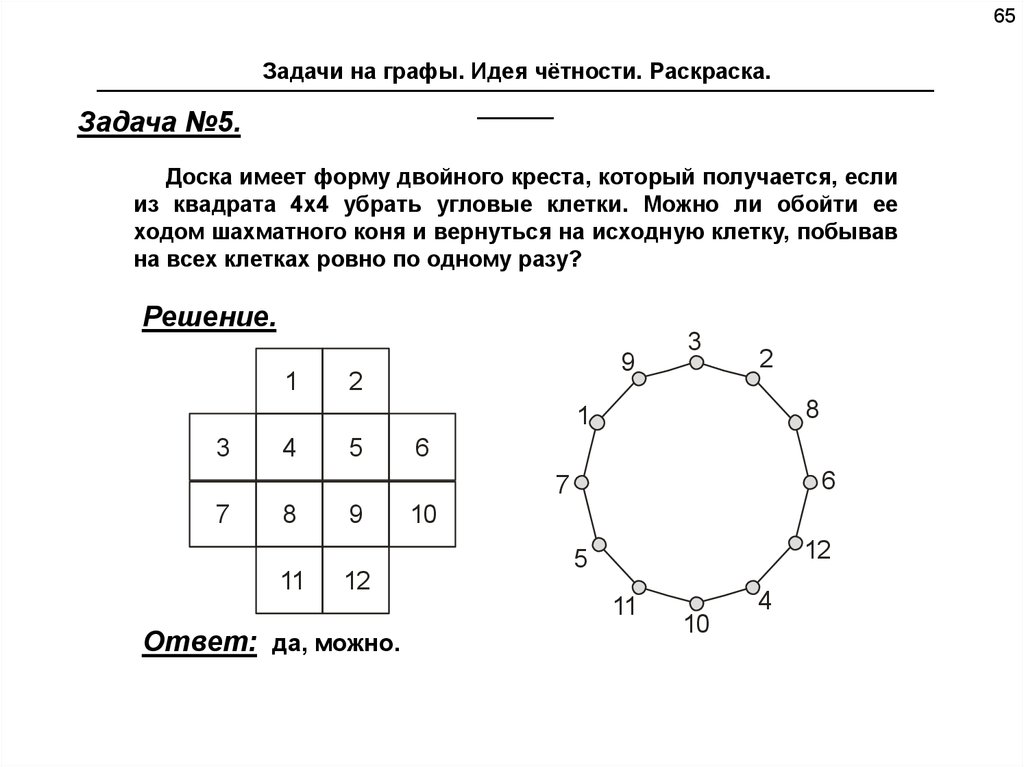
Задача №5.
Доска имеет форму двойного креста, который получается, если
из квадрата 4x4 убрать угловые клетки. Можно ли обойти ее
ходом шахматного коня и вернуться на исходную клетку, побывав
на всех клетках ровно по одному разу?
Решение.
1
9
2
3
2
8
1
3
4
5
6
6
7
7
8
11
9
12
10
12
5
11
Ответ: да, можно.
4
10
66.
66Задачи на графы. Идея чётности. Раскраска.
__________________________________________________________________
______
Задача №6.
Раскрасить вершины графа так, чтобы любые две
смежные вершины были раскрашены в разные цвета,
при этом число использованных цветов должно быть
наименьшим.
Это число называется
хроматическим (цветным) числом
графа.
В данной задаче хроматическое
число равно 3.
67.
67Задача №7.
Шахматный турнир проводится по круговой
системе, при которой каждый участник
встречается с каждым ровно один раз,
участвуют семь школьников.
Известно, что в настоящий момент:
1) Ваня сыграл шесть партий;
2) Толя сыграл пять партий;
3) Леша и Дима сыграли по три партии;
4) Семен и Илья сыграли по две партии;
5) Женя сыграл одну партию.
Требуется определить:
с кем сыграл Леша.
68.
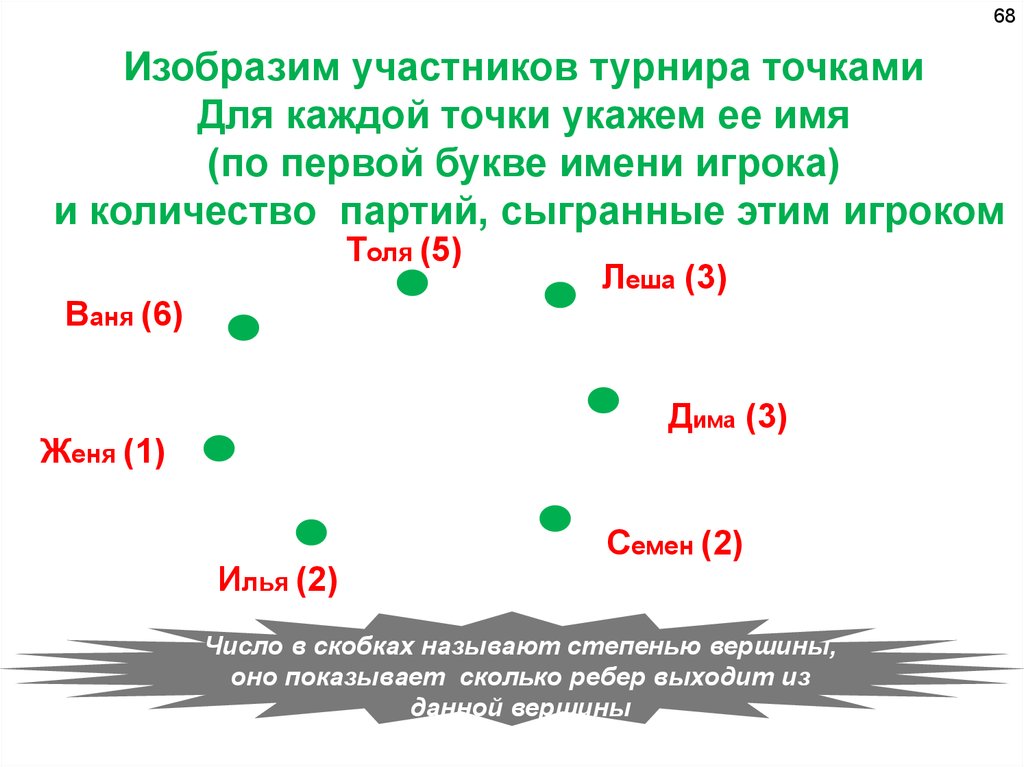
68Изобразим участников турнира точками
Для каждой точки укажем ее имя
(по первой букве имени игрока)
и количество партий, сыгранные этим игроком
Толя (5)
Ваня (6)
Леша (3)
Дима (3)
Женя (1)
Илья (2)
Семен (2)
Число в скобках называют степенью вершины,
оно показывает сколько ребер выходит из
данной вершины
69.
69Будем строить ребра графа с учетом степеней вершин
Начать построение ребер следует с вершины В,
так как это единственная вершина,
которая соединяется со всеми другими вершинами
графа
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Женя (1)
Семен (2)
Илья (2)
70.
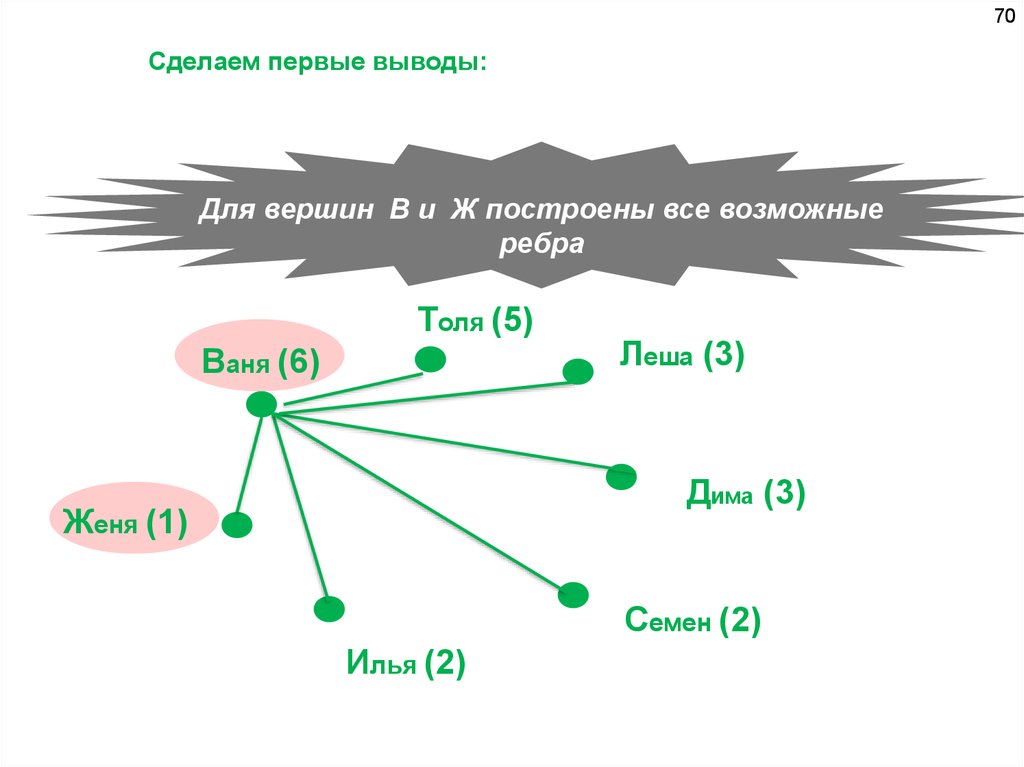
70Сделаем первые выводы:
Для вершин В и Ж построены все возможные
ребра
Толя (5)
Ваня (6)
Леша (3)
Дима (3)
Женя (1)
Семен (2)
Илья (2)
71.
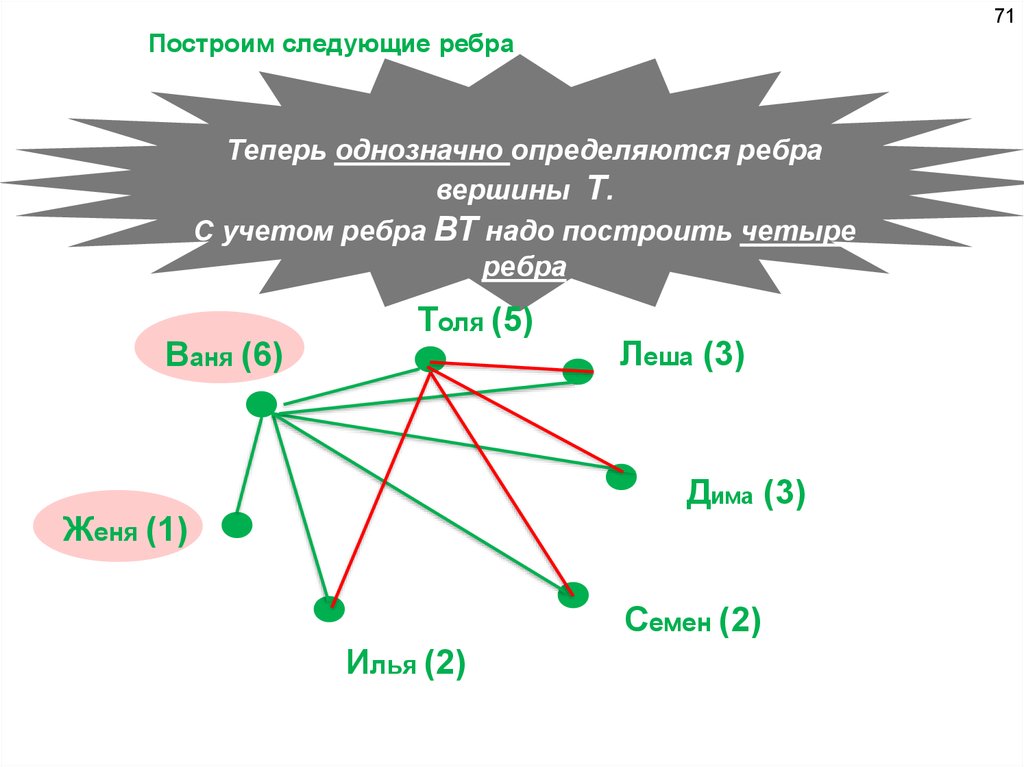
71Построим следующие ребра
Теперь однозначно определяются ребра
вершины Т.
С учетом ребра ВТ надо построить четыре
ребра
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Женя (1)
Семен (2)
Илья (2)
72.
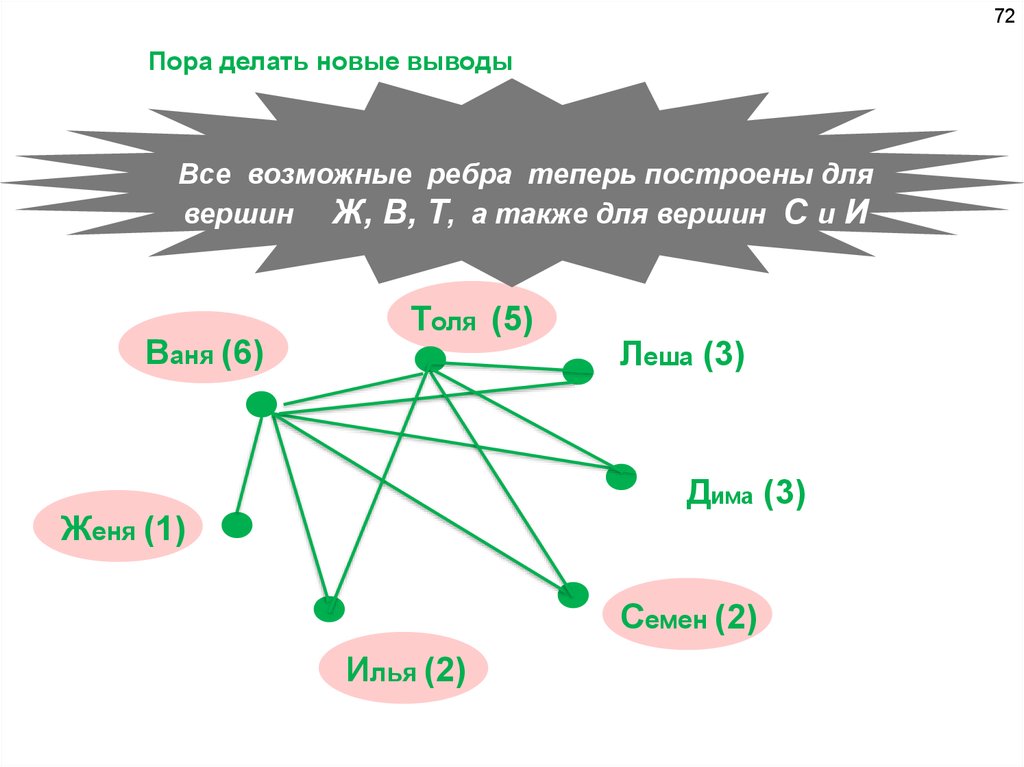
72Пора делать новые выводы
Все возможные ребра теперь построены для
вершин Ж, В, Т, а также для вершин С и И
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Женя (1)
Семен (2)
Илья (2)
73.
73Граф к задаче построен
Требовалось определить: с кем сыграл
Леша.
Толя (5)
Ваня (6)
Леша (3)
Дима (3)
Женя (1)
Илья (2)
Семен (2)
ОТВЕТ: Леша играл с Толей, Ваней и Димой
74.
74Задача №8.
В одном дворе живут четыре друга.
Вадим и шофер старше Сергея,
Николай и слесарь занимаются боксом,
Электрик-младший из друзей.
По вечерам Андрей и токарь играют в
домино против Сергея и электрика.
Определите профессию каждого из
друзей.
75.
75Вадим
слесарь
Сергей
токарь
Коля
электрик
Андрей
шофер
Начинаем анализировать полученную схему.
От каждого верхнего кружка должно исходить 4 линии к кружкам нижнего
ряда,одна из которых сплошная(прочная связь) ,три-пунктирные.
(разрывная связь). И от кружков нижнего ряда-аналогично.
От Сергея отходит 3 разрывные связи, значит, четвертая- прочная связь
Ответ готов:
Вадим-токарь, Сергей-слесарь, Коля-электрик, Андрей-шофер
76.
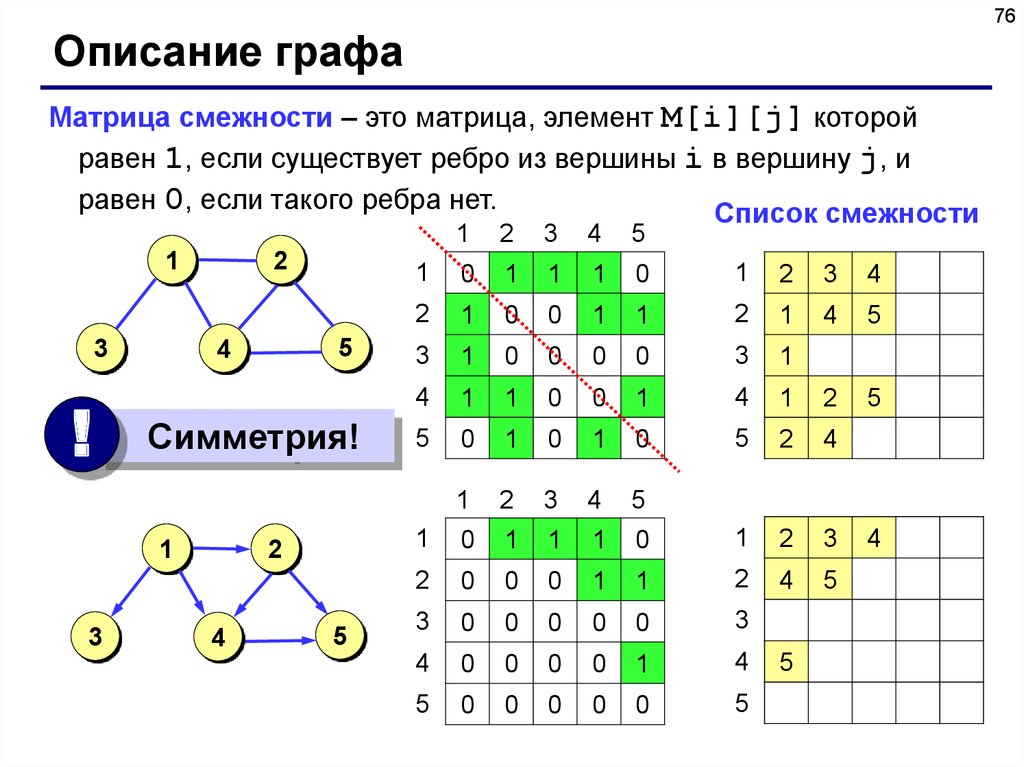
76Описание графа
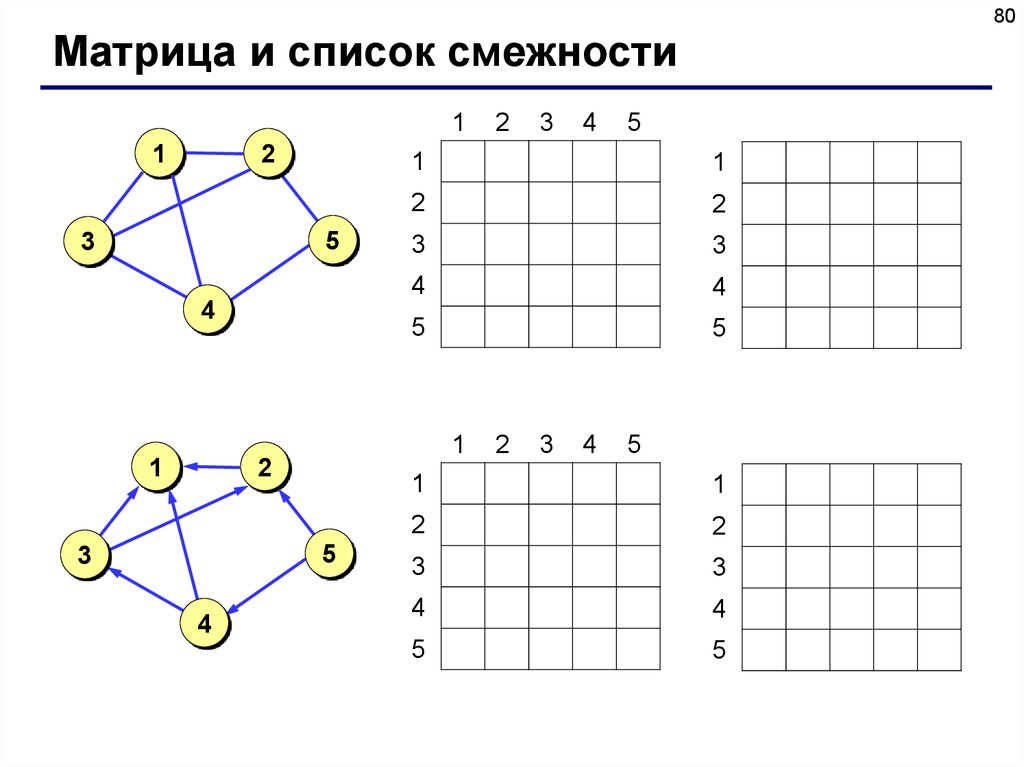
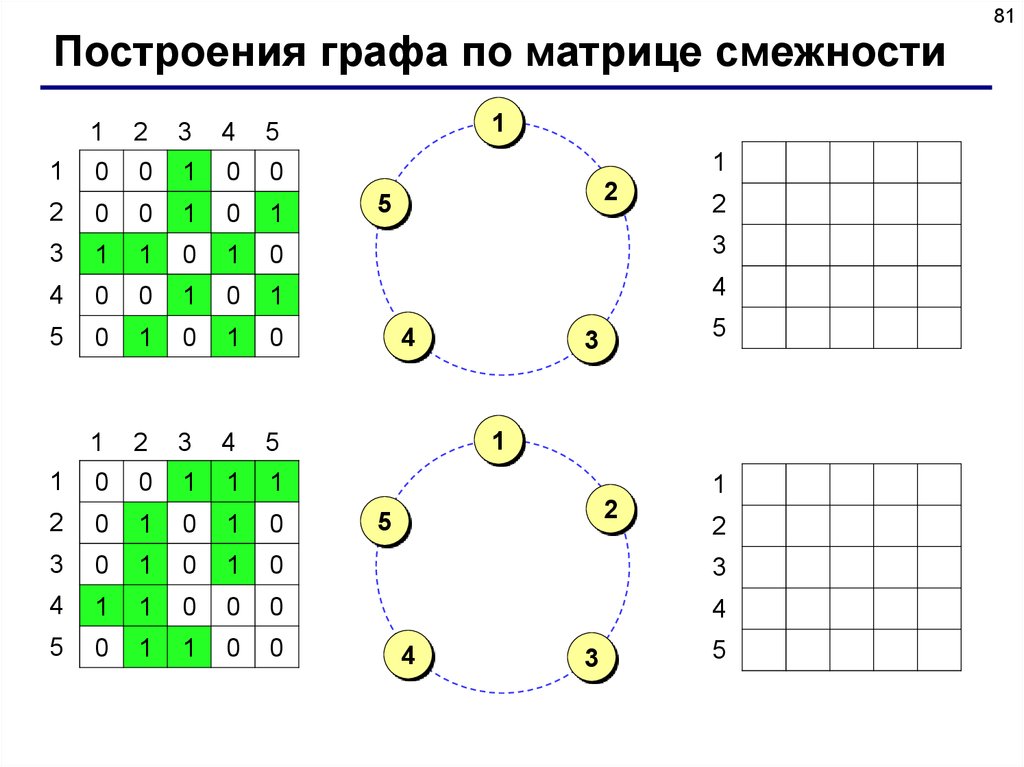
Матрица смежности – это матрица, элемент M[i][j] которой
равен 1, если существует ребро из вершины i в вершину j, и
равен 0, если такого ребра нет.
Список смежности
1
3
!
2
Симметрия!
1
3
5
4
2
4
5
1
2
3
4
5
1
0
1
1
1
0
1
2
3
4
2
1
0
0
1
1
2
1
4
5
3
1
0
0
0
0
3
1
4
1
1
0
0
1
4
1
2
5
5
0
1
0
1
0
5
2
4
1
2
3
4
5
1
0
1
1
1
0
1
2
3
2
0
0
0
1
1
2
4
5
3
0
0
0
0
0
3
4
0
0
0
0
1
4
5
0
0
0
0
0
5
5
4
77.
77Матрицей
инцидентности
называется
таблица, состоящая из n строк (вершины) и т
столбцов (рёбра), в которой:
• для неориентированного графа:
bij 1, если вершина Vi инцидентна ребру X j ;
bij 0 , если вершина не инцидентна ребру ;
• для ориентированного графа:
bij 1, если вершина является началом дуги ;
bij 0 , если вершина не инцидентна дуге ;
bij 1 , если вершина является концом дуги.
78.
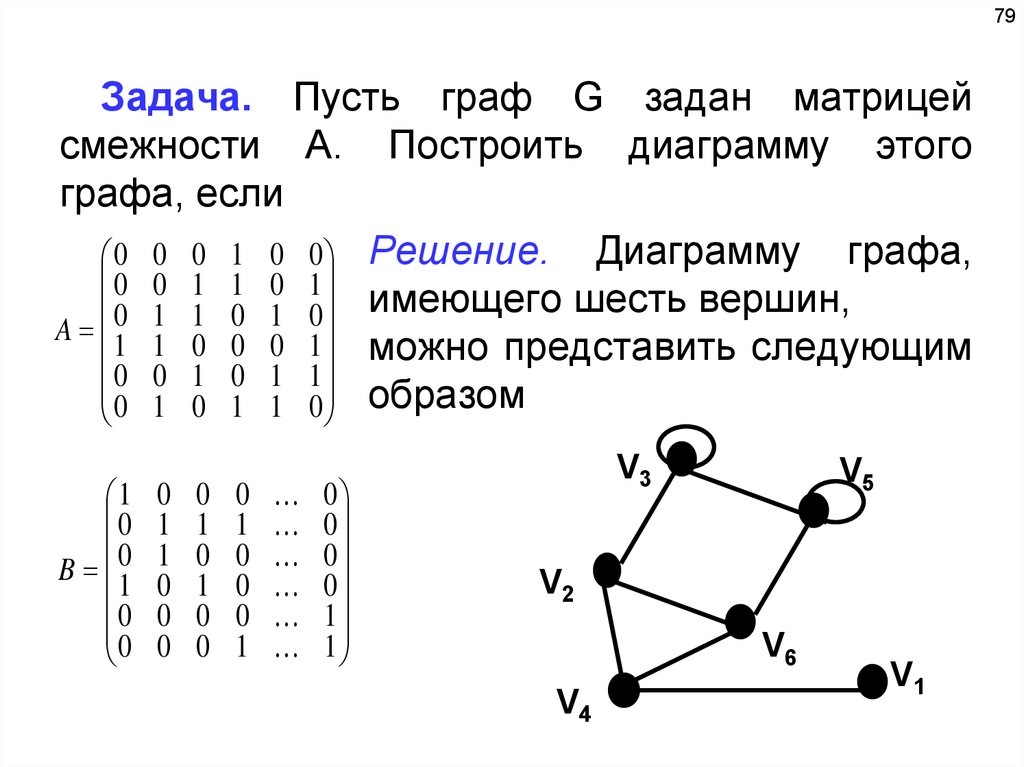
78Задача. Пусть граф G задан матрицей
смежности А. Построить диаграмму этого
графа, если
0 1 0 1 0 1 Решение. Поскольку матрица
1 0 1 1 0 1
0 1 0 1 0 1 А несимметрична (например
A 1 1 1 1 0 0
a35 a53 ), то
она
может
0 0 1 0 0 1
1 1 1 1 1 0 задавать только ориентиро
ванный граф.
1
1
0
B
0
0
0
1 0
0 0 0
0 0 0
1 0 0
0 0 1
0 1 1
1
V3
V2
V4
V1
V6
V5
79.
79Задача. Пусть граф G задан матрицей
смежности А. Построить диаграмму этого
графа, если
0 0 0 1 0 0 Решение. Диаграмму графа,
0 0 1 1 0 1
0 1 1 0 1 0 имеющего шесть вершин,
A 1 1 0 0 0 1
можно представить следующим
0 0 1 0 1 1
0 1 0 1 1 0 образом
1
0
B 10
0
0
0
1
1
0
0
0
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
1
V3
V5
V2
V6
V4
V1
80.
80Матрица и список смежности
1
1
2
5
3
4
1
5
3
4
3
4
5
1
1
2
2
3
3
4
4
5
5
1
2
2
2
3
4
5
1
1
2
2
3
3
4
4
5
5
81.
81Построения графа по матрице смежности
1
1
2
3
4
5
0
0
1
0
0
1
1
2
5
2
2
0
0
1
0
1
3
1
1
0
1
0
3
4
0
0
1
0
1
4
5
0
1
0
1
0
1
2
3
4
5
1
0
0
1
1
1
2
0
1
0
1
0
3
0
1
0
1
0
3
4
1
1
0
0
0
4
5
0
1
1
0
0
4
5
3
1
1
2
5
4
3
2
5
82.
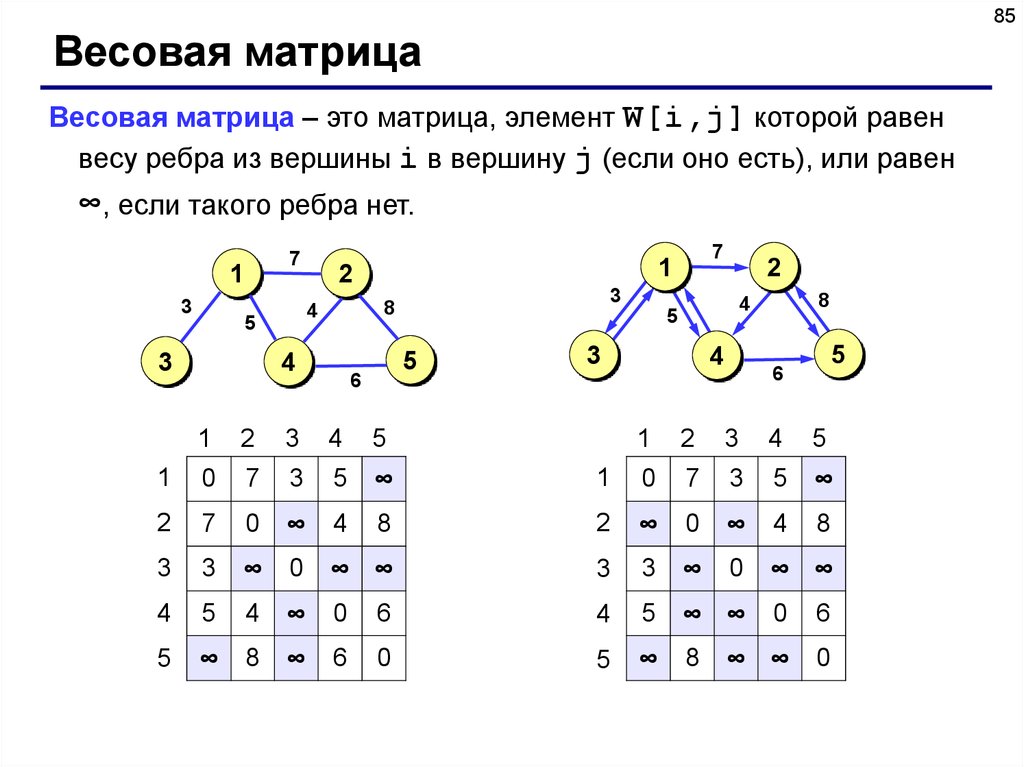
85Весовая матрица
Весовая матрица – это матрица, элемент W[i,j] которой равен
весу ребра из вершины i в вершину j (если оно есть), или равен
∞, если такого ребра нет.
7
1
3
5
3
2
4
1
2
3
4
5
1
0
7
3
5
∞
2
7
0
∞ 4
3
8
4
5
5
6
2
3
8
4
7
1
3
4
5
6
1
2
3
4
5
1
0
7
3
5
∞
8
2
∞ 0 ∞ 4
8
3
∞ 0 ∞ ∞
3
3
∞ 0 ∞ ∞
4
5
4
∞ 0
6
4
5
∞ ∞ 0
5
∞ 8 ∞ 6
0
5
∞ 8 ∞ ∞ 0
6
83.
86Задача Прима-Краскала
Задача: соединить N городов телефонной сетью так,
чтобы длина телефонных линий была минимальная.
Та же задача: дан связный граф с N вершинами, веса
ребер заданы весовой матрицей W. Нужно найти набор
ребер, соединяющий все вершины графа (остовное
дерево) и имеющий наименьший вес.
7
1
3
3
2
4
2
3
4
5
1
0
7
3
5
∞
2
7
0
∞ 4
8
3
3
∞ 0 ∞ ∞
4
5
4
∞ 0
6
5
∞ 8 ∞ 6
0
8
4
5
1
6
5
84.
87Жадный алгоритм
Жадный алгоритм – это многошаговый алгоритм, в котором на
каждом шаге принимается решение, лучшее в данный момент.
!
В целом может получиться не оптимальное
решение (последовательность шагов)!
Шаг в задаче Прима-Краскала – это выбор еще невыбранного
ребра и добавление его к решению.
7
1
3
3
8
4
5
4
!
2
6
5
В задаче Прима-Краскала
жадный алгоритм дает
оптимальное решение!
85.
88Реализация алгоритма Прима-Краскала
Проблема: как проверить, что
1) ребро не выбрано, и
2) ребро не образует цикла с выбранными ребрами.
Решение: присвоить каждой вершине свой цвет и перекрашивать
вершины при добавлении ребра.
7
1
3
3
2
8
4
5
4
6
5
Алгоритм:
1) покрасить все вершины в разные цвета;
2) сделать N-1 раз в цикле:
выбрать ребро (i,j) минимальной длины из всех ребер,
соединяющих вершины разного цвета;
перекрасить все вершины, имеющие цвет j, в цвет i.
3) вывести найденные ребра.
86.
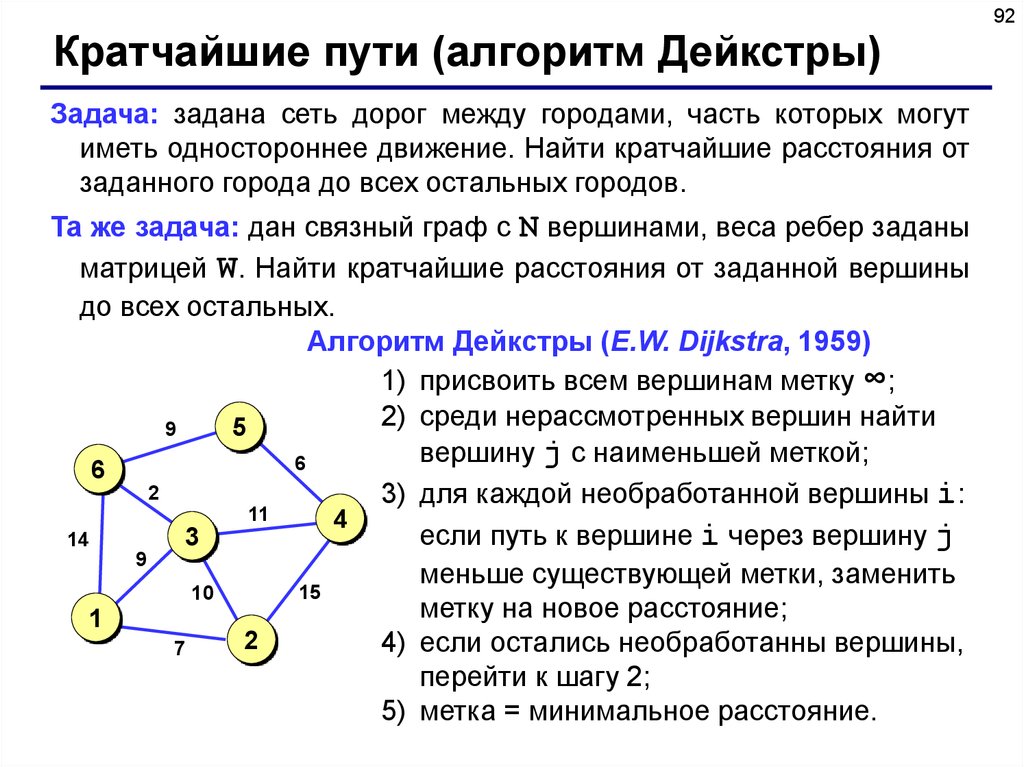
92Кратчайшие пути (алгоритм Дейкстры)
Задача: задана сеть дорог между городами, часть которых могут
иметь одностороннее движение. Найти кратчайшие расстояния от
заданного города до всех остальных городов.
Та же задача: дан связный граф с N вершинами, веса ребер заданы
матрицей W. Найти кратчайшие расстояния от заданной вершины
до всех остальных.
Алгоритм Дейкстры (E.W. Dijkstra, 1959)
1) присвоить всем вершинам метку ∞;
2) среди нерассмотренных вершин найти
9
5
вершину j с наименьшей меткой;
6
6
2
3) для каждой необработанной вершины i:
11
4
если путь к вершине i через вершину j
3
14
9
меньше существующей метки, заменить
15
10
метку на новое расстояние;
1
2
4) если остались необработанны вершины,
7
перейти к шагу 2;
5) метка = минимальное расстояние.
87.
93Алгоритм Дейкстры
∞
6
14
2
∞
3
9
∞
5
9
11
0
7
11
9
5
2
9
9
3
∞
7
9
7
2
9
9
3
∞
14
7
5 20
11
7
7
3
9
15
2
7
5 20
9
6
2
9
9
3
7
4 20
11
15
10
1
0
4 22
11
10
7
14
15
2
9
2
6
4 20
11
∞
6
1
0
10
1
0
4
5
9
6
6
6
15
2
9
14
14
15
2
7
11
4 20
11
10
0
∞
11
10
1
3
1
6
6
0
14
9
2
15
2
14
∞
∞
6
6
4
10
1
14
6
5
9
2
7
88.
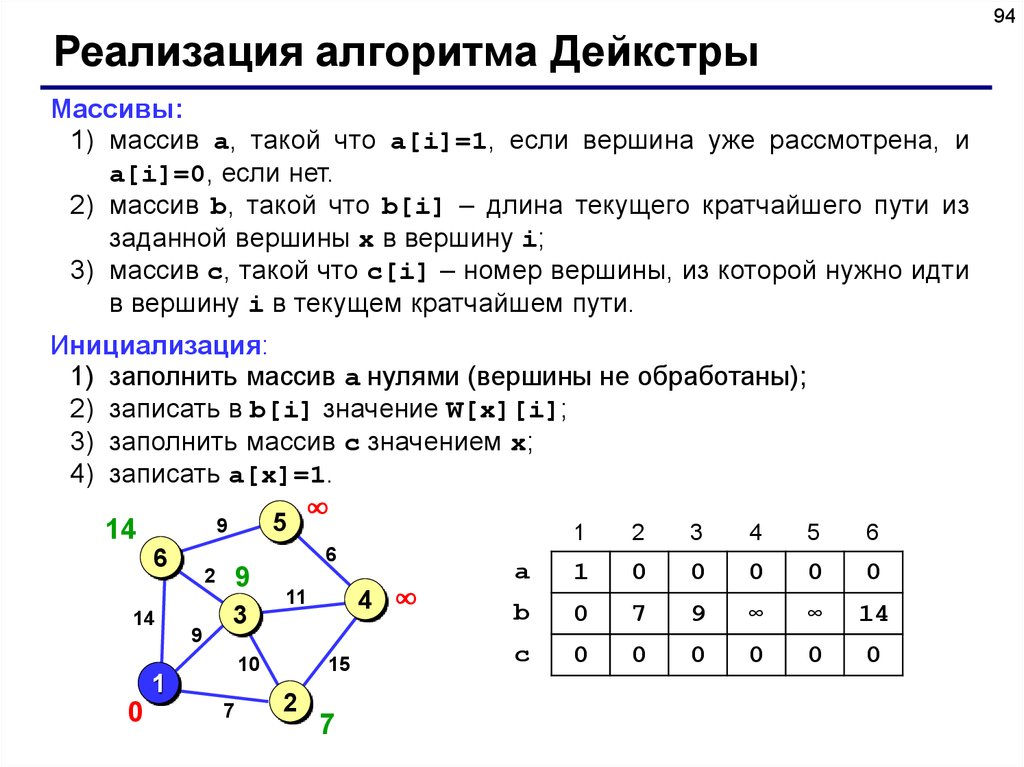
94Реализация алгоритма Дейкстры
Массивы:
1) массив a, такой что a[i]=1, если вершина уже рассмотрена, и
a[i]=0, если нет.
2) массив b, такой что b[i] – длина текущего кратчайшего пути из
заданной вершины x в вершину i;
3) массив c, такой что c[i] – номер вершины, из которой нужно идти
в вершину i в текущем кратчайшем пути.
Инициализация:
1) заполнить массив a нулями (вершины не обработаны);
2) записать в b[i] значение W[x][i];
3) заполнить массив c значением x;
4) записать a[x]=1.
5
9
14
6
6
14
2
9
9
3
11
7
4
15
10
1
0
∞
2
7
∞
1
2
3
4
5
6
a
1
0
0
0
0
0
b
0
7
9
∞
∞
14
c
0
0
0
0
0
0
89.
95Реализация алгоритма Дейкстры
Основной цикл:
1) если все вершины рассмотрены, то стоп.
2) среди всех нерассмотренных вершин (a[i]=0) найти
вершину j, для которой b[i] – минимальное;
3) записать a[j]:=1;
4) для всех вершин k: если путь в вершину k через вершину j
короче, чем найденный ранее кратчайший путь, запомнить
его: записать b[k]:=b[j]+W[j,k] и c[k]=j.
Шаг 1:
5
9
14
2
9
9
3
7
4 22
11
15
10
1
0
1
2
3
4
5
6
a
1
1
0
0
0
0
b
0
7
9
22
∞
14
c
0
0
0
1
0
0
6
6
14
∞
2
7
90.
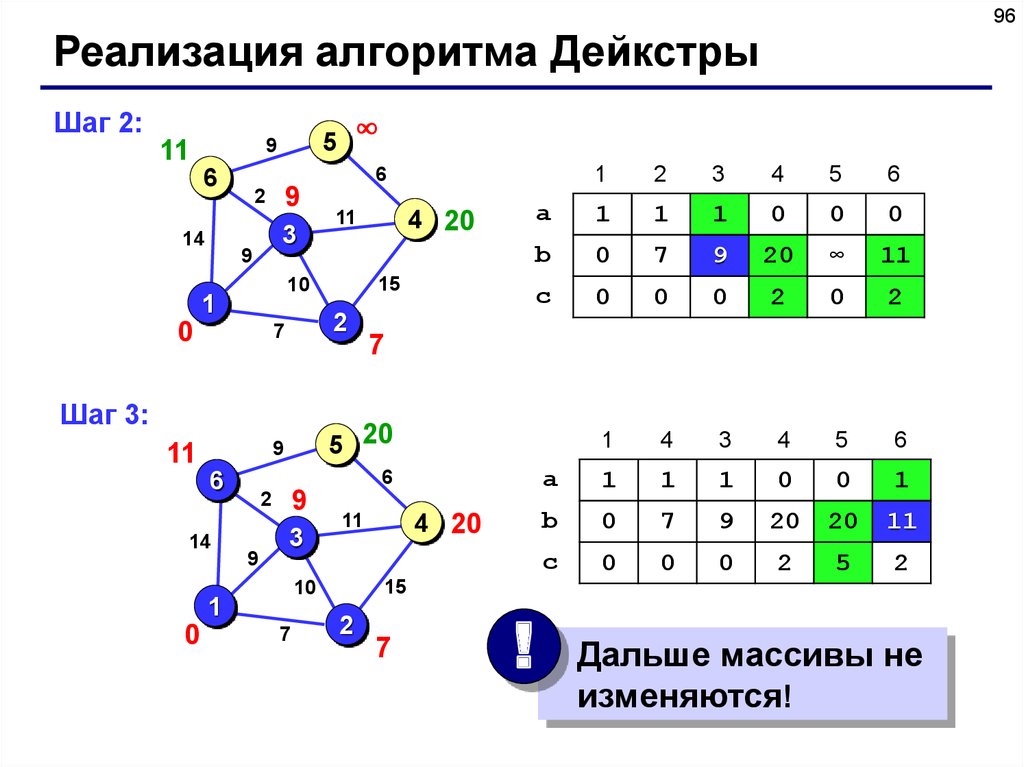
96Реализация алгоритма Дейкстры
Шаг 2:
11
9
2
3
9
4 20
11
15
10
1
0
7
2
11
9
5 20
Шаг 3:
2
9
9
3
7
4 20
11
3
4
5
6
a
1
1
1
0
0
0
b
0
7
9
20
∞
11
c
0
0
0
2
0
2
1
4
3
4
5
6
a
1
1
1
0
0
1
b
0
7
9
20
20
11
c
0
0
0
2
5
2
15
10
1
0
2
7
6
6
14
1
6
6
14
∞
5
9
2
7
!
Дальше массивы не
изменяются!
91.
97Как вывести маршрут?
Результат работа алгоритма Дейкстры:
1
2
3
4
5
6
a
1
1
1
1
1
1
b
0
7
9
20
20
11
c
0
0
0
2
5
2
длины путей
Маршрут из вершины 0 в вершину 4:
4
5
2
0
Вывод маршрута в вершину i (использование массива c):
1) установить z:=i;
2) пока c[i]<>x присвоить z:=c[z] и вывести z.
Сложность алгоритма Дейкстры:
два вложенных цикла по N шагов
O(N2)
92.
98Алгоритм Флойда-Уоршелла
Задача: задана сеть дорог между городами, часть которых могут
иметь одностороннее движение. Найти все кратчайшие
расстояния, от каждого города до всех остальных городов.
for k: =1 to N
for i: = 1 to N
for j: = 1 to N
if W[i,j] > W[i,k] + W[k,j] then
W[i,j] := W[i,k] + W[k,j];
k
W[i,k]
i
W[k,j]
j
W[i,j]
!
Если из вершины i в
вершину j короче ехать
через вершину k, мы едем
через вершину k!
Нет информации о маршруте, только
кратчайшие расстояния!
93.
100Задача коммивояжера
Задача коммивояжера. Коммивояжер (бродячий торговец) должен
выйти из первого города и, посетив по разу в неизвестном
порядке города 2,3,...N, вернуться обратно в первый город. В
каком порядке надо обходить города, чтобы замкнутый путь (тур)
коммивояжера был кратчайшим?
!
Это NP-полная задача, которая строго решается
только перебором вариантов (пока)!
Точные методы:
большое время счета для
1) простой перебор;
больших N
2) метод ветвей и границ;
O(N!)
3) метод Литтла;
4) …
Приближенные методы:
не гарантируется
1) метод случайных перестановок (Matlab);
оптимальное
2) генетические алгоритмы;
решение
3) метод муравьиных колоний;
4) …
94.
101Другие классические задачи
Задача на минимум суммы. Имеется N населенных пунктов, в
каждом из которых живет pi школьников (i=1,...,N). Надо
разместить школу в одном из них так, чтобы общее расстояние,
проходимое всеми учениками по дороге в школу, было
минимальным.
Задача о наибольшем потоке. Есть система труб, которые имеют
соединения в N узлах. Один узел S является источником, еще
один – стоком T. Известны пропускные способности каждой
трубы. Надо найти наибольший поток от источника к стоку.
Задача о наибольшем паросочетании. Есть M мужчин и N
женщин. Каждый мужчина указывает несколько (от 0 до N)
женщин, на которых он согласен жениться. Каждая женщина
указывает несколько мужчин (от 0 до M), за которых она согласна
выйти замуж. Требуется заключить наибольшее количество
моногамных браков.
95.
102Конец презентации































































 Математика
Математика








