Похожие презентации:
Применение рассеяния нейтронов для решения структурных и материаловедческих задач (нейтронография)
1. Применение рассеяния нейтронов для решения структурных и материаловедческих задач (нейтронография)
2.
МУРНДифракция
10
1
Спектрометр
с фильтром-анализатором
105
ТOF
спектрометр
-13
10
-12
r,Å
100
10-14
10
Рефлектометрия
4
10
Спектрометр
обратного рассеяния
103
2
t, c
10
-10
10
Трехосевой
спектрометр
-9
DE, mэВ
10-11
101
10
0
10
10-8
10-1
Спин-эхо спектрометр
-7
10
-2
10
0.01
0.1
Q, Å -1
1
10
Рис. 1-1. Диаграмма, иллюстрирующая доступные для различных нейтронных
спектрометров области на плоскости переданный импульс – переданная энергия.
Переданный импульс (в Å-1) указан на нижней шкале, соответствующие ему
характерные расстояния (в Å) – на верхней шкале. Там же указаны интервалы
характерных расстояний, доступных для дифракции, рефлектометрии и малоуглового
рассеяния нейтронов. По правой и левой шкалам отложены переданные энергии (в μэВ)
и соответствующие им характерные времена процессов (в секундах).
3.
ВЗАИМОДЕЙСТВИЕНЕЙТРОНОВ С КРИСТАЛЛАМИ
РАССЕЯНИЕ
ПОГЛОЩЕНИЕ
НЕУПРУГОЕ
УПРУГОЕ
(динамика теплового
движения)
КОГЕРЕНТНОЕ
ЯДЕРНОЕ
Положение атомов в ячейке
(кристаллическая структура)
НЕКОГЕРЕНТНОЕ
МАГНИТНОЕ
Величина и направление магнитных моментов
(магнитная структура)
Рис. 1-2. Основные типы взаимодействия тепловых нейтронов с веществом. Для
получения информации об атомной структуре кристалла следует использовать ядерное,
когерентное, упругое рассеяние нейтронов. Для получения информации о магнитной
структуре кристалла следует использовать магнитное, когерентное, упругое рассеяние
нейтронов.
4.
Плотность потока нейтроновT = 293 K ( =1.8 Å)
T = 105 K ( =3 Å)
0
1
2
3
Длина волны, Å
4
5
Рис. 2-1. Спектральное распределение плотности нейтронного потока для разных
температур замедлителя, представленное в шкале длин волн. λ0 – характерная длина волны
максвелловского распределения.
5.
Normalized intensity1.0
Normalized intensity
c542-h
C60
T=293 K
1.5
2.0
d, Å
2.5
3.0
al2o3
Al2O3
0.8
1.0
1.2
1.4
1.6
1.8
d, Å
Рис. 3-1. Сравнение нейтронных дифракционных спектров, измеренных от
“хорошего” (Al2O3, внизу) и “плохого” (фуллерен C60, вверху) кристаллов. В
структуре С60 степень дальнего порядка понижена, что проявляется в уменьшении
интенсивности пиков при малых d и большом диффузном фоне.
6.
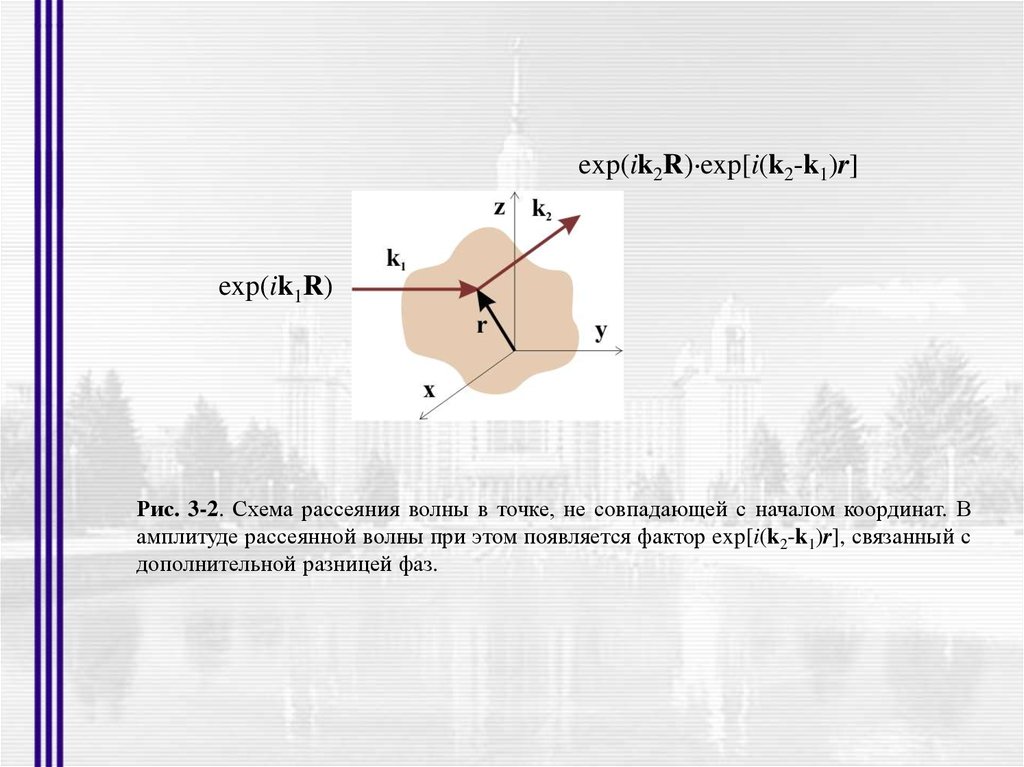
exp(ik2R) exp[i(k2-k1)r]exp(ik1R)
Рис. 3-2. Схема рассеяния волны в точке, не совпадающей с началом координат. В
амплитуде рассеянной волны при этом появляется фактор exp[i(k2-k1)r], связанный с
дополнительной разницей фаз.
7.
Рис. 3-3. Схема рассеяния волны на совокупности объектов, положениякоторых в общей системе координат фиксируются векторами Rm.
8.
24
1
3
5
Рис. 4-1. Схема центральной части стационарного исследовательского нейтронного
реактора. Обозначены: 1 - активная зона, 2 - горячий источник, 3 - холодный
источник. Показаны выходы горизонтальных каналов (4) и один из вертикальных
каналов (5).
9.
мс1 00
мс
200
Рис. 4-2. Схема образования нейтронных импульсов на реакторе ИБР-2. Рядом с активной
зоной вращаются лопасти подвижного отражателя, навстречу друг другу с частотой 5 Гц
(вспомогательный ротор) и 10 Гц (основной ротор). Когда роторы встречаются около
активной зоны (5 раз в секунду, т.е. с периодом 200 мс), возникает мощный нейтронный
импульс. Через 100 мс после основного импульса возникает дополнительный импульс
(сателлит), что связано с прохождением основного ротора возле зоны.
10.
Normalized intensitynac-hrpt
HRPT
NAC, =1.886 Å
20
40
60
80
100
2 , grad.
120
140
160
Рис. 4-3. Дифракционный спектр Na2Al2Ca3F14 (NAC стандарт), измеренный на HRPT
при λ = 1.886 Å.
11.
ЗамедлительФоновый
прерыватель
Зеркальный
нейтроновод
Детекторы
обратного рассеяния
90°-детектор
Образец
Накопление и
обработка
информации
Рис. 4-4. Схема TOF-дифрактометра. Как правило, расстояние от активной зоны до места
расположения образца составляет от 10 до 30 м.
12.
Рис. 4-5. Схема фурье-прерывателя (вверху),его функция пропускания и фазировка
двоичного
сигнала.
Прозрачные
и
непрозрачные для нейтронов промежутки на
роторе
и
статоре
расположены
эквидистантно.
Сигналы
+1
и
-1
присваиваются, если пропускание больше
или меньше 1/2 от максимального.
13.
Рис. 4-6. Функциональная схема фурье-дифрактометра. На корреляционнуюэлектронику подаются сигналы, моделирующие импульс источника и пропускание
прерывателя, а также сигнал от детектора.
14.
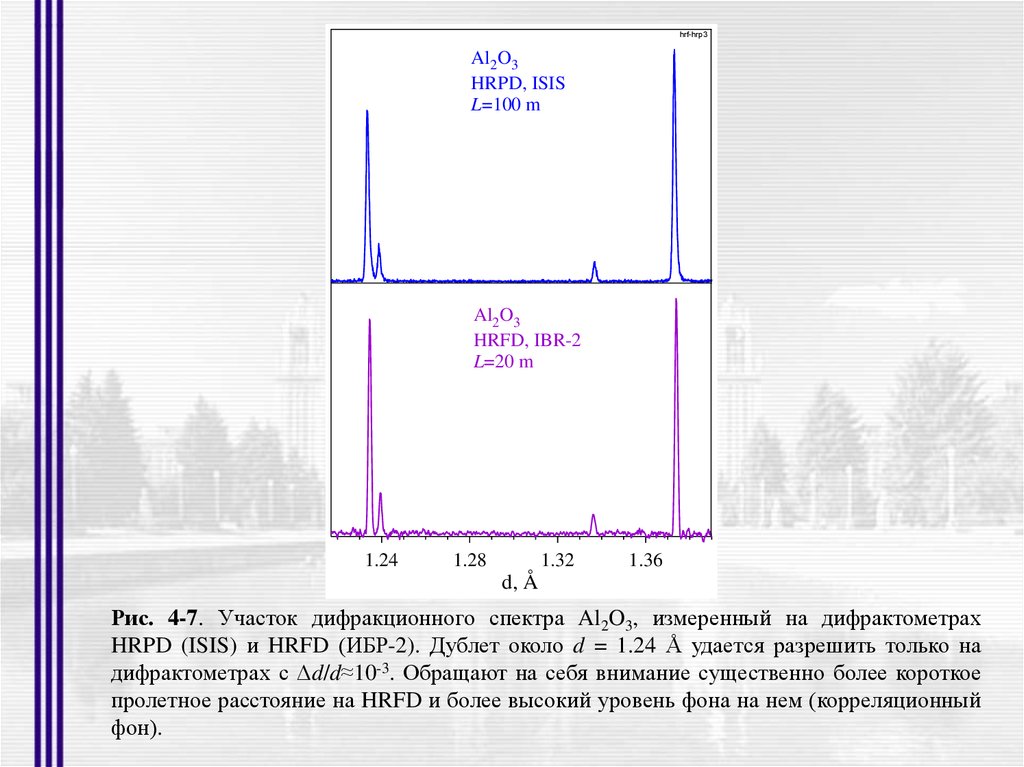
hrf-hrp3Al2O3
HRPD, ISIS
L=100 m
Al2O3
HRFD, IBR-2
L=20 m
1.24
1.28
1.32
1.36
d, Å
Рис. 4-7. Участок дифракционного спектра Al2O3, измеренный на дифрактометрах
HRPD (ISIS) и HRFD (ИБР-2). Дублет около d = 1.24 Å удается разрешить только на
дифрактометрах с Δd/d≈10-3. Обращают на себя внимание существенно более короткое
пролетное расстояние на HRFD и более высокий уровень фона на нем (корреляционный
фон).
15.
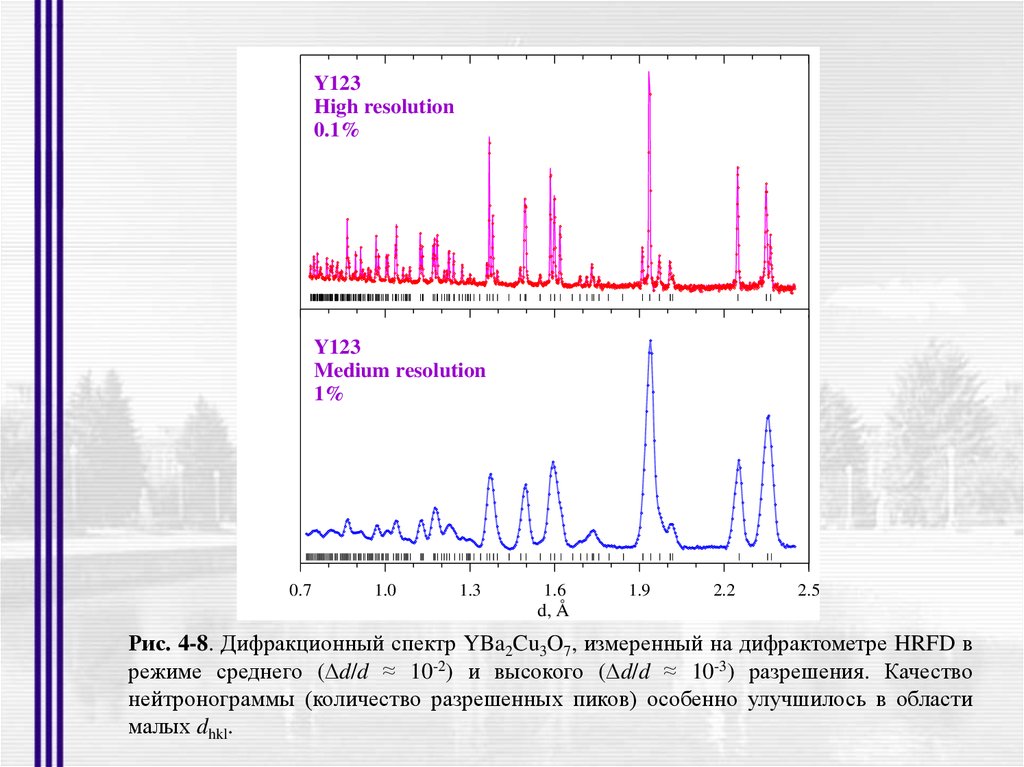
Y123High resolution
0.1%
Y123
Medium resolution
1%
0.7
1.0
1.3
1.6
1.9
2.2
2.5
d, Å
Рис. 4-8. Дифракционный спектр YBa2Cu3O7, измеренный на дифрактометре HRFD в
режиме среднего (Δd/d ≈ 10-2) и высокого (Δd/d ≈ 10-3) разрешения. Качество
нейтронограммы (количество разрешенных пиков) особенно улучшилось в области
малых dhkl.
16.
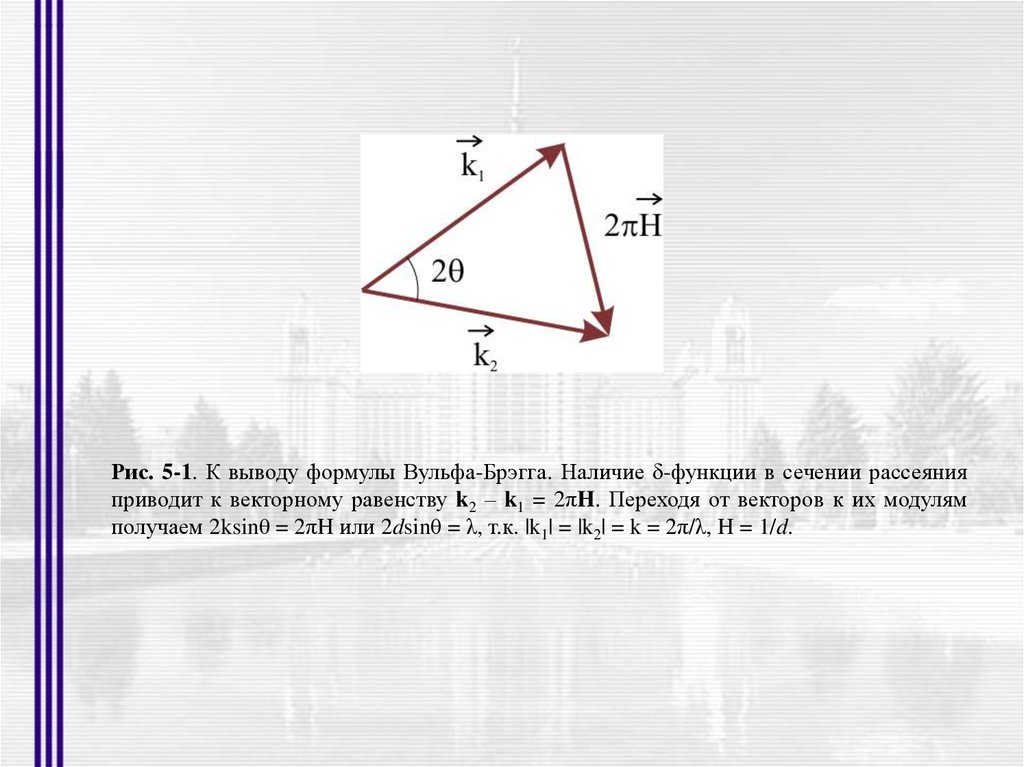
Рис. 5-1. К выводу формулы Вульфа-Брэгга. Наличие δ-функции в сечении рассеянияприводит к векторному равенству k2 – k1 = 2πH. Переходя от векторов к их модулям
получаем 2ksinθ = 2πH или 2dsinθ = λ, т.к. |k1| = |k2| = k = 2π/λ, H = 1/d.
17.
Рис. 5-2. Диаграмма Эвальда. Изображено сечение (b1, b2) обратной решетки ивекторный треугольник k´2 – k´1 = H, где штрих означает деление на 2π. В этом примере
ориентация векторов k´2 и k´1 обеспечивает наблюдение дифракционного пика (220).
18.
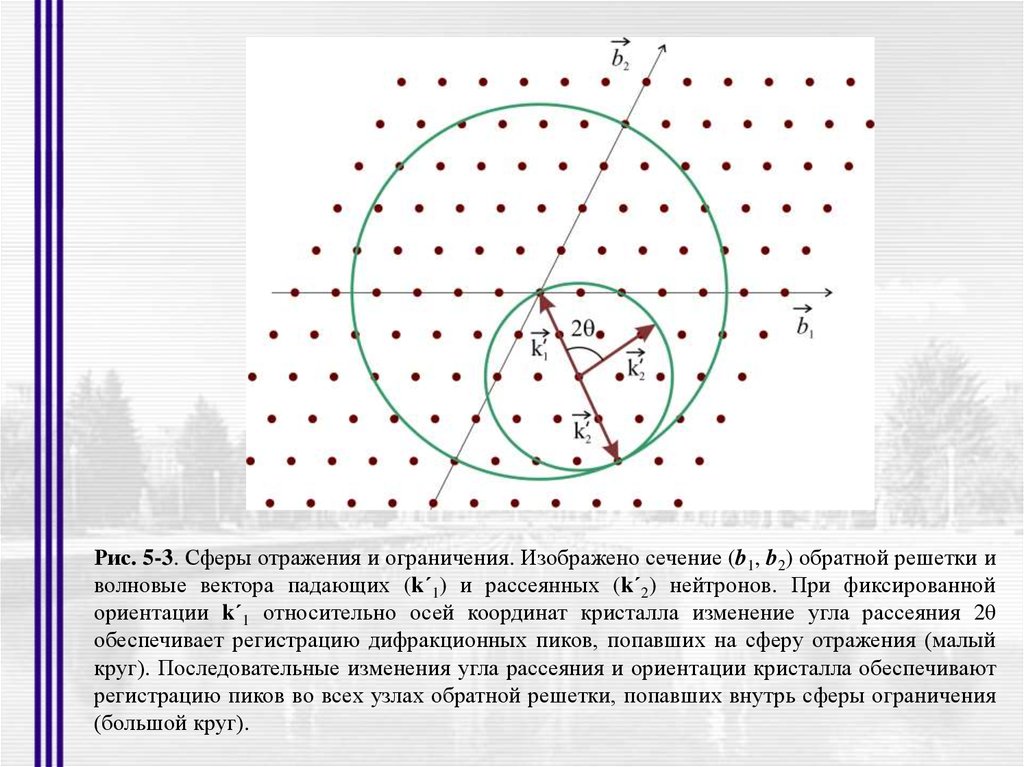
Рис. 5-3. Сферы отражения и ограничения. Изображено сечение (b1, b2) обратной решетки иволновые вектора падающих (k´1) и рассеянных (k´2) нейтронов. При фиксированной
ориентации k´1 относительно осей координат кристалла изменение угла рассеяния 2θ
обеспечивает регистрацию дифракционных пиков, попавших на сферу отражения (малый
круг). Последовательные изменения угла рассеяния и ориентации кристалла обеспечивают
регистрацию пиков во всех узлах обратной решетки, попавших внутрь сферы ограничения
(большой круг).
19.
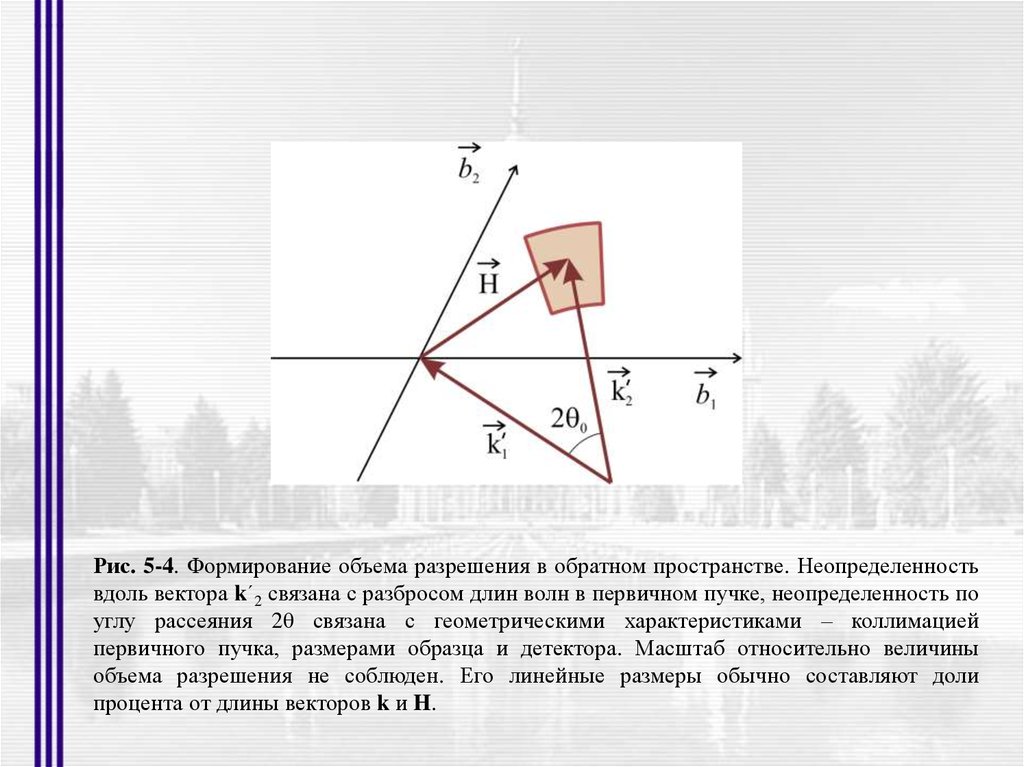
Рис. 5-4. Формирование объема разрешения в обратном пространстве. Неопределенностьвдоль вектора k´2 связана с разбросом длин волн в первичном пучке, неопределенность по
углу рассеяния 2θ связана с геометрическими характеристиками – коллимацией
первичного пучка, размерами образца и детектора. Масштаб относительно величины
объема разрешения не соблюден. Его линейные размеры обычно составляют доли
процента от длины векторов k и H.
20.
Maxwell-wav-limitПлотность потока нейтронов
1
T = 293 K
0.1
0.01
max
min
0.001
0
1
2
3
Длина волны, Å
4
5
6
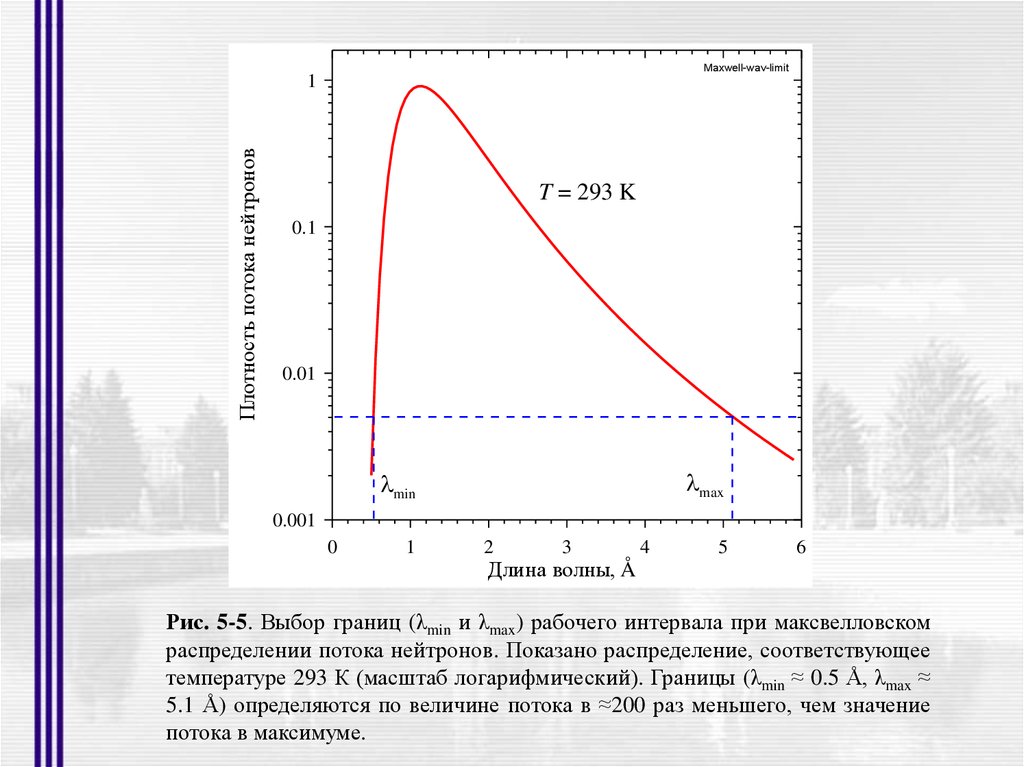
Рис. 5-5. Выбор границ (λmin и λmax) рабочего интервала при максвелловском
распределении потока нейтронов. Показано распределение, соответствующее
температуре 293 К (масштаб логарифмический). Границы (λmin ≈ 0.5 Å, λmax ≈
5.1 Å) определяются по величине потока в ≈200 раз меньшего, чем значение
потока в максимуме.
21.
Рис. 5-6. Сканирование обратного пространства на TOF-дифрактометре спомощью точечного детекторa. Сканирование идет вдоль направления (100).
При фиксированном угле рассеяния 2θ0 будут регистрироваться порядки
отражения (100), (200) и т.д. Поскольку треугольник, образованный векторами
k´1, k´2 и H, равнобедренный, то перпендикуляр, восстановленный из точки
пересечения k´1 и k´2, делит соответствующий вектор H пополам.
22.
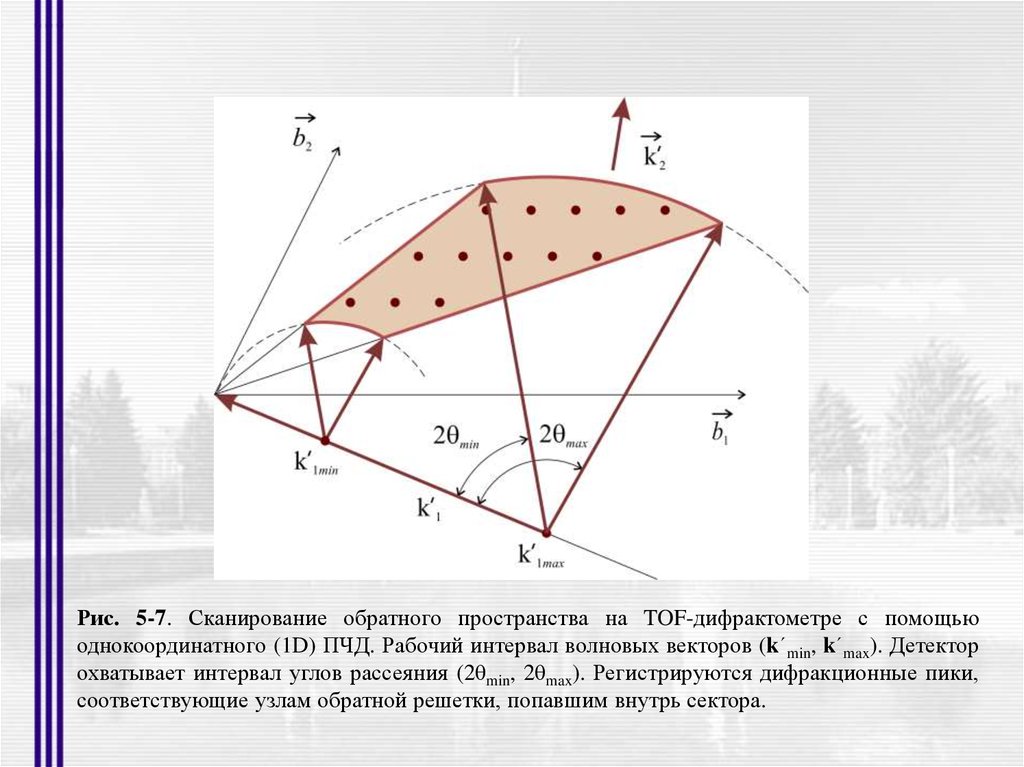
Рис. 5-7. Сканирование обратного пространства на TOF-дифрактометре с помощьюоднокоординатного (1D) ПЧД. Рабочий интервал волновых векторов (k´min, k´max). Детектор
охватывает интервал углов рассеяния (2θmin, 2θmax). Регистрируются дифракционные пики,
соответствующие узлам обратной решетки, попавшим внутрь сектора.
23.
hkl5
buras.grf
111
2dsin =
200
4
111
3
Å
220
113
222
400
2
0=1.6 Å
1
0=450
111
0
0
10
20
30
40
50
60
70
80
90
Угол Брэгга
Рис. 5-8. Схема формирования дифракционного спектра от поликристалла на λ0дифрактометре с λ0 = 1.6 Å и TOF-дифрактометре с детектором при θ0 = 45°. Показаны кривые,
соответствующие уравнению Вульфа-Брэгга для разных dhkl. Дифракционные пики будут
зарегистрированы при углах Брэгга или длинах волн, соответствующих пересечениям
горизонтальной линии λ0 = 1.6 Å или вертикальной линии θ0 = 45° с кривыми λ = 2dsinθ.
Отмечены значения θ и λ для пика (111).
24.
Рис. 5-9. Схема эксперимента на TOF-дифрактометре с источником (1) и детектором (3)конечных размеров. Размеры монокристалла (2) пренебрежимо малы. Вектора k1, k2 и H,
соответствующие средним направлениям первичного и рассеянного пучков и средней
ориентации мозаичных блоков монокристалла, отмечены индексом 0. Вектора без индекса 0
соответствуют возможному варианту рассеяния нейтронов на одном из мозаичных блоков
монокристалла.
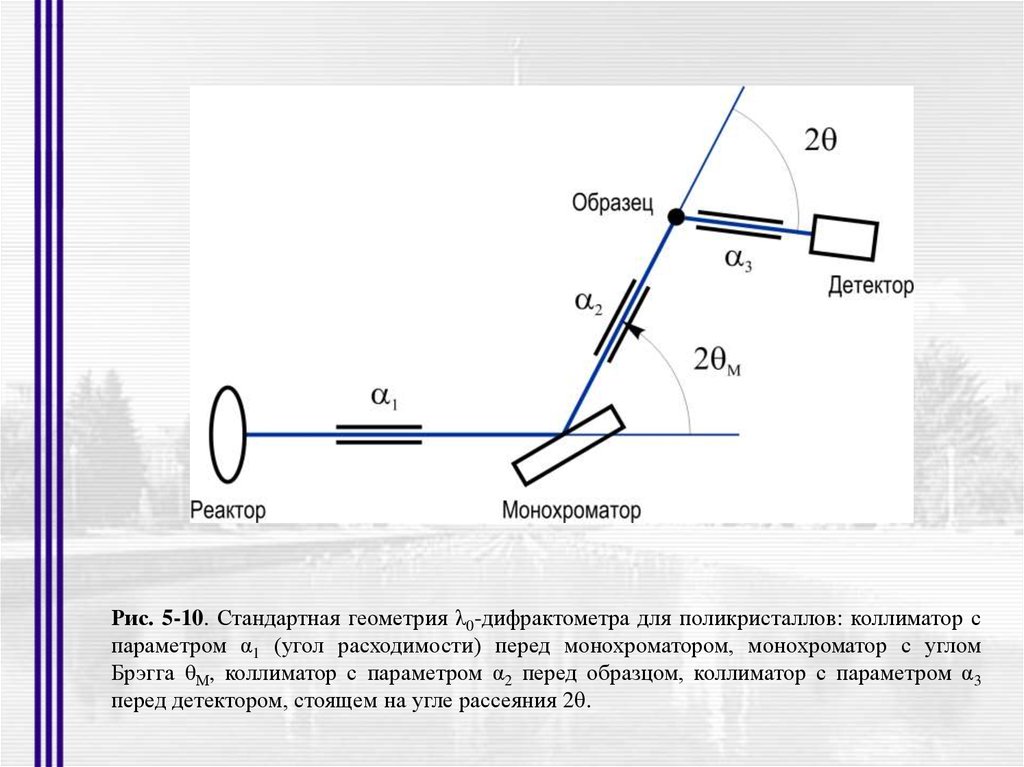
25.
Рис. 5-10. Стандартная геометрия λ0-дифрактометра для поликристаллов: коллиматор спараметром α1 (угол расходимости) перед монохроматором, монохроматор с углом
Брэгга θМ, коллиматор с параметром α2 перед образцом, коллиматор с параметром α3
перед детектором, стоящем на угле рассеяния 2 .
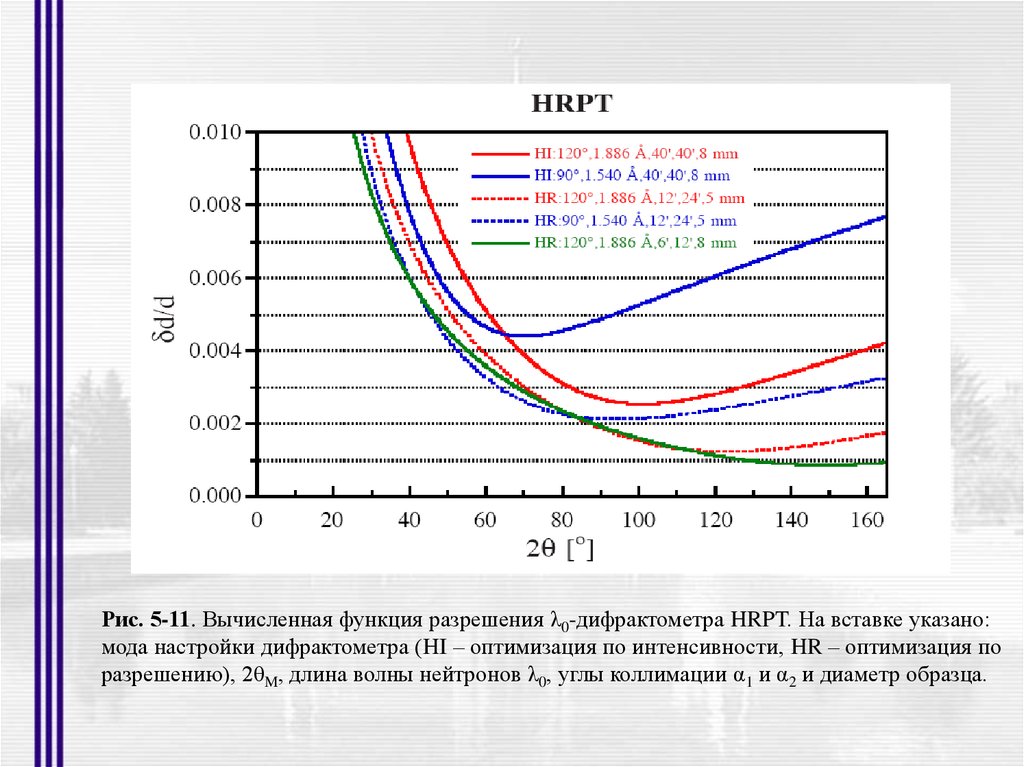
26.
Рис. 5-11. Вычисленная функция разрешения λ0-дифрактометра HRPT. На вставке указано:мода настройки дифрактометра (HI – оптимизация по интенсивности, HR – оптимизация по
разрешению), 2θM, длина волны нейтронов λ0, углы коллимации α1 и α2 и диаметр образца.
27.
0.002Относительная ширина функции разрешения
TOF_Resolut
0.0015
HRFD
HRPD
0.001
0.0005
0
0
1
2
3
4
5
6
7
8
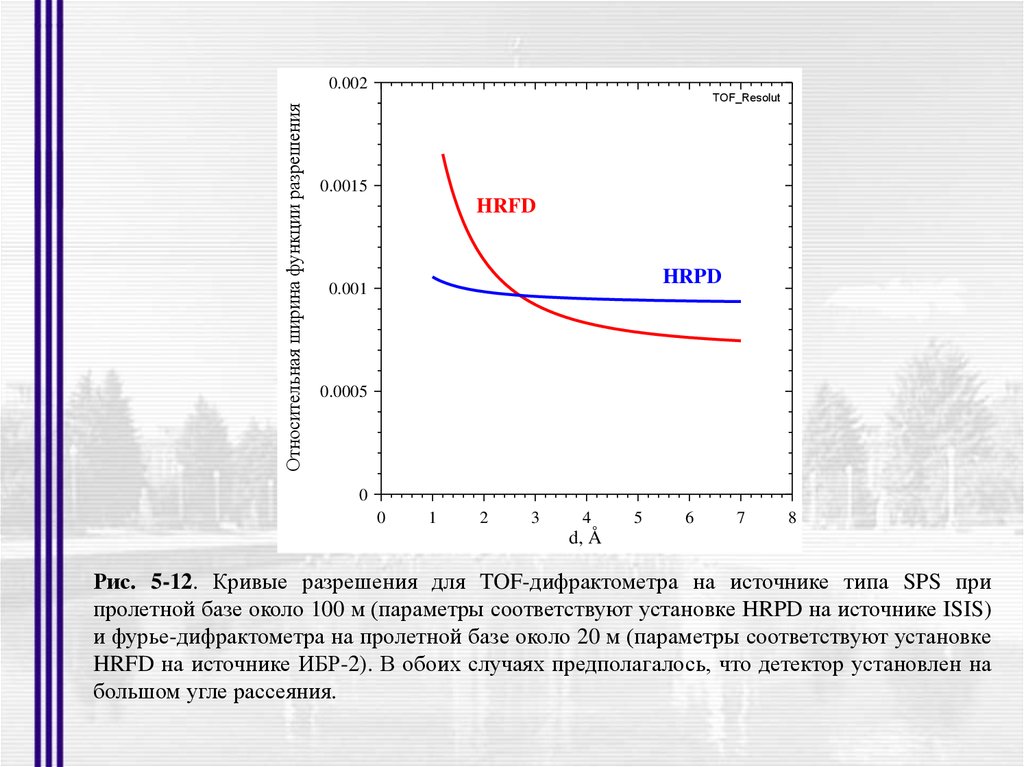
d, Å
Рис. 5-12. Кривые разрешения для TOF-дифрактометра на источнике типа SPS при
пролетной базе около 100 м (параметры соответствуют установке HRPD на источнике ISIS)
и фурье-дифрактометра на пролетной базе около 20 м (параметры соответствуют установке
HRFD на источнике ИБР-2). В обоих случаях предполагалось, что детектор установлен на
большом угле рассеяния.
28.
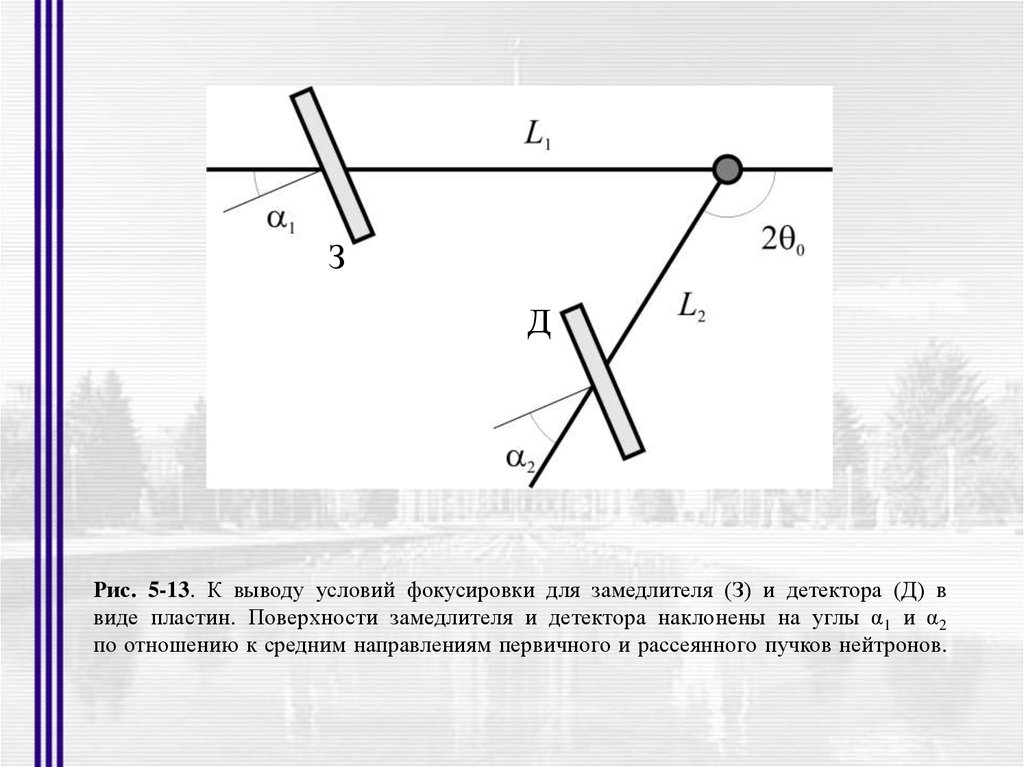
ЗД
Рис. 5-13. К выводу условий фокусировки для замедлителя (З) и детектора (Д) в
виде пластин. Поверхности замедлителя и детектора наклонены на углы α1 и α2
по отношению к средним направлениям первичного и рассеянного пучков нейтронов.
29.
Reflect-wavКоэффициент отражения
1
R( )
0.5
0
0
0.005
0.01
Угол отражения, рад.
0.015
0.02
Рис. 5-14. Коэффициент отражения нейтронов от гладкой плоской поверхности.
Критический угол составляет γcr = 0.01, т.е. около 34 угл. минут. Такая кривая отражения
реализуется при отражении пучка с 0 ≈ 6 Å от идеально гладкой поверхности Ni.
30.
tran-ma1.0
Пропускание
нейтроновода
Поток (отн. ед.)
0.8
0.6
0.4
0.2
0.0
0
1
2
3
4
Длина волны (Å)
5
6
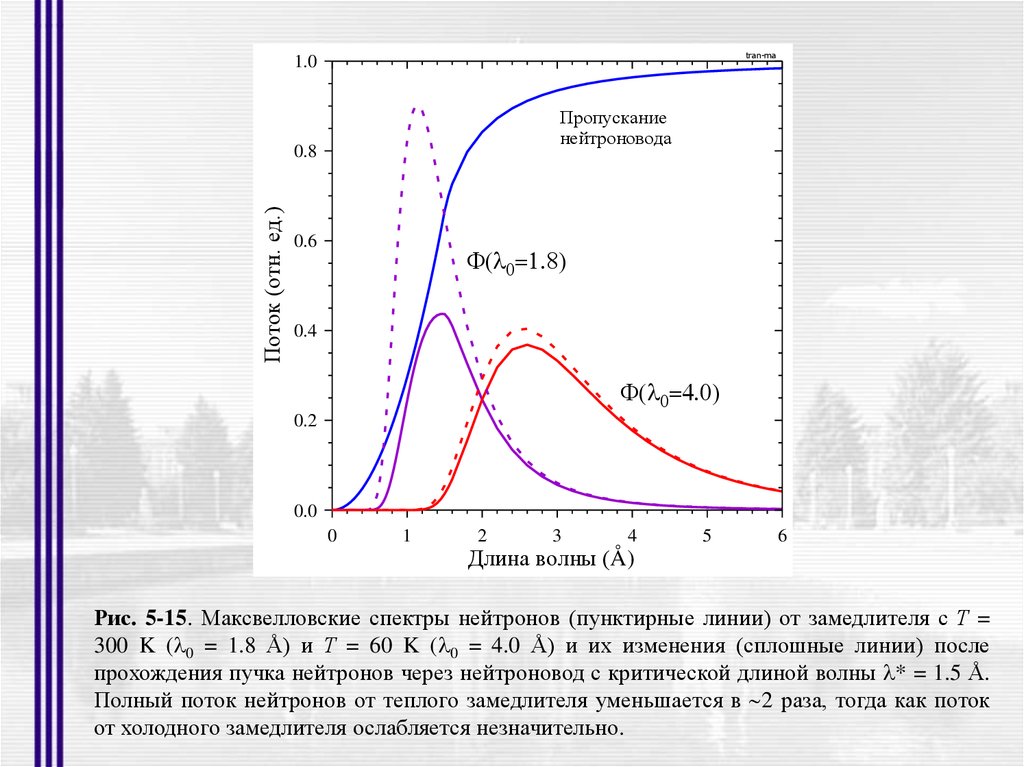
Рис. 5-15. Максвелловские спектры нейтронов (пунктирные линии) от замедлителя с Т =
300 K ( 0 = 1.8 Å) и Т = 60 K ( 0 = 4.0 Å) и их изменения (сплошные линии) после
прохождения пучка нейтронов через нейтроновод с критической длиной волны * = 1.5 Å.
Полный поток нейтронов от теплого замедлителя уменьшается в 2 раза, тогда как поток
от холодного замедлителя ослабляется незначительно.
31.
2correct-wav
1.5
( )
1
( )
y( )
0.5
0
0
1
2
3
Длина волны, Å
4
5
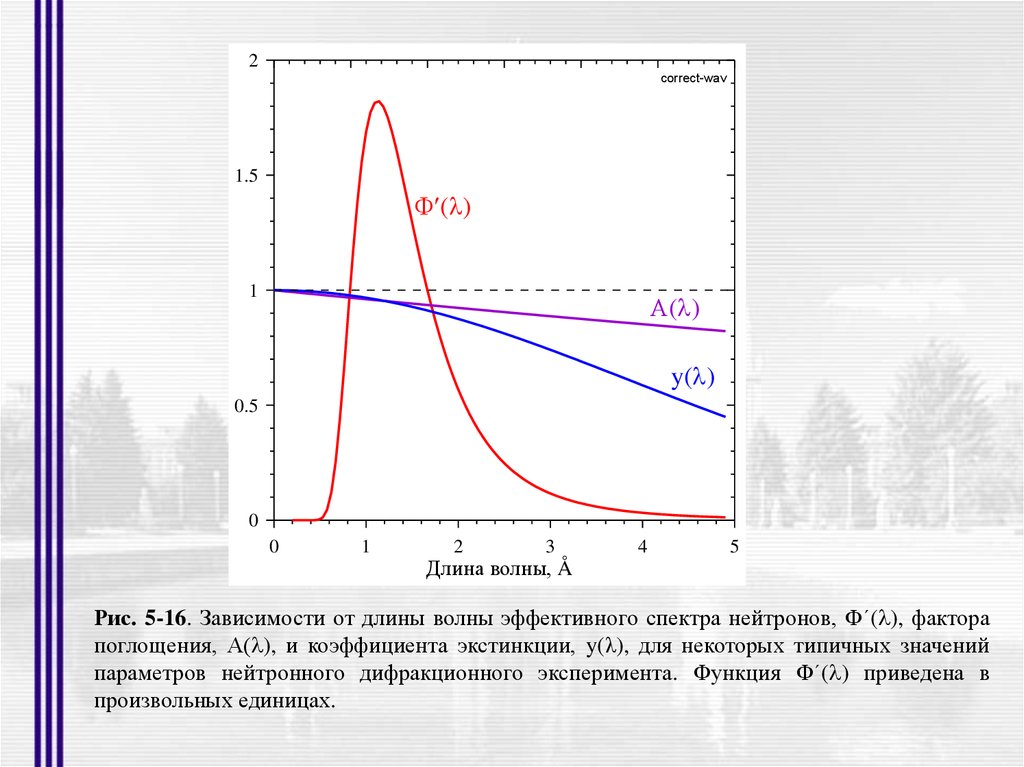
Рис. 5-16. Зависимости от длины волны эффективного спектра нейтронов, Ф´( ), фактора
поглощения, А( ), и коэффициента экстинкции, y(λ), для некоторых типичных значений
параметров нейтронного дифракционного эксперимента. Функция Ф´( ) приведена в
произвольных единицах.
32.
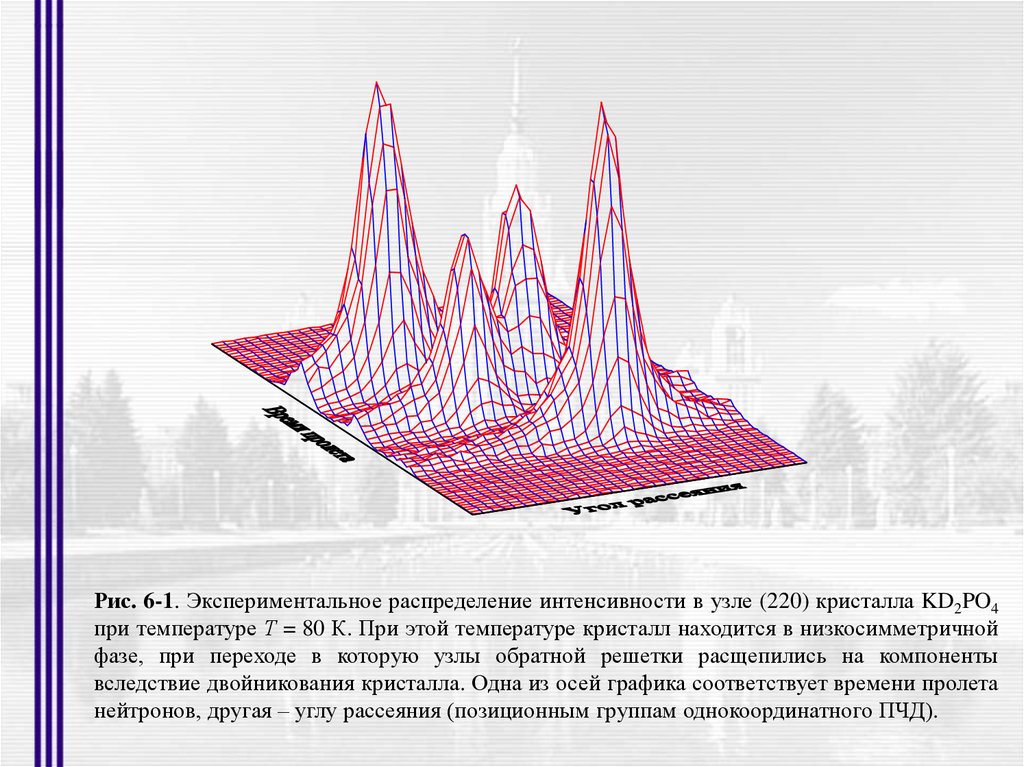
Рис. 6-1. Экспериментальное распределение интенсивности в узле (220) кристалла KD2PO4при температуре Т = 80 К. При этой температуре кристалл находится в низкосимметричной
фазе, при переходе в которую узлы обратной решетки расщепились на компоненты
вследствие двойникования кристалла. Одна из осей графика соответствует времени пролета
нейтронов, другая – углу рассеяния (позиционным группам однокоординатного ПЧД).
33.
Рис. 6-2. Участок дифракционного спектра кристалла SBN, измеренный на TOFдифрактометре с 1D ПЧД в сечении [hk0]. Вверху спектр представлен в увеличенноммасштабе. Внизу справа показана ориентация сектора в направлении узла (810),
ограниченного пределами ±2.5° по углу Брэгга. Индексы Миллера основных пиков указаны
в скобках, начиная от (6 1 0) до (14 1 0). Индексы сателлитов второго порядка указаны без
скобок, например, 5 0 1 2, со знаками, указывающими смещение вдоль a* и b*.
34.
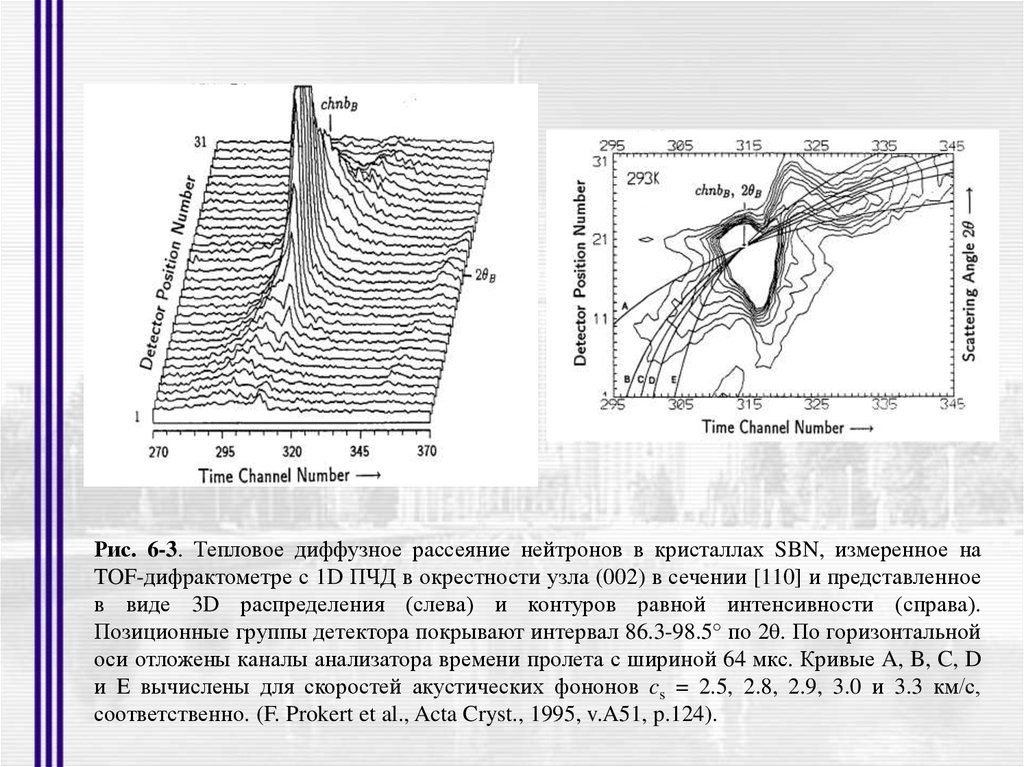
Рис. 6-3. Тепловое диффузное рассеяние нейтронов в кристаллах SBN, измеренное наTOF-дифрактометре с 1D ПЧД в окрестности узла (002) в сечении [110] и представленное
в виде 3D распределения (слева) и контуров равной интенсивности (справа).
Позиционные группы детектора покрывают интервал 86.3-98.5° по 2θ. По горизонтальной
оси отложены каналы анализатора времени пролета с шириной 64 мкс. Кривые A, B, C, D
и E вычислены для скоростей акустических фононов cs = 2.5, 2.8, 2.9, 3.0 и 3.3 км/с,
соответственно. (F. Prokert et al., Acta Cryst., 1995, v.A51, p.124).
35.
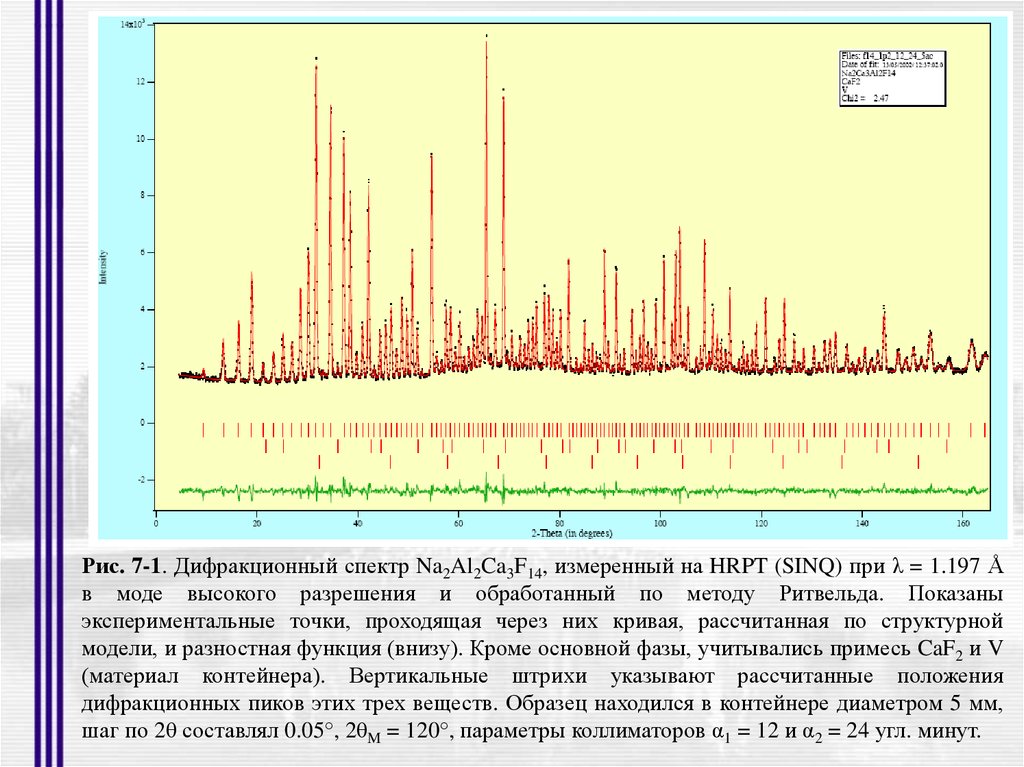
Рис. 7-1. Дифракционный спектр Na2Al2Ca3F14, измеренный на HRPT (SINQ) при λ = 1.197 Åв моде высокого разрешения и обработанный по методу Ритвельда. Показаны
экспериментальные точки, проходящая через них кривая, рассчитанная по структурной
модели, и разностная функция (внизу). Кроме основной фазы, учитывались примесь CaF2 и V
(материал контейнера). Вертикальные штрихи указывают рассчитанные положения
дифракционных пиков этих трех веществ. Образец находился в контейнере диаметром 5 мм,
шаг по 2θ составлял 0.05°, 2θM = 120°, параметры коллиматоров α1 = 12 и α2 = 24 угл. минут.
36.
1.98158
mn-o1c
ang-O1c
Along b-axes
Mn-O1-Mn (deg.)
Mn - O1 (Å)
O-16
O-18
1.97
1.96
O-16
1.95
TFM (O-16)
TAFM
50
100
150
157
156
O-18
155
TCO
TFM (O-16) TAFM
1.94
0
200
250
1.970
0
1.955
TCO
150
200
250
300
200
Temperature (K)
159
O-16 / O-18
158
157
TFM (O-16)
1.950
100
150
ang-O2c
Mn-O2-Mn (deg.)
<Mn - O2> (Å)
1.960
50
100
In plane
O-16 / O-18
0
50
160
mn-o2c
TFM (O-16) TAFM
TCO
154
300
In plane
1.965
Along b-axes
250
300
TAFM
TCO
156
0
50
100
150
200
250
300
Temperature (K)
Рис. 7-2. Зависимости от температуры межатомных расстояний Mn-O (слева) и валентных
углов Mn-O-Mn (справа) в соединении (La0.25Pr0.75)0.7Ca0.3MnO3, обогащенном изотопами
кислорода 16О (синие значки) и 18О (красные значки). Указаны температуры фазовых
переходов в состояние зарядового (ТСО), антиферромагнитного (ТАFM) и ферромагнитного в составе с
16О
(ТFM) упорядочений. Показаны расстояния и углы в базисной плоскости (in plane) и вдоль b-оси ячейки.
37.
1Функция разрешения
0.8
0.6
0.4
1
2
0.2
0
-0.2
-12 -10 -8
-6
-4
-2
0
2
4
6
8
10 12
x
Рис. 7-3. Форма пика, измеряемого на фурье-дифрактометре с разными частотными
распределениями вращения фурье-прерывателя: g( ) = const (кривая 1), распределение
Блэкмана (кривая 2).
38.
Normalized neutron countsnac-1r
Na2Al2Ca3F14
HRFD
0.7
0.8
0.8
1.0
0.9
1.0
8
4
0
-4
-8
1.2
1.4
1.6
1.8
2.0
2.2
2.4
d, Å
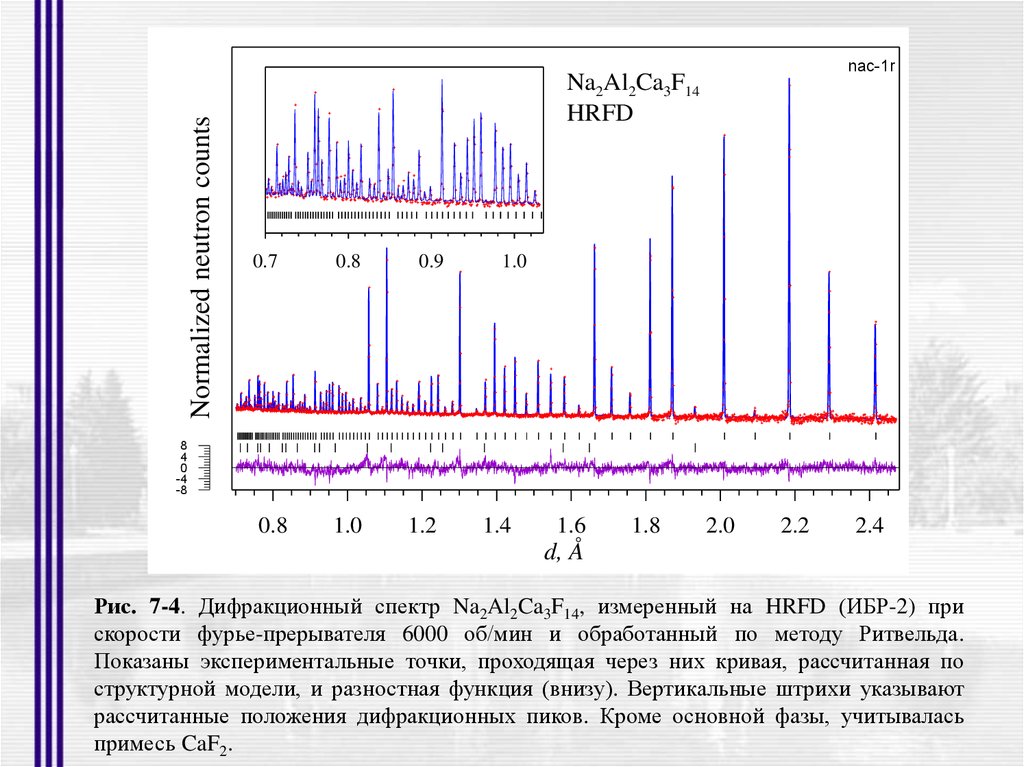
Рис. 7-4. Дифракционный спектр Na2Al2Ca3F14, измеренный на HRFD (ИБР-2) при
скорости фурье-прерывателя 6000 об/мин и обработанный по методу Ритвельда.
Показаны экспериментальные точки, проходящая через них кривая, рассчитанная по
структурной модели, и разностная функция (внизу). Вертикальные штрихи указывают
рассчитанные положения дифракционных пиков. Кроме основной фазы, учитывалась
примесь CaF2.
39.
2000l=1
Dd2, отн. ед.
1600
l>1
Ni(OH)2
1200
l=0
800
400
Resolution
0
0
1
2
3
4
5
6
7
8
d2 , Å 2
Рис. 7-5. Зависимость ширины дифракционных пиков -Ni(OH)2 для различных значений
индекса l от dhkl. Сплошные линии – аппроксимация многочленом 4-й степени, пунктирной
линией показан вклад от функции разрешения дифрактометра.
40.
Рис. 7-6. Дифракционный спектр Na2Al2Ca3F14, измеренный на D20 (ILL) за 2 мин.41.
Spectr_temp1temp1
T, K
570
Stet
600
Stet
Scub
Intensity
Temperature, K
800
780
400
(103)
470
20
40
60
80
100
Time, sec/80
1.5
2.0
2.5
d, Å
3.0
3.5
Рис. 7-7. Анализ структурного фазового перехода в шпинели CuLi0.1V0.1Fe1.8O4 на ДН-2
(ИБР-2) в реальном времени с Δt = 80 сек. График изменения температуры образца
показан на рисунке слева. Справа показаны характерные дифракционные спектры при
нагревании (T = 470 K, тетрагональная фаза Fd3m), после перехода в кубическую фазу
(T = 780 K, I41/adm) и в ходе охлаждения (T = 570 K, Fd3m).
42.
0.39param
Oxz
c
8.50
Oxygen coordinates
Lattice parameters, Å
8.60
8.40
a=b
8.30
8.20
Stet
Scub
Stet
Ox
0.38
0.38
Oz
0.37
Stet
Stet
0.36
8.10
20
40
60
80
20
100
40
6
20
40
Scub
60
Time, sec/80
100
0.90
Scattering factor
7
Stet
80
occ
Width
8
5
60
Time, sec/80
Time, sec/80
Peak width
Scub
Stet
80
0.80
0.70
100
Stet
20
40
Scub
60
Stet
80
100
Time, sec/80
Рис. 7-8. Температурные
зависимости
структурных
параметров
шпинели
CuLi0.1V0.1Fe1.8O4, измеренные в ходе перехода из тетрагональной фазы (Fd3m) в
кубическую (I41/adm) и обратно. Слева показаны изменения параметров решетки (вверху)
и ширины пиков (внизу). Справа показаны изменения координаты Oz (вверху) и фактора
заполнения катионами различных позиций в ячейке. Границы перехода показаны
вертикальными линиями.
43.
Дифракционные пики(2212)
(2201)
Рассеяние на малые углы
15 Å
12 Å
1000
Bi-graph
Temperature, oC
800
Temp.
600
15 Å
400
200
12 Å
0
0
10
20
30
40
Изменения температуры и интенсивности
дифракционных пиков с d = 12 и 15 Å.
Time, min/15
Рис. 7-9. Температурные зависимости интенсивностей дифракционных пиков (вверху
слева) в диапазоне d = 10 – 18 Å и малоуглового рассеяния (справа) в диапазоне Q = 0.02
– 0.06 Å-1, измеренные в реальном времени с Δt = 5 мин в ходе превращений в
BiSrCaCu2Ox. При нагревании в аморфном составе сначала кристаллизуется фаза Bi2201, которая переходит в фазу Bi-2212. После плавления при Т > 800°С и охлаждения
кристаллизуются обе фазы.
44.
40mol-e
Intensity per 0.2 sec
One pulse
30
Источник
20
10
L1
0
10000
8000
(110)
6000
(200)
4000
Образец
Детекторы
Intensity per 1 min
300 pulses
(211)
2000
0
70
90
110
130
150
170
190
TOF channel number
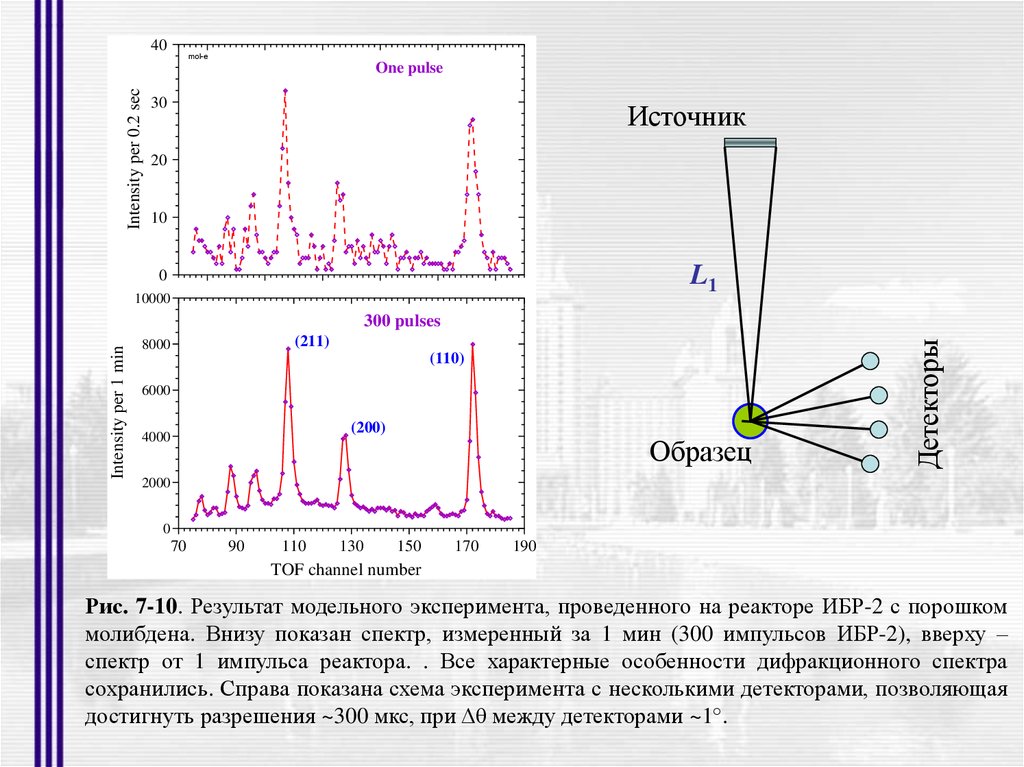
Рис. 7-10. Результат модельного эксперимента, проведенного на реакторе ИБР-2 с порошком
молибдена. Внизу показан спектр, измеренный за 1 мин (300 импульсов ИБР-2), вверху –
спектр от 1 импульса реактора. . Все характерные особенности дифракционного спектра
сохранились. Справа показана схема эксперимента с несколькими детекторами, позволяющая
достигнуть разрешения ~300 мкс, при Δθ между детекторами ~1°.
45.
1. Корпус.2. Поршень.
3. Нагрузочные винты.
4. Опоры из твердого
сплава.
5. Юстировочные винты.
6. Наковальни из
монокристаллов сапфира.
7. Прокладка.
8. Образец.
9. Первичный пучок
нейтронов.
10. Пучок рассеянных
нейтронов.
Рис. 7-11. Камера высокого давления с сапфировыми наковальнями.
46.
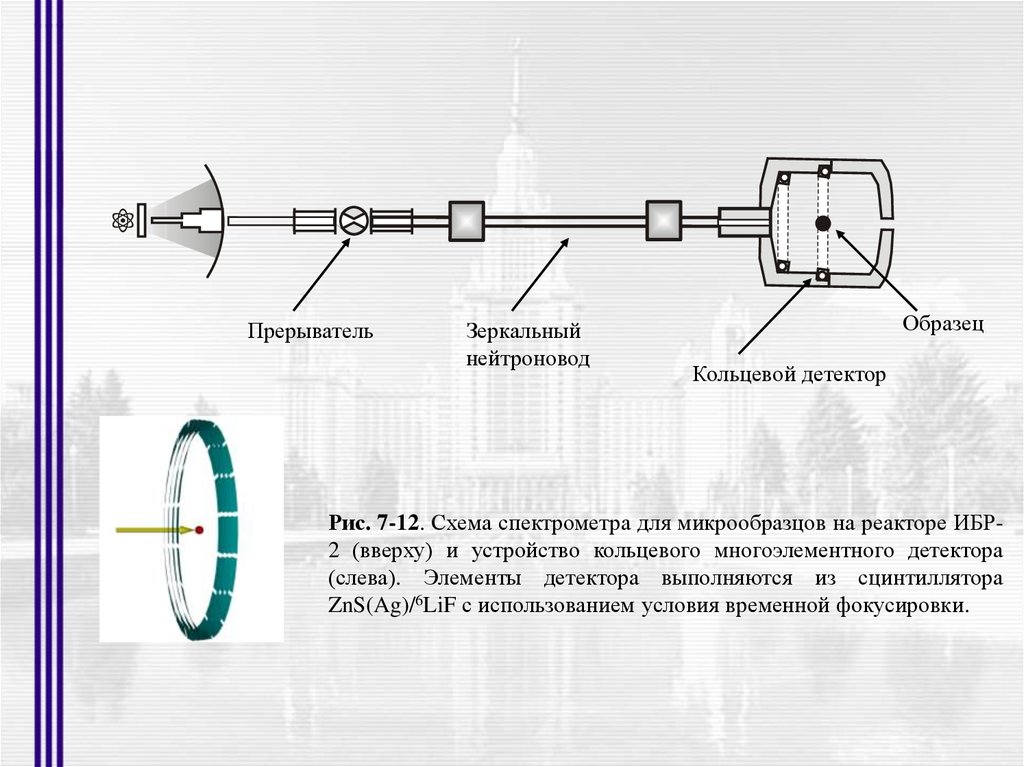
ПрерывательЗеркальный
нейтроновод
Образец
Кольцевой детектор
Рис. 7-12. Схема спектрометра для микрообразцов на реакторе ИБР2 (вверху) и устройство кольцевого многоэлементного детектора
(слева). Элементы детектора выполняются из сцинтиллятора
ZnS(Ag)/6LiF с использованием условия временной фокусировки.
47.
Рис. 7-13. Приведенный структурный фактор F(Q) кристаллического Ni, измеренный доQmax ≈ 30 A-1 (слева). На вставке показана область больших Q, где видны
дифракционные пики, которые необходимо учитывать при вычислении преобразования
Фурье. Справа показаны экспериментальная (точки) функция G(r), полученная фурьепреобразованием F(Q), и вычисленная (гладкая кривая) по структурной модели функция
PDF. Внизу показана разностная кривая.
48.
Рис. 7-14. Экспериментальная и вычисленные функции G(r) в области малых r дляLa0.75Ca0.25MnO3. Вычисления проведены для двухфазной модели (сплошная линия),
предполагающей наличие в образце искаженной фазы (точки) и регулярной фазы
(пунктир). При низкой температуре (20 K) доминирует регулярная фаза, при 220 K
присутствуют обе фазы. Слева показано поведение доли регулярной фазы.
49.
11
χ
T
χ 0
χ
χ 0
T
M
1
θ 0
TC
T
θ 0
χ
TN
T
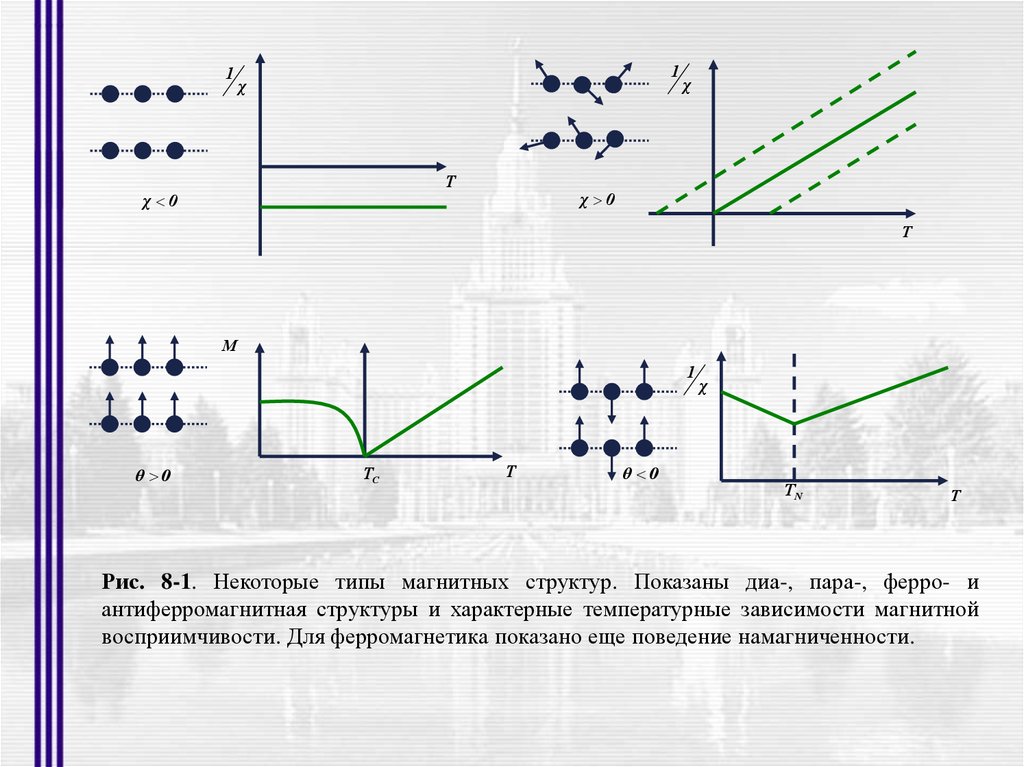
Рис. 8-1. Некоторые типы магнитных структур. Показаны диа-, пара-, ферро- и
антиферромагнитная структуры и характерные температурные зависимости магнитной
восприимчивости. Для ферромагнетика показано еще поведение намагниченности.
50.
dmc-c.grf20000
FM+AFM
O-16
1/2 0 1/2
10000
1/2 0 0
Intensity
15000
200/121
101/020
DMC
T=12 K
AFM
5000
O-18
0
10
20
30
40
50
60
70
80
90
Scattering angle
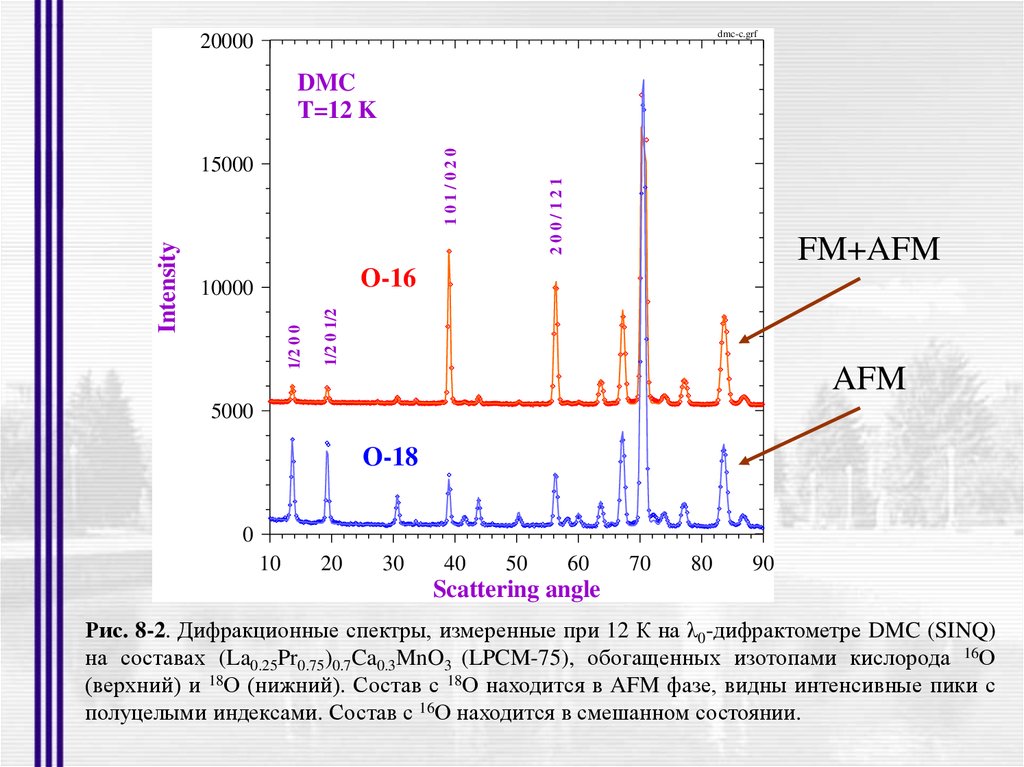
Рис. 8-2. Дифракционные спектры, измеренные при 12 К на λ0-дифрактометре DMC (SINQ)
на составах (La0.25Pr0.75)0.7Ca0.3MnO3 (LPCM-75), обогащенных изотопами кислорода 16О
(верхний) и 18О (нижний). Состав с 18О находится в AFM фазе, видны интенсивные пики с
полуцелыми индексами. Состав с 16О находится в смешанном состоянии.
51.
44
o16-mc
o18-mc
16
3
18
LPCM-75, O
FM
Magnetic moment
Magnetic moment
LPCM-75/ O
2
1
AFM,
pseudo-CE
k1=(0,0,1/2)
k2=(1/2,0,1/2)
3
2
1
AFM
0
0
0
50
100
Temperature, K
150
200
0
50
100
150
200
Temperature, K
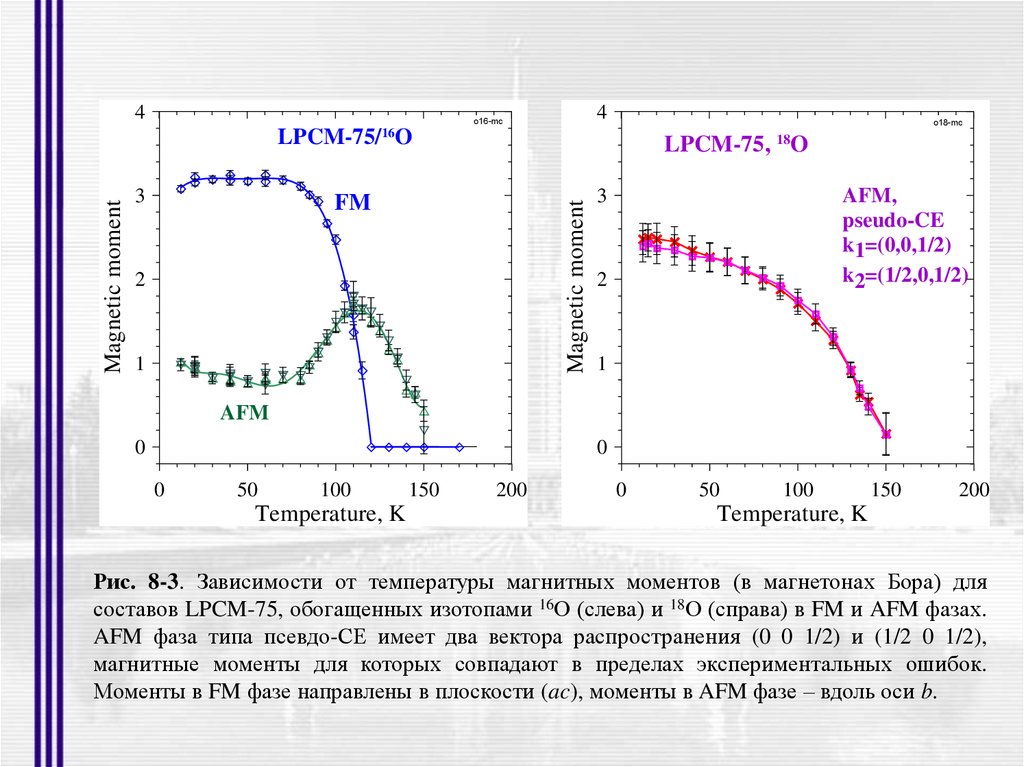
Рис. 8-3. Зависимости от температуры магнитных моментов (в магнетонах Бора) для
составов LPCM-75, обогащенных изотопами 16О (слева) и 18О (справа) в FM и AFM фазах.
AFM фаза типа псевдо-СЕ имеет два вектора распространения (0 0 1/2) и (1/2 0 1/2),
магнитные моменты для которых совпадают в пределах экспериментальных ошибок.
Моменты в FM фазе направлены в плоскости (ac), моменты в AFM фазе – вдоль оси b.
52.
0n
Пучок нейтронов
Диафрагмы
Q2
Detector 2
Detector 1
Q1
Изделие
Рис. 9-1. Постановка эксперимента по измерению внутренних напряжений в объемном
материале или изделии. Малый объем в изделии (gauge volume) выделяется с помощью
диафрагм в первичном пучке нейтронов (вверху) и перед детекторами. Регистрация
нейтронограмм двумя детекторами позволяет одновременно определять деформации в
двух взаимно перпендикулярных направлениях Q1 и Q2.
53.
-Fe(110)
fe-str
W2 = C1 + C2d2 + C3d4
1000
(a-a0)/a0=0.001
(200 MPa)
800
W2, arb. un.
(a-a0)/a0=-0.0001
(20 MPa)
Ni
600
400
200
Al2O3
2.020
2.025
2.030
d, Å
2.035
wid-Ni-3
0
0
1
2
3
4
(d, Å)2
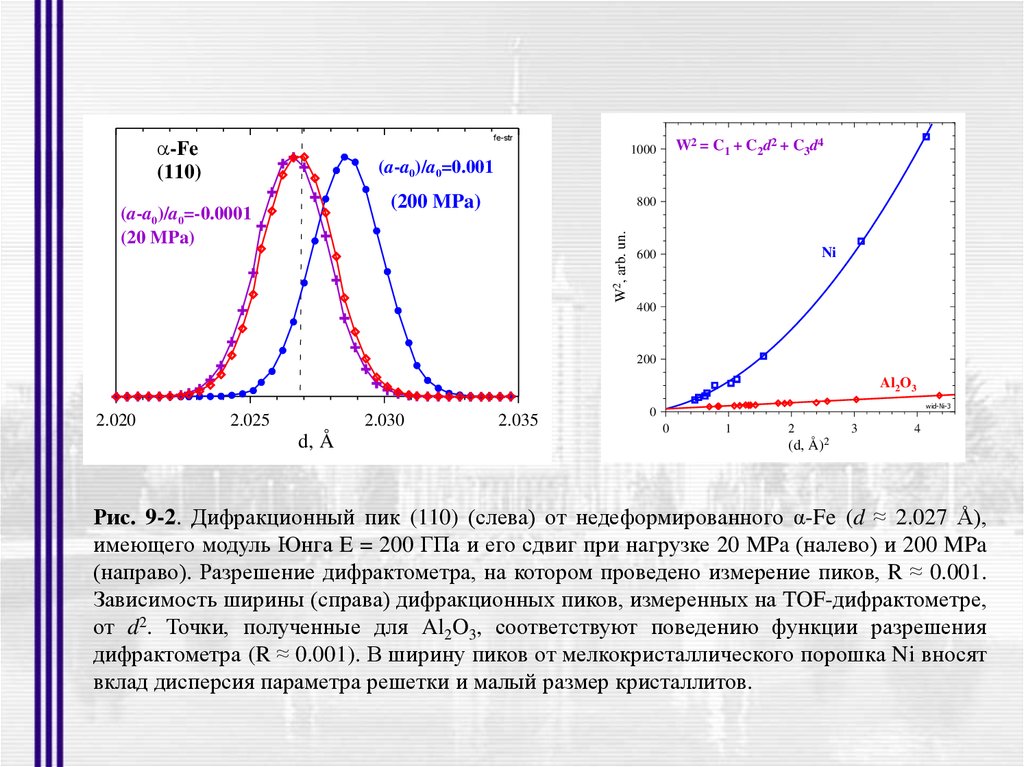
Рис. 9-2. Дифракционный пик (110) (слева) от недеформированного α-Fe (d ≈ 2.027 Å),
имеющего модуль Юнга E = 200 ГПа и его сдвиг при нагрузке 20 MPa (налево) и 200 MPa
(направо). Разрешение дифрактометра, на котором проведено измерение пиков, R ≈ 0.001.
Зависимость ширины (справа) дифракционных пиков, измеренных на TOF-дифрактометре,
от d2. Точки, полученные для Al2O3, соответствуют поведению функции разрешения
дифрактометра (R ≈ 0.001). В ширину пиков от мелкокристаллического порошка Ni вносят
вклад дисперсия параметра решетки и малый размер кристаллитов.
54.
Zr200 m m
сталь
88 m m
Рис. 9-3. Биметаллический переходник сталь – сплав циркония. Показаны область А-В и
сечения 1, 2 (слева), в которых производились нейтронные измерения остаточных
деформаций, а0 – место, где был измерен параметр решетки стали, принятый за исходное
значение. Справа показана стенка биметаллического переходника в разрезе. Виден переход
от стали к Zr.
55.
-180-200
-220
Residual Stress, MPa
-240
-260
-280
-300
-320
-340
-360
Stress1
Stress2
-380
-400
-420
-0.5 0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
6.0
X , mm
Рис. 9-4. Величины радиальных остаточных напряжений в сечении 3 (черные квадраты) и
сечении 2 (красные кружки) биметаллического переходника. Координата x соответствует
расстоянию от границы раздела нержавеющая сталь – цирконий (x = 0 – граница раздела).
56.
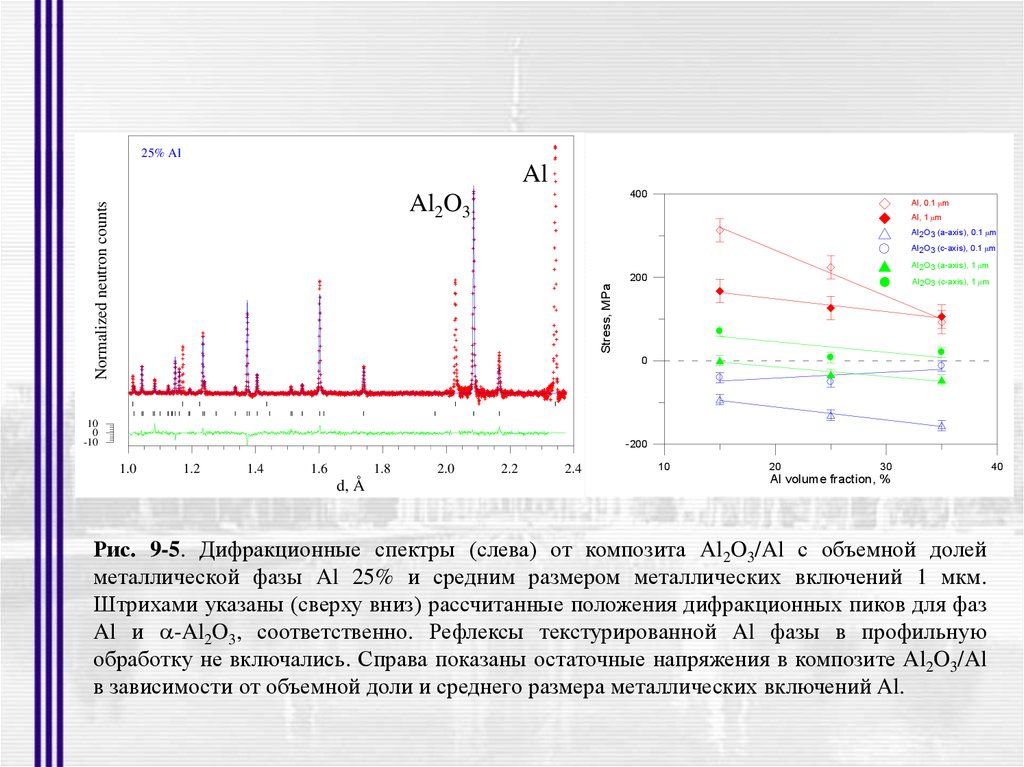
25% AlAl
400
Normalized neutron counts
Al2O3
Al, 0.1 mm
Al, 1 mm
Al2O3 (a-axis), 0.1 mm
Al2O3 (c-axis), 0.1 mm
Al2O3 (a-axis), 1 mm
200
Stress, MPa
Al2O3 (c-axis), 1 mm
0
10
0
-10
-200
1.0
1.2
1.4
1.6
1.8
d, Å
2.0
2.2
2.4
10
20
30
Al volume fraction, %
Рис. 9-5. Дифракционные спектры (слева) от композита Al2O3/Al с объемной долей
металлической фазы Al 25% и средним размером металлических включений 1 мкм.
Штрихами указаны (сверху вниз) рассчитанные положения дифракционных пиков для фаз
Al и -Al2O3, соответственно. Рефлексы текстурированной Al фазы в профильную
обработку не включались. Справа показаны остаточные напряжения в композите Al2O3/Al
в зависимости от объемной доли и среднего размера металлических включений Al.
40































 Физика
Физика








