Арксинус. Решение уравнения sin t = a

1. Арксинус. Решение уравнения sin t = a. урок алгебры, 10 класс, УМК А.Г. Мордкович

Автор: Лазарчук Владимир Николаевич,
учитель математики и физики
МБОУ СОШ № 4
н.п. Енский Ковдорского района Мурманской
области

2. Цели

• Изучить определение арксинуса числа.
• Изучить формулы решения
простейшего тригонометрического
уравнения sin t = a.

3.

Что называется синусом
числа t на числовой
окружности.
t
М(х ;у)
у
Синусом числа t на
числовой окружности
называют ординату
соответствующей точки
окружности
у sin t

4.

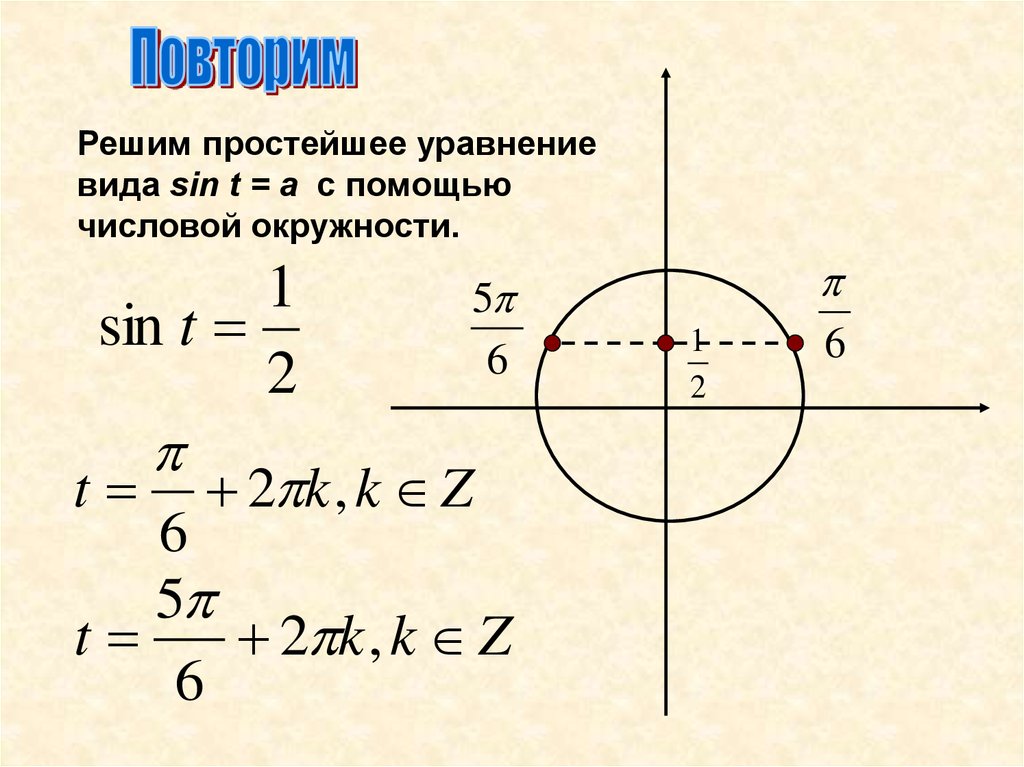
Решим простейшее уравнение
вида sin t = a с помощью
числовой окружности.
1
5
sin t
6
2
t 2 k , k Z
6
5
t
2 k , k Z
6
1
2
6

5.

3
sin t
5
С помощью числовой
окружности получим
решение.
В
Р(t2 )
С
M (t1 )
3
5
А
t t1 2 k , k Z
t t2 2 k , k Z
Поскольку АР АС - РС,
t1 длина дуги АМ
АС , а РС АМ, получаем,
t2 длина дуги АP
что t 2 - t1

6.

?
Что это за число t1?
В рассмотрение введён
новый символ
3
arcsin
5
«арксинус трёх пятых»
Р(t2 )
M (t1 )
3
5

7.

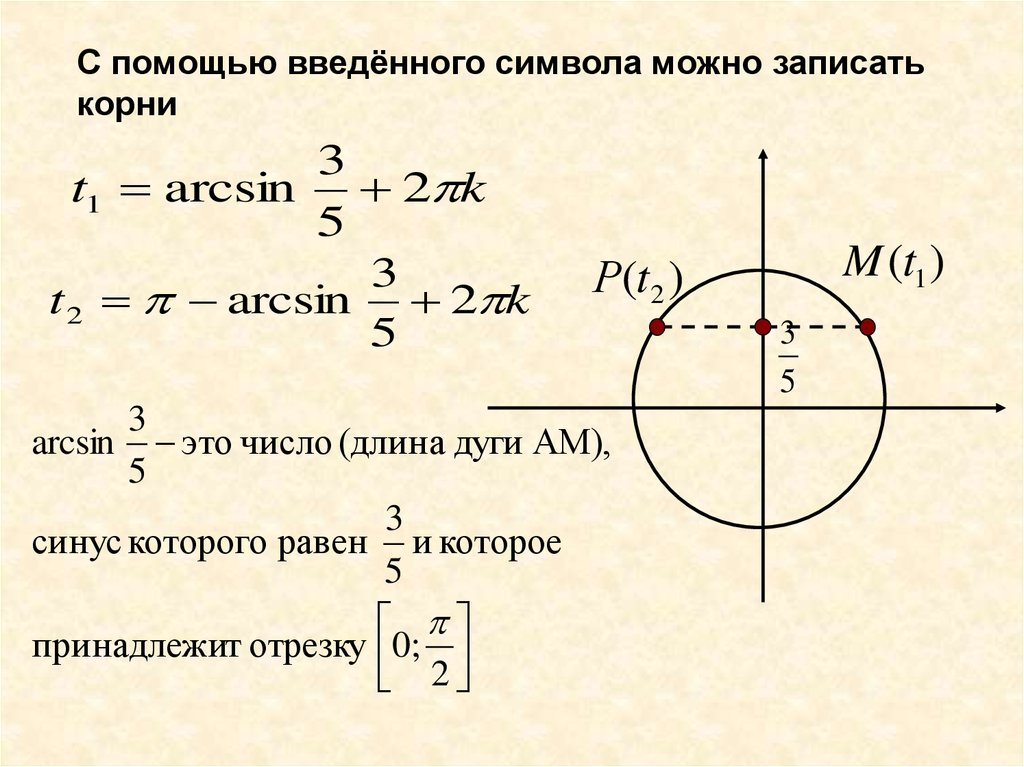
С помощью введённого символа можно записать
корни
3
t1 arcsin 2 k
5
3
t 2 arcsin 2 k
5
M (t1 )
Р(t2 )
3
arcsin это число (длина дуги АМ),
5
3
синус которого равен и которое
5
принадлежит отрезку 0;
2
3
5

8.

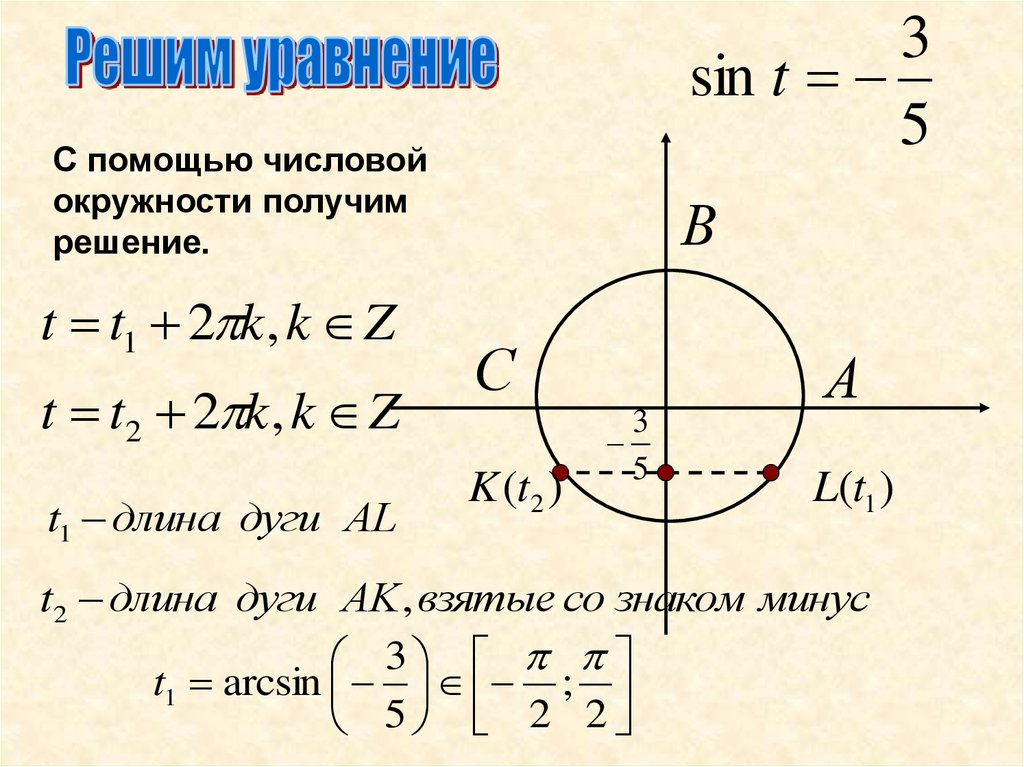
3
sin t
5
С помощью числовой
окружности получим
решение.
t t1 2 k , k Z
t t2 2 k , k Z
t1 длина дуги АL
В
С
K (t2 )
3
5
А
L(t1 )
t2 длина дуги АK , взятые со знаком минус
3
t1 arcsin ;
5 2 2

9.

С помощью числовой окружности сравним
3
arcsin
5
3
и arcsin
5
Дуги AM и AL
равны по длине и
противоположны
по направлению
M
3
5
3
5
3
3
arcsin arcsin
5
5
3
arcsin
5
А
3
arcsin
5
L

10.

3
t arcsin 2 k , k Z
5
3
sin t
5
В
С
K (t2 )
3
5
3
t arcsin 2 k , k Z
5
А
L(t1 )

11.

Если а 1, то arcsin a (арксинус а) это
такое число из отрезка ; , синус
2 2
которого равен а.
Если а 1, то
sin t a
arcsin a t
.
2 t 2

12.

Если а 1, то уравнение sin t a
имеет две серии решения
t arcsin a 2 k , k Z ,
t arcsin a 2 k , k Z .
Существует три частных случая решения уравнения
sin t = a
t k ;
sin t 0,
sin t 1,
sin t 1,
t
2 k ;
2
t 2 k .
2

13.

Пример 1.
Вычислить:
1
а) arcsin
2
1
1
Пусть arcsin t. Тогда sin t и t ; .
2
2
2 2
1
Значит, t , поскольку sin и ; .
6
6 2 6 2 2
1
arcsin .
2 6

14.

Пример 1.
Вычислить:
2
б ) arcsin
2
2
2
t. Тогда sin t
и t ; .
Пусть arcsin
2
2
2 2
2
Значит, t , поскольку sin
и ; .
4
2
4 2 2
4
2
arcsin
2
4

15.

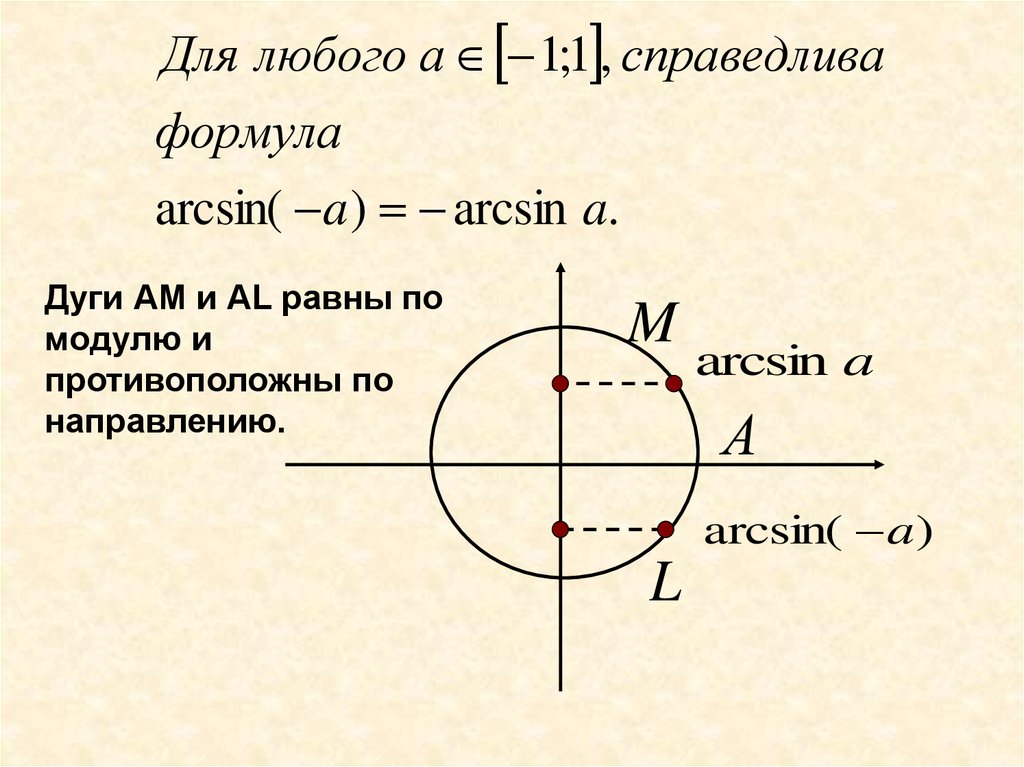
Для любого а 1;1 , справедлива
формула
arcsin( a ) arcsin a.
Дуги АМ и АL равны по
модулю и
противоположны по
направлению.
M
arcsin a
А
arcsin( a )
L

16.

Пример 2.
Решить уравнение
3
a) sin t
2
3
3
t arcsin
2 k , t arcsin
2 k .
2
2
3
arcsin
2
3
2
t 2 k , t
2 k , k Z
3
3

17.

Пример 2.
Решить уравнение
3
б ) sin t
2
3
3
2 k , t arcsin
t arcsin
2
2
3
3
arcsin
arcsin
2
2
3
4
t 2 k , k Z , t
2 k , k Z
3
3

18.

Пример 2.
Решить уравнение
7
в ) sin t
12
7
7
t arcsin
2 k , t arcsin
2 k , k Z
12
12
г ) sin t 1,2
Т .к. 1,2 1, то уравнение sin t 1,2
не имеет корней .

19.

Принята общая формула решения
тригонометрического уравнения sin t = a
t arcsin a 2 k , k Z ,
t arcsin a 2 k , k Z .
t arcsin a 2k , k Z ,
t arcsin a (2k 1), k Z .
t 1 arcsin a n, n Z ,
n

20.

Пример 3.
Решить неравенство
sin t 0,6
arcsin 0,6
Строим окружность
M
Учитываем, что синус –
это ордината точки
числовой окружности.
Следовательно
arcsin 0,6
P
0,6
у 0,6
Данному неравенству соответствуют
точки открытой дуги MP
Получим
arcsin 0,6 2 k t arcsin 0,6 2 k , k Z

21. Решите из учебника

• № 16.1, 16.3, 16.5, 16.9, 16.11

22. Задание на дом

• § 16 выучить
• № 16.2, 16.4, 16.6

23.

Список используемых источников
Алгебра и начала математического анализа. 10 – 11 классы. В
2ч. Ч. 1. Учебник для учащихся общеобразовательных
учреждений (базовый уровень)/А.Г.Мордкович. – 11-е изд.,
стер. – М.: Мнемозина, 2010. – 399 с. : ил.