Düz xətt və nöqtə müstəvinin əsas anlayışlarıdır. İstənılən düz xəttə aid olan nöqtələr və aid olmayan nöqtələr var

1.

Düz xətt və nöqtə müstəvinin əsas anlayışlarıdır.İstənılən düz xəttə aid olan nöqtələr və aid olmayan nöqtələr var.
a
C
D
B
A
Düz xətt üzərində yerləşən üç nöqtədən biri digər ikisi arasında yerləşir.
a
A
B
C
Parçanın uzunluğu , onun istənilən nöqtəsi ilə bölündüyü hissələrinin uzunluqları cəminə bərabərdir.
M
N
K
MK=MN+NK
Düz xətt və onun üzərində yerləşməyən nöqtədən bu düz xəttə paralel bir və yalnız bir düz xətt keçirmək olar.
A
b
a

2.

Müstəvi üzərində verilmiş iki düz xətt ya kəsişmir .ya da bir nöqtədə kəsişir. Kəsişməyən düz xətlər paraleldir.
a
b
a║b
b
İki düz xətt kəsişdikdə dörd bucaq əmələ gəlir.
2
3
4
1
a
‹1və‹3
‹2və‹4 qarşılıqlı bucaqlardır. Qarşılıqlı bucaqlar bərabərdir. ‹1=‹3. ‹2=‹4.
‹1və‹2. ‹1və‹4.....qonşu bucaqlardır. Qonşu bucaqların cəmi 180°-yə bərabərdir. ‹1+‹2=180° . ‹1+‹4=180°
İti bucağa qonşu olan bucaq kor bucaqdır. Kor bucağa qonşu olan bucaq iti bucaqdır.
135°
Düz bucağa qonşu olan bucaq düz bucaqdır.
Düz bucaq altında kəsişən düz xətlər ┴ düz xətlərdir.
45°

3.

İstənilən yarımdüzxətt üzərində onun başlanğıc nöqtəsindən başlayaraq verilmiş uzunluqda bir parça ayırmaq olar.
A
B
Ortaq başlanğıclı iki müxtəlif şüanın əmələ gətirdiyi fiqur bucaqdır.
A
O
)
‹O , ‹AOB , ‹BOA
Kimi yazılır.
B
Bucağın dərəcə ölçüsü onun bölündüyü bucaqların dərəcə ölçüləri cəminə bərabərdir.
A
B
C
‹AOD=‹AOB+‹BOC+‹COD olar.
D
O
Bucağın təpəsindən çıxan şüa onu iki bərabər bucağa bölərsə, onda bu şüa bucağın tənbölənidir.
B
‹BAC=‹CAD olar.
C
)
D
A
)
Üçbucaq həndəsi fiqurdur. Üçbucağın əsas 6 elementi var. 3 bucağı və 3 tərəfi.
∆ABC üçün
Bucaqlar: ‹A ,‹B ,‹C ;
A
Tərəflər: AB , BC , CA .
B
C

4.

Yan tərəfləri bərabər olan üçbucaq bərabəryanlıdır.
B
AB=BC
Bərabəryanlı üçbucaqda oturacağa bitişik bucaqlar bərabərdir.
A
‹A=‹C
Bərabəryanlı üçbucaqda təpədən çəkilmiş median həm
tənbölən, həm də hündürlükdür.
NK┴MP , MK=KP , ‹NMK=‹NPK olar.
N
C
M
P
K
B
Bütün tərəfləri bərabər olan üçbucaq bərabərtərəflidir. Bərabərtərəfli üçbucaqda bucaqlar 60°-dir.
∆ABC bərabərtərəflidirsə, AB=BC=AC və ‹A=‹B=‹C=60° olar.
Bərabərtərəfli üçbucaqda hündürlüklər, medianlar, tənbölənlər eynidir.
Onlar bir nöqtədə kəsişir və onlar arasındakı bucaqlar 60°-dir.
C
A
Bucaqlarından biri düz bucaq olan üçbucaq düzbucaqlı üçbucaqdır.
Düzbucaqlı üçbucaqda iti bucaqların cəmi 90°-dir.
‹B+‹C= 90°
Düzbucaqlı üçbucaqda iti bucağa bitişik tərəflər katetlər, iti bucaq
qarşısındakı tərəf isə hipotenuzdur: AB və AC katetlər.
BC hipotenuz.
60
B
A
C
60 60
60
60 60

5.

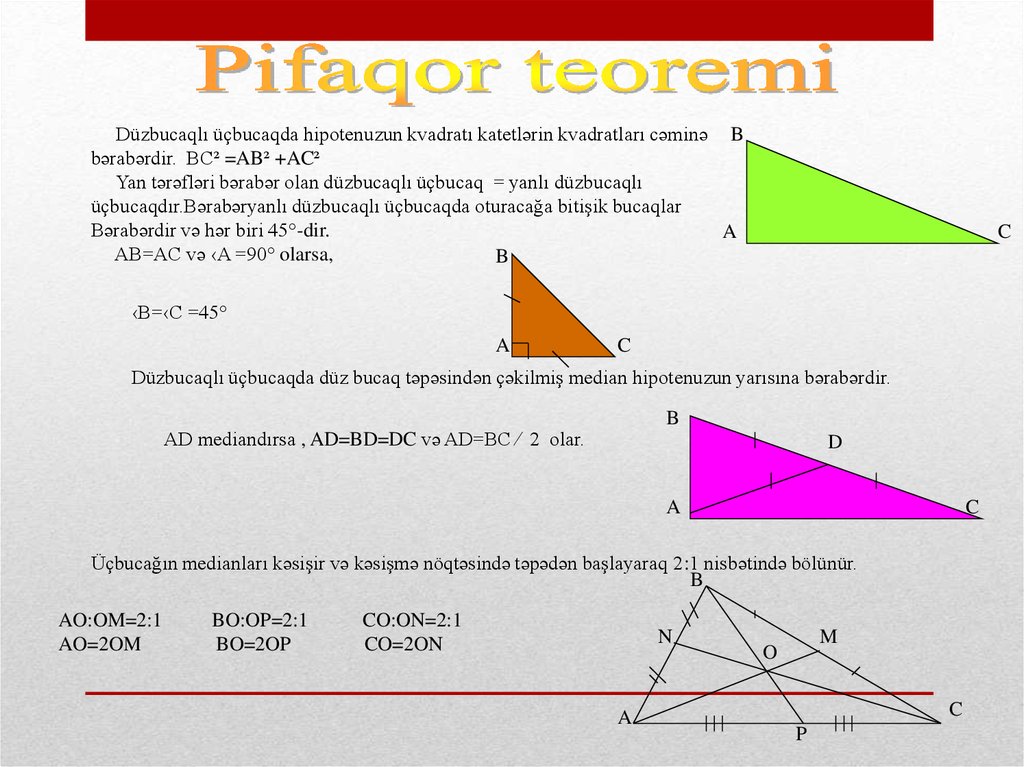
Düzbucaqlı üçbucaqda hipotenuzun kvadratı katetlərin kvadratları cəminə B
bərabərdir. BC² =AB² +AC²
Yan tərəfləri bərabər olan düzbucaqlı üçbucaq = yanlı düzbucaqlı
üçbucaqdır.Bərabəryanlı düzbucaqlı üçbucaqda oturacağa bitişik bucaqlar
Bərabərdir və hər biri 45°-dir.
A
AB=AC və ‹A =90° olarsa,
B
C
‹B=‹C =45°
A
C
Düzbucaqlı üçbucaqda düz bucaq təpəsindən çəkilmiş median hipotenuzun yarısına bərabərdir.
B
AD mediandırsa , AD=BD=DC və AD=BC ⁄ 2 olar.
D
A
C
Üçbucağın medianları kəsişir və kəsişmə nöqtəsində təpədən başlayaraq 2:1 nisbətində bölünür.
B
AO:OM=2:1
AO=2OM
BO:OP=2:1
BO=2OP
CO:ON=2:1
CO=2ON
N
A
M
O
C
P

6.

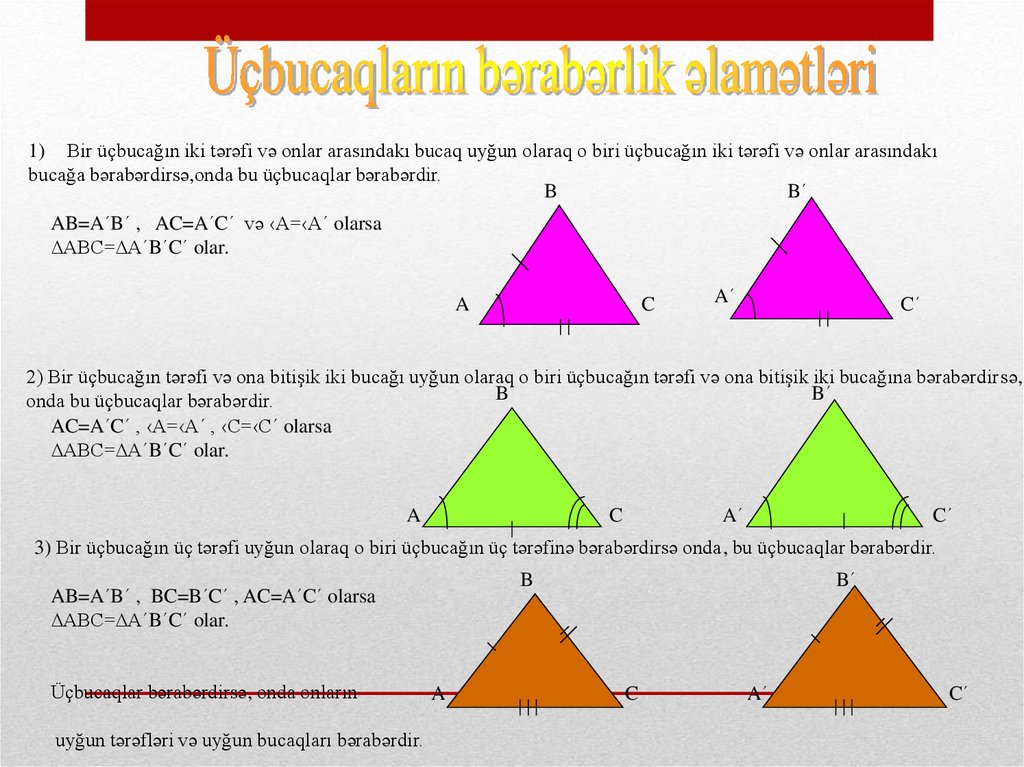
1) Bir üçbucağın iki tərəfi və onlar arasındakı bucaq uyğun olaraq o biri üçbucağın iki tərəfi və onlar arasındakı
bucağa bərabərdirsə,onda bu üçbucaqlar bərabərdir.
B
B΄
AB=A΄B΄ , AC=A΄C΄ və ‹A=‹A΄ olarsa
∆ABC=∆A΄B΄C΄ olar.
A
C
A΄
C΄
2) Bir üçbucağın tərəfi və ona bitişik iki bucağı uyğun olaraq o biri üçbucağın tərəfi və ona bitişik iki bucağına bərabərdirsə,
B
B΄
onda bu üçbucaqlar bərabərdir.
AC=A΄C΄ , ‹A=‹A΄ , ‹C=‹C΄ olarsa
∆ABC=∆A΄B΄C΄ olar.
A
C
A΄
C΄
3) Bir üçbucağın üç tərəfi uyğun olaraq o biri üçbucağın üç tərəfinə bərabərdirsə onda, bu üçbucaqlar bərabərdir.
B
AB=A΄B΄ , BC=B΄C΄ , AC=A΄C΄ olarsa
∆ABC=∆A΄B΄C΄ olar.
Üçbucaqlar bərabərdirsə, onda onların
uyğun tərəfləri və uyğun bucaqları bərabərdir.
A
B΄
C
A΄
C΄

7.

Müstəvi üzərində iki düz xətt kəsişmirsə, onlara paralel düz xətlər deyilir.
a
a║b
b
Eyni bir düz xəttə paralel olan iki düz xətt bir-birinə paraleldir.
m║n və n║c olarsa , onda m║c olar.
m
c
n
a
İki paralel düz xətt üçüncü ilə kəsişdikdə
1) Daxili çarpaz bucaqlar bərabərdir;
‹4=‹6 , ‹3=‹5.
.
2) Uyğun bucaqlar bərabərdir;
‹1=‹5 , ‹2=‹6 , ‹3=‹7 , ‹4=‹8
3)Daxili birtərəfli bucaqların cəmi 180°-yə bərabərdir.
‹4+‹5=180° , ‹3+‹6=180° .
b
2 1
3 4
6 5
7 8
c

8.

c
Düz xətt iki paralel düz xətdən birinə ┴-dırsa, o birinə də ┴-dır.
a
b
Müstəvinin istənilən nöqtəsindən verilmiş düz xəttə bir və yalnız bir ┴ düz xətt çəkmək olar.
Düz xətt üzərində olmayan nöqtədən bu düz xəttə çəkilmiş ┴-ın
uzunluğuna həmin nöqtədən düz xəttə qədər məsafə deyilir.
Şəkildəki AC məsafəsi A nöqtəsindən a düz xəttinə qədər məsafədir.
Nöqtə düz xətt üzərində olduqda bu nöqtədən düz xəttə qədər məsafə
sıfra bərabərdir.
Paralel düz xətlərdən birinin bütün nöqtələri o biri düz xətdənbərabər məsafədədir.
a
C
Paralel düz xətlərdən birinin ixtiyari nöqtəsindən o biri düz xəttə qədər olan
məsafəyə bu düz xətlər arasındakı məsafə deyilir.
M
.
A
MN m və n düz xətləri arasındakı məsafədir.
n
N
m

9.

O α
α
O
A
γ
O'
γ
α=γ
O'
α+γ=180°
Uyğun tərəfləri┴ olan bucaqlar ya bir birinə bərabərdir, ya da onların cəmi 180°-yə bərabərdir.
B
Üçbucaqların bucaqları cəmi 180°-yə bərabərdir.
İxtiyari üçbucağın heç olmasa iki bucağı iti bucaqdır.
C
A
‹A+‹B+‹C=180°
N
Üçbucağın hər hansı bucağına qonşu olan bucağa bu üçbucağın xarici bucağı deyilir.
.
m+n=180°
y
M
x
n
m
K
m=x+y
Uyğun tərəfləri paralel olan bucaqlar ya bir-birinə bərabərdir, ya da onların cəmi 180°-yə bərabərdir.
Üçbucağın xarici bucağı özünə qonşu olmayan daxili
bucaqların cəminə bərabərdir.Üçbucağın xarici bucağı özünə qonşu olmayan daxili bucaqların hər birindən böyükdür.

10.

hipotenuz
katet
Itibucaqlı üçbucaq
katet
Düzbucaqlı üçbucaq
Korbucaqlı üçbucaq
B
Üçbucaqda: 1) böyük tərəf qarşısında böyük bucaq durur.
2) böyük bucaq qarşısında böyük tərəf durur.
a
c
C
A
b
b>a>c olduğundan , ‹B > ‹A > ‹C olar.
B
İki bucağı bərabər olan üçbucaq bərabəryanlıdır.
‹A=‹C olarsa , AB=BC olar.
Üçbucağın hər bir tərəfi digər iki tərəfinin cəmindən kiçikdir.
a‹b+c
b‹a+c
c‹a+b
A
C

11.

1) Bir düzbucaqlı üçbucağın katetləri o birinin katetlərinə bərabərdirsə, bu üçbucaqlar bərabərdir.
AB=A'B'
AC=A'C' olarsa,
∆ABC=∆A'B'C' olar.
B
B'
C
A
C'
A'
2) Bir düzbucaqlı üçbucağın kateti və iti bucağı uyğun olaraq o biri düzbucaqlı üçbucağın kateti və iti bucağına
bərabərdirsə, bu üçbucaqlar bərabərdir.
B'
B
AC=A'C' və ‹C=‹C' olarsa,
∆ABC=∆A'B'C' olar.
C
A'
A
3) Bir düzbucaqlı üçbucağın hipotenuzu və iti bucağı uyğun olaraq o birinin hipotenizu və iti bucağına
bərabərdirsə, bu üçbucaqlar bərabərdir.
B
B'
C'
BC=B'C' və ‹C=‹C' olarsa,
∆ABC=∆A'B'C' olar.
C'
A
C
A'

12.

Bir düzbucaqlı üçbucağın hipotenuzu və kateti uyğun olaraq o birinin hipotenuzu və katetinə bərabərdirsə, bu
düzbucaqlı üçbucaqlar bərabərdir.
B
B'
BC=B'C' və AC=A'C' olarsa,
∆ABC=∆A'B'C' olar.
C
A
Düzbucaqlı üçbucaqda iti bucaqların cəmi 90°-yə bərabərdir.
‹B+‹C=90°
Düzbucaqlı üçbucaqda 30°-li bucaq qarşısında duran katet
hipotenuzun yarısına bərabərdir.Və yaxud düzbucaqlı
AB=BC/2
üçbucaqda katet hipotenuzun yarısına bərabərdirsə, bu
katetin qarşısındakı bucaq 30°-dir.
B
C'
A'
B
A
30
C
D
Düzbucaqlı üçbucaqda düz bucaq təpəsindən çəkilmiş
median hipotenuzun yarısına bərabərdir. AD=BC/2 olar.
C
A
AH parçası A nöqtəsindən a düz xəttinə çəkilmiş perpendikulyardır və M nöqtəsi isə
a düz xəttinin H –dan fərqli ixtiyari nöqtəsidir. Onda AM parçası A nöqtəsindən a düz
xəttinə çəkilmiş mail adlanır. H nöqtəsinə perpendikulyarın otiracağı, M nöqtəsinə isə
mailin oturacağı deyilir. Mailin oturacağını perpendikulyarın oturacağı ilə birləşdirən
parçaya mailin proyeksiyası deyilir. Nöqtədən düz xəttə çəkilmiş perpendikulyar
bu nöqtədən çəkilən bütün maillərdən kiçikdir.
A
M
H
a

13.

Düz xətt üzərində yerləşməyən nöqtədən bu düz xəttəperpendikulyar və maillər çəkilərsə:
a) Proyeksiyaları bərabər olan mallər bərabərdir;
b) bərabər maillərin proyeksiyaları bərabərdir;
c) proyeksiyası böyük mail böyükdür;
d) böyük mailin proyeksiyası böyükdür.
B
Verilmiş nöqtədən bərabər məsafədə olan bütün nöqtələrdən ibarət olan fiqura çevrə deyilir.
Verilmş nöqtəyə çevrənin mərkəzi deyilir. Çevrənin mərkəzindən hər hansı nöqtəsinə
qədər məsafəyə radius deyilir. Çevrənin ixtiyari iki nöqtəsini biləşdirən parçaya vətər
dryilir. Mərkəzdən keçən vətər diametr adlanır. Diametr vətərdən iki dəfə böyükdür.
Çevrə ilə onun daxili oblastınin əmlə gətirdiyi fiqura dairə deyilir.
Çevrənin nöqtəsindən keçib bu nöqtədən çəkilən radiusa perpendikulyar
Olan düz xəttə bu çevrəyə toxunan deyilir.Çevrənin həmin nöqtəsinə
Çevrə ilə düz xəttin toxunma nöqtəsi deyilir.
Çevrəyə toxunan düz xətt toxunma nöqtəsində çəkilmiş radiusa perpendikulyardır.
OA┴a olar.
Bir nöqtədən çevrəyə iki toxunan çəkilərsə, həmin nöqtədən toxunma nöqtələrinə qədər
məsafələr bərabərdir.
B
AB=AC
A
C
N
C
A
O
M
O
A
a

14.

İki çevrə eyni bir nöqtədə müəyyən bir düz xəttə toxunursa , deyirlər ki ,çevrələr bir-birinə toxunur.Toxunan
Çevrələr toxunma nöqtəsindən keçən düz xəttə nəzərən bir tərəfdə yerləşərsə belə toxunma daxildən toxunmadır.
Daxildən toxunan çevrələrin mərkəzləri arasındakı məsafə böyük radiusla kiçik radiusun fərqinə bərabərdir.
OO‘=R‘-R olar.
R
O
O'
O' R'
R'
O
R
a
·
O
·
O΄
·
R΄
Çevrələr toxunma nöqtəsindən keçən düz xəttə nəzərən müxtəlif tərəfkərdə
R
yerləşərsə, onda deyirlər ki, çevrələr xaricdən toxunur.
Xaricdən toxunan çevrələrin mərkəzləri arasındakı məsafə onların radiusları
cəminə bərabərdir. OO΄=R+R΄ olar.
Çevrələr toxunmursa ,onların mərkəzləri
Konsentrik çevrələrin mərkəzləri üst-üstə düşür.
arasındakı məsafə radiusları cəmindən
A
böyükdür.
O
O΄
R
R΄
Çevrələr kəsişirsə, onların mərkəzləri arasındakı məsafə onların radiusları cəmindən kiçikdir. OO΄‹ R+R΄ olar.

15.

Altıbucaqlı
dördbucaqlı
beşbucaqlı
Çoxbucaqlının bütün tərəflərinin uzunluqları cəminə onun perimetri deyilir.
n sayda təpəsi olan çoxbucaqlıya n bucaqlı da deyilir. n bucaqlınin n tərəfi olur.
Çoxbucaqlının bir tərəfinə aid olan iki təpəsinə onun qonşu təpələri deyilir. Çoxbucaqlının qonşu olmayan iki təpəsini
birləşdirən parçaya onun diaqonalı deyilir.
B
C
ABCDEF çoxbucaqlısında , məsələn, A və B təpələri qonşu təpələr;
A və C təpələri isə qonşu olmayan təpələr; deməli AC , BE diaqonaldır.
D
A
Qabarıq n bucaqlının daxili bucaqlarının cəmi 180°(n-2) – bərabərdir.
Qabarıq çoxbucaqlının xarici bucaqlarının cəmi 360° - yə bərabərdir.
F
Qabarıq n bucaqlınin bir təpədən çıxan diaqonallarınin sayı (n-3) saydadır.Qabarıq n bucaqlının
Bir təpədən çıxan dıaqonalları onu (n-2) sayda üçbucaqlara ayırır.
E

16.

Qarşı tərəfləri paralel olan dördbucaqlıya paraleloqram deyilir.
B
C
A
Paraleloqramın qarşı tərəfləri və qarşı bucaqları bərabərdir.
D
B
ABCD paraleloqramında AB=CD, BC=AD və ‹A=‹C , ‹B=‹D olar.
C
(
A )
Paraleloqramın diaqonalları kəsişir və kəsişmə nöqtəsində yarıya bölünür.
B
AO=OC və BO= OD olar.
İki qarşı tərəfi bərabər və paralel olan dördbucaqlı paraleloqramdır.
Qarşı tərəfləri cüt-cüt bərabər olan dördbucaqlı paraleloqramdır.
Dördbucaqlının diaqonalları kəsişirsə və kəsişmə nöqtəsində yarıya
A
bölünürsə bu dördbucaqlı paraleloqramdır.
Paraleloqramın diaqonalları onu sahələri bərabər olan 4 üçbucağa
ayırır.Paraleloqramın diaqonalı onu 2 bərabər üçbucağa ayırır.
Bu mənada S(ABO)=S(BOC)=S(COD)=S(DOA) və ∆ABC=∆ADC=∆ABD=∆CDB olar.
D
C
o
D

17.

B
C
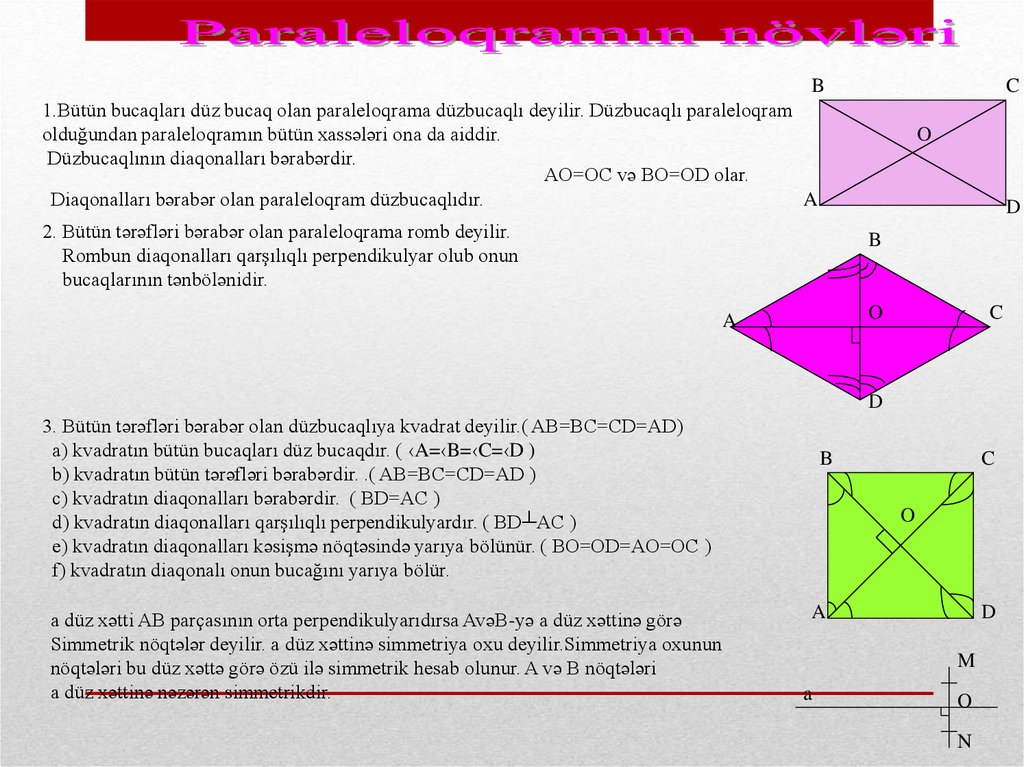
1.Bütün bucaqları düz bucaq olan paraleloqrama düzbucaqlı deyilir. Düzbucaqlı paraleloqram
olduğundan paraleloqramın bütün xassələri ona da aiddir.
Düzbucaqlının diaqonalları bərabərdir.
AO=OC və BO=OD olar.
Diaqonalları bərabər olan paraleloqram düzbucaqlıdır.
A
O
D
2. Bütün tərəfləri bərabər olan paraleloqrama romb deyilir.
Rombun diaqonalları qarşılıqlı perpendikulyar olub onun
bucaqlarının tənbölənidir.
B
O
A
C
D
3. Bütün tərəfləri bərabər olan düzbucaqlıya kvadrat deyilir.( AB=BC=CD=AD)
a) kvadratın bütün bucaqları düz bucaqdır. ( ‹A=‹B=‹C=‹D )
b) kvadratın bütün tərəfləri bərabərdir. .( AB=BC=CD=AD )
c) kvadratın diaqonalları bərabərdir. ( BD=AC )
d) kvadratın diaqonalları qarşılıqlı perpendikulyardır. ( BD┴AC )
e) kvadratın diaqonalları kəsişmə nöqtəsində yarıya bölünür. ( BO=OD=AO=OC )
f) kvadratın diaqonalı onun bucağını yarıya bölür.
a düz xətti AB parçasının orta perpendikulyarıdırsa AvəB-yə a düz xəttinə görə
Simmetrik nöqtələr deyilir. a düz xəttinə simmetriya oxu deyilir.Simmetriya oxunun
nöqtələri bu düz xəttə görə özü ilə simmetrik hesab olunur. A və B nöqtələri
a düz xəttinə nəzərən simmetrikdir.
B
C
O
A
D
M
a
O
N

18.

D
- İstənilən bucağın tənbölənini saxlayan düz xətt bu bucağın simmetriya oxudur.
A
C
O
M
B
N
- Bərabəryanlı üçbucağın oturacağına çəkilmiş medianını özündə saxlayan düz xətt onun simmetriya oxudur.
B
A
C
D
- Bərabərtərəfli üçbucağın 3 simmetriya oxu var.
-Düzbucaqlının tərəfinin orta perpendikulyarı onun simmetriya oxudur.
Düzbucaqlının 2 simmetriya oxu var.

19.

-Rombun diaqonalını saxlayan düz xətt onun simmetriya oxudur.Rombun 2 simmetriya oxu var.
-Kvadratın 4 simmetriya oxu var.
- Çevrənin mərkəzindən keçən istənilən düz xətt onun simmetriya oxudur.
O
·
-O nöqtəsi AB parçasının orta nöqtəsidirsə, A və B-yə O nöqtəsinə nəzərən
Simmetrik nöqtələr deyilir.O nöqtəsi simmetriya mərkəzi adlanır.Simmetriya
mərkəzi özü ilə simmetrik hesab olunur.
B
O
·
A
AO=OB
-Paraleloqramın simmetriya oxu yoxdur. Onun simmetriya mərkəzi var. Paraleloqramın simmetriya mərkəzi onun
diaqonallarının kəsişmə nöqtəsidir.

20.

C
Bucağin tərəflərini kəsən paralel düz xətlər bu bucağın
bir tərəfi üzərində bərabər parçalar ayırırsa, həmin düz xətlər
o biri tərəf üzərində də bərabər parçalar ayırır.
OB=BC olarsa, OA=AD olar.
B
O
D
A
Verilmiş iki düz xətti kəsən paralel düz xətlər onlardan biri üzərində bərabər parçalar ayırırsa, o biri düz xətt
Üzərində də bərabər parçalar ayırır.
Üçbucağın iki tərəfinin orta nöqtəsini birləşdirən parçaya bu üçbucağın orta xətti deyilir.
Üçbucağın 3 orta xətti var.
Üçbucağın orta xətti oturacağa paralel olub onun yarısına bərabərdir.
B
M
A
MN=AC / 2
A
N
C
B
C

21.

Yalnız iki qarşı tərəfi paralel olan dördbucaqlıya trapesiya deyilir. Trapesiyanın paralel tərəflərinə onun oturacaqları,
Paralel olmayan tərəflərinə isə yan tərəfləri deyilir.
C
B
Yan tərəflər; AB və CD
oturacaqlar; BC və AD
D
A
Yan tərəfləri bərabər olan trapesiyaya bərabəryanlı trapesiya deyilir.
Bərabəryanlı trapesiyada oturacağa bitişik bucaqlar bərabərdir.
‹A=‹D və ‹B=‹C olar.
Bərabəryanlı trapesiyanın diaqonalları bərabərdir.BD=AC olar.
B
C
D
A
Yan tərəfi oturacağına perpendikulyar olan trapesiyaya düzbucaqlı
trapesiya deyilir.
Trapesiyanın orta xəttinin diaqonallar arasında qalan hissəsi
oturacaqları fərqinin yarısına bərabərdir. X=(a-b)/2
B
Düzbucaqlı trapesiyada diaqonallar perpendikulyardırsa ; h² = ab olar.
h
A
a
C
O
b
D

22.

B
Trapesiyanın diaqonalları yan tərəfə ┴-dırsa; h a 2 b 2 olar.
2
Bərabəryanlı trapesiyanın kor bucaq təpəsindən oturacağa
çəkilmiş
perpendikulyar böyük oturacağı iki hissəyə bölür ki, onlardan böyüyü
trapesiyanın orta xəttinə bərabərdir.
a
h
D
A
Trapesiyanın yan tərəflərinin ortasını birləşdirən parçaya trapesiyanın
orta xətti deyilir.
Trapesiyanın orta xətti oturacaqlara paralel olub onların cəminin
yarısına bərabərdir. MN=(a+b) / 2 olar.
C
b
a
N
M
b
-Hər bir sadə fiqurun seçilmiş ölçü vahidi ilə ifadə olunmuş müsbət sahəsi var.
-Bərabər üçbucaqların sahələri bərabərdir.
Fiqur daxili ortaq nöqtəsi olmayan sonlu sayda fiqurlardan ibarətdirsə,onun sahəsi bu fiqurların sahələri
cəminə bərabərdir.
-Tərəfi a olan kvadratın sahəsi, a² -na bərabərdir.
B
-Düzbucaqlının sahəsi onun iki qonşu tərəfinin hasilinə bərabərdir.
a
S(ABCD)=ab olar.
-Düzbucaqlı üçbucağın sahəsi onun katetləri hasilinin yarısına bərabərdir.
S(∆)=(ab) / 2 olar.
a
b
A
C
D
b

23.

İxtiyari üçbucağın sahəsi onun tərəfi ilə
bu tərəfə çəkilmiş hündürlüyün hasilinin
yarısına bərabərdir.
S(ABC) = (AC·h) / 2 olar.
B
B
h
h
A
C
C
A
B
Rombun sahəsi onun diaqonallarının hasilinin yarısına bərabərdir.
S(ABCD) = (AC·BD) / 2 olar.
A
O
C
D
Paraleloqramın sahəsi onun tərəfi ilə bu tərəfə çəkilən hündürlüyü hasilinə bərabərdir
B
S(ABCD) = AD·h olar..
h
A
S
S
S
S
C
D

24.

M nöqtəsi BC tərəfi üzərindədirsə alınan üçbucağın
sahəsi paraleloqramın sahəsinin yarısına bərabərdir.
S(AMD) = S(ABCD) / 2 olar.
M
B
A
C
D
M nöqtəsi BC tərəfinin N nöqtəsi CD tərəfinin orta
nöqtəsi olarsa alınan üçbucağın sahəsi paraleloqramın
sahəsinin 8-dən 3-nə bərabərdir.
S(AMN) =⅜ S(ABCD) olar.
B
M
C
N
A
D
Trapesiyanın hər hansı oturacağının nöqtəsindən digər oturacağı saxlayan düz xəttə çəkilən perpendikulyara
bu trapesiyanın hündürlüyü deyilir.
B
C
h
A
Trapesiyanın sahəsi onun oturacaqları cəminin yarısı ilə
hündürlüyünün hasilinə bərabərdir.
Trapesiyanın sahəsi onun orta xətti ilə hündürlüyünün
hasilinə bərabərdir.
S ABCD
D
BC AD
h
2
a
Düzbucaqlı üçbucaqda hipotenuzun kvadratı katetlərin kvadratları cəminə bərabərdir.
c2 a2 b2
c
b

25.

-Düzbucaqlı üçbucaqda hipotenuz üzərində qurulmuş kvadratın sahəsi katetlər üzərində qurulmuş kvadratların
sahələri cəminə bərabərdir.
-Üçbucaqda bir tərəfin kvadratı qalan iki tərəfin kvadratları cəminə bərabərdirsə bu üçbucaq düzbucaqlı üçbucaqdır.
-Üçbucağın sahəsi üçün heron düsturu.
a b c üçbucağın yarım perimetridir.
2
-Düzbucaqlı üçbucağın sahəsi onun katetləri hasilinin yarısına bərabərdir. S 1 ab
a
2
2
-Bərabərtərəfli üçbucağın sahəsi. S 1 a 2 sin 60 və S a 3 olar.
60
2
4
S ( a)( b)( c)
burada,
a
a
Üçbucağın hündürlüyü h=b sinα olduğundan, onun sahəsi iki tərəf və onlar arasındakı bucağın
sinusu hasilinin yarısına bərabərdir.
S
1
ab sin
2
a
α
b
AB
CD
Uzunluqları mütənasib olan parçalara mütənasib parçalar deyilir. AB, CD A1 B1və C1 D1 parçaları üçün A B C D
1 1
1 1
Olarsa deyirlər ki bu parçalar mütənasibdir.
Üçbucağın iki tərəfini onların daxili nöqtələrində kəsib üçüncü tərəfinə paralel olan düz xətt həmin tərəflərdən
onlara mütənasib parçalar ayırır.
B
M
N
BM
BN
BA
BC
A
C

26.

İki düz xətti kəsən üç və daha artıq paralel düz xətt onlar üzərində mütənasib parçalar ayırır.
KL LM KM
k
AB BC
AC
a
C
B
A
AB MN
BC NK
M
N
K
b
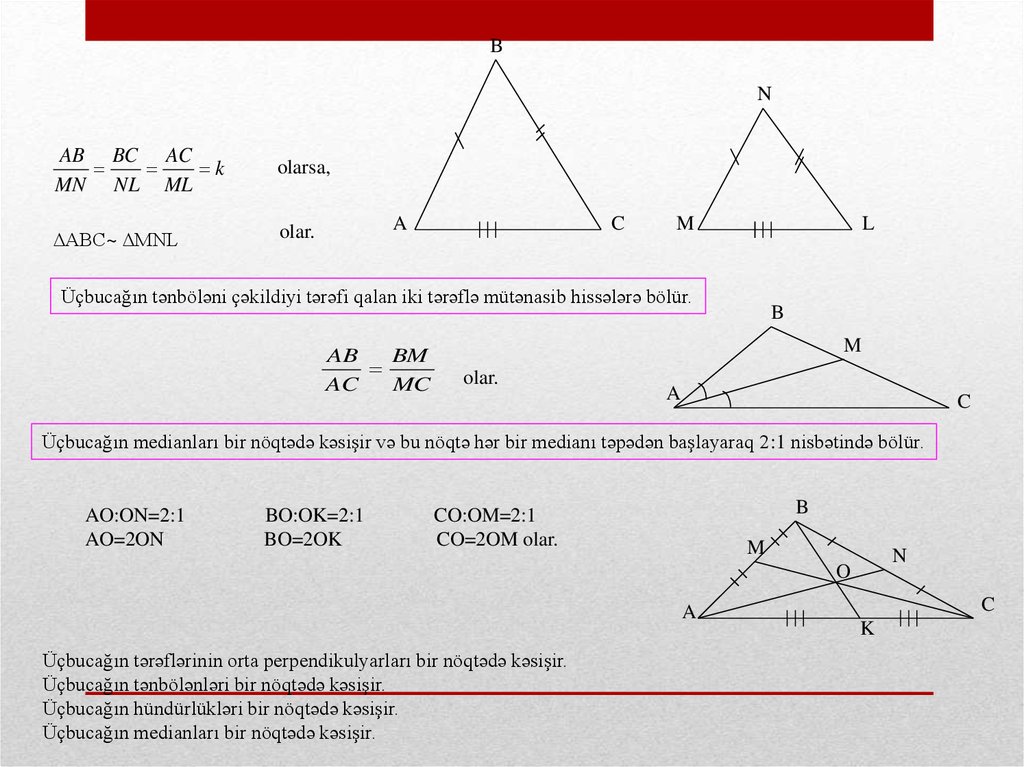
Uyğun bucaqları bərabər olub, uyğun tərəfləri mütənasib olan üçbucaqlara oxşar üçbucaqlar deyilir.
KL LM KM
k
AB BC
AC
L
B
‹A= ‹K, ‹B= ‹L, ‹C= ‹M
A
C
K
Olarsa, onda bu üçbucaqlara oxçar üçbucaqlar deyilir və aşağıdaki kimi işarə olunur:
Bərabər üçbucaqlar k=1 əmsalı ilə bir-birinə oxşardır.
Üçbucağın iki tərəfini onların daxili nöqtələrində kəsib onun üçüncü tərəfinə paralel olan düz xətt, həmin üçbucaqdan
özünə oxşar üçbucaq ayırır.
M

27.

1. Bir üçbucağın iki tərəfi o biri üçbucağın iki tərəfi ilə mütənasib və bu tərəflər arasında bucaqlar bərabərdirsə,
bu üçbucaqlar oxşardır.
B
‹A= ‹M və
AB
AC
MN
ML
∆ABC~ ∆MNL
N
olarsa,
olar.
C
A
M
L
2. Bir ücbucağın iki bucağı, o biri üçbucağın iki bucağına bərabərdirsə, bu üçbucaqlar oxşardır.
B
‹A= ‹M , ‹B= ‹N
∆ABC ~ ∆MNL
N
olarsa,
olar.
A
C
M
L
Nəticə. Bir düzbucaqlı üçbucağın iti bucağı o biri düzbucaqlı üçbucağın iti bucağına bərabərdirsə, onlar oxşardır.
3. Bir üçbucağın üç tərəfi, o biri üçbucağın üç tərəfi ilə mütənasibdirsə, bu üçbucaqlar oxşardır.

28.

B
N
AB BC AC
k
MN NL ML
olarsa,
∆ABC~ ∆MNL
olar.
A
C
M
L
Üçbucağın tənböləni çəkildiyi tərəfi qalan iki tərəflə mütənasib hissələrə bölür.
AB
BM
AC
MC
B
M
olar.
A
C
Üçbucağın medianları bir nöqtədə kəsişir və bu nöqtə hər bir medianı təpədən başlayaraq 2:1 nisbətində bölür.
AO:ON=2:1
AO=2ON
BO:OK=2:1
BO=2OK
B
CO:OM=2:1
CO=2OM olar.
M
N
O
A
Üçbucağın tərəflərinin orta perpendikulyarları bir nöqtədə kəsişir.
Üçbucağın tənbölənləri bir nöqtədə kəsişir.
Üçbucağın hündürlükləri bir nöqtədə kəsişir.
Üçbucağın medianları bir nöqtədə kəsişir.
C
K

29.

Düzbucaqlı üçbucaqda düz bucaq təpəsindən çəkilmiş hündürlük bu üçbucağın katetlərinin hipotenuz üzərində
proyeksiyaları ilə orta mütənasibdir.
Həmin üçbucağın kateti hipotenuz və bu katetin hipotenuz üzərindəki proyeksiyası ilə orta mütənasibdir.
h 2 AD CD
B
A
BC 2 AC CD
h
AB 2 AC AD
D
İti bucaq qarşısındakı katetin hipotenuza nisbətinə bu bucağın
sinusu deyilir və belə içarə olunur: sinα=a / c
İti bucağa bitişik katetin hipotenuza nisbətinə bu bucağın kosinusu
deyilir və belə işarə olunur: cosα=b / c
İti bucağın qarşısındakı katetin bu bucağa bitişik katetə nisbətinə
həmin bucağın tangensi deyilir və belə yazılır: tgα=a / b
İti bucağa bitişik katetin bu bucağın qarşısındakı katetə nisbətinə
həmin bucağın cotangensi deyilir və belə yazılır:ctgα=b / a .
c
a
α
b
C

30.

İti bucağın qiyməti artdıqca həmin bucağın sinusu və tangensi artır və cosinusu və kotangensi isə azalır.
α
o
sinα
0
cosα
1
tgα
0
30
60
2
2
3
2
1
2
2
0
2
2
1
2
0
-
2
2
-1
1
2
3
2
1
135
180
45
90
1
3
--------
-1
0
1
1
0
-1
-------
3
ctgα
------
3
Təpəsi çevrənin mərkəzində olan bucağa mərkəzi bucaq deyilir.
Mərkəzi bucağın dərəcə ölçüsü uyğun qövsün dərəcə ölçüsünə
bərabərdir..
AmB AOB
3
A
O
·
m
B
Əgər qövs yarımçevrədirsə və ya kiçik qövsdürsə, həmin qövsün dərəcə ölçüsü, tərəfləri onun
uclarından keçən mərkəzi bucağın dərəcə ölçüsünə bəraberdir.
Qövs yarımçevrədirsə, onda mərkəzi bucaq 180-yə bərabərdir.
O
·

31.

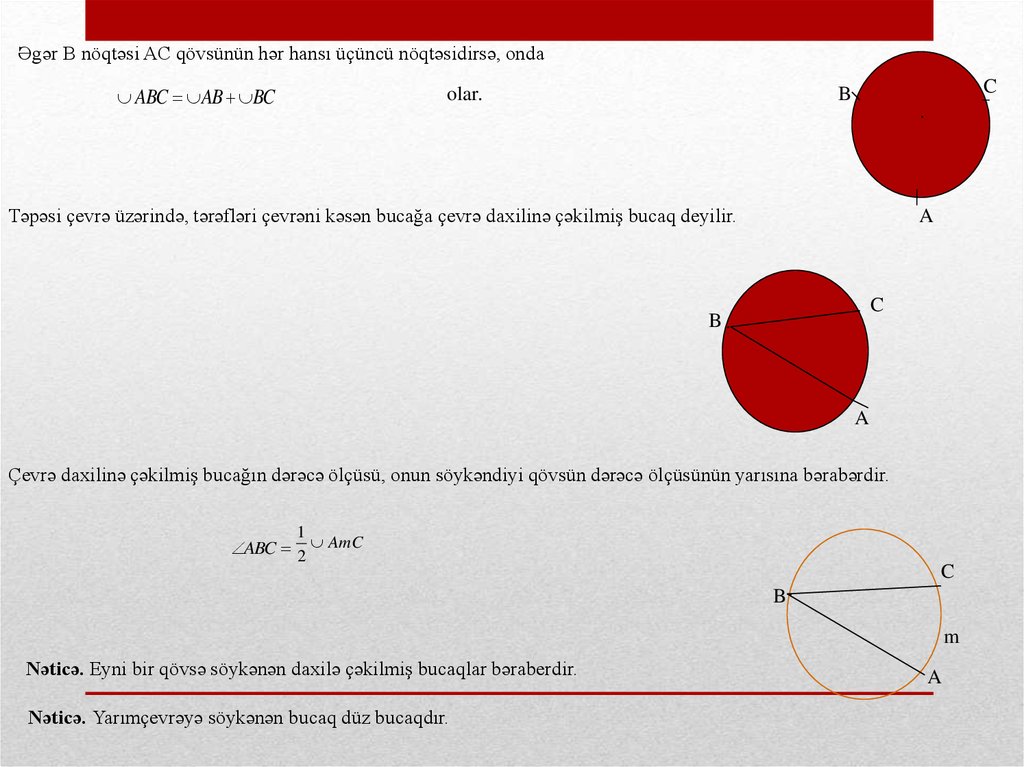
Əgər B nöqtəsi AC qövsünün hər hansı üçüncü nöqtəsidirsə, onda
ABC AB BC
olar.
C
B
·
Təpəsi çevrə üzərində, tərəfləri çevrəni kəsən bucağa çevrə daxilinə çəkilmiş bucaq deyilir.
A
C
B·
A
Çevrə daxilinə çəkilmiş bucağın dərəcə ölçüsü, onun söykəndiyi qövsün dərəcə ölçüsünün yarısına bərabərdir.
1
ABC 2 AmC
C
B·
m
Nəticə. Eyni bir qövsə söykənən daxilə çəkilmiş bucaqlar bəraberdir.
Nəticə. Yarımçevrəyə söykənən bucaq düz bucaqdır.
A

32.

Çevrənin iki vətəri kəsişirsə,kəsişmə nöqtəsinin birinci vətərdən ayırdığı parçaların hasili ikinci vətərdən
ayırdığı parçaların hasilinə bərabərdir.
C
B
M
AM·MB=CM·MD
A
D
P nöqtəsindən çevrəni uyğun olaraq A, B və C, D nöqtələrində kəsən iki düz xətt çəkilərsə,
AP·BP=CP·DP bəraberliyi doğrudur.
D
C
P
A
B
Çoxbucaqlının bütün tərəfləri çevrəyə toxunursa, bu çevrəyə çoxbucaqlının daxilinə çəkilmiş çevrə, çoxbucaqlıya isə
çevrənin xaricinə çəkilmiş çoxbucaqlı deyilir.
N
B
C
·O
A
·O
D
M
P

33.

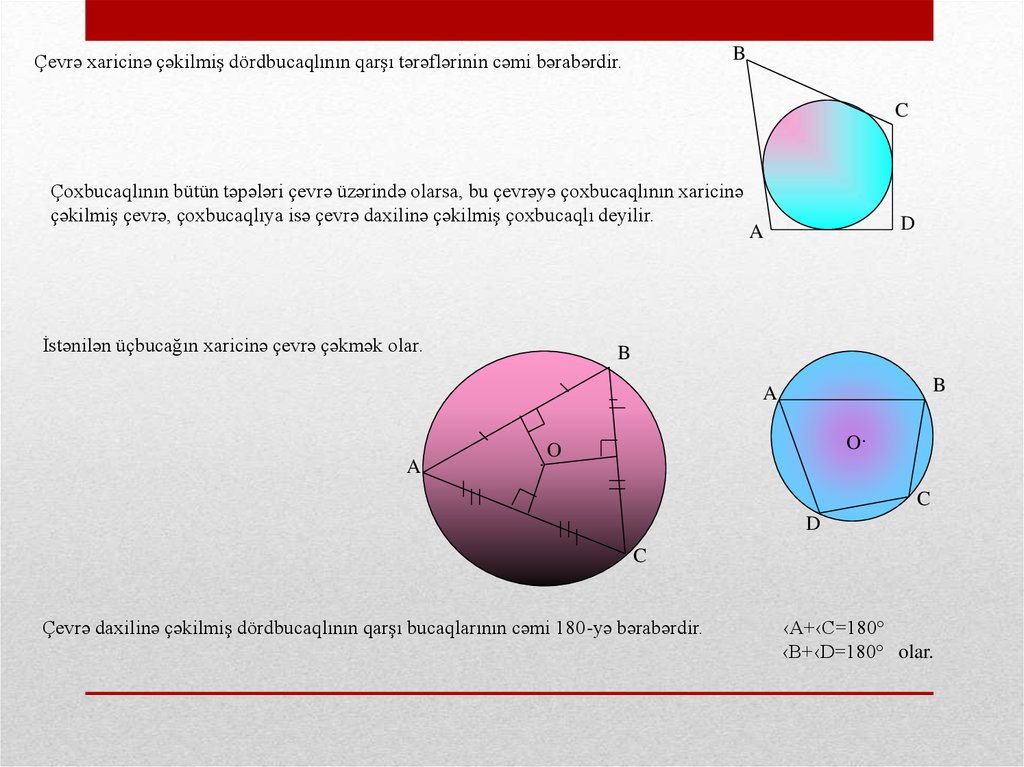
B
Çevrə xaricinə çəkilmiş dördbucaqlının qarşı tərəflərinin cəmi bərabərdir.
C
Çoxbucaqlının bütün təpələri çevrə üzərində olarsa, bu çevrəyə çoxbucaqlının xaricinə
çəkilmiş çevrə, çoxbucaqlıya isə çevrə daxilinə çəkilmiş çoxbucaqlı deyilir.
İstənilən üçbucağın xaricinə çevrə çəkmək olar.
D
A
B
B
A
A
·
O·
O
C
D
C
Çevrə daxilinə çəkilmiş dördbucaqlının qarşı bucaqlarının cəmi 180-yə bərabərdir.
‹A+‹C=180°
‹B+‹D=180° olar.

34.

Fərz edək ki, AB və CD şüaları paraleldir. Yəni pralel düz xətlər üzərindədir.
Əgər bu şüalar, onların başlanğıclarından keçən AC düz xəttinə nəzərən eyni yarımmüstəvidə yerləşirsə onlara eyni
istiqamətli şüalar, müxtəlif yarımmüstəvillərdə yerləşirsə, onlara əks istiqamətli süalar deyilir.
D
A
B
D
A
B
C
C
AB↑↓CD olar.
AB↑↑CD
Başlanğıc və son nöqtələri göstərilmiş parçaya vektor deyilir.
A
B
AB parçasının uzunluğuna AB vektorunun uzunluğu yaxud mütləq qiyməti deyilir və AB kimi işarə olunur.
AB parçasın istiqamətinə isə AB vektorunun istiqaməti deyilir.
Əgər vektorun başlanğıc və son nöqtələri eyni nöqtələrdirsə belə vektora sıfır vektor deyilir və 0 kimi işarə olunur.
AB və CD şüaları eyni istiqamətlidirsə, AB və CD
vektorları eyni istiqamətli vektorlar, AB və CD şüaları əks
istiqamətlidirsə, AB
vektorları əks istiqamətli vektorlar adlanır. Sıfır vektor istənilən vektorla
və
CD
eyni istiqamətlidir. Eyni bir düz xətt üzərində və ya paralel düz xətlər üzərində yerləşən vektorlara kollinear vektorlar
deyilir. Uüunluqları bərabər və istiqamətləri eyni olan iki vektora bərabər vektorlar deyilir.

35.

1) Vektorların toplanmasının üçbucaq qaydası:
a
b
c a b
b
2) Vektorların toplanmasının paraleloqram qaydası:
a
c a b
a
b
3) Vektorların çıxılması:
b
c a b
a
b
c a b
a
a
b

36.

Uzunluqları bərabər əks istiqamətli iki vektora əks vektorlar deyilir
a MN
a a MN NM MM 0
a NM
M
MB BA MA
MA MB BA
4) Vektorların toplanmasının paralelepiped qaydası:
a b c
c
b
a
N

37.

Üzərində hesablama başlanğıcı, ölçü vahidi və müsbət istiqamət seçilmiş düz xəttə ədəd oxu deyilir.
N
-3
-2
O
-1
0
1
2
3
Nöqtənin ədəd oxu üzərindəki vəziyyətini təyin edən ədəddə bu nöqtənin koordinatı deyilir.
Üfüqi düz xəttə absis oxu (OX ilə işarə olunur), şaquli düz xəttə ordinat oxu (OY ilə işarə olunur) deyilir.
Bu iki düz xəttə koordinat oxları deyilir.
Y
II rüb
(-;+)
Müstəvi üzərində koordinat sistemi seçilibsə, ona koordinat müstəvisi deyilir.
III rüb
(-;-)
I rüb
(+;+)
O
IV rüb
(+;-)
Koordinat oxları, müstəvinin bu oxlar üzərində olmayan nöqtələrini dörd çoxluğa bölür. Bu çoxluqların
hər birinə rüb deyilir. Hər bir rübün daxilində nöqtənin koordinatlarının işarəsi dəyişməz qalır.
Absis oxu koordinat müstəvisini iki yarımfəzaya ayırır. Bu oxdan yuxarıda qalan yarımmüstəviyə yuxarı yarımmüstəvi, ondan aşağıda qalan
yarımmüstəviyə aşağı yarımmüstəvi deyilir. Ordinat oxundan sağ tərəfdə qalan yarımmüstəvi sağ yarımmüstəvi , ondan solda qalan
yarımmüstəviyə sol yarımmüstəvi deyəcəyik. Absis oxunun sağ yarımmüstəviyə, ordinat oxunun isə, yuxarı yarımmüstəviyə aid şüalarına
onların müsbət yarımoxları deyilir.
X

38.

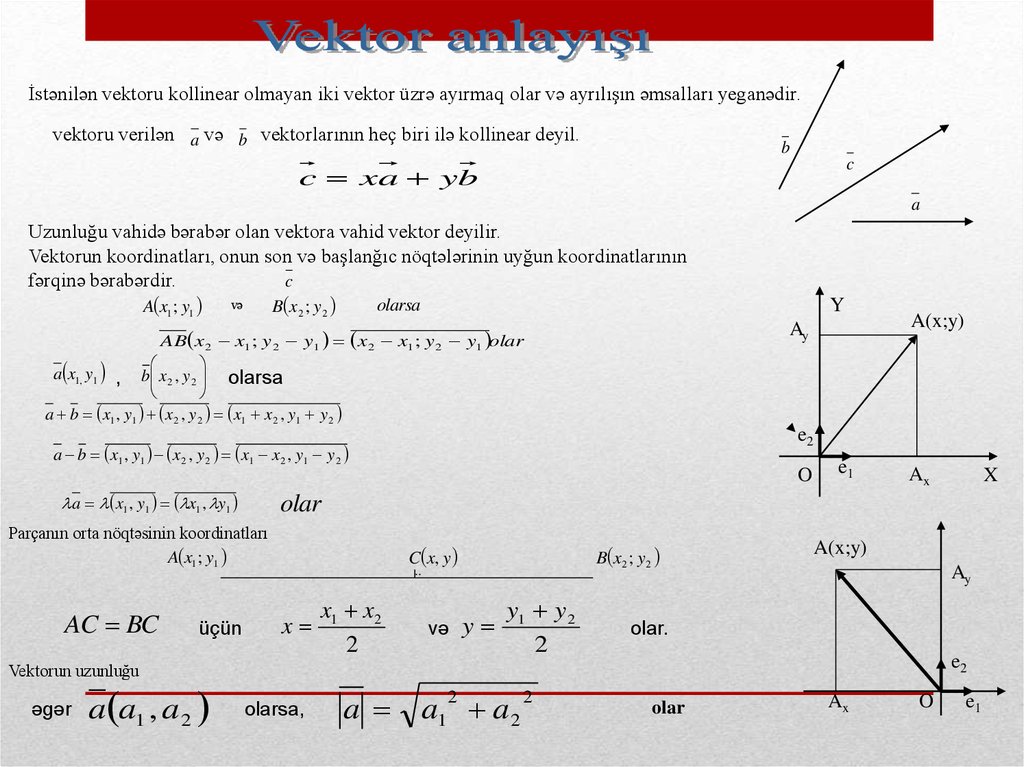
İstənilən vektoru kollinear olmayan iki vektor üzrə ayırmaq olar və ayrılışın əmsalları yeganədir.
vektoru verilən a və b vektorlarının heç biri ilə kollinear deyil.
b
c
c x a yb
a
Uzunluğu vahidə bərabər olan vektora vahid vektor deyilir.
Vektorun koordinatları, onun son və başlanğıc nöqtələrinin uyğun koordinatlarının
fərqinə bərabərdir.
c
A x1 ; y1
B x2 ; y 2
və
Y
olarsa
Ay
AB x 2 x1 ; y 2 y1 x 2 x1 ; y 2 y1 olar
a x1, y1 , b x2 , y 2 olarsa
a b x1 , y1 x 2 , y 2 x1 x 2 , y1 y 2
e2
a b x1 , y1 x 2 , y 2 x1 x 2 , y1 y 2
O
a x1 , y1 x1 , y1
üçün
e1
Ax
C x, y
B x2 ; y 2
..
x
x1 x2
2
və y
y1 y 2
2
A(x;y)
Ay
olar.
e2
Vektorun uzunluğu
əgər
a a1 , a 2
X
olar
Parçanın orta nöqtəsinin koordinatları
A x1 ; y1
AC BC
A(x;y)
olarsa,
a a1 a 2
2
2
olar
Ax
O
e1

39.

Koordinat müstəvisində iki nöqtə arasındakı məsafə
A x1 ; y1
və
B x2 ; y 2
olarsa
AB
x2 x1 2 y2 y1 2
olar
Koordinatları verilmiş ikidəyişənli tənliyin həlli olan nöqtələrin həndəsi yeri F fiqurudursa, bu tənliyə F fiquru deyilir.
Koordinat müstəvisində Mərkəzi M0(a;b) nöqtəsində, radiusu r olan çevrənin tənliyini yazaq. İxtiyari M(x;y) nöqtəsində
M0(a;b) nöqtəsinə qədər məsafə:
y
MM0= x a 2 y b 2 = r
M(x;y)
M 0(a;b)
(x-a)2+(y-b)2=r2
Xüsusi halda, çevrənin mərkəzi koordinat başlanğıcındadırsa, onda çevrənin tənliyi
aşağıdakı kimi olar:
x2+y2=r2
Düz xəttin ümumi tənliyi.
x
O
ax+by+c=0
Koordinat sistemində düz xəttin yerləşməsi.
Düz xəttin ax+by+c=0 tənliyinin bəzi xüsusi şəkillərində bu düz xəttin koordinat oxlarına nəzərən
necə yerləşdiyini aydınlaşdıraq.
y
-c/b
1) a=0, b≠0. Bu halda düz xəttin tənliyini. y= -c / b olar.
O
x

40.

2) b=0, a≠0. Bu halda düz xəttin tənliyi.
y
x= - c / b
3) c=0, a≠0, b≠0. olduqda, düz xəttin tənliyi ax+by=0 şəklində yazılır.
-c/b
a
y x
b
x
O
Düz xətlə çevrənin qarşılıqlı vəziyyətləri.
Müstəvi üzərində radiusu r olan çevrə və hər hansı düz xətt verilmişdir. Çevrənini mərkəzindən verilmiş düz xəttə
y
qədər məsafəni d ilə işarə edək.
r>d olduqda bu düz xətt verilən çevrəni kəsir.
r>d
r
r=d olarsa, sistemin bir həlli var.
y
y
d
r<d
r=d
d
r
d
x
r<d olduqda sistemin həlli yoxdur.
x
r
x

41.

Əgər düz xəttin a1 x b1 y c1 0
həll edə bilərik:
y
a1
c
x 1
b1
b1
tənliyində y dəyişəninin əmsalı b1 0
,
a1
k
b1
və
c1
b
b1
olarsa, tənliyi y dəyişəninə qörə
ilə işarə etsək, y=kx+b tənliyini alarıq.
k əmsalının koordinat müstəvisində düz xəttin vəziyyəti ilə əlaqəsini aydınlaşdıraq.
Fərz edək ki, y=kx+b tənliyi MN düz xəttinin tənliyidir. MN düz xətti üzərində A(x1 ; y1 ) və B( x 2 ; y 2 ) nöqtələrini
qeyd edək (x 2 > x1 ). Bu nöqtələrin koordinatları
y=kx+b tənliyini ödəyir. y1 kx1 b
y2 kx2 b
Bərabərlikləri tərəf-tərəfə çıxsaq,
Beləliklə
tg
y 2 y1
k
x2 x1
y2 y1 k x2 x1
yaxud:
k
y 2 y1
x 2 x1
bərabərliyini alırıq.
alırıq.
Üçbucaöın sahəsi onun iki tərəfi ilə bi tərəflər arasında qalan bucağın sinusu hasilinin yarısına bərabərdir.
B
S
1
AB AC sin
2
A
α
C

42.

Paraleloqramın sahəsi onun iki tərəfi ilə bu tərəflər arasındakı bucaöın sinusu hasilinə bərabərdir.
S a b sin
a
α
b
Sinuslar teoremi
Üçbucağın tərəfləri qarşı bucaqların sinusları ilə mütənasibdir.
γ
a
β
a
b
c
2R
sin sin sin
b
α
c
(burada R üçbucağın xaricinə çəkilmiş çevrənin radiusudur).
Üçbucağın tərəfinin, bu tərəf qarşıcındakı bucağın sinusuna nisbəti həmin üçbucağın xaricinə çəkilmiş çevrənin
diametrinə bərabərdir.
a
b
c
2R
sin sin sin
=d

43.

A
İki vektor arasındakı bucaq.
a
O
B
b
‹AOB-yə
a
və
b
vektorları arasındakı bucaq deyilir.
a
və
b
vektorları eyni istiqamətlidirsə, yaxud bu
vektorlardan biri sıfır vektordursa onlar arasındakı bucaq 0°-yə bərabər hesab edilir.
a
və
b
arasındakı bucaq 90°-yə bərabər olduqda, onlara perpendikulyar vektorlar deyilir və
işarə olunur.
a b
a
İki vektorun skalyar hasili.
b
Iki vektorun uzunluqları ilə onlar arasındakı bucağın kosinusu hasilinə bu vektorların skalyar hasili deyilir.
a b a b cos
Perpendikulyar vektorların skalyar hasili 0-ra bərabərdir.
a b
olarsa ,
a b 0
olar.
kimi

44.

İki vektorun fərqinin skalyar kvadratı bərabərdir: birinci vektorun skalyar kvadratı, pilus ikinci vektorun
skalyar kvadratı, minus bu vektorların skalyar hasilinin iki misli.
a b
2
a a1 ; a 2
və
b b1 ; b2
-Sıfır vektorundan fərqli
2
a b 2a b
vektorlarının skalyar hasili
a a1 ; a 2
və
b b1 ;b2
a1 b1 a2 b2 0
Sıfır vektordan fərqli
2
a a1 ; a 2
və
a b a1 b1 a 2 b2
düsturu ilə ifadə olunur.
Vektorları onda və yalnız onda, perpendikulyardır ki,
olsun.
b b1 ;b2
vektorları arasındakı bucağın kosinusu aşağıdakı düsturla ifadə olunur;
cos
a1 b1 a 2 b2
a1 a 2 b1 b2
2
-Vektorun hər bir koordinatı, bu vektorun uyğun koordinat vektoru ilə skalyar hasilinə bərabərdir.
Yəni ixtiyari
a a1 ; a 2
vektoru üçün:
a1 a e1
a 2 a e2
olar.
2
2
2

45.

Skalyar hasilin xassələri
İxtiyari a, b, c vektorları və x ədədi üçün aşağıdakı münasibətlər doğrudur.
və a 0 olduqda a 2 >0.
(yerdəyişmə qanunu)
a b b a
2
1. a 0
2.
(paylama qanunu)
3. (a b) c a c b c
4. ( x a) b x a b
(qruplaşdırma qanunu)
Kosinuslar teoremi
Üçbucağın hər hansı tərəfinin kvadratı bərabərdir: qalan iki tərəfin kvadratları cəmi, minus bu tərəflərlə
onlar arasındakı bucağın kosinusu hasilinin iki misli.
β
a2=b2+c2-2cb cosα
b2=a2+c2-2ac
a
cosβ
c2=a2+b2-2ab cosγ
γ
Üşbucağın sahəsini hesablamaq üçün Heron düsturu:
Üçbucağın xaricinə və daxilinə çəkilmiş çevrələrin radiusları üçün düsturlar.
S=
p( p a)( p b)( p c)
c
(burada a, b, c üçbucağın tərəfləri, p isə yarımperimetrdir) yəni
α
b
p=
a b c
2
Üçbucağın xaricinə və daxilinə çəkilmiç çevrələrin radiusları uyğun olaraq R və r olarsa:
abc
2S
R= 4 S
, r=
olar.
a b c
-Üçbucağı təyin edən hər hansı üç əsas elementi məlum olduqda onun digər əsas elementlərinin tapılmasına
üçbucağın həlli deyilir.

46.

Ox simmetriyası və mərkəzi simmetriya çevrilmələri uyğun nöqtələr arasındakı məsafəni saxlayır.Yəni bu çevrilmələrdə
M nöqtəsi M1 nöqtəsinə, N nöqtəsi N1 nöqtəsinə çevrilirsə, M1N1=MN olur.
N
M1
M
A
M1
N
O
N1
B
M
N1
a
Ox simmetriyası
Mərkəzi simmetriya
-O nöqtəsinə görə F fiqurunun nöqtələrinə simmetrik olan bütün nöqtələrdən ibarət olanF 1 fiquruna, O nöqtəsinə görə
F fiquruna simmetrik fiqur deyilir.
-a düz xəttinə görə F fiqurunun nöqtələrinə simmetrik olan bütün nöqtələrdən ibarət olan F 1 fiquruna, bu düz xəttə görə
F fiquruna simmetrik fiqur deyilir.
-Müstəvinin özünə çevrilməsində nöqtələr arasındakı məsafələr saxlanarsa ona hərəkət deyilir.
-Düz xətt üzərində olan nöqtələr, hərəkət zamanı düz xətt üzərində olan nöqtələrə çevrilir və onların qarşılıqlı
yerləşməsi nizamı saxlanılır.
-Hərəkətdə düz xətt düz xəttə, şüa şüaya, parça özünə bərabər parçaya çevrilir.
-Hərəkətdə bucaq özünə bərabər bucağa çevrilir
-Tutaq ki,
a verilmiş vektordur.Müstəvinin özünə çevrilməsində ixtiyari M nöqtəsi və onun çevrildiyi M
MM 1 a
bərabərliyi ödənərsə, bu çevrilməyə
a
vektoru qədər paralel köçürmə deyilir.
1
nöqtəsi üçün

47.

M1
N1
a
-Paralel köçürmə hərəkətdir.
-Koordinat müstəvisində paralel köçürmə bir cüt ədədlə təyin olunan düsturla verilir:
M
N
x‘=x+a
y‘=y+b
Dönmə.
Fərz edək ki , O nöqtəsi və α bucağı verilmişdir.Müstəvinin hərəkəti zamanı O nöqtəsindən çıxan ixtiyari şüa eyni
istiqamətdə α bucağı qədər dönərsə , bu hərəkətə müstəvinin O nöqtəsi ətrafında α bucağı qədər dönməsi deyilir.
O nöqtəsinə dönmə mərkəzi , α bucağına dönmə bucağı deyilir.
A
-Dönmə hərəkətdir.
O
30°
C2
A1
Hərəkət çevirməsi ilə F fiquru F1fiquruna çevrilirsə onlara bərabər fiqurlar deyilir.
a
A
C
B
A1
B2
C1
B1
b

48.

Müstəvinin özünə çevrilməsində istənilən iki nöqtə arasındakı məsafə eyni ədəd dəfə dəyişərsə , ona oxşarlıq
çevirməsi deyilir.
Yəni oxşarlıq çeriməsi ilə müstəvinin ixtiyari X və Y nöqtələri , uyğun olaraq , X1 və Y1 nöqtələrinə çevrilərsə, onda :
X1Y1=k·XY
k>0 ədədi oxşarlıq əmsalı adlanır. Qeyd edək ki , hərəkət k=1 əmsallı oxşarlıq çevirməsidir.
Homotetiya.
Tutaq ki , O verilmiş nöqtə , k>0 verilmiş ədəddir. Müstəvinin özünə çevrilməsində ixtiyari X nöqtəsi və onun
çevrildiyi X1 nöqtəsi üçün : OX1=k·OX olarsa bu çevrilməyə homotetiya deyilir.
O nöqtəsinə homotetiya mərkəzi , k ədədinə homotetiya əmsalı , X1 nöqtəsinə isə X-ə homotetik nöqtə deyilir.
X1 nöqtəsi X nöqtəsi ilə homotetikdirsə deyirlər ki , homotetiyada X nöqtəsi X1 nöqtəsinə çevrilir.
F fiqurunun nöqtələrinə homotetik bütün nöqtələrdən ibarət F 1 fiquruna F-ə homotetik fiqur deyilir.
-k əmsallı homotetiya k əmsallı oxşarlıq çevirməsidir.
Oxşarlıq çevirməsində bir düz xətt üzərində olan üç A , B , C nöqtələri , uyğun olaraq , bir düz xətt üzərində olan
A1 ,, B1 , C1 nöqtələrinə çevrilir. B nöqtəsi A və C nöqtələri arasındadırsa , B1 nöqtəsi də A1 və C1 nöqtələri arasındadır.
-Oxşarlıq çevirməsində düz xətt düz xəttə , şüa şüaya , parça parçaya çevrilir.
-Oxşarlıq çevirməsində şüalar arasındakı bucaq saxlanılır.
FİQURLARIN OXŞARLIĞI.
-Oxşarlıq çevirməsi ilə F1 fiquru F2 fiquruna çevrilirsə, onlara oxşar fiqurlar deyilir.
-F1 fiquru F2 fiquruna , F2 fiquru isə F3 fiquruna oxşardırsa , F1 fiquru F3 fiquruna oxşardır və onun oxşarlıq əmsalı
əvvəlki oxşarlıq əmsallarının hasilinə bərabərdir.
-Uyğun bucaqları bərabər və uyğun tərəfləri mütənasib olan çoxbucaqlılar oxşardır.
-Oxşar çoxbucaqlıların perimetrləri nisbəti, onların uyğun tərəflərinin nisbətinə, yəni oxşarlıq əmsalına bərabərdir.
P1: P2 =k

49.

Oxşar çoxbucaqlıların sahələri nisbəti oxşarlıq əmsalının kvadratına bərabərdir.
S1:S2=k2
Oxşar çoxbucaqlıların sahələri nisbəti ,onların uyğun xətti ölçülərinin kvadratları nisbətinə bərabərdir.
ABCDEF ... ~
A1 B1C1 D1 E1 F1
AB 2
… olarsa,
A1 B1
2
BC 2
B1C1
2
CD 2
C1 D1
2
... k 2 olar .
Bütün tərəfləri və bucaqları bərabər olan qabarıq çoxbucaqlıya düzgün çobucaqlıya deyilir.
İstənilən düzgün çoxbucaqlının daxilinə və xaricinə çevrə çəkmək olar
Təpəsi düzgün çoxbucaqlının mərkəzində olan, tərəfləri isə onun qonşu təpələrindən keçən bucağa düzgün
çoxbucaqlının mərkəzi bucağı deyilir.
Düzgün çoxbucaqlının xaricinə və daxilinə çəkilmiş çevrələrin radiusları üçün düsturlar
Tərəfi an olan düzgün çoxbucaqlının xaricinə çəkilmiş çevrənin R və daxilinə çəkilmiş çevrənin r radiuslarını tapaq.
R=
an
180 0
2 sin
n
və
r=
an
180 0
2tg
n
olar.

50.

1. Bərabərtərəfli üçbucaqlar üçün:
2. Düzgün dördbucaqlı (kvadrat) üçün
3. Düzgün dördbucaqlı üçün
a3
r= 2tg 60 0
a3
R=
2 sin 60 0
R=
a6
R=
2 sin 30 0
a4
2 sin 45 0
r=
a4
2tg 450
a6
r= 2tg30 0
Çevrənin uzunluğu və dairənin sahəsi
Çevrəniin daxilinə çəkilmiş düzgün çoxbucaqlıların tərəflərinin sayını qeyri-məhdud artırdıqda, onların perimetrlərinin
limitinə çəvrənin uzunluğu deyilir.
C=2 R
Dairəni hüdudlandıran çevrənin daxilinə çəkilmiş düzgün çoxbucaqlıların tərəfləri sayını qeyri-məhdud artırdıqda onların
sahələrinin limitinə dairənin sahəsi deyilir.
Çoxbucaqlının daxilinə və xaricinə çəkilmiş çevrələrlə hüdudlanmış dairələrə,
uyğun olaraq, həmin çoxbucaqlının daxilinə və xaricinə çəkilmiş dairələr,
çoxbucqalıya isə, uyğun olaraq, dairə xaricinə və daxilinə çəkilmiş
çoxbucaqlı deyilir.
h
OO·
·
R

51.

Dairənin sahəsi
S= R
2
d 2
S=
4
R-dairənin sahəsi, d-diametridir.
Dairə sektorunun sahəsi
Dairənin , onu hududlandıran çevrənin hər hansı qövsü və bu qövsün uclarından çəkilmiş radiuslarla məhdud
A
edilmiş hissəsinə dairə sektoru deyilir.
R 2
S=
360
O
M
N
B
Dairənin, onu hüdudlandıran çevrənin hər hansı qövsü və bu qövsün uclarını birləşdirən vətəri ilə məhdud edilmiş
hissəsinə dairə seqmenti deyilir.
S
A
R 2
360
S AOB
S
R 2
360
S AOB
A
B
B
O
O·
α › 180° olarsa,
α ‹ 180° olarsa.

52.

Stereometriya aksiomları
1) Düz xəttin üzərində olan nöqtələr və onun üzərində olmayan nöqtələr var.
2) İki nöqtədən bir və yalnız bir düz xətt keçir.
3) Düz xəttin ixtiyari üç nöqtəsindən biri və yalnız biri qalan ikisi arasında yerləşir.
4) Düz xəttin ixtiyari A nöqtəsi bu düz xəttin qalan nöqtələrini a.ağıdakı şərtləri ödəyən iki çoxluğa ayırır:eyni
çoxluğa aid olan iki nöqtə A nöqtəsinin bir tərəfində yerləşir, müxtəlif çoxluqlara aid iki nöqtə A nöqtəsinin
müxtəlif tərəflərində yerləşir.
5) Uzunluq vahidi seçməklə hər bir parçanın uzunluğunu ölçmək olar, yəni onun uzunluğunu müsbət ədədlə ifadə
etmək olar.
6) Parçanın uzunluğu , onun hər hansı daxili nöqtəsi ilə bölündüyü parçaların uzunluqları cəminə bərabərdir.
7) Şüanın başlanğıcından , uzunluğu verilmiş , bir və yalnız bir parça ayırmaq olar.
8) Hər bir bucağın sıfırdan böyük müəyyən dərəcə ölçüsü var. Açıq bucaq 180°-yə bərabərdir.
9) Bucağın dərəcə ölçüsü , onun daxili şüası ilə bölündüyü bucaqların dərəcə ölçüləri cəminə bərabərdir.
10)Üçbucağın təpələrindən keçməyən düz xətt onun bir tərəfini kəsirsə , onda həmin düz xətt digər iki tərəfdən yalnız
birini kəsər.
11) İstənilən şüadan başlayaraq verilmiş yarımmüstəvidə , bir tərəfi həmin şüa olan və dərəcə ölçüsü 180°-dən kiçik
bir və yalnız bir bucaq qurmaq olar.
12) Bir üçbucağın iki tərəfi və onlar arasındakı bucaq , uyğun olaraq , o biri üçbucağın iki tərəfi və onlar arasındakı
bucağa bərabərdirsə , bu üçbucaqlar bərabərdir.
13) Düz xəttin üzərində olmayan nöqtədən bu düz xəttə ən çoxu bir paralel düz xətt çəkmək olar.
14) Hər bir sadə fiqurun seçilmiş ölçü vahidi ilə ifadə olunan müsbət sahəsi var.
15) Bərabər üçbucaqların sahələri bərabərdir.

53.

16) Əgər sadə fiqur , ortaq daxili nöqtəsi olmayan sonlu sayda sadə fiqurlardan ibarətdirsə , bu fiqurun sahəsi onun
hissələrinin sahələri cəminə bərabərdir.
17) Ttərəfi a olan kvadratın sahəsi S=a2 olar.
O
kub
silindr
Kürə
tetraedr
Belə fiqurlar fəza fiqurları adlanır
Həndəsənin fəza fiqurlarını öyrənən bölməsi stereometriya(yunan sözü-stereos fəza, metreo ölçürəm) adlanır.
Stereometriyada baxılan bütün nöqtələr çoxluğuna fəza deyilir.
Stereometriyada üç anlayış: nöqtə, düz xətt və müstəvi tərifsiz qəbul olunub.
Fəzada düz xətlər və müstəvilər var. Hər bir düz xəttə və hər bir müstəviyə aid olan və aid olmayan nöqtələr var.
Bir düz xəttin üzərində olmayan üç nöqtədən bir və yalnəz bir müstəvi keçir.
Planimetriyanın bütün aksiomları və teoremləri fəzanın hər bir müstəvisində doğrudur.
β
İki müxtəlif müstəvinin ortaq nöqtəsi varsa, onlar bu nöqtədən keçən düz xətt boyunca kəsişirlər.
Fəzada hər bir müstəvi fəzanın bu müstəviyə aid olmayan nöqtələrini aşağıdakı şərt ödəyən iki
çoxluğa ayırır:
a) Eyni çoxluğa aid olan ixtiyari iki nöqtəni birləşdirən parça bu müstəvini kəsmir
b) Müxtəlif çoxluqlara aid olan istənilən iki nöqtəni birləşdirən parça müstəvini kəsir.
α
a

54.

Düz xətlə müstəvinin iki ortaq nöqtəsi varsa, bu düz xətt müstəvi üzərindədir.
Düz xətt və ona aid olamayan nöqtədən bir və yalnəz bir müstəvi keçir.
İki kəsişən düz xətdən bir və yalnız bir müstəvi keçir.
Fəzada yalnız bir ortaq nöqtəsi olan iki düz xəttə kəsişən düz xətlər deyilir.
Bir müstəvi üzərində olan və kəsişməyən iki düz xəttə paralel müstəvilər deyilir.
Fəzada düx xətt xaricində götürülmüş nöqtədən həmin düz xəttə paralel bir və yalnız bir düz xətt keçir.
Eyni bir düz xəttə paralel olan iki düz xətt paraleldir.
Ortaq nöqtəsi olmayan düz xətt və müstəviyə paralel düz xətt və müstəvi deyilir.
Müstəvi üzərində olmayan düz xətt, müstəvi üzərindəki hər hansı bir düz xəttə paraleldirsə,
onda bu müstəvinin özünə də paraleldir.
Bir müstəvi ikinci müstəviyə paralel olan düz xətdən keçib və onu kəsərsə, alınan kəsişmə xətti verilən düz xəttə
paralel olar.
Bir müstəvi üzərində olmayan iki düz xəttə çarpaz düz xətlər deyilir.
İki düz xətdən biri ikincidən hər hansı bir müstəvini ikinci düz xəttə aid
olmayan nöqtədə kəsərsə, onda bu düz xətlər çarpazdır.
N
N
M
a
M
a
Uyğun tərəfləri eyniistiqamətli olan iki bucaq bərabərdir.
Uyğun tərəfləri paralel olan bucaqlar ya bərabərdir, ya da onların cəmi 180 0-dir

55.

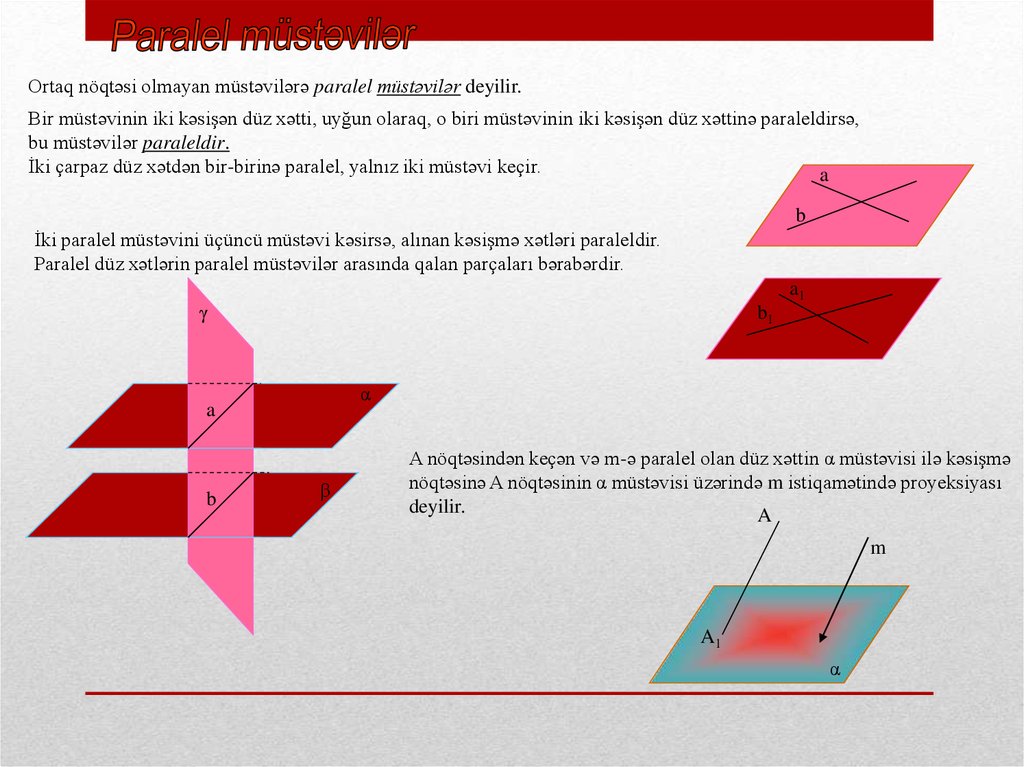
Ortaq nöqtəsi olmayan müstəvilərə paralel müstəvilər deyilir.
Bir müstəvinin iki kəsişən düz xətti, uyğun olaraq, o biri müstəvinin iki kəsişən düz xəttinə paraleldirsə,
bu müstəvilər paraleldir.
İki çarpaz düz xətdən bir-birinə paralel, yalnız iki müstəvi keçir.
a
b
İki paralel müstəvini üçüncü müstəvi kəsirsə, alınan kəsişmə xətləri paraleldir.
Paralel düz xətlərin paralel müstəvilər arasında qalan parçaları bərabərdir.
a1
γ
b1
α
a
b
β
A nöqtəsindən keçən və m-ə paralel olan düz xəttin α müstəvisi ilə kəsişmə
nöqtəsinə A nöqtəsinin α müstəvisi üzərində m istiqamətində proyeksiyası
deyilir.
A
m
A1
α

56.

Düz xəttin müstəvi üzərində proyeksiyası düz xətdir. Xüsusi halda bu nöqtə də ola bilər.
Paralel düz xətlərin müstəvi üzərində proyeksiyaları paralel düz xətlərdir. Xüsusi halda bu proyeksiyalar üst-üstə düşə bilər
və ya nöqtələr ola bilər
İki paralel parçanın müstəvi üzərində proyeksiyaları nisbəti bu parçaların nisbətinə bərabərdir.
Müstəvi fiqur proyeksiya müstəvisinə paralel olduqda, onun proyeksiyası özünə bərabərdir.
Nöqtə parçanı hansı nisbətdə bölürsə, onun proyeksiyası da parçanın proyeksiyasını həmin nisbətdə bölür.
Fəzada perpendikulyar düz xətlər
Paralel düz xətlərdən birinə perpendikulyar olan düz xətt onların hər birinə perpendikulyardır.
Müstəvi üzərindəki hər bir düz xəttə perpendikulyar olan düz xəttə, müstəviyə perpendikulyar düz xətt,
müstəviyə isə düz xəttə perpendikulyar müstəvi deyilir.
Müstəvini kəsən düz xətt, onun üzərindəki iki kəsişən düz xəttə perpendikulyardırsa, müstəvinin özünə də
perpendikulyardır.
c
Fəzanın ixtiyari nöqtəsindən verilmiş müstəviyə perpendikulyar bir və yalnız
bir düz xətt keçirmək olar.
Paralel müstəvilərdən birinə perpendikulyar olan düz xətt,
o birinə də perpendikulyardır.
a
O
b
Perpendikulyar və mail . Düz xətt və müstəvi arasındakı bucaq.
Paralel proyeksiyada istiqamət proyeksiya müstəvisinə paralel olmayan düz xəttdir. Bu düz xətt xüsusi halda həmin
müstəviyə perpendikulyar da ola bilər. İstiqaməti proyeksiya müstəvisinə perpendikulyar olan paralel proyeksiyaya
ortoqonal proyeksiya deyilir.
Qeyd: Bundan sonra “proyeksiya” dedikdə “ortoqonal proyeksiya” başa düşəcəyik.
Şəkildə ortoqonal proyeksiyada A,B,C nöqtələrinin A1,, B1 , C1 proyeksiyaları göstərilmişdir.

57.

A
B
C
a
α
B1
C1
A1
Şəkildə AB parçasının müxtəlif vəziyyətlərinin proyeksiyaları göstərilmişdir.
B
B
A
A1
α
A
B1
α
A nöqtəsindən α müstəvisinə perpendikulyar düz xətt çəkək.
Bu düz xəttin α müstəvisi ilə kəsişmə nöqtəsi A1 olsun. AA1
parçasına A nöqtəsindən α müstəvisinə çəkilmiş perpendikulyar deyilir.
A1 nöqtəsinə perpendikulyarın müstəvi üzərindəki oturacağı deyilir.
A nöqtəsi ilə α müstəvisinin qalan nöqtələrini birləşdirən parçalara
mail deyilir. Mailin müstəvi üzərindəki uc nöqtəsinə onun oturacağı
deyilir. Mailin otiracağı ilə perpendikulyarın oturacağını birləşdirən
parçaya mailin proyeksiyası deyilir.
B1
A
Perpendikulyar
A1
mail
proyeksiya
M

58.

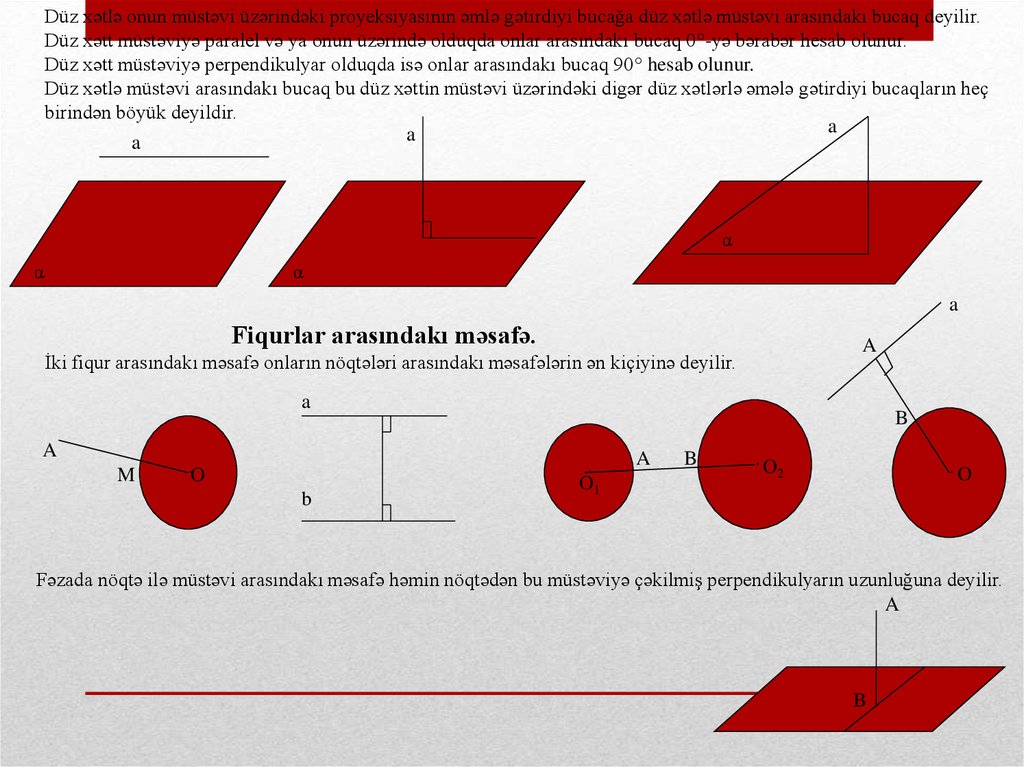
Düz xətlə onun müstəvi üzərindəki proyeksiyasının əmlə gətirdiyi bucağa düz xətlə müstəvi arasındakı bucaq deyilir.
Düz xətt müstəviyə paralel və ya onun üzərində olduqda onlar arasındakı bucaq 0°-yə bərabər hesab olunur.
Düz xətt müstəviyə perpendikulyar olduqda isə onlar arasındakı bucaq 90° hesab olunur.
Düz xətlə müstəvi arasındakı bucaq bu düz xəttin müstəvi üzərindəki digər düz xətlərlə əmələ gətirdiyi bucaqların heç
birindən böyük deyildir.
a
a
a
α
α
α
a
Fiqurlar arasındakı məsafə.
A
İki fiqur arasındakı məsafə onların nöqtələri arasındakı məsafələrin ən kiçiyinə deyilir.
a
A
M
.O
b
B
.
O1
A
B
.O
.O
2
Fəzada nöqtə ilə müstəvi arasındakı məsafə həmin nöqtədən bu müstəviyə çəkilmiş perpendikulyarın uzunluğuna deyilir.
A
B

59.

-Ortaq nöqtəsi olan fiqurlar arasındakı məsafə “sıfra” bərabər hesab olunur.
-Paralel düz xətt və müstəvi arasındakı məsafə düz xəttin ixtiyari nöqtəsindən bu müstəviyə çəkilmiş perpendikulyarın
uzunluğuna bərabərdir.
A
B
-İki paralel müstəvi arasındakı məsafə bu müstəvilərdən birinin ixtiyari nöqtəsindən o birinə çəkilmiş perpendikulyarın
uzunluğuna bərabərdir.
A
B
-İki çarpaz düz xəttə perpendikulyar və onları kəsən bir və yalnız bir düz xətt vardır.
-Çarpaz düz xətlərin ortaq perpendikulyarının uzunluğuna bu çarpaz düz xətlər arsındakı məsafə deyilir.
-İki çarpaz düz xətt arasındakı məsafə bu çarpaz düz xətlərdən keçən və bir-birinə paralel olan müstəvilər arasındakı
məsafəyə bərabərdir.
Üç perpendikulyar teoremi.
Müstəvi üzərində olan düz xətt , mailin bu müstəvi üzərindəki proyeksiyasına perpendikulyardırsa , bu mailin özünə də
perpendikulyardır.Tərsinə: Müstəvi üzərində olan düz xətt mailə perpendikulyardırsa , mailin bu müstəvi üzərindəki
proyeksiyasına da perpendikulyardır.
a

60.

a┴AB olarsa , a┴CB olar.
və tərsinə a┴CB olarsa, a┴AB olar.
A
aa
C
B
-Sərhədləri eyni olan iki yarımmüstəvidən ibarət fiqura ikiüzlü bucaq deyilir. Yarımmüstəvilərə ikiüzlü bucağın üzləri ,
onların ortaq sərhəddinə isə ikiüzlü bucağın tili deyilir.
a
üz
til
üz
üz
-İkiüzlü bucağın tilinə perpendikulyar olan müstəvi ilə kəsişməsindən alınan bucağa ikiüzlü bucağın xətti bucağı deyilir.
-İkiüzlü bucağın xətti bucağının qiymətinə ikiüzlü bucağın
qiyməti deyilir.
-İkiüzlü bucağın qiyməti 0°-dən 180°-yə qədər olur.
-İki müstəvinin kəsişməsindən alınan ikiüzlü bucaq 90° olduqda,
müstəvilərə perpendikulyar müstəvilər deyilir.
-Perpendikulyar olmayan iki müstəvinin kəsişməsindən alınan iküzlü
bucaqların qiymətcə kiçiyinə bu müstəvilər arasındakı bucaq deyilir.
-Paralel müstəvilər arasındakı bucaq 0° qəbul olunur.

61.

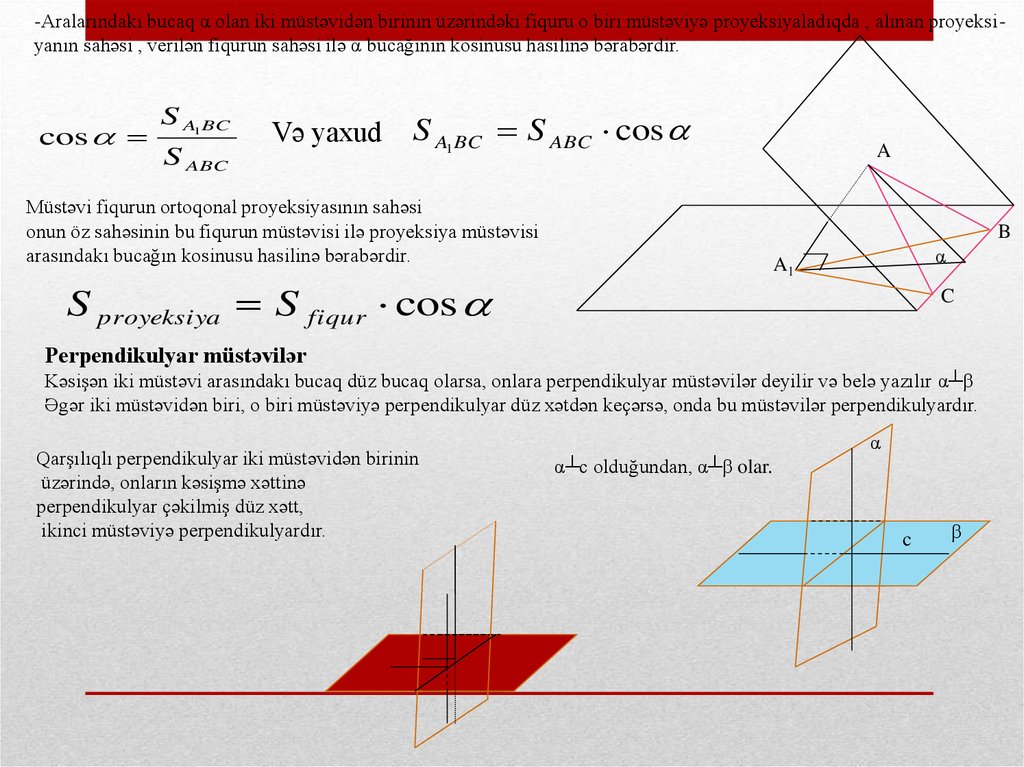
-Aralarındakı bucaq α olan iki müstəvidən birinin üzərindəki fiquru o biri müstəviyə proyeksiyaladıqda , alınan proyeksiyanın sahəsi , verilən fiqurun sahəsi ilə α bucağının kosinusu hasilinə bərabərdir.
cos
S A1BC
S ABC
Və yaxud
S A1BC S ABC cos
Müstəvi fiqurun ortoqonal proyeksiyasının sahəsi
onun öz sahəsinin bu fiqurun müstəvisi ilə proyeksiya müstəvisi
arasındakı bucağın kosinusu hasilinə bərabərdir.
A
B
α
A1
S proyeksiya S fiqur cos
C
Perpendikulyar müstəvilər
Kəsişən iki müstəvi arasındakı bucaq düz bucaq olarsa, onlara perpendikulyar müstəvilər deyilir və belə yazılır α┴β
Əgər iki müstəvidən biri, o biri müstəviyə perpendikulyar düz xətdən keçərsə, onda bu müstəvilər perpendikulyardır.
Qarşılıqlı perpendikulyar iki müstəvidən birinin
üzərində, onların kəsişmə xəttinə
perpendikulyar çəkilmiş düz xətt,
ikinci müstəviyə perpendikulyardır.
α
α┴c olduğundan, α┴β olar.
c
β

62.

Üçüzlü bucaq.
Ortaq S təpəsi olan və bir müstəvi üzərində olmayan (a1a2) , (a2a3) və (a3a1) bucaqlarının əmələ gətirdiyi fiqura üçüzlü
ucaq deyilir.
S
Üçüzlü bucağın hər bir müstəvi bucağı onun qalan
müstəvi bucaqlarının cəmindən kiçikdir.
Üçüzlü bucağın hər bir müstəvi bucağı o biri müstəvi
bucaqların fərqindən böyükdür.
a1
a3
a2
Ortaq S təpəsi olan və ortaq tərəfli bucaqları bir müstəvi üzərində olmayan (a 1a2) , (a2a3) , (a3a4) ... (ana1) müstəvi
bucaqlarının əmələ gətirdiyi fiqura çoxüzlü bucaq deyilir.
S
Çoxüzlü bucağın bütün müstəvi bucaqlarının cəmi 360°-dən
kiçikdir
a1
a2
a3
a4
a5
Səthi sonlu sayda müstəvi çoxbucaqlılardan ibarət olan cismə çoxüzlü deyilir.
Çoxüzlünün səthini təşkil edən müstəvi çoxbucaqlılara çoxüzlünün üzləri deyilir.Çoxbucaqlıların tərəflərinə
çoxüzlünün tilləri , təpələrinə isə çoxüzlünün təpələri deyilir.

63.

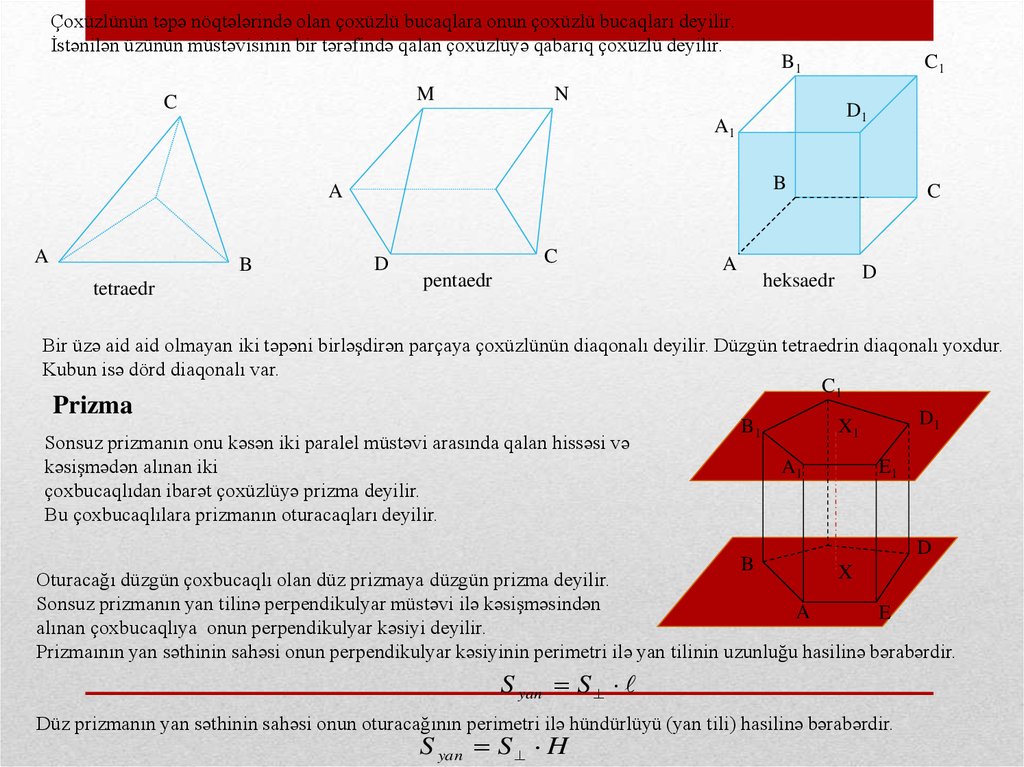
Çoxüzlünün təpə nöqtələrində olan çoxüzlü bucaqlara onun çoxüzlü bucaqları deyilir.
İstənilən üzünün müstəvisinin bir tərəfində qalan çoxüzlüyə qabarıq çoxüzlü deyilir.
M
C
N
D1
A1
B
A
A
B
tetraedr
C1
B1
D
C
pentaedr
A
C
D
heksaedr
Bir üzə aid aid olmayan iki təpəni birləşdirən parçaya çoxüzlünün diaqonalı deyilir. Düzgün tetraedrin diaqonalı yoxdur.
Kubun isə dörd diaqonalı var.
C1
Prizma
Sonsuz prizmanın onu kəsən iki paralel müstəvi arasında qalan hissəsi və
kəsişmədən alınan iki
çoxbucaqlıdan ibarət çoxüzlüyə prizma deyilir.
Bu çoxbucaqlılara prizmanın oturacaqları deyilir.
B1
D1
X1
A1
E1
B
D
X
Oturacağı düzgün çoxbucaqlı olan düz prizmaya düzgün prizma deyilir.
Sonsuz prizmanın yan tilinə perpendikulyar müstəvi ilə kəsişməsindən
A
E
alınan çoxbucaqlıya onun perpendikulyar kəsiyi deyilir.
Prizmaının yan səthinin sahəsi onun perpendikulyar kəsiyinin perimetri ilə yan tilinin uzunluğu hasilinə bərabərdir.
S yan S
Düz prizmanın yan səthinin sahəsi onun oturacağının perimetri ilə hündürlüyü (yan tili) hasilinə bərabərdir.
S yan S H

64.

Tam səthi tapmaq üçün yan səthin sahəsinə oturacaqların sahələrini
Əlavə etmək lazımdır.
B1
C1
Stam=Syan+2Sot
A1
D1
Paralelepiped
O
O
Oturacağı paraleloqram olan prizmaya paralelepiped deyilir.
Paralelepipedin qarşı üzləri paralel və bərabərdir.
Paralelepipedin diaqonalları bir nöqtədə kəsişir və bu nöqtədə yarı bölünür.
A1O=OC
və
B
C
B1O=OD
A
D
Oturacağı düzbucaqlı olan düz paralelepipedə düzbucaqlı paralelepiped deyilir.
Düzbucaqlı paralelepipedin bütün üzləri düzbucaqlıdır. Onun 12 tili var. Bir təpədən çıxan tillərinə onun ölçüləri
deyilir. Bu
Ölçülər en (a) , uzunluq (b) və hündürlük (c vəya h) adlanır.
Düzbucaqlı paralelepipedin tillərindəki bütün ikiüzlü bucaqlar düz ikiüzlü bucaqlar və təpələrindəki ikiüzlü bucaqların
müstəvi bucaqları düz bucaqlardır. Onun bütün tillərinin uzunluqları cəmi: L =4(a+b+c)
Yan səthinin sahəsi :
Syan=2(ac+bc)
Tam səthinin sahəsi:
Stam=2(ab+ac+bc)
Diaqonalı:
d2=a2+b2+c2
Həcmi:
V=abc və ya V=Sot.h
Düzbucaqlı paralelepipedin diaqonalları bir nöqtədə kəsişir və həmin nöqtədə yarıya bölünür.
Düzbucaqlı paralelepipedin diaqonalının kvadratı onun bir təpədən çıxan tillərinin kvadratları cəminə brabərdir.
Ölçüləri bərabər olan düzbucaqlı paralelepipedə kub (heksaedr) deyilir. Kub üçün L=12a
Syan=4a2
S =6a2

65.

Piramida
Bir çoxüzlü bucaq götürək və onun bütün tillərini kəsən müstəvi keçirək. Onda çoxüzlü bucaöın S təpəsinin aid olduğu
Yarımfəzada SABCDEF çoxüzlüsü alınır.Bu çoxüzlünün bir üzü ABCDEF çoxbucaqlısı (çoxüzlü bucaqla müstəvinin
kəsişməsi) , qalan üzləri isə bir təpəsi S olan ortaq təpəli üçbucaqlardır: ASB , BSC , ... ,FSA.Belə çoxüzlülər piramida
adlanır.
Bir üzü hər hansı çoxbucaqlı , qalan üzləri ortaq təpəli üçbucaqlar olan çoxüzlüyə piramida deyilir.
Ortaq təpəli üçbucaqlara piramidanın yan üzləri , onların birləşməsinə piramidanın yan səthi , çoxbucaqlıya piramidanın oturacağı , bütün yan üzlərin ortaq nöqtəsinə piramidanın təpəsi , yan üzlərin ortaq tərəflərinə piramidanın yan
tilləri , təpədən oturacaq müstəvisinə çəkilmiş perpendikulyara isə piramidanın hündürlüyü deyilir.
Piramida oturacağındakı çoxbucaqlının adı ilə adlandırılır. Üçbucaqlı , dördbucaqlı , ... , n – bucaqlı piramida.
Yan üzdə təpədən oturacağın tərəfinə çəkilmiş hündürlüyə apofem deyilir.
təpə S
SM apofem-dir
hündürlük
Oturacağı düzgün çoxbucaqlı və hündürlüyünü oturacağı
bu çoxbucaqlının mərkəzi olan piramidaya
düzgün piramida deyilir.
yan üz
til
B
C
D
A
O
oturacaq M
F
E

66.

Tetraedrin təpəsi ilə qarşı üzün medianlarının kəsişmə nöqtəsini birləşdirən parçaya onun medianı deyilir.
Düzgün piramidanın yan səthinin sahəsi oturacağın perimetri ilə apofemi hasilinin yarısına bəraberdir.
S
Sortoqonal=Syan·cosφ
A1
φ
K
Kəsik piramida
A2
A3
Piramidanın oturcağına paralel və onu kəsən müstəvi:
1)Piramidanın yan tillərini və hündürlüyünü mütənasib parçalara bölür;
2)kəsikdə alınan çoxbucaqlı oturacağa oxşardır və oxşarlıq əmsalı onların
təpədən olan məsafələri nisbətinə bərabərdir;
3)kəsiyin və oturacağın sahələri nisbəti oxşarlıq əmsalının kvadratına, yaxud onların təpədən olan məsafələrinin
kvadratları nisbətinə bərabərdir;
Piramidanın oturacağına paralel və onu kəsən müstəvi ilə oturacağı arasında qalan çoxüzlüyə kəsik piramida deyilir.
Düzgün piramidanı oturacağına paralel müstəvi ilə kəsdikdə alınan kəsik piramidaya düzgün kəsik piramida deyilir.

67.

B1
a
C1
O1
L
h isə piramidanın apofemidir
Syan= P1 P2 ·h
2
C
B
O
Düzgün kəsik piramidanın yan səthinin sahəsi onun oturacaqlarının
M
perimetrləri cəminin yarısı ilə apofemi hasilinə bərabərdir.
Kəsik piramidanın tam səthinin sahəsini tapmaq üçün onun üzlərinin sahələrini
toplamaq lazımdır.
Stam=Salt+Süst+Syan
E
d
A
Düzgün kəsik piramidanın xassələrini yada salaq;
1) Yan tilləri bərabərdir;
2) Yan üzləri bərabərdir ;
3) Apofemləri bərabərdir ;
4) Oturacağı tərəfindəki ikiüzlü bucaqlar bərabərdir ;
5) Yan tildəki ikiüzlü bucaqlar bərabərdir ;
6) Ox üzərindəki nöqtə hər oturacağın təpələrindən bərabər məsafədədir ;
7) Düzgün kəsik piramidada L yan til, R alt oturacağın, R1 üst oturacağın xaricinə çəkilmiş çevrənin radiusları,
H isə hündürlük olarsa,
L2=(R-R1)2+H2
olar.
Kəsik piramidada bir üz üzərində olmayan iki yan tilindən keçən müstəvi ilə kəsiyinə diaqonal kəsiyi dyilir.

68.

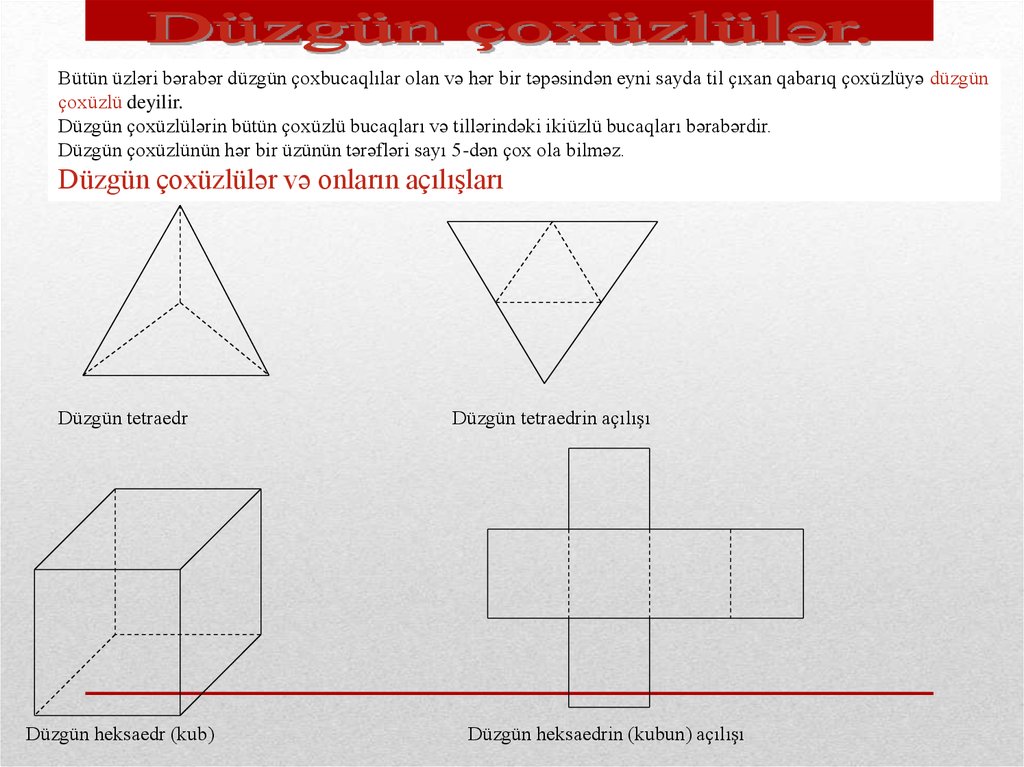
Bütün üzləri bərabər düzgün çoxbucaqlılar olan və hər bir təpəsindən eyni sayda til çıxan qabarıq çoxüzlüyə düzgün
çoxüzlü deyilir.
Düzgün çoxüzlülərin bütün çoxüzlü bucaqları və tillərindəki ikiüzlü bucaqları bərabərdir.
Düzgün çoxüzlünün hər bir üzünün tərəfləri sayı 5-dən çox ola bilməz.
Düzgün çoxüzlülər və onların açılışları
Düzgün tetraedr
Düzgün heksaedr (kub)
Düzgün tetraedrin açılışı
Düzgün heksaedrin (kubun) açılışı

69.

Düzgün oktaedr
Düzgün ikosaedr
Düzgün oktaedrin açılışı
Düzgün ikosaedrin açılışı

70.

71.

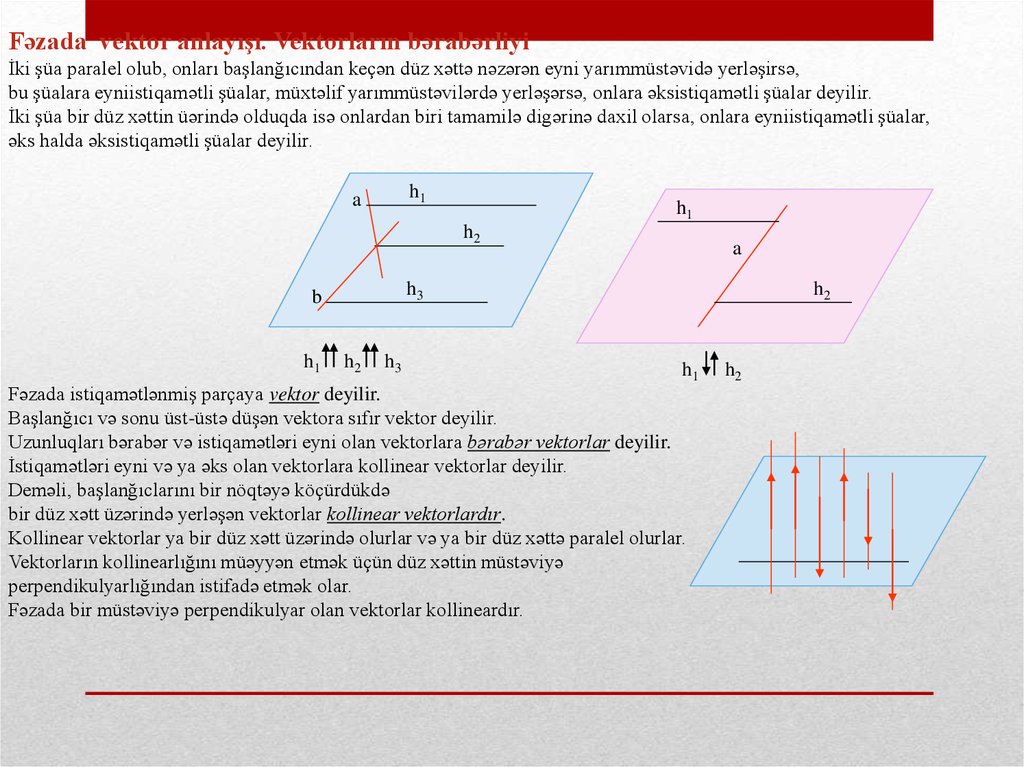
Fəzada vektor anlayışı. Vektorların bərabərliyi
İki şüa paralel olub, onları başlanğıcından keçən düz xəttə nəzərən eyni yarımmüstəvidə yerləşirsə,
bu şüalara eyniistiqamətli şüalar, müxtəlif yarımmüstəvilərdə yerləşərsə, onlara əksistiqamətli şüalar deyilir.
İki şüa bir düz xəttin üərində olduqda isə onlardan biri tamamilə digərinə daxil olarsa, onlara eyniistiqamətli şüalar,
əks halda əksistiqamətli şüalar deyilir.
h1
a
h1
h2
h3
b
h1
a
h2
h3
h2
h1
Fəzada istiqamətlənmiş parçaya vektor deyilir.
Başlanğıcı və sonu üst-üstə düşən vektora sıfır vektor deyilir.
Uzunluqları bərabər və istiqamətləri eyni olan vektorlara bərabər vektorlar deyilir.
İstiqamətləri eyni və ya əks olan vektorlara kollinear vektorlar deyilir.
Deməli, başlanğıclarını bir nöqtəyə köçürdükdə
bir düz xətt üzərində yerləşən vektorlar kollinear vektorlardır.
Kollinear vektorlar ya bir düz xətt üzərində olurlar və ya bir düz xəttə paralel olurlar.
Vektorların kollinearlığını müəyyən etmək üçün düz xəttin müstəviyə
perpendikulyarlığından istifadə etmək olar.
Fəzada bir müstəviyə perpendikulyar olan vektorlar kollineardır.
h2

72.

a vektorunun sonunda b vektorunu ayıraq.
a vektorunun başlanğıcı ilə b vektorunun sonunu birləşdirən vektora a və b vektorlarının cəmi deyilir. c a b
Vektorların toplanmasının üçbucaq qaydası deyilir.
və yazılır.
a
İstiqamətləri əks və modulları bərabər olan vektorlara əks vektorlar deyilir.
b
a
a və b vektorlarının fərqi elə c vektoruna deyilir ki,
onu b vektoru ilə topladıqda a vektoru alınsın.
Tərəfləri a və b vektorları olan paraleloqramın bir diaqonalı a b
O biri diaqonalı a b bərabərdir.
a b
a b
-a
a b
b
Vektorun ədədə vurulması
Sıfır olmayan a vektorunun sıfırdan fərqli m ədədinə hasili
a
elə vektora deyilir ki, bu vektorun uzunluğu m a bərabərdir.
m>0 olduqda a vektoru ilə eyniistiqamətli, m<0 olduqada isə a vektoru ilə əksistiqamətlidir.
Sıfır ədədi ilə istənilən vektorun hasili sıfır vektor qəbul olunmuşdur.
a 0 və b vektorları kollineardırsa, onda elə yeganə k ədədi var ki, b k a və tərsinə, a və b vektorları üçün b k a
bərabərliyi ödənirsə, onda onlar kollineardırlar.
Bir müstəviyə paralel və ya bir müstəvi üzərində olan vektorlara komplanar vektorlar deyilir.
a , b və c komplanar vektorlar, a və b isə kollinear olmayan vektorlar olarsa, c vektorunu c x a y b
şəklində yeganə qaydada gostərmək olar.
İstənilən x və y ədələri üçün a , b və x a y b vektorları komplanardır.
Fəzada istənilən d vektorunu komplanar olmayan üç b , a və c vektorları üzrə ayırmaq olar və bu ayrılış yeganədir:
d x a y b z c

73.

İxtiyari O nöqtəsi götürək və bu nöqtədən bir-birinə cüt-cüt
perpendikulyar olan üç düz xətt keçirək.Bu düz xətləri uyğun
olaraq , Ox , Oy və Oz , onlardan keçən müstəviləri isə xOy ,xOz və
yOz adlandıraq.O nöqtəsini başlanğıc qəbul edək və düz xətlər
üzərində istiqamətlər seçərək onları koordinat düz xəttinə çevirək.
Bu qayda ilə yaradılmış sistemə düzbucaqlı koordinat sistemi deyilir.
Koordinat başlanğıcının koordinatları—O(0,0,0)
Absis oxu üzərində olan nöqtələrin koordinatları—(x,0,0)
Ordinat oxu üzərində olan nöqtələrin koordinatları—(0,y,0)
Aplikat oxu üzərində olan nöqtələrin koordinatları—(0,0,z)
(xy) müstəvisində olan nöqtənin koordinatları—(x,y,0)
(yz) müstəvisində olan nöqtənin koordinatları—(0,y,z)
(xz) müstəvisində olan nöqtənin koordinatları—(x,0,z) olar.
z
yz
xz
y
o
xy
x
Vektorun koordinatları
Oxyz kordinat fəzası götürək. Koordinat başlanğıcından çıxan OM vektoruna radius- vektor deyilir.
Vektorun uc nöqtəsinin koordinatlarına OM vektorunun koordinatları deyilir.M(x 0,y0,z0) olduqda OM x , y , z
0
0
0
kimi yazılır. Ox , Oy və Oz koordinat oxlarının müsbət istiqaməti üzrə yönələn , koordinat başlanğıcından çıxan və
Uzunluğu vahidə bərabər olan e1 1,0,0 , e2 0,1,0 , e3 0,0,1 vektorlarını götürək.
Koordinat başlanğıcından çıxan, koordinat oxlarının müsbət istiqaməti üzrə yönələn və uzunluğu vahidə bərabər olan
e1 , e2 , e3 vektorlarına bazis vektorlar, onların üçlüyünə isə fəzanın bazisi deyilir.

74.

OA ( x1 , y1 , z1 )
Və
OB ( x2 , y2 , z 2 ) vektorlarının cəminin koordinatları onların uyğun koordinatları cəminə bərabər-
dir. OC OA OB ( x x , y y , z z )
1
2
1
2 1
2
a ( x, y , z )
və k ıxtiyari ədəd olarsa,
k a (kx, ky, kz) . Yəni vektoru ədədə vurmaq üçün onun koordinatlar-
ını həmin ədədə vurmaq lazımdır.
Parçanın orta nöqtəsinin koordinarları
A(x1,y1,z1) , B(x2,y2,z2) və C(x,y,z) nöqtələri üçün C nöqtəsi AB parçasının orta nöqtəsidirsə,
x
x1 x2
2
,
y
y1 y 2 ,
2
z
z1 z 2 olar.
2
İki nöqtə arasındakı məsafə.Vektorun uzunluğu.
A(x1,y1,z1) və B(x2,y2,z2) nöqtələri arasındakı məsafə aşağıdakı düsturla hesablanır.
AB
x2 x1 2 y2 y1 2 z2 z1 2
Müstəvi üzərində olduğu kimi fəza koordinat sistemində də iki vektorun skalyar hasili onların uyğun koordinatları
hasilinin cəminə bərabərdir.
Sıfır olmayan iki vektorun skalyar hasili yalnız sıfra bərabər olduqda , onlar qarşılıqlı perpendikulyardır.
Müstəvinin tənliyi
Fəzanın hər bir müstəvisi üçdəyişənli birdərəcəli tənliklə təyin olunur.Həmçinin, hər bir üçdəyişənli xətti tənlik fəzada
bir müstəviyə uyğundur. Müstəvinin ümumi tənliyi aşağıdakı kimidir.
ax+by+cz+d=0
1)
2)
3)
4)
5)
a=b=d=0 olarsa, z=0 olar. Bu (xy) müstəvisinin tənliyidir.
a=b=0 olasa, cz+d=0, z=-d/c . Bu (xy) müstəvisinə paralel və applikatı z=-d/c olan müstəvinin tənliyidir.
a=c=d=0 olarsa, y=0 olar. Bu (xz) müstəvisinin tənliyidir.
a=c=0 olarsa, by+d=0, y=-d/b .Bu (xz) müstəvisinə paralel və ordinatı y=-d/b olan müstəvinin tənliyidir.
b=c=d=0 olarsa,x=0 olar. Bu (yz) müstəvisinin tənliyidir.

75.

6) b=c=0 olarsa, ax+d=0 , x=-d/a . Bu (yz) müstəvisinə paralel olan və absisi x=-d/a olan müstəvinin tənliyidir.
z
3
Z=3
y
0
-1
Z=0
Z=-1
x