Похожие презентации:
Нарощення та дисконтування грошових сум
1. Тема 1. Нарощення та дисконтування грошових сум
2. Методика складних відсотків
Формула нарощування за методикою складнихвідсотків має вигляд
(9)
Величину
називають множником
нарощування складних відсотків.
3.
Операцію багаторазового дисконтування заметодикою складних відсотків виконують так
(9)
Наприклад, якщо певна сума через три роки
оцінюється як 3 993 грн при річній ставці дохідності
10%, то теперішня (дисконтована) вартість цих
грошей становить
PV = 3 993 / (1 + 0.1)3 = 3 993 / 1.331 = 3000.0 грн.
4.
5.
6. Номінальна та ефективна ставка складних відсотків
7. Визначення терміну кредиту та величини відсоткової ставки
8.
9.
10.
11. Врахування податків та інфляції
12.
13.
14.
15.
16.
17. Фінансова еквівалентність
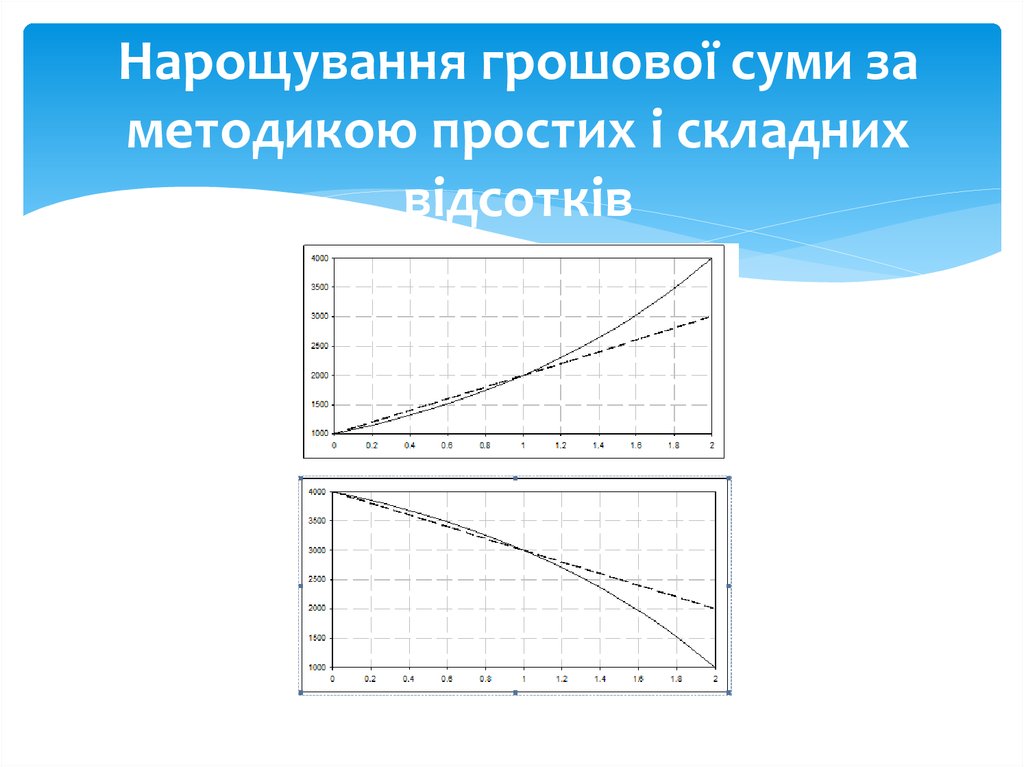
18. Нарощування грошової суми за методикою простих і складних відсотків
19. Визначення еквівалентної ставки дохідності при утриманні комісійних
20.
21. Застосування програмного забезпечення
При виконанні фінансових розрахунків зручновикористовувати електронні таблиці MS Excel. При цьому
слід знати позначення основних фінансових функцій.
БС (Ставка, Кпер, Плт, Пс, Тип) – майбутня вартість FV;
ПС (Ставка, Кпер, Плт, Бс, Тип) – теперішня вартість PV;
СТАВКА (Кпер, Плт, Пс, Бс, Тип) – ставка дохідності r;
КПЕР (Ставка, Плт, Пс, Бс, Тип) – кількість періодів n;




















 Финансы
Финансы








