Графы. Информация и информационные процессы

1. Графы

2. Графы

Информация и информационные процессы, 10 класс
2
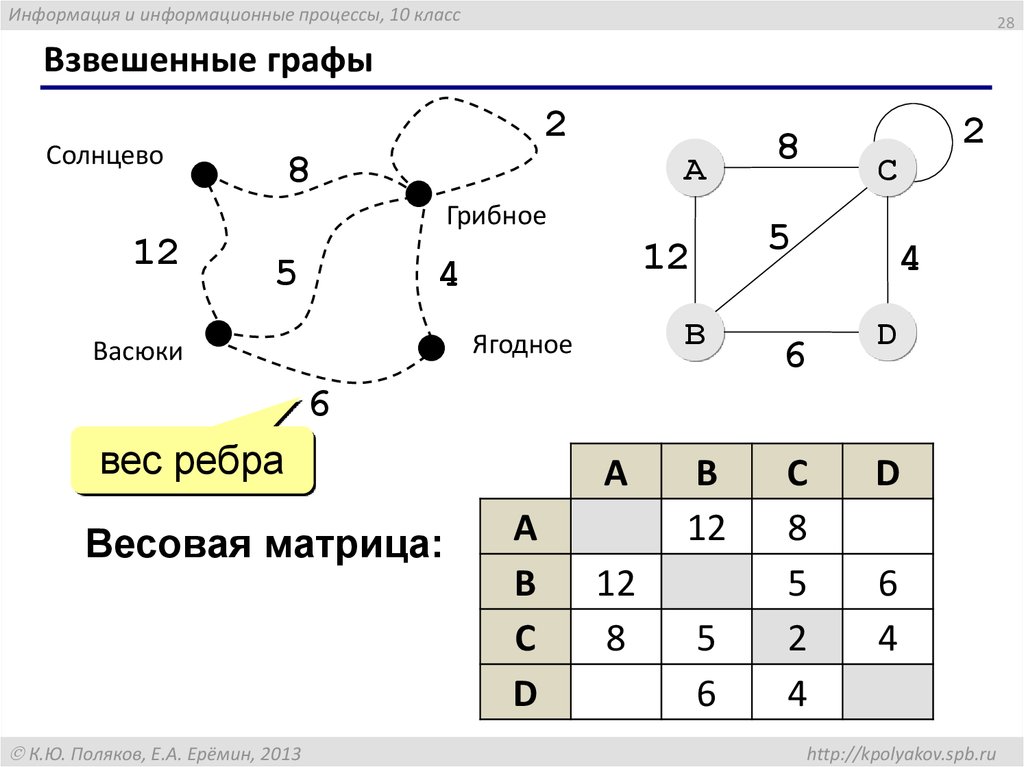
Графы
«От посёлка Васюки три дороги идут в
посёлки Солнцево, Грибное и Ягодное. Между
Солнцевым и Грибным и между Грибным и
Ягодным также есть дороги. Кроме того,
есть дорога, которая идет из Грибного в лес
и возвращается обратно в Грибное».
?
К.Ю. Поляков, Е.А. Ерёмин, 2013
Как структурировать?
http://kpolyakov.spb.ru

3. Графы

Информация и информационные процессы, 10 класс
3
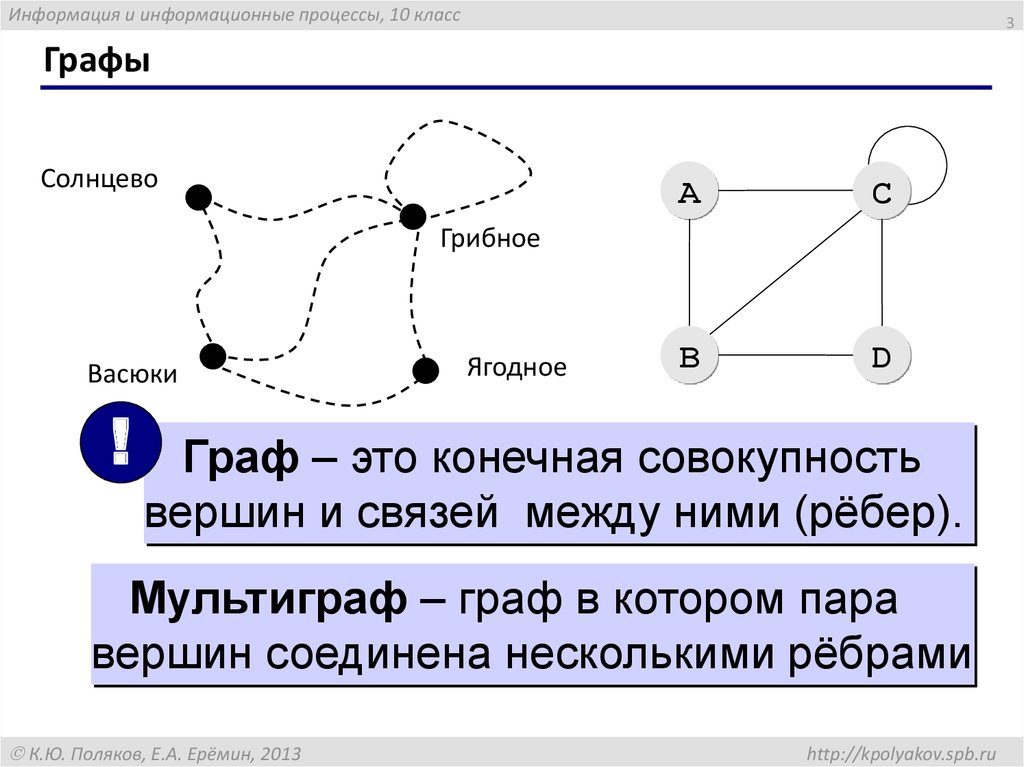
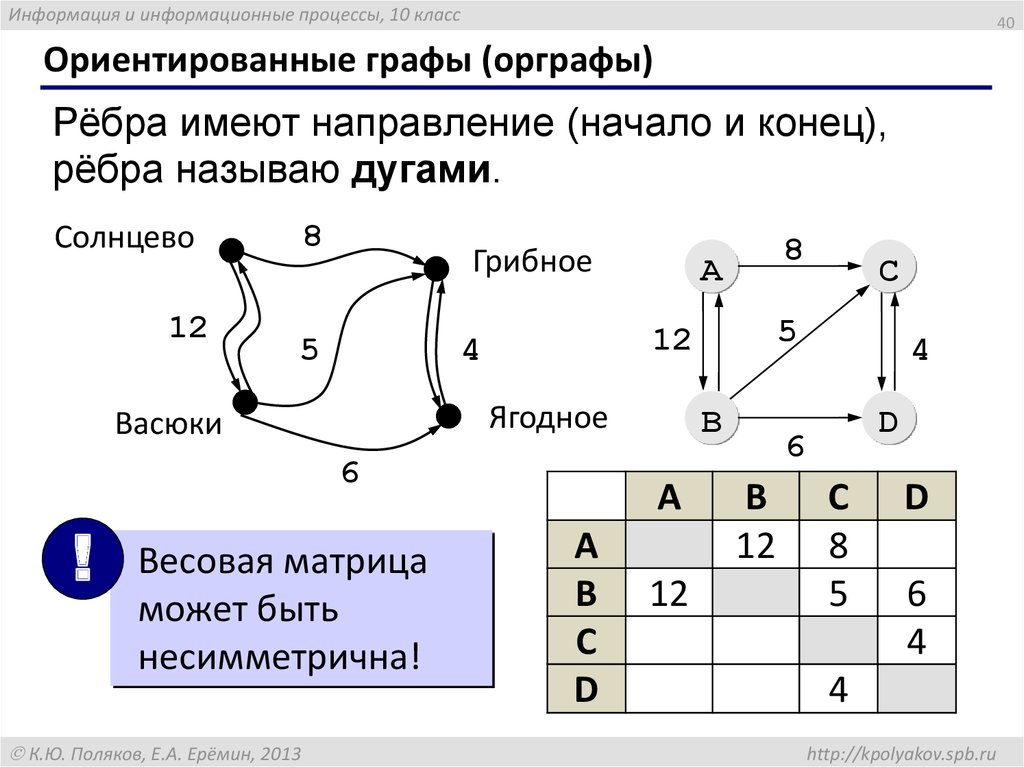
Графы
Солнцево
A
C
B
D
Грибное
Васюки
!
Ягодное
Граф – это конечная совокупность
вершин и связей между ними (рёбер).
Мультиграф – граф в котором пара
вершин соединена несколькими рёбрами
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

4.

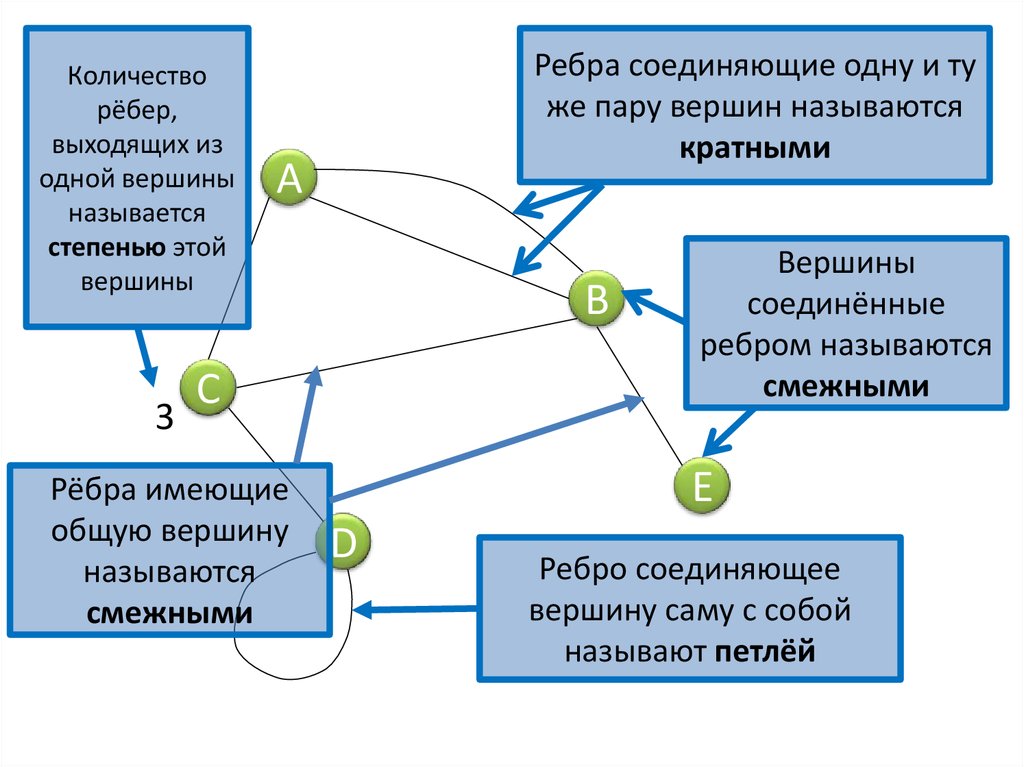
Количество
рёбер,
выходящих из
одной вершины
называется
степенью этой
вершины
3
Ребра соединяющие одну и ту
же пару вершин называются
кратными
А
B
C
Рёбра имеющие
общую вершину
называются
смежными
Вершины
соединённые
ребром называются
смежными
E
D
Ребро соединяющее
вершину саму с собой
называют петлёй

5.

Теорема о сумме степеней вершин
графа
для неориентированного графа
Сумма степеней всех вершин графа (или
мультиграфа без петель) — равна
удвоенному числу рёбер
1. Если взять вершины, вообще не связанные друг с другом,
то сумма степеней этих вершин равна нулю.
2. Прибавляя любое ребро, которое связывает две
вершины, увеличиваем сумму всех степеней на 2
единицы.
3. Таким образом, сумма всех степеней вершин четна и
равна удвоенному количеству рёбер.

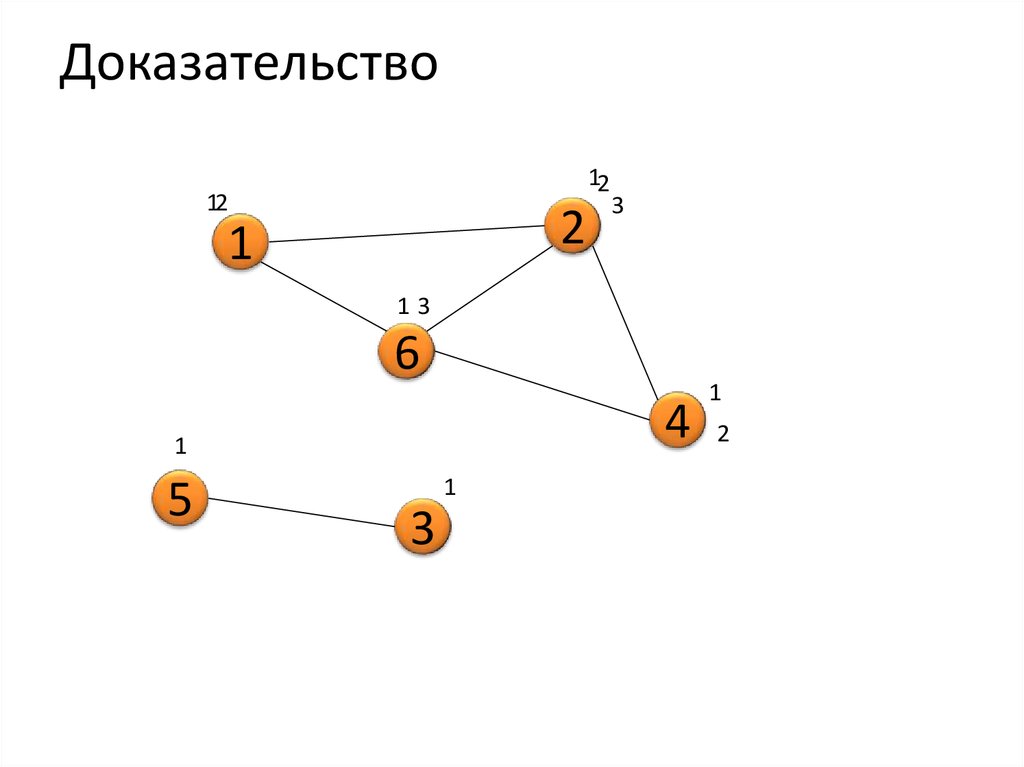
6.

Доказательство
12
12
2
1
3
13
6
4
1
5
1
3
1
2

7.

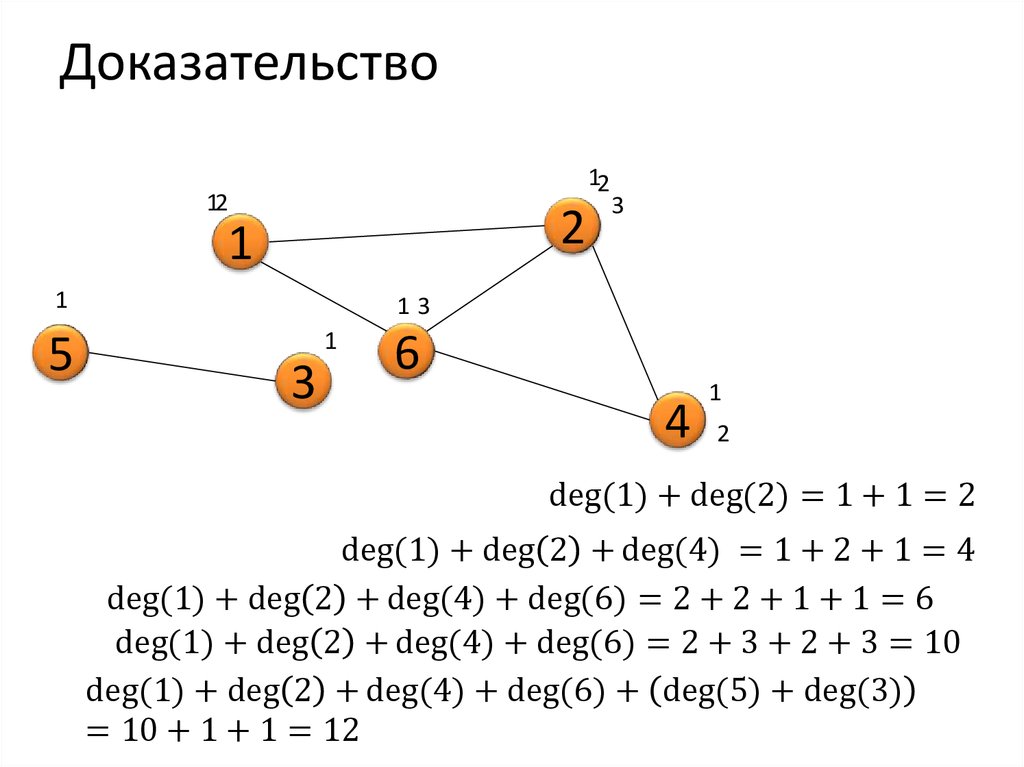
Доказательство
12
12
2
1
1
5
3
13
1
3
6
4
1
2
deg(1) + deg(2) = 1 + 1 = 2
deg(1) + deg 2 + deg(4) = 1 + 2 + 1 = 4
deg(1) + deg 2 + deg(4) + deg(6) = 2 + 2 + 1 + 1 = 6
deg(1) + deg 2 + deg(4) + deg(6) = 2 + 3 + 2 + 3 = 10
deg(1) + deg 2 + deg(4) + deg(6) + deg(5) + deg(3)
= 10 + 1 + 1 = 12

8.

Лемма о рукопожатиях
В любом графе число вершин нечётной
степени чётно.
1. Сумма степеней всех вершин в графе (или мультиграфе
без петель) должна быть четной.
2. Удаляя из этой суммы степени четных вершин, получим,
что сумма степеней нечетных вершин, должна быть
четной.
3. Значит, само число таких вершин должно быть четным.
Лемма доказана.
В любой момент времени количество людей,
сделавших нечетное число рукопожатий, чётно

9. Теорема о сумме степеней вершин графа

Теорема о существовании вершин
одинаковой степени
В любом графе есть по крайней мере две
вершины, имеющие одинаковую степень.

10. Доказательство

Теорема о существовании вершин
одинаковой степени
Число рёбер в полном графе