Похожие презентации:
Параллельные алгоритмы вычислительной алгебры. Разделение переменных
1. Спецкурс кафедры «Вычислительной математики» Параллельные алгоритмы вычислительной алгебры
Александр КалинкинСергей Гололобов
2. Часть 5: Разделение переменных
•Разделение переменных для оператора Лапласа•Вычислительный алгоритм
•OMP и MPI реализация
3. Сеточная аппроксимация оператора Лапласа
2u 2u2 2 f ; 0 x 1; 0 y 1;
y
x
u u u u 0;
x 1
y 0
y 1
x 0
Кусочно-линейная аппроксимация,
квадратная сетка
1
4 1
1 4 1
1
1 4 1
1
1 4
1
1
4 1
1
1
1 4 1
1
1
1 4 1
1
1 4
1
1
4 1
h2
1
1 4
1
1
1
1
1
1
1
4
1
1
1
u i f i
1
1
1
1
4
1
4 1
1 4 1
1 4 1
1
1 4
4. Сеточная аппроксимация оператора Лапласа
Как найти собственные вектора и собственные значения матрицы А?1
4 1
1 4 1
1
1 4 1
1
1 4
1
1
4 1
1
1
1 4 1
1
1
1 4 1
1
1 4
1
1
4 1
h2
1
1 4
1
1
1
1
1
1
1
4
1
1
1
A
1
1
1
1
4
1
4 1
1 4 1
1 4 1
1
1 4
5. Базисные функции оператора Лапласа
Пусть k (i, j ) k(1) (i) * k( 2) ( j) - собственный вектор матрицы A.1
2
Тогда оказывается:
k
4
2 k h
sin
,
2
h
2
k 1,2,..., N 1
k1 i
, k1 1,2,..., N 1
1
N
k j
k(22) ( j ) 2 sin 2 , k 2 1,2,..., N 1
N
k(1) (i ) 2 sin
Следовательно для нашей матрицы A:
k1 i k1 j
sin
; 0 i, j N
N N
2
4
k h
1
2
k k1 k2 2 sin 2
2
1 h
k (i, j ) 2 sin
6. Базисные функции оператора Лапласа
Разложим теперь решение задачи и правую часть по базисным функциям матрицы Au (i, j )
N1 1 N 2 1
u
k1 1 k 2 1
f (i, j )
k1k 2
k(1) (i ) k( 2 ) ( j )
N1 1 N 2 1
f
k1 1 k 2 1
k1k 2
1
2
k(1) (i ) k( 2) ( j )
1
2
Подставим полученные выражения в изначальное уравнение получим и учтя
собственные значения матрицы A:
N1 1 N 2 1
k1 1 k 2 1
uk1k2
1
k1
f k1k2
k1 k2
1
N1 1 N 2 1
k2 uk1k2 (i ) ( j ) f k1k2 k(11 ) (i ) k(22 ) ( j )
2
(1)
k1
( 2)
k2
k1 1 k 2 1
; 1 k1 N 1, 1 k 2 N 1
2
f k1k2
u (i, j ) 1 2 uk1k2 k(11 ) (i) k(22) ( j ); 0 i, j N
k1 1 k 2 1 k1 k 2
N1 1 N 2 1
7. Вычислительный алгоритм (двойной ряд)
k 2 j;
N
N 1
k (i ) f (i, j ) sin
2
j 1
N 1
k1 i
;
N
k k k (i ) sin
1` 2
i 1
2
1 i, k 2 N 1;
1 k1 , k 2 N 1;
k1k2 k1 i
; 1 i, k 2 N 1;
1
2 sin
N
k1 1 k1 k 2
4 N 1
k j
u (i, j ) 2 uk2 (i ) sin 2 ; 1 i, j N 1;
N k2 1
N
uk2 (i )
N1 1
k i
yk ai sin
; - Тригонометрическое разложение, трудоемкость С*N*log(N)
n
j 1
N 1
8. Вычислительный алгоритм (двойной ряд)
k 2 j;
N
N 1
k (i ) f (i, j ) sin
2
j 1
N 1
k1 i
;
N
k k k (i ) sin
1` 2
i 1
2
1 i, k 2 N 1;
1 k1 , k 2 N 1;
k1k2 k1 i
; 1 i, k 2 N 1;
1
2 sin
N
k1 1 k1 k 2
4 N 1
k j
u (i, j ) 2 uk2 (i ) sin 2 ; 1 i, j N 1;
N k2 1
N
uk2 (i )
N1 1
k i
yk ai sin
; - Тригонометрическое разложение, трудоемкость С*N*log(N)
n
j 1
N 1
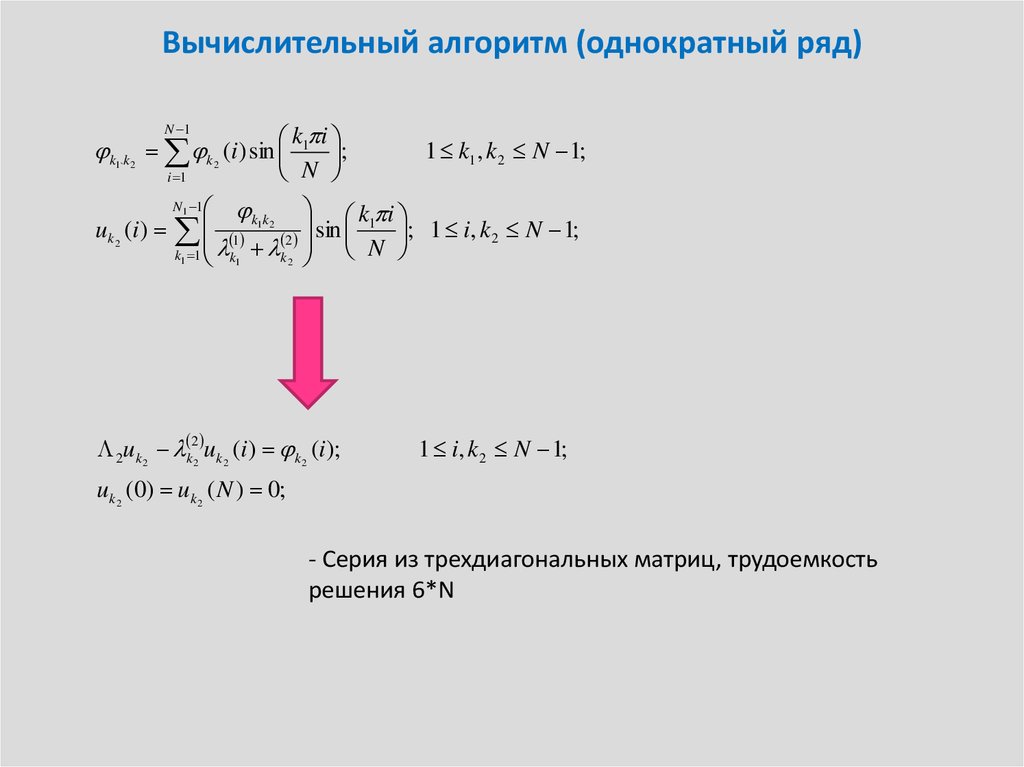
9. Вычислительный алгоритм (однократный ряд)
N 1k1 i
;
N
k k k (i ) sin
1` 2
u k 2 (i )
i 1
2
1 k1 , k 2 N 1;
k1k 2 k1 i
sin
; 1 i, k 2 N 1;
1
2
N
k1 1 k1 k 2
N1 1
2uk2 k22 uk2 (i ) k2 (i );
1 i, k 2 N 1;
uk2 (0) uk2 ( N ) 0;
- Серия из трехдиагональных матриц, трудоемкость
решения 6*N
10. Вычислительный алгоритм (однократный ряд)
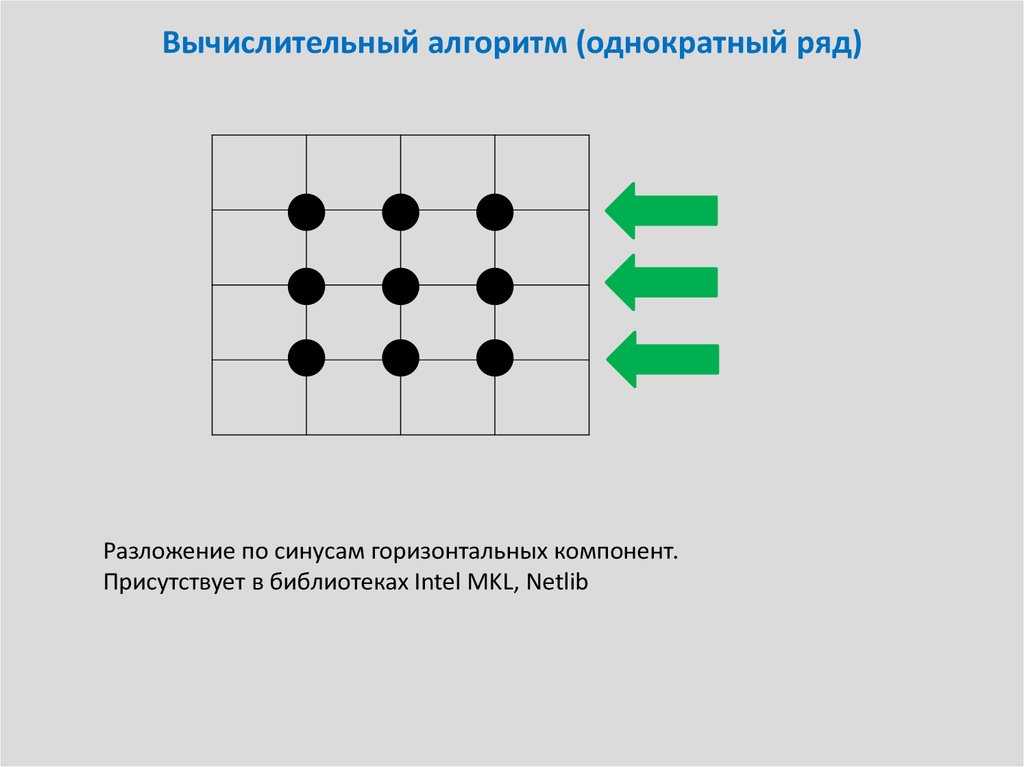
11. Вычислительный алгоритм (однократный ряд)
Разложение по синусам горизонтальных компонент.Присутствует в библиотеках Intel MKL, Netlib
12. Вычислительный алгоритм (однократный ряд)
Решение трехдиагональных систем (каждая системаразная!!! к диагонали добавляютя различные
собственные числа)
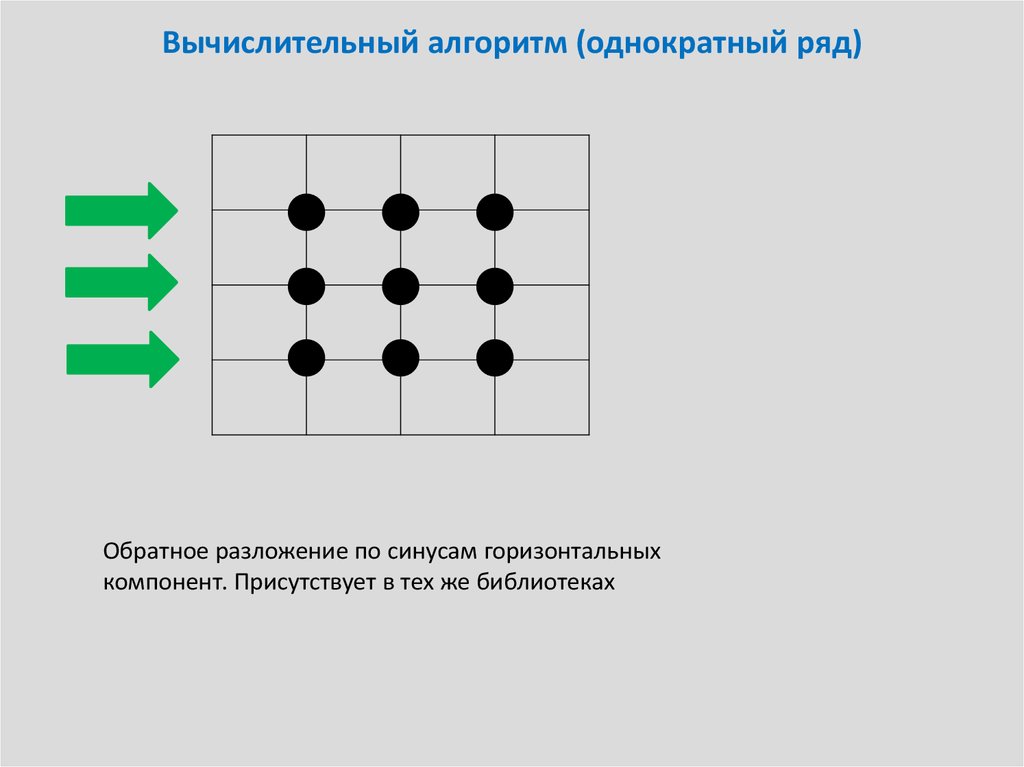
13. Вычислительный алгоритм (однократный ряд)
Обратное разложение по синусам горизонтальныхкомпонент. Присутствует в тех же библиотеках
14. Вычислительный алгоритм (однократный ряд)
subroutine laplas_solution(f(*,*),N)……
Do i=1,N
Call forward_trig_transform(f(i,*),….)
enddo
Do j=1,N
Call three_diagonal_lu(f(*,j),lambda(j),…)
enddo
Do i=1,N
Call backward_trig_transform(f(i,*),….)
enddo
…..
End subroutine
15. Вычислительный алгоритм (однократный ряд) (OMP)
subroutine laplas_solution(f(*,*),N)……
C$OMP PARALLEL DO
Do i=1,N
Call forward_trig_transform(f(i,*),….)
enddo
C$OMP END PARALLEL DO
C$OMP PARALLEL DO
Do j=1,N
Call three_diagonal_lu(f(*,j),lambda(j),…)
enddo
C$OMP END PARALLEL DO
C$OMP PARALLEL DO
Do i=1,N
Call backward_trig_transform(f(i,*),….)
enddo
C$OMP END PARALLEL DO
…..
End subroutine
16. Вычислительный алгоритм (однократный ряд) ( MPI)
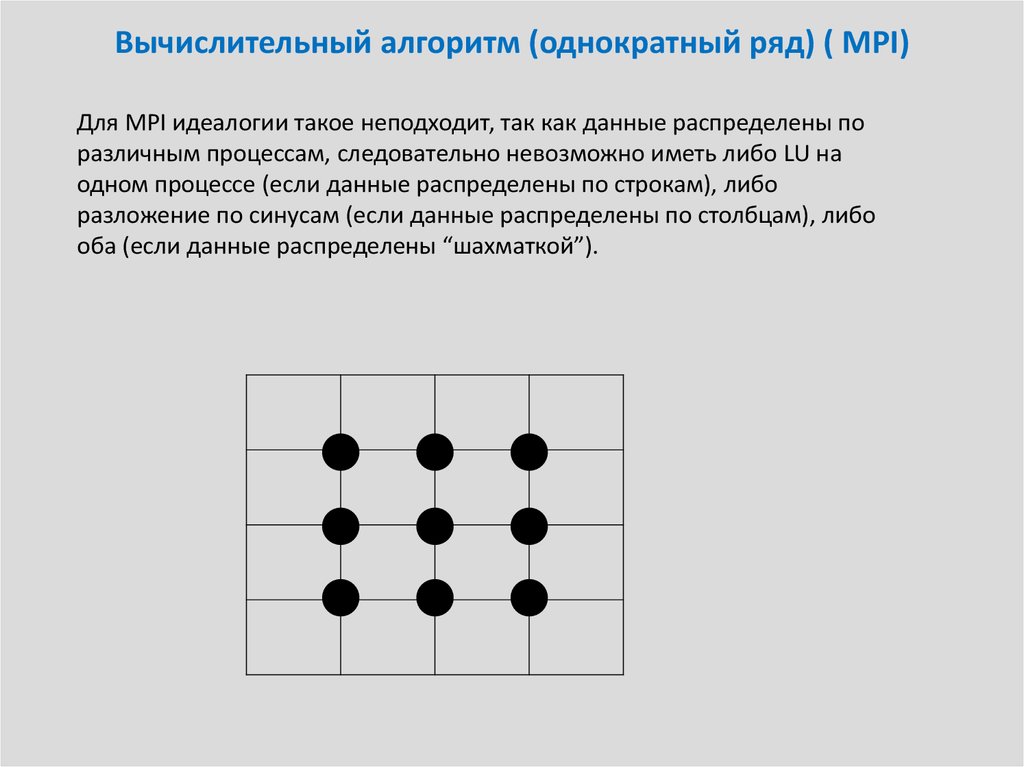
Для MPI идеалогии такое неподходит, так как данные распределены поразличным процессам, следовательно невозможно иметь либо LU на
одном процессе (если данные распределены по строкам), либо
разложение по синусам (если данные распределены по столбцам), либо
оба (если данные распределены “шахматкой”).
17. Вариант 1 (транспонирование, MPI)
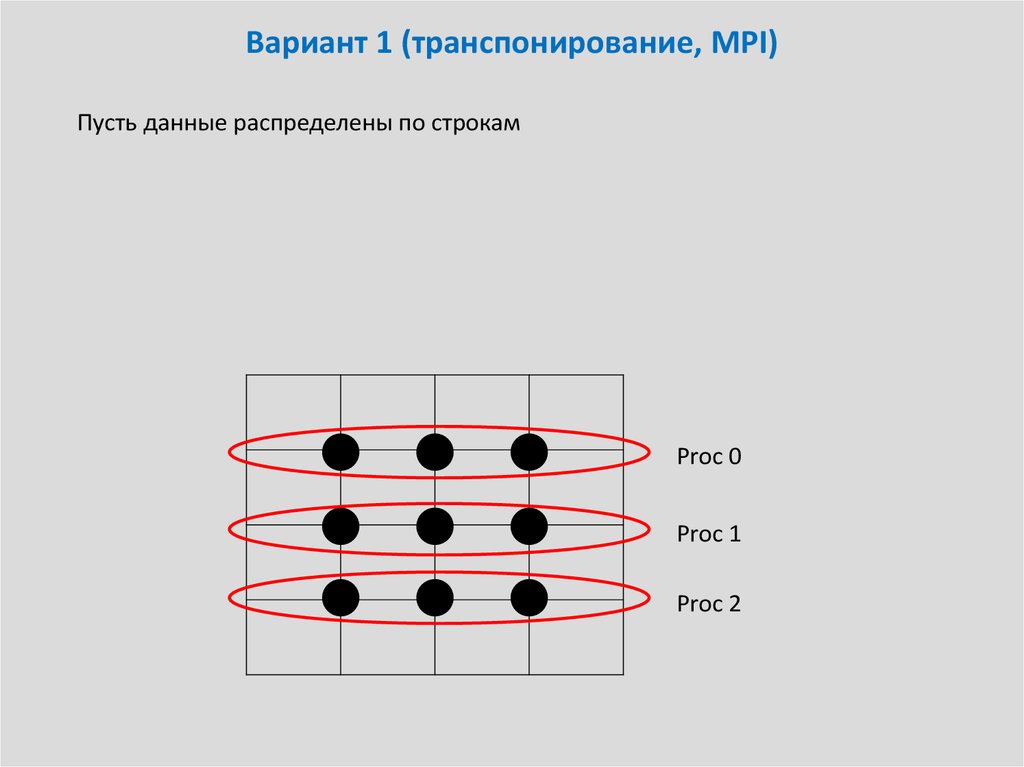
Пусть данные распределены по строкамProc 0
Proc 1
Proc 2
18. Вариант 1 (транспонирование, MPI)
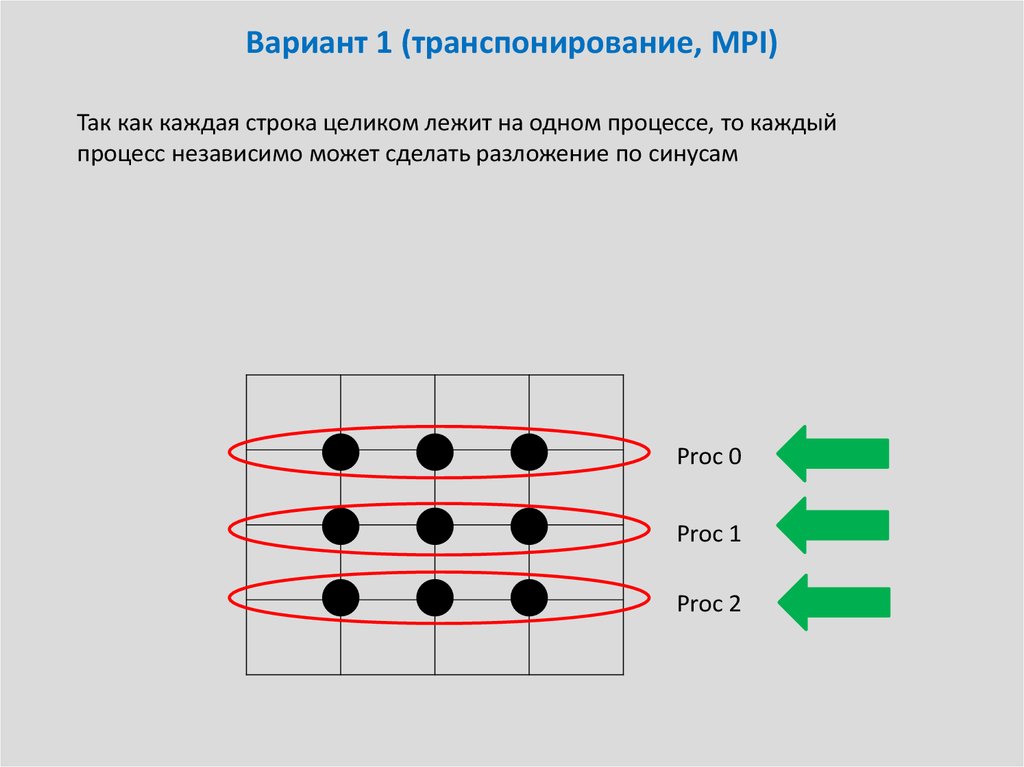
Так как каждая строка целиком лежит на одном процессе, то каждыйпроцесс независимо может сделать разложение по синусам
Proc 0
Proc 1
Proc 2
19. Вариант 1 (транспонирование, MPI)
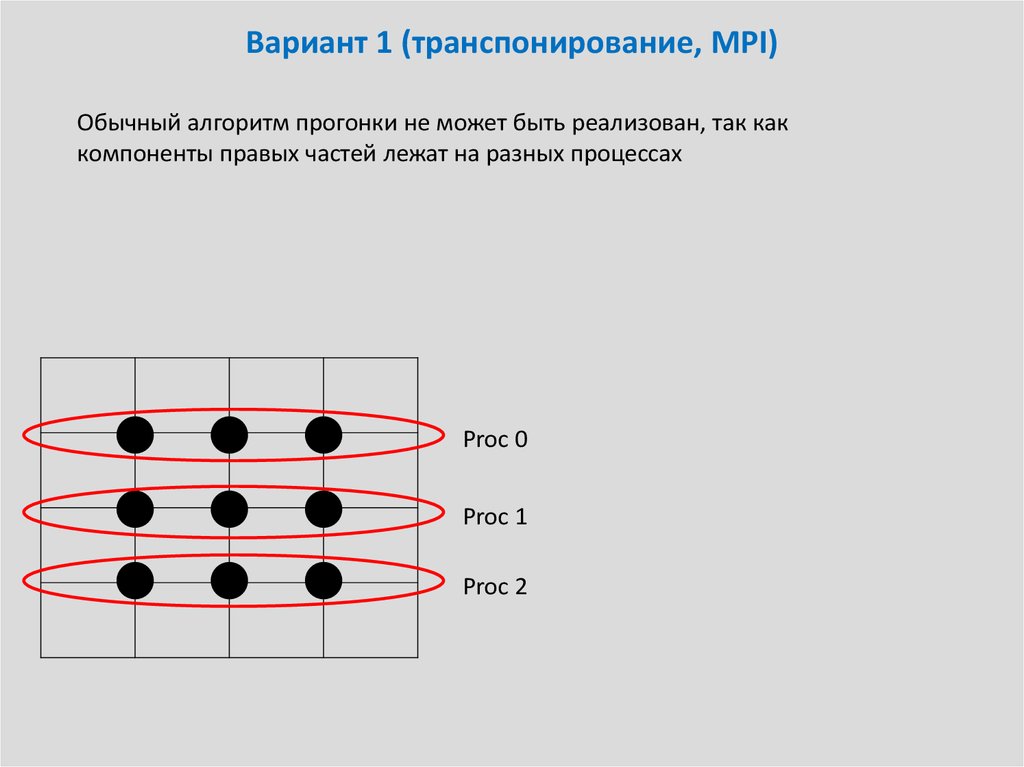
Обычный алгоритм прогонки не может быть реализован, так каккомпоненты правых частей лежат на разных процессах
Proc 0
Proc 1
Proc 2
20. Вариант 1 (транспонирование, MPI)
Данные можно транспонировать между процессами.ВАЖНО! Не забыть про порядок нумерации на процессах
MPI_Alltoallv
Proc 0
Proc 1
Proc 2
Proc 0
Proc 1
Proc 2
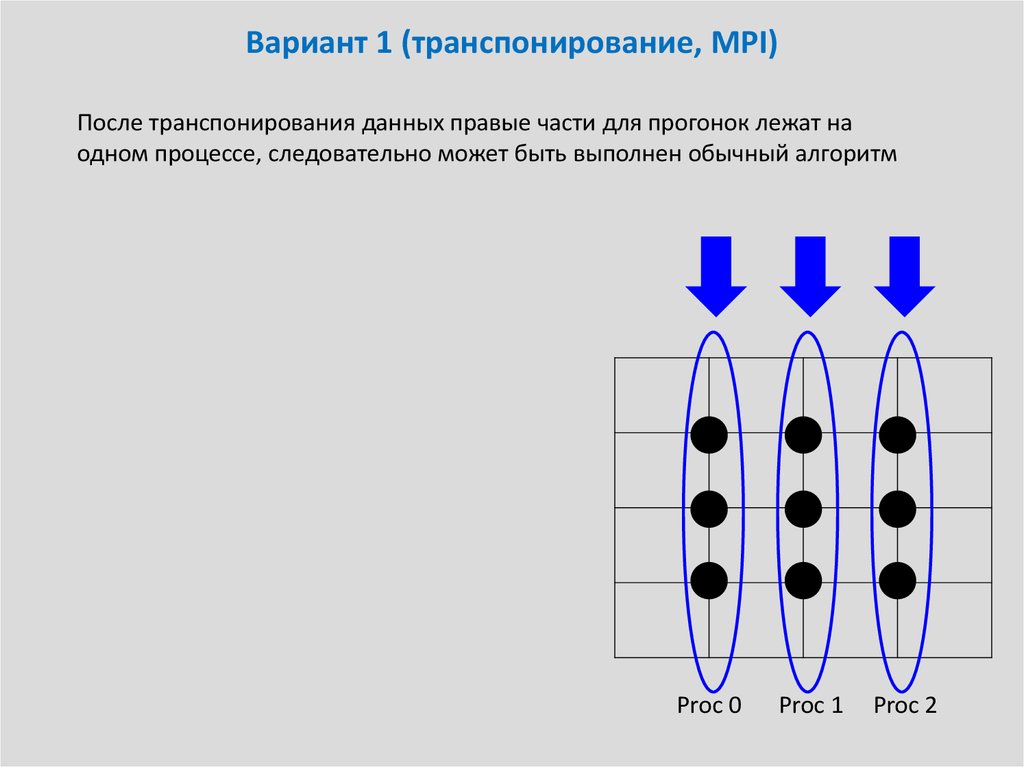
21. Вариант 1 (транспонирование, MPI)
После транспонирования данных правые части для прогонок лежат наодном процессе, следовательно может быть выполнен обычный алгоритм
Proc 0
Proc 1
Proc 2
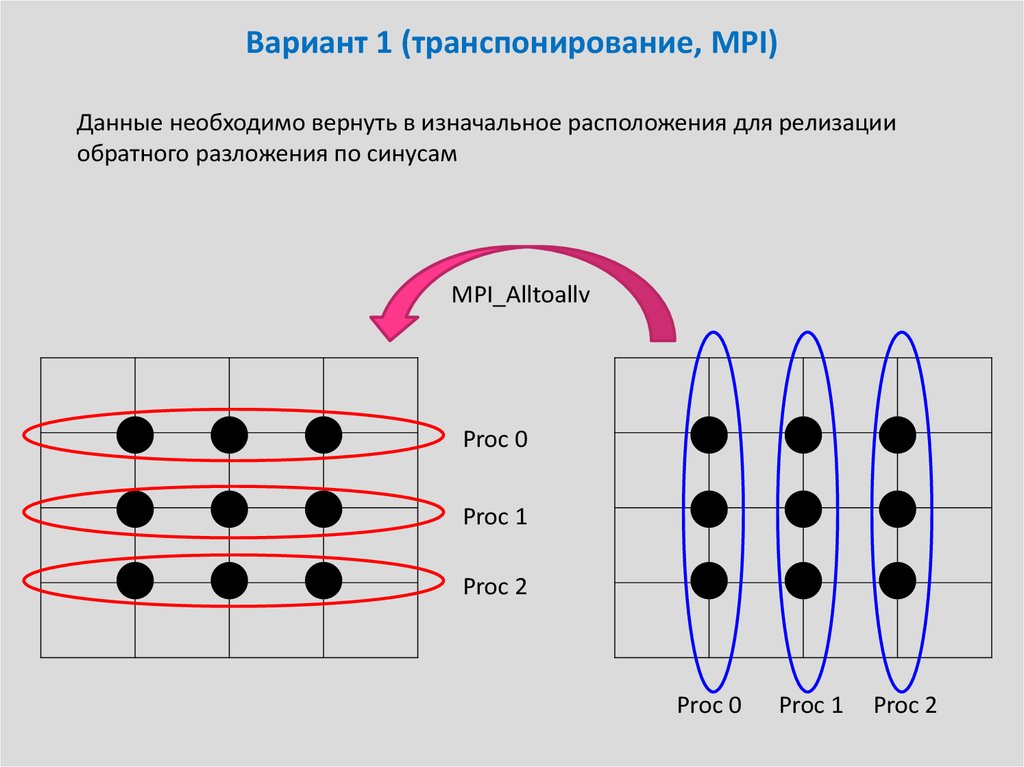
22. Вариант 1 (транспонирование, MPI)
Данные необходимо вернуть в изначальное расположения для релизацииобратного разложения по синусам
MPI_Alltoallv
Proc 0
Proc 1
Proc 2
Proc 0
Proc 1
Proc 2
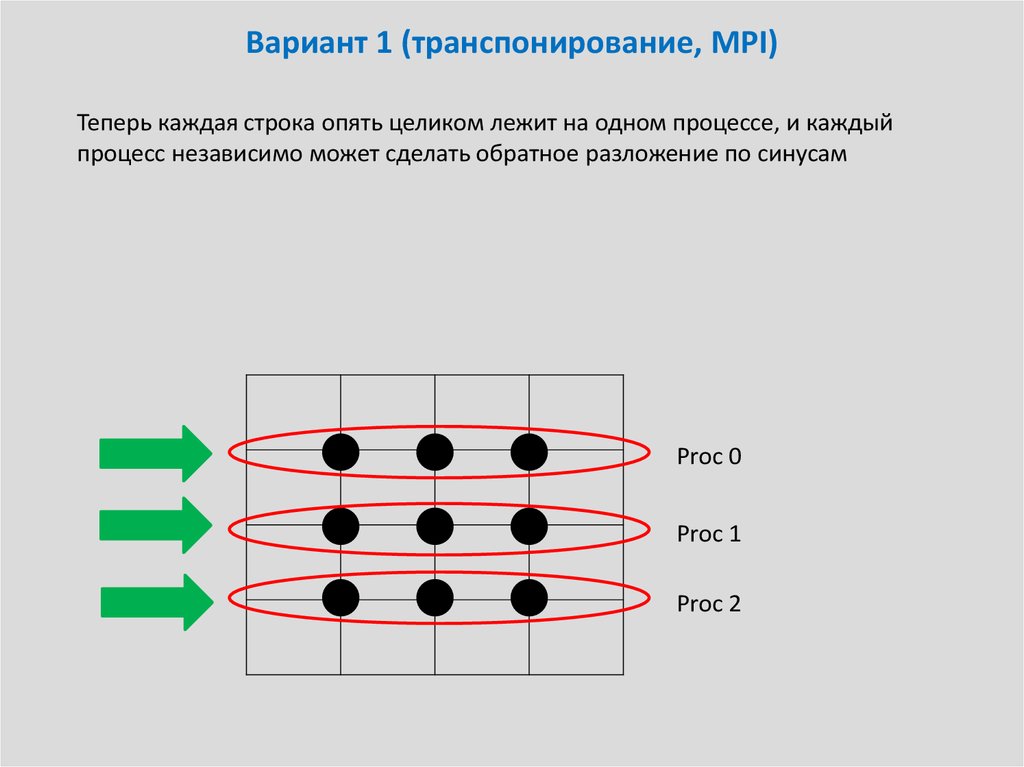
23. Вариант 1 (транспонирование, MPI)
Теперь каждая строка опять целиком лежит на одном процессе, и каждыйпроцесс независимо может сделать обратное разложение по синусам
Proc 0
Proc 1
Proc 2
24. Вариант 1 (транспонирование, MPI)
subroutine laplas_solution(f(*,*),N)……
Call MPI_Init();
Do i=ny_first,ny_last
Call forward_trig_transform(f(i-ny_first+1,*),….)
enddo
call transpose _y_to_x(f,f_work,…)
call MPI_All_to_allv(f_work,f,…,MPI_COMM_WORLD)
Do j=nx_first,nx_last
Call three_diagonal_lu(f(*,j-nx_first+1),lambda(j),…)
enddo
call MPI_All_to_allv(f,f_work,…,MPI_COMM_WORLD)
call transpose _x_to_y(f_work,f,…)
Do i=ny_first,ny_last
Call backward_trig_transform(f(i-ny_first+1,*),….)
Enddo
…..
Call MPI_Finalize();
End subroutine
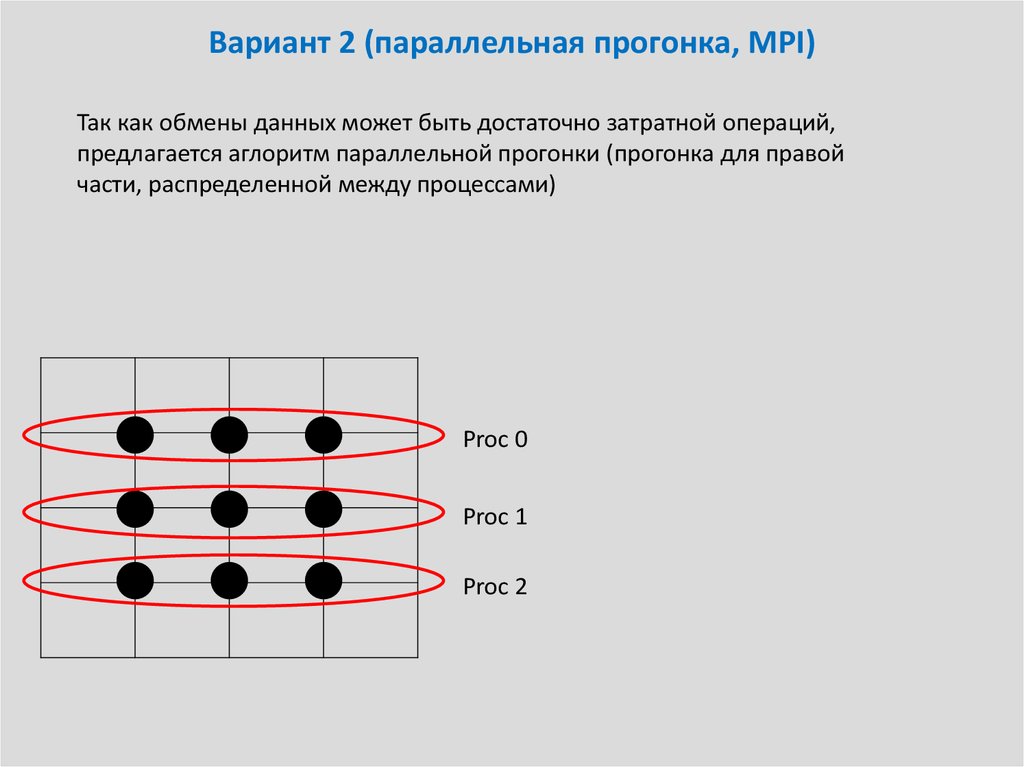
25. Вариант 2 (параллельная прогонка, MPI)
Так как обмены данных может быть достаточно затратной операций,предлагается аглоритм параллельной прогонки (прогонка для правой
части, распределенной между процессами)
Proc 0
Proc 1
Proc 2
26. Вариант 2 (параллельная прогонка, MPI)
Разобьем компоненты вектора решения (X)i и правой части (F)I междупроцессами таким образом, чтоб на каждом процессоре лежала часть
вектора с компонентами [k,k+M], каждая компонента хранилась только на
одном процессе.
b1
a
2
c1
b2
c2
a3
b3
c3
.
.
.
.
.
.
.
.
ck 1
ak
bk
ck
.
.
.
ak M
bk M
ck M
.
.
.
.
.
.
.
.
.
.
.
an 1
bn 1
an
( X )i ( F )i
cn 1
bn
27. Вариант 2 (параллельная прогонка, MPI)
Теорема: Если вектор решения записать в следующем виде:X x01 ,.., x1M , x02 ,..., x0ya ,..., xMya ,..., xMmax_ proc ( X 1 ,.., X ya ,..., X max_ proc )
,где max_proc – число процессов, то решение задачи с трехдиагональной
матрицей записывается в следующем виде:
X ya R ya P ya Wya 1 Q ya Wya ; Wi x0i 1
ai Pjya 1 bi Pjya ci Pjya 1 0; P0ya 1, PMya 0;
ai Q jya 1 bi Q jya ci Q jya 1 0; Q0ya 0, PMya 1;
ai R jya 1 bi R jya ci R jya 1 f j ; R0ya 0, RMya 0;
j 0, M ; i ( ya 1) M j
28. Вариант 2 (параллельная прогонка, MPI)
Теорема: Если вектор решения записать в следующем виде:X x01 ,.., x1M , x02 ,..., x0ya ,..., xMya ,..., xMmax_ proc ( X 1 ,.., X ya ,..., X max_ proc )
,где max_proc – число процессов, то решение задачи с трехдиагональной
матрицей записывается в следующем виде:
X ya R ya P ya Wya 1 Q ya Wya ; Wi x0i 1
ai Pjya 1 bi Pjya ci Pjya 1 0; P0ya 1, PMya 0;
ai Q jya 1 bi Q jya ci Q jya 1 0; Q0ya 0, PMya 1;
ai R jya 1 bi R jya ci R jya 1 f j ; R0ya 0, RMya 0;
j 0, M ; i ( ya 1) M j
Относительно Wk записывается трехдиагональная система уравнений, с
коэффициентами, зависящими от a,b,c,P,Q.
29. Вариант 2 (параллельная прогонка, MPI)
Алгоритм:1. Решаем на каждом процессора 3 системы уравнений методом прогонки с
одной и той же матрицей, разными правыми частями
2. Рассылаем с каждого процесса малый объем данных на один процесс для
того, чтоб собрать трехдиагональную систему уравнений
размерностью=число процессов
3. Полученные компоненты решения рассылаем на каждый процесс (по два
значения на процесс) и собираем на них требуемые компоненты решения
30. Вариант 1 (транспонирование, MPI)
subroutine laplas_solution(f(*,*),N)……
Call MPI_Init();
Do i=ny_first,ny_last
Call forward_trig_transform(f(i-ny_first+1,*),….)
enddo
Do j=1,nx
Call MPI_three_diagonal_lu(f(*,j),lambda(j),…)
enddo
Do i=ny_first,ny_last
Call backward_trig_transform(f(i-ny_first+1,*),….)
Enddo
…..
Call MPI_Finalize();
End subroutine



















 Математика
Математика Информатика
Информатика








