Похожие презентации:
Радиотехнические системы передачи информации
1. Радиотехнические системы передачи информации
Профессор, д.ф.-м.н. А.Г. ФлаксманКафедра радиоэлектронных систем НГТУ
1.
2.
3.
4.
5.
Литература (основная)
Прокис Д. Цифровая связь. Пер. с англ. – М: Радио и связь, 2000. 800с.
Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Пер. с англ.
М:, Вильямс, 2003. 1104 с.
Ермолаев В.Т., Маврычев Е.А., Флаксман А.Г. Современные методы обработки сигналов в
беспроводных системах связи. Учебное пособие. / Нижний Новгород: Изд-во НГТУ им.
Р.Е. Алексеева, 2011. – 140 с.
Ермолаев В.Т., Флаксман А.Г. Современные методы пространственной обработки сигналов
в радиосистемах с антенными решетками. Учебное пособие. / Нижний Новгород: Изд-во
НГТУ им. Р.Е. Алексеева, 2008. - 171 с.
В.Т. Ермолаев, А.А. Мальцев, А.Г. Флаксман, О.В. Болховская, А.В. Клюев. Мобильная
связь: вопросы теории и типовые задачи. Учебное пособие. / Нижний Новгород: Изд-во
Нижегородского госуниверситета ННГУ им. Н.И. Лобачевского, 2014. 234 с.
03.01.2018
1
2.
Лекция 1. ВведениеЧисло пользователей мобильной связи (в млн.)
140 (1996 г.)
205 (1997 г.)
290 (1998 г.)
380 (1999 г.)
500 (2000 г.)
680 (2001 г.)
Страны с наибольшим удельным числом пользователей (на конец 20 века)
1. Финляндия. 2. Швеция.
3. Норвегия.
4. Дания
• Первый стандарт беспроводного доступа в Интернет (стандарт 802.11
Wi-Fi (Wireless Fidelity)) на передачу данных со скоростью до 2 Мбит/с
в диапазоне 2,4 ГГц ратифицирован в 1997 году
•Стандарт 802.11b на передачу данных со скоростью до 11 Мбит/с в
диапазоне 2,4 ГГц ратифицирован в 1999 году
• Стандарт 802.11а ратифицирован в 1999 году и регламентирует
скорость передачи данных до 54 Мбит/с в частотном диапазоне 5 ГГц
03.01.2018
2
3. Основные концепции построения сотовых сетей
Особенности сотовой архитектуры:- передатчики небольшой мощности
- небольшие зоны покрытия сотами
- повторное использование частот
- дробление сот для уменьшения мощности
- управление передачей вызова (handoff)
Макросота ~ 35 км
Сота ~ 3-5 км
Микросота ~ 0.8-1 км
Пикосота ~ 0.2 км
03.01.2018
3
4. Гексагональная структура сотовой сети
Пример используемой антенны (2100 МГц)Столбец излучателей (10 излучателей)
Поляризация – двойная, линейная с наклоном +45 и -45 град.
Высота столбца - 697 мм
Ширина столбца - 167 мм
Глубина столбца - 58 мм
Ширина луча (по уровню половинной мощности):
горизонтальная плоскость - 65 град.
Вертикальная плоскость - 13 град.
03.01.2018
4
5.
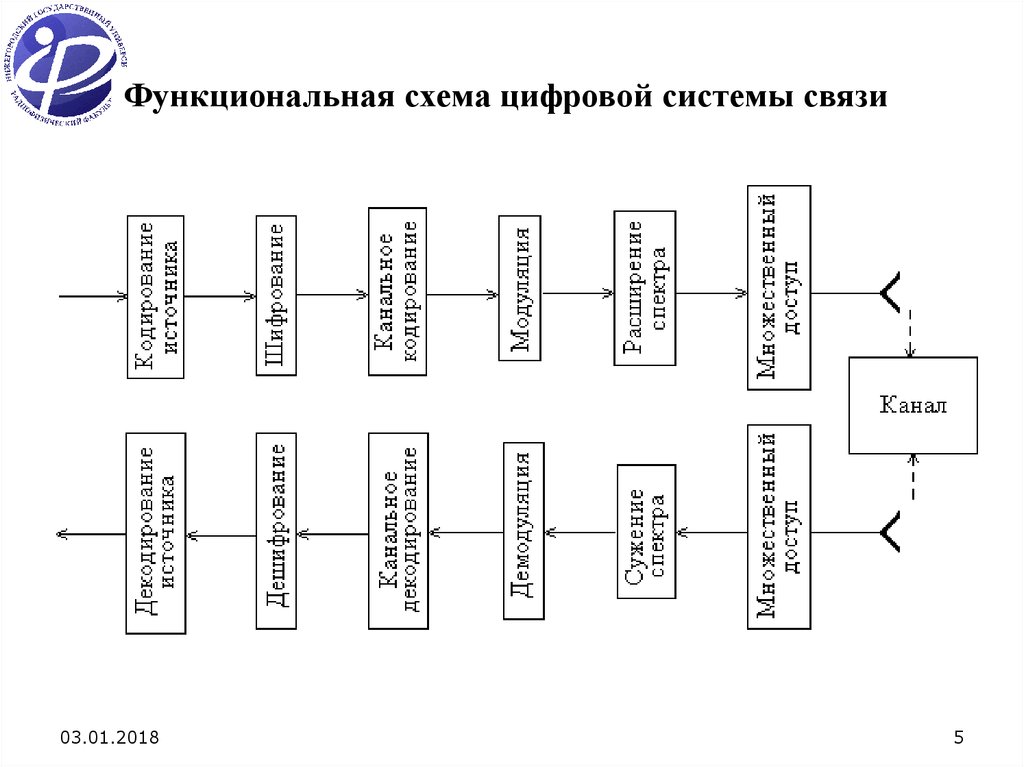
Функциональная схема цифровой системы связи03.01.2018
5
6. Повторное использование частот (frequency reuse)
Повторное использование частот заключается в том, что в соседних сотах используютсяразные полосы частот, которые повторяются через несколько сот.
Кластер (cluster) – группа сот с различным набором частот.
3-х частотный
кластер (f1, f2, f3)
7-ми частотный
кластер
( f1, f2, …, f7)
Цифра внутри соты показывает используемую частоту
Расстояние между центрами сот с одинаковыми частотами, D R 3N
R – радиус соты (радиус описанной окружности), N – число сот в кластере.
N=3, D=3R;
N=7, D=4.58R;
N=19, D=7.55R
Отношение D/R=q называется коэффициентом уменьшения соканальных помех или
коэффициентом соканального повторения.
Обратная величина C=1/N называется коэффициентом повторного использования частот
Расстояние между центрами сот с одинаковыми частотами D R 3 C
03.01.2018
6
7. Жесткая «Handoff»-процедура
Жесткий handoff - обслуживание лучшей базовой станцией (БС)Пример двух БС (А и Б)
Жесткий handoff приводит к
кратковременной передаче
пользователя от одной БС к
другой, то есть возможны
перерывы в сеансе связи
Сигналы, принимаемые базовыми
станциями А и Б
03.01.2018
Результирующий сигнал
формируется путем коммутации и
«склеивания» сигналов от разных
базовых станций
7
8.
Мягкая «Handoff»-процедураМягкий handoff - обслуживание лучшей базовой станцией (БС)
Пример двух БС
Пороговое ОСШ
(выбор кандидатных
БС)
Нет Handoff
Пороговое ОСШ
(замена
обслуживающей БС)
Мягкий handoff уменьшает
число передач пользователя
от одной БС к другой, то есть
число возможных перерывах
в сеансе связи
Handoff
03.01.2018
Сигналы, принимаемые
базовыми станциями А и Б
8
9.
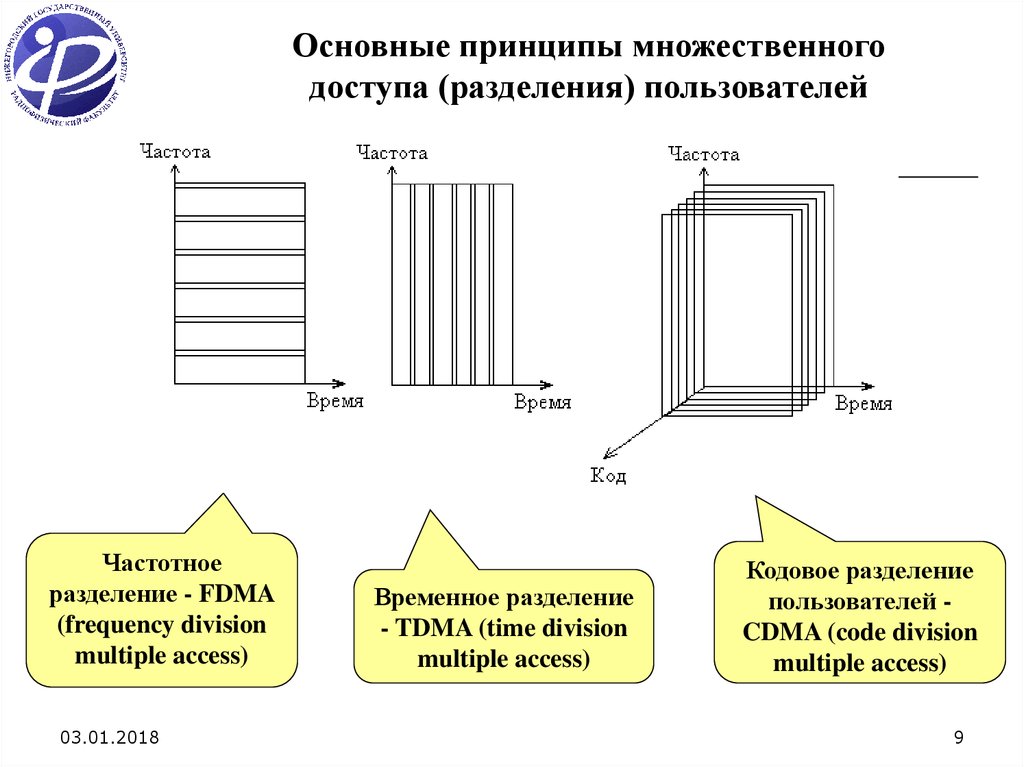
Основные принципы множественногодоступа (разделения) пользователей
Частотное
разделение - FDMA
(frequency division
multiple access)
03.01.2018
Временное разделение
- TDMA (time division
multiple access)
Кодовое разделение
пользователей CDMA (code division
multiple access)
9
10. Частотное разделение пользователей
Скорость передачи данных R бит/сек (один пользователь).М – число пользователей (число отдельных полос).
Длительность импульсов увеличивается в M раз, то есть все M пользователей
одновременно передают информацию, но с уменьшенной скоростью R/M бит/сек.
1. Взаимное влияние каналов должно быть минимально возможным;
2. Время ожидания пакета для всех пользователей одинаково;
3. При замираниях в канале некоторые частотные каналы могут быть сильно ослаблены.
М – число пользователей;
b – число бит в пакете;
Т – время передачи пакета.
03.01.2018
Скорость передачи
RFD M
b
бит / сек
T
10
11. Временное разделение пользователей
времяСкорость передачи данных R бит/сек (один пользователь).
М – число пользователей (число временных интервалов).
Каждый пользователь использует всю полосу и передает
информацию со скоростью R бит/сек (длительность
импульсов не изменяется), но за время T/M.
М – число пользователей;
b – число бит в пакете;
Т – время передачи пакета.
Скорость передачи
Пакет передается
за меньшее время
RTD
b
бит / сек
T /M
Скорость передачи одинакова для
частотного и временного разделения
RFD RTD
Время ожидания пакета для всех пользователей различно
03.01.2018
11
12. Производительность частотного и временного разделения пользователей
Время задержки пакета состоит из среднего времени w ожиданияпакета и из среднего времени передачи пакета
D w
Частотное разделение - пакет передается без задержки
в течение T секунд
wFD 0; FD T
Временное разделение - пакет передается с задержкой
в течение T/M секунд.
Время задержки m-го пакета (m 1)T / M
1
wTD
Среднее время ожидания m-го пакета
M
FD T / M
DTD
T
1
1
2 M
T
M
DTD DFD
T
1
1
2 M
M
(m 1)
m 1
DTD DFD
T T
1
1
M 2 M
b
M 1
2R
Временное разделение является более производительным,
если учитывать время задержки пакета
03.01.2018
12
13. Понятие о кодовом разделении пользователей
- Разделение пользователей осуществляется за счет модуляции символов кодовымипсевдослучайными последовательностями (КПШП).
- Каждому пользователю назначается своя КПШП.
Передаваемые импульсы
dA=1, dB=1, dC= –1, dD= 1
(простой сигнал)
03.01.2018
Модулированные импульсы
(сигнал с расширенным
спектром)
13
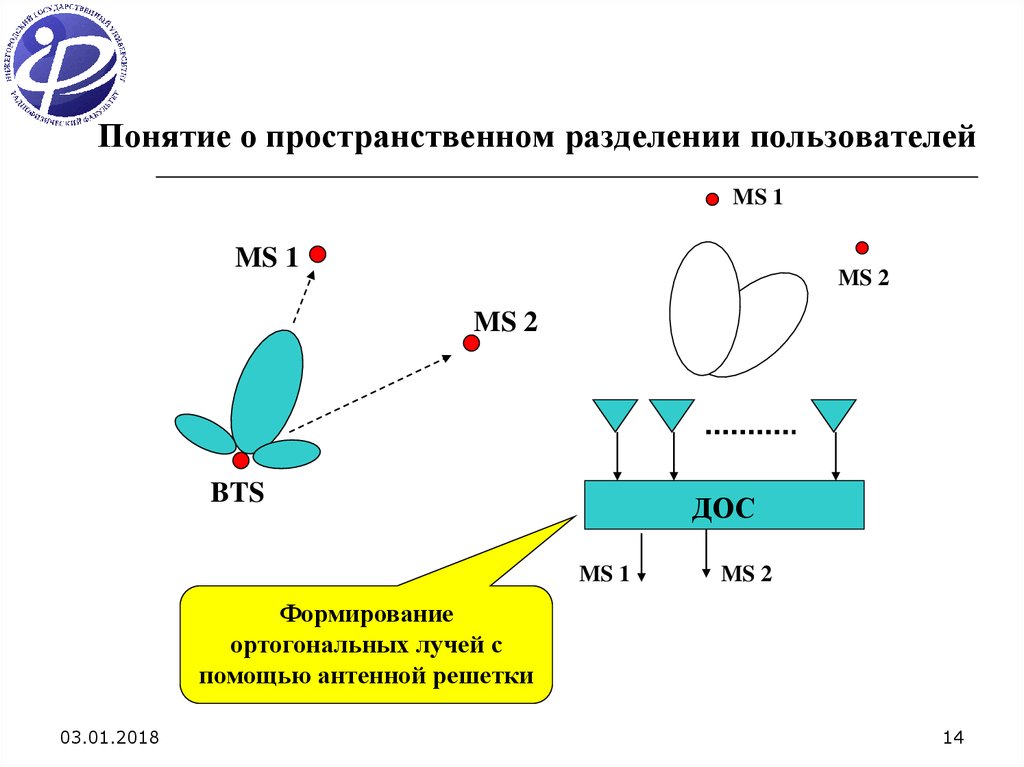
14. Понятие о пространственном разделении пользователей
MS 1MS 1
MS 2
MS 2
BTS
ДОС
MS 1
MS 2
Формирование
ортогональных лучей с
помощью антенной решетки
03.01.2018
14
15.
Управление мощностью (powercontrol - PC) на мобильной станции
Стандарт CDMA (IS-95)
15 дБ
Без РС
с РС
- Фрейм (20 мсек) состоит из 288
символов.
- Эти символы делятся на 16 групп
PC (18 символов в группе).
- Длительность группы 1.25 мсек.
- Частота управления мощностью 800 Гц
- Шаг управления мощностью 1 дБ
- Управление мощностью основано
на оценке ОСШП для каждой группы
символов
8 дБ
Замирания сигналов в канале связи
0 дБ
-5 дБ
Мощность передатчика
03.01.2018
15
16.
Лекция 2. Преобразование аналоговойинформации в дискретную форму
1. Дискретизация аналогового сигнала
X ( ) 2 ( 0 ) - спектр сигнала x(t), где - круговая частота; (x) - дельта-функция
1
j 0t
j t
x(t )
2
(
)
e
d
e
0
2
Периодический сигнал с периодом T имеет линейчатый спектр
X ( )
2 X n ( n 0 )
n
0 2 T
1
jn 0t
j t
2
X
(
n
)
e
d
X
e
Сигнал представляется рядом Фурье x(t )
n
0
n
n 2
n
2
2 n
Докажем, что (t k t )
t
t
k
n
03.01.2018
периодическая последовательность
-импульсов имеет линейчатый
спектр в виде периодической
последовательности -компонент
16
17.
Последовательность импульсов(t k t )
имеет период t
k
Коэффициенты ряда Фурье
Спектр
t / 2
1
2 n
1
Xn
(
t
)
exp
j
t
dt
t t / 2
t
t
2 2
2 n
X ( ) 2 X n ( n 0 ) 2 X n n
t
t
t
n
n
n
Доказали
Операция дискретизации.
s (t )
(t n t )
n
xs (t ) x(t ) s (t ) x(t )
Так как
03.01.2018
(t n t )
n
- дискретный (семплированный) сигнал
x(t ) (t t0 ) x(t0 ) (t t0 ) то xs (t )
x(n t ) (t n t )
n
17
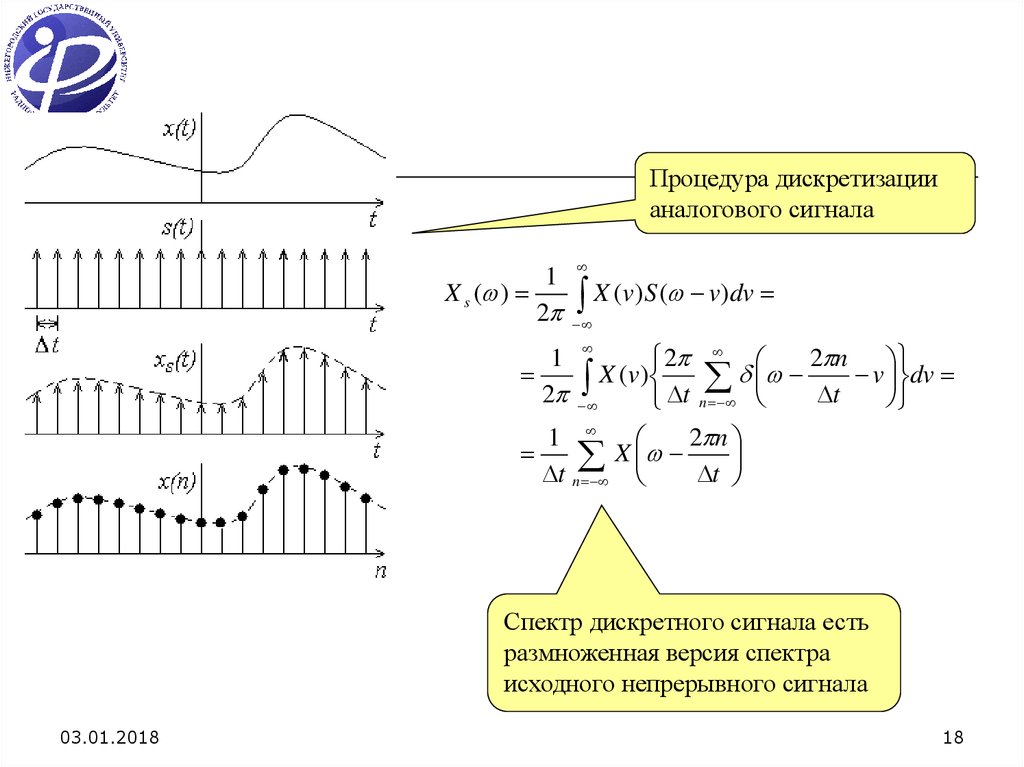
18.
Процедура дискретизациианалогового сигнала
1
X s ( )
2
X (v)S ( v)dv
2
2 n
X
(
v
)
v
dv
t n
t
1
2 n
X
t n
t
1
2
Спектр дискретного сигнала есть
размноженная версия спектра
исходного непрерывного сигнала
03.01.2018
18
19.
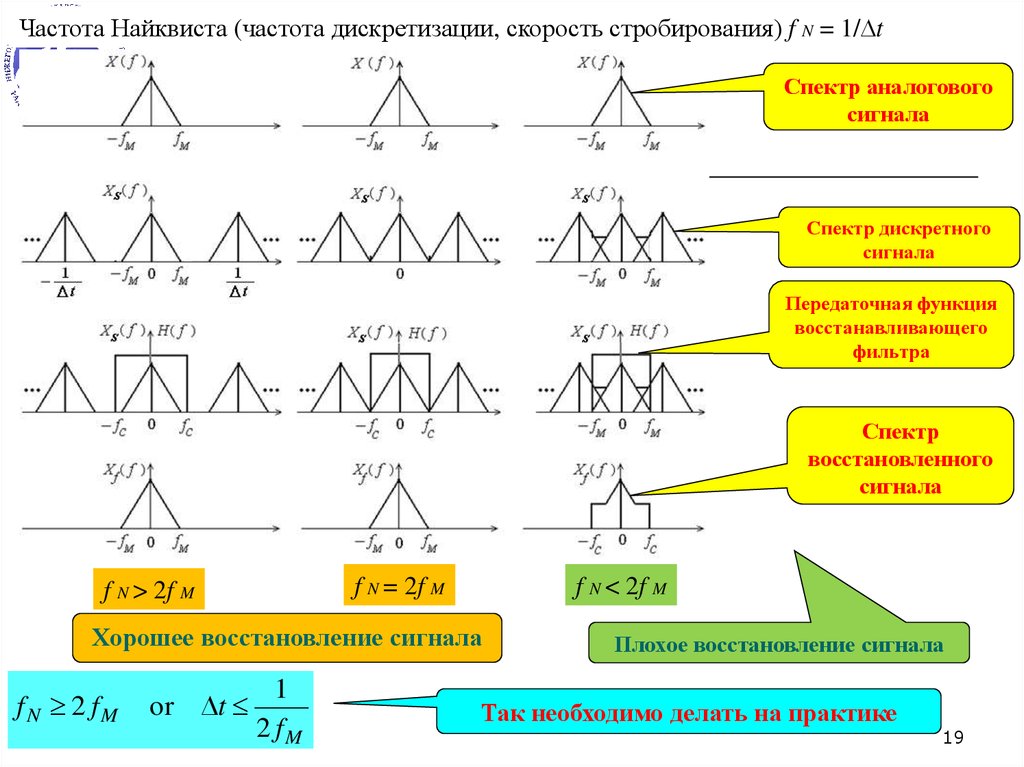
Частота Найквиста (частота дискретизации, скорость стробирования) f N = 1/ tСпектр аналогового
сигнала
Спектр дискретного
сигнала
Передаточная функция
восстанавливающего
фильтра
Спектр
восстановленного
сигнала
f N = 2f M
f N > 2f M
f N < 2f M
Хорошее восстановление сигнала
f N 2 fM
or t
03.01.2018
1
2 fM
Плохое восстановление сигнала
Так необходимо делать на практике
19
20.
2. Теорема КотельниковаНепрерывный сигнал с ограниченной полосой [ fM fM] может быть восстановлен по
его отсчетам (выборкам), взятым через интервал времени t 1/(2fM) с помощью
интерполяционной формулы
tmax=1/(2fM) - максимальный интервал
sin[ (t n t ) t ]
между временными отсчетами сигнала,
x f (t ) x(n t )
(t n t ) t
определяемый шириной полосы
n
Доказательство. Сигнал можно восстановить в частотной
области, используя идеальный низкочастотный фильтр
X f ( ) X s ( ) H ( )
x f (t ) xs (t ) h(t x(n t ) (t n t ) h(t
n
x(n t ) ( n t )h(t )d x(n t )h(t n t )
n
Идеальная передающая функция
(см. рисунок на слайде выше)
n
t ,
H ( )
0,
Идеальная импульсная характеристика
03.01.2018
t t
t.
h(t )
sin ( t t )
( t t )
Доказали
20
21.
3. Квантование аналоговых сигналовРавномерная импульсно-кодовая модуляция (ИКМ)
Каждый отчет квантуется в один из N=2b уровней, где b – число двоичных цифр (разрядов)
Динамический диапазон сигнала [ Emax Emax].
Размер шага квантования
q 2Emax 2b
Амплитудная характеристика
3-битового квантователя
03.01.2018
21
22.
x x eПроцесс квантования ~
p ( e) 1 q
где e – ошибка квантования, трактуемая как аддитивный шум
( 0.5q e 0.5q)
с равномерной плотностью вероятности
Мощность
ошибки квантования
0.5 q
0.5 q
1
1 2 (2 Emax ) 2
e p(e)de e de q
q
12
12(22b )
0.5 q
0.5 q
2
q
2
Мощность входного сигнала x при
равномерной плотности вероятности
на интервале от -Emax до +Emax
ОСШ
2x
2q
2 2b
2
2x
Emax
Emax
Emax
Emax
(2 Emax ) 2
1
x
dx
2 Emax
12
2
ОСШдБ 10 lg( ОСШ) 10 lg( 22b ) 20b lg( 2) 6 b
Пример: 8-разрядный (b=8) АЦП (256 уровней).
ОСШ = 48 дБ.
03.01.2018
x p( x)dx
2
ОСШ увеличивается
на 6 дБ на каждый
разряд АЦП
22
23.
При неравномерной плотности вероятности сигнала на интервале от -Emax до +EmaxОСШдБ 6 b C (C 0)
Пример. Сигнал x занимает часть динамического диапазона квантователя и имеет
равномерную плотность вероятности на интервале Emax a Emax a (a >1)
Мощности сигнала
2x
Emax a
x p( x)dx
Emax a
ОСШ 22b a 2
2
(2 Emax ) 2
12a 2
ОСШдБ 10 lg( ОСШ) 6 b 20 lg a
Пример: a=4. Тогда C=12 дБ.
03.01.2018
23
24.
Неравномерная импульсно-кодовая модуляция.
Устройство неравномерного
квантования
В природе более вероятны
более слабые сигналы.
Входной сигнал преобразуется
в нелинейном устройстве
(компрессор или сжиматель) и
затем квантуется с помощью
равномерной ИКМ.
При восстановлении сигнала
используется обратное
преобразование, выполняемое
с помощью экспандера
(расширителя)
Характеристика компрессора y=C(x). Размер шага квантования
Дисперсия ошибки квантования (плотность вероятности
p(x) и характеристика компрессора y=C(x) произвольные)
2
Дисперсия сигнала x
y (dC dx ) x
x
q 2
q 2 max p( x)
dx
2
12 x dC dx
max
2
x
p( x)dx
03.01.2018
24
25.
xmaxx2
ОСШ 2 2
q
q
2
x
p( x)dx
xmax
xmax
12 xmax
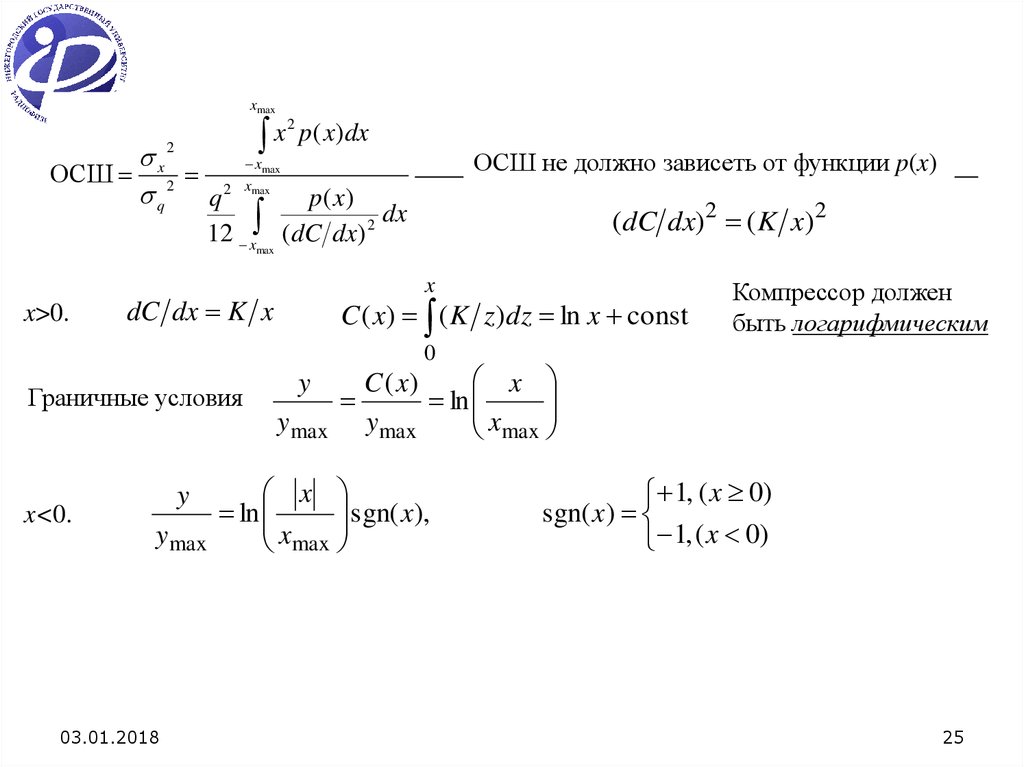
x>0.
ОСШ не должно зависеть от функции p(x)
p( x)
dx
(dC dx) 2
(dC dx) 2 ( K x) 2
x
dC dx K x
C ( x) ( K z )dz ln x const
Компрессор должен
быть логарифмическим
0
Граничные условия
y
ymax
x<0.
y
ymax
03.01.2018
x
C ( x)
ln
ymax
xmax
x
sgn( x),
ln
xmax
1, ( x 0)
sgn( x)
1, ( x 0)
25
26.
Плавное соединение междулогарифмической функцией
и линейным отрезком,
проходящим через начало
координат
Функции логарифмического
сжатия
03.01.2018
-закон (Северная Америка)
A-закон (Европа)
26
27.
Амплитудная характеристика -компрессораy ymax
ln[1 ( x xmax )]
ln(1 )
sgn x
Амплитудная характеристика A-компрессора
A( x xmax )]
y
sgn x,
0 x xmax 1 A
max
1 ln( A)
y
1 A( x xmax )]
y
sgn x,
1 A x xmax 1.
max
1 ln( A)
В стандарте США и Канады при кодировании
речи =255 при 8-битовом АЦП.
A=87.56 - стандартное значение параметра A.
Амплитудная характеристика
компрессора при =1, 15 и 255
(кривые
1, 2, 3, соответственно)
03.01.2018
27
28.
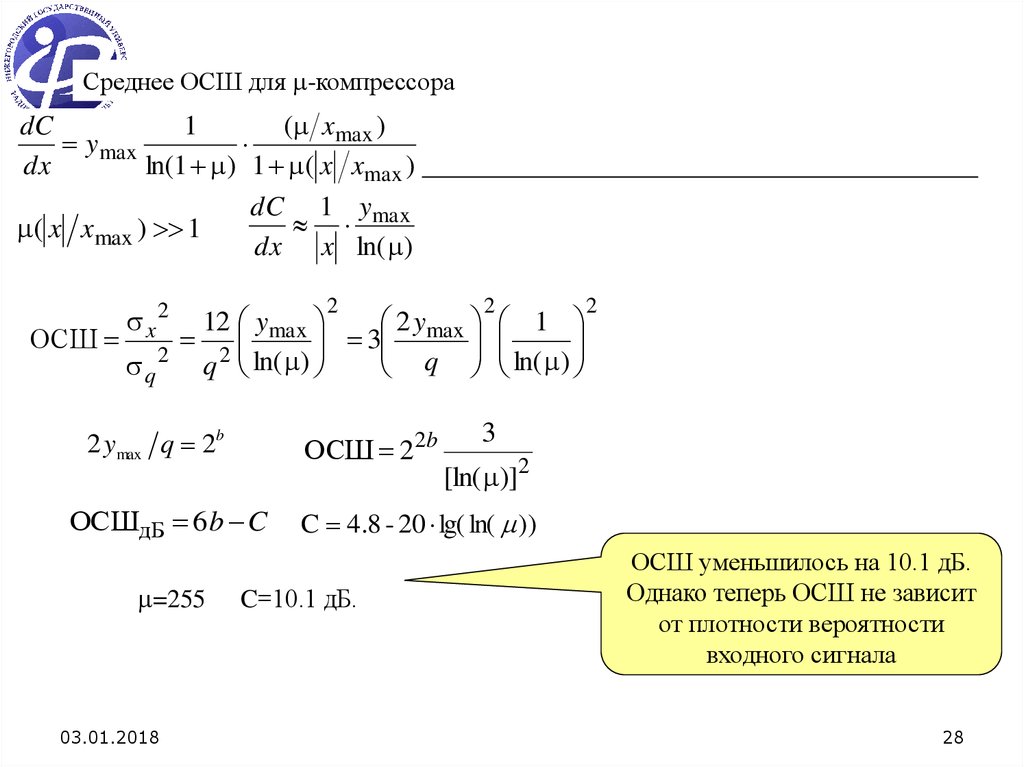
Среднее ОСШ для -компрессора( xmax )
dC
1
ymax
dx
ln(1 ) 1 ( x xmax )
dC 1 ymax
( x x max ) 1
dx x ln( )
ОСШ
x2
q 2
2
2y
12 y
2 max 3 max
q ln( )
q
2 ymax q 2b
ОСШ 22b
ОСШдБ 6 b C
=255
03.01.2018
2
1
ln( )
2
3
[ln( )]2
C 4.8 - 20 lg( ln( ))
C=10.1 дБ.
ОСШ уменьшилось на 10.1 дБ.
Однако теперь ОСШ не зависит
от плотности вероятности
входного сигнала
28
29. 4. Кодирование дискретных источников
X множество всевозможных дискретных сообщений x1, x2, …, xn передается по каналусвязи с вероятностями p(x1), p(x2), …, p(xn).
Условие непрерывной передачи: p(x1)+p(x2)+ … +p(xn)=1.
Энтропия источника (среднее количество информации
при передаче одного символа сообщения)
n
H ( X ) p ( xi ) log p ( xi )
i 1
H max log n - при равновероятных символах (p(xi)=1/n),
Кодовые слова фиксированной длины (при равновероятных символах источника)
Каждому из n символов источника ставится в соответствие R бит.
Эффективность кодирования – H/R (H – энтропия)
- n равно целой степени основания 2: число бит на символ источника R=log2(n), H/R=1
-n не равно целой степени основания 2: число бит на символ R= log2(n) +1, H/R<1
Кодовые слова переменной длины (при не равновероятных символах источника)
Должны выполняться два условия:
- требуется минимальное количество кодовых символов (бит) для передачи сообщения;
- отсутствуют потери передаваемой информации (однозначное декодирование)
Для выполнения второго условия используются префиксные (мгновенные) коды, в
которых начало более длинного кодового слова не совпадает с более коротким кодом.
В этом случае исключается неоднозначность при декодировании.
03.01.2018
29
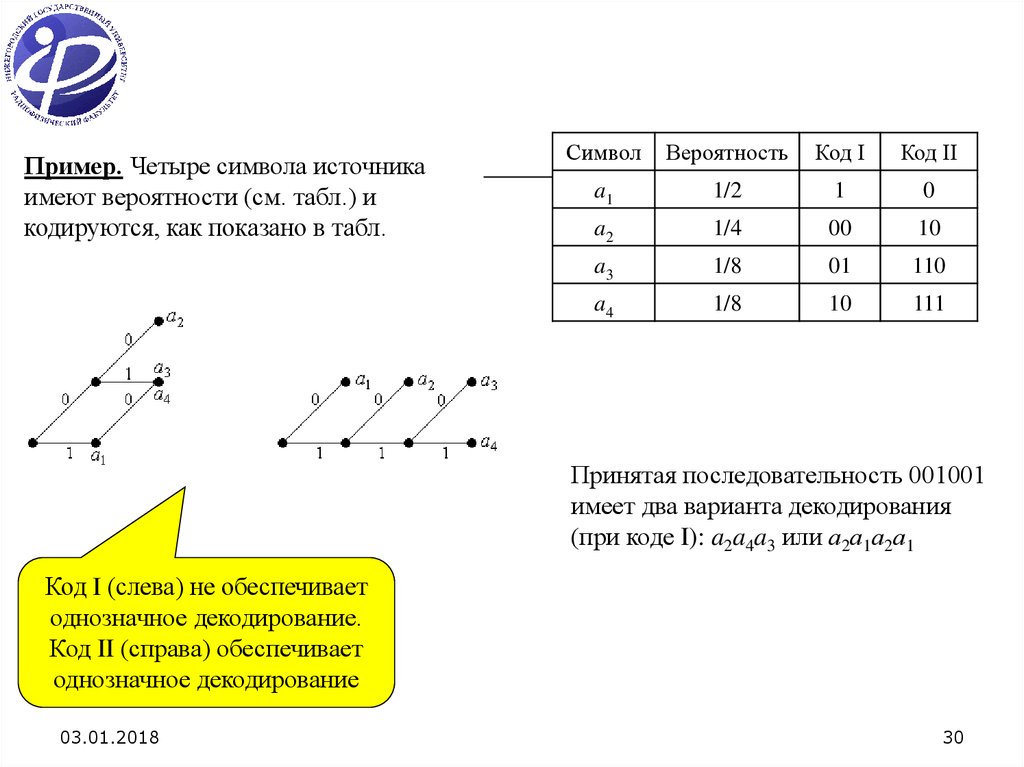
30.
Пример. Четыре символа источникаимеют вероятности (см. табл.) и
кодируются, как показано в табл.
Символ
Вероятность
Код I
Код II
a1
1/2
1
0
a2
1/4
00
10
a3
1/8
01
110
a4
1/8
10
111
Принятая последовательность 001001
имеет два варианта декодирования
(при коде I): a2a4a3 или а2а1а2а1
Код I (слева) не обеспечивает
однозначное декодирование.
Код II (справа) обеспечивает
однозначное декодирование
03.01.2018
30
31. Код Хаффмена
Энтропия источника H(X)=2.11.Средняя длина кодового слова R=2.21.
Эффективность кодирования
H(X)/R=95.5%.
Длина кодовой посылки обратно
пропорциональна его априорной
вероятности
Символ
сообщения
x1
x2
х3
х4
х5
x6
x7
Вероятность
символа
0.35
0.3
0.2
0.1
0.04
0.005
0.005
Двоичный
код символа
11
10
01
001
0001
00001
00000
03.01.2018
31
32. Код Шеннона-Фэно
Длина кодовой посылки обратнопропорциональна его априорной
вероятности
Символ сообщения
x1
x2
х3
х4
х5
x6
x7
Вероятность
символа
0.3
0.25
0.25
0.15
0.04
0.005
0.005
Двоичный код
символа
00
01
10
110
1110
11110
11111
03.01.2018
32
33. Лекции 3-4. 1. Некоторые сведения из теории информации.
1.1. Логарифмическая мера информации.Передается сообщение о событии, вероятность которого (априорная) равна P1.
После приема сообщения вероятность (апостериорная) события для получателя
равна P2. Прирост количества информации I log P2 log P2 log P1
P1
Идеальный канал связи без помех и искажений сигналов (P2=1)
I log P1
Чем меньше вероятность P1 (больше неопределенность) события, тем большая
информация о нем получается в результате приема сообщения. Если в качестве
основания логарифма выбрать 2, то единицей измерения информации является бит.
1.2. Количество информации в дискретных сообщениях.
Найдем информационное содержание сообщения, состоящего из n символов, при
алфавите, насчитывающем L символов S1, S2,…, SL.
Сколько различных последовательностей из n символов можно составить при
заданном алфавите из L различных символов? Рассмотрим частные случаи:
n=1 (одно сообщение содержит один символ) число возможных сообщений равно L;
03.01.2018
33
34.
n=2 (одно сообщение содержит два символа) число возможных сообщенийравно L L и возможные сообщения образуют следующую совокупность:
S1S1
S1S 2
...
S 2 S1
S2 S2
... S 2 S L
...
...
S L S1
S L S2
...
S1S L
...
... S L S L
при произвольном n число возможных сообщений
N (n) Ln
Символы сообщения равновероятны.
Количество информации в сообщении
I n log P1 log( 1 Ln ) n log L
H I n n log L бит/символ
Энтропия случайной величины (или сообщения)
Два свойства сообщений при равновероятных и независимых символах:
а) количество информации в сообщении пропорционально полному числу n
символов и логарифму от числа L различных символов в алфавите;
б) средняя информация, приходящаяся на один символ, зависит только от числа
различных символов в алфавите.
Символы сообщения не равновероятны.
n
Энтропия случайной величины (или сообщения) H j log Pj Pj log Pj бит/символ
j
03.01.2018
n
j
34
35.
Пример. Источник сообщений выдает дванезависимых символа: 0 с вероятностью q
и 1 с вероятностью (1-q). Энтропия
H (q) q log q (1 q) log( 1 q)
Два фактора уменьшают энтропию:
а) неравные вероятности символов в сообщении;
б) наличие связей (корреляции) между
отдельными символами в сообщении.
Передаваемые сообщения обладают избыточностью и число символов
в сообщении больше, чем это требуется при их независимости и
равномерном использовании. Поэтому фактическая энтропия H
меньше максимальной Hmax. Избыточность
H
R 1
03.01.2018
H max
35
36.
1.3. Информационная емкость дискретного сигналаДвоичный сигнал (-1, +1). Энтропия - 1 бит/символ.
и - длительность импульса. T=n и - длительность сообщения.
Количество информации n бит.
Полоса частот w 1/ и.
I n n T и Tw
Количество информации в сигнале
Информационная емкость сигнала C I / T w бит / сек
n
.
Информационная емкость
двоичного сигнала равна
полосе частот сигнала
2. Дискретный сигнал с различными амплитудами.
L - число возможных уровней амплитуды (число различных символов).
Количество информации в сигнале I n n log L (T / и ) log L Tw log L
Информационная емкость сигнала C I n / T w log L бит / сек
03.01.2018
Информационная
емкость является
предельной скоростью
передачи информации 36
37.
1.4. Информационная емкость непрерывного сигналаT - длительность сигнала. w=Fmax-Fmin – ширина полосы частот.
1/(2Fmax) – расстояние между выборками (теорема Котельникова).
Число выборок сигнала N
T
1 2 Fmax T 1
1 /( 2 Fmax )
Pс – мощность сигнала, Pш - СКО шума
Число L различимых уровней (приблизительно)
L
Pс Pш
Pш
Число L можно рассматривать как число различных символов алфавита,
а N – как общее число символов в сообщении
Полная информация в непрерывном сообщении
I T N log L (2 Fmax T 1) log
Pс Pш
Pш
Информационная емкость сигнала (предельная скорость безошибочной передачи
информации) при условии 2Fmax T 1
C
P Pш
I T (2 Fmax T 1) 1
log с
Fmax log( 1 ОСШ)
T
T
2
Pш
03.01.2018
Точное выражение
(несмотря на
приблизительное
определение L)
37
38.
1.5. Энтропия случайной непрерывной величины.p(x) - плотность вероятности.
p(xi) xi - вероятность попадания случайной величины x в интервал xi, xi+ xi.
i-ое дискретное сообщение - попадание x в этот интервал.
Энтропия непрерывного распределения
H lim
p
(
x
)
x
log[
p
(
x
)
x
]
i
i
i
i
xi 0
i
H lim
p( xi )[log p ( xi )] xi lim
p ( xi )[log xi ] xi
xi 0
i
xi 0 i
p ( x) log p( x)dx lim
p ( xi )[log xi ] xi .
Не зависит от
плотности вероятности
xi 0 i
Пусть xi= x. Второе слагаемое
lim
p( xi )[log xi ] xi lim
log x p( xi ) x lim
log x p( x)dx lim
log x
xi 0 i
x 0
x 0
i
x 0
Дифференциальная энтропия
H p( x) log p( x)dx
03.01.2018
38
39.
Примеры.1. Гармоническое колебание со случайной фазой , равномерно
распределенной на интервале [0 2 ], и с амплитудой A0.
p1( x)
Плотность вероятности
1
A02 x 2
2
Средняя мощность сигнала P0 0.5 A0
Энтропия
H 1 log 2
P0
2
2. Случайный процесс с нулевым средним и амплитудой,
равномерно распределенной на интервале [ A0 A0].
Плотность вероятности p2 ( x) 1 2 A0
Энтропия
H 2 log 2 12P0
3. Гауссов случайный процесс с нулевым средним и дисперсией (мощностью) P0.
Энтропия
H 3 log 2 2 eP0
H 3 H 2 log 2
03.01.2018
e
6
0.26
H 2 H1 log 2
24
2
0.64
39
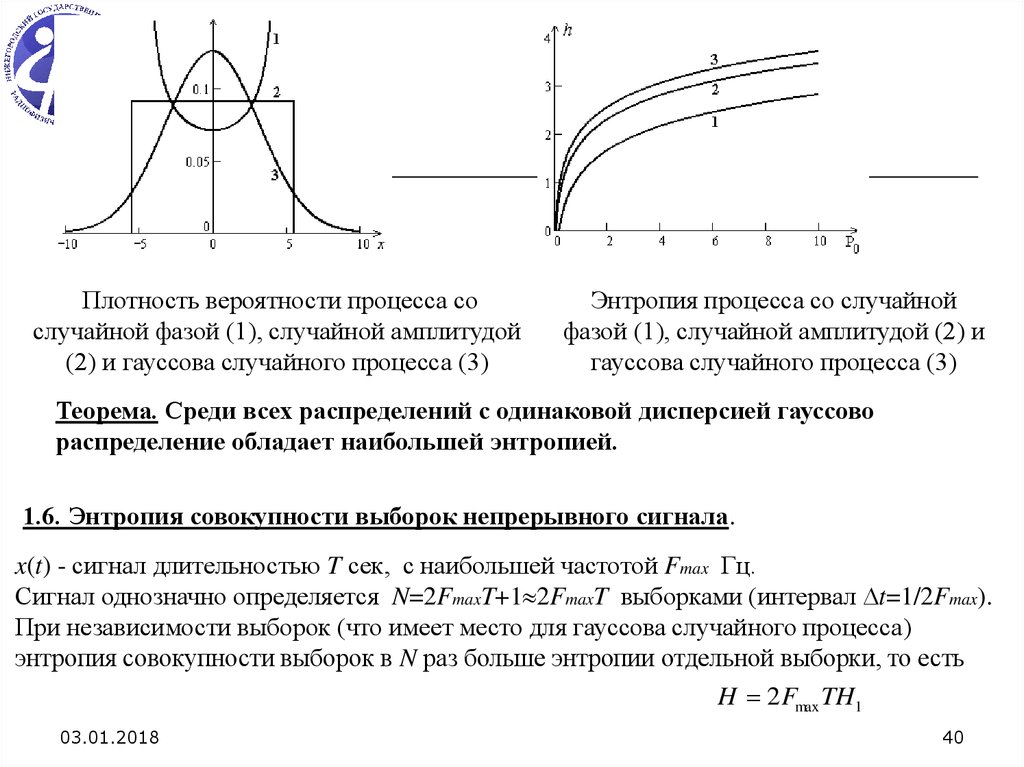
40.
Плотность вероятности процесса сослучайной фазой (1), случайной амплитудой
(2) и гауссова случайного процесса (3)
Энтропия процесса со случайной
фазой (1), случайной амплитудой (2) и
гауссова случайного процесса (3)
Теорема. Среди всех распределений с одинаковой дисперсией гауссово
распределение обладает наибольшей энтропией.
1.6. Энтропия совокупности выборок непрерывного сигнала.
x(t) - сигнал длительностью T сек, с наибольшей частотой Fmax Гц.
Сигнал однозначно определяется N=2FmaxT+1 2FmaxT выборками (интервал t=1/2Fmax).
При независимости выборок (что имеет место для гауссова случайного процесса)
энтропия совокупности выборок в N раз больше энтропии отдельной выборки, то есть
H 2 Fmax TH1
03.01.2018
40
41. 2. Модели каналов без памяти.
2.1. Двоичный симметричный канал без памяти (ДСКБП).Это канал с аддитивным шумом. В канал включены модулятор и демодулятор, как его
составные части (составной канал).
ДСКБП характеризуется набором X={0,1}
возможных входов, набором Y={0,1} возможных
выходов, а также набором условных вероятностей
P Y 1 X 0 P Y 0 X 1 p
возможных выходов при условии возможных входов
P Y 0 X 0 P Y 1 X 1 1 p
(вероятностей ошибок и правильной передачи)
Двоичный
симметричный канал
без памяти
03.01.2018
41
42.
2.2. Дискретный канал без памяти (ДКБП).Это канал с аддитивным шумом. В канал включены модулятор и демодулятор, как его
составные части (составной канал).
ДКБП характеризуется набором X={x0, x1, …, xq-1} возможных входов, набором
Y={y0, y1, …, yQ-1} возможных выходов, а также набором qQ условных вероятностей
возможных выходов при условии возможных входов
i=(1,2,…,Q-1), j=(1,2,…,q-1)
P(Y yi X x j ) P( yi x j )
- u1, u2, …, un – входная последовательность из n символов,
выбираемых из алфавита X,
- v1, v 2 , …, vn - выходная последовательность из n символов
из алфавита Y,
- совместные условные вероятности при отсутствии памяти
в канале равны
n
Дискретный канал
без памяти
03.01.2018
P(v1 , v2 ,..., vn u1 , u2 ,..., un ) P(vk uk )
k 1
42
43.
2.3. Канал с дискретным входом и непрерывным выходом.Это канал с аддитивным шумом. В канал включены модулятор и демодулятор, как его
составные части (составной канал).
Канал характеризуется набором X={x0, x1, …, xq-1} возможных
входов, непрерывным выходом Y={ , }, и условными
плотностями вероятностей P( y X x )
k=0,1,…,q-1
k
Наиболее важный канал этого типа – канал с аддитивным гауссовым шумом
Y=X+n, где n – гауссовы случайные величины с нулевым средним и СКО ,
X=xk (k=1,2,…,q-1).
( y xk )2
1
N ( xk , )
exp
Условная плотность вероятностей для X=xk P( y X xk )
2
2
2
- x1, x2, …, xn – входная последовательность из n символов,
- y1, y2, …, yn - выходная последовательность, yi=xi+ni (i=1,2,…,n).
- совместные условные вероятности при отсутствии памяти в канале
n
P( y1 , y2 ,..., yn x1 , x2 ,..., xn ) P( yk xk )
k 1
03.01.2018
43
44.
2.4. Сигнальный канал.Это физический канал (без модулятора и демодулятора) с аддитивным шумом,
в котором вход x(t) и выход y(t) являются сигналами (сигнальный канал).
Канал имеет единичный коэффициент передачи в полосе частот W.
y (t ) x(t ) n(t )
Выходной сигнал
Разложения x(t), y(t) и n(t) в полный ряд по ортонормированным функциям fi(t)
y(t ) yi f i (t );
x(t ) xi f i (t );
i
n(t ) ni f i (t )
i
T
Условия ортонормированности
0
i
1, (i j )
*
f i (t ) f j (t )dt ij
0, (i j )
T
Коэффициенты разложения
yi y(t ) f i (t )dt ,
*
0
yi xi ni
Выходной сигнал
TT
ni n j n(t )n ( )
*
*
*
ni – статистически независимые
случайные величины
03.01.2018
T
xi x(t ) f i (t )dt , ni n(t ) f i (t )dt
*
*
0
p( yi / xi )
fi (t ) f j ( )dtd i2
00
T
T
0
(y x )
1
exp i 2i
2 i
2 i
2
N ( xi , i )
fi* (t ) f j (t )dt i2 ij
0
N
p( y1 , y2 ,..., y N / x1 , x2 ,..., x N ) p( yi / xi )
i 1
44
45.
3. Спектральная эффективность каналов без памяти.3.1. Дискретный канал без памяти (ДКБП).
ДКБП характеризуется набором X={x0, x1, …, xq-1} возможных входов, набором
Y={y0, y1, …, yQ-1} возможных выходов, а также набором qQ условных вероятностей
P ( yi x j )
i=(1,2,…,Q-1), j=(1,2,…,q-1)
log P( yi x j ) P( yi ) - взаимная информация о событии X=xj, когда имеет место событие Y=yi
q 1
P( yi ) P( xk ) P( yi / xk )
k 0
q 1 Q 1
I ( X , Y ) P x j P yi / x j log 2
j 0 i 0
P yi / x j
P yi
- средняя взаимная информация о событии
X, когда имеет место событие Y
Спектральной эффективностью (СЭ) канала называется максимальное значение
величины I(X,Y) по набору вероятностей P ( x j ) входных символов.
q 1 Q 1
C max I ( X , Y ) max P x j P yi / x j log 2
P( x j )
P( x j )
j 0 i 0
при условиях P( x j ) 0,
03.01.2018
q 1
P yi / x j
P yi
Единица измерения
СЭ - бит/символ
P( x ) 1
j 0
j
45
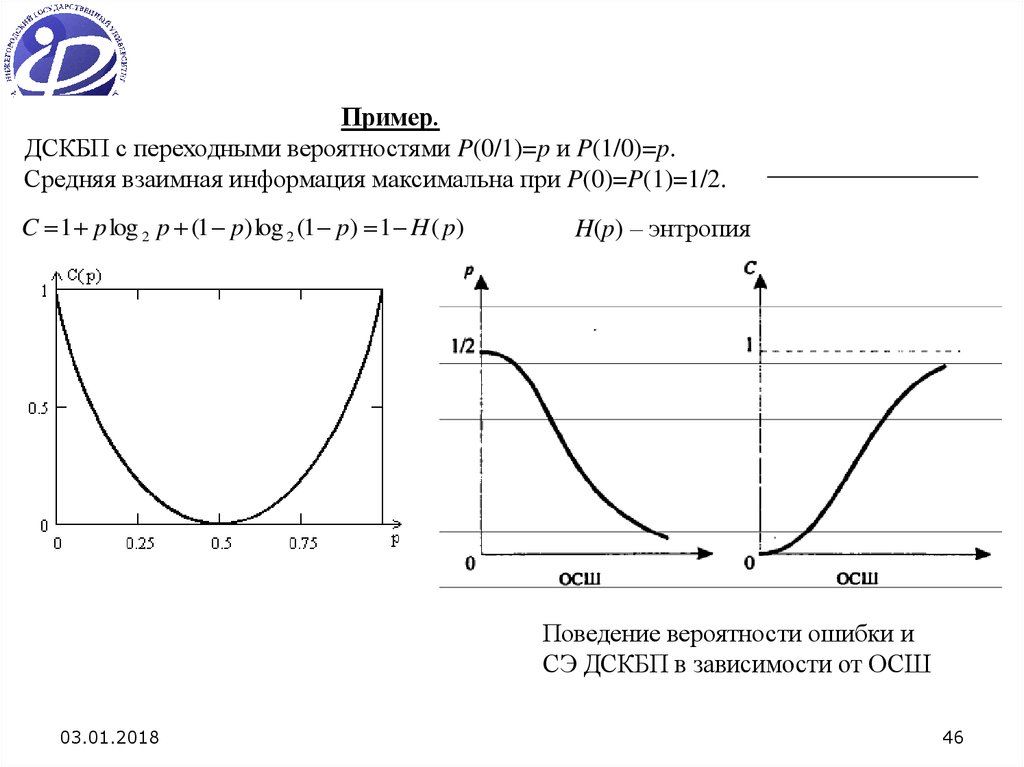
46.
Пример.ДСКБП с переходными вероятностями P(0/1)=p и P(1/0)=p.
Средняя взаимная информация максимальна при P(0)=P(1)=1/2.
C 1 p log 2 p (1 p) log 2 (1 p) 1 H ( p)
H(p) – энтропия
Поведение вероятности ошибки и
СЭ ДСКБП в зависимости от ОСШ
03.01.2018
46
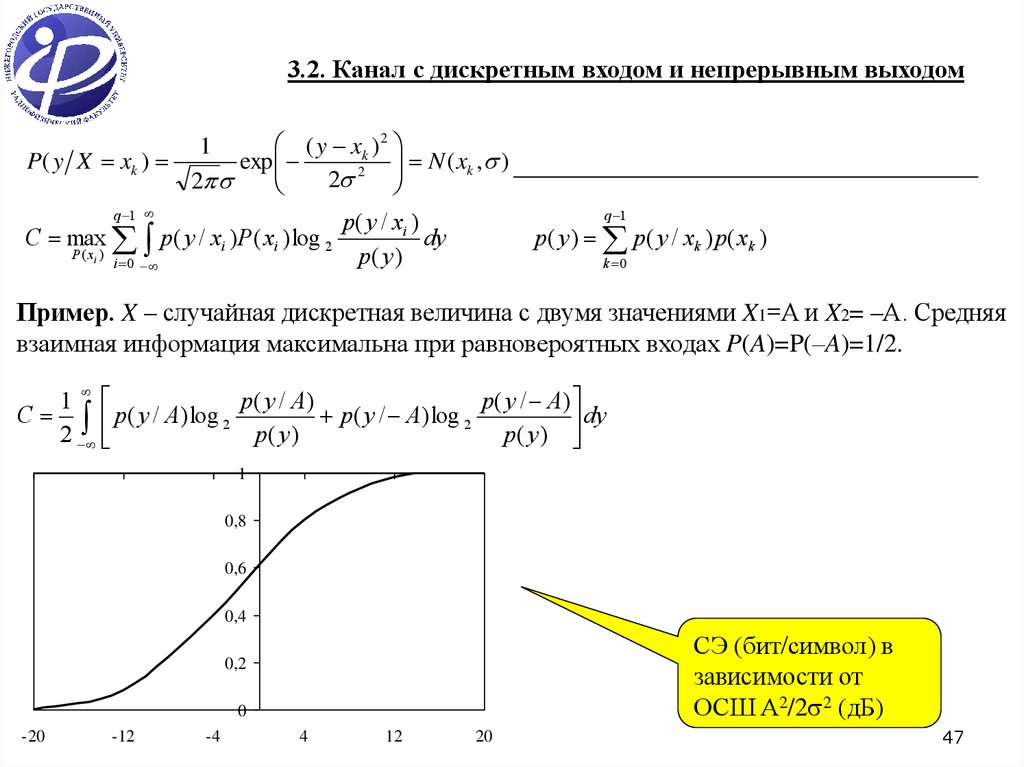
47.
3.2. Канал с дискретным входом и непрерывным выходом( y xk )2
1
N ( xk , )
P( y X xk )
exp
2
2
2
q 1
q 1
p ( y / xi )
C max p( y / xi ) P( xi ) log 2
dy
P ( xi )
p
(
y
)
i 0
p ( y ) p ( y / xk ) p ( xk )
k 0
Пример. X – случайная дискретная величина с двумя значениями X1=A и X2= –A. Средняя
взаимная информация максимальна при равновероятных входах P(A)=P(–A)=1/2.
1
p( y / A)
p ( y / A)
C p( y / A) log 2
p ( y / A) log 2
dy
2
p( y)
p( y )
1
0,8
0,6
0,4
СЭ (бит/символ) в
зависимости от
ОСШ A2/2 2 (дБ)
0,2
0
-20 03.01.2018
-12
-4
4
12
20
47
48.
3.3. Ограниченный по полосе частот канал с аддитивным шумом и дискретнымвременем (канал с непрерывным входом и непрерывным выходом).
C lim max
СЭ такого канала в единицу времени (Шеннон, 1948 год)
Средняя взаимная информация между X и Y
T p ( x )
I ( X ;Y )
1
I ( X ;Y )
T
p( x) p( y / x) log
p( y / x)
dxdy
p( y )
Непрерывные функции y(t), x(t) и n(t) заменяем их выборками {yi}, {xi} и {ni}, взятыми
через интервалы времени t=1/2W (теорема отсчетов).
Затем находим среднюю взаимную информацию между векторами XN ={x1, …, xN} и
YN ={y1, …, yN} размерности N=2WT. Имеем yi xi ni
Выборки шума статистически независимыми между собой.
Средняя взаимная информация между XN и YN равна сумме
средних взаимных информаций между отдельными выборками
N
I ( X N ; YN )
i 1
p( yi / xi ) p( xi ) log
I ( xi , yi ) H ( yi ) H ( yi / xi )
03.01.2018
N
I ( X N ; YN ) I ( xi ; yi )
i 1
p( yi / xi )
dxi dyi
p ( yi )
I ( xi , yi ) H ( yi ) H (ni )
48
49.
Энтропия N=2WT выборок шумаH (N N ) 2WT log 2 2 e 02
xi – гауссовы случайные величины с нулевым
средним и стандартным отклонением x
Энтропия N=2WT выборок выходной смеси
xi 2
1
p( xi )
exp 2 N (0, x )
2 x
2 x
H (YN ) 2WT log 2 2 e( x2 02 )
x2
1 x2
C N log 1 2 WT log 1 2
2 0
0
СЭ канала в единицу времени (удельная СЭ)
x2
C W log 1 2 W log 1 ОСШ
0
Нормированная СЭ
(бит/символ)
03.01.2018
49
50.
Спектральная плотность мощности шума - N 0 02 WC W log 1
WN 0
2
x
W
2x
W ln 1
WN 0
2x
C
ln 2
N 0 ln 2
C 14.4
Удельная СЭ при
x2 N 0 10
Eb – энергия одного бита, а СЭ C определена в бит/символ.
Спектральная плотность мощности шума - x2 CEb / T C Eb
C E
C W log 1 b
W N0
03.01.2018
Eb 2 C W 1
N0
C W
C W 1
Eb N 0 1
50
51.
1. C WEb 2C W
C
C
exp ln 2 ln
N0 C W
W
W
2. C W 0
Eb
2C W 1
lim
ln 2 1,6 дБ
N 0 C W 0 C W
Теорема кодирования в
канале с шумами
(теорема Шеннона)
Существуют кодеры канала (и декодеры),
которые могут обеспечить надежную связь
со сколь угодно малой вероятностью
ошибки, если скорость передачи R<C.
Если R>C, то не существуют кодеры
канала (и декодеры), которые могут
обеспечить стремление вероятности
ошибки к нулю.
Смысл теоремы Шеннона: шум может определять СЭ канала, а не точность передачи
информации. В пределе можно получить сколь угодно высокую безошибочность
передачи данных, применяя кодирование достаточно больших блоков.
03.01.2018
51
52.
Лекция 5.Модуляции, используемые в системах цифровой связи
1. Цифровой модулятор преобразует битовую последовательность в последовательность
узкополосных электрических сигналов, имеющих форму импульсов.
2. Модуляция M-го порядка. Если последовательность {an} из b бит преобразуется в
сигнал, то модулятор должен иметь возможность вырабатывать M=2b
детерминированных сигналов {sm(t), m=1,2,…,M}, так как число возможных двоичных
последовательностей, которые можно получить из b бит, равно 2b.
3. Если двоичную последовательность необходимо передавать со скоростью R бит/сек,
то она входит в модулятор за время b/R секунд, т.е. длительность сигналов должна
составлять b/R секунд, а символьная скорость равна R/b символов в секунду.
4. Когда отображение цифровой последовательности {an} в сигнал осуществляется так,
что сигнал, передаваемый на данном временном интервале, зависит от одного или более
сигналов, переданных раньше, то говорят, что модулятор имеет память.
5. Если отображение цифровой последовательности {an} в сигналы {sm(t)},
осуществляется так, что передаваемые сигналы не зависят от ранее переданных
сигналов, то модулятор называют модулятором без памяти.
03.01.2018
52
53.
1. Одномерная амплитудная модуляция (АМ).Цифровой АМ сигнал на интервале времени (0 t T) можно представить как
sm (t ) Re Am g (t ) exp( j 2 f c t ) Am g (t ) cos 2 f 0t
где Am (m=1,2,…,M) - возможные амплитуды, соответствующие M=2b сигналам.
Функция g(t) описывает форму вещественного сигнального импульса, которая
определяет спектр передаваемого сигнала.
Амплитуда сигнала Am принимает дискретные значения
Am 2m 1 M d , m 1,2, , M ,
Таким образом, имеем, что
где 2d – расстояние между соседними амплитудами
A1 ( M 1)d ,..., AM ( M 1)d .
Двоичная последовательность на входе модулятора имеет скорость R бит/сек.
Скорость передачи символов (скорость изменения амплитуды несущей ) равна R/b.
Tb 1 / R
- информационный или битовый временной интервал
T k / R kTb - сигнальный интервал
03.01.2018
53
54.
Tm
2
sm
(t )dt
0
T
1 2 2
1
Am g (t )dt Am2 g
2
2
0
- энергия сигналов АМ,
Eg - энергия импульса g(t)
АМ сигналы являются одномерными и их можно представить в виде
sm (t ) sm f (t )
где
s m Am 0.5 g
f (t ) (2 g ) g (t ) cos 2 f c t
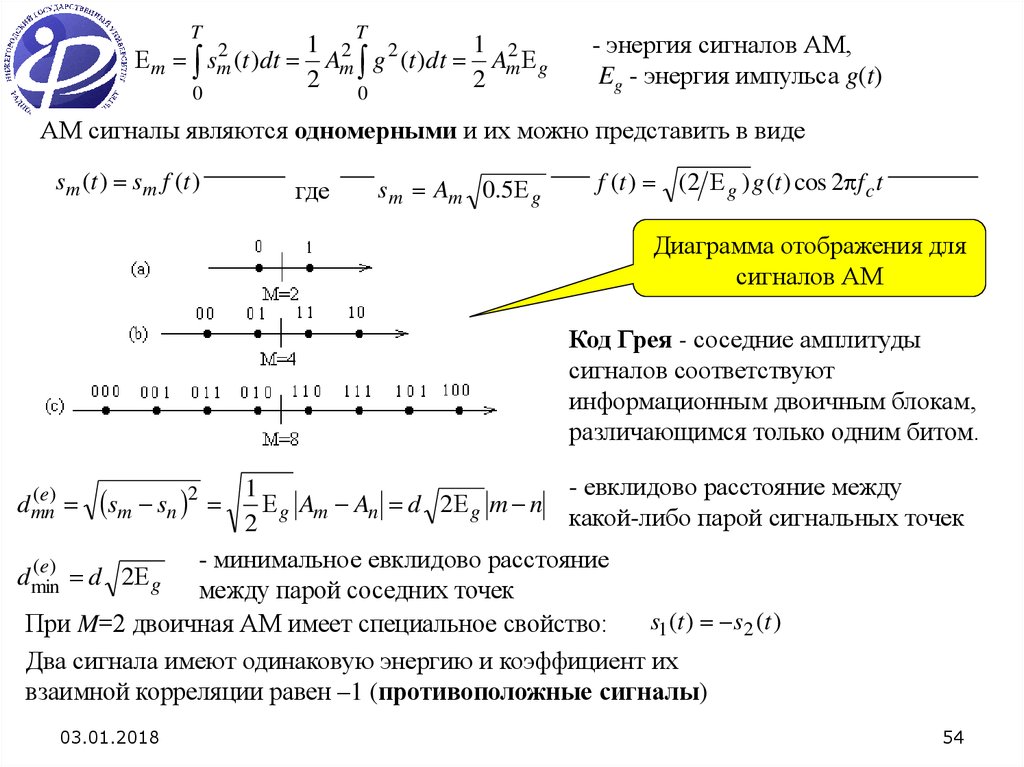
Диаграмма отображения для
сигналов АМ
Код Грея - соседние амплитуды
сигналов соответствуют
информационным двоичным блокам,
различающимся только одним битом.
- евклидово расстояние между
1
g Am An d 2 g m n
какой-либо парой сигнальных точек
2
- минимальное евклидово расстояние
( e)
dmin
d 2 g
между парой соседних точек
s1 (t ) s2 (t )
При M=2 двоичная АМ имеет специальное свойство:
Два сигнала имеют одинаковую энергию и коэффициент их
взаимной корреляции равен –1 (противоположные сигналы)
(e)
d mn
sm sn 2
03.01.2018
54
55.
2. Двумерная фазовая модуляция (ФМ).При ФМ M сигналов на интервале времени (0 t T) можно представить в виде
2 (m 1)
sm (t ) Re g (t )e j 2 ( m 1) / M e j 2 f 0t g (t ) cos 2 f 0t
M
2 (m 1)
2 (m 1)
g (t ) cos
cos 2 f 0t g (t ) sin
sin 2 f 0t ,
M
M
m 2 (m 1) / M
- M возможных значений фазы несущей, которая переносит
передаваемую информацию
T
ФМ сигналы имеют одинаковую энергию
E
T
2
sm
(t )dt
0
1
1
g 2 (t )dt E g
20
2
Сигналы с ФМ являются двумерными и их можно представить в виде
sm (t ) sm1 f1 (t ) sm 2 f 2 (t )
S m sm1, sm2 T
sm1
g
где f1 (t ) (2 g ) g (t ) cos 2 f 0t ,
- двумерный вектор с компонентами
g
2 (m 1)
2 (m 1)
cos
, sm 2
sin
,
2
M
2
M
03.01.2018
f 2 (t ) (2 g ) g (t ) sin 2 f 0t
(m 1,2, , M ).
55
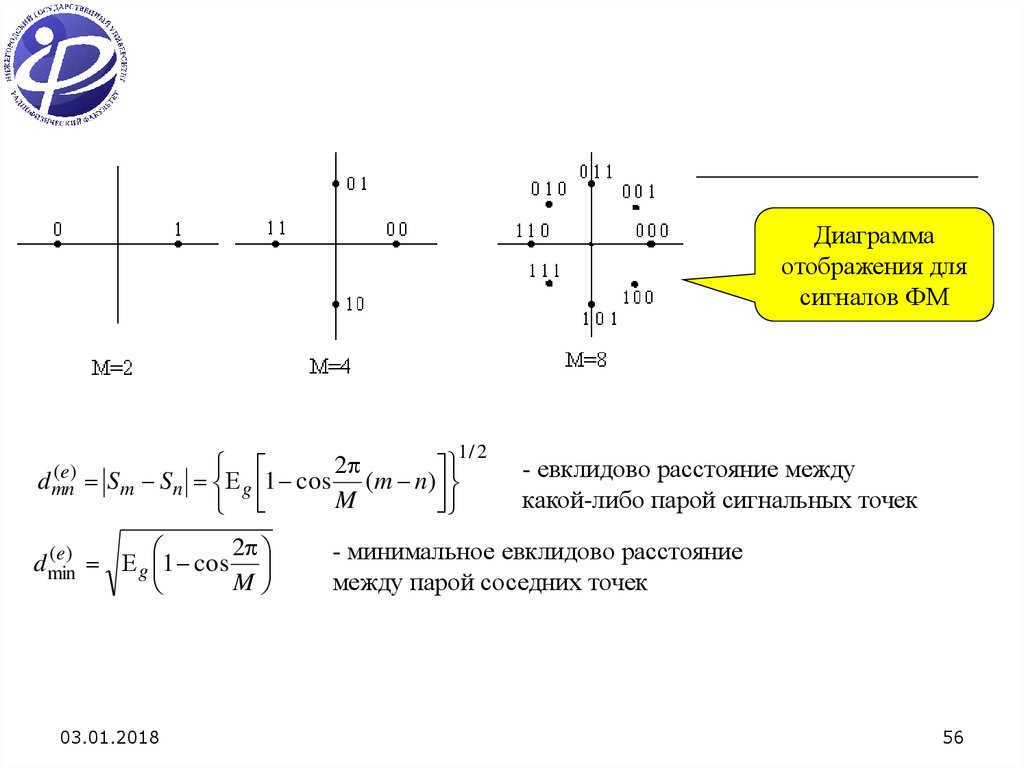
56.
Диаграммаотображения для
сигналов ФМ
1/ 2
(e)
d mn
2
Sm Sn g 1 cos (m n)
M
2
(e)
d min
g 1 cos
M
03.01.2018
- евклидово расстояние между
какой-либо парой сигнальных точек
- минимальное евклидово расстояние
между парой соседних точек
56
57.
3. Двумерная квадратурная амплитудная модуляция (КАМ)Одновременная передача двух отдельных b-битовых информационных блоков на двух
несущих, находящихся в квадратуре (cos2 f0t и sin2 f0t), называется квадратурной АМ
или КАМ.
Два представления сигналов КАМ на интервале времени (0 t T)
sm (t ) Re Amc jAms g (t )e j 2 f0t Amc g (t ) cos 2 f 0t Ams g (t ) sin 2 f 0t
где Amc и Ams – информационные амплитуды для квадратурных несущих
2
2
sm (t ) Re Vme j m g (t )e j 2 f ct Vm g (t ) cos 2 fct m , Vm Amc Ams
m arctg Ams Amc
Сигнал КАМ можно рассматривать как комбинацию АМ и ФМ.
Можно образовать определенную комбинацию М1-уровневой АМ и М2-позиционной ФМ
В результате получается сигнальное созвездие комбинированной АМ-ФМ, содержащее
М=М1 М2 точек пространства сигналов.
Если М1=2n и М2=2m, то сигнальное созвездие позволяет передавать m+n=logM1M2
двоичных символов со скоростью R/(m+n).
03.01.2018
57
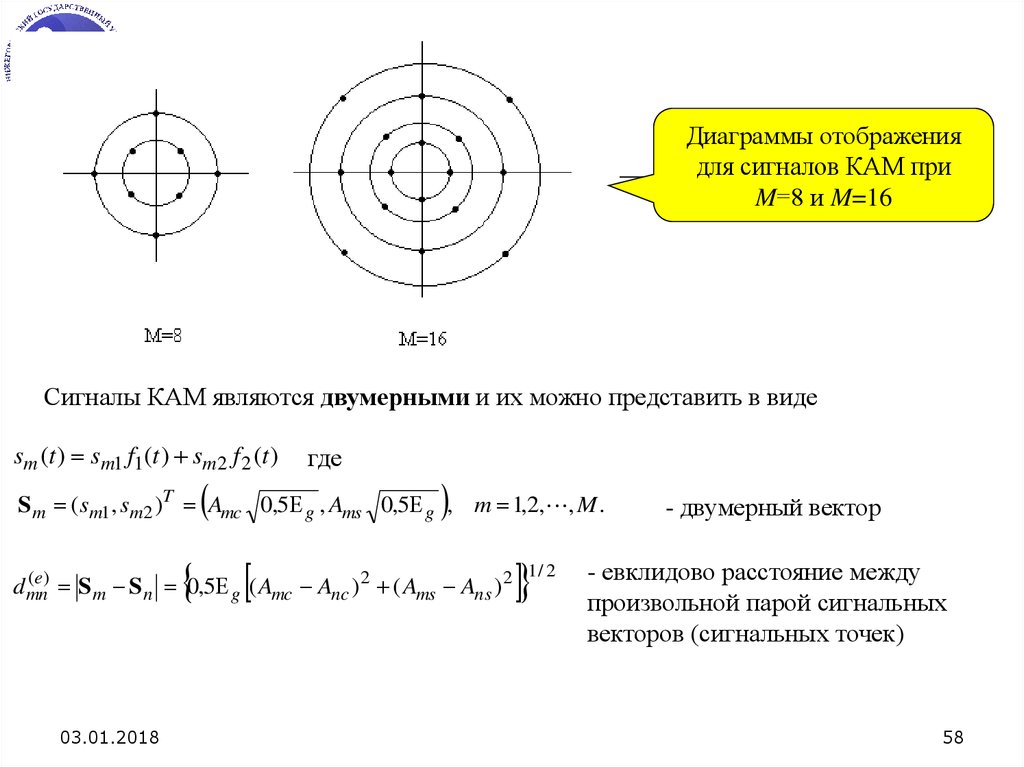
58.
Диаграммы отображениядля сигналов КАМ при
M=8 и M=16
Сигналы КАМ являются двумерными и их можно представить в виде
sm (t ) sm1 f1 (t ) sm 2 f 2 (t )
где
S m (sm1, sm2 )T Amc 0,5 g , Ams 0,5 g , m 1,2, , M .
( e)
d mn
S m S n 0,5 g ( Amc Anc ) 2 ( Ams Ans ) 2
03.01.2018
1/ 2
- двумерный вектор
- евклидово расстояние между
произвольной парой сигнальных
векторов (сигнальных точек)
58
59.
Наиболее интересен случай, когда амплитудыквадратурных сигналов принимают дискретные значения
2m 1 M d , (m 1,2, , M )
Диаграмма отображения становится прямоугольной
Диаграммы отображения для
сигналов КАМ при разных M
( e)
dmin
d 2 g
03.01.2018
- минимальное евклидово расстояние между парой соседних точек
59
60.
Двумерные 4-ФМ, 16-КАМ и 64-КАМ сигналы имеют вид( I jQ )
d (t ) Re
g (t ) exp(2 f c t )
k
нормирующий множитель (выбирается из
условия единичной средней мощности сигналов)
2-ФМ сигналы: I= 1; Q=0.
k=1
d min 2
4-ФМ сигналы: I= 1; Q= 1
k 2
d min 2
16-КАМ сигналы: I= 1, 3; Q= 1, 3
k 10
d min 2
64-КАМ сигналы: I= 1, 3, 5, 7; Q= 1, 3, 5, 7
03.01.2018
k 42
dmin 2
10
42
60
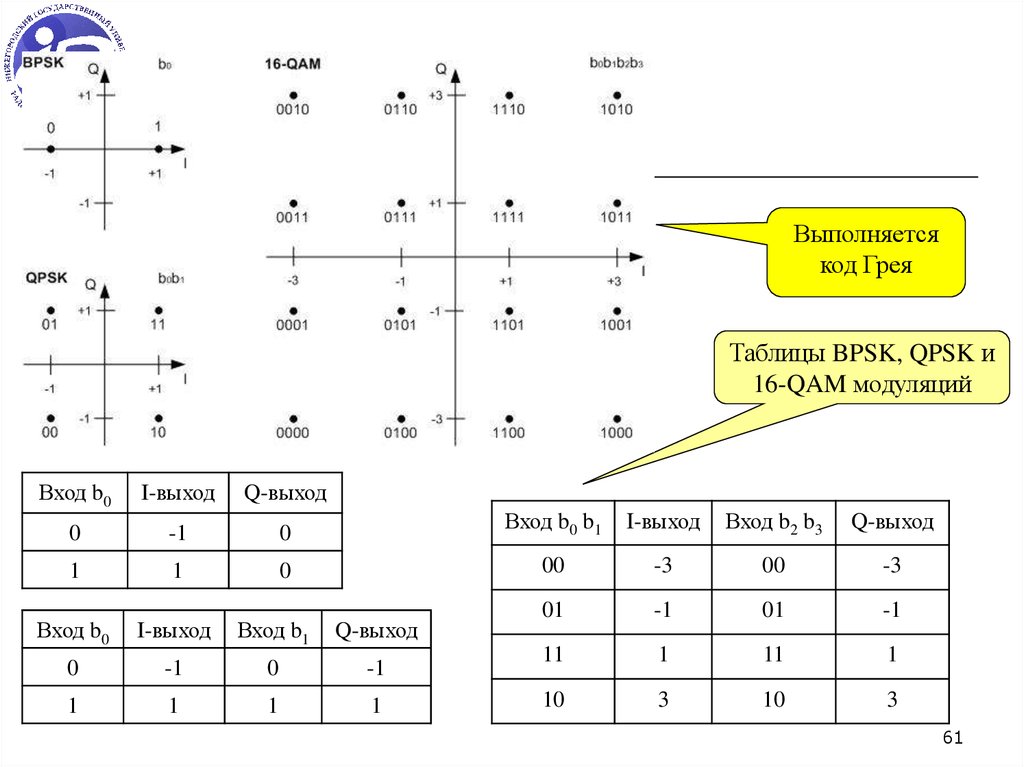
61.
Выполняетсякод Грея
Таблицы BPSK, QPSK и
16-QAM модуляций
Вход b0
I-выход
Q-выход
0
-1
0
Вход b0 b1
I-выход
Вход b2 b3
Q-выход
1
1
0
00
-3
00
-3
Вход b0
Вход b1
01
-1
01
-1
I-выход
Q-выход
0
-1
0
-1
11
1
11
1
1
1
1
1
10
3
10
3
61
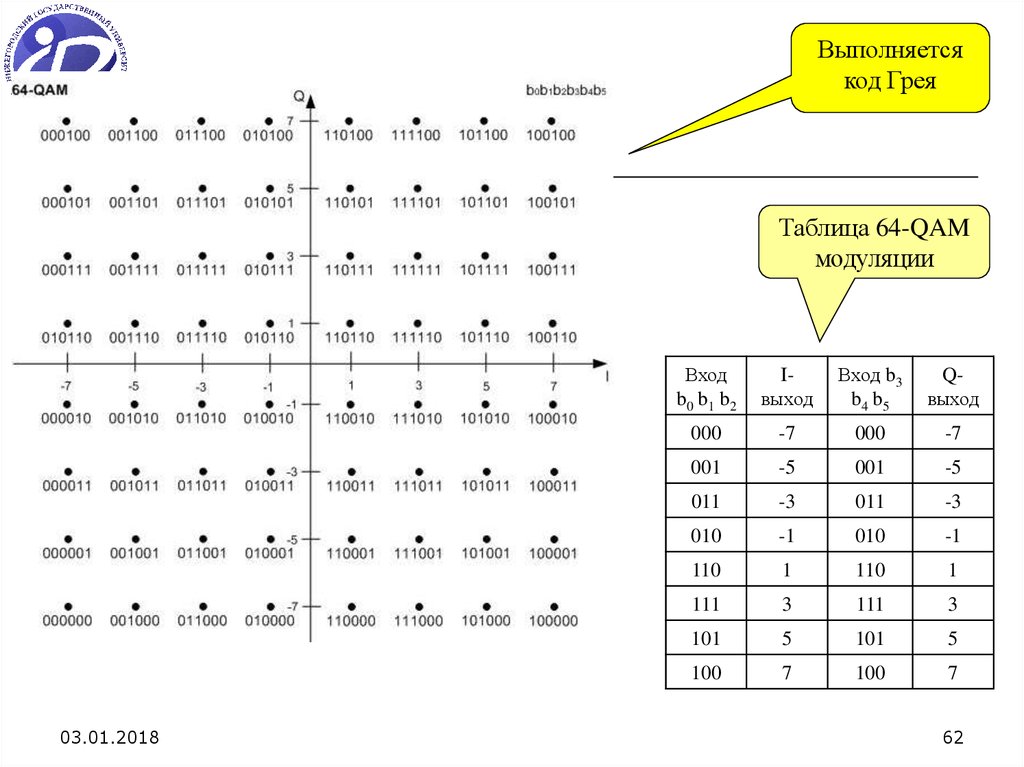
62.
Выполняетсякод Грея
Таблица 64-QAM
модуляции
03.01.2018
Вход
b0 b1 b2
Iвыход
Вход b3
b4 b5
Qвыход
000
-7
000
-7
001
-5
001
-5
011
-3
011
-3
010
-1
010
-1
110
1
110
1
111
3
111
3
101
5
101
5
100
7
100
7
62
63.
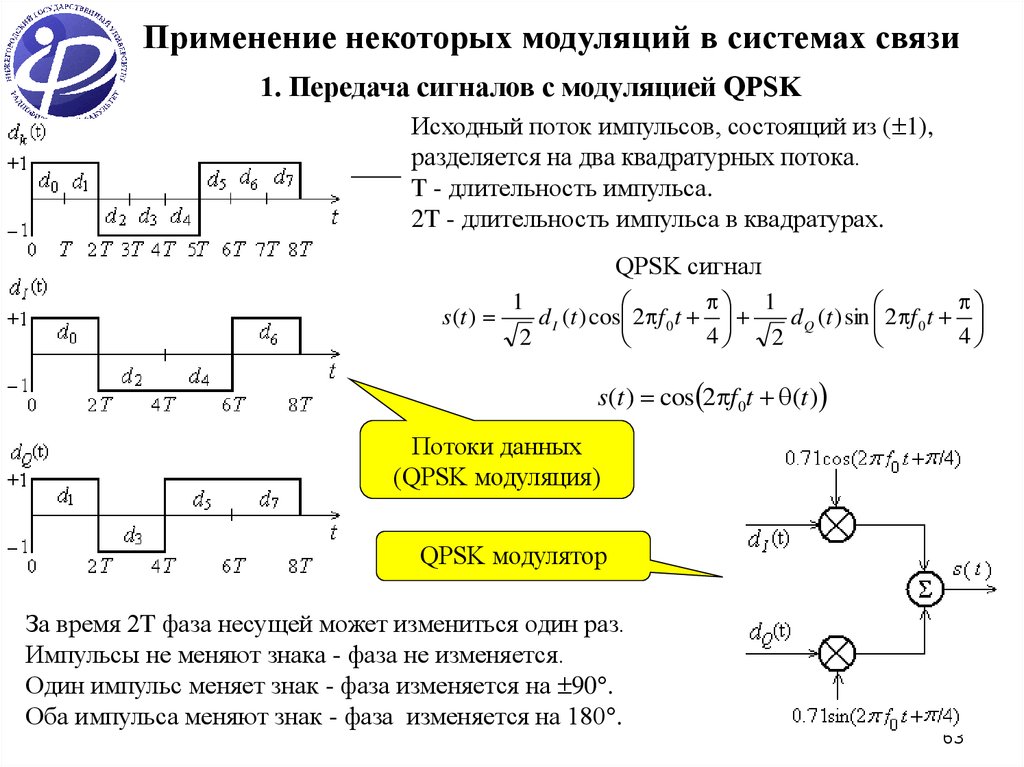
Применение некоторых модуляций в системах связи1. Передача сигналов с модуляцией QPSK
Исходный поток импульсов, состоящий из ( 1),
разделяется на два квадратурных потока.
T - длительность импульса.
2T - длительность импульса в квадратурах.
QPSK сигнал
s (t )
1
d I (t ) cos 2 f 0 t
d Q (t ) sin 2 f 0 t
4
4
2
2
1
s(t ) cos 2 f 0t (t )
Потоки данных
(QPSK модуляция)
QPSK модулятор
За время 2T фаза несущей может измениться один раз.
Импульсы не меняют знака - фаза не изменяется.
Один импульс меняет знак - фаза изменяется на 90 .
Оба импульса меняют знак - фаза изменяется на 180 .
63
64.
2. Передача сигналов с модуляцией OQPSK (Offset QPSK)В QPSK потоки импульсов dI(t) и dQ(t)
синхронизированы так, что их переходы
совпадают по времени (см. предыдущий слайд).
В OQPSK эти потоки синхронизированы со
сдвигом на T. Поэтому фаза несущей не может
измениться на 180 . За каждые T секунд фаза
может измениться только на 0 или 90 .
Потоки данных (OQPSK модуляция)
Потоки данных
(OQPSK модуляция)
QPSK и OQPSK
сигналы
64
65.
3. Манипуляция с минимальным частотным сдвигом (ММС)ММС - разновидность OQPSK с
синусоидальным взвешиванием символов.
Это модуляция по частоте с памятью.
t
t
s (t ) d I (t ) cos
cos 2 f 0t dQ (t ) sin
sin 2 f 0t
2
T
2
T
d I 1, d Q 1,
d I 1, d Q 1,
t
s (t ) cos 2 f 0t
2T
t
s (t ) cos 2 f 0t
2T
1. Сигнал s(t) имеет постоянную составляющую
2. Фаза несущей непрерывна при изменении
значений dI(t) и dQ(t)
3. Сигнал s(t) - частотно манипулированный
сигнал с частотами передачи
f1 f 0
1
4T
f2 f0
1
4T
4. Разнесение между частотами - 1 2T
Формирование сигнала ММС
65
66.
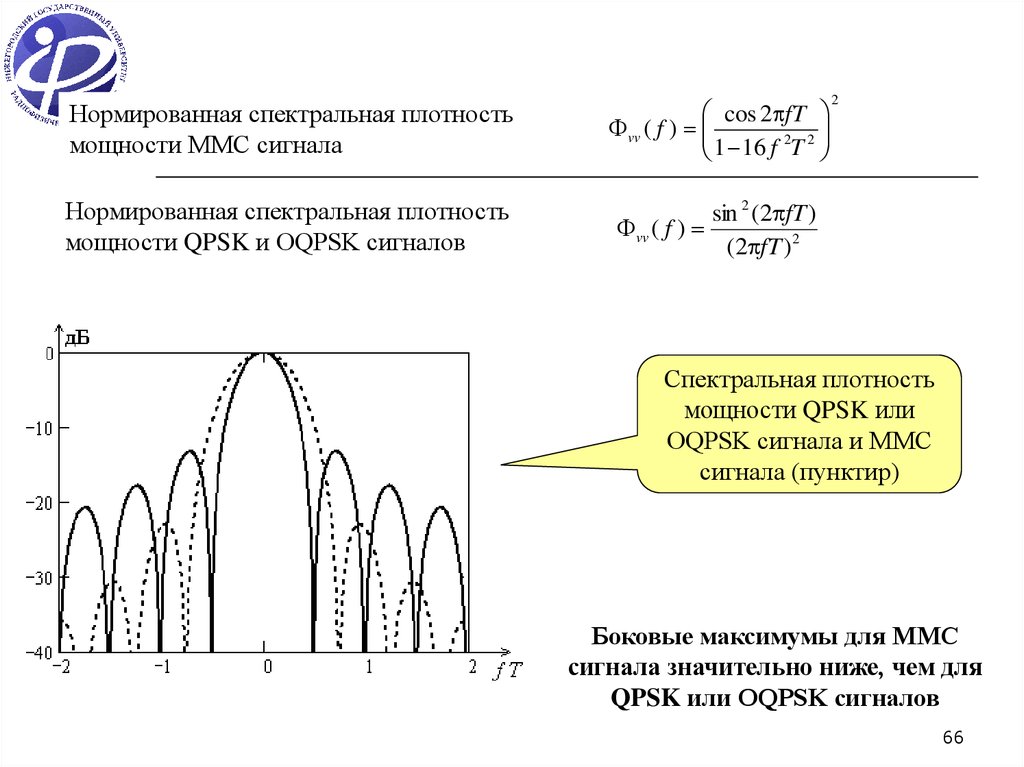
Нормированная спектральная плотностьмощности ММС сигнала
cos 2 fT
vv ( f )
2 2
1
16
f
T
Нормированная спектральная плотность
мощности QPSK и OQPSK сигналов
sin 2 (2 fT )
vv ( f )
(2 fT ) 2
2
Спектральная плотность
мощности QPSK или
OQPSK сигнала и ММС
сигнала (пунктир)
Боковые максимумы для ММС
сигнала значительно ниже, чем для
QPSK или OQPSK сигналов
66
67.
4. Гауссова частотная манипуляция с минимальным частотнымсдвигом (GMSK - Gaussian Minimum Shift Keying) -
На интервале одного символа фаза
несущей частоты изменяется на 90
град. и непрерывна при переходе
от одного символа к другому
Амплитуда изменяется только
при передаче 1.
Это - дифференциальное
кодирование.
bk ak b k 1
ak – входная двоичная информационная последовательность кодера,
bk – выходная последовательность кодера, - суммирование по модулю 2.
bk=1, передаваемый сигнал – положительный прямоугольный импульс,
bk=0, передаваемый сигнал – это отрицательный прямоугольный импульс.
Операция дифференциального кодирования вводит память в сигнал.
67
68.
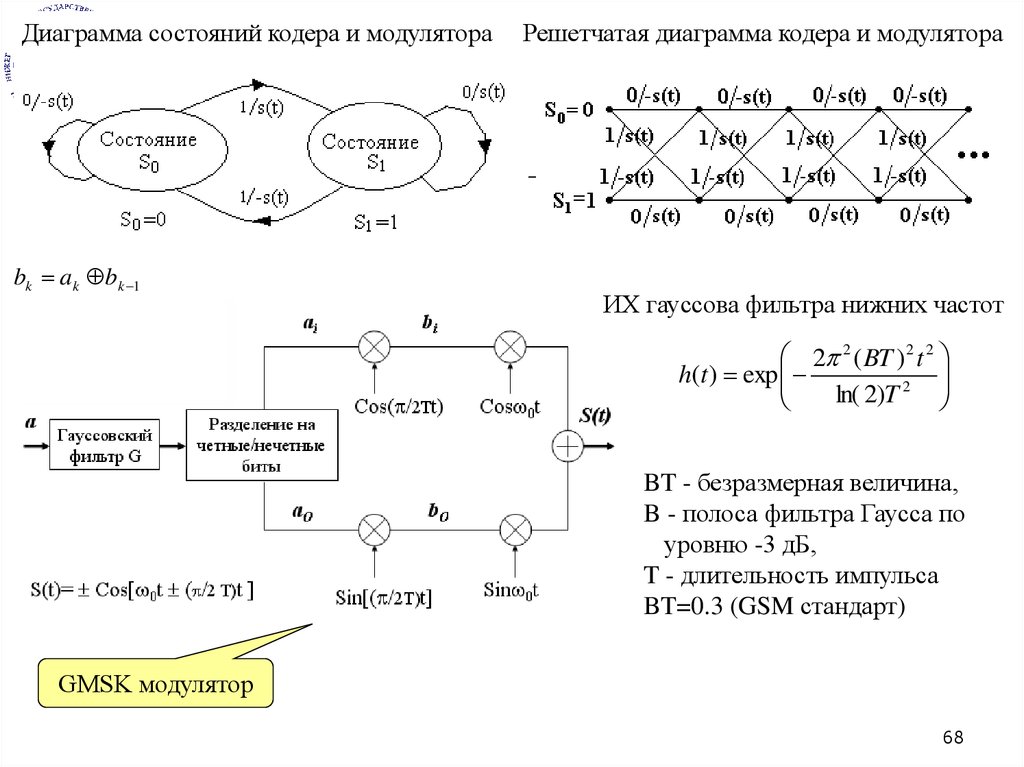
Диаграмма состояний кодера и модулятораbk ak b k 1
Решетчатая диаграмма кодера и модулятора
ИХ гауссова фильтра нижних частот
2 2 ( BT ) 2 t 2
h(t ) exp
2
ln(
2
)
T
BT - безразмерная величина,
B - полоса фильтра Гаусса по
уровню -3 дБ,
T - длительность импульса
BT=0.3 (GSM стандарт)
GMSK модулятор
68
69.
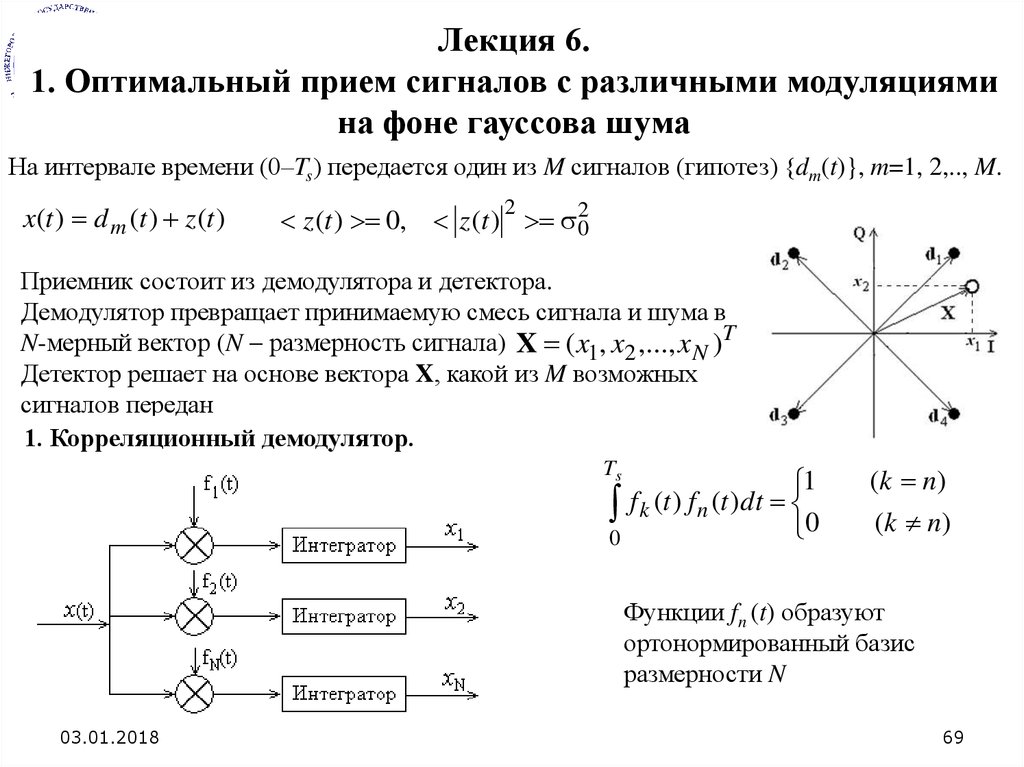
Лекция 6.1. Оптимальный прием сигналов с различными модуляциями
на фоне гауссова шума
На интервале времени (0–Ts) передается один из M сигналов (гипотез) {dm(t)}, m=1, 2,.., M.
x(t ) d m (t ) z (t )
2
z (t ) 0, z (t ) 02
Приемник состоит из демодулятора и детектора.
Демодулятор превращает принимаемую смесь сигнала и шума в
N-мерный вектор (N размерность сигнала) X ( x1, x2 ,..., x N )T
Детектор решает на основе вектора X, какой из M возможных
сигналов передан
1. Корреляционный демодулятор.
Ts
0
1
f k (t ) f n (t )dt
0
( k n)
( k n)
Функции fn (t) образуют
ортонормированный базис
размерности N
03.01.2018
69
70.
2-ФМ сигналы (N=1)g
Ts
g
2
d1 (t ) g (t ) cos 2 f ct ,
d 2 (t ) g (t ) cos 2 f ct
(t )dt – энергия импульса g(t).
0
d1 (t ) d1 f1 (t )
d 2 (t ) d 2 f1 (t )
d1( 2) 0.5 E g
Прямоугольный импульс – g(t)=const на интервале (0–Ts)
f1 (t ) 2 E g g (t ) cos 2 f ct
f1 (t ) 2 Ts cos 2 f ct
Демодулятор состоит из одного коррелятора.
4-ФМ-сигналы
(N=2)сигналы (N=2)
4-ФМ,
16- и 64-КАМ
Прямоугольный импульс
f1 (t ) 2 Ts cos 2 f ct
f 2 (t ) 2 Ts sin 2 f ct
Демодулятор состоит из двух корреляторов.
03.01.2018
70
71.
Проекции на базисные функцииTs
Ts
0
0
x(t ) f k (t )dt [d m (t ) z(t )] f k (t )dt
Ts
Ts
Ts
0
0
0
xk x(t ) f k (t )dt , d mk d m (t ) f k (t )dt , zk z (t ) f k (t )dt
xk d mk z k
(k 1, 2,..., N )
Ts
z k z (t ) f k (t )dt 0
0
zk zm
Ts Ts
Ts Ts
00
00
z (t ) z ( ) f k (t ) fm ( )dtd z
Ts
0.5 N 0 f k (t ) f m ( )dt 0.5 N 0 km,
0
2z 0.5N0
z k2
1
p( z k )
exp 2
2
2 z
z
03.01.2018
2
(t ) (t ) f k (t ) f m ( )dtd
0.5N0 – спектральная плотность мощности шума в
области положительных и отрицательных частот
xk d mk
2x 2z 0.5N 0
xk dmk 2
1
p( xk )
exp
2
2 x
2 x
Статистически независимые гауссовы случайные величины
71
72.
Np( X / d m ) p( x1 , x2 ,..., x N / d m1d m2 ,..., d mN ) p( xk / d mk )
k 1
( xk d mk ) 2
1
p( xk / d mk )
exp
N
N 0
0
N ( xk d mk ) 2
p( X / d m )
exp
N 2
N
( N 0 )
0
k 1
1
m=1,2, …, M
2. Согласованный фильтр (СФ) как демодулятор.
ИХ k-го согласованного фильтра
согласована с k-й базисной функцией
f k (Ts t ),
hk (t )
0,
03.01.2018
0 t Ts
t 0, t Ts
72
73.
Выходные сигналы СФ (интеграл Дюамеля)t
t
0
0
xk (t ) x( )hk (t )d x( ) f k (Ts t )d
Отсчет в момент времени t=Ts
Совпадение с выходными
сигналами корреляторов
Ts
xk (Ts ) x( ) f k ( )d
0
3. Основные критерии, используемые для принятия решений.
- Критерий максимума апостериорной вероятности
- Критерий максимального правдоподобия
Критерий максимума апостериорной вероятности.
на вычислении апостериорных вероятностей
Алгоритм оценки переданного сигнала
d m arg max { p(d m X)}
p(d m X)
(m=1,2,…,M)
d m (d m1, d m2 ,..., d mN )T - N-мерный вектор
dm
Тождество
p(d m , X) p(d m X) p(X) p(X d m ) p(d m )
Правило Байеса
03.01.2018
p(d m
p( X d m ) p(d m )
X)
p( X)
p ( X)
M
p(X dm ) p(d m )
m 1
73
74.
Критерий максимального правдоподобия.Используется когда априорная вероятность неизвестна
(любая из M гипотез равновероятна)
p(d m
p(d m ) 1 M
(m=1,2,…,M)
p( X d m ) p(d m )
X)
p( X)
Алгоритм оценки переданного сигнала
d m arg max { p( X d m )}
d m (d m1, d m2 ,..., d mN )T
- N-мерный вектор
dm
Условная плотность вероятности
1
1
ln p( X d m ) N ln( N 0 )
2
N0
D( X, d m )
N
p( X d m )
называется правдоподобием dm
N
( xk d mk ) 2
k 1
( xk d mk ) 2 X d m
2
Дистанционная
метрика (метрика
расстояний)
k 1
d m arg min {D( X, d m )}
Алгоритм оценки - минимизация евклидова расстояния
dm
03.01.2018
74
75.
Пример. 4-ФМ сигналы (N=2)Обозначение
D( X, d m ) Dm
Детектирование по
минимуму расстояния
D( X, d m )
N
k 1
xk2
N
N
k 1
k 1
2
2 xk d mk d mk
X 2 XT d m d m
D ( X, d m ) 2XT d m d m
03.01.2018
2
2
C ( X, d m ) 2XT d m d m
2
2
Корреляционная
метрика
75
76.
NC ( X, d m ) 2 xk d mk Em
k 1
Ts
N
0
k 1
Ts
xk x(t ) f k (t )dt
0
C ( X, d m ) 2 x(t ) d mk f k (t )dt Em
Ts
C ( X, d m ) 2 x(t )d m (t )dt Em .
0
Оптимальный
приемник
03.01.2018
76
77.
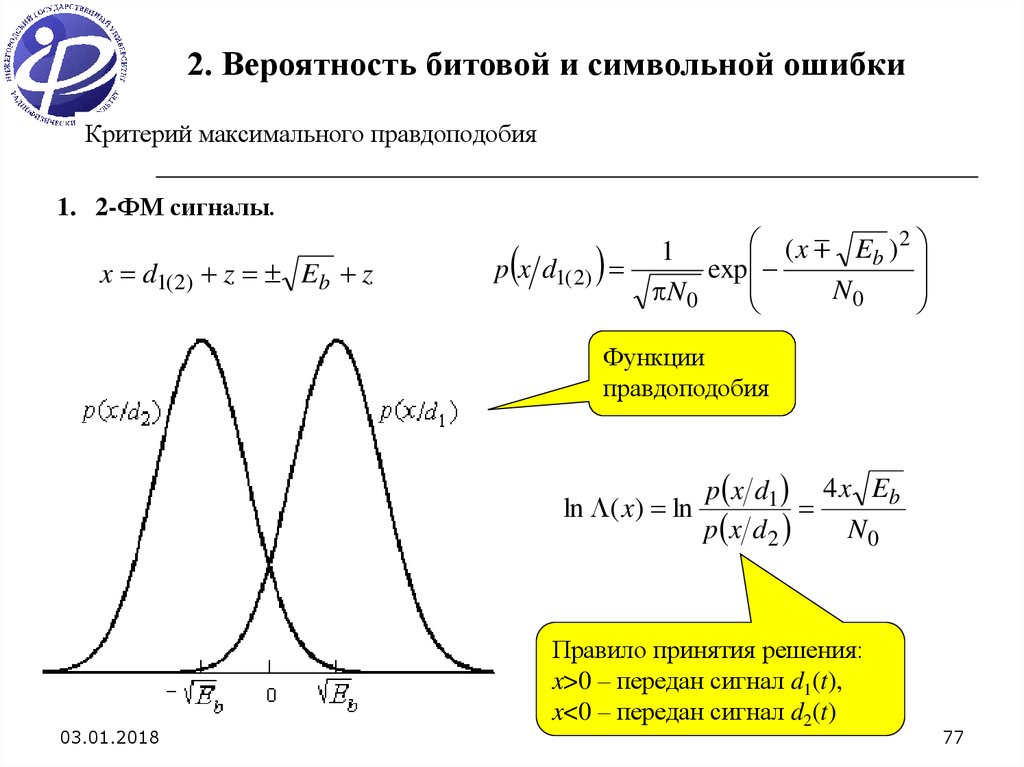
2. Вероятность битовой и символьной ошибкиКритерий максимального правдоподобия
1. 2-ФМ сигналы.
x d1( 2) z Eb z
p x d1( 2)
( x Eb ) 2
1
exp
N
N 0
0
Функции
правдоподобия
ln ( x) ln
03.01.2018
p x d1 4 x Eb
p x d 2
N0
Правило принятия решения:
x>0 – передан сигнал d1(t),
x<0 – передан сигнал d2(t)
77
78.
Вероятность битовой ошибки при передаче первого сигнала2 Eb
BER1 p( x d1 )dx Q
N0
0
1
2
Q( x )
exp(
0
.
5
t
)dt
2 x
Q(x) – функция Маркума
Вероятность битовой ошибки при передаче второго сигнала
2 Eb
BER2 p( x d 2 )dx Q
N0
0
Вероятность битовой ошибки
2 Eb
1
BER ( BER1 BER2 ) Q
2
N0
b Eb / N 0 – ОСШ на бит
2-ФМ-сигналы b 0 Es N 0 – ОСШ на символ
0>>1
0 0
1
0.5 x 2
Q( x)
e
x 2
BER 0.5
BER
Q( 2 b )
1
e 0
2 0
BER не может превышать 0.5
Вероятность
битовой ошибки совпадает с вероятностью символьной ошибки
03.01.2018
78
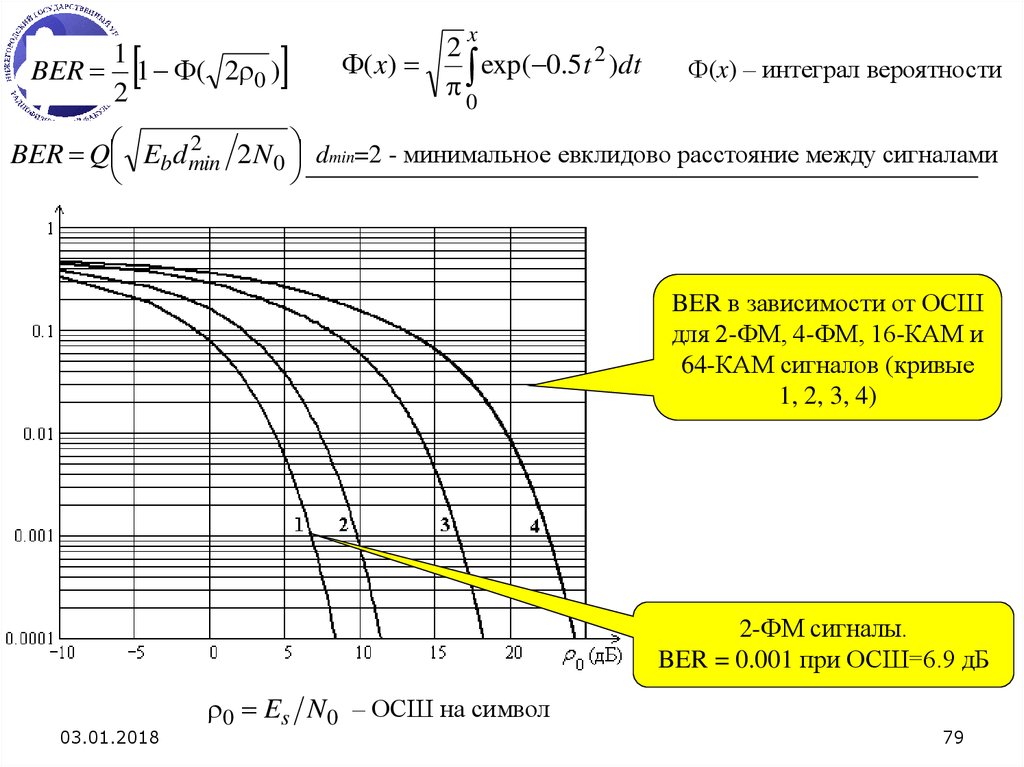
79.
BER1
1 ( 2 0 )
2
x
2
( x)
exp( 0.5 t 2 )dt
0
(x) – интеграл вероятности
2
BER Q Eb d min
2N0 dmin=2 - минимальное евклидово расстояние между сигналами
BER в зависимости от ОСШ
для 2-ФМ, 4-ФМ, 16-КАМ и
64-КАМ сигналов (кривые
1, 2, 3, 4)
2-ФМ сигналы.
BER = 0.001 при ОСШ=6.9 дБ
03.01.2018
0 Es N 0 – ОСШ на символ
79
80.
2. 4-ФМ сигналы.Eb
PT
PT
P
0 s 0 b 0
N 0 kb N 0
N0
N 0 Rb
E
E
Связь ОСШ с ОСШ на бит b b s 0
N0 2N0
2
ОСШ на бит b
4-ФМ (kb=2) реализуется с помощью одновременной
передачи 2-ФМ в двух квадратурах.
В каждой квадратуре - половина мощности (0.5P0).
Скорость передачи исходного потока – Rb.
Скорость передачи в каждой квадратуре - 0.5Rb.
ОСШ на бит в каждом квадратурном канале такое же,
как для 2-ФМ сигналов.
BER в зависимости от отношения Eb/N0 одинаково
для 2-ФМ и 4-ФМ сигналов.
4-ФМ модулятор
d min 2 - минимальное евклидово расстояние между 4-ФМ сигналами
BER Q 0
03.01.2018
BER
1
1 ( 0 )
2
2
BER Q Eb d min
N 0
80
81.
Связь ОСШ с ОСШ на бит 0P0
02
Es
E
kb b
Ts N 0W
N0
Одинаковая BER достигается для 4-ФМ при ОСШ большем в 2 раза (на 3 дБ),
чем для 2-ФМ.
BER в зависимости от ОСШ
для 2-ФМ, 4-ФМ, 16-КАМ и
64-КАМ сигналов (кривые
1, 2, 3, 4)
0 Es N 0 – ОСШ на символ
03.01.2018
4-ФМ сигналы.
BER = 0.001 при ОСШ=9.9 дБ
81
82.
Вероятность символьной ошибки (SER)Вероятность правильного приема для 4-ФМ-сигнала
( M 4)
pcorrect
( M 2) 2
1 BER
( M 4)
pcorrect
1 Q 2 b
2
1
( M 4)
SER( M 4) 1 pcorrect
2Q 2 b 1 Q 2 b
2
b>>1
SER( M 4) 2Q 2 b
03.01.2018
SER = 2 BER
Следствие
кода Грея
82
83.
3. 16-КАМ сигналы.3 0 1 0 1 0
Q 3
Q 5
BER Q
4 5 2
5 4
5
SER 4 BER
Следствие
кода Грея
BER в зависимости от ОСШ
для 2-ФМ, 4-ФМ, 16-КАМ и
64-КАМ сигналов (кривые
1, 2, 3, 4)
03.01.2018
0 Es N 0 – ОСШ на символ
16-КАМсигналы.
BER = 0.001 при
ОСШ=16.7 дБ
83
84.
4. 64-КАМ сигналы.BER
7 0 1 0 1 0 1 0 1
Q 3
Q 5
Q 9
Q 13 0
Q
12 21 2 21 12 21 12 21 12
21
SER 6 BER
Следствие
кода Грея
BER в зависимости от ОСШ
для 2-ФМ, 4-ФМ, 16-КАМ и
64-КАМ сигналов (кривые
1, 2, 3, 4)
03.01.2018
0 Es N 0 – ОСШ на символ
64-КАМ сигналы.
BER = 0.001 при
ОСШ=22.7 дБ
84
85.
Приближенная формула для достаточно высоких уровней модуляцииd2
SER N Q 0 min
2
N 4 – число точек, наиболее близко расположенных к выбранной точке в диаграмме
отображения бит в символы, dmin – минимальное евклидово расстояние.
d min
2
10
(16 КАМ), d min
Q( x) exp( 0.5x )
2
2
42
(64 КАМ),
2
0 d min
SER N exp
4
BER SER kb
Следствие
кода Грея
03.01.2018
85
86.
0P0
02
Es
E
kb b
Ts N 0W
N0
kb= 1, 2, 4 и 6 для 2-ФМ, 4-ФМ, 16-КАМ и 64-КАМ, соответственно
BER = 0.001
Eb/N0 = 6.9, 6.9, 10.7 и 15.9 дБ
(2-ФМ, 4-ФМ, 16-КАМ и 64-КАМ
сигналы)
BER в зависимости от Eb/N0
для 2-ФМ, 4-ФМ, 16-КАМ и
64-КАМ сигналов (кривые
1, 2, 3, 4)
03.01.2018
b Eb / N 0 – ОСШ на бит
86
































































 Информатика
Информатика








