Похожие презентации:
Основные понятия теории колебаний
1.
Семинар 1. Основные понятия теории колебаний1.1. Понятия о колебаниях
Пусть состояние системы в каждый момент времени дописывается
некоторым набором параметров.
Возьмем один из числовых параметров системы и.
Рассмотрим изменение этого параметра во времени t .
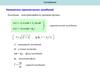
Это изменение может быть монотонным, немонотонным, существенно
немонотонным (рис. 1).
Рис. 1. Изменение параметра u(t):
а) монотонное
б) немонотонное
в, г) существенно немонотонное
2.
1.4. Кинематические характеристики периодическихколебательных процессов
Пусть процесс характеризуется одной скалярной переменной и(t) (например,
перемещение).
Периодические колебания. Колебания называются периодическими,
если любые значения колеблющейся величины повторяются через равные отрезки
времени. .
Более точно, колебания называются периодическими, если существует
такое число Т, что для любого t выполняется условие (рис. 2) и(t + Т) = и(t).
Наименьшее из этих значений называется периодом колебаний.
3.
Обозначим его через Т. Величина, обратная периоду колебаний,называется частотой колебаний: f = 1/ Т.
В технике период колебаний обычно измеряется в секундах; частота f,
следовательно, имеет размерность 1/с ( с -1 )
В теоретические формулы входит величина, называемая угловой
(циклической) частотой
2
2 f
T
( 3)
Она также измеряется в с -1. Эта частота равна числу периодов колебаний,
которые укладываются на отрезке времени продолжительностью 2 с.
Необходимо остерегаться смешения частот f и
.
Частоту f обычно измеряют в герцах (Гц).
Для угловой частоты наряду с размерностью с - 1 часто используют
размерность рад/с.
4.
Гармонические колебания. Простейшим (и наиболее важным) видомпериодических колебаний являются гармонические (синусоидальные) колебания,
при которых колеблющаяся величина изменяется во времени по закону
u (t ) A sin( t ) (4)
A, ,
- постоянные параметры.
Параметр А равен наибольшему значению колеблющейся величины и
называется амплитудой.
называется начальной фазой колебаний.
t
называется фазой колебаний в момент времени t .
является угловой частотой.
Период гармонических колебаний выражается через угловую частоту:
T
2
(5)
5.
Для наглядного представления гармонических колебаний можноиспользовать круговую диаграмму (рис. 3).
Для этого на плоскости вводится вектор длиной А, который вращается с
постоянной угловой скоростью, равной
Начальное положение вектора задается углом
.
Проектируя конец вектора на вертикальную ось, получим закон движения
в форме (4).
6.
Скорость при гармонических колебанияхdu
v
A cos( t ) (6)
dt
а ускорение
d 2u
w 2 2 A sin( t ) (7)
dt
Скорость v(t) и ускорение w(t) при гармонических колебаниях также
изменяются во времени по синусоидальному закону с той же частотой, что и
перемещение u(t).
Амплитуды скорости и ускорения равны соответственно
A и 2 A
В технической литературе перемещение, скорость и ускорение при
колебательном движении называют соответственно виброперемещением,
виброскоростью и виброускорением.
7.
Сумма двух гармонических колебаний с одинаковыми частотами будетгармоническим колебанием с той же частотой:
A1 cos t A2 cos( t ) A cos( t ) (8)
Амплитуда и фаза результирующих колебаний могут быть найдены,
например, из круговой диаграммы (рис. 4):
A
A12 A22 2 A1 A2 cos ;
A2 sin
tg
A1 A2 cos
(9)
8.
Полигармонические колебания. Полигармоническими называютколебания, которые могут быть представлены в виде суммы двух или более
гармонических колебаний с частотами (периодами), находящимися между собой в
рациональном соотношении.
Пример: колебательный процесс, являющийся суммой двух
гармонических процессов
u(t ) A1 cos 1 t A2 cos 2 t (10)
Существенно, чтобы отношение частот было рациональным числом.
Пусть 1 m , 2 n выражаются через некоторую частоту
где m и n - целые числа, причем m/ n - несократимая дробь.
Тогда сумма (10) будет периодической функцией с периодом
,
2 / .
9.
Примеры полигармонических колебаний.Пример 1
u(t ) A1 cos m t A2 cos n t (10)
0,5 c
m= 1
n= 2
f1 = 4
f2 = 8
Гц
Гц
10.
Пример 2u(t ) A1 cos m t A2 cos n t (10)
0,25 c
m= 1
n= 4
f1 = 8 Гц
f2 = 32 Гц
11.
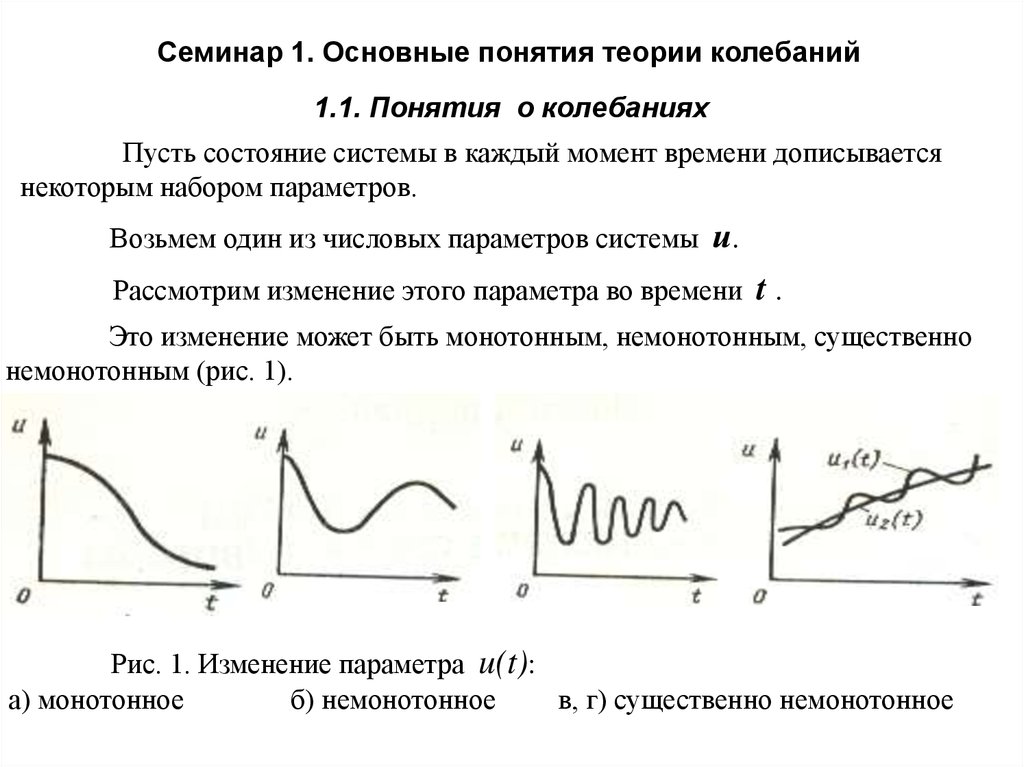
Пример 3u(t ) A1 cos m t A2 cos n t (10)
1,0 c
m= 1
n= 6
f1 = 1
f2 = 6
Гц
Гц
12.
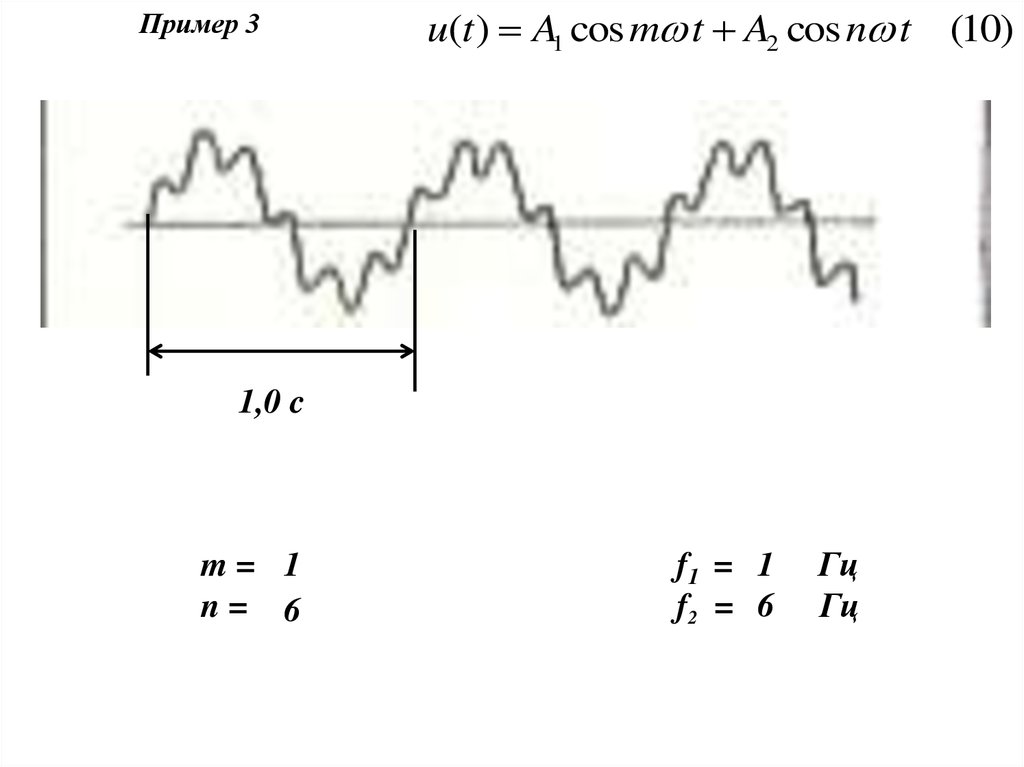
Пример 4u(t ) A1 cos m t A2 cos n t (10)
0,25 c
m= 1
n= 3
f1 = 8 Гц
f2 = 24 Гц
13.
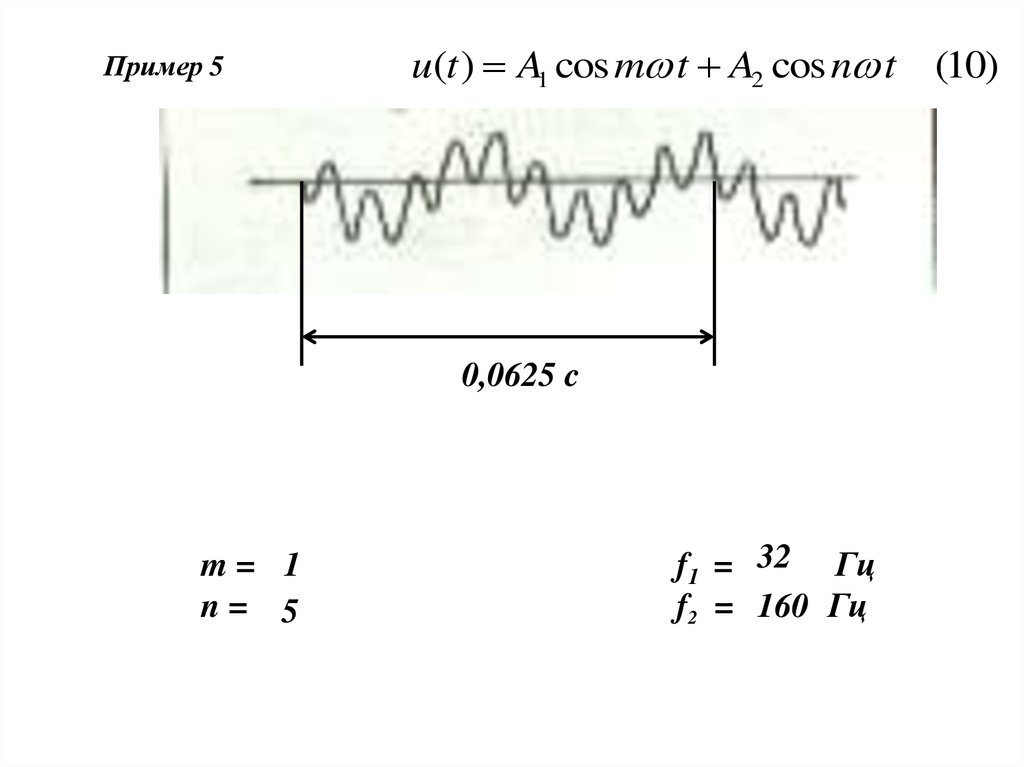
Пример 5u(t ) A1 cos m t A2 cos n t (10)
0,0625 c
m= 1
n= 5
f1 = 32 Гц
f2 = 160 Гц
14.
Пример 6u(t ) A1 cos m t A2 cos n t (10)
3c
m= 1
n = 10
f1 = 0,67
f2 = 6,7
Гц
Гц










 Физика
Физика