Деревья. Связность. Дерево и его виды

1.

ЛЕКЦИЯ 11.
ДЕРЕВЬЯ

2. Связность. Дерево и его виды

Неорграф
на рис.
1 имеет
Множество
вершин
графа
таких,
что
любые
две
Орграф
на
рис.
2
имеет
Связность.
Дерево
и
его
виды
4
компоненты
связности:
из него связаны, а связи с вершинами
несвязности:
из этого
2 компоненты
{v1}, {v2,v3,v4},нет,
{v5,v6,vназывается
7}, {v8}.
множества
компонентой
{v1, v2, v3}, {v4, v5, v6, v7}.
связности графа.
Граф, содержащий одну компоненту связности,
называется связным.
v
v3 v1
v2
v5
v2
v8
Рис. 1
v5
v1
v4
v7
4
v6
v3
v6
v7
Рис. 2

3.

Связность означает наличие хотя бы
одного пути - последовательности смежных
неповторяющихся рёбер (дуг) между любой
парой вершин графа (графы на рис. 1, 2
несвязные).
Например, все компьютеры, включённые
в Интернет, образуют связный граф.
Два конкретных компьютера могут быть
не соединёнными напрямую, но от каждого
информацию можно передать на любой
другой.

4.

В орграфах связность может быть
сильной или слабой.
В первом случае существует
ориентированный путь из любой вершины
в любую другую (рис. 3).
Во втором случае связным является
неорграф, полученный заменой дуг
исходного орграфа рёбрами (рис. 4).
v2
v1
v6
v3
Рис. 3
v4
v5
v7
Рис. 4

5.

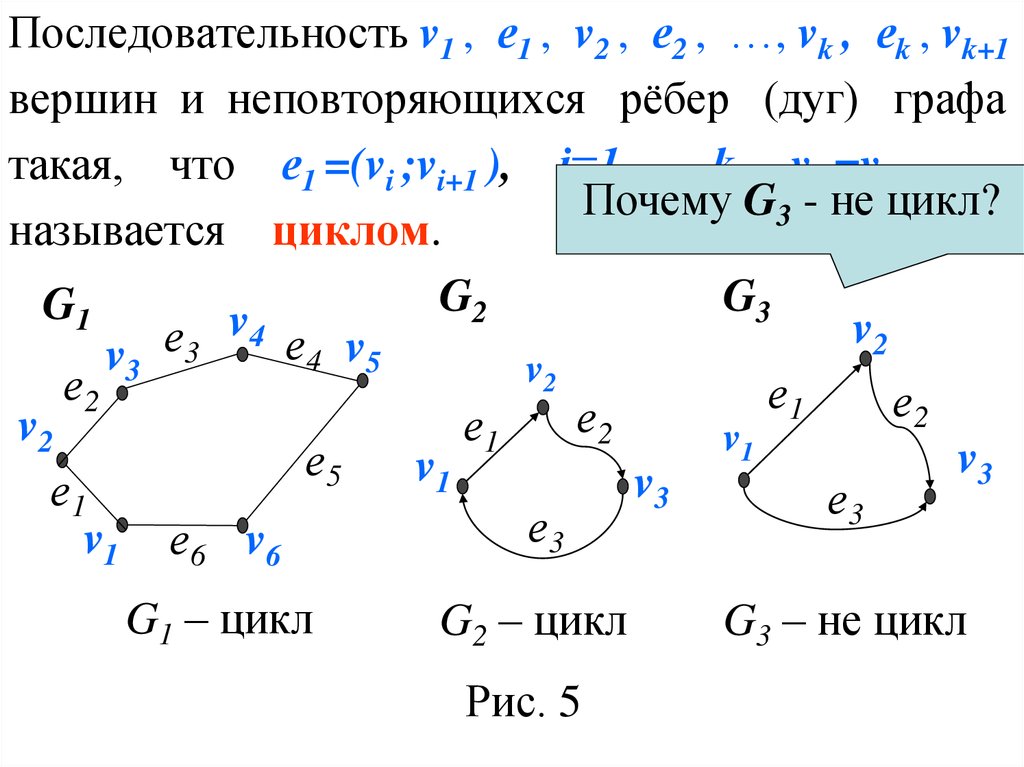
Последовательность v1 , е1 , v2 , е2 , …, vk , еk , vk+1
вершин и неповторяющихся рёбер (дуг) графа
такая, что е1 =(vi ;vi+1 ), i=1, …, k, v1 =vk+1
Почему G3 - не цикл?
называется циклом.
G2
G3
G1
v4
v2
е
е
v
3
v3
4 5
v2
е2
е1
е2
е
v2
е1
2
v1
v3
е5
v1
v3
е1
е3
е3
v1 е6 v6
G1 – цикл
G2 – цикл
Рис. 5
G3 – не цикл

6.

Связный неориентированный граф, не имеющий
циклов, называется деревом.
G1
G2
G3
G1Определите,
– дерево G2какой
– не дерево
G3 – –недерево.
дерево
из графов
Рис. 6

7.

Следующие утверждения эквивалентны:
1. G – дерево.
2. G – связный неорграф и в нём число
ребер m на единицу меньше числа вершин n:
m = n - 1.
3. Любые две вершины дерева соединяет
единственный путь.
4. G – неорграф без циклов и если любую
пару несмежных вершин соединить ребром,
то G будет содержать единственный цикл.

8.

Изобразите все деревья (неизоморфные),
которые можно построить на 6 вершинах
(деревья образуют лес).
Рис. 7

9.

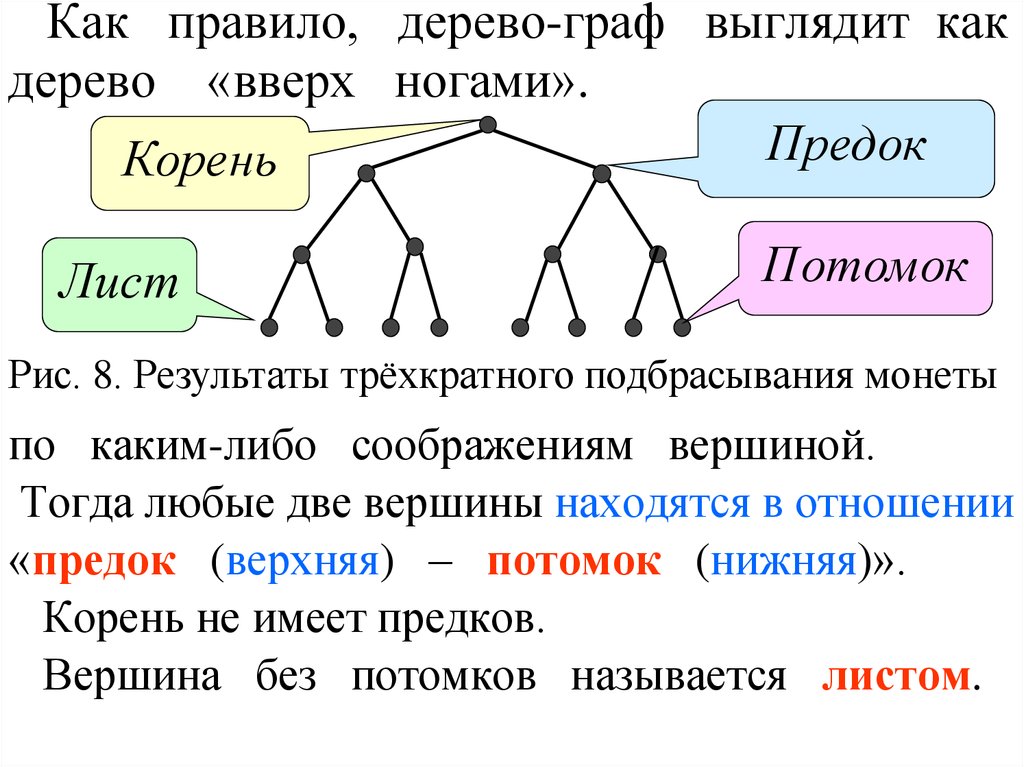
Как правило, дерево-граф выглядит как
дерево «вверх ногами».
Предок
Корень
Лист
Потомок
Рис.
8. Результаты
трёхкратного
подбрасывания
монеты
Корневым
называется
дерево
с выделенной
по каким-либо соображениям вершиной.
Тогда любые две вершины находятся в отношении
«предок (верхняя) – потомок (нижняя)».
Корень не имеет предков.
Вершина без потомков называется листом.

10.

Ориентированным деревом называется орграф
без циклов и петель, у которого:
- есть ровно одна вершина (корень), в которую
не входит ни одна дуга (степень входа d+ корня
равна нулю);
Корень
- в каждую вершину, кроме корня,
v1
входит ровно одна дуга (то есть
степень входа d+ вершин кроме v2
v5
корня равна единице);
v3
v4 v6
v7
- из корня в каждую вершину
v8
идёт ровно один путь (рис. 9).
Рис. 9

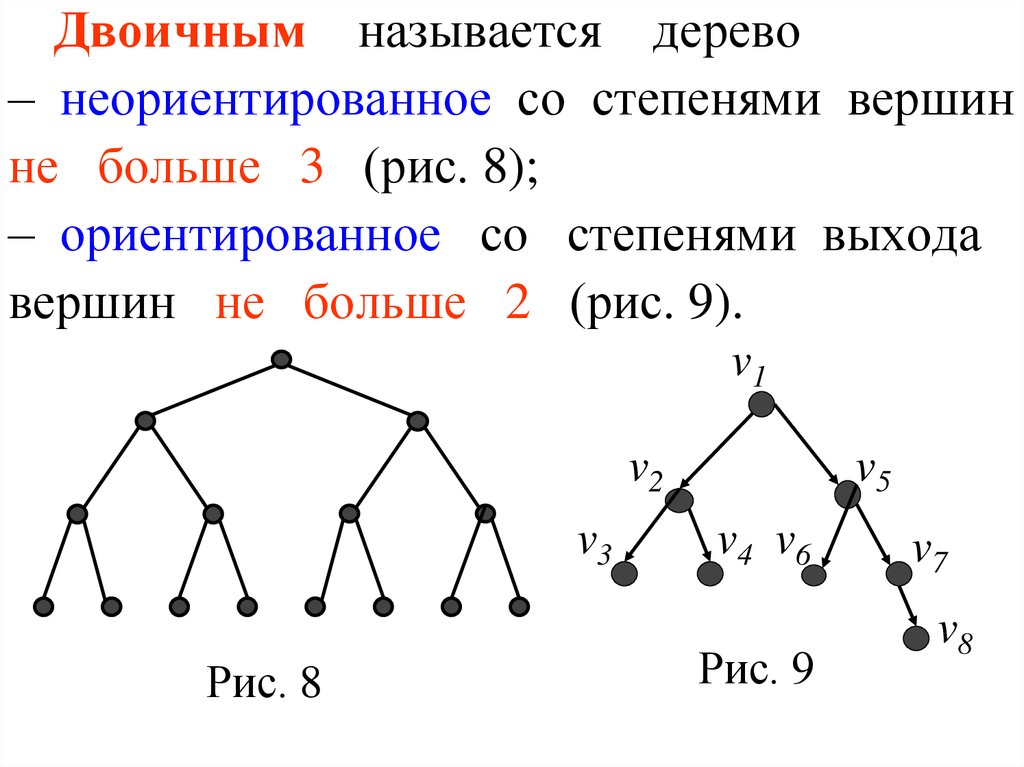
11.

Двоичным называется дерево
– неориентированное со степенями вершин
не больше 3 (рис. 8);
– ориентированное со степенями выхода
вершин не больше 2 (рис. 9).
v1
v2
v3
Рис. 8
v5
v 4 v6
Рис. 9
v7
v8

12. Остовы

Граф G называется
подграфом графа G,
Остовы
если множества их вершин совпадают,
а множество рёбер G образовано
некоторыми рёбрами G .
Остовным деревом (каркасом, остовом)
графа G называется его связный без циклов
подграф G .
Теорема 1 (Кирхгофа). Число различных
остовов связного графа G с n вершинами
(n ≥ 2) равно алгебраическому
vi и элемента
v j смежные;
1, если
дополнению
любого
матрицы
Кирхгофа
из элементов
k
0K(G),
, если состоящей
v и v несмежные
и i j;
ij
i
d(vi ), если i j.
j

13.

Пример. Найти число различных остовов
графа G (рис. 10).
v1
v6
v5
v2
v3
Рис. 10
v7
v4

14.

Решение. Матрица
графа
v1 v2 Кирхгофа
v3 v4 vданного
5 v6 v7
имеет вид:
v
2 1 0 0 1 0 0
v2 1 3 1 0 1 0 0
v3 0 1 2 1 0 0 0
v4 0 0 1 2 1 0 0
v5 1 1 0 1 4 1 0
v6 0 0 0 0 1 2 1
v7 0 0 0 0 0 1 1
1
K (G)

15.

Вычислим алгебраическое дополнение
элемента k11:
3 1
1
A11
0
0
0
0
0
2 1
0
0
4 1
0
2 1
0 1
1
0 1
0 1
0
0
0 1
0
0
0
2 1
0 1
1

16.

3 1
1
2 1
0 1
1
0 1
0 0
0
0 0
2 1
0 0
0 1
4 1 0
0
0
0 1
0
0
0
1 0
0 1 1

17.

3 1
1
2 1
6 6
1 ( 1) 0 1
1
0
0 1
2 1
0 1
0
0
0
0
1
1
1
0
0 1 0
2 1
0 0 1
4 1
0 1
3 1
2 1 0
0 1
0
0 0
3 0
0 1 1

18.

5 5
1 ( 1)
3 1 0 1
3
1 2 1 0
1 2 1 0
0 1 2 1
1 0 1 3
1
1 4
( 1) ( 1) 3
1 0 1
3 0
2
0
8 3 1 0
2 1
0
2 11.
8 3 1

19.

Значит, данный граф имеет 11 различных
остовов.
Рис. 11

20.

Теорема 2. Число рёбер неорграфа G,
которые
нужно удалить
для получения
Цикломатическое
число графа
G
остова, не зависит от порядка их удаления
и равно ν(G) = m – n + k, где m – число рёбер,
n – число вершин, k – число компонент
n – k = ν (G) - коранг графа G
cвязности графа G.
ν (G) = m – n + k = m - (n - k)
Ясно, что ν (G) + ν(G) = m .
Для графа на рис. 12
ν (G) = 9 – 7 + 2 = 4,
ν (G) = 7 – 2 = 5.
Рис. 12

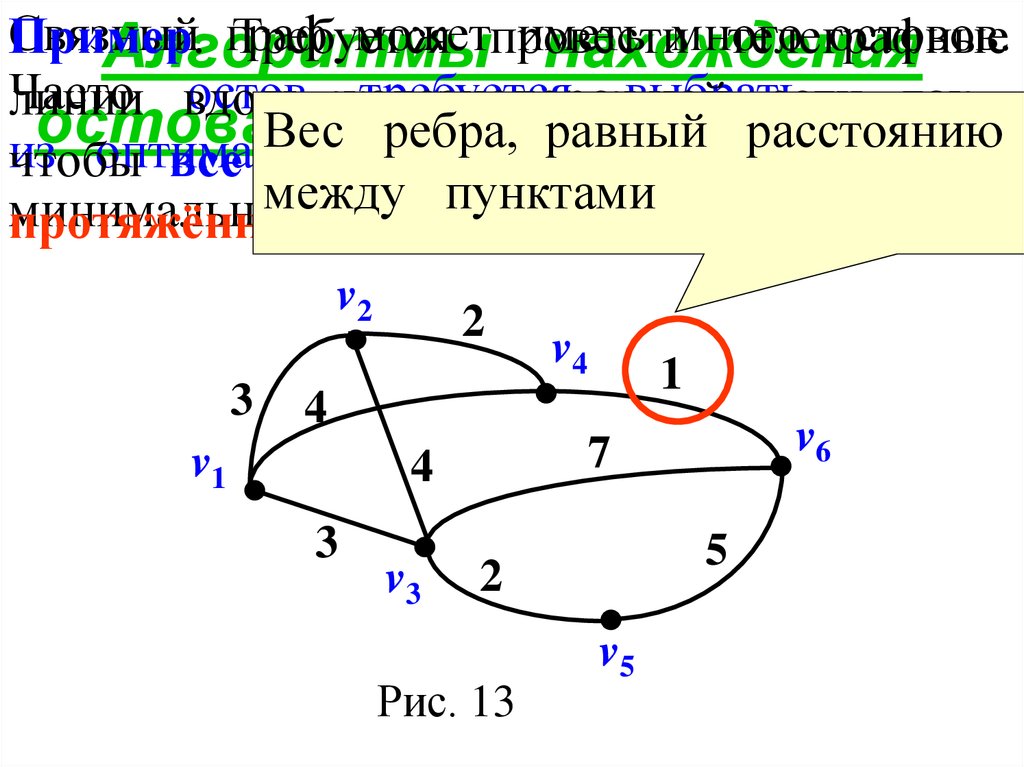
21. Алгоритмы нахождения остова минимального веса

Связный
граф
можетпровести
иметь
много
остовов.
Пример.
Требуется
телеграфные
Алгоритмы
нахождения
Часто
остов железнодорожной
требуется выбрать
линии вдоль
сети так,
остова
минимального
веса
Вес
ребра,
равный
расстоянию
из
оптимальных
чтобы
все пункты соображений:
были связаны,его
а общая
между
пунктами
минимального
или
максимального
веса.
протяжённость линий
была наименьшей.
v2
3
2
v4
1
4
v1
4
3
v3
v6
7
5
2
Рис. 13
v5

22.

Другими словами, в задаче нужно
найти остов графа минимального веса.
Алгоритм Прима
Разобьём множество вершин V на два
подмножества V и V таких, что V V,
V V , V V V, V V Ø.
Число
d (V ,V ) min { ω(vi , v j ) | vi V , v j V }
называется пошаговым
между V и V .
расстоянием

23.

Шаг 1. Присвоение начальных значений
Пусть V {v1} (v1 – произвольная вершина),
V V \ V , U Ø.
Шаг 2. Обновление данных
Найдём ребро (vi;vj) такое, что vi V , v j V ,
d (V ,V ) min { ω(vi , v j ) | vi V , v j V }.
Полагаем V V {v j } , V V \ V ,
U U {(vi ; v j )}.
Шаг 3. Проверка на завершение
Если V = V, то G =( V , U ) – искомый остов.
Иначе - переход к шагу 2.

24.

Пример. Найти остов минимального веса
графа (рис.13) с помощью алгоритма Прима.
v2
3
2
v4
1
4
v1
7
4
3
v3
v6
5
2
Рис. 13
v5

25.

Шаг 1. Пусть V = {v1}, тогда
= {v2, v3, v4, vвершине
Из трёх рёбер,Vинцидентных
v1,
5, v6},
наименьший
вес имеют два.
U = Ø.
Первая итерация
Шаг 2. d (V ,V ) ω(v1 , v2 ) ω(v1 , v3 ) 3 .
Включим, например, вершину v2 в V :
V {v1 , v2 }, тогда V {v3 , v4 , v5 , v6 }
U {(v1; v2 )}
Шаг 3. V V, переход к шагу 2.

26.

Шаг 1.
V
v1
v2
Первая итерация Шаг 2.
2
V
v4
3
1
4
Ребро (v1,v2) включено
в
остов
v6
7
4
3
Чтобы найти пошаговое расстояние
5
v
между V 3 и V 2 , рассмотрим рёбра,
инцидентные вершинам этих множеств.
v5

27.

Вторая итерация
d (V ,V ) ω(v2 , v4 ) 2
V {v1 , v2 , v4 } V {v3 , v5 , v6 }
Шаг 2.
U {(v1; v2 ), (v2 ; v4 )}
Шаг 3. V V, переход к шагу 2.

28.

(v2,v4)
Вторая итерация Шаг Ребро
2.
v2
2 включено в остов
V
v1
v4
3
1
4
V
4
v6
7
3
v3
5
Чтобы найти пошаговое
расстояние
2
между V и V , рассмотрим
рёбра,
v5
инцидентные вершинам этих множеств.

29.

Третья итерация
d (V ,V ) ω(v4 , v6 ) 1
V {v1 , v2 , v4 , v6 } V {v3 , v5 }
Шаг 2.
U {(v1; v2 ), (v2 ; v4 ), (v4 ; v6 )}
Шаг 3. V V, переход к шагу 2.

30.

Третья итерация Шаг 2.Ребро (v4,v6)
v2
2 включено в остов
v4
3
V
1
4
v1
4
3
v3
v6
7
V
5
2
Чтобы найти пошаговое
расстояние
между V и V , рассмотрим
рёбра,
v5
инцидентные вершинам этих множеств.

31.

Четвёртая итерация
d (V ,V ) ω(v1 , v3 ) 3
V {v1 , v2 , v3 , v4 , v6 } V {v5 }
Шаг 2.
U {(v1; v2 ), (v1; v3 ), (v2 ; v4 ), (v4 ; v6 )}
Шаг 3. V V, переход к шагу 2.

32.

Четвёртая итерация Шаг 2.
v2
2
V 3
v4
1
4
v1
v6
7
4
3
v3
5
2
Чтобы
Ребро найти
(v1,v3) пошаговое расстояние
V
v5
между Vв иостов
V , рассмотрим
рёбра,
включено
инцидентные вершинам этих множеств.

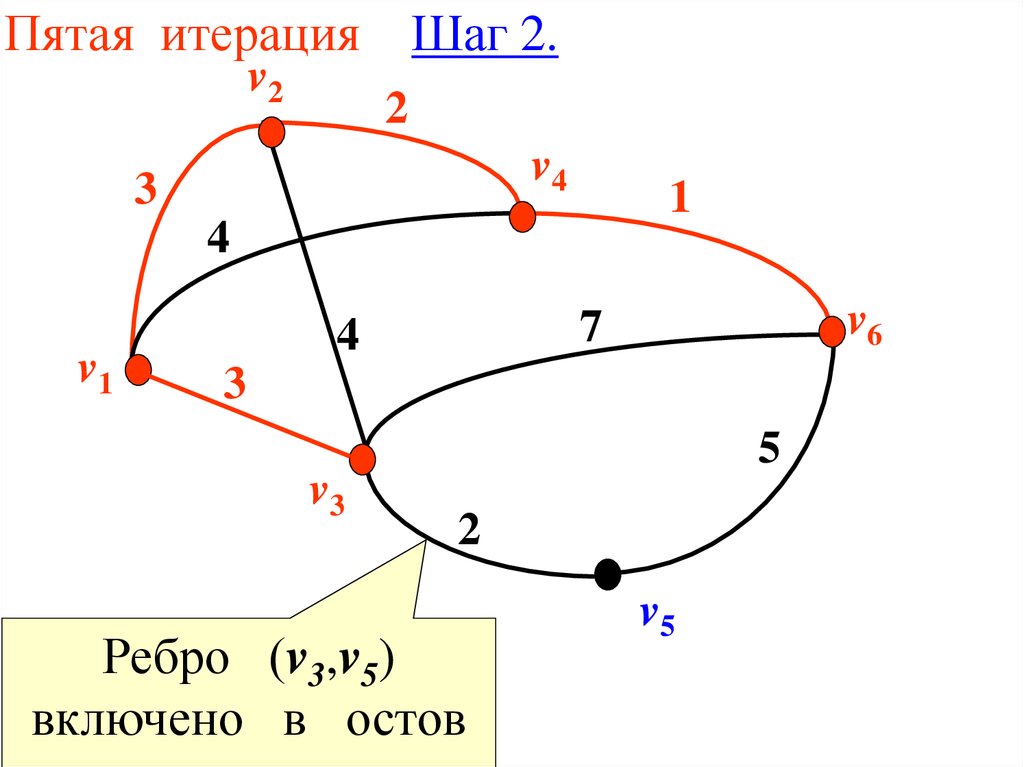
33.

Пятая итерация
d (V ,V ) ω(v3 , v5 ) 2
V {v1 , v2 , v3 , v4 , v5 , v6 } V Ø
Шаг 2.
U {(v1; v2 ), (v1; v3 ), (v2 ; v4 ), (v3 ; v5 ), (v4 ; v6 )}
Шаг 3. V = V

34.

Пятая итерация
v2
Шаг 2.
2
v4
3
1
4
v1
v6
7
4
3
v3
5
2
Ребро (v3,v5)
включено в остов
v5

35.

Получен остов
минимального веса (рис. 14):
ω 1 2 3 3 2 11.
v1
v2 3
v4
2
3
v3
2
v5
1
v6
Рис. 14

36.

Алгоритм Краскала
Из всех рёбер выбирают одно с наименьшим
весом. Затем из оставшихся находят ребро
с наименьшим весом. Если оно не образует
цикла с выбранными ранее рёбрами, то
вводится в остов. Построение
прекращается
после n-1 шагов (n – число вершин).

37.

Пример. Найти остов минимального
веса графа (рис.13) с помощью алгоритма
Краскала.
v2
3
2
v4
1
4
v1
7
4
3
v3
v6
5
2
Рис. 13
v5

38.

Выбираем ребро с минимальным весом:
(v4; v6) c весом 1.
Снова выбираем ребро с минимальным
весом, не образующее цикла с ребром,
выбранным ранее: ребро (v2; v4) c весом 2.
Включаем его в строящийся остов.
v2
3
2
v4
1
4
v1
7
4
3
v3
v6
5
2
v5

39.

Из оставшихся наименьший вес 2 имеет
ребро (v3; v5). Оно не образует цикла
с рёбрами, выбранными раньше, поэтому
включаем его в остов.
v2
3
2
v4
1
4
v1
7
4
3
v3
v6
5
2
v5

40.

Следующим ребром, включённым в остов,
будет (v1; v2) с весом 3, не образующее
цикла с тремя предыдущими.
Последнее ребро, включённое в остов,
это (v1; v3) с весом 3.
v2
3
2
v4
1
4
v1
7
4
3
v3
v6
5
2
v5

41.

Выполнено 5 шагов, поэтому алгоритм
закончен. Найдём вес найденного остова:
ω 1 2 3 3 2 11.