Похожие презентации:
Блочные методы возведения в степень по модулю. Методы окна
1. Блочные методы возведения в степень по модулю (методы окна)
Вариант 1: “традиционный” блочный методR x mod N ;
k (kt 1kt 2 k1k0 ) 2 , kt 1 0;
k
t
k (kd 1kd 2 k1k0 ) 2 w , d , kd 1 0;
w
k 2
d 1 w
x x
k
kd 1 2
2 d 1 w kd 1
21-05-2008
d 2 w
kd 2 22 w k2 2 w k1 k0 ;
x
22 w k2
x
Лк № __ - Блочные методы
2 w k1
x mod N ;
k0
1
2.
k kd 1 2 kd 2 2 k2 2 k1 2 k0 ;w
w
w
w
d 1
2w
w
2
w
2
w
2
k d 1
k d 2
k2
k
x x
x
x x k1 x k0 .
d 1
21-05-2008
Лк № __ - Блочные методы
2
3.
01
2 w 1
2
1. (Предвычисления: x , x , x , , x
)
1.1. X [0] = 1; X [1] = x ;
w
1.2. for (i = 2; i <= 2 1 ; i + +)
X [i] = X [i-1] x mod N;
2. R = 1;
3. for (i = d-1 ; i >= 0 ; i - - ) {
2w
3.1. R = R mod N ;
ki
3.2. R = R X [k i ] mod N ; // R *= x
}
21-05-2008
Лк № __ - Блочные методы
3
4.
01
2 w 1
2
1. (Предвычисления: x , x , x , , x
)
1.1. X [0] = 1; X [1] = x ;
w
1.2. for (i = 2; i <= 2 1 ; i + +)
X [i] = X [i-1] x mod N;
kd 1
2. R = X [kd-1 ] ; // x
3. for (i = d-2 ; i >= 0 ; i - - ) {
2w
3.1. R = R mod N ;
ki
3.2. R = R X [k i ] mod N ; // R *= x
}
21-05-2008
Лк № __ - Блочные методы
4
5. Пример 1.
k = 23<10> = 17<16> = (10 111)2 = (k1 k0 ) = (27)8 ;w = 3, b = 2w = 8 ; {[X [0],X [1],] X [2],…,X [7]} =
= {[1,x,] x2, x3, x4, x5, x6, x7 } .
23<10> = ( (10)
i
1
3.1
2
x
R
3.2
3
)2
(111)
0
x x
2 8
16
x16 X [7] x16 x 7 x 23
(d-1)w = 3
(d-1) = 1
I1block=1∙IM+3∙IS; Iblock=4∙IM+6∙IS (I0block=3∙IM+3∙IS);
Ibin= (wt (k)-1)∙IM+(t-1)∙IS = 3∙IM+ 4∙IS.
21-05-2008
Лк № __ - Блочные методы
5
6. Пример 2.
k=283<10>=11B<16>=(1 0001 1011)2==(100 011 011)2=(k2 k1 k0 )=(433)8;
w = 3, b = 2w = 8 ; {[X [0],X [1],] X [2],…,X [7]} =
= {[1,x,] x2, x3, x4, x5, x6, x7 } .
i
ki
2
4
4 8
(3.1)
R
(3.2)
x
1
3
x4
x
32
x 32 X [3]
x
32
x x
3
35
x
35 8
0
3
x 280
x 280 X [3]
x
280
x x
3
283
(d-1)w=6
d-1=2
I1block=2∙IM+6∙IS; Iblock=5∙IM+9∙IS (I0block=3∙IM+3∙IS);
Ibin = (wt (k)-1)∙IM + (t-1)∙IS = 4∙IM+8∙IS.
21-05-2008
Лк № __ - Блочные методы
6
7. Оценки средней вычислительной сложности
Для этапа предвычислений:0
I block
0
I block
21-05-2008
2 2 IM ;
(2
w
w 1
1) I M I S .
Лк № __ - Блочные методы
7
8. Для основного цикла алгоритма:
2 1d 1 w I M w I S ;
2
w
w
1
I block
1
I block
t 2 1
1 w I M t w I S .
w 2
1
I block
N 2 2w 1
1
I
t
w
I
.
M
S
w
2w
21-05-2008
Лк № __ - Блочные методы
8
9.
2w 1
t 1
t
2 1 1
w
w
;
2 t 1
.
t w w 1
w
2 1 1 2 2 1
w
w 1
21-05-2008
Лк № __ - Блочные методы
9
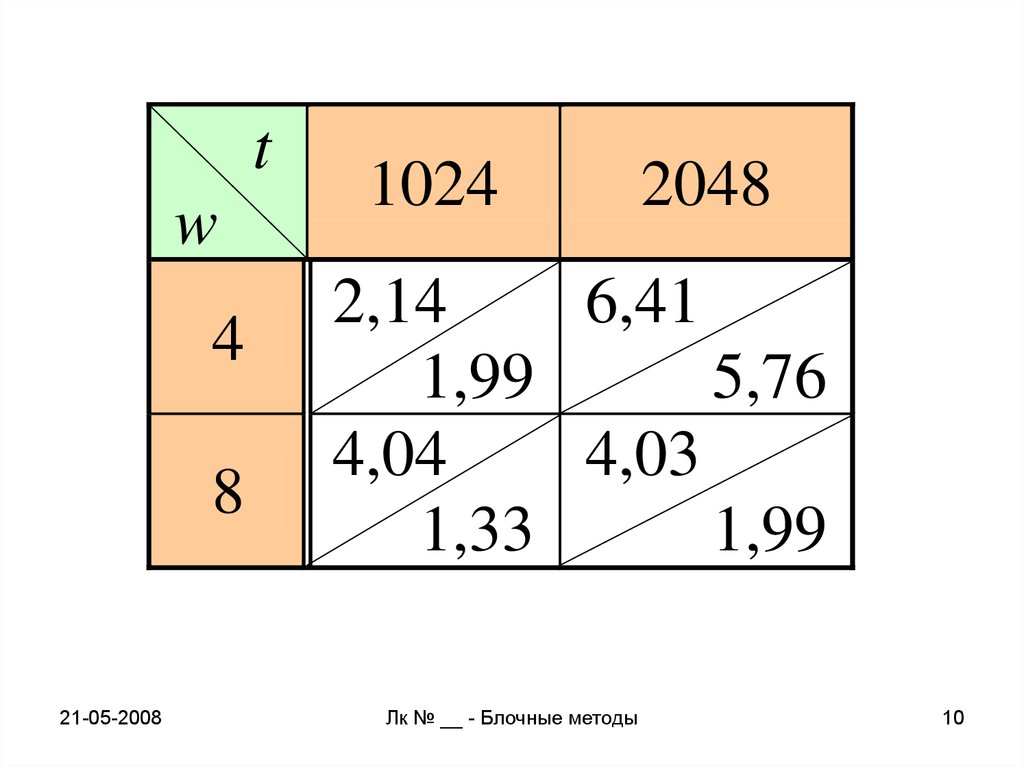
10.
tw
4
8
21-05-2008
1024
2048
2,14
6,41
1,99
5,76
4,04
4,03
1,33
1,99
Лк № __ - Блочные методы
10
11.
tw
512
255.5
511
192.3
2
511
151.8
3
513
126.1
4
515
113.8
5
525
114.7
6
541
135.4
7
574
189.8
8
631
310.9
9
759
562.0
21-05-2008
10
1021
1
1 024
511.5
1023
384.3
1023
301.4
1026
246.1
1027
212.6
1035
198.3
1051
207.9
1085
253.5
1143
367.8
1272
612.9
1531
2 048
4 096
1023.5
2047.5
2047
4095
768.3
1536.3
2047
4095
599.8
1197.4
2049
4098
486.1
966.1
2051
4099
411.2
808.4
2060
4110
366.7
702.3
2077
4123
352.7
643.4
2107
4158
381.0
636.0
2167
4215
481.6
709.1
2298
4350
714.8
919.6
Лк № __ - Блочные
методы
2551
4601
8 192
16 384
4095.5
8191
3072.3
8191
2391.8
8193
1926.1
8195
1601.8
8205
1374.7
8221
1223.9
8253
1146.0
8311
1163.2
8445
1329.2
8701
8191.5
16383
6144.3
16383
4781.4
16386
3846.1
16387
3188.6
16395
2718.3
16411
2384.7
16443
2166.0
16503
2071.4
16635
2147.4 11
16891
12.
tw
512
335804672
1 024
2685399552
2 048
21479023616
4 096
171815454720
8 192
1374456614912
16 384
10995384655872
1
392448
1571328
6288384
25159680
100651008
402628608
302578688
2418276352
19336785920
154656563200
1237101559808
9896208596992
2
360064
1441024
5765632
23065600
92268544
369086464
282092544
2249031424
17935208448
143358557184
1145956614144
9165684076544
3
340352
1359232
5424640
21689856
86710272
346806272
269387584
2134494848
16993656064
135620278784
1083646833664
8663914047488
4
328224
1303616
5195904
20746496
82911744
331498496
266897472
2076906240
16422183808
130605858048
1041128260608
8314154987520
5
327072
1277568
5061056
20145792
80337408
320858112
273660848
2072133824
16155356864
127373411072
1012249180928
8068102360064
6
335704
1279328
5004640
19764608
78607744
313415168
297583544
2145673440
16227149696
126277262784
995226879744
7901864082432
7
363228
1323888
5037504
19666656
77634432
308473344
348606980
2332865032
16842333200
127463069728
990615679040
7808596926592
8
420226
1430020
5218312
19869712
77471776
305872960
462737040
2775981628
18511093992
133315515280
1006418648640
7810983696640
9
547784
1679134
5692532
20722120
78710560
306486400
697979597
3698574644
22061676752
146699279160
1054473542864
7954853958464
10
810470.5
21-05-2008
2195354
Лк6688360
№ __ - Блочные22612380
методы
82167400
311925152
12
13.
tw
1
2
3
4
5
6
7
8
9
10
512
1 024
2 048
4 096
336197120
302938752
282432896
269715808
267224544
273996552
297946772
349027206
463284824
698790067
2686970880
2419717376
2250390656
2135798464
2078183808
2073413152
2146997328
2334295052
2777660762
3700769998
21485312000
19342551552
17940633088
16998851968
16427244864
16160361504
16232187200
16847551512
18516786524
22068365112
171840614400
154679628800
143380247040
135641025280
130626003840
127393175680
126296929440
127482939440
133336237400
146721891540
21-05-2008
Лк № __ - Блочные методы
8 192
16 384
1374557265920 10995787284480
1237193828352 9896577683456
1146043324416 9166030882816
1083729745408 8664245545984
1041208598016 8314475845632
1012327788672 8068415775232
995304514176 7902172555776
990693150816 7808902799552
1006497359200 7811290183040
1054555710264 7955165883616
13



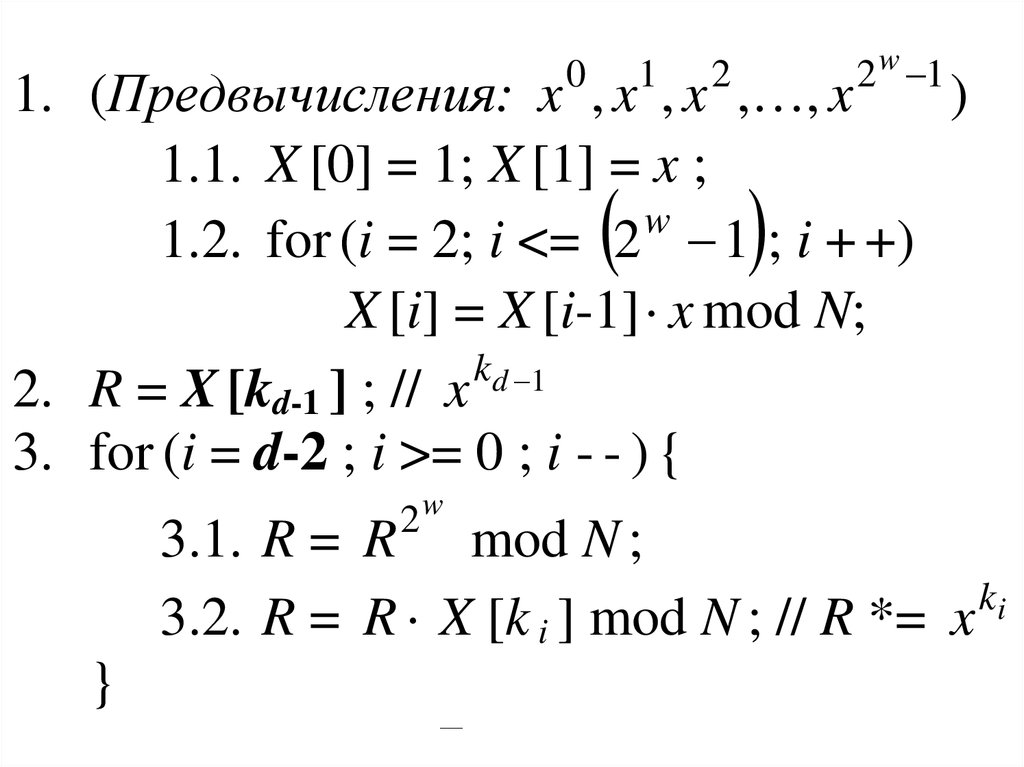








 Информатика
Информатика








