Реология горных пород

1. Реология горных пород

С помощью какого механического
воздействия можно распознать
природу тел (отличить одно тело от
другого)?

2. Виды деформаций

Упругая
Пластическая
Вязкая

3. Упругость

• Способность тела восстанавливать
свою форму и объем (у твердых тел)
или
• только объем (жидкость, газы) после
прекращения действия сил.
• Упругая деформация исчезает после
снятия нагрузки.

4. Пластичность

• Пластичность - свойство горной породы
необратимо изменять свою форму под
действием сдвигового напряжения без
разрушения. Пластичность возникает тогда,
когда максимальное касательное напряжение
достигает предельного значения,
называемого пределом текучести τТ.
• Уравнение состояния можно записать так:
max T const ;
v 0.

5. Механизмы пластической деформации

• Пластическая деформация обеспечивается:
- межзерновым скольжением;
- трансляцией;
- перекристаллизацией.
Межзерновое скольжение - смещение отдельных зерен породы относительно друг друга.
Трансляция – скольжение одного слоя кристаллической решетки минерала относительно
другого.
Перекристаллизация - искажение и изменение
кристаллической решетки.

6. Вязкость

• Свойство тела оказывать сопротивление перемещению молекул относительно друг друга.

7.

Идеальные реологические тела
- носители идеальных деформаций
Механические
модели
Реологические
уравнения
H
StV
i = G · gi,
sср = K· ср
Реологичеcкие
диаграммы
H
H
Гук
N
StV
СенStV
Венан
N
Ньютон
N
gi = 0 при i < т,
i g i
gi при i т,
sср = K· ср
v = 0
τi
τт
i
А
β
0
γi р
γi
gi

8. Аксиомы реологии

• Первая аксиома: под действием
равномерного всестороннего давления
все материалы ведут себя одинаково –
как идеально упругие тела.

9. Возвращение в исходному вопросу:

• С помощью какого механического
воздействия можно распознать
природу тел (отличить одно тело от
другого)?
• ОТВЕТ:

10. Вторая аксиома

• Каждый реальный материал
обладает всеми реологическими
свойствами, хотя и в разной степени.
• H, StV, N
H,
H
StV,
N
, StV, N

11. Третья аксиома

• Существует иерархия реологических тел: тело, низшее по иерархии,
должно получаться из тела, высшего по иерархии, если в последнем
приравнять нулю некоторые реологические параметры.
• Последовательное и параллельное
соединение идеальных тел:
моделирование реальных тел.

12.

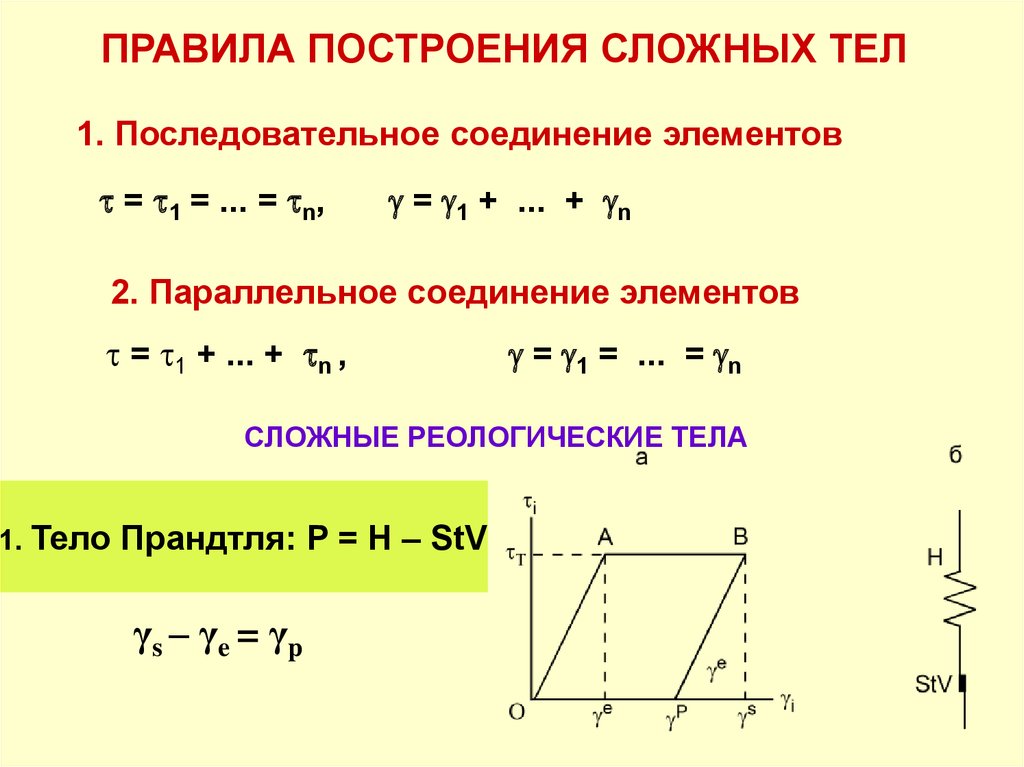
ПРАВИЛА ПОСТРОЕНИЯ СЛОЖНЫХ ТЕЛ
1. Последовательное соединение элементов
= 1 = ... = n,
g = g1 + ... + gn
2. Параллельное соединение элементов
= 1 + ... + n ,
g = g1 = ... = gn
СЛОЖНЫЕ РЕОЛОГИЧЕСКИЕ ТЕЛА
1. Тело Прандтля: P = H – StV
γs – γe = γp

13.

Ползучесть горных пород
g
gо
go
II - тело Максвелла
I - тело ПойнтингаТомсона
t
Н1
Н2
Тело Пойнтинга-Томсона
N
PT = M | H1

14. Ползучесть горных пород

Кривые изменения сдвиговой
деформации во времени
Затухающая ползучесть
Незатухающая ползучесть
τ = const
τ = const
g
gпр
g
Д
В
g0
g0
t
В
С
А
tразр. t

15. Кривые изменения сдвиговой деформации во времени

Ползучесть и пластическая
деформация
• По внешним признакам ползучесть похожа на
пластическое течение горных пород.
Принципиальная же разница в том, что пластичность проявляется за пределами
упругости при возрастающих нагрузках.
• Ползучесть может возникнуть при нагрузках,
меньших предела упругости (текучести)
горных пород, причем длительность воздействия нагрузки для фиксирования ползучести,
как правило, велика.

16. Ползучесть и пластическая деформация

К чему приводит ползучесть горных
пород стенки скважины
• Потеря устойчивости пород в открытом
стволе, смятие обсадных колонн, потери стволов при наклонном бурении.

17. К чему приводит ползучесть горных пород стенки скважины

Ползучесть горных пород стенки
скважины
• Инициатор ползучести у горных пород
разный:
- Ползучесть глин и глинистых пород является следствием наличия водно-коллоидных
связей в этих породах. Водные пленки играют
роль смазочного материала, по которому
ползут частицы минерального скелета.
- Ползучесть песчаников и других осадочных
пород, имеющих глинистый цемент,
объясняется свойства-ми этого цемента.

18. Ползучесть горных пород стенки скважины

• В мерзлых горных породах роль цементирующего вещества играет лед, который вызывает ползучесть минерального скелета.
• Ползучесть соленосных пород определяется
наличием в них солей. Эти горные породы
начинают течь при весьма малых нагрузках,
так как соли не имеют несущей способности и
передают нагрузку так же, как жидкости.

19. Ползучесть горных пород стенки скважины

Ползучесть
• Склонны к ползучести соленосные
породы, многолетние мерзлые пласты
горных пород, аргиллиты, глинистые
сланцы, песчаники с глинистым
цементом.

20. Ползучесть

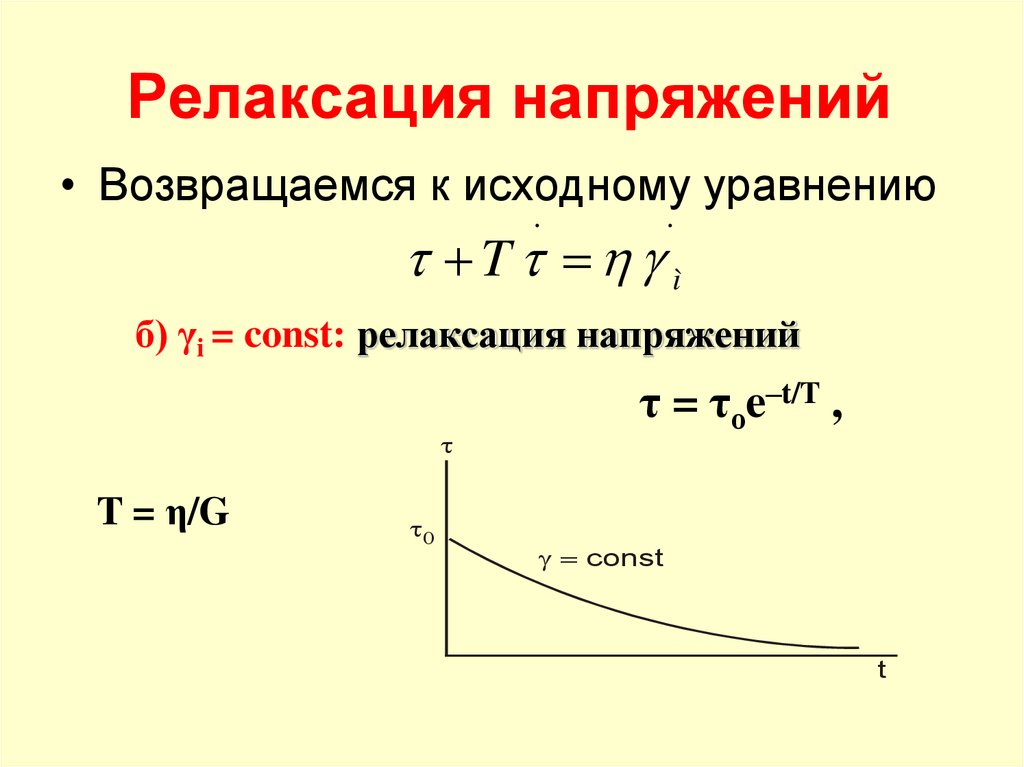
Релаксация напряжений
• Возвращаемся к исходному уравнению
.
.
T g ì
б) γi = const: релаксация напряжений
T = η/G
0
τ = τоe–t/T ,
g const
t

21. Релаксация напряжений

• Релаксация напряжений характеризуется периодом
(временем) релаксации (время, в течение которого
напряжение убывает в «е» раз (е = 2,71 – основание
натурального логарифма).
• Время релаксации:
Известняки – 1,05 · 105 – 1010 с;
Песчаники – (1,07 - 2,6) · 105 с;
Глинистые сланцы (2,6 – 34,5) · 105 с;
Плотные глины – (8,6 – 17,3) · 105 с.
Лед – 102 -103 c;
Вода – 10– 11 с.

22. Релаксация напряжений

Тело Максвелла
• Тело Максвелла – упруго-вязкое тело.
Его поведение при деформировании определяется соотношением времени действия нагрузки t и времени релаксации T:
- при t >> T – тело М ведет себя как жидкость,
- при t << T – тело М ведет себя как твердое тело

23. Тело Максвелла

СЛОЖНЫЕ РЕОЛОГИЧЕСКИЕ ТЕЛА
3. Тело Шведова SW
SW H 1 (M | StV )
τ
τо
т
g
G
g 0
τ*
t
0
SW B
( o )e
t
T

24.

Физические уравнения
a) Упругий массив горных пород
εx = [σx – v (σy + σz)]/Е
εy = [σy – v (σx + σz)]/Е
εz = [σy – v (σx + σz)]/Е
γxy = τxy/G,
γxz = τxz/G,
γyz = τyz
б) Пластический массив горных пород
εx – εср = [(σх – σср)/2G] ∙ ω
εy – εср = [(σy – σср)/2G] ∙ ω
εz – εср = [(σz – σср)/2G] ∙ ω
γxy = τxy ∙ ω/G,
γxz = τxz∙ ω/G,
γyz = τyz ∙ ω/G

25. Физические уравнения

• в) Вязкий массив горных пород
• теория старения
• теория упрочнения

26. Физические уравнения

Примерные вопросы к
рейтингу
• Тело Максвелла, время релаксации и проявление упругих и
вязких свойств в этом теле..
• Дать определение понятию «ползучесть». Затухающая и
незатухающая ползучесть. Кривые ползучести горных пород.
Где при бурении ствола скважины возникают условия
появления ползучести. К чему это приводит?
• Охарактеризовать тело Прандтля. Привести деформационную
кривую, характерную для этого тела?
• Аксиомы реологии.
• Написать реологические уравнения состояния,
характеризующее изменение объема и формы тела Ньютона.
Привести соответствующие графики.
• Тела Гука, Сен-Венана, Ньютона.
• Реологические параметры и их размерности.