Похожие презентации:
Алгоритм умножения
1. Алгоритм умножения
2 курслекция №3
2. Определение операции умножения
Если a,b-целые неотрицательные числа, то произведением
называется число, удовлетворяющее следующим условиям:
1)
a b a
a
a
a
...
a, еслиb 1
b раз
2)
3)
a b a, еслиb 1
a b 0, еслиb 0
a b
3. Умножение однозначных чисел можно выполнить , основываясь на определении
• При умножении многозначных чиселсмысл умножения сохраняется, но
меняется техника вычислений.
• При умножении многозначных чисел
используют правило умножения
многозначного числа на однозначное.
(правило умножения суммы на число)
4. Например :
428∙3=(400+20+8) ∙3=
=400 ∙3+20 ∙3+8 ∙3=1200+60+24=
=(1000+200)+60+(20+4)=
∙
=1000+200+(60+20)+4=
=1000+200+80+4=
=1284
5.
• Согласно записи чисел в десятичнойсистеме счисления, 428 = 4 10 2 2 10 8
2
• 428∙3= (4 10 2 10 8) 3
2
• = 4 10 3 2 10 3 8 3
2
• = 12 10 6 10 24
При умножении 428 на 3 используется
ассоциативный закон умножения,
дистрибутивный и коммутативный
6.
• Сейчас коэффициенты: 12 и 24 больше10, поэтому полученный результат не
является десятичной записью числа
• Преобразуем полученный результат:
(10 2) 10 6 10 2 10 4
2
7.
• На основании ассоциативного,коммутативного законов сложения и
дистрибутивного закона умножения
относительно сложения, получаем:
1 10 2 10 (6 2) 10 4
3
2
1 10 2 10 8 10 4
3
2
8.
В практике используется запись в столбик428
263
01284
25680
85600
112564
9.
• Для получения ответа нам пришлосьумножать 428 на 3, на 6, на 2.
• Умножая на 3, мы получаем единицы;
• Умножая на 6 (д), мы получаем десятки;
• Умножая на 2 (с), мы получаем сотни.
• Записываем разряд под разрядом.
10.
Умножение многозначного числа на
однозначное основывается на знаниях
(фактах):
1. Записи чисел в десятичной системе
счисления;
2. Свойствах сложения и умножения;
3. Таблицы сложения и умножения
однозначных чисел.
11. Правило умножения многозначного числа на однозначное в общем виде
Пустьx a n 10 a n 1 10
n
n 1
a n 2 10
y-однозначное число.
n 2
... a1 10 a0
12.
Тогда, имеемn
n 1
n 2
(
a
10
a
10
a
10
... a1 10 a0 ) y
• x·y = n
n 1
n 2
13.
• Применив основные свойства умноженияполучаем,
(an y)10n (an 1 y)10n 1 (an 2 y)10n 2 ... (a1 y)10 a0 y
Заменим все произведения,
ak y
где 0 ≤ k ≤ n
Если они больше или равны 10
Соответствующими значениями
ak y bk 10 c
14.
• Получаем:• x·y= bn 10 cn 10 n bn 1 10 cn 1 10 n 1 ...
b1 10 c1 10 b0 10 c0
=
bn 10
n 1
cn bn 1 10 ... c1 b0 10 c0
n
15.
• Суммыc k bk 1 ,
где
0≤k≤n
Заменим ее значением.
И это значение запишем в ответ.
16. Алгоритм умножения многозначного числа на однозначное
1.Записываем второй множитель под первым;
2.
Умножаем цифру разряда единиц числа х на число
у. Если произведение меньше 10, его записываем
в разряд единиц ответа и переходим к следующему
разряду(десятков)
17.
3. Если произведение цифры единиц числа х начисло у больше, или равно10, то
представляем его в виде 10 g1 c0
где
c0
- есть однозначное число.
Записываем
и запоминаем
g1
c0
в разряд единиц ответа
-перенос в следующий разряд
18.
4. Умножаем цифру разряда десятков на числоу, прибавляем к полученному произведению
число g 1
И повторяем процесс, описанный в пункте 2 и 3
19.
5. Процесс умножения заканчивается,когда окажется умноженной цифра
старшего разряда.
Замечание:
Умножение числа x на 10 n
Сводится к приписыванию к десятичной записи
числа x n нулей справа
20. Умножение многозначного на многозначное число
428·263=428·(200+60+3)=
=428·200+428·60+428·3=
=428·(2·100) +428·(6·10)+428 ·3=
=(428 ·2) ·100+(428 ·6) ·10+428 ·3
Умножение многозначного на
многозначное свелось к умножению
многозначного на однозначное
число.
21. Основой выполнения преобразований являются:
• Представление каждого множителя ввиде суммы разрядных слагаемых
( запись числа в десятичной системе)
• Правило умножения суммы на число
(дистрибутивность умножения
относительно сложения)
• Законы сложения
• Умножение круглых чисел
22. Алгоритм умножения числа на число
____________Алгоритм умножения
x an an 1...a1a0
____________числа
на число у bnbn 1...b1b0
1. Записываем второе число под первым
2. Умножаем число х на младший разряд
b0 числа у и записываем произведение
x b0
под числом у
23.
3. Умножаем число x на следующийразряд b1 числа у,
Записываем результат,
но со сдвигом на один разряд влево,
что соответствует умножению
на 10
x b1
24.
4. Продолжаем вычислениепроизведений до вычисления x bk
5. Полученные k+1 произведение
складываем.
25.
Спасибо за внимание













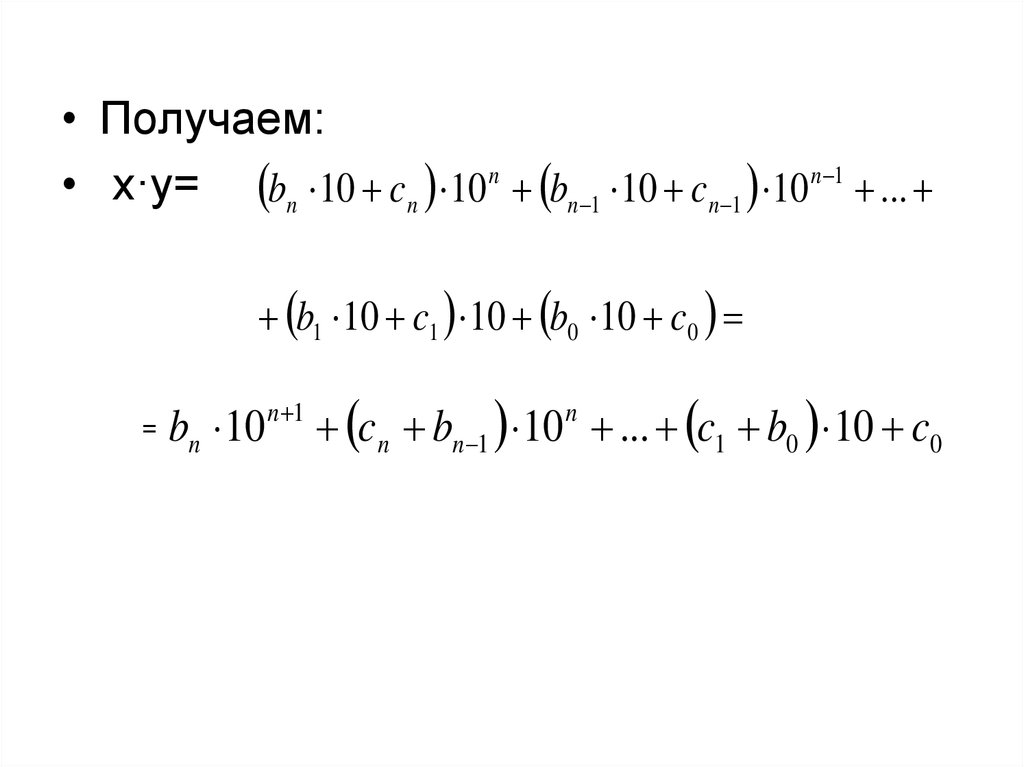











 Математика
Математика








