Похожие презентации:
Классификация структур данных. (Лекция 8)
1. Элементарные структуры данных на основе статической памяти.
Лекция 82. Классификация структур данных
По сложности:простые
интегрированные
По способу представления:
физическая
логическая
По наличию связей между элементами данных:
несвязные
связные
По изменчивости:
Статические
полустатические
динамические
По характеру упорядоченности элементов в структуре:
линейные
нелинейные
По виду памяти, используемой для сохранности данных:
для оперативной
для внешней памяти
3. Список
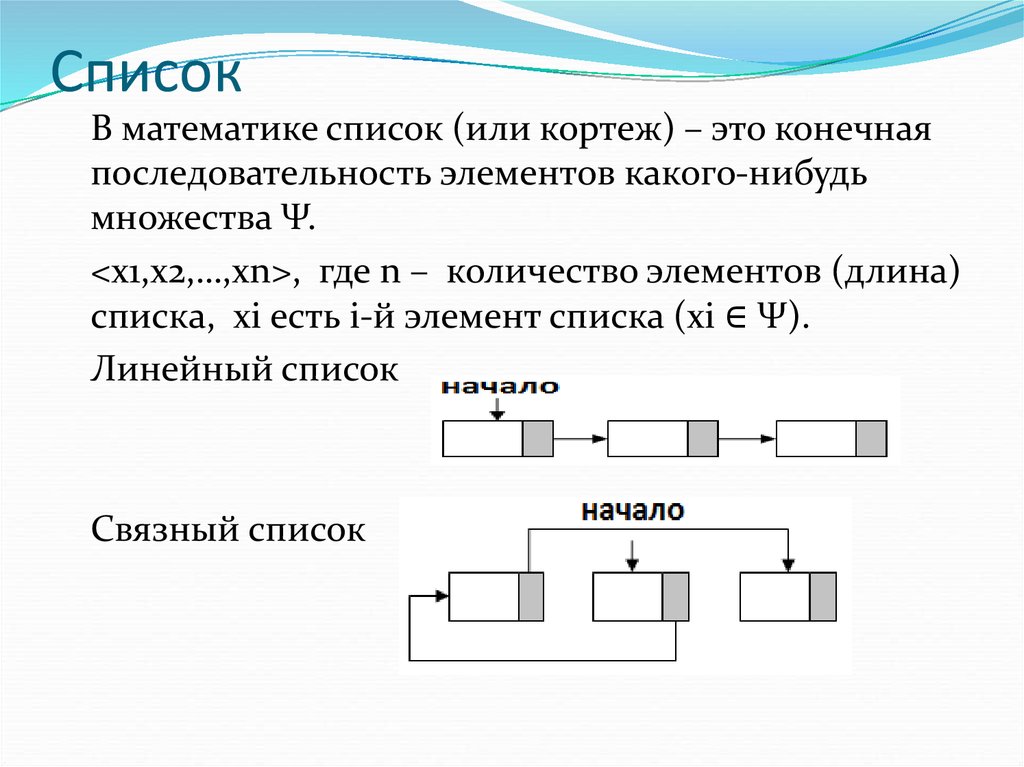
В математике список (или кортеж) – это конечнаяпоследовательность элементов какого-нибудь
множества Ψ.
<x1,x2,…,xn>, где n – количество элементов (длина)
списка, xi есть i-й элемент списка (xi ∈ Ψ).
Линейный список
Связный список
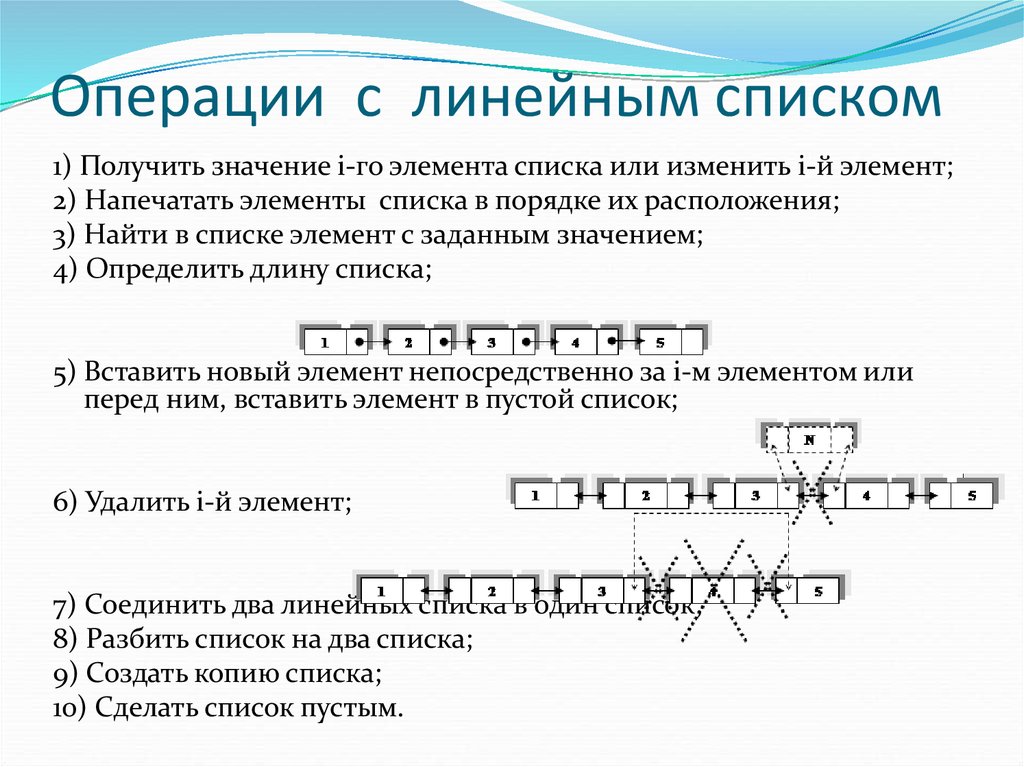
4. Операции с линейным списком
1) Получить значение i-го элемента списка или изменить i-й элемент;2) Напечатать элементы списка в порядке их расположения;
3) Найти в списке элемент с заданным значением;
4) Определить длину списка;
5) Вставить новый элемент непосредственно за i-м элементом или
перед ним, вставить элемент в пустой список;
6) Удалить i-й элемент;
7) Соединить два линейных списка в один список;
8) Разбить список на два списка;
9) Создать копию списка;
10) Сделать список пустым.
5. Реализация списков посредством массивов
Линейный списокconst
maxlen = … {для конкретной задачи целое}
type
elemtype = … {для задачи тип элементов};
list = record
elems: array [1..maxlen] of elemtype;
last: integer
end;
var L: list;
L.elems[i] - i -й элемент списка
L
elems
4
5
procedure make_null(var L: list);
begin
L.last:=0
end;
2
3
Last
6.
Операция вставки элемента x перед i-м элементомprocedure insert(var L: list; x: elemtype; i:integer);
var p: integer;
после 1-го этапа вставки:
begin
4
3
for p:=L.last downto i do
5
3-я компонента свобоL.elems[p+1]:=L.elems[p];
дна для записи
2
L.elems[i]:=x;
нового
L.last:=L.last+1;
2
значения
end;
для вставки элемента в пустой список
make_null(L); insert(L, 9,1):
Для удаления i-го элемента
procedure delete(var L: list; i:integer);
var p: integer;
begin
for p:=i to L.last-1 do
L.elems[p]:=L.elems[p+1];
L.last:=L.last-1
end;
бывшие третий
теперь занимает
четвертую
компоненту
после 2-го этапа вставки:
4
4
5
6
2
в 3-ей
компоненте
новое
значение
function is_full(var L: list):boolean;
begin
is_full:=L.last=maxlen
end;
function is_empty(var L: list):boolean;
begin
is_empty:=L.last=0
end;
function is_valid(var L: list;i:integer):boolean;
begin
is_valid:=(1<=i) and (i<=L.last)
end;
7. Поиск элемента X
function is_present(var L: list; x: elemtype):boolean;var p:integer;
begin
is_present:= false;
p:=1;
while not is_present and (p <= L.last) do
begin
is_present:= x = L.elems[p];
p:= p+1
end;
end;
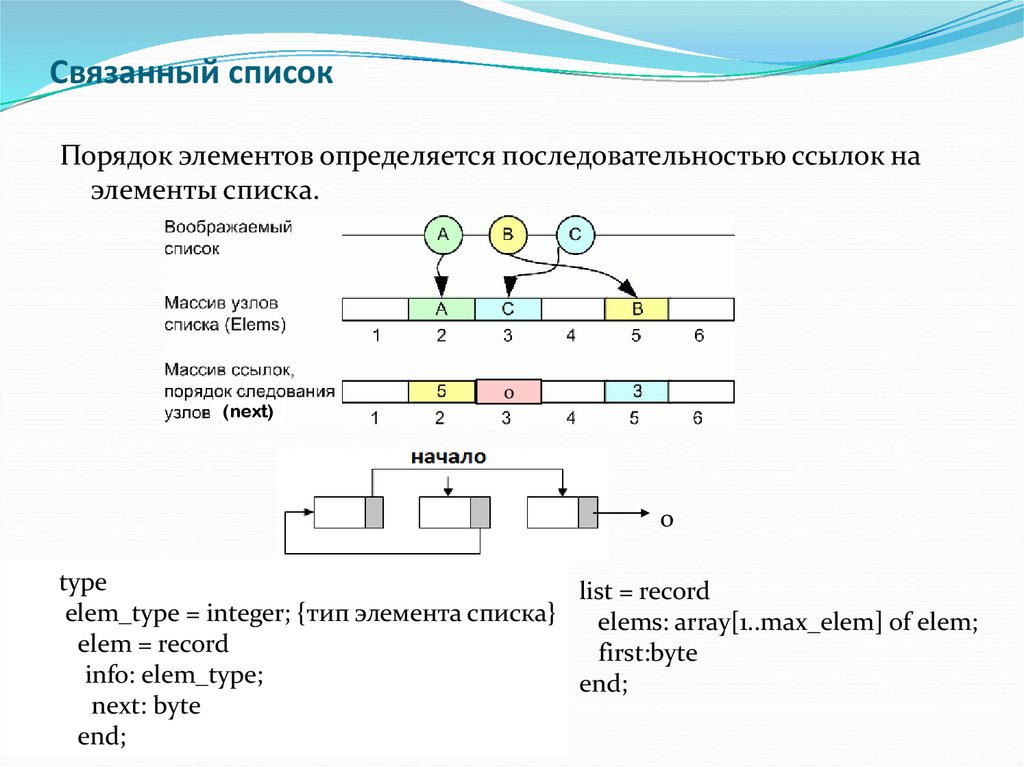
8. Связанный список
Связанный списокПорядок элементов определяется последовательностью ссылок на
элементы списка.
(next)
0
0
type
list = record
elem_type = integer; {тип элемента списка}
elems: array[1..max_elem] of elem;
elem = record
first:byte
info: elem_type;
end;
next: byte
end;
9. Создать связный список положительных и отрицательных элементов
const max_elem = 20;Type
elem_type = integer;
elem = record
info: elem_type; next: byte
end;
list = record
elems:array[1..max_elem] of elem;
first:byte
end;
var t1,t2: list;
r: elem_TYPE;
begin
t1.first := 0; t2.first2 := 0;
repeat
read (r); if r>0 then add_beg(t1, r);
if r<0 then add_beg(t2, r);
until r=0;
writeln(' список положительных элементов:');
trav_info(t1);
writeln(‘список отрицательных элементов:');
trav_info(t2);
end.
procedure add_beg (var t: list; X:elem_type);
var cur:byte;
begin
cur:=t.first+1;
t.elems[cur].info := X;
t.elems [cur].next := first;
t.first := cur
end;
procedure trav_info (var t:list);
var
cur: byte;
begin
cur := t.first;
while (cur <> 0) do
begin write(t.elems [cur].info,' * ');
cur := t.elems [cur].next
end
end;
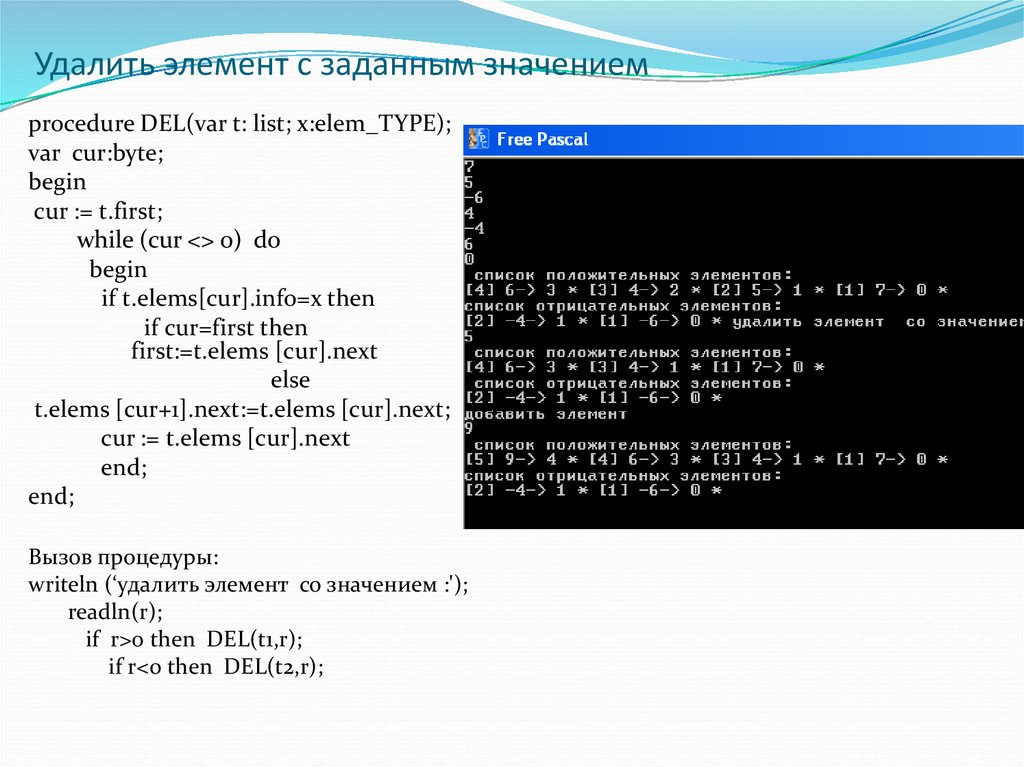
10. Удалить элемент с заданным значением
procedure DEL(var t: list; x:elem_TYPE);var cur:byte;
begin
cur := t.first;
while (cur <> 0) do
begin
if t.elems[cur].info=x then
if cur=first then
first:=t.elems [cur].next
else
t.elems [cur+1].next:=t.elems [cur].next;
cur := t.elems [cur].next
end;
end;
Вызов процедуры:
writeln (‘удалить элемент со значением :');
readln(r);
if r>0 then DEL(t1,r);
if r<0 then DEL(t2,r);
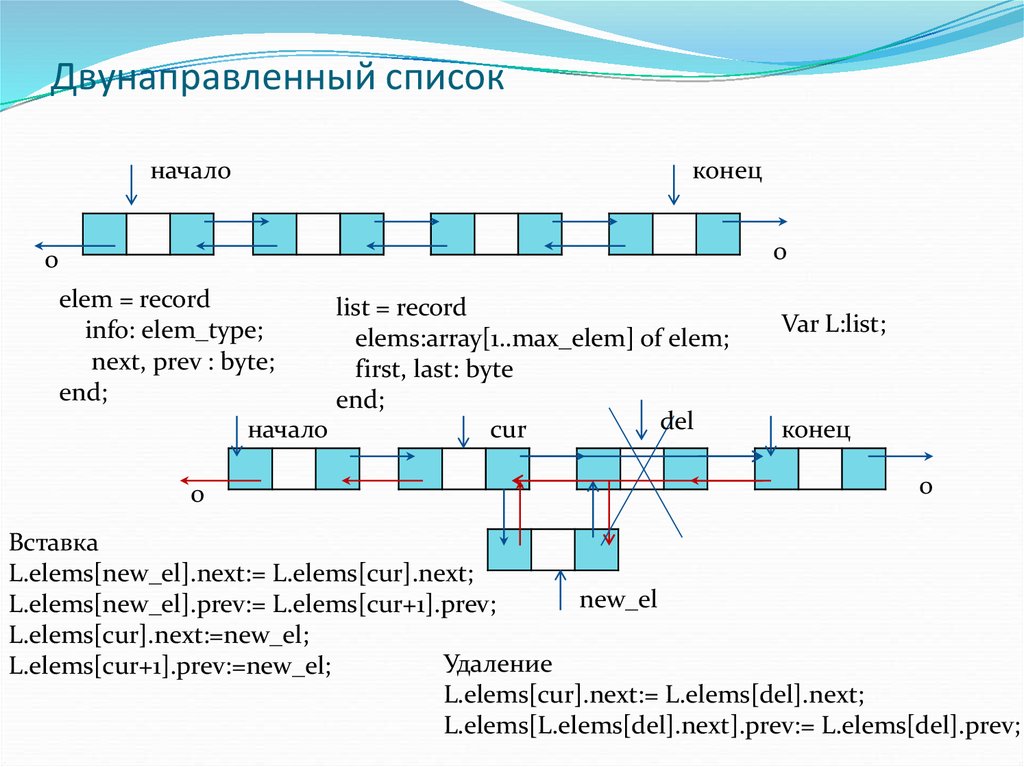
11. Двунаправленный список
началоконец
0
0
elem = record
list = record
info: elem_type;
elems:array[1..max_elem] of elem;
next, prev : byte;
first, last: byte
end;
end;
del
начало
cur
0
Var L:list;
конец
0
Вставка
L.elems[new_el].next:= L.elems[cur].next;
new_el
L.elems[new_el].prev:= L.elems[cur+1].prev;
L.elems[cur].next:=new_el;
Удаление
L.elems[cur+1].prev:=new_el;
L.elems[cur].next:= L.elems[del].next;
L.elems[L.elems[del].next].prev:= L.elems[del].prev;
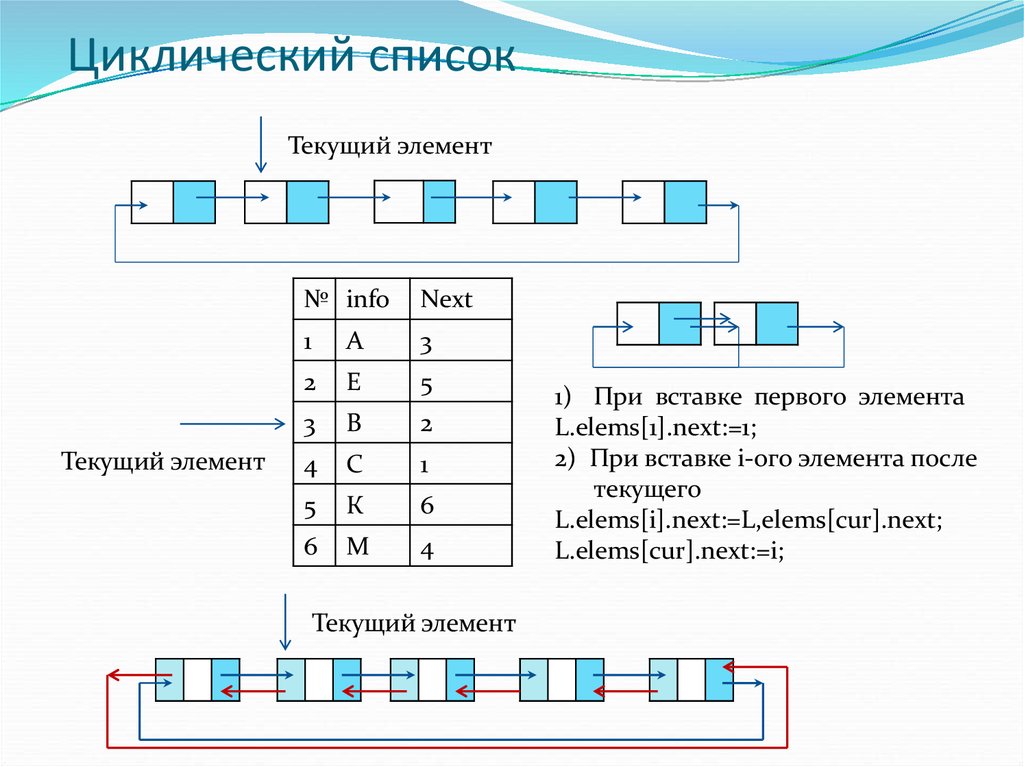
12. Циклический список
Текущий элементТекущий элемент
№ info
Next
1
А
3
2
Е
5
3
В
2
4
С
1
5
К
6
6
М
4
Текущий элемент
1) При вставке первого элемента
L.elems[1].next:=1;
2) При вставке i-ого элемента после
текущего
L.elems[i].next:=L,elems[cur].next;
L.elems[cur].next:=i;
13. Стек, очередь, дек
В очереди (queue) всегда удаляетсяэлемент, который содержится в
множестве дольше других. Стратегия
"первым вошел - первым вышел" (first-in,
first-out ).
Первым из стека (stack)
удаляется элемент, который
был помещен туда последним.
Стратегия "последним вошел
— первым вышел" (last-in,
first-out )
14. Стек
Операции, производимые надстеками:
1) Занесение элемента в стек.
Push(S,x), где S - идентификатор стека, x
- заносимый элемент.
2) Выборка элемента из стека.
Pop(S)
3) Определение пустоты стека.
Empty(S)
4) Прочтение элемента без его выборки из
стека.
StackTop(S) эквивалентно x =
Pop(Stack) Push(Stack, x).
2
5
top
Push (S,5)
Push (S,2)
Pop (S)
Pop (S)
15. Реализация стека на базе массива
conststacksize = … {максимальное число элементов};
type
elemtype = … {тип элементов стека};
stack = record
elems: array [1..stacksize] of elemtype;
top: integer {индекс вершины стека}
end;
var S: stack;
procedure push (var S: stack;x:elemtype);
Begin
S.top:=S.top+1;
S.elems[S.top]:=x
end;
procedure pop (var S: stack; var x:elemtype);
begin
x:=S.elems[S.top];
S.top:=S.top-1;
end;
function Stacktop : integer;
begin
Stacktop := S.elems[S.top];
end;
procedure init_stack (var S: stack);
begin
S.top:=0;
end;
function full_stack(var S: stack):boolean;
Begin
full_stack:=S.top=stacksize
end;
function empty_stack(var S: stack):boolean
Begin
empty_stack:=S.top=0
end;
16. Очередь
Очередью FIFO (First In First Out - "первым пришел - первым вышел”называется такой последовательный список с переменной длиной, в котором
включение элементов выполняется только с одной стороны списка (эту сторону
часто называют хвостом (tail) очереди), а исключение - с другой стороны
(называемой головой (head) очереди).
Для очереди определены три примитивные операции.
1. Очистка очереди;
2. Считывание первого элемента очереди; Операция remove(q) удаляет
элемент из начала очереди q и присваивает его значение переменной х.
3. Вставка элемента в конец очереди; Операция insert (q,x) помещает
элемент х в конец очереди q.
4. Проверка, является ли очередь пустой. Третья операция, empty (q),
возвращает значение true или false в зависимости от того, является ли данная
очередь пустой или нет
17. Пример реализации очереди в виде одномерного массива
Tail=0Tail=1
A
Head=1
B
Head=2
Insert(q,A)
Insert(q,B)
Insert(q,C)
Remove(q)
Remove(q)
Tail=2
C
Head=3
Tail=3
18.
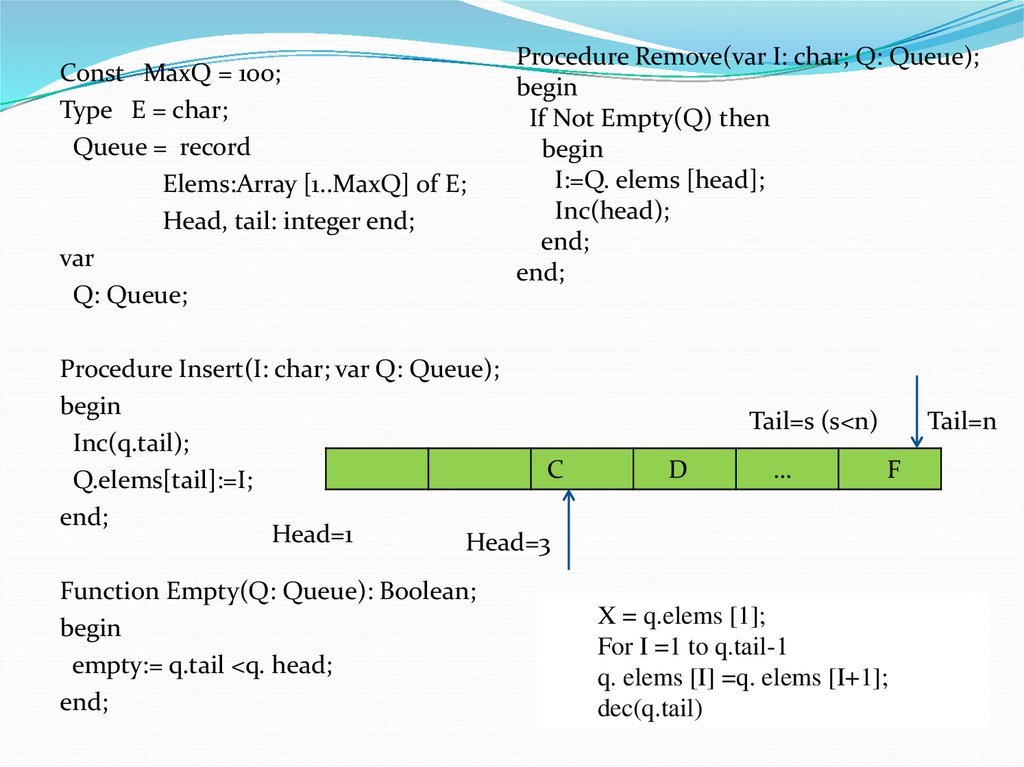
Const MaxQ = 100;Type E = char;
Queue = record
Elems:Array [1..MaxQ] of E;
Head, tail: integer end;
var
Q: Queue;
Procedure Remove(var I: char; Q: Queue);
begin
If Not Empty(Q) then
begin
I:=Q. elems [head];
Inc(head);
end;
end;
Procedure Insert(I: char; var Q: Queue);
begin
Inc(q.tail);
C
Q.elems[tail]:=I;
end;
Head=1
Head=3
Function Empty(Q: Queue): Boolean;
begin
empty:= q.tail <q. head;
end;
Tail=s (s<n)
D
…
Tail=n
F
X = q.elems [1];
For I =1 to q.tail-1
q. elems [I] =q. elems [I+1];
dec(q.tail)
19. Организация кольцевой очереди
TAIL=1 TAIL=21
2
15
TAIL=9
3
17
4
5
3
HEAD=4
Insert (q,15);
Insert (q,17);
6
5
7
12
8
1
9
4
10
20.
Const size=100;Type Data= integer;
Queue= record
elems: array[1..SIZE] of data;
tail, head : integer;
end;
Var q:queue;
Procedure QInit; { инициализация }
begin q. tail :=1; q.head:=1; end;
Procedure Qclr; {очистка}
begin q. tail :=q.head; end;
Function QSize : integer;
begin
if q.head <= q. tail then
QSize:=q. tail -q.head
else QSize:=q.tail+SIZE-q.head+1;
end;
Function Insert(a : data) : boolean;
begin
if (Q.tail mod SIZE)+1=Q.head then
insert:=false
else begin
Q.ELEMS[tail]:=a;
Q.tail:=(Q.tail mod SIZE)+1;
Insert:=true;
end;
end;
Function Remove(var a: data) : boolean;
begin
if Q.tail=Q.head then
Remove:=false
else
begin
a:=Q.elems[head];
q.head:=(q.head mod SIZE) + 1;
Remove:=true;
end;
end;
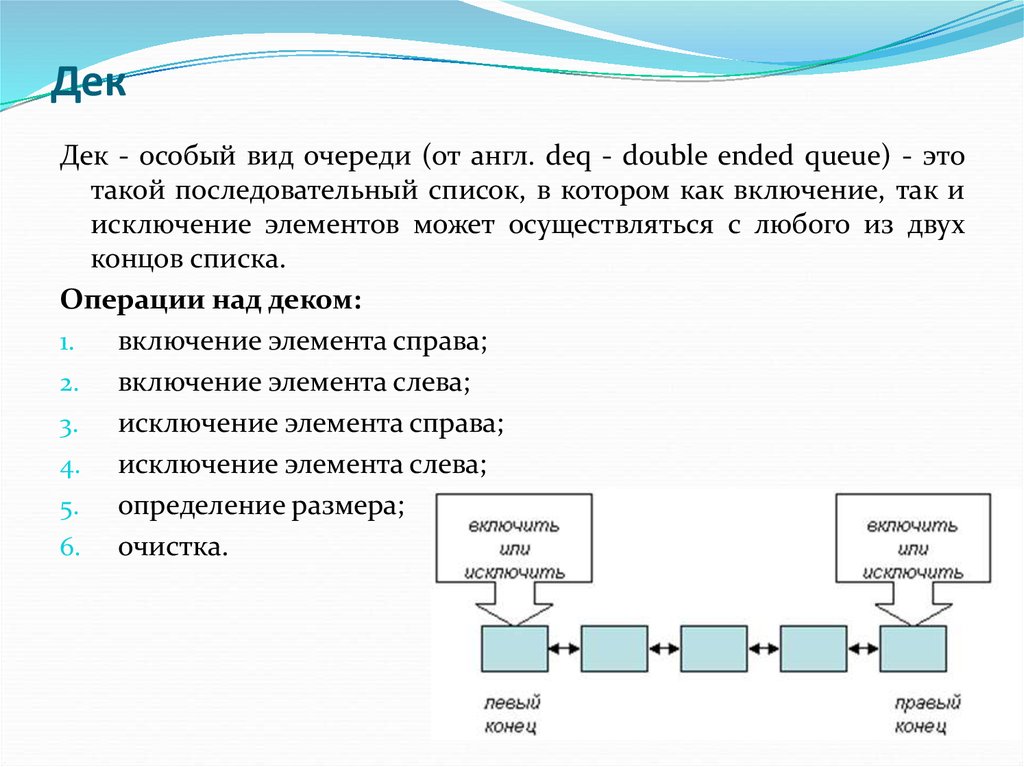
21. Дек
Дек - особый вид очереди (от англ. deq - double ended queue) - этотакой последовательный список, в котором как включение, так и
исключение элементов может осуществляться с любого из двух
концов списка.
Операции над деком:
1.
включение элемента справа;
2. включение элемента слева;
3. исключение элемента справа;
4. исключение элемента слева;
5. определение размера;
6. очистка.
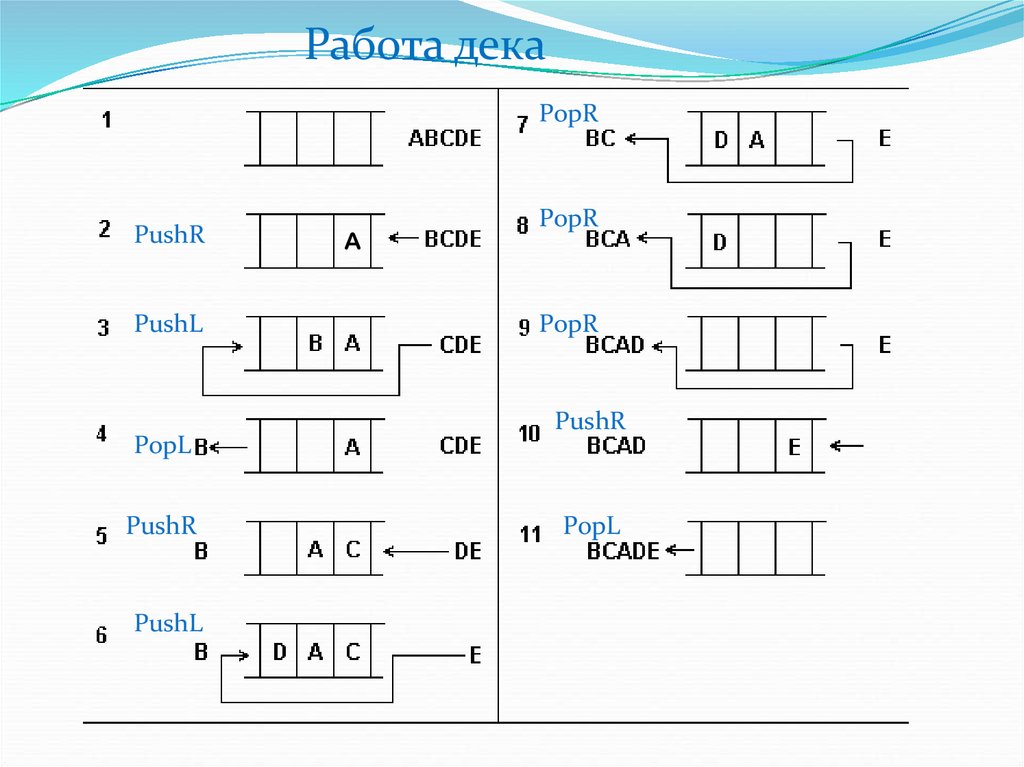
22.
Работа декаPорR
PushR
PushL
PорL
PushR
PushL
A
PорR
PорR
PushR
PорL
23. Дерево
— это совокупность элементов, называемых узлами и отношений,образующих иерархическую структуру узлов
1
2
4
3
5
8
7
6
9
10
Дерево характеризуется следующими признаками:
дерево имеет 1 элемент, на которого нет ссылок от других
элементов. Этот элемент называется корнем дерева;
в дереве можно обратиться к любому элементу путем прохождения
конечного числа вершин;
каждый элемент дерева связан только с одним предыдущим
элементом.
Высота - это количество уровней дерева.
Количество ветвей, растущих из узла дерева, называется степенью
исхода узла.
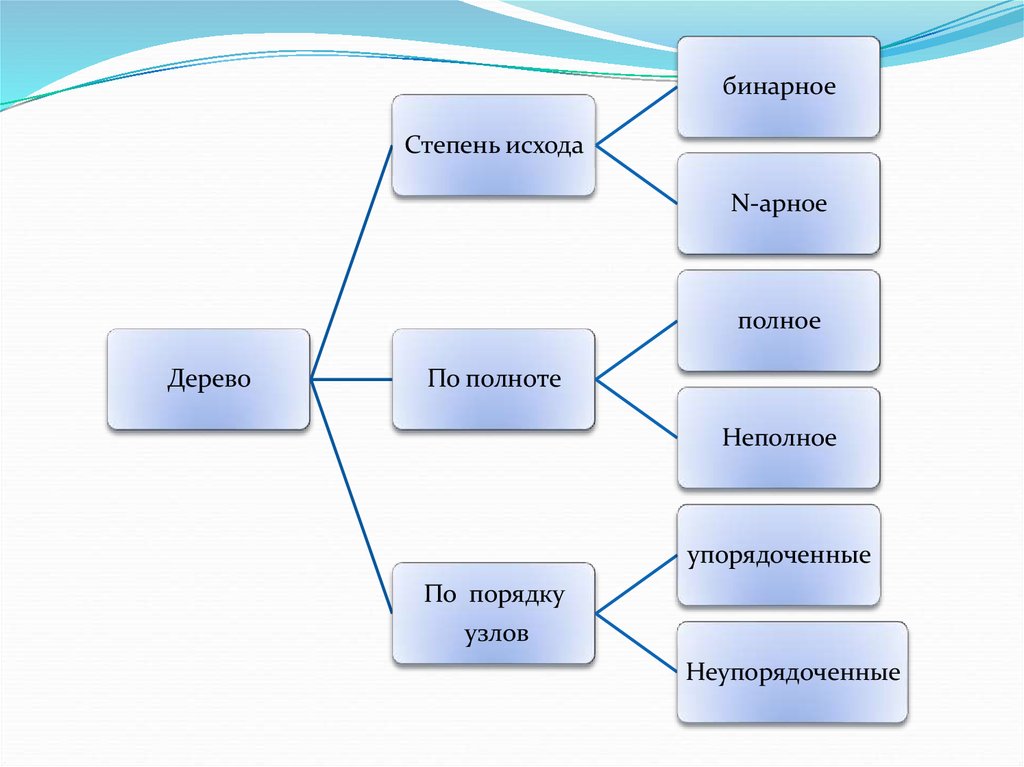
24.
бинарноеСтепень исхода
N-арное
полное
Дерево
По полноте
Неполное
упорядоченные
По порядку
узлов
Неупорядоченные
25.
Способы обхода узлов дереваобход в прямом порядке -от корня к левой ветви, затем к правой;
1 2 3 5 8 9 6 10 4 7
обход в обратном порядке -проходится левая ветвь, затем правая, затем
корень
2 8 9 5 10 6 3 7 4 1
симметричный обход - дерево проходится, начиная с левой ветви вверх к
корню, затем к правой ветви;
2 1 8 5 9 3 10 6 7 4
1
2
4
3
5
8
7
6
9
10
26. Представление дерева
12
3
4
5
6
9
7
10
8
j 1
2
3
4
5
6
7
8
9
10
A 0
1
1
2
2
5
5
5
3
3
j info count
sun
1
1
2
2
3
2
2
2
3
3
2
4
5
4
4
0
9
10
5
5
3
6
6
0
7
7
0
8
8
0
9
9
0
10 10
0
6 7 8
type
node= record
info: char;
count: integer;
sun: array [1..max] of integer
end;
tree= array [1..max] of node;
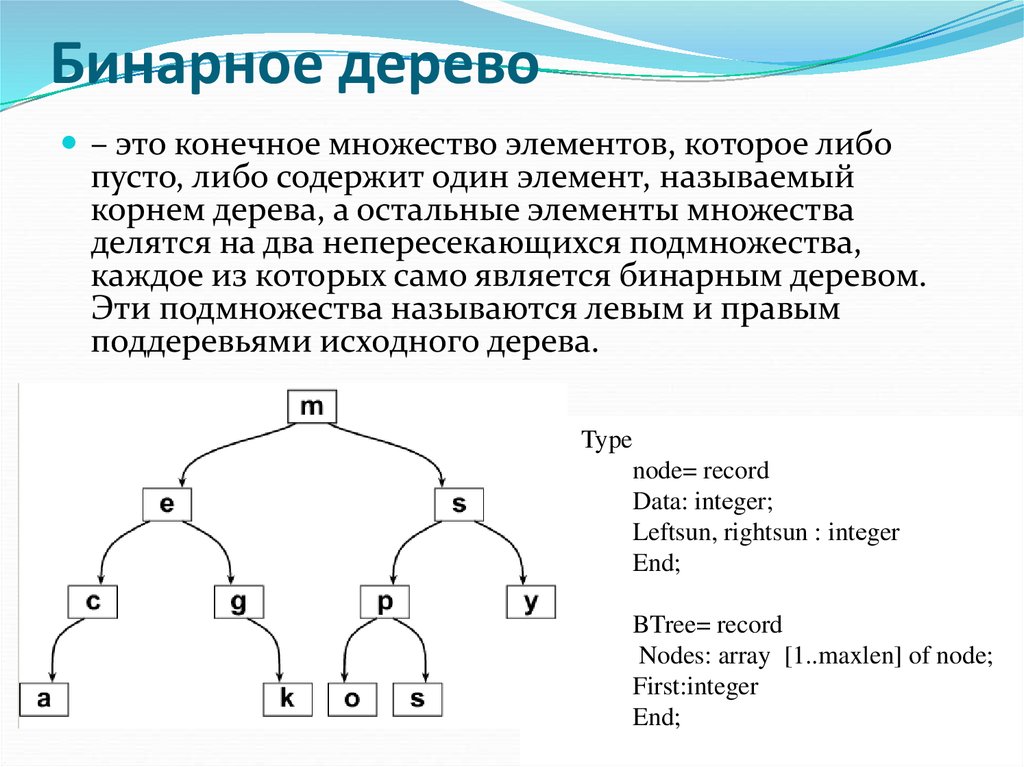
27. Бинарное дерево
– это конечное множество элементов, которое либопусто, либо содержит один элемент, называемый
корнем дерева, а остальные элементы множества
делятся на два непересекающихся подмножества,
каждое из которых само является бинарным деревом.
Эти подмножества называются левым и правым
поддеревьями исходного дерева.
Type
node= record
Data: intеger;
Leftsun, rightsun : intеger
End;
BTree= record
Nodes: array [1..maxlen] of node;
First:integer
End;
28. Основные операции с деревьями
1. Обход дерева.Обработка корня.
Обработка левой ветви.
Обработка правой ветви.
2. Удаление поддерева.
Поиск родителя поддерева
Разрыв связи с удаляемым поддеревом
Декремент степени исхода
3. Вставка поддерева.
Определения родителя для нового поддерева
Установка связи с новым поддеревом
Инкремент степени исхода
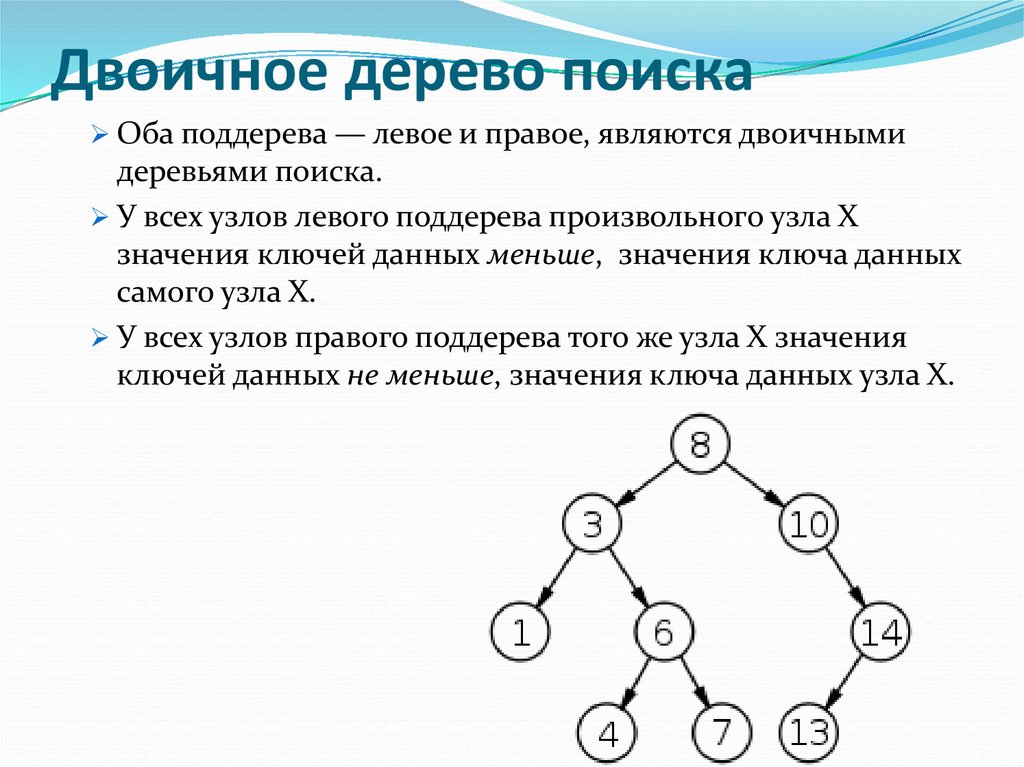
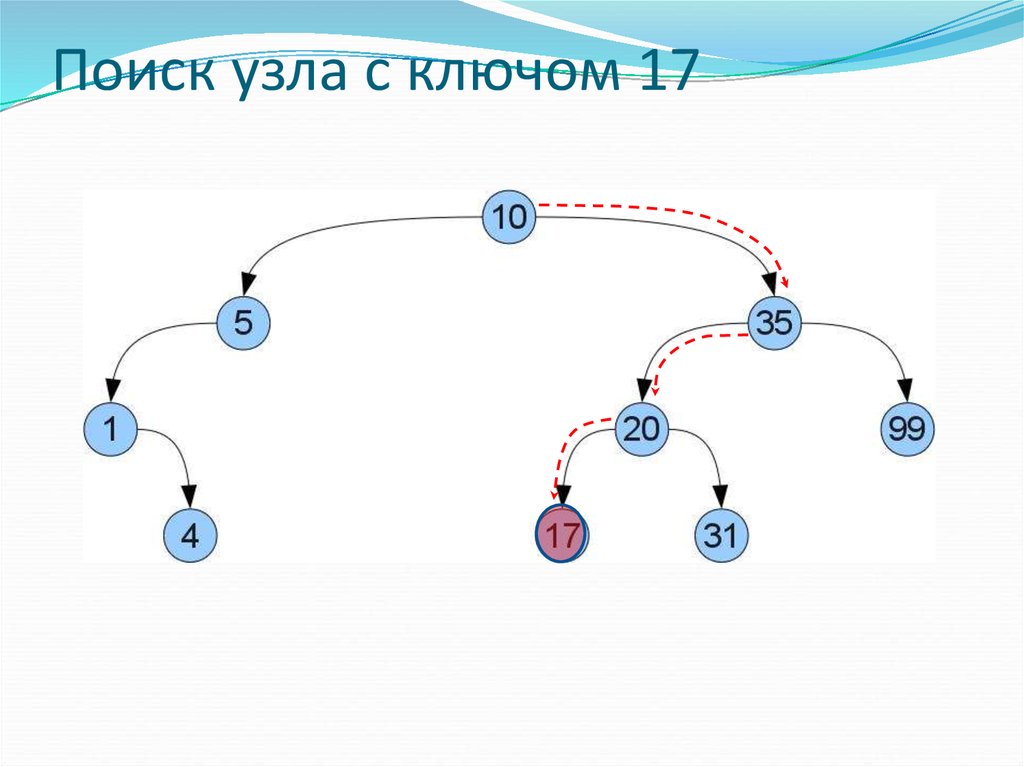
29. Двоичное дерево поиска
Оба поддерева — левое и правое, являются двоичнымидеревьями поиска.
У всех узлов левого поддерева произвольного узла X
значения ключей данных меньше, значения ключа данных
самого узла X.
У всех узлов правого поддерева того же узла X значения
ключей данных не меньше, значения ключа данных узла X.
30. Поиск узла с ключом 17
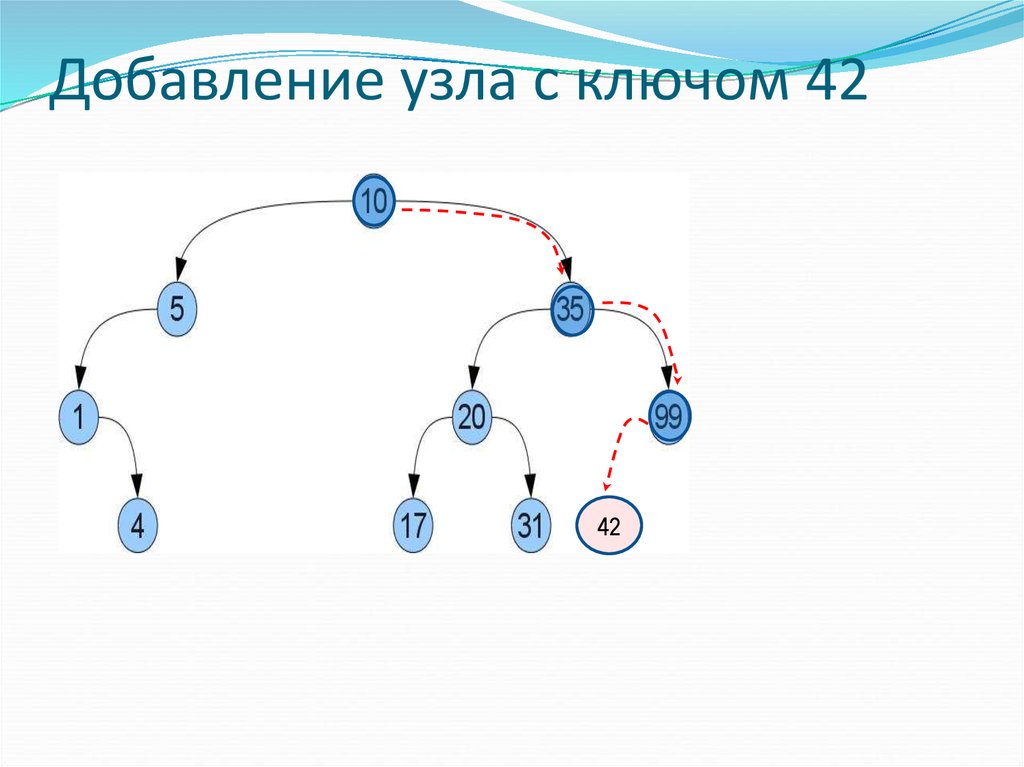
31. Добавление узла с ключом 42
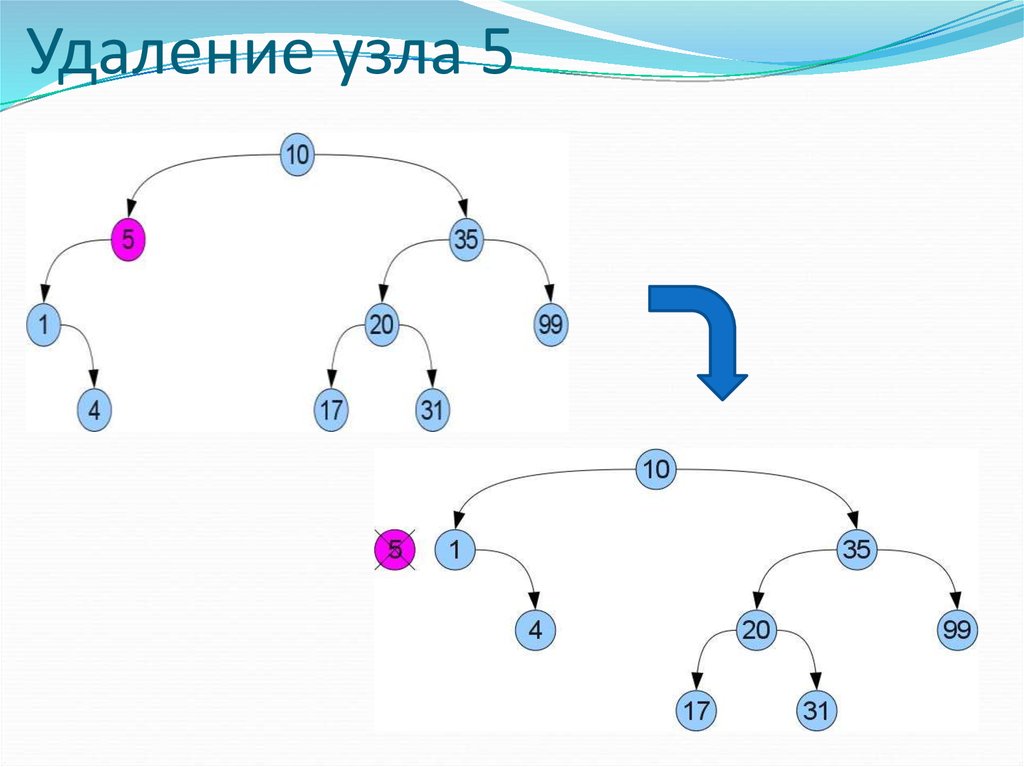
4232. Удаление узла 5
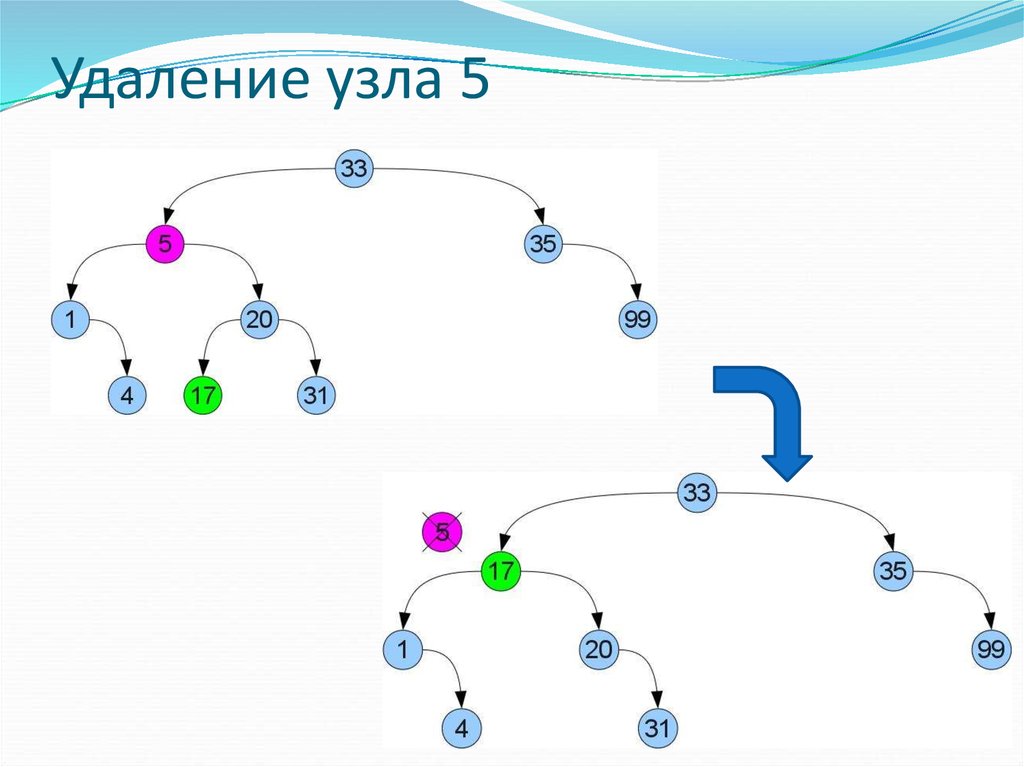
33. Удаление узла 5
34. Ку́ча
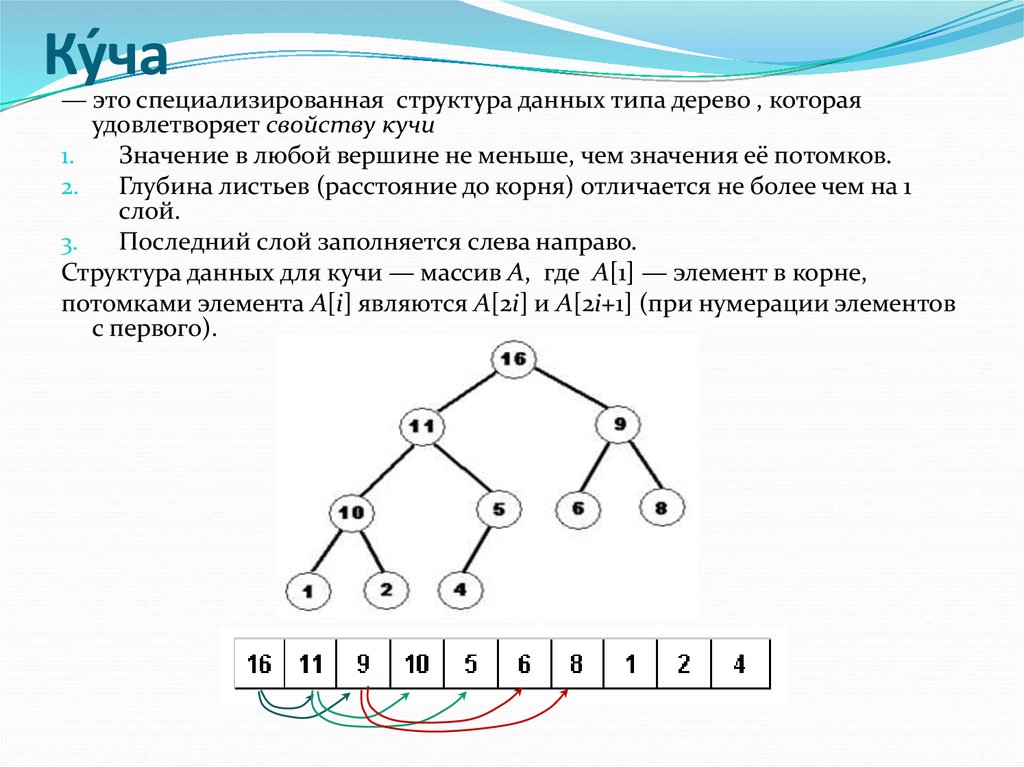
Куч́ а— это специализированная структура данных типа дерево , которая
удовлетворяет свойству кучи
1.
Значение в любой вершине не меньше, чем значения её потомков.
2.
Глубина листьев (расстояние до корня) отличается не более чем на 1
слой.
3.
Последний слой заполняется слева направо.
Структура данных для кучи — массив A, где A[1] — элемент в корне,
потомками элемента A[i] являются A[2i] и A[2i+1] (при нумерации элементов
с первого).
35. Основные операции с кучей
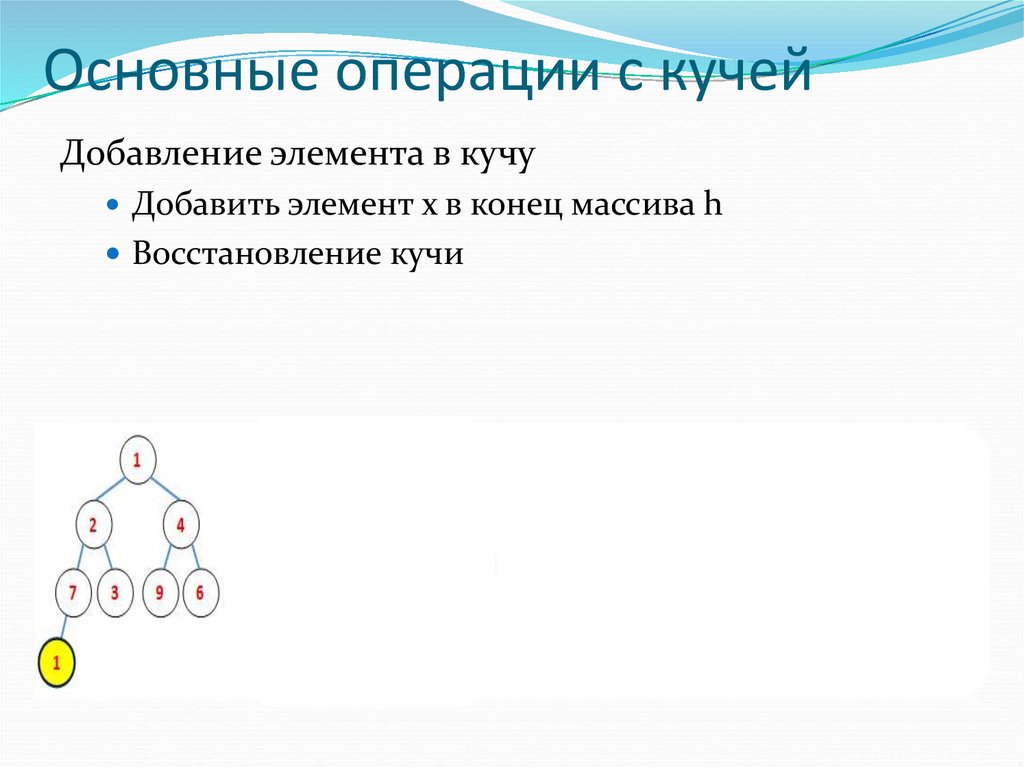
Добавление элемента в кучуДобавить элемент х в конец массива h
Восстановление кучи



















 Программирование
Программирование








