Характеристические числа графов

1. Дискретная математика

Характеристические
числа графов

2. Цикломатическое число

Цикломатическим
числом графа G
называется число ребер,
которые надо убрать, что
бы граф стал ацикличным.

3. Цикломатическое число

Рис. 1
Рис. 2

4. Цикломатическое число

Цикломатическое число графа G
находится по формуле:
G e v с
e число ребер ,
v число вершин,
с число компонент связности .

5. Цикломатическое число

Замечание 1. Цикломатическое
число дерева равно 0.
Замечание 2. Цикломатическое
число леса равно 0.
Замечание 3. Если
цикломатическое число графа
равно 1, то в графе ровно 1 цикл.

6. Цикломатическое число

Пример 1.
G e v с
7 5 1 3.

7. Цикломатическое число

Пример 2. G
e v с
10 7 2 5.

8. Число внутренней устойчивости

Внутренне устойчивым
множеством графа G называется
множество вершин S, все вершины
которого попарно несмежны.
Число внутренней устойчивости:
G max S
S V

9. Число внутренней устойчивости

S1 a , S2 a , c , S3 g, c , S4 a , d .
G max Si 2.

10. Число внешней устойчивости

Внешне устойчивым множеством
графа G называется множество
вершин Q, таких, что из всех
вершин множества ┐Q ведут
ребра в вершины множества Q.
Число внутренней устойчивости:
G min Q
Q V

11. Число внешней устойчивости

Q1 a , b, c , Q2 g, d .
G min Qi 2.

12. Хроматическое число

Граф G называется h- хроматическим,
если его вершины можно раскрасить h
различными красками так, чтобы
никакие две смежные (различные)
вершины не были окрашены в один
цвет. Хроматическое число графа –
это наименьшее число красок.
G min h

13. Хроматическое число

H1 a , d , H 2 g, c , H3 b .
G min h 3.

14. Хроматическое индекс

Граф G называется k-раскрашиваемым,
если его ребра можно раскрасить k
различными красками так, чтобы
никакие два смежные ребра не были
окрашены в один цвет.
Хроматический индекс графа – это
наименьшее число красок.
G min k

15. Хроматическое индекс

Согласно теореме Визинга, если
максимальная локальная степень
вершины графа равна k, то
хроматический индекс подчиняется
условию:
k G k 1

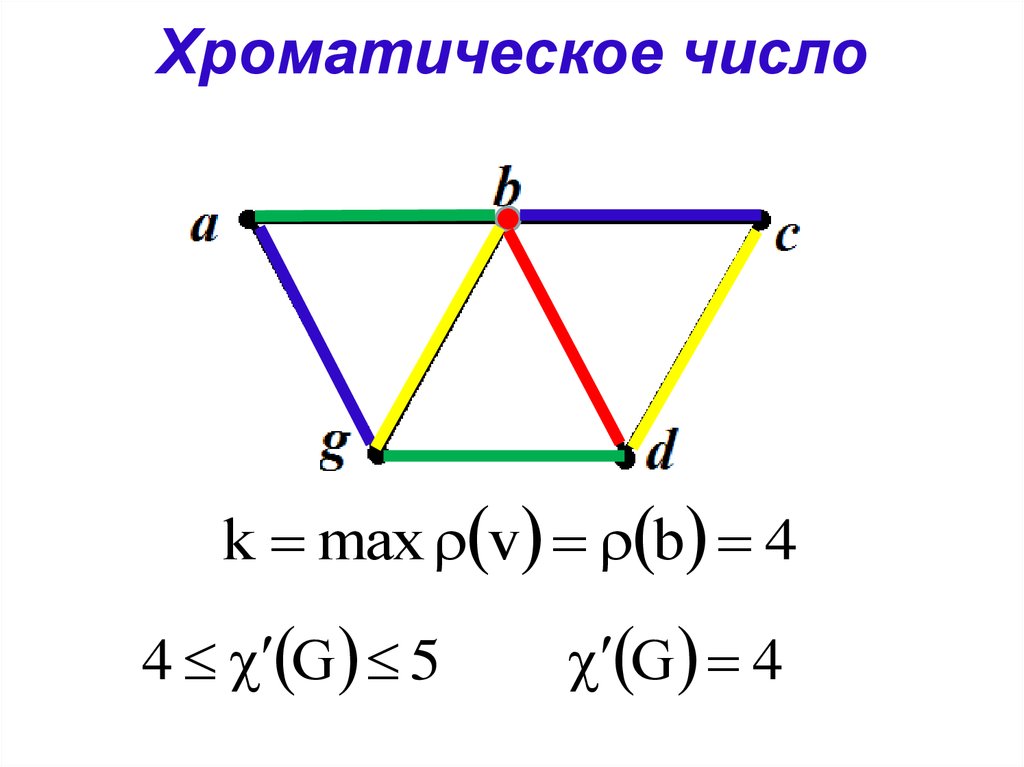
16. Хроматическое число

k max v b 4
4 G 5
G 4

17. Пример 1

В пунктах Х1, Х2, Х3, Х4, Х5, Х6 могут
быть источники излучения. Если
источники расположены в пунктах Xi
и Xj влияют друг на друга (поражают
друг друга), то на графе они
соединены ребром (Xi, Xj). Можно ли
расположить в каких-либо из данных
пунктов 4 или 3 источника, не
поражающих друг друга?

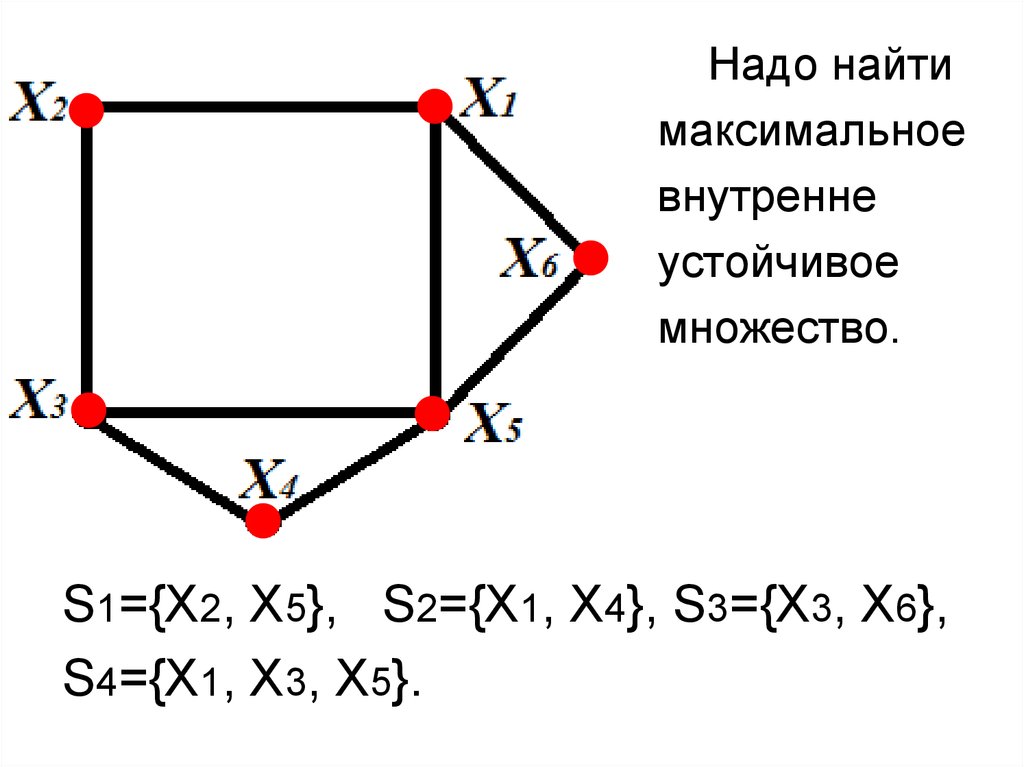
18.

Надо найти
максимальное
внутренне
устойчивое
множество.
S1={X2, X5}, S2={X1, X4}, S3={X3, X6},
S4={X1, X3, X5}.

19. Пример 2

Объекты Х1, Х2, … , Х9
расположены так, как показано
на графе. Объекты, которые
просматриваются друг из друга
соединены ребрами. Определить
в каких объектах достаточно
поставить камеры наблюдения,
чтобы они в совокупности
просматривали все объекты.

20.

21.

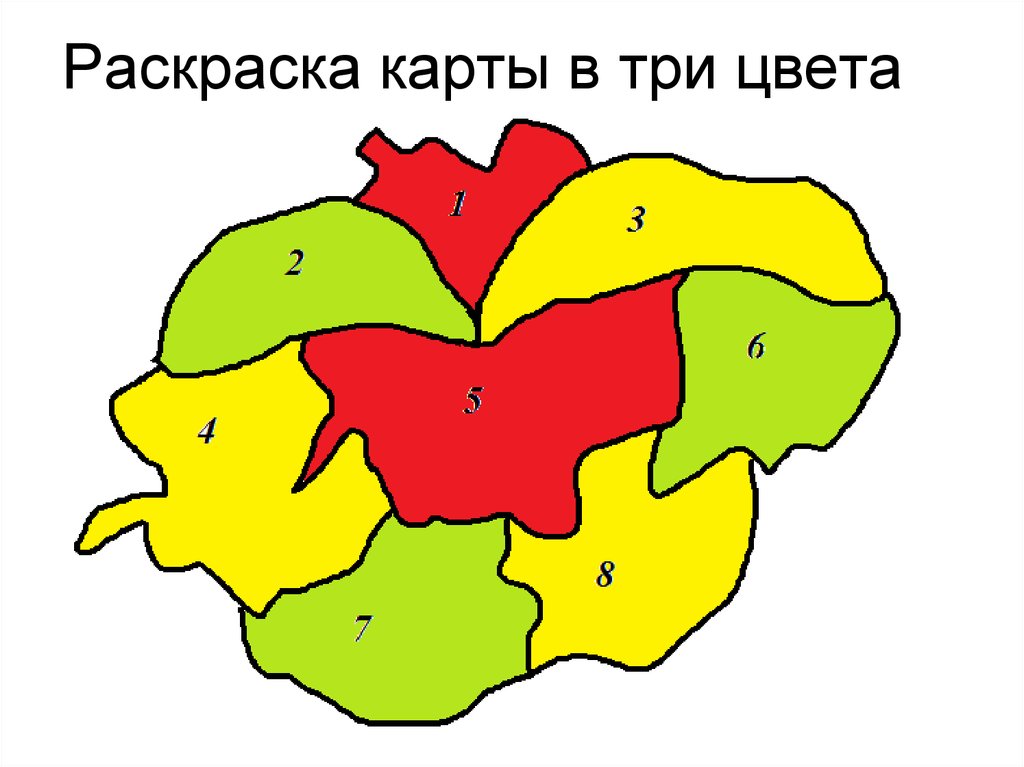
Пример 3. Дана политическая карта
континента. Найти минимальное число
цветов, чтобы раскрасить карту.

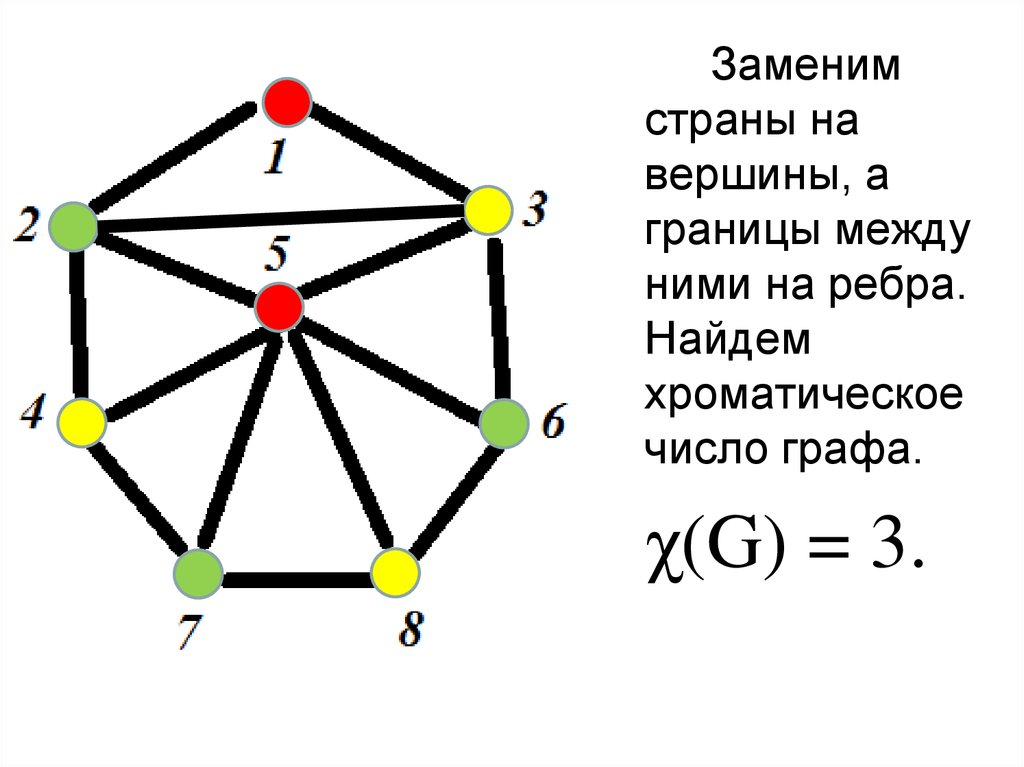
22.

Заменим
страны на
вершины, а
границы между
ними на ребра.
Найдем
хроматическое
число графа.
χ(G) = 3.

23.

Раскраска карты в три цвета