Потенциальные поля простой трёхмерной фрактальной модели среды (губка Менгера)

1. ПОТЕНЦИАЛЬНЫЕ ПОЛЯ ПРОСТОЙ ТРЁХМЕРНОЙ ФРАКТАЛЬНОЙ МОДЕЛИ СРЕДЫ (ГУБКА МЕНГЕРА)

Глазнев В.Н., Ли А.Т., Кочетов М.В.
Воронежский государственный университет, Воронеж

2.

Фрактальный объект обладает некоторой сложной,
приближённо, самоподобной структурой,
проявляющейся на различных, как правило кратных,
уровнях масштабирования.
Фракталы используются для описания геометрии
природных объектов сложной самоподобной формы
(Мандельброт, 2002), анализа структуры рудных
полей, геофизических аномалий и результатов
петрофизических измерений (Keilis-Borok et.al., 1996,
2001, 2004; Горяинов, Иванюк, 1998, 2001;
Galitchanina et. al., 1995; Козлов и др., 2006).

3.

В плане применения методов фрактальной геометрии к
анализу потенциальных полей, интерес представляют
работы Ю.И.Блоха с соавторами (Бабаянц и др., 2005;
Блох, 2007), в которых исследовалась простейшая 2D
модель фрактальной среды - «ковер Серпинского»,
обладающая нецелой Хаусдорфовой размерностью
ln 8
1.89
ln 3
Авторами указанных работ было показано, что
магнитное поле такой структуры, также представляет
некоторую фрактальную структуру.

4.

Задача:
Численное моделирование потенциальных полей от 3D
фрактальных моделей среды, примером которых
является «губка Менгера» – трёхмерный куб, каждая
грань которого выглядит как «ковёр Серпинского».
N

5.

Губка Менгера обладает масштабным самоподобием и
характеризуется нецелой Хаусдорфовой размерностью
ln 20
ln 3
2.73
Объём куба Менгера (для итерации N)
VN 20 27
N
В пределе (для N→∞) куб Менгера имеет нулевой
объём и бесконечную площадь граней.

6.

Численное моделирование:
исходный куб размером 1000 х 1000 х1000 м с
избыточной плотность 1000 кг/м3;
формирование модели куба Менгера для текущей
итерации;
вычисление полей Vz и Vzz с заданной точностью на
плоскости над верхней гранью куба Менгера.
Проблемы моделирования: сложность модели (число
непустых элементов куба Менгера) и линейные
размеры элемента изменяются как
Num 20
N
l L 3N

7.

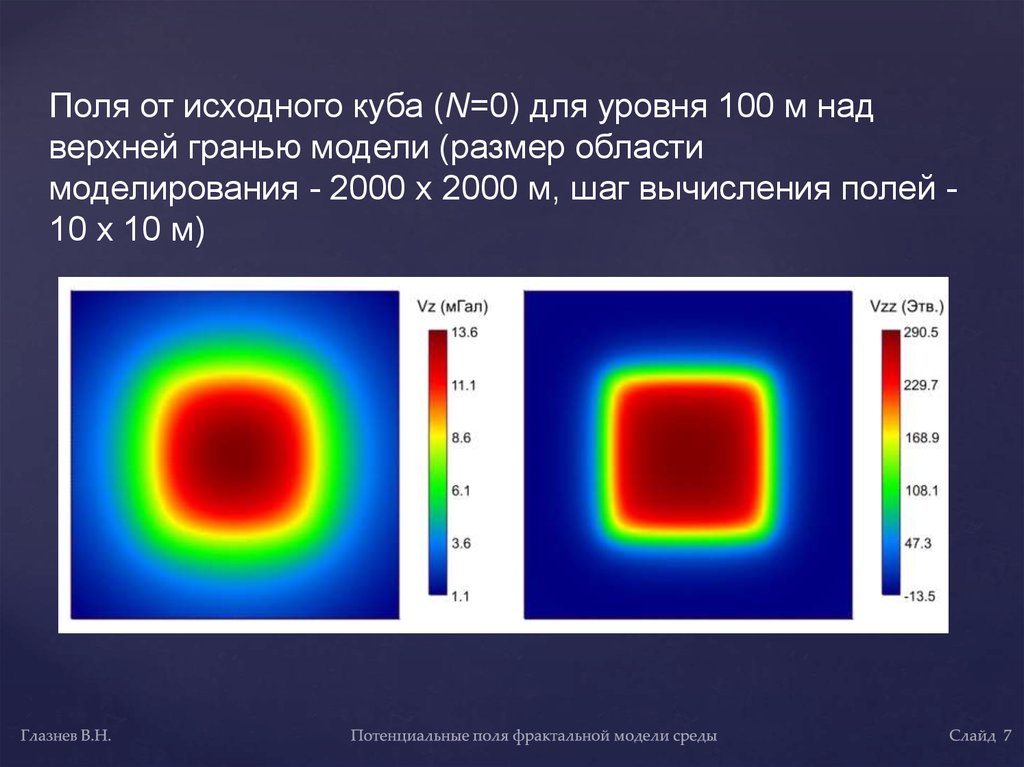
Поля от исходного куба (N=0) для уровня 100 м над
верхней гранью модели (размер области
моделирования - 2000 х 2000 м, шаг вычисления полей 10 х 10 м)

8.

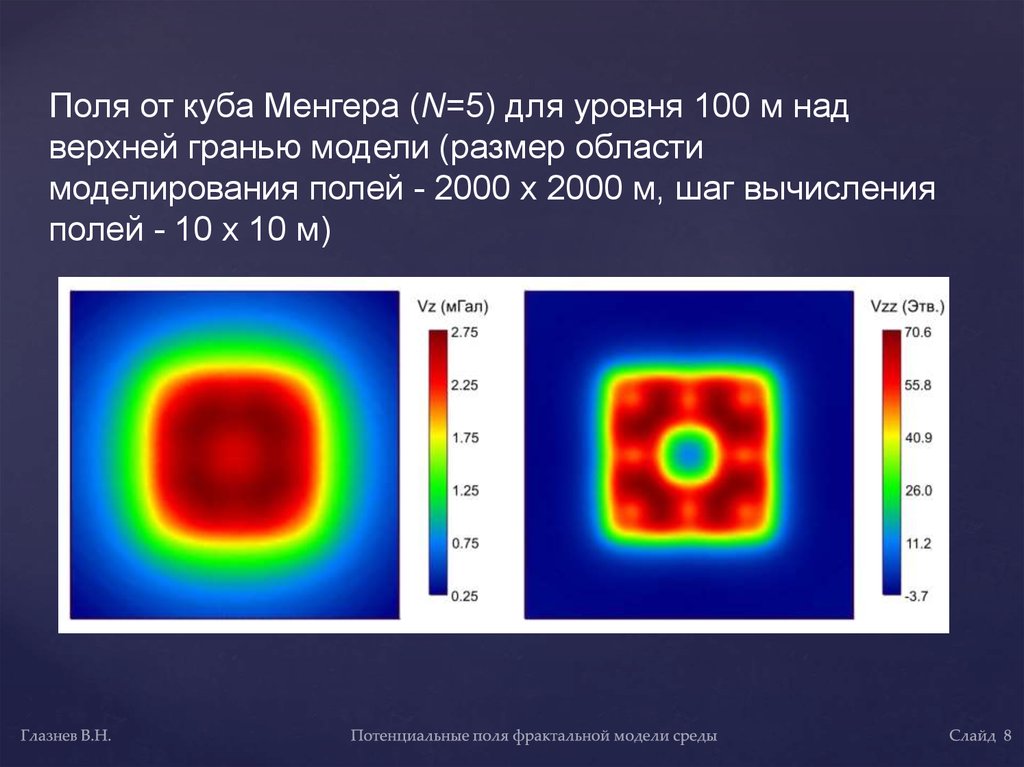
Поля от куба Менгера (N=5) для уровня 100 м над
верхней гранью модели (размер области
моделирования полей - 2000 х 2000 м, шаг вычисления
полей - 10 х 10 м)

9.

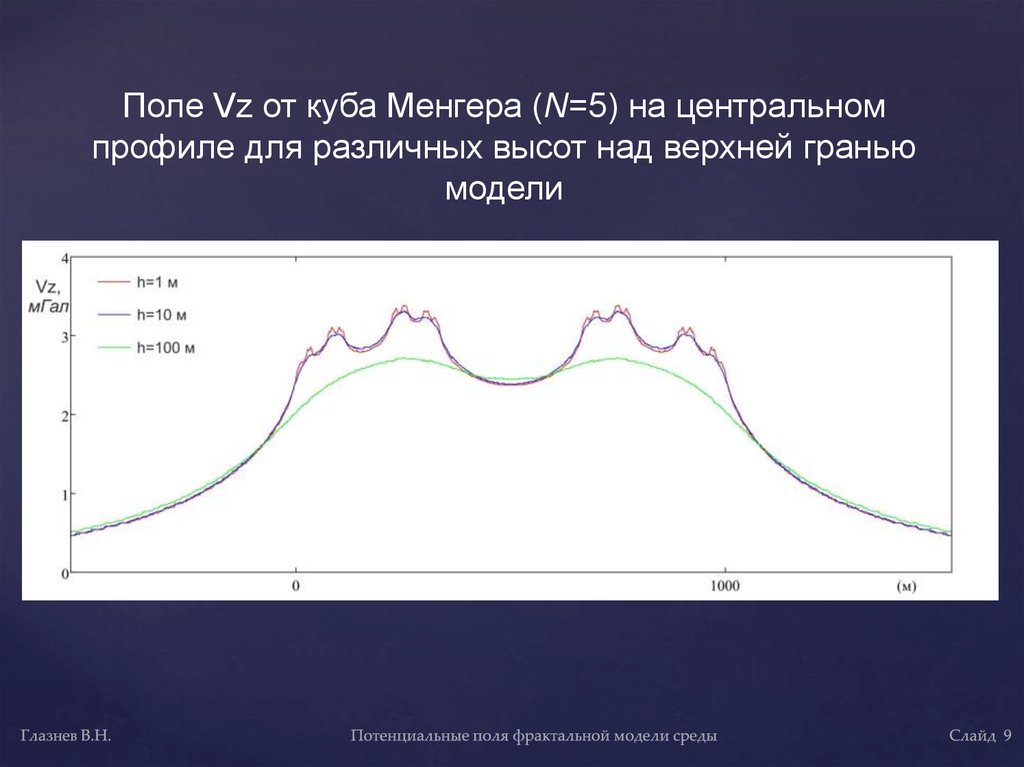
Поле Vz от куба Менгера (N=5) на центральном
профиле для различных высот над верхней гранью
модели

10.

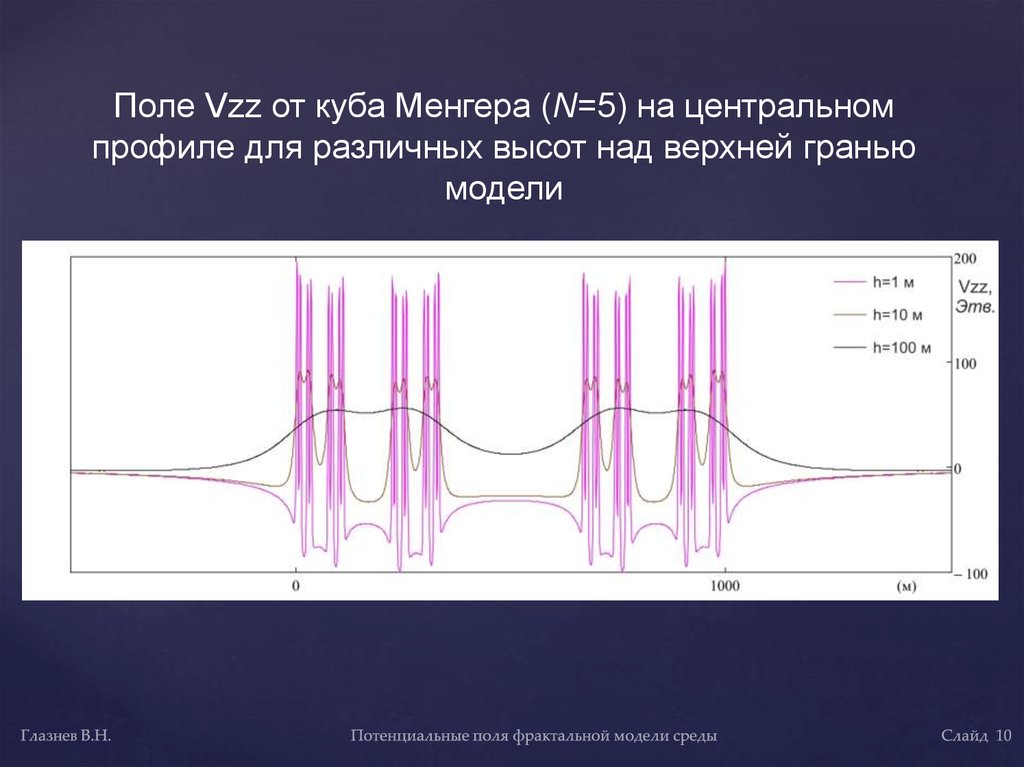
Поле Vzz от куба Менгера (N=5) на центральном
профиле для различных высот над верхней гранью
модели

11.

Амплитудный спектр поля
Vz от куба Менгера (N=5).
h=100 м
Порог ошибок округления
данных
h=10 м
Ws q 2 12
где q – значение младшего
значащего разряда (q=0.01
мГал).
h=1 м

12.

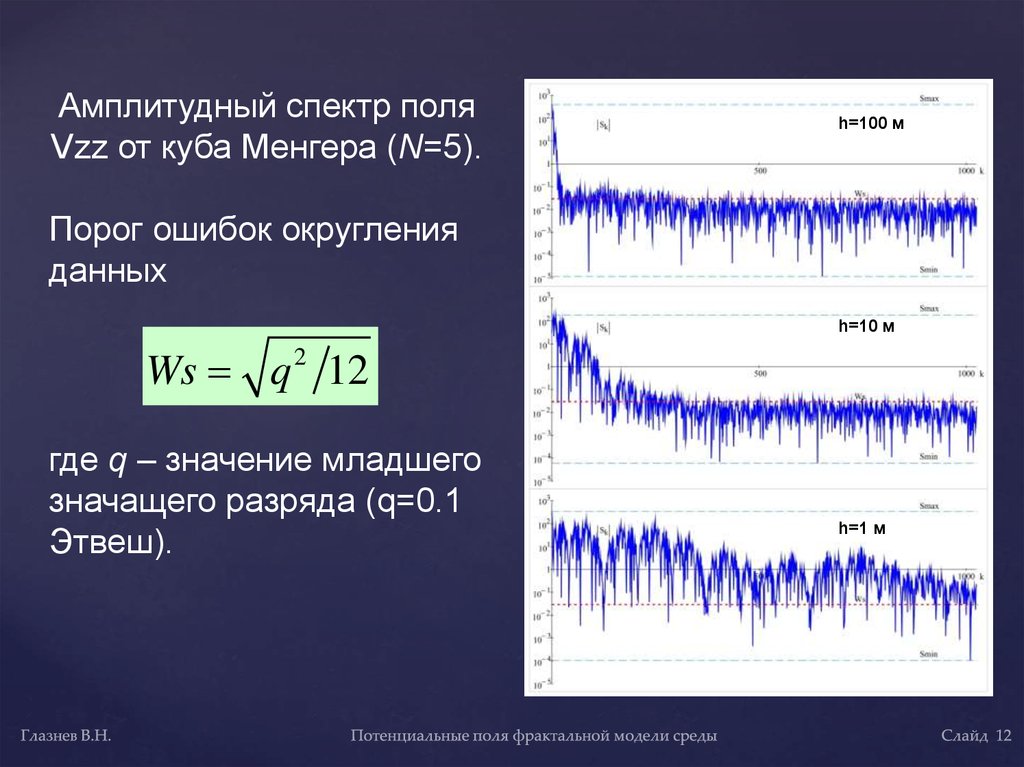
Амплитудный спектр поля
Vzz от куба Менгера (N=5).
h=100 м
Порог ошибок округления
данных
h=10 м
Ws q 2 12
где q – значение младшего
значащего разряда (q=0.1
Этвеш).
h=1 м

13.

Для спектра мощности самоподобного (фрактального)
процесса известно
G
Соотношение между спектрами плотности в слое Ss и
поля SF на уровне z
S F , z Ss , m S R , z m
N
m
где SF – спектр оператора Пуассона
exp z m
, для Vz
S R , z m
exp z m , для Vzz

14.

Вывод:
Исследование фрактальных свойств потенциальных
полей требует чёткого определения реальной
точности представления данных, а равно и
результатов их аналитических преобразований.
Для более глубокого анализа данных потенциальных
полей требуются более высокие точности их
практического определения и, вероятно, переход к
измерениям высших производных полей.

15. Благодарю за внимание

16.

Поле Vz от куба Менгера (N=0) на центральном
профиле для различных высот над верхней гранью
модели

17.

Поле Vzz от куба Менгера (N=0) на центральном
профиле для различных высот над верхней гранью
модели