Похожие презентации:
Механическое движение. Виды движений. Кинематика материальной точки. Силы в механике
1. ФИЗИКА
2.
Литература:1.Сазонова З.С., Ткачева Т.М., Чечеткина
Н.В.
Литература:
1.Смык А.Ф.
Курс Физики,2016
2.Захаров В.Г.
Физика для бакалавров
3.Трофимова Т.И.
Курс физики
3.
Лекция 11. Механическое движение. Виды движений
2. Кинематика
материальной
точки.
Криволинейное
движение.
Тангенциальное и нормальное ускорения
3. Динамика материальной точки. Основное
уравнение поступательного движения (2
закон Ньютона)
4. Силы в механике
4. 1.Механическое движение
• Механическое движение- изменение положениятел друг относительно друга с течением времени.
• Физическое тело:
1. Тело, размерами которого в условиях данной
задачи можно пренебречь, называется
материальной точкой (МТ).
2. Система материальных точек.
3. Абсолютно твердое тело (АбсТвТ)– тело,
деформациями которого в условиях данной задачи
можно пренебречь .
5. Определение положения тела
• Совокупность неподвижных друготносительно друга тел, по отношению к
которым рассматривается движение, и
отсчитывающих время часов образуют
систему отсчета (СО).
• С телами, образующими систему отсчета,
связывают системы координат (СК).
6.
Декартова система координатРене Декарт (1596–1650).
7. Степени свободы
• Числом степеней свободымеханической системы называется
число независимы величин, с
помощью которых может быть
задано положение системы.
• Положение МТ в пространстве
определяется тремя координатами МТ имеет три степени свободы.
• Система МТ, состоящая из N точек,
между которыми нет жестких связей,
имеет 3 N степеней свободы.
• Число степеней свободы АбсТвТ
будет равно шести
8. Поступательное движение
• Движение АбсТвТ можно разложить на дваосновных вида движения – поступательное
и вращательное.
• Поступательное движение- это такое
движение, при котором любая прямая,
связанная с движущимся телом, остается
параллельной самой себе.
9. Поступательное движение АбТвТ
• При поступательном движении АТТ все его точкиперемещаются по одинаковым траекториям и
имеют одинаковые скорость и ускорение.
Поэтому при поступательном движении АТТ
используются модель МТ и кинематические
параметры для МТ.
В этом случае выбирается одна точка, связанная с
телом и описывается ее движение. Все остальные
точки в движении отличаются только по
координатам.
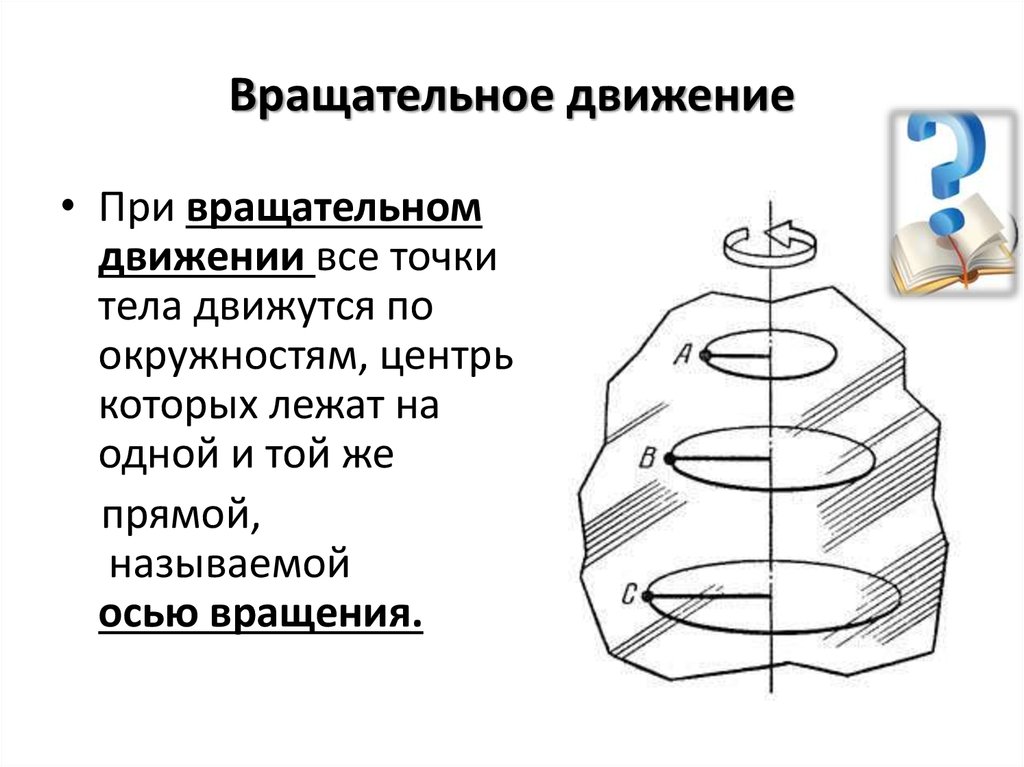
10. Вращательное движение
• При вращательномдвижении все точки
тела движутся по
окружностям, центры
которых лежат на
одной и той же
прямой,
называемой
осью вращения.
11. Кинематика МТ
• МТ при своем движении описываетнекоторую линию, которая называется
траекторией.
• Расстояние между начальным и конечным
положением частицы, отсчитываемое вдоль
траектории, называется пройденным путем.
• Прямолинейный отрезок (кратчайшее
расстояние), проведенный из начального
положения частицы в конечное, называется
перемещением.
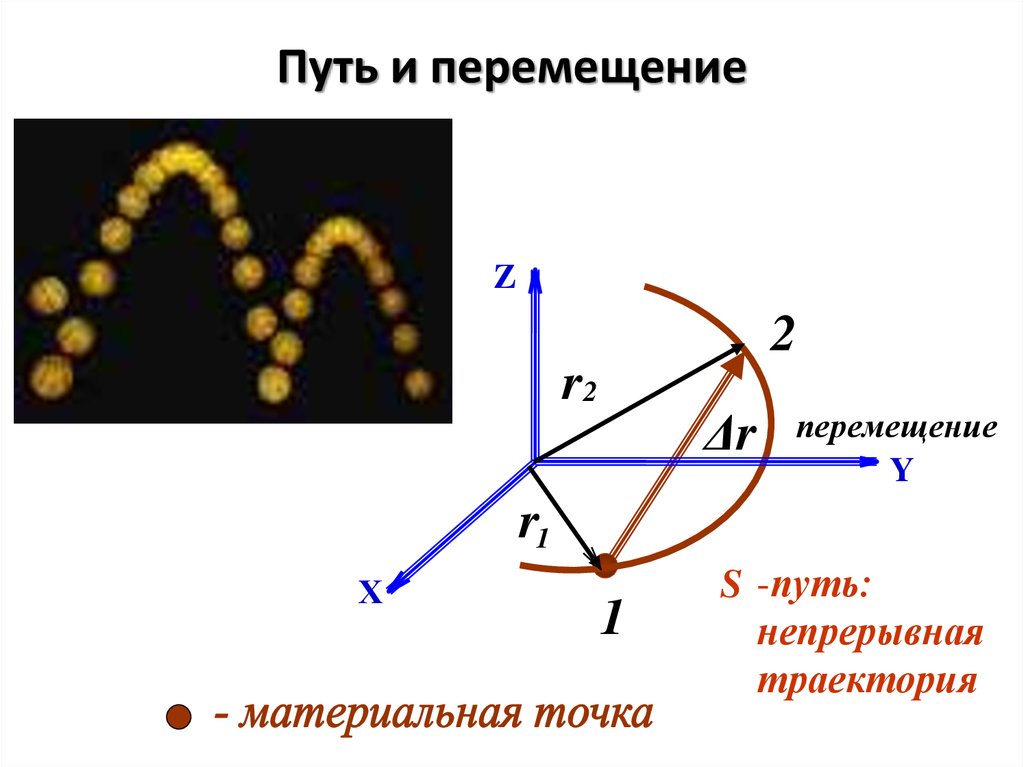
12.
Путь и перемещениеZ
2
r2
Δr
перемещение
Y
r1
Х
1
S -путь:
непрерывная
траектория
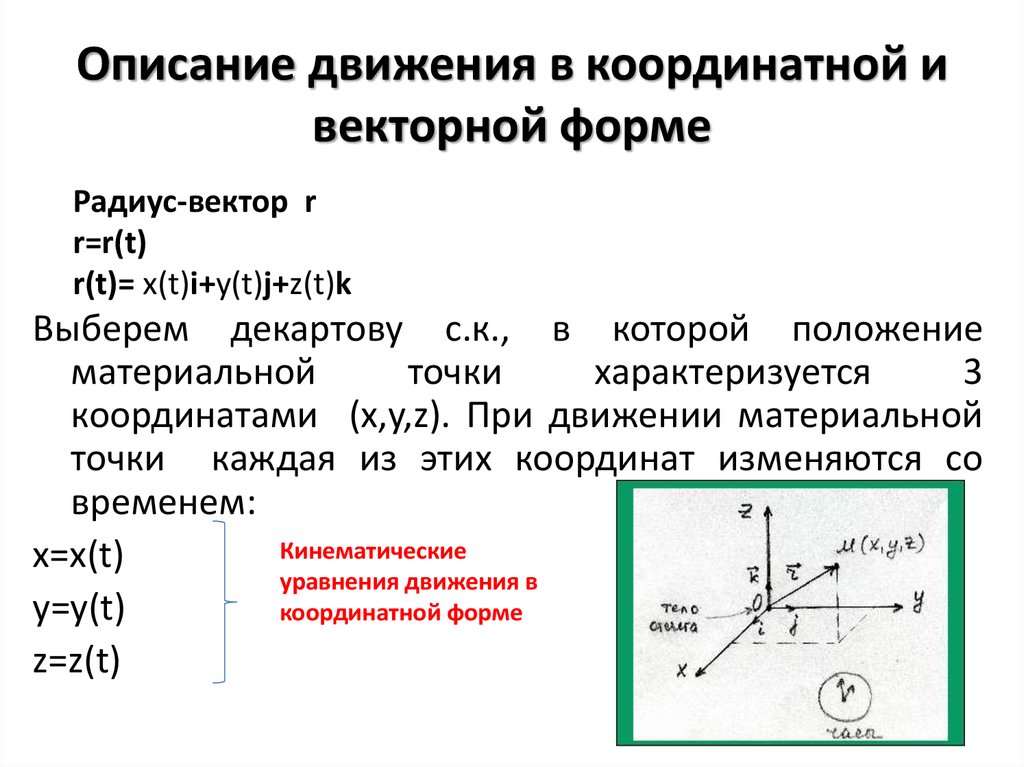
13. Описание движения в координатной и векторной форме
Радиус-вектор rr=r(t)
r(t)= x(t)i+y(t)j+z(t)k
Выберем декартову с.к., в которой положение
материальной
точки
характеризуется
3
координатами (x,y,z). При движении материальной
точки каждая из этих координат изменяются со
временем:
Кинематические
x=x(t)
уравнения движения в
y=y(t)
координатной форме
z=z(t)
14. Средняя скорость перемещения и средняя путевая скорость
• Средняя скоростьперемещения- это
векторная величина, равная
отношению вектора
перемещения к промежутку
времени, за которое это
перемещение произошло
r r2 r1
Vср
t t2 t1
Средняя путевая
(модуль скорости)это скалярная величина, равная
первой производной пути от
времени
Vср
dS
dt
14
15. Скорость
Мгновеннаяскорость:
r
r dr
r
v lim
lim t t t
t
dt
t 0 t t 0
v=v x i+v y j+v z k
dх
dy
dz
Vх , Vу , Vz
dt
dt
dt
Модуль скорости :
2
2
2
v V v v v
x
y
z
16. Ускорение
Мгновенное ускорение:v dv
a lim
t 0 t
dt
a ax i ay j azk
dVy
dVx
dVz
aх
, aу
, az
dt
dt
dt
Модуль ускорения:
2
2
2
a a ax a y az
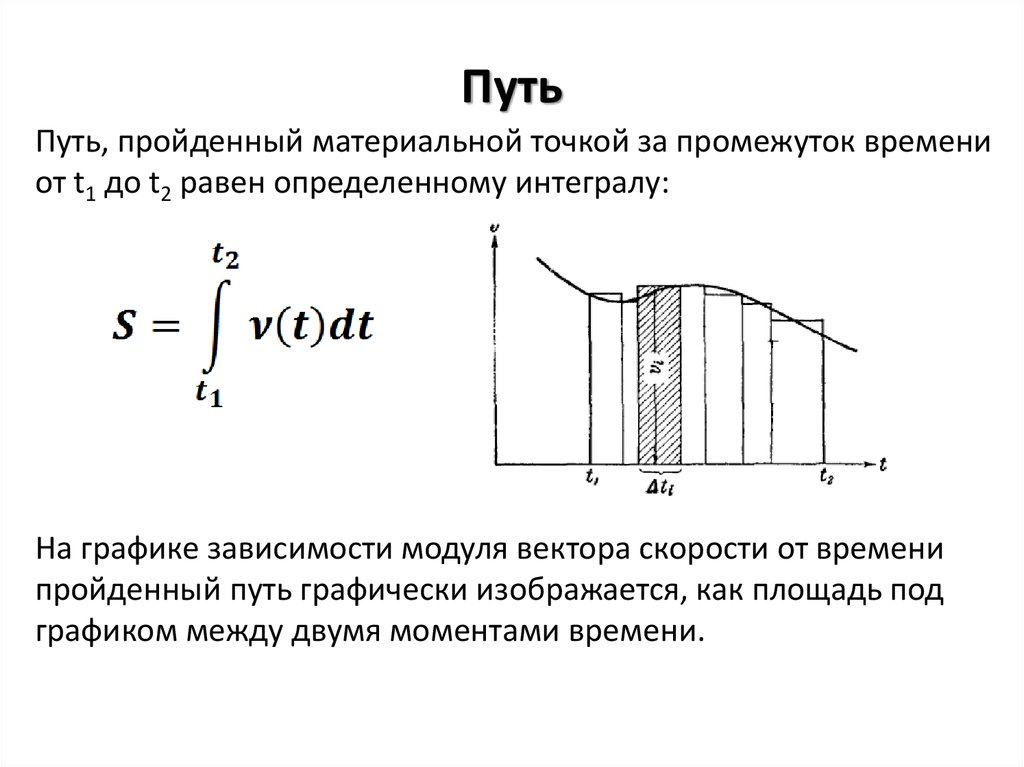
17. Путь
Путь, пройденный материальной точкой за промежуток времениот t1 до t2 равен определенному интегралу:
На графике зависимости модуля вектора скорости от времени
пройденный путь графически изображается, как площадь под
графиком между двумя моментами времени.
18.
19. Уравнения равноускоренного движения
a соnstV V0 at
at 2
S S0 V0t
2
axt 2
x x0 0 x t
2
a yt 2
y y0 0 y t
2
azt 2
z z0 0 z t
2
Уравнение равноускоренного
движения
в скалярной форме
Уравнение равноускоренного
движения
в проекциях
на оси координат
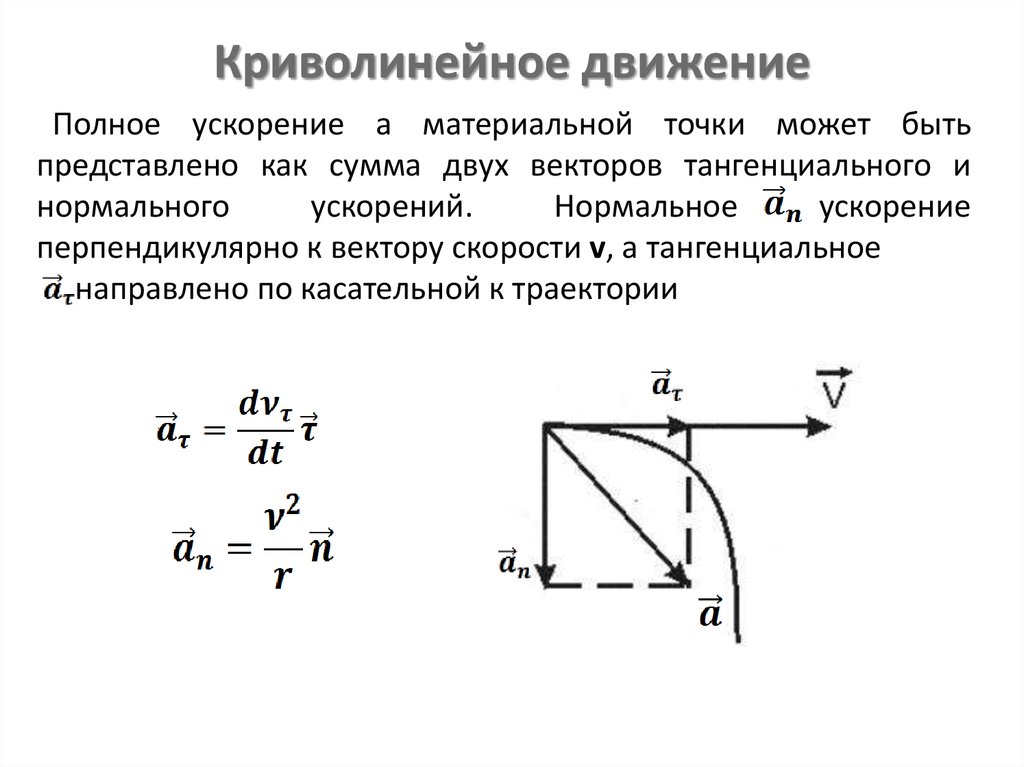
20. Криволинейное движение
Полное ускорение a материальной точки может бытьпредставлено как сумма двух векторов тангенциального и
нормального
ускорений.
Нормальное
ускорение
перпендикулярно к вектору скорости v, а тангенциальное
направлено по касательной к траектории
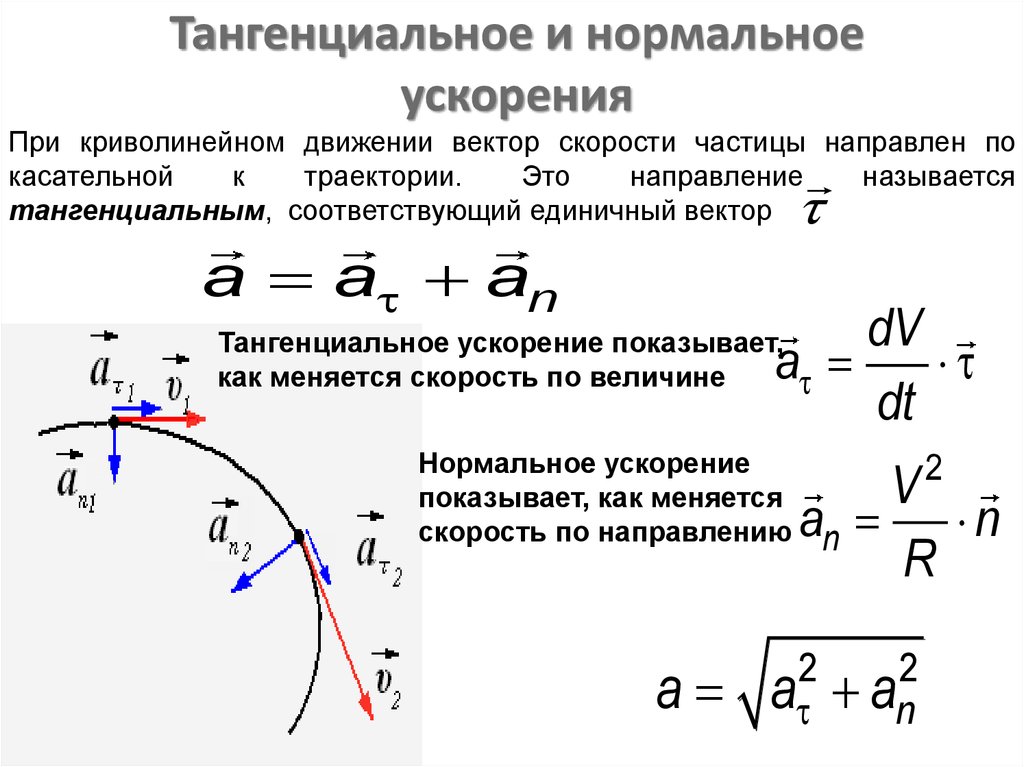
21. Тангенциальное и нормальное ускорения
При криволинейном движении вектор скорости частицы направлен покасательной
к
траектории.
Это
направление
называется
тангенциальным, соответствующий единичный вектор
a a an
dV
а
dt
Тангенциальное ускорение показывает,
как меняется скорость по величине
Нормальное ускорение
показывает, как меняется
скорость по направлению
a
2
V
аn n
R
2
a
2
an
22.
Пример . Тело брошено под углом α кгоризонту со скоростью V0 . Чему равно
нормальное и тангенциальное ускорение в
начальный момент и в точке максимального
подъема?
g
23. Динамика МТ
• Динамика изучает движение тел в связи с темипричинами(силами), которые обуславливают тот
или иной характер движения.
• Силой называется векторная величина,
характеризующая воздействие на данное тело со
стороны других тел, в результате которого тело
приобретает ускорение или изменяет свою форму
и размеры.
• Векторная сумма всех сил, действующих на тело,
называется равнодействующей
n
F Fi
i 1
24.
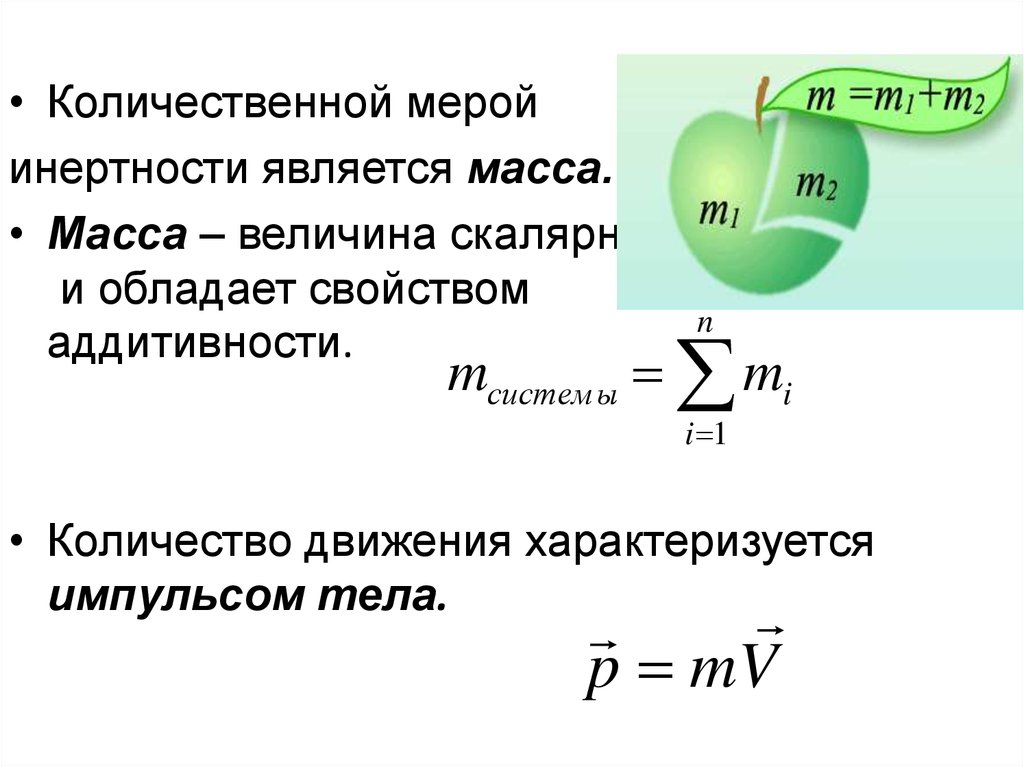
• Количественной меройинертности является масса.
• Масса – величина скалярная
и обладает свойством
аддитивности.
n
mсистем ы mi
i 1
• Количество движения характеризуется
импульсом тела.
p mV
25. Законы Ньютона
28 апр. 1686 г. представилЛондонскому королевскому
обществу
свою
новую
теорию – механику земных
и небесных процессов.
«Математические
начала
натуральной философии».
Исаак Ньютон (1642-1727)
26. 1 закон Ньютона
• Всякое тело находится в состояниипокоя или равномерного и
прямолинейного движения, пока
воздействие со стороны других тел не
заставят его изменить это состояние.
• Системы отсчета, в которых выполняется
1зН, называется инерциальной.
• Системы отсчета, в которых не выполняется
1зН, называются неинерциальной.
Законы Ньютона справедливы в инерциальных
системах отсчета при скоростях, много
меньших скорости света.
27. Инерциальные системы отсчета
УстановленоГелиоцентрическая (звездная)
опытным
система отсчета:
путем
• начало координат – в центре Солнца,
• оси проведены в направлении
определенных звезд
Инерциальных систем существует ∞ множество
Все ИСО образуют класс
систем, движущихся
друг относительно
друга равномерно и
прямолинейно
28. (2 закон Ньютона)
Основное уравнение динамикипоступательного движения
(2 закон Ньютона)
• Скорость изменения импульса тела
равна действующей на тело силе:
dp
F;
dt
F Fi
i
• Если масса тела остается постоянной
dp d (mv )
dv
m
ma F
dt
dt
dt
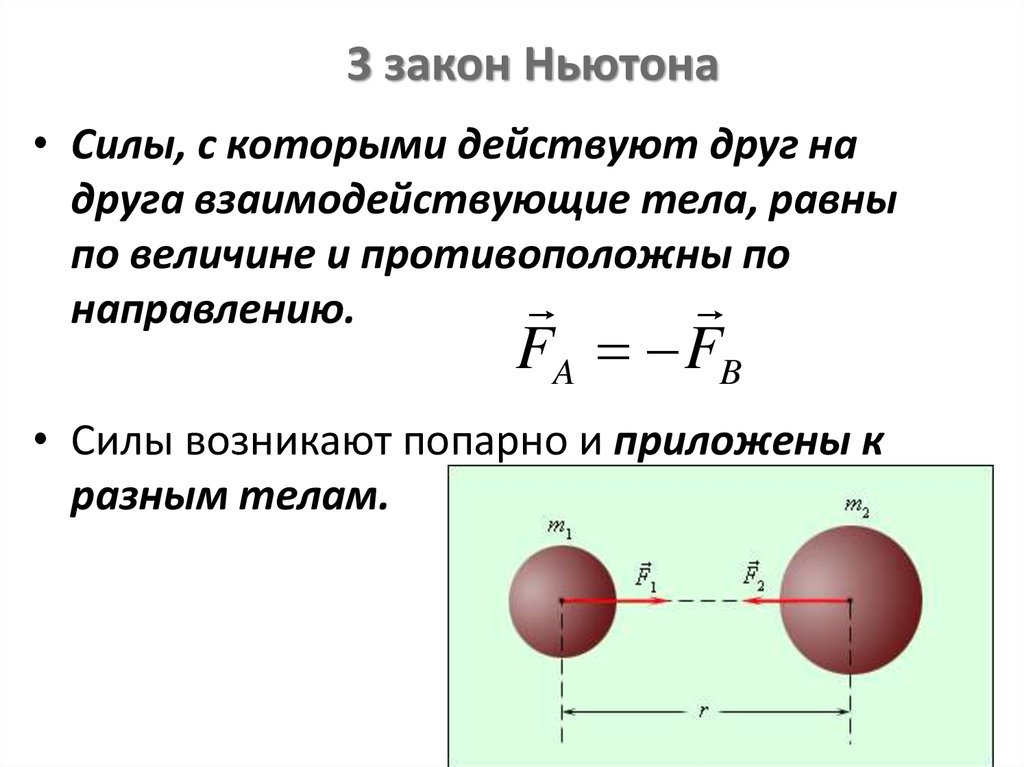
29. 3 закон Ньютона
• Силы, с которыми действуют друг надруга взаимодействующие тела, равны
по величине и противоположны по
направлению.
FA FB
• Силы возникают попарно и приложены к
разным телам.
30. Принцип относительности Галилея
Уравнения динамики неизменяются при
переходе от одной
инерциальной СО к
другой.
Все механические
явления в различных
инерциальных системах
протекают одинаковым
образом.
Галилео Галилей
(1564 – 1642)
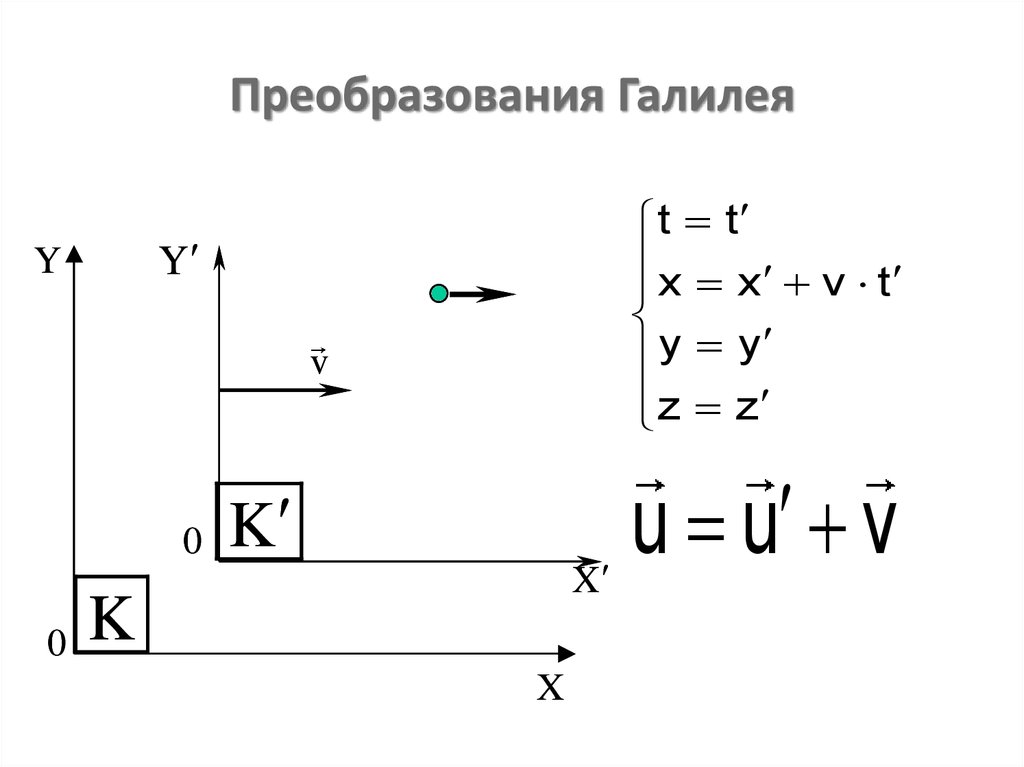
31. Преобразования Галилея
t tx x v t
y y
z z
Y
Y
v
0
0
K
X
K
X
u u v
32. Силы
Фундаментальныевзаимодействия:
гравитационные,
электромагнитные,
сильные,
слабые.
В классической механике рассматриваются:
– гравитационные силы (сила тяжести)
– электромагнитные силы (упругие силы и силы
трения)
33.
34. Сила тяжести и вес тела
• В система отсчета, связанной с Землей, навсякой тело действует сила F=mg, называемая
силой тяжести.
На поверхности
Земли:
GM
F 2 m mg
R
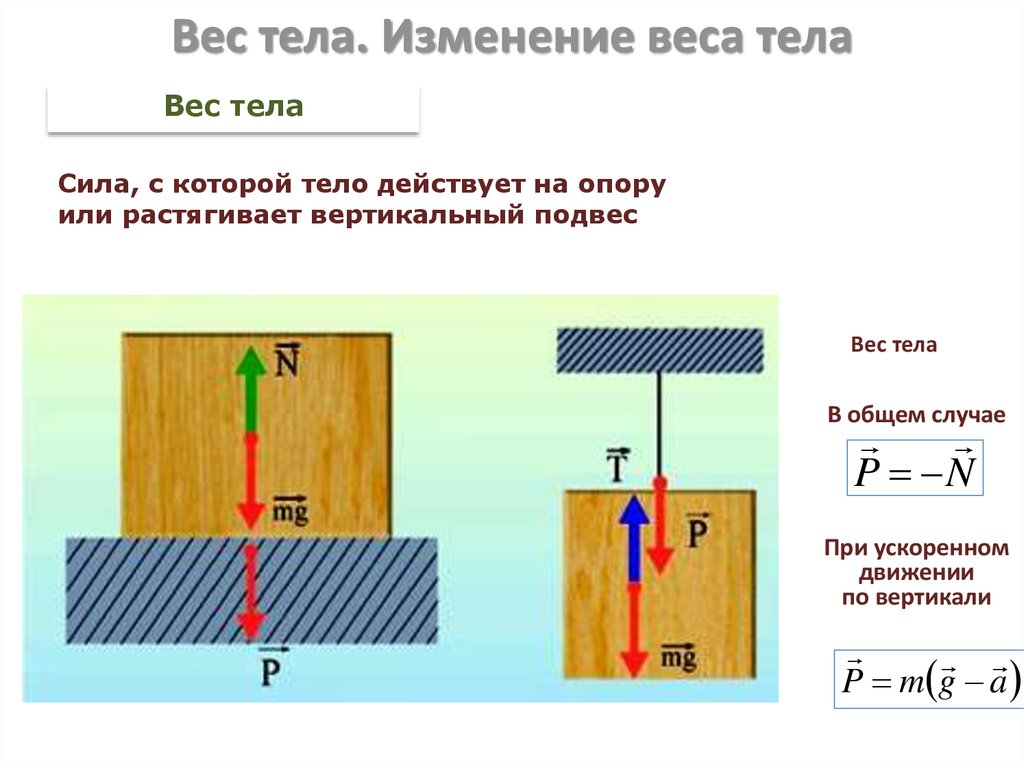
35. Вес тела. Изменение веса тела
Вес телаСила, с которой тело действует на опору
или растягивает вертикальный подвес
Вес тела
В общем случае
P N
При ускоренном
движении
по вертикали
P m g a
36. Закон Гука
• Опыт показывает, что при небольшихдеформациях удлинение пружины
оказывается пропорциональным внешней
силе F=k L, где к - коэффициент жесткости
пружины.
• В пружине при деформации возникает сила
упругости, равная по величине внешней силе
и тоже пропорциональная
удлинению пружины.
Fупр k L
ΔL
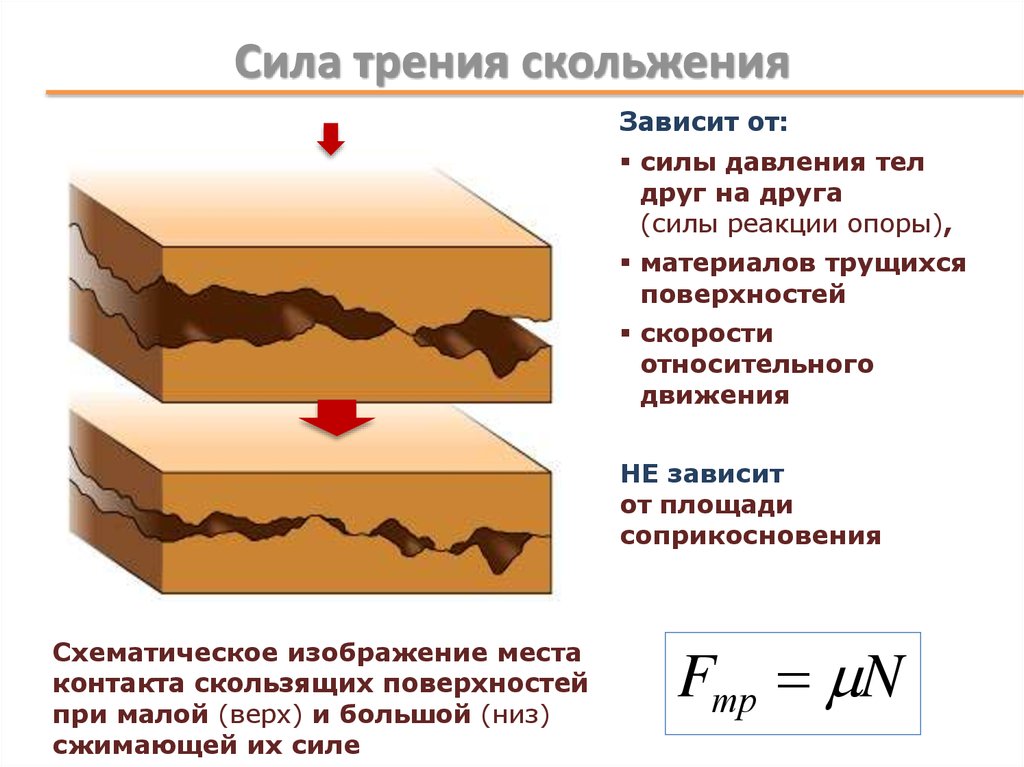
37. Сила трения скольжения
Зависит от:силы давления тел
друг на друга
(силы реакции опоры),
материалов трущихся
поверхностей
скорости
относительного
движения
НЕ зависит
от площади
соприкосновения
Схематическое изображение места
контакта скользящих поверхностей
при малой (верх) и большой (низ)
сжимающей их силе
Fтр N
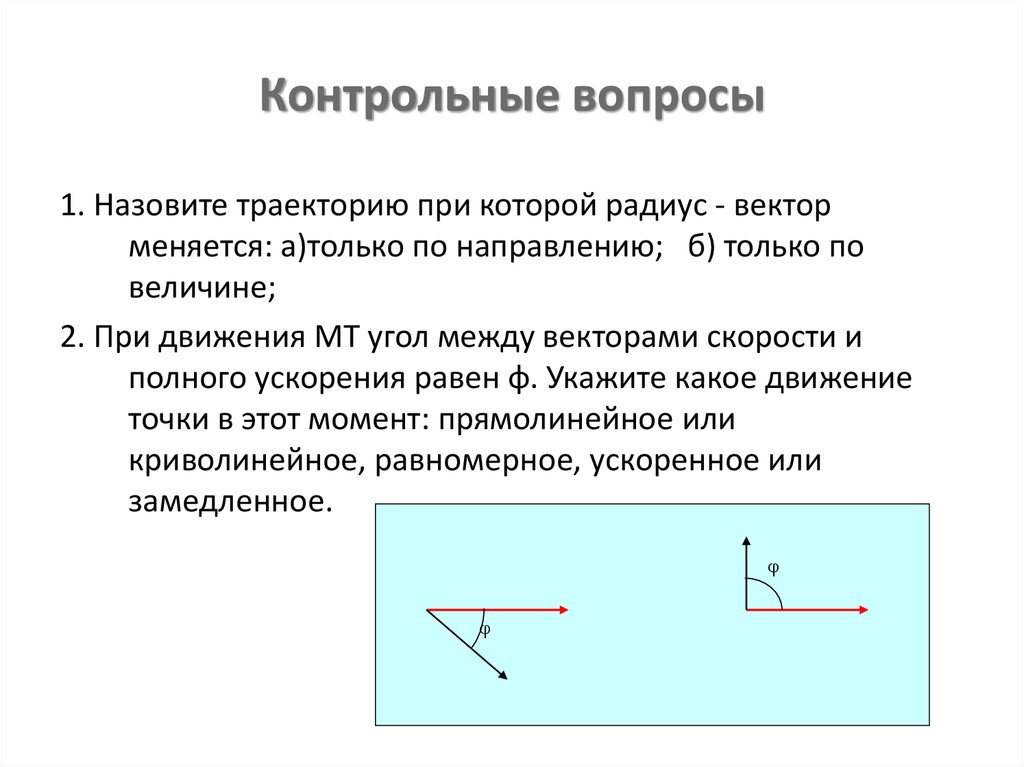
38. Контрольные вопросы
1. Назовите траекторию при которой радиус - векторменяется: а)только по направлению; б) только по
величине;
2. При движения МТ угол между векторами скорости и
полного ускорения равен φ. Укажите какое движение
точки в этот момент: прямолинейное или
криволинейное, равномерное, ускоренное или
замедленное.
φ
φ


























 Физика
Физика Механика
Механика








