Логические основы

1. Информатика

Лектор: Подвесовская
Марина Александровна
к.т.н., доцент кафедры
«Информатика и
программное обеспечение»

2. § 7. Логические основы

2

3.

7.1. Логика и компьютер
Высказывание
это
повествовательное
предложение, про которое можно однозначно сказать, что
оно истинно или ложно.
1.Сейчас идет дождь.
2.Вчера жирафы улетели на север.
3.Красиво!
4.Который час?
5.В городе N живут более 2 миллионов человек.
6.Посмотрите на улицу.
7.У квадрата 10 сторон, и все разные.
8.История — интересный предмет.
3

4.

Алгебра логики — это математический аппарат, с
помощью которого записывают, вычисляют, упрощают и
преобразовывают логические высказывания.
Алгебра логики определяет правила выполнения
операций с логическими величинами, которые могут быть
равны только 0 или 1, то есть с двоичными данными.
Используя эти правила, можно строить элементы памяти и
выполнять арифметические действия.
4

5.

7.2. Логические операции
Отрицание
A
0
1
1
0
Отрицание – инверсия – операция «НЕ»
Таблица
состоит
из
двух
частей:
слева
перечисляются все возможные значения исходного
высказывания, а в последнем столбце записывают
результат выполнения логической операции для каждого
из этих вариантов. Такая таблица называется таблицей
истинности логической операции.
Таблица
истинности
задает
логическую
функцию, то есть правила преобразования входных
логических значений в выходные.
5

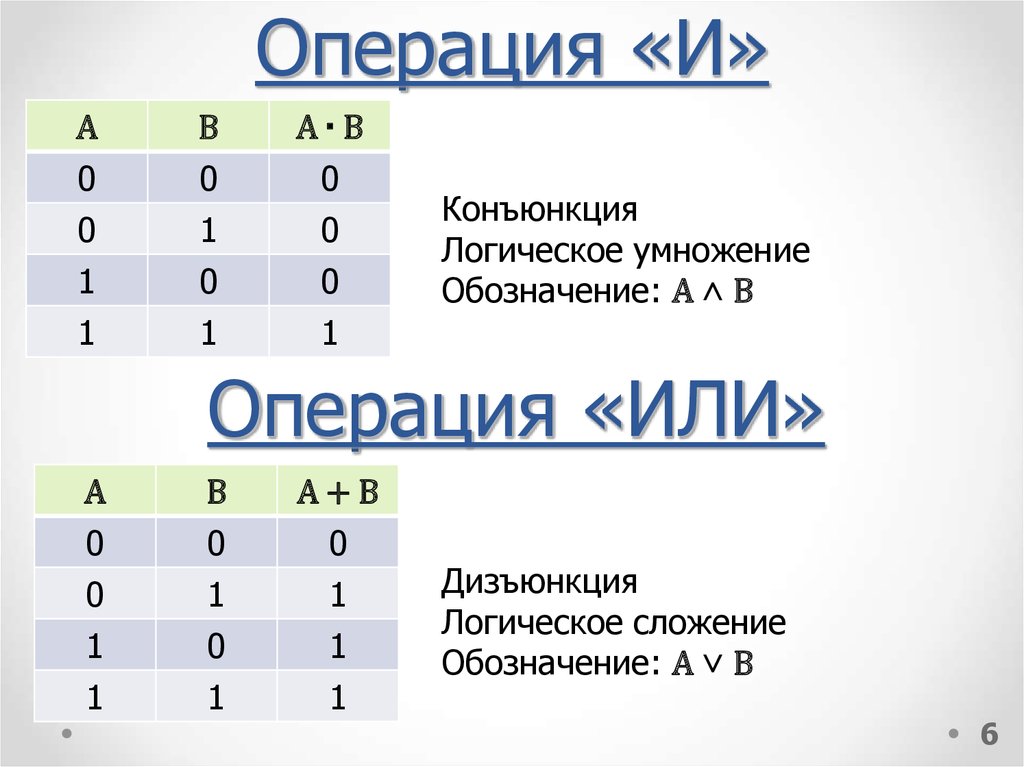
6. Операция «И»

A
B
A B
0
0
1
1
0
1
0
1
0
0
0
1
Конъюнкция
Логическое умножение
Обозначение: A ˄ B
Операция «ИЛИ»
A
B
A+B
0
0
0
0
1
1
1
0
1
1
1
1
Дизъюнкция
Логическое сложение
Обозначение: A ˅ B
6

7. Эквивалентность

A
B
0
0
0
1
1
0
1
1
0
1
0
1
7

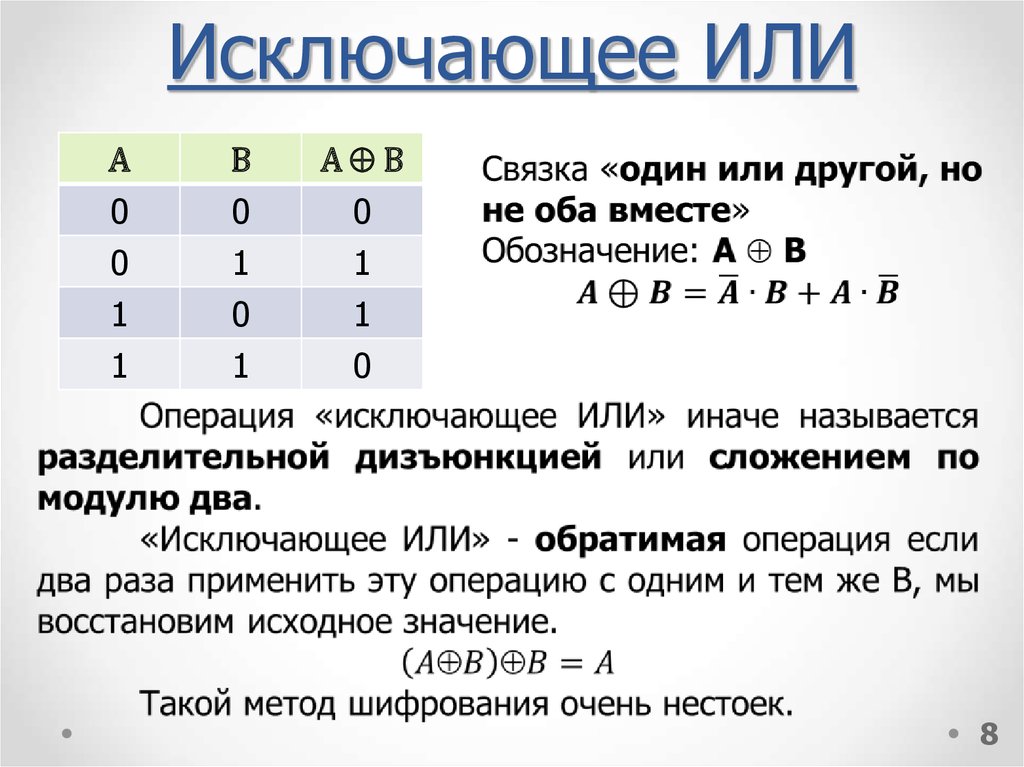
8. Исключающее ИЛИ

A
B
A B
0
0
1
0
1
0
0
1
1
1
1
0
8

9. Импликация

A
B
A B
0
0
1
0
1
0
1
1
0
1
1
1
Примеры: Если пойдет дождь, то я надену плащ.
Если все стороны прямоугольника равны, то это квадрат.
Следует отличать импликацию от высказывания
«Если А, то В» в обычной жизни. В быту имеется в виду,
что существует причинно-следственная связь между А и
В, в алгебре логики истинность A B говорит только о
возможности такой связи.
9

10.

Если хорошо работаешь, то получаешь большую
зарплату.
Пусть A: хорошо работаешь,
В: получаешь большую зарплату
Если высказывание A→B истинно, то все, кто
хорошо работают (A=1), должны получать большую
зарплату (B=1). Если же кто-то работает хорошо
(A=1), а получает мало (B=0), то высказывание A→B
ложно.
Лодыри и бездельники (A=0) могут получать как
маленькую (B=0), так и большую зарплату (B=1), это
не нарушает справедливость высказывания A→B.
10

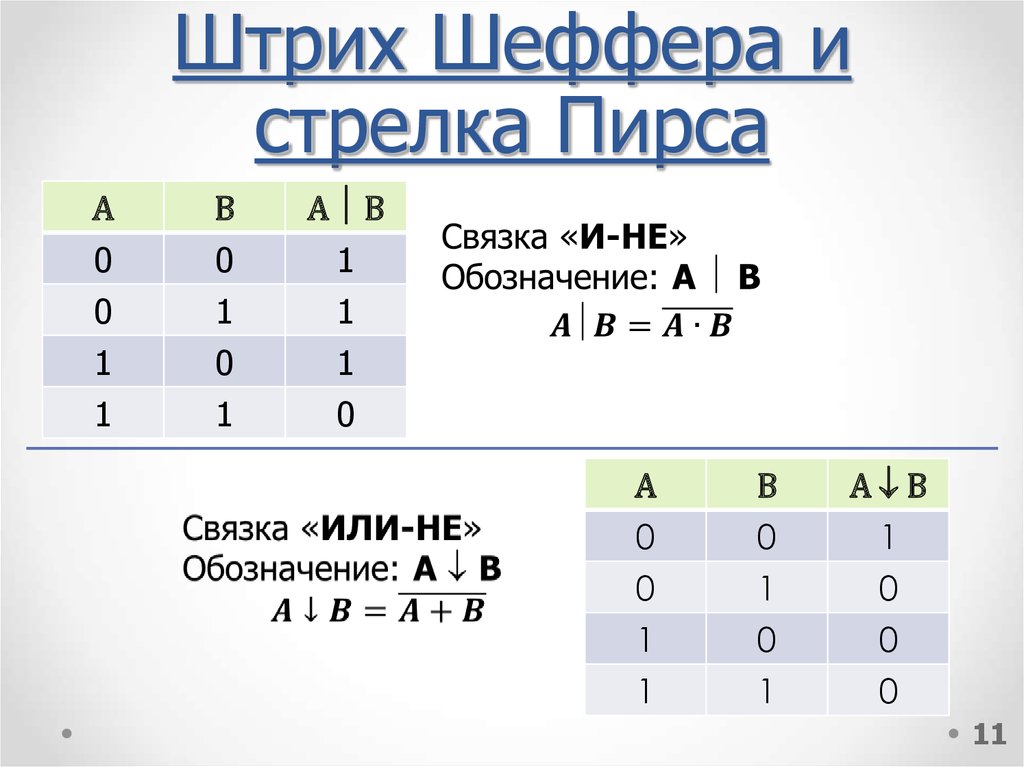
11. Штрих Шеффера и стрелка Пирса

A
B
A B
0
0
1
0
1
0
1
1
1
1
1
0
A
B
A B
0
0
1
0
1
1
1
0
1
0
0
0
11

12. Штрих Шеффера и стрелка Пирса

12

13. Логические выражения

13

14. Логические выражения

Таким образом, мы выполнили формализацию.
Формализация — это переход от конкретного
содержания к формальной записи с помощью некоторого
языка.
В логических выражениях операции выполняются в
следующем порядке:
1.действия в скобках;
2.отрицание (НЕ);
3.логическое умножение (И);
4.логическое сложение (ИЛИ) и «исключающее ИЛИ»;
5.импликация;
6.эквивалентность.
14

15. Логические выражения

Высказывание «Вася — школьник, или он не учится
в школе» всегда истинно (для любого Васи). Выражение,
истинное при любых значениях переменных, называется
тождественно истинным, или тавтологией.
Высказывание «сегодня безветрие, и дует сильный
ветер»
никогда
не
может
быть
истинным.
Соответствующее логическое выражение всегда ложно,
оно
называется
тождественно
ложным,
или
противоречием.
Если два выражения принимают одинаковые
значения при всех значениях переменных, они называются
равносильными, или тождественно равными.
15

16. Логические выражения

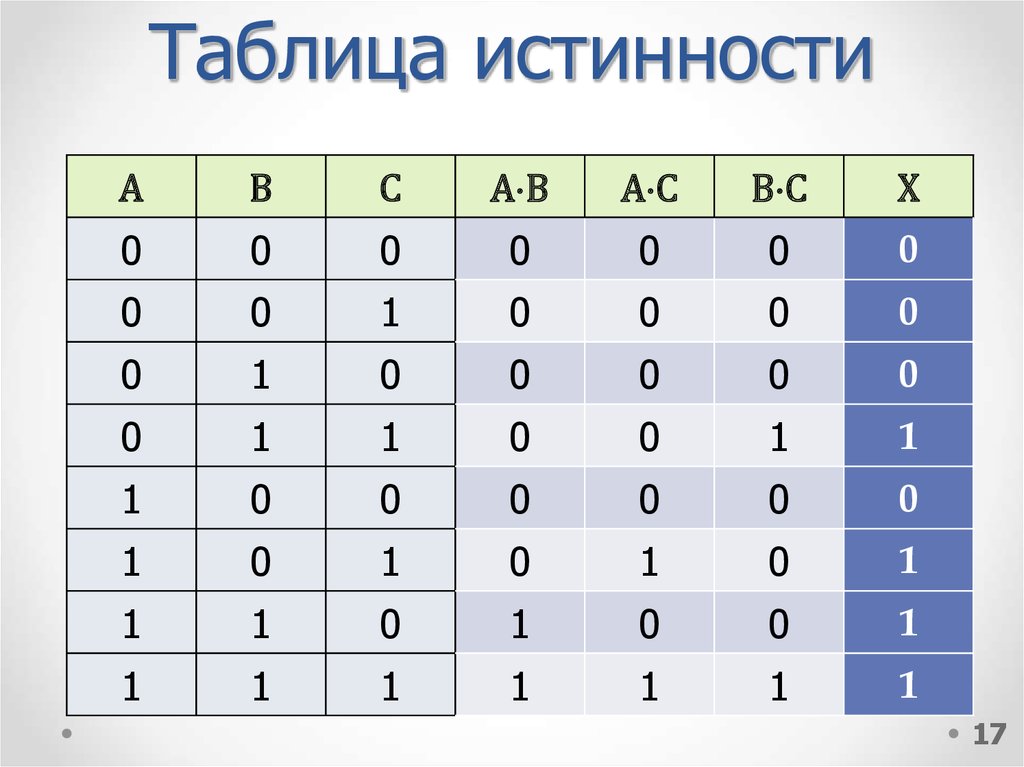
16

17. Таблица истинности

A
B
C
A B
A C
B C
X
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
1
1
1
0
0
0
0
0
0
1
0
1
0
1
0
1
1
1
0
1
0
0
1
1
1
1
1
1
1
1
17

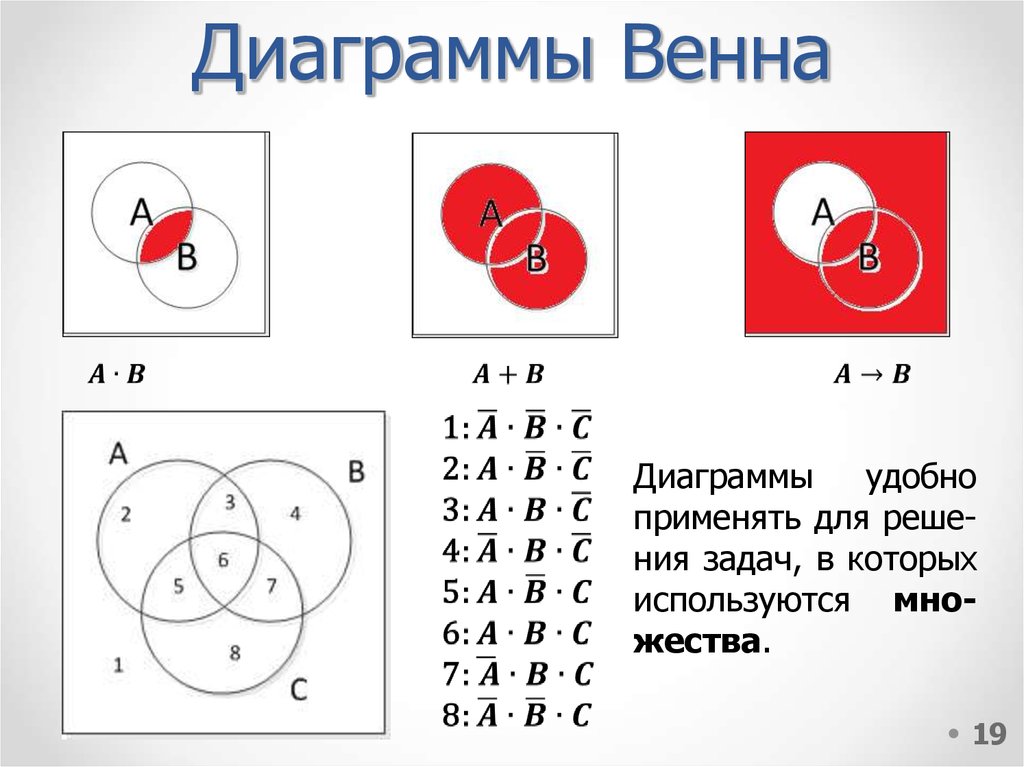
18. 7.3. Диаграммы Венна

Выражения, зависящие от небольшого количества
переменных (обычно 4), удобно изображать в виде
диаграмм, которые называют диаграммами Венна, или
кругами Эйлера.
На
такой
диаграмме
каждой
переменной соответствует круг, внутри
которого она равна единице, а вне его нулю. Круги пересекаются, каждый с
каждым. Области, в которых рассматриваемое логическое выражение истинно,
закрашиваются каким-либо цветом.
18

19. Диаграммы Венна

Диаграммы
удобно
применять для решения задач, в которых
используются множества.
19

20. Предварительные замечания

Поисковый запрос для поисковой
системы в Интернете – ключевое слово
или
несколько
ключевых
слов,
соединенных между собой знаками
логических операций И, ИЛИ, НЕ.
Операция И (&, ˄) сокращает объем
получаемого при поиске результата.
Операция ИЛИ (|, ˅) увеличивает
объем
получаемого
при
поиске
результата.
20

21. Пример 1 задачи №11 РГР

В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по
этим запросам в некотором сегменте Интернета:
Запрос
Количество страниц (тыс.)
пирожное & выпечка
3200
пирожное
8700
выпечка
7500
Сколько страниц (в тысячах) будет найдено по
запросу пирожное | выпечка?
21

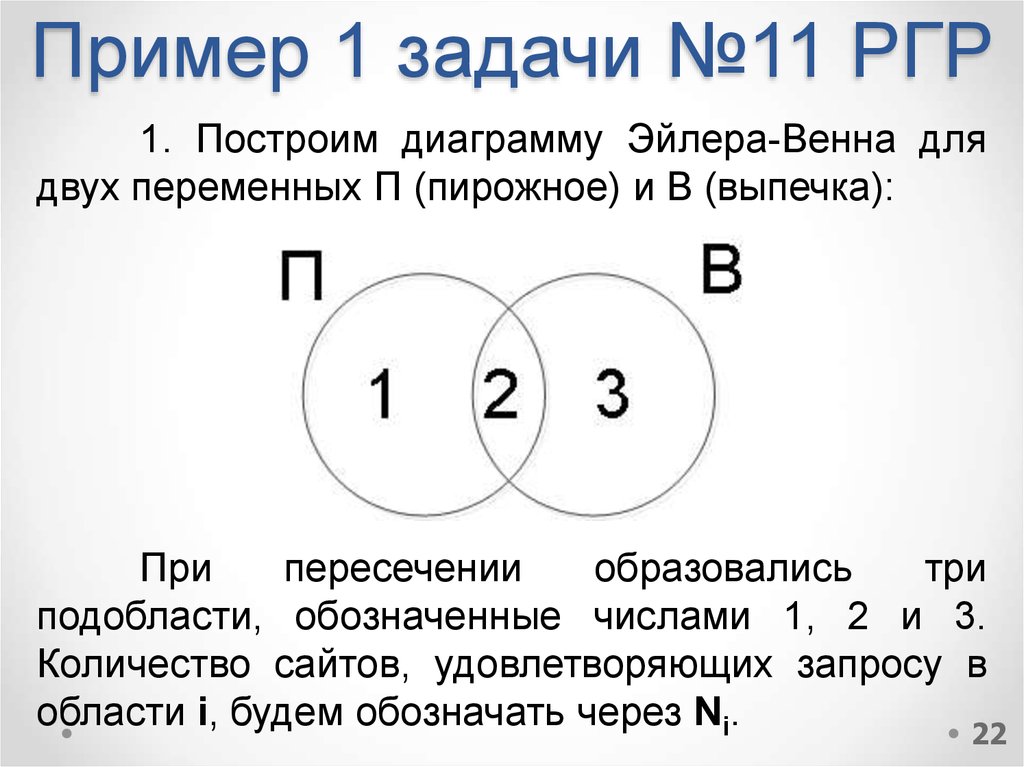
22. Пример 1 задачи №11 РГР

1. Построим диаграмму Эйлера-Венна для
двух переменных П (пирожное) и B (выпечка):
При
пересечении
образовались
три
подобласти, обозначенные числами 1, 2 и 3.
Количество сайтов, удовлетворяющих запросу в
области i, будем обозначать через Ni.
22

23. Пример 1 задачи №11 РГР

2.
Составляем
уравнения,
которые
определяют запросы, заданные в условии:
пирожное & выпечка N2 = 3200
пирожное
N1 + N2 = 8700
выпечка
N2 + N3 = 7500
23

24. Пример 1 задачи №11 РГР

3. Подставляя значение N2 из первого
уравнения в остальные, получаем
N1 = 8700 - N2 = 8700 – 3200 = 5500
N3 = 7500 - N2 = 7500 – 3200 = 4300
4. Количество сайтов по запросу пирожное |
выпечка равно
N1 + N2 + N3 = 5500 + 3200 + 4300 = 13000
24

25. Пример 2 задачи №11 РГР

В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по
этим запросам в некотором сегменте Интернета:
Запрос
Динамо & Рубин
Спартак & Рубин
(Динамо | Спартак) & Рубин
Количество
страниц (тыс.)
320
280
430
Сколько страниц (в тысячах) будет найдено
по запросу Рубин & Динамо & Спартак?
25

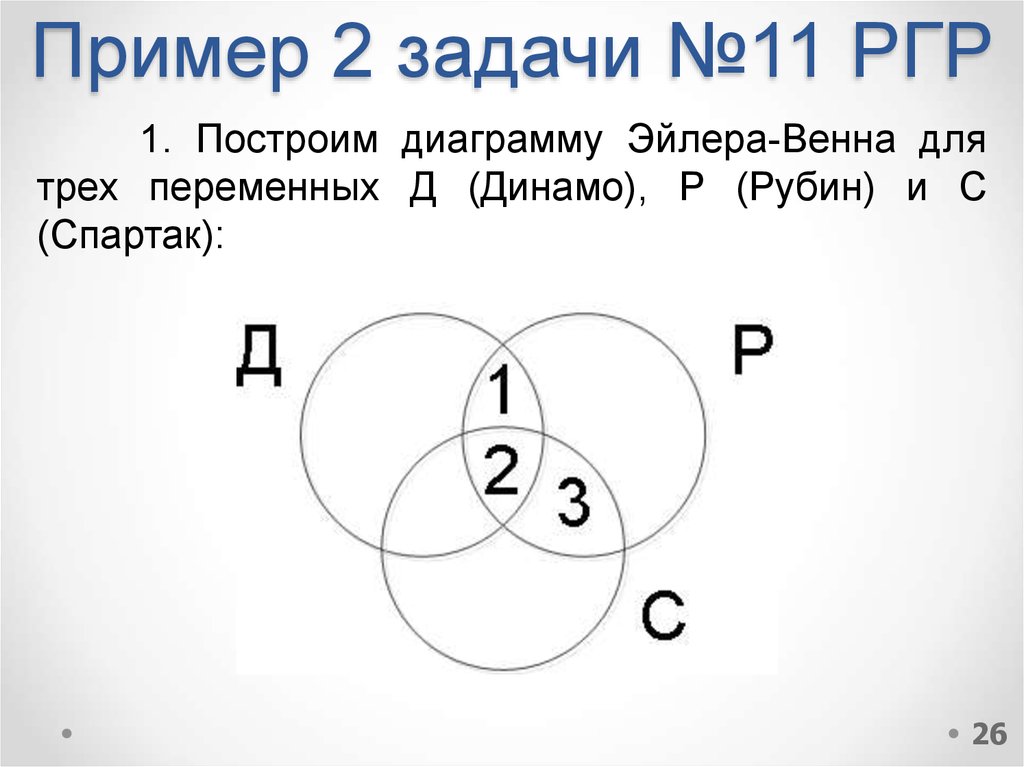
26. Пример 2 задачи №11 РГР

1. Построим диаграмму Эйлера-Венна для
трех переменных Д (Динамо), Р (Рубин) и С
(Спартак):
26

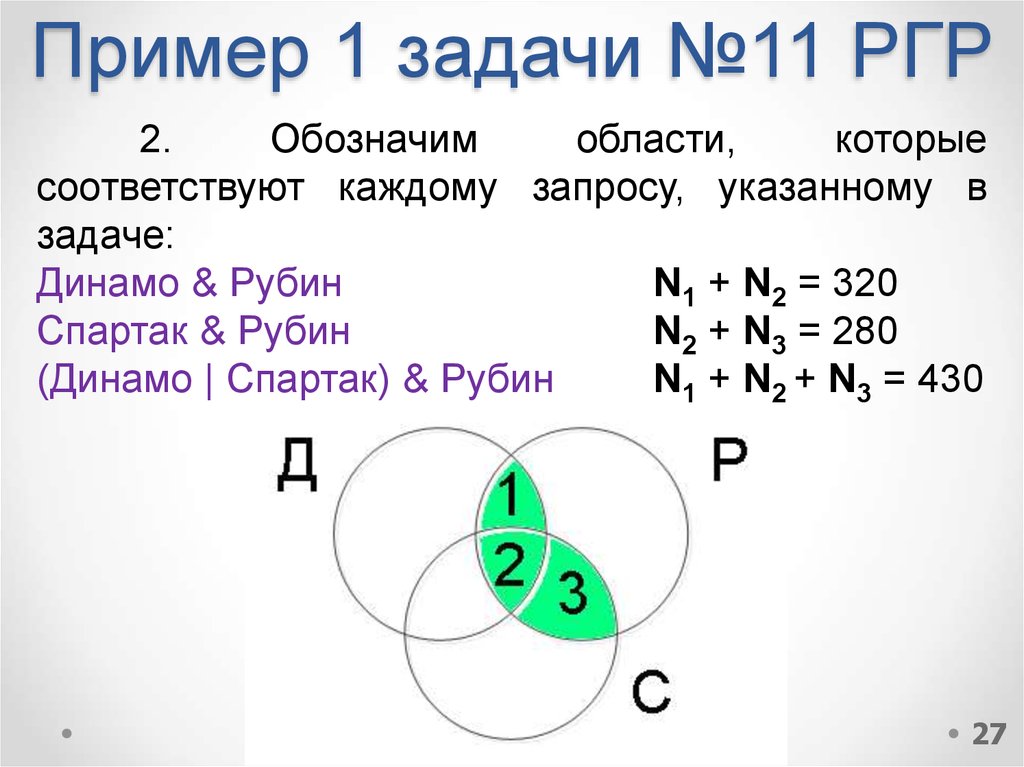
27. Пример 1 задачи №11 РГР

2.
Обозначим
области,
которые
соответствуют каждому запросу, указанному в
задаче:
Динамо & Рубин
N1 + N2 = 320
Спартак & Рубин
N2 + N3 = 280
(Динамо | Спартак) & Рубин
N1 + N2 + N3 = 430
27

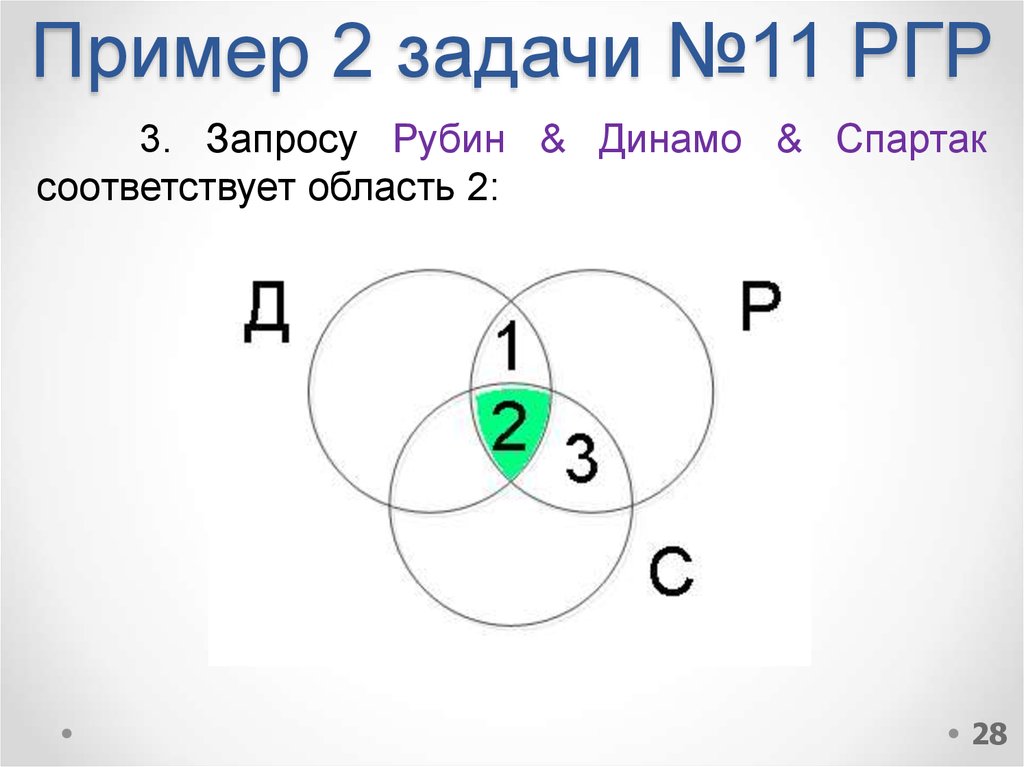
28. Пример 2 задачи №11 РГР

3. Запросу Рубин & Динамо & Спартак
соответствует область 2:
28

29. Пример 2 задачи №11 РГР

4. В суммарный результат первых двух
запросов область 2 входит дважды (1 + 2 + 2 + 3),
поэтому, сравнивая этот результат с третьим
запросом (1 + 2 + 3), сразу находим результат
четвертого:
N2 = (320 + 280) – 430 = 170
5. Таким образом, ответ – 170.
29

30. 7.4. Упрощение логических выражений

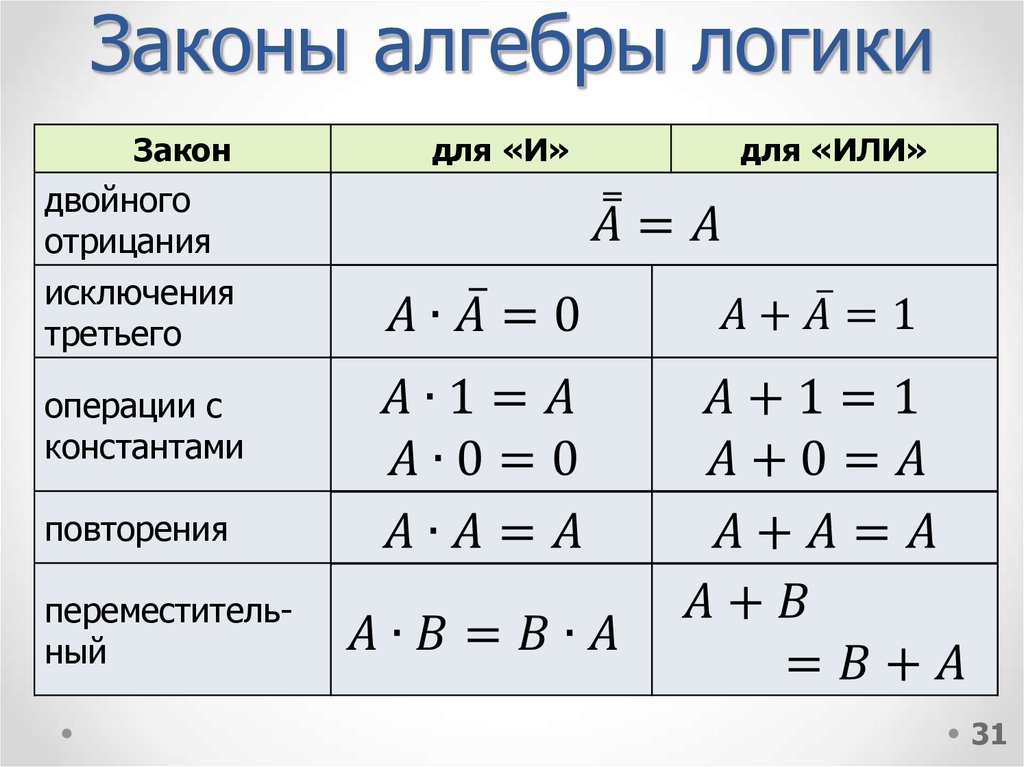
30

31. Законы алгебры логики

Закон
для «И»
для «ИЛИ»
двойного
отрицания
исключения
третьего
операции с
константами
повторения
переместительный
31

32. Законы алгебры логики

Закон
для «И»
для «ИЛИ»
сочетательный
распределительный
поглощения
законы де
Моргана
32

33.

В общем случае можно рекомендовать такую
последовательность действий:
1.Заменить
все
«небазовые»
операции
(исключающее ИЛИ, импликацию, эквивалентность и др.) на их выражения через базовые
операции «НЕ», «И» и «ИЛИ».
2.Раскрыть отрицания сложных выражений
по законам де Моргана так, чтобы операции
отрицания
остались
только
у
отдельных
переменных.
3.Используя вынесение общих множителей за
скобки, раскрытие скобок и другие законы
алгебры логики, упростить выражение.
33

34.

34

35. 7.5. Синтез логических выражений

Задача анализа - задача, где логическое
выражение уже задано и требуется построить таблицу
истинности.
Обратная задача – задача синтеза - строить
логическое выражение по готовой таблице истинности,
которая описывает нужное правило обработки данных.
Эта задача возникает при проектировании различных
логических устройств, в том числе и узлов компьютеров.
Пример. Построим логическое выражение по
следующей таблице истинности:
35

36.

Шаг 1. Определяем количество нулей и единиц в
выражении F:
«0» - 2
«1» - 6
A
B
C
F
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
1
36

37.

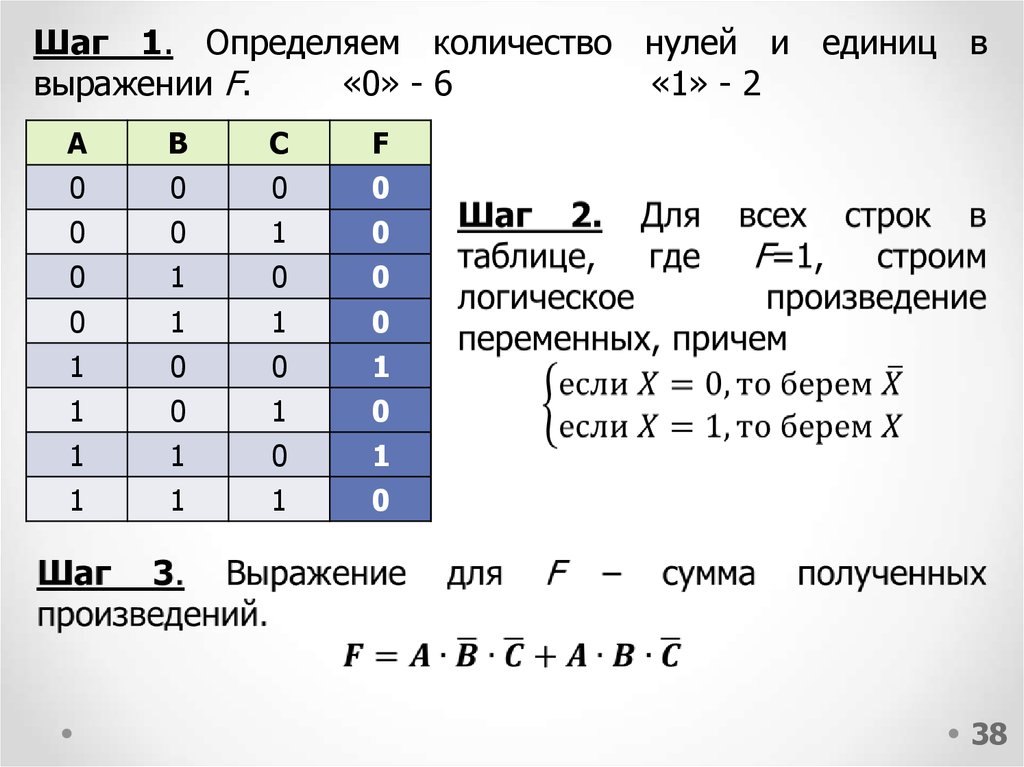
37

38.

Шаг 1. Определяем количество нулей и единиц в
выражении F.
«0» - 6
«1» - 2
A
B
C
F
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
1
1
1
1
0
38

39.

39

40. 7.6. Логические задачи

40

41. Метод рассуждений

Задача 1. Среди трех приятелей (их зовут Сеня, Вася и
Миша) один всегда говорит правду, второй говорит правду
через раз, а третий все время обманывает.
Как-то
раз
они
впервые
прогуляли
урок
информатики. Директор школы вызвал их в свой кабинет
для разговора.
Сеня сказал: «Я всегда прогуливаю информатику.
Не верьте тому, что скажет Вася».
Вася сказал: «Я раньше не прогуливал этот
предмет».
Миша сказал: «Все, что говорит Сеня, — правда».
Директору стало все понятно. Кто из них правдив, кто
лгун, а кто говорит правду через раз?
41

42. Метод рассуждений

1. Точная информация: все трое прогуляли урок
информатики в первый раз.
2. Запишем высказывания мальчиков:
Сеня: 1. Я всегда прогуливаю информатику.
2. Вася сейчас соврет.
Вася: Я раньше не прогуливал информатику.
Миша: Сеня говорит правду.
3. Известно, что один из них говорит правду всегда,
второй - через раз, а третий все время лжет. Отметим,
что если у нас есть только одно высказывание
«полулжеца», оно может быть как истинным, так и
ложным.
42

43. Метод рассуждений

«Все трое прогуляли урок в первый раз» и Сеня: «Я
всегда прогуливаю информатику»
Сеня соврал.
«Все трое прогуляли урок в первый раз» и Вася: «Я
раньше не прогуливал информатику»
Вася сказал правду.
Сеня: «Вася сейчас соврет» и предыдущий вывод
Сеня всегда лжет.
Миша: «Сеня говорит правду» и предыдущий
вывод
Миша лжет и говорит правду через раз
43

44. Табличный метод

Задача 2. Перед началом турнира по шахматам
болельщики высказали следующие предположения по поводу результатов:
А.
Максим победит, Борис - второй;
Б.
Борис - третий, Коля - первый;
В.
Максим - последний, а первый - Дима.
Когда соревнования закончились, оказалось,
что каждый из болельщиков был прав только в
одном из своих прогнозов. Как распределились
призовые места?
44

45. Табличный метод

А
Б
В
I
Максим?
Коля?
Дима?
II
Борис?
III
IV
Борис?
Максим?
Начнем с той строки, где больше всего
информации.
Пусть Максим действительно занял I
место, как и сказал болельщик «A». В этом
случае «В» ошибся, поставив на I место Диму.
Тогда
получается,
что
второй
прогноз
болельщика «В» верен, и Максим — IV.
45

46. Табличный метод

А
1 Максим?
2
3
4
Б
В
Коля?
Дима?
Борис?
Борис?
Максим?
Получается противоречие первый прогноз «А»
не сбылся, тогда верен его второй прогноз, и Борис занял
II место. При этом он не мог занять еще и III место
первый прогноз болельщика «Б» неверный, верен
второй: Коля - I.
Дима не может быть I верен первый прогноз «В»:
Максим - IV. Диме осталось III место.
В результате места распределились так: I - Коля,
II - Борис, III - Дима и IV - Максим.
46

47. Использование алгебры логики

Задача 3. Следующие два высказывания истинны:
1. Неверно, что если корабль A вышел в море, то
корабль C — нет.
2. В море вышел корабль B или корабль C, но не оба
вместе.
Определить, какие корабли вышли в море.
Введем три высказывания:
A — корабль A вышел в море;
B — корабль B вышел в море;
C — корабль C вышел в море.
47

48. Использование алгебры логики

48

49. Использование алгебры логики

49