Фигурные числа

1. Цифры (числа) не управляют миром, но они показывают, как управляется мир. (И. Гете)

ЦИФРЫ (ЧИСЛА) НЕ
УПРАВЛЯЮТ МИРОМ, НО
ОНИ ПОКАЗЫВАЮТ, КАК
УПРАВЛЯЕТСЯ МИР.
(И. ГЕТЕ)

2. Фигурные числа.

ФИГУРНЫЕ
ЧИСЛА.
Федоров Даниил
МБУЗ СОШ 24
Научный руководитель:
Андрейчикова Светлана Владимировна
учитель математики

3. Проблемный вопрос:

ПРОБЛЕМНЫЙ ВОПРОС:
Какие числа называются фигурными, на какие
виды эти числа делятся, применение и история
возникновения фигурных чисел, научиться
самому «выкладывать» фигурные числа и
познакомить своих одноклассников с фигурными
числами.

4.

Мотивы выбора темы.
Ещё вначале VI века до н.э. греческие математики
обнаружили интересный способ рассмотрения
чисел,
который
можно
назвать
как
полуарифметический
полугеометрический.
Способ состоял в том, что, используя камешки
одинаковой
величины
и
формы,
можно
выкладывать
числа
с
помощью
фигур.
Я
заинтересовался
этим
и
решил
выяснить,
действительно ли существуют числа, которые
можно выкладывать в виде геометрических фигур?.

5. Гипотеза.

ГИПОТЕЗА.
В наше время фигурные числа не
потеряли свою актуальность, они
могут оказать помощь ученику в
изучении математики

6. История возникновения

ИСТОРИЯ
ВОЗНИКНОВЕНИЯ
В строительстве сооружений древности — пирамид, дворцов и
храмов — применялись плиты и кирпичи, имеющие грани в виде
треугольника, четырёхугольника, квадрата и некоторых других
фигур. С этими же фигурами человек встречался при межевании и
измерении
земельных
участков.
Знакомясь
с
различными
геометрическими фигурами, люди начали подмечать их общие
свойства. Так постепенно складывалась геометрия — наука о
геометрических фигурах. Геометрия достигла высокого развития в
Древней Греции в школе Пифагора (VI–V вв. до н. э.). Пифагор и его
ученики развивали не только геометрию, но и арифметику, причём
их учение о числах тесно переплеталось с учением о
геометрических фигурах. Пифагорейцы составляли различные
фигуры из камешков или костяшек, изображая числа в виде точек,
группируемых в геометрические фигуры. Такое представление
чисел облегчало пифагорейцам изучать свойства чисел. Числа,
которые можно представить с помощью геометрических фигур,
получили название фигурных чисел.

7.

Со времён пифагорейцев традиционно различают
следующие виды фигурных чисел
•Линейные числа — числа, не разлагающиеся на сомножители, то
есть их ряд совпадает с рядом простых чисел, дополненным
единицей : 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,
61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139,
149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227,
229, 233, 239, 241, 251, 257, 263, 269, 271 и т.д.
Линейное число 5

8.

Плоские числа — числа, представимые в виде произведения
двух сомножителей, то есть составные: 4, 6, 8, 9, 10, 12, 14, 15,
16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40,
42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65,
66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88 и
т.д.
Плоское число 6

9.

•Телесные числа — числа, представимые произведением трёх
сомножителей: 8, 12, 16, 18, 20, 24, 27, 28, 30, 32, 36, 40, 42, 44,
45, 48, 50, 52, 54, 56, 60, 63, 64, 66, 68, 70, 72, 75, 76, 78, 80, 81, 84,
88, 90, 92, 96, 98, 99, 100, 102, 104, 105, 108, 110, 112, 114, 116,
117, 120, 124, 125, 126, 128, 130, 132, 135, 136, 138, 140, 144 и т.д.
•Телесное число 8
8=2х2х2

10.

МНОГОУГОЛЬНЫЕ ЧИСЛА —числа, связанные определенным
образом с плоским многоугольником. Простейшими из
многоуголных чисел являются треугольные числа
.1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351,
378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741 и т.д.
1
3=1+2
6=1+2+3
10=1+2+3+4
15=1+2+3+4+5
Треугольные числа 1,3,6,10,15,21
21=1+2+3+4+5+6

11.

Квадратные числа представляют собой
произведение двух одинаковых натуральных
чисел, то есть являются полными квадратами:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484,
529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521,
1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500 и т.д.
4=1+3
9=1+3+5
16=1+3+5+7
25=1+3+5+7+9

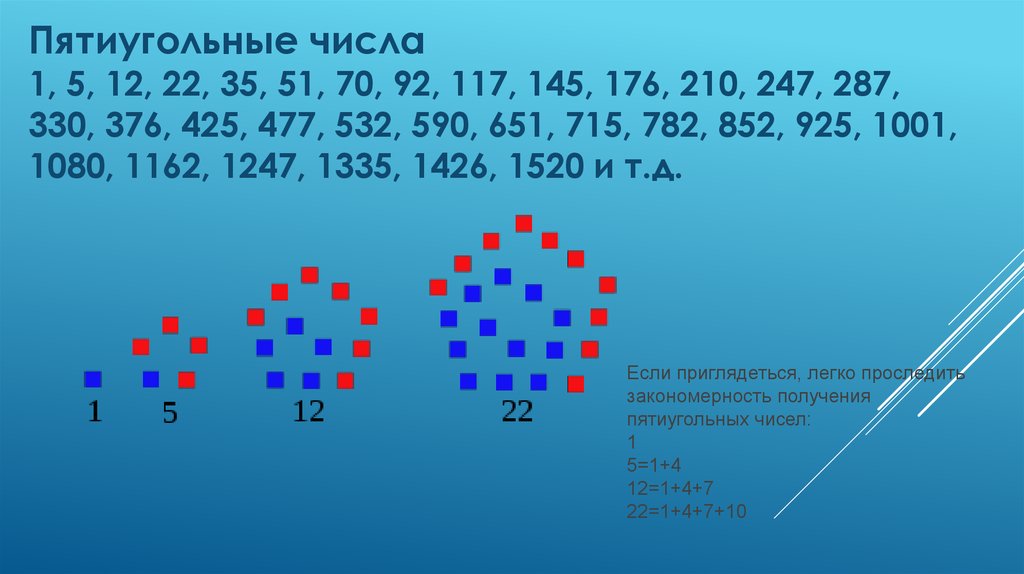
12.

Пятиугольные числа
1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287,
330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001,
1080, 1162, 1247, 1335, 1426, 1520 и т.д.
Если приглядеться, легко проследить
закономерность получения
пятиугольных чисел:
1
5=1+4
12=1+4+7
22=1+4+7+10

13.

Фигурные числа в математике.
На мой взгляд, с помощью плоских фигурных чисел легко проиллюстрировать законы умножения.
А) Так, представляя число 6 в двух формах: 3×2=2×3, легко "увидеть" переместительный закон умножения:
a×b=b×a.
Б)Можно "разглядеть" распределительный закон сложения относительно умножения: (a+b)c=ac+bc. Тоже
можно с помощью плоских чисел.
Берем число 10. (2+3)×2=2×2+3×2=10 - это свойство видим

14.

Наконец, если "камешки", образующие фигурные
числа, мыслить в виде равных по площади квадратиков,
то, укладывая их в прямоугольное число ab,
автоматически получаем формулу для вычисления
площади прямоугольника S=ab.
Аналогично, применяя телесные числа, получаем
формулу для вычисления объема прямоугольного
параллелепипеда V=abc.

15.

Итак, работая по данной теме, я пришёл к
следующим выводам:
•Фигурные числа, действительно, существуют: они
выкладываются в виде геометрических фигур;
•Выделяются несколько видов данных чисел;
•Фигурные числа – это интересно.