Сходство и различие радиотехнических САУ и других автоматических систем

1.

Федеральное государственное автономное образовательное
учреждение высшего образования
«Сибирский федеральный университет»
РАДИОАВТОМАТИКА
Демонстрационная презентация лекционного курса
Красноярск
2017

2.

Предмет и задачи курса
Предмет изучения дисциплины – системы автоматического
управления (САУ), охватывающие широкий класс систем
автоматического управления, применяемых в радиосвязи,
радиолокации, радионавигации, радиоуправлении и других областях
радиоэлектроники.
Основными задачами курса являются изучение основ теории
автоматического управления, принципов действия типовых систем
автоматического управления, методов их анализа, синтеза и
оптимизации.

3.

Сходство и различие радиотехнических САУ и других
автоматических систем
Сходство радиотехнических САУ с автоматическими системами
другого назначения определяется, прежде всего, единством теории –
теории автоматического управления, а также общностью многих
элементов, из которых строятся эти системы (усилители,
корректирующие и исполнительные элементы, управляющие ЭВМ и
другие)

4.

Краткая история развития систем автоматического управления
Первые радиотехнические САУ – системы автоматической регулировки
усиления (АРУ) – появились в 30-е годы нашего столетия. Системы
АРУ широко используются в приемниках современных радиосистем
самого разного назначения.
Большое применение находят системы частотной и фазовой
автоподстройки частоты (ЧАП и ФАП): для стабилизации
промежуточной частоты приемников, в качестве демодуляторов
сигналов с частотной и фазовой модуляцией, в синтезаторах частот, в
следящих измерителях координат и скорости подвижных объектов.
В радиолокации и радионавигации широкое применение находят
системы слежения за задержкой сигнала (ССЗ), на основе которых
строятся следящие измерители дальности. Кроме того, они
используются в радиосвязи в качестве систем синхронизации.
Системы слежения за направлением (ССН) применяются
в
радиолокации и радионавигации в качестве следящих измерителей
угловых координат, в радиоуправлении крылатыми ракетами, а также в
радиосвязи (наведение направленных антенн).

5.

Тема 1: «Общая характеристика систем автоматического
управления»
Содержание
1. Основные понятия и определения
2. Функциональная схема замкнутой САУ
3. Классификация САУ
4. Примеры характеристик нелинейных звеньев

6.

Основные понятия и определения
Автоматика – отрасль науки и техники, охватывающая
теорию и практику автоматического управления, а также
принципы построения автоматических систем.
Автоматическое регулирование – поддержание заданного
значения
какой
либо
физической
величины
без
непосредственного участия человека с помощью специальных
автоматических регуляторов.
Автоматическое управление – изменение по некоторому
закону какой - либо физической величины без непосредственного
участия человека с помощью специальных автоматических
управителей.
Элемент автоматики – звено автоматической системы,
выполняющее определенную функцию и характеризующееся
назначением, принципом действия, устройством (конструкцией),
электронной схемой.

7.

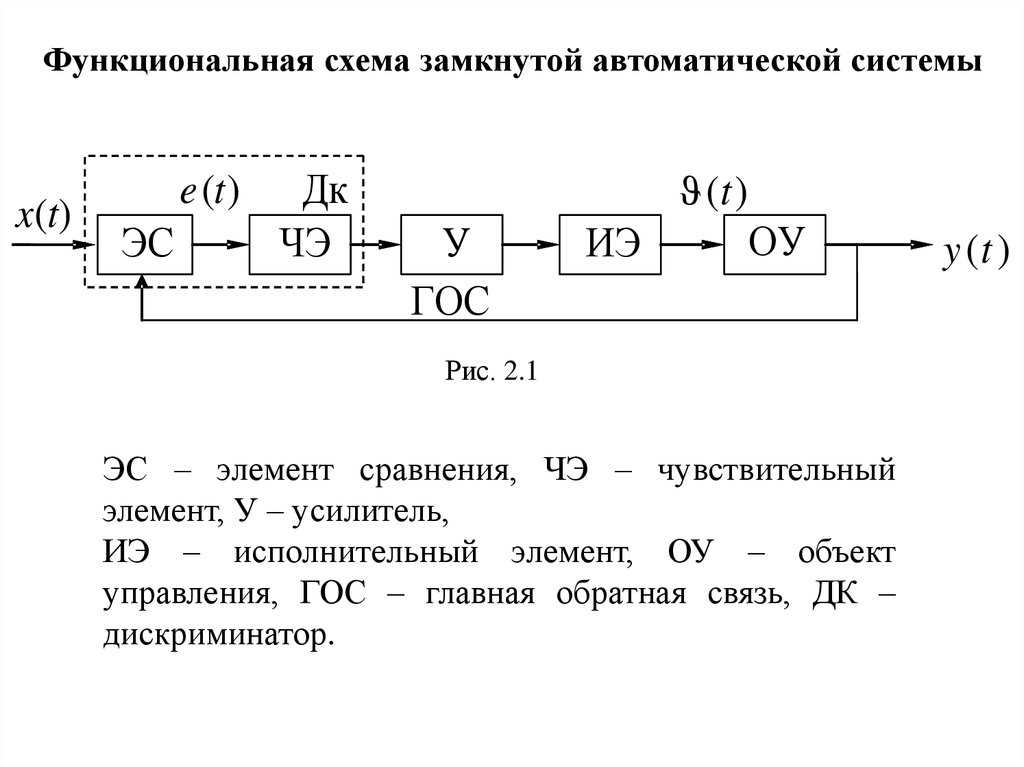
Функциональная схема замкнутой автоматической системы
x(t)
e (t)
ЭС
Дк
ЧЭ
(t)
У
ГОС
ИЭ
ОУ
Рис. 2.1
ЭС – элемент сравнения, ЧЭ – чувствительный
элемент, У – усилитель,
ИЭ – исполнительный элемент, ОУ – объект
управления, ГОС – главная обратная связь, ДК –
дискриминатор.
y (t )

8.

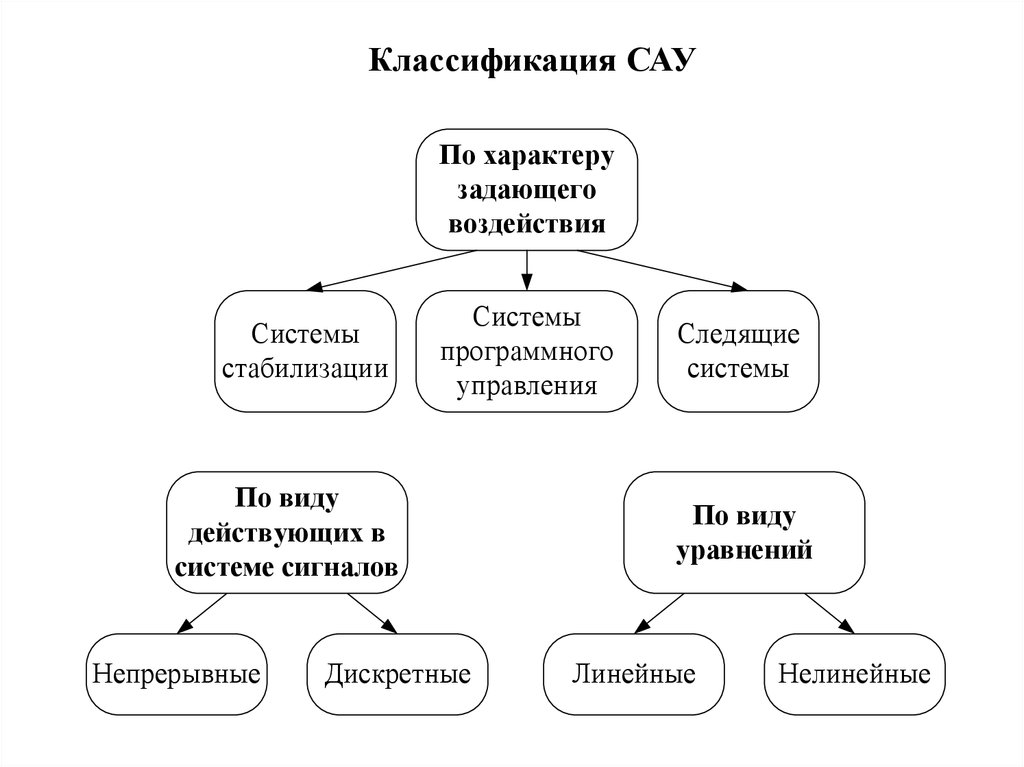
Классификация САУ
По характеру
задающего
воздействия
Системы
стабилизации
Системы
программного
управления
По виду
действующих в
системе сигналов
Непрерывные
Дискретные
Следящие
системы
По виду
уравнений
Линейные
Нелинейные

9.

По виду управляемой переменной
Системы
АРУ
Системы
слежения за
частотой (АПЧ)
По стабильности
параметров
системы
Стациорнарные
Нестационарные
Системы
слежения за
фазой (ФАПЧ)
Системы
слежения за
задержкой (ССЗ)
По числу
управляемых
переменных
Одномерные
Многомерные
Системы слежения
за направлением
(ССН)
По виду
используемой
для управления
энергии
Электромеханические
Электронные

10.

Примеры характеристик нелинейных звеньев САУ
y
y
0
0
x
x
б
а
y
y
0
в
x
0
y
г
0
д
Рис. 2.2
x
x

11.

Статическая характеристика – алгебраическое уравнение y=ƒ(x)
(для описания безынерционных звеньев);
Динамические характеристики (дифференциальные уравнения
или передаточные функции).
Пример: RC-фильтр нижних частот (ФНЧ):
дифференциальное
уравнение:
передаточная функция:
T
dy (t )
y (t ) x (t )
dt
K ( p)
1
1 Tp

12. Литература

В.Н. Бондаренко
Основы автоматики : учеб. пособие, 2004
либо – Радиоавтоматика: учеб. пособие, 2013
Радиоавтоматика. Методические указания по курсовому проектированию, 2011
Радиоавтоматика. учеб.-метод. пособие для лаб. практикума, 2012
Радиоавтоматика. учеб.-метод. пособие для практ. занятий, 2012
Дополнительная литература:
Соколов А. И. Радиоавтоматика : учеб. пособие, 2011.
Первачев, С.В. Радиоавтоматика. / М.: Радио и связь, 1982 – с., 296.
Чердынцев, В.А. Радиотехнические системы. / Минск: Высш. школа, 1988. – 368 с.
Бесекерский, В.А. Радиоавтоматика / М.: Высш. школа, 1985.
Коновалов, Г.Ф. Радиоавтоматика / М.: Высш. школа, 1990.
Бесекерский, В.А. Теория систем автоматического управления / СПб. : Профессия, 2003.
Ерофеев, А.А. Теория автоматического управления / СПб. : Политехника, 1998.
Шавров, А.В. Автоматика / М. : Колос, 2000.

13.

Тема 2: «Типовые звенья систем автоматического
управления»
Содержание
1.
2.
3.
4.
5.
6.
7.
8.
Интегрирующее звено
Частотные и временные характеристики интегрирующего звена
Форсирующее звено
Характеристики форсирующего звена
Способы реализации форсирующего звена
Колебательное звено
Частотные характеристики колебательного звена
Переходная характеристика колебательного звена

14.

Интегрирующее звено
Уравнение динамики интегрирующего звена
y(t ) kи x( )d , dy(t ) kи x(t ) ,
dt
0
t
(7.1)
где kи – коэффициент передачи, с –1.
Передаточная функция
kи
K ( p) ,
p
(7.2)
Частотные характеристики
K (ω)
kи ,
ω
(ω) arctg( ) π 2 .
ЛАХ: L( )=20lgK( )=20lgkи – 20lg .
(7.3)
(7.4)

15.

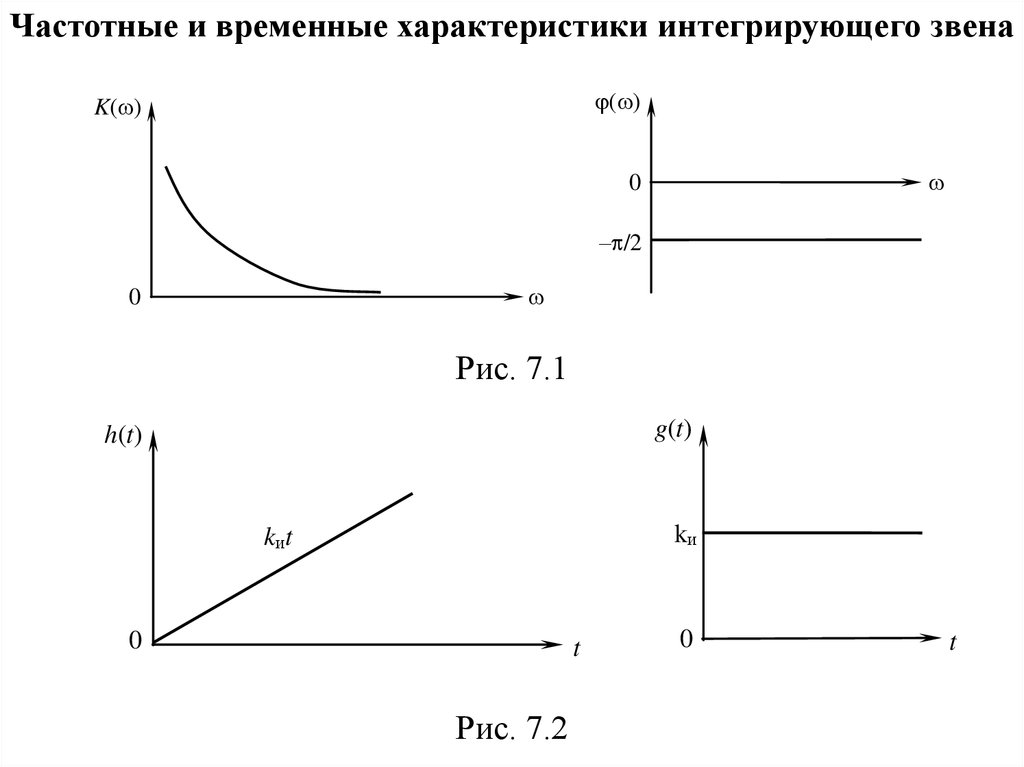
Частотные и временные характеристики интегрирующего звена
( )
K( )
0
– /2
0
Рис. 7.1
g(t)
h(t)
kи
kиt
0
t
Рис. 7.2
0
t

16.

Форсирующее звено
y(t ) kT dx(t ) kx(t ) ,
dt
(7.5)
где k – коэффициент передачи звена, Т – постоянная времени.
Передаточная функция
К(р)=k(1+Тр).
(7.6)
K (ω) k 1 (ωT )2 ,
(7.7)
( )=arctg T.
(7.8)
АЧХ и ФЧХ звена

17.

Характеристики форсирующего звена
( )
K( )
/2
2
k
/4
1
0
2
1
0
Рис. 7.3
L( )=20lgk+20lg(1+ 2T2)1/2.
(7.9)
h(t)
L ( )=20lgk при 1/T,
L ( )=20lgk+20lg T при > 1/Т. (7.10)
k
0
t
Рис. 7.4 – Переходная
характеристика
форсирующего звена

18.

Способы реализации форсирующего звена
K ( p) (k0 k ) k (1 Tp) ,
p
p
где T
(7.11)
k0
– постоянная времени, а k – общий коэффициент передачи.
k
y
x
x
k0
y
k/p
1 + Tp
k/p
K(p)
K(p)
б
a
Рис. 7.5
x
R1
y
R2
C
Рис. 7.6
Передаточная функция фильтра
K ( p) (k0 k ) k (1 Tp) , (7.12)
p
p
где постоянные времени Т1=R2C и
Т2=(R1+R2)C.

19.

Колебательное звено
Уравнение динамики
2
d
y(t ) 2γ T dy(t ) y(t ) kx(t ) ,
T
dt
dt 2
где Т – постоянная времени, – коэффициент затухания
(демпфирования), k – коэффициент передачи.
Передаточная функция
K ( p) 2 2 k
,
T p 2γ Tp 1
Частотные характеристики колебательного звена
k
K (ω)
2
2
2
,
ω 4γ 2 ω
1
ω
ω
0
0
2
(7.14)
(7.15)
2γ (ω /ω0 )
φ ω arctg
,
2
1 (ω/ω0 )
где 0=1/Т собственная частота.
(7.13)
(7.16)

20.

Частотные характеристики колебательного звена
K(ω)
ω = ωр
φ(ω)
4
3
2
K
1
K/2
0
ω0
1
0
ω
– π/2
–π
Рис. 7.7
( 1>1, 2=1, 3=0,5, 4<0,5)
2
3
4
ω0
ω

21.

Резонансная частота
р 0 1 2γ 2
K max K р
k
2γ 1 γ
, K( 0)=k/2 .
2
При 1 звено апериодическое.
ЛАХ
2
2
L( )=20lgK( )=20lgk – 20lg 1 ω/ω0 4γ 2 ω/ω0 .
2
(7.17)
L ( ) 20lgk.
(7.18)
L ( ) 20lgk – 40lg( / 0).
(7.19)

22.

Переходная характеристика колебательного звена
h(t ) k 1
e γt / T sin
1 γ2
1
1 γ2
t arctg
T
1 γ2
γ
( <1). (7.20)
tп 3 / γω0 . Период собственных колебаний Т0 равен 2π / ω0 1 2γ 2 .
h(t)
T0
5%
1
0
tп
t

23.

Тема 8: «Передаточные функции систем
радиоавтоматики»
Содержание
1. Обобщенная функциональная схема САУ
2. Обобщенная структурная схема САУ
3. Дискриминационная характеристика
4. Флуктуационная характеристика
5. Правила преобразования структурных схем
6. Передаточные функции замкнутой системы
7. САУ как фильтр

24.

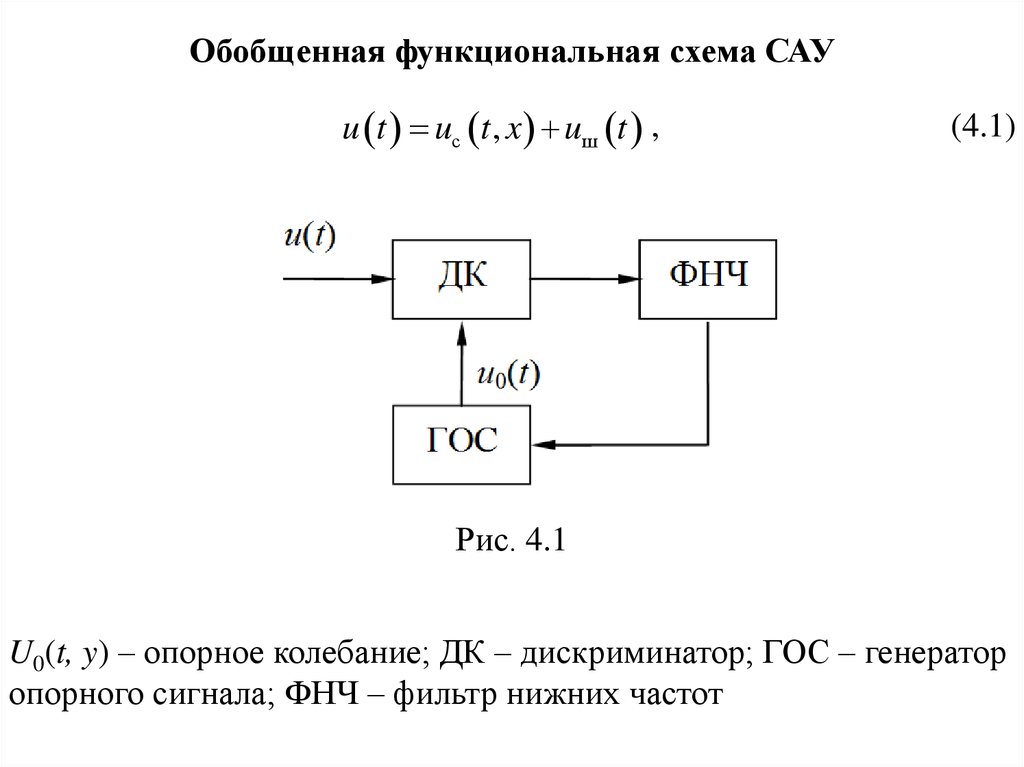
Обобщенная функциональная схема САУ
u t uс t , x uш t ,
(4.1)
Рис. 4.1
U0(t, y) – опорное колебание; ДК – дискриминатор; ГОС – генератор
опорного сигнала; ФНЧ – фильтр нижних частот

25.

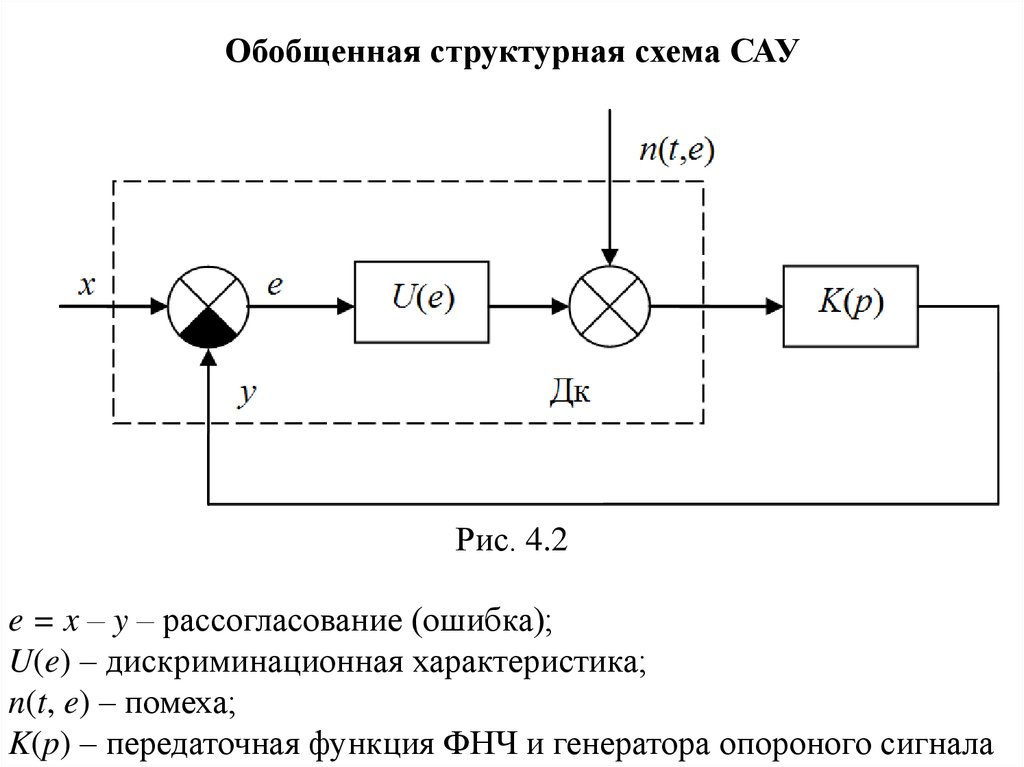
Обобщенная структурная схема САУ
Рис. 4.2
e = x – y – рассогласование (ошибка);
U(e) – дискриминационная характеристика;
n(t, e) – помеха;
K(p) – передаточная функция ФНЧ и генератора опороного сигнала

26.

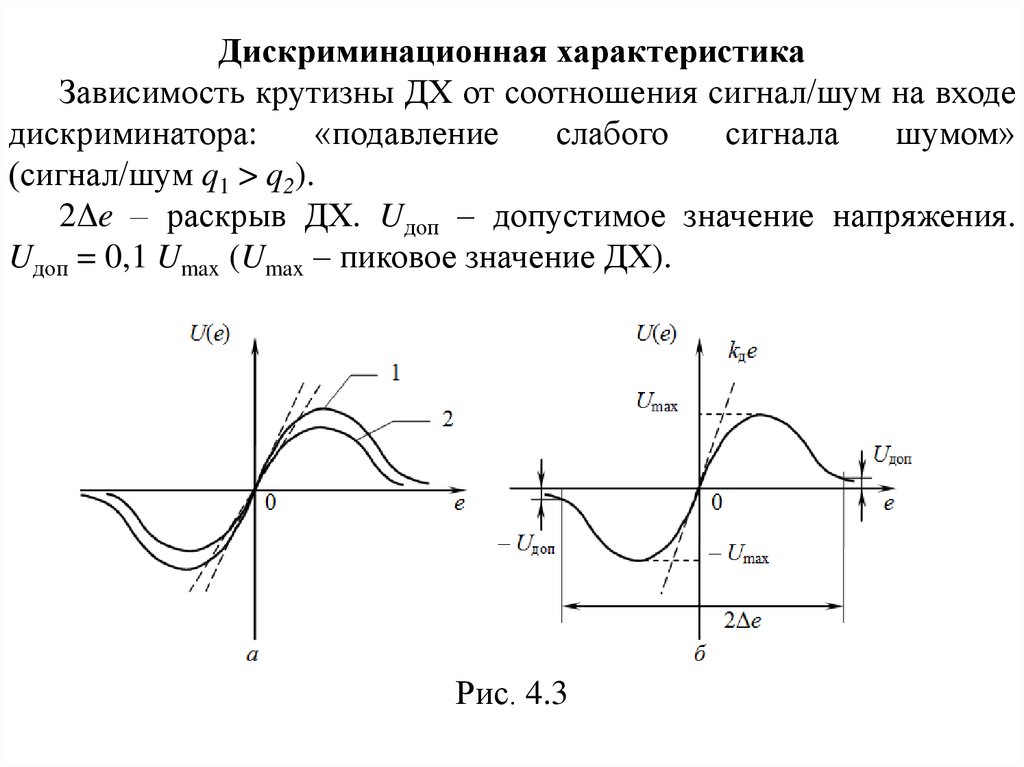
Дискриминационная характеристика
Зависимость крутизны ДХ от соотношения сигнал/шум на входе
дискриминатора:
«подавление
слабого
сигнала
шумом»
(сигнал/шум q1 > q2).
2Δe – раскрыв ДХ. Uдоп – допустимое значение напряжения.
Uдоп = 0,1 Umax (Umax – пиковое значение ДХ).
Рис. 4.3

27.

Флуктуационная характеристика
Флуктуационная характеристика (ФХ) – зависимость спектральной плотности
помехи на входе дискриминатора от ошибки.
n(t, e) – белый шум со спектральной плотномтью N0(e) Вт/Гц.
Форма N0(e) зависит от усиления предшествующего тракта, способа
нормировки сигнала, отношения сигнал/шум, типа дискриминатора и его
параметров.
Рис. 4.4

28.

Дифференциальное уравнение системы
y(t) = K(p)[U(e)+ n(t, e)].
(4.2)
Линеаризация дискриминационной характеристики (e → 0)
dU e
kA
, N 0 e N 0 const.
de e 0
y(t) =kд K(p)e(t)+K(p) n(t).
Рис. 4.5
(4.3)

29.

Правила преобразования структурных схем
Последовательное соединение звеньев
n
K p Y p / X p Ki p .
i 1
Рис. 4.6

30.

Параллельное соединение звеньев
n
K p Y p / X p Ki p
i 1
Рис. 4.7

31.

Передаточные функции замкнутой системы
Рис. 5.1
Передаточная функция замкнутой системы
kд K p
Y p
K з p K xy p
.
X p 1 kд K p
Передаточная функция «от воздействия к ошибке»
E p
1
K xe p
, K xe p
, K xe p 1 K з p
X p
1 kд K p
(5.1)

32.

САУ как фильтр
Рис. 5.2
Kз(jω) – комплексный коэффициент передачи (АФХ).
Модуль АФХ Kз(ω) – амплитудно-частотная характеристика,
аргумент АФХ φз(ω) – фазо-частотная характеристика замкнутой
системы.
Экспериментальное опретеделение АЧХ замкнутой системы:
x(t) = Xmsin(ωt). Xm – «амплитуда» (девиация частоты, индекс
фазовой модуляции, …). АЧХ замкнутой системы – зависимость от
частоты отношения «амплитуды» Ym выходной переменной к
«амплитуде» Xm входной переменой.

33.

САУ – фильтр нижних частот по отношению к воздействию x(t).
Рис. 5.3
Кривая 1 соответствует системе с монотонной переходной
характеристикой, а кривая 2 – система с колебательной ПХ

34.

Тема 9: «Устойчивость автоматических систем»
Содержание
1. Общие требования к устойчивости систем
2. Алгебраические критерии устойчивости
3. Частотные критерии устойчивости
4. Запас устойчивости

35.

Общие требования к устойчивости систем
Характеристическое уравнение замкнутой системы:
a0 pn a1 pn 1 ..... an 1 p an 0,
(6.1)
Однородное дифференциальное уравнение:
n
n 1
d
y
(
t
)
d
yc (t ) .....a dyc (t ) a y (t ) 0,
c
a0
a
n c
1
n 1 dt
dt n
dt n 1
(6.2)
где а0, а1, …, аn – коэффициенты, определяемые параметрами системы; yc(t) –
составляющая выходной переменной, определяющая свободное движение
системы.
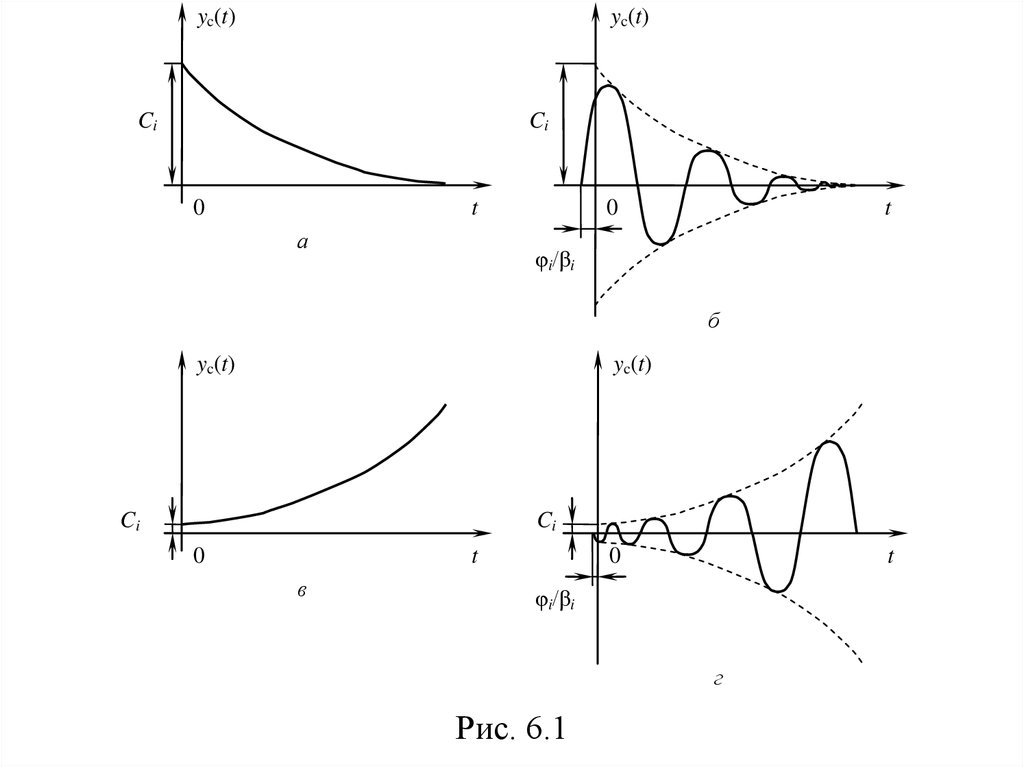
• отрицательные вещественные корни (рис. 6.1, а);
• комплексные корни с отрицательной вещественной частью (рис. 6.1, б);
• положительный вещественный корень (рис. 6.1, в);
• комплексные корни с положительной вещественной частью (рис. 6.1, г).

36.

yc(t)
yc(t)
Ci
Ci
0
t
а
0
t
φi/βi
б
yc(t)
yc(t)
Ci
Ci
0
t
в
0
t
φi/βi
г
Рис. 6.1

37.

Составляющие свободного движения
,
αi t
yci (t ) Cie sin(βit φi ),
yci (t ) Cieαi t ,
(6.3)
где Сi – постоянные интегрирования; i – вещественная часть корня
(интенсивность затухания колебаний); i – мнимая часть корня
(частота собственных колебаний); i – начальная фаза.
Im
Критерии устойчивости:
•алгебраические;
•частотные.
α2 + jβ2
α1
α1
0
α2 – jβ2
Рис. 6.2
Re

38.

Алгебраические критерии устойчивости
Критерий Гурвица: главный определитель, а также все его
диагональные миноры 1, 2, … должны быть положительными.
Главный определитель Гурвица для уравнения n-й степени:
2
a
a
1
0
a
a
3
2
,
a1
a3
a5 ... ...
...
0
a0
a2
... ... ...
...
0
a0
a1
a3 ... ...
...
0
...
...
... ... ...
...
0
...
...
... ... ... an 1
0
0
...
... ... ...
an
a
a
1
3
0
0
a
a
a
3
2
1
...
a
a ,
a
5
4
.
n n 1an .
3
Если все миноры, кроме предпоследнего, положительны, а
минор n – 1 равен нулю, то система находится на границе
устойчивости.

39.

Частотные критерии устойчивости
Критерий Найквиста: замкнутая система устойчива, если АФХ
разомкнутой системы для 0 не охватывает точку с
координатами (–1, j0).
АФХ – кривая на комплексной плоскости, представляющая
геометрическое место конца вектора комплексного коэффициента
передачи Kр(j ) при изменении частоты от нуля до бесконечности
(годографом).
Для астатических (рис. 6.3, б) систем АФХ дополняется дугой
бесконечно большого радиуса и определется её расположение
относительно точки (–1, j0).

40.

Im
ω=∞
Im
ω=0
ω=∞
–1
–1
0
Re
R→∞
ω→0
а
б
Рис. 6.3
Re

41.

Использование логарифмических частотных характеристик для
исследования устойчивости замкнутых систем по критерию
Найквиста: точке АФХ с координатами (–1, j0) соответствуют
критические значения ЛАХ и ЛФХ Lкp 20lg1 0 дБ, кp = – рад.
L(ω), дБ
ωср
0
ω, с–1
π
–φ(ω), рад
Рис. 6.4

42.

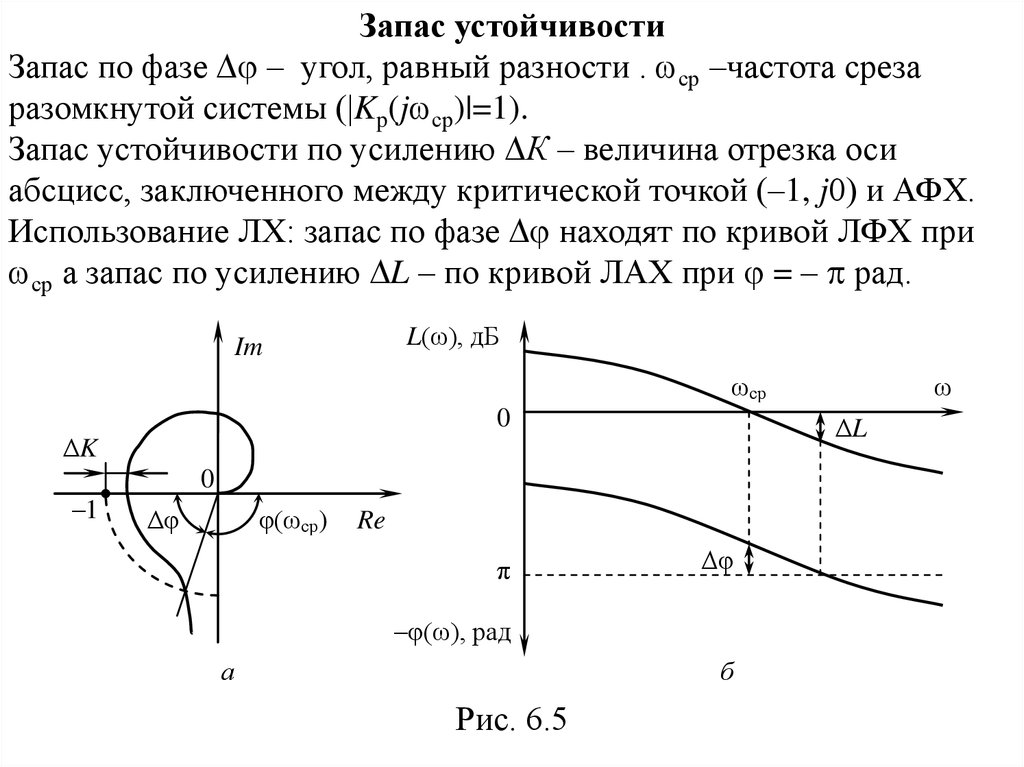
Запас устойчивости
Запас по фазе – угол, равный разности . ср –частота среза
разомкнутой системы (|Kp(j ср)|=1).
Запас устойчивости по усилению К – величина отрезка оси
абсцисс, заключенного между критической точкой (–1, j0) и АФХ.
Использование ЛХ: запас по фазе находят по кривой ЛФХ при
ср а запас по усилению L – по кривой ЛАХ при = – рад.
L(ω), дБ
Im
ωср
0
ΔL
ΔK
0
–1
Δφ
φ(ωср)
Re
π
∆φ
–φ(ω), рад
а
б
Рис. 6.5
ω

43.

Запретные области по заданным запасам K и
L(ω), дБ
20lg(1 + ΔK)
ω
20lg(1 – ΔK)
– Δφ
Δφ
π
– φ(ω), рад
Рис. 6.6
Достаточный запас по фазе > /6 рад и по усилению L >6 дБ
(или K>0,5).

44.

Тема 10: «Оценка качества автоматических систем в
переходном режиме»
Содержание
1. Цифровое моделирование непрерывных систем
2. Анализ качества переходного процесса по АЧХ замкнутой системы
3. Анализ качества переходного процесса по АФХ разомкнутой системы
4. Оценка качества переходного процесса по ЛАХ разомкнутой системы
5. ЛАХ типовых систем

45.

Типовые воздействия в виде детерминированных функций времени:
•постоянное (ступенчатое),
•линейное,
•квадратичное.
Методы анализа качества переходного процесса:
•прямые (по переходной характеристике замкнутой системы),
•косвенные (по АЧХ замкнутой системы, по АФК разомкнутой
системы, по ЛАХ разомкнутой системы).

46.

y
e
emax
emax
2δ
2δ
x0
0
emax
t
tп
а
t
emax
б
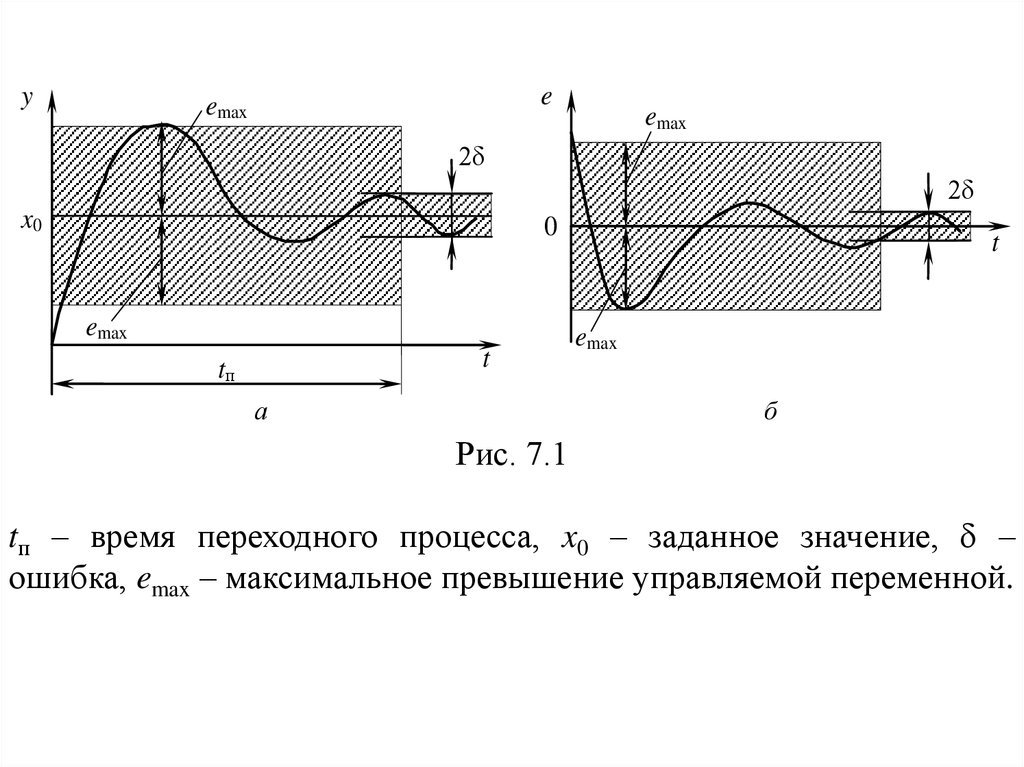
Рис. 7.1
tп – время переходного процесса, x0 – заданное значение, –
ошибка, emax – максимальное превышение управляемой переменной.

47.

Переходный процесс: монотонный (кривая 1), апериодический
(кривая 2), колебательный (кривая 3).
=(emax/x0) 100% – перерегулирование (максимальное отклонение,
выраженное в процентах).
Быстродействие системы – время переходного процесса tп (время,
по истечении которого ошибка управления не превосходит заданной
величины от значения x0, обычно 5%).
– степень колебательности (число колебаний за время
переходного процесса).
y
3
e′′′
max
2
e′′
max
x0
0
2δ
1
t
tп′
tп′′′
Рис. 7.2

48.

Цифровое моделирование непрерывных САУ
Разностное уравнение – программа рекуррентного вычисления
переходного процесса.
Дискретная передаточная функция цифровой модели
1 T 1 z 1 ,
(7.1)
p 2 1 z 1
где T интервал дискретизации, z=e pT переменная Z –
преобразования
(z – 1=e – pT оператор задержки на T).
1
b
... bm z m
0 b1 z
K ( z)
,
(7.2)
1 a1 z 1 ... an z n
Разностное уравнение
m
n
y k bi x k i ai y k i , k 0,1,2,...,
i 0
i 1
(7.3)
где y[k] текущее значение управляемой переменной, x[k–i] и y[k–i]
предыдущие значения процессов на (k–i)-м шаге.

49.

Анализ качества переходного процесса по АЧХ
замкнутой системы
Кз(ω)
y
1
1
2
2
3
x0
3
4
4
0
ω
0
а
t
б
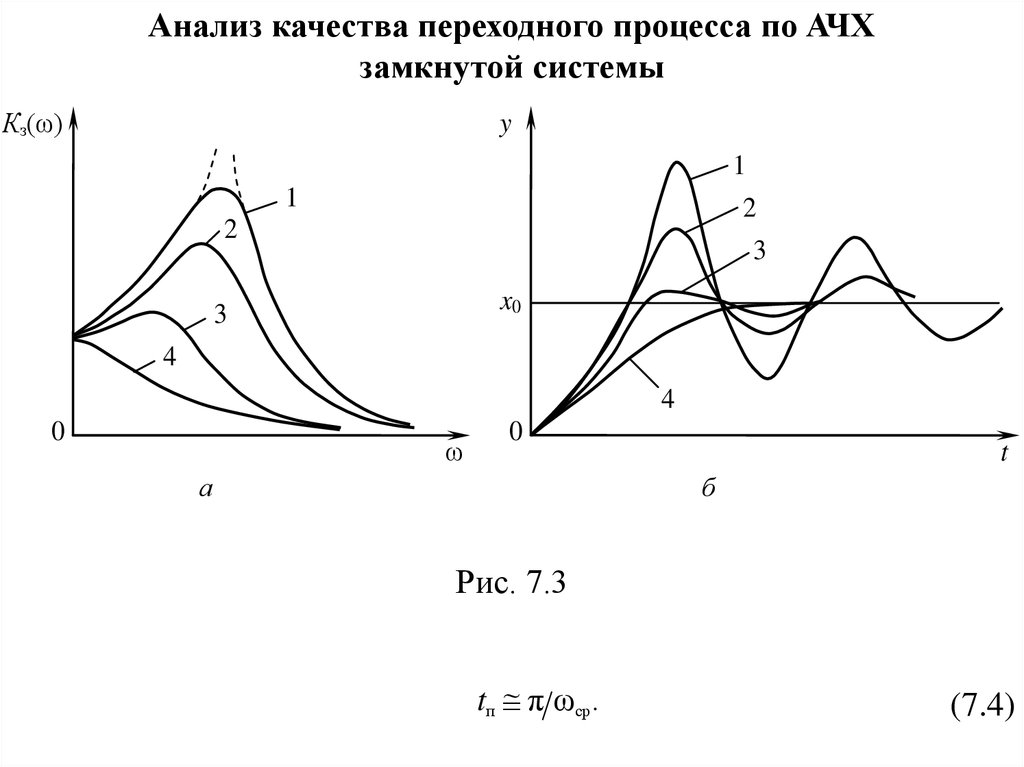
Рис. 7.3
tп π ωcp .
(7.4)

50.

Kр ( jω)
Kз (ω) Kз ( jω)
.
1 Kр ( jω)
Кз(ω)
1
M
0
ω0
ср
ω
Рис. 7.4
M – показатель колебательности; – собственная частота; – частота
среза.

51.

Анализ качества переходного процесса по АФХ разомкнутой
системы
Im
Im
β(ωi)
1
→∞ 0
Re
1
0,5
0
Re
φр(ωi)
1 + Кр(jωi)
ср
Кр(jωi)
ωi
φ(ωi)
ω→
0
1
а
2
3
б
Рис. 7.5
Кривая 1 АЧХ замкнутой системы имеет пик, переходный процесс
колебательным с перерегулированием;
кривая 3 АЧХ замкнутой системы является убывающей функцией,
переходный процесс монотонный.

52.

Оценка качества переходного процесса по ЛАХ
разомкнутой системы
h(ω0t)
M = 1,7
M = 1,5
M = 1,3
1,2
1,0
0,8
M = 1,1
0
0,5 1,0 1,5
3,5
ω0 t
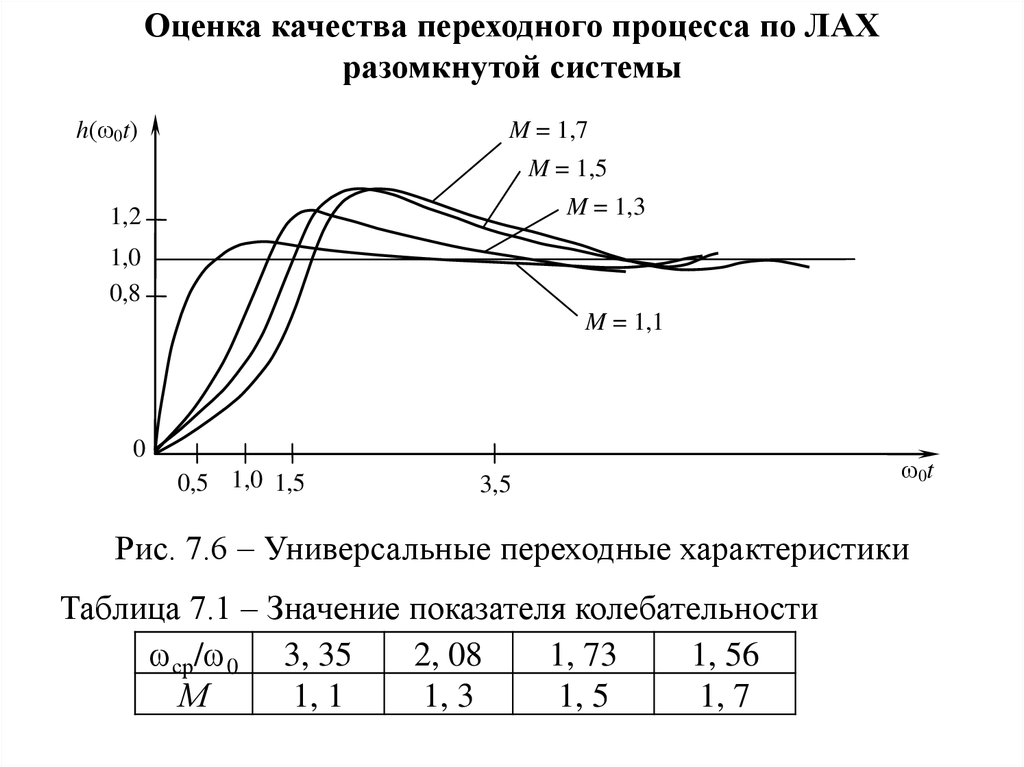
Рис. 7.6 Универсальные переходные характеристики
Таблица 7.1 – Значение показателя колебательности
2, 08
1, 73
1, 56
ср/ 0 3, 35
М
1, 1
1, 3
1, 5
1, 7

53.

ЛАХ типовых систем
– 20
– 20
– 40
– 40
– 20
1
τ1
1
τ2
1
τ3
1
– 20
ω
ω0
– 40
1
τ1
1
τ2
1
τ3
1
– 60
а
б
– 40
– 40
– 20
1
τ1
ω
ω0
1
τ2
1
– 20
ω
ω0
– 40
1
τ1
1
τ2
1
τ3
1
– 40
– 60
г
в
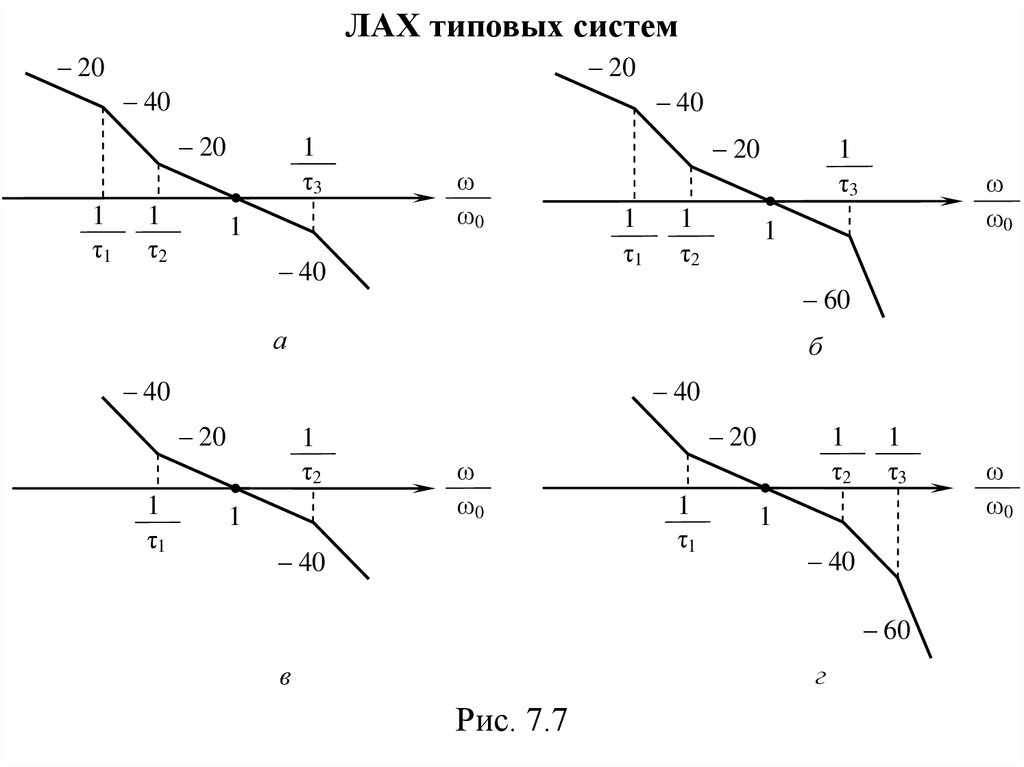
Рис. 7.7
ω
ω0

54.

Тема 11: «Точность автоматических систем при типовых
воздействиях»
Содержание
1. Статические ошибки
2. Динамические ошибки

55.

Точность САУ при типовых воздействиях
Точность АС – величина ошибки в установившемся режиме.
Детерминированные воздействия:
постоянное (ступенчатое),
линейное,
квадратичное.
Передаточная функция, описывающая систему радиоавтоматики:
Kp ( p)
Ki B( p)
,
i
p A( p)
(8.1)
где Ki общее усиление разомкнутой системы, i – число
интегрирующих звеньев, определяющее порядок астатизма
системы;
A( p) a0 p n a1 p n 1 ... 1,
B( p) b0 p m b1 p m 1 ... 1

56.

Статические ошибки
Статическая ошибка – ошибка системы при постоянном
(ступенчатом) воздействии x(t)=x0=const.
pi A( p)
pi x0
x
x
0
0
ecт lim
e(t ) lim
pKe ( p) lim
p
lim
.
t
p 0
p p 0 pi A( p) Ki B( p) p p 0 pi Ki (8.2)
Ошибка статической системы (не содержащей интегрирующих
звеньев)
eст x0 .
(8.3)
1 K0
Ошибка астатических
воздействии
систем
eст 0.
(i
1)
при
постоянном

57.

Динамические ошибки
Динамическая ошибка eд(t) – ошибка, характеризующая
точность замкнутой системы при меняющемся воздействии
1 2
x(t ) x0 υ xt υ xt ...
(8.4)
2
где x0 начальное значение, скорость изменения, ускорение и
т. д.
Выражение для ошибки в операторной форме:
E ( p) K e ( p) X ( p).
C2 2
E ( p ) C0 C1 p
p ... X ( p ),
2!
где C0, C1, C2, … коэффициенты ошибок.
d k K e ( p)
Ck
dp k
.
p 0
(8.5)
(8.6)
(8.7)

58.

Установившееся значение ошибки
eд ( t )
n
lim e ( t )
t
k
Ck d x (t )
k 0 k
!
dt
k
.
pi A( p)
pi
C0 Ke (0) i
i
p A( p) Ki B( p) p 0 p Ki
(8.8)
p 0
Для статических систем (i=0) C0=1/(1+K0), для астатических
систем C0=0.
Динамические ошибки типовых систем при линейном
воздействии (изменение с постоянной скоростью) x(t)= xt.
Динамическая ошибка (ошибка по скорости):
eд (t ) C0 xt C1 x
Для статической системы она равна
x
eд (t )
t.
1 K0

59.

Установившееся значение ошибки
eд (t ) C1 x .
C2 2
p i A( p )
C0 C1 p
p i
.
2
p A( p) K i B( p)
(8.9)
C
p i A( p ) K i B( p ) C0 C1 p 2 p 2 p i A( p ).
2
(8.10)
i = 1 (астатическая система первого порядка):
C0 (1 bm 1 K1 ) C1K1 1
C1=1/K1, так как C0=0.
Скоростная ошибка системы первого порядка астатизма eд= x/K1
определяется усилением разомкнутой системы K1 и не зависит от
времени. Параметр K1, имеющий размерность c –1, называется
добротностью системы по скорости.

60.

Для астатической системы второго порядка скоростная ошибка
равна нулю (C0=C1=0).
Динамические ошибки типовых систем при квадратичном
воздействии (изменение с постоянным ускорением) x(t ) ν xt 2 / 2.
Для динамической ошибки (ошибки по ускорению)
C0 2
C2
eд (t ) xt C1 xt x .
2
2
Для статической системы ошибка по ускорению равна
eд (t )
(8.11)
νx t 2,
2(1 K0 )
Для системы первого порядка астатизма ошибка по ускорению
равна
eд (t ) C1 xt
x
K1
t
(8.12)

61.

Для астатической системы второго порядка ошибка по
ускорению равна
C2
eд (t ) x
2
C2
C0 (1 K 2bm 2 ) K 2bm 1C1 K 2
1
2
(8.13)
Откуда C2/2=1/K2, так как C0=C1=0.
Ошибка по ускорению в системе второго порядка астатизма
равна постоянной величине . Параметр K2, характеризующий
точность системы, называется добротностью по ускорению (имеет
размерность c –2).

62.

Тема 12: «Точность автоматических систем при воздействии
помех»
Содержание
1. Составляющие ошибки слежения
2. Дисперсия динамической ошибки при случайном воздействии
3. Оптимизация шумовой полосы замкнутой системы

63.

Составляющие ошибки слежения
e=x–y
x
x + nэ
x
y
KЗ(p)
nэ
1 – KЗ(p)
eд
e = eд + eп
– eп
KЗ(p)
а
б
Рис. 9.1
e 2 eд2 en2 ,
e2 e2д en2

64.

Дисперсия шумовой ошибки
1
2
2
σ en
S э (ω) K з (ω)dω,
(9.1)
2π
где Sэ( )=Sn( )/k2д энергетический спектр эквивалентного шума,
Sn( ) – энергетический спектр помехи n(t) на выходе
дискриминатора, n(t) – белый шум с равномерным спектром
Sn(f)=N0 Вт/Гц в полосе частот от 0 до .
Эквивалентный шум – белый шум со спектральной плотностью
мощности Sэ(f)=Nэ=N0/k2д, размерность [х]2/Гц ([х] – размерность
задающего воздействия).
Дисперсия шумовой ошибки
N0 1 2
N0 2
2
σ en 2 K з (ω) dω 2 K з ( f ) df
2k д π 0
kд 0
(9.2)

65.

Шумовая полоса замкнутой системы
1 2
2
Fш K з ( f )df
K з (ω)dω
2π 0
0
2
σ en
N0
Fш
2
kд
(9.3)
(9.4)
Для типовых систем радиоавтоматики определенный интеграл в
(6.16) сводится к табличному интегралу
Bn (ω)dω
1
In
π 0 An ( jω) An ( jω)
(9.5)
где полиномы An(j ) и Bn( )
An ( jω) a0 ( jω) n a1 ( jω) n 1 ... an ;
2 n 2
2 n 4
Bn (ω) b0ω
b1ω
... bn 1.
(9.6)

66.

b0
I1
,
2a0 a1
b0 a0b1 / a2
I2
,
2a0 a1
I3
a2b0 a0b1 a0 a1b2 / a3
.
2a0 (a0 a3 a1a2 )
KЗ2(f)
Sn(f)
1
N0
0
f
а
0
б
Рис. 9.2
Fш
f

67.

Дисперсия динамической ошибки при случайном воздействии
1
2
σ S x (ω) 1 K з ( jω) dω
π0
2
eд
Подавляемые частоты
Воспроизводимые частоты
Sx( )
(9.7)
Sn( )
N0
ω
0
ω
0
K2з( )
|1-Kз(j )|
1
1
0
Sед( )
ω
0
2πFш
ω
2πFш
Sеn( )
ω
0
ω
0
б
а
Рис. 9.3

68.

Оптимизация шумовой полосы замкнутой системы
Kз( ω )
1
1
0
а
б
Рис. 9.4
σ ед2(ед2),
σ ен 2,
σ е2(е)
1
3
мин
2
Fшопт
Рис. 9.5
Fш

69.

Тема 15: «Методы анализа нелинейных систем
радиоавтоматики»
Содержание
1. Анализ нелинейной системы ЧАП
2. Графо-аналитический метод анализа нелинейной системы ЧАП
3. Графический метод определения полос захвата и удержания
4. Зависимость статической ошибки от частотной расстройки

70.

Методы анализа нелинейных систем радиоавтоматики
•метод фазовой плоскости
•метод кусочно-линейной аппроксимации
•метод гармонической линеаризации
•метод статистической линеаризации
•метод моделирования на ЭВМ
Нелинейные режимы работы АС:
Поиск – устранение начальной расстройки (уменьшение ее
до значений, определяемых полосой захвата). (|e|<eдоп).
Срыв слежения возникает, когда расстройка выходит за
пределы раскрыва ДХ.
Полоса захвата характеризует способность захватывать
сигнал и осуществлять слежение при максимально допустимой
расстройке (2eдоп).

71.

Δfc
Анализ нелинейной системы ЧАП
Δf
U(Δf)
Kф(p)
Δfг
kг
Рис.10.1 – Структурная схема системы ЧАП
Дифференциальное уравнение системы
fг kг Kф ( p)U ( fc fг )
(10.1)
f c f г
fг
U ( fc f г )
kг Kф ( p) kг /(1 Tp)
(1 Tp)U ( f c f г ) ( f c f г ) / kг .
В установившемся режиме
f c f
U ( f c f г )
.
kг
(10.2)

72.

Графо-аналитический метод анализа нелинейной системы ЧАП
Рис.10.2
A – устойчивое
A, C – устойчивое
слежение; Δf=Δf0, Δf0 – слежение, если
остаточная частотная Δfc1→ Δfc2
расстройка;
С – устойчивый срыв
слежения, если Δfc1→
Δfc3. Захват
невозможен если Δfc=
Δfc3

73.

Передаточная функция замкнутой (линеаризованной) системы
K зi ( p )
K pi ( p )
1 K pi ( p )
, i 1, 2, 3,
K0i e j i
(10.3)
Kpi ( p)
1 Tp
K pi ( p ) -передаточная функция разомкнутой системы,
соответствующая точкам А, В и С(i 1, 2, 3), K0i ki kг
0i
– модуль и аргумент комплексного коэффициента
передачи разомкнутой системы (k1= kА ,k2 =kВ ,k3 =kС).
Ai ( p) a0 p a1i ,
a0 T , a1i 1 K 0i e j i .
(10.4)
1 k1 kг 0,
a1 1 k2 kг 0, т.к. k2 1/ kг ,
1
k
k
0,
т.к.
k
1/
k
.
3 г
3
г
(10.5)
n=1. Необходимое и достаточное условие устойчивости: >0,
φi : φ1 =0, φ2= π, φ3= π.

74.

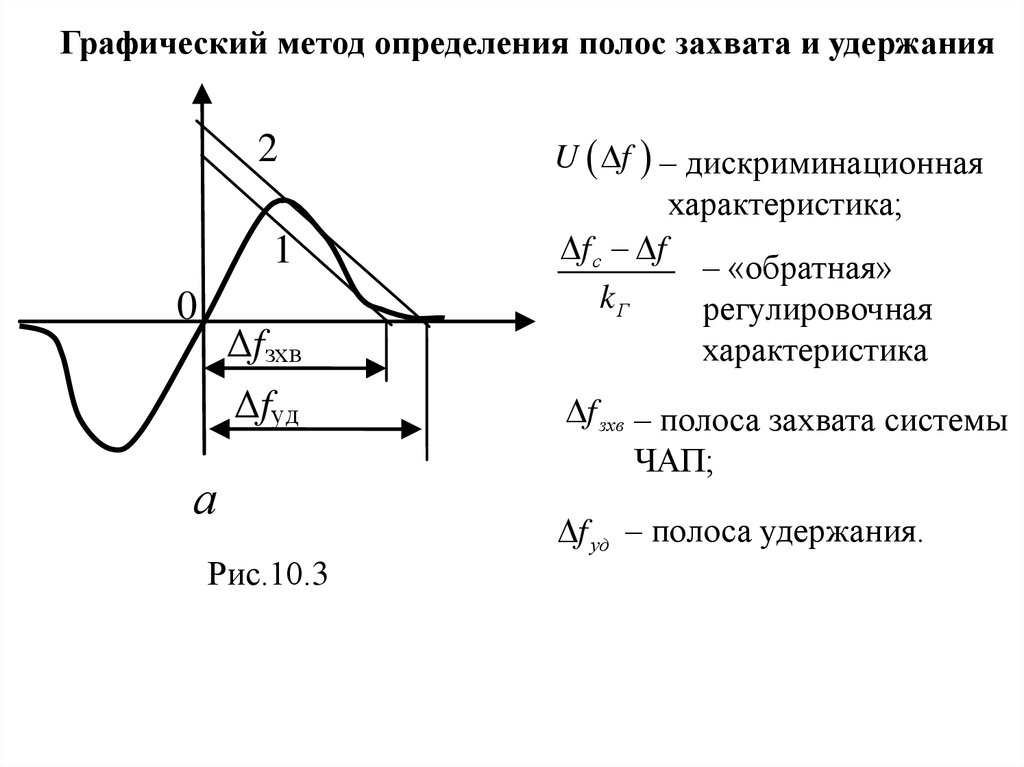
Графический метод определения полос захвата и удержания
2
1
0
Δfзхв
Δfуд
а
Рис.10.3
U f – дискриминационная
характеристика;
f с f
– «обратная»
kГ
регулировочная
характеристика
f зхв – полоса захвата системы
ЧАП;
f уд – полоса удержания.

75.

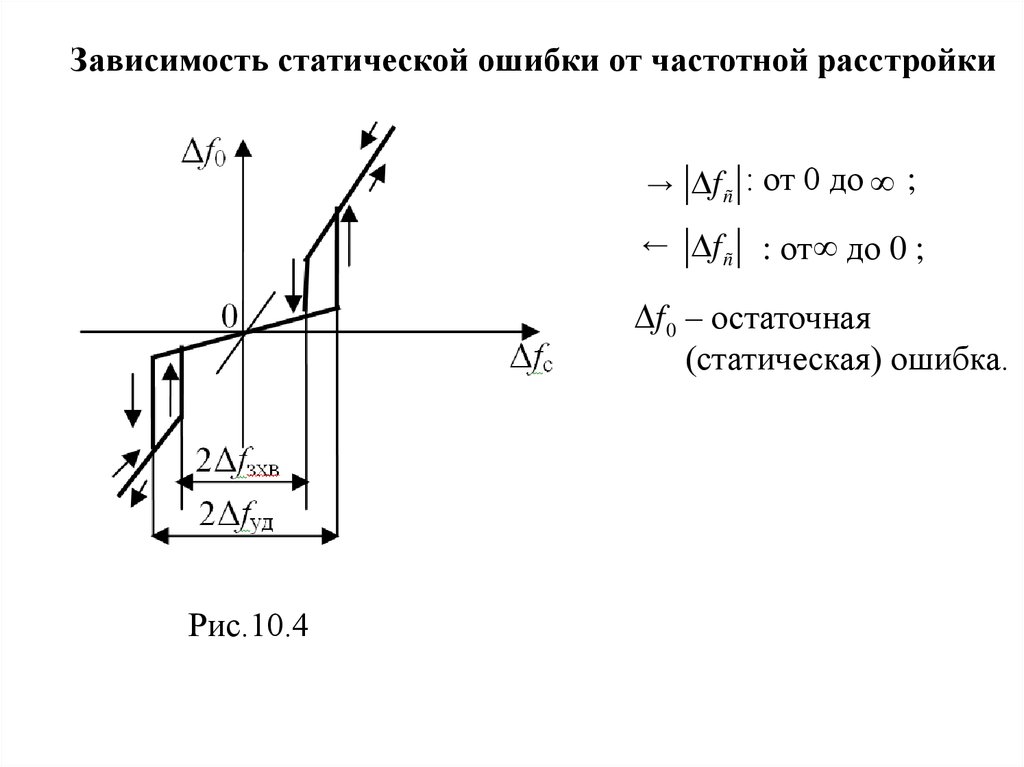
Зависимость статической ошибки от частотной расстройки
→
f ñ : от 0 до ;
←
f ñ : от до 0 ;
f 0 – остаточная
(статическая) ошибка.
Рис.10.4

76.

Тема 16: «Анализ дискретных систем радиоавтоматики»
Тема 17: «Показатели качества управления дискретных
систем радиоавтоматики»
Содержание
1. Математическое описание дискретных САУ
2. Обобщенная структурная схема линейной дискретной САУ
3. Анализ точности дискретной САУ при детерминированном
воздействии
4. Анализ точности дискретной САУ при воздействии помех

77.

Математическое описание дискретных АС
Дискретное преобразование Лапласа записывается в виде
X ( p ) x(nT )e pnT ,
x(nT ) x(t nT ), n 0,1...,
(11.1)
n 0
дискретная (решетчатая) функция.
X ( z ) x(nT ) z n z x(t ) ,
n 0
z e
pT
(11.2)
z 1 e pT , – оператор задержки на T, Т – интервал дискретизации.
Х(z) – Z-преобразование непрерывной функции х(t),
Z
. оператор
Z-преобразования.
m
n
y[k ] bi x k i ai y k i , k 0,1, 2...
i 0
i 1
(11.3)

78.

Обобщенная структурная схема линейной дискретной САУ
n(kT)
x(kT)
e(kT)
x(kT)
e(kT)
Kp(z)
y(kT)
Kд
K(z)
y(kT)
а
б
Рис.11.1
Kp ( z)
Y ( z)
K3 ( z )
,
X ( z) 1 Kp ( z)
Ke ( z )
E( z)
1
1 K з ( z ),
X ( z) 1 Kp ( z)
(11.4)
(11.5)

79.

Анализ точности дискретной САУ при детерминированном
воздействии
.
..
e(kT ) C0 x(kT ) C1 x(kT ) C2 x(kT ),
С0, С1 и С2–коэффициенты ошибок по положению, по
скорости и по ускорению.
..
d
d2
x(t ) x(t ) и x(t ) 2 x(t )
dt
dt
.
1 dj
pT
cj
K
(
e
)
e
j
j ! dp
C0 K e ( z )
z 1
C1 zTK e/ ( z )
p 0, j 0,1,2,
,
z 1
C2 2 zT K e/ ( z ) zK e// ( z )
z 1
2
d
d
Ke/ ( z ) Ke ( z ), K e// ( z ) 2 K e ( z ).
dz
dz
(11.6)

80.

Анализ точности дискретной САУ при воздействии помех
Результирующая среднеквадратическая ошибка
e 2 eд2 e2 ,
eд – математическое ожидание (динамическая ошибка).
Дисперсия ошибки
T
2
2
e
2
T
Se (w) 1 jw 2 dw,
Se(w) – спектральная плотность ошибки, w – псевдочастота.

81.

Тема 2: «Системы автоматической регулировки усиления
(АРУ)»
Содержание
1. Система АРУ с управлением по рассогласованию
2. Амплитудные характеристики РУ
3. Математическое описание системы АРУ
4. Структурная схема системы АРУ как системы стабилизации

82.

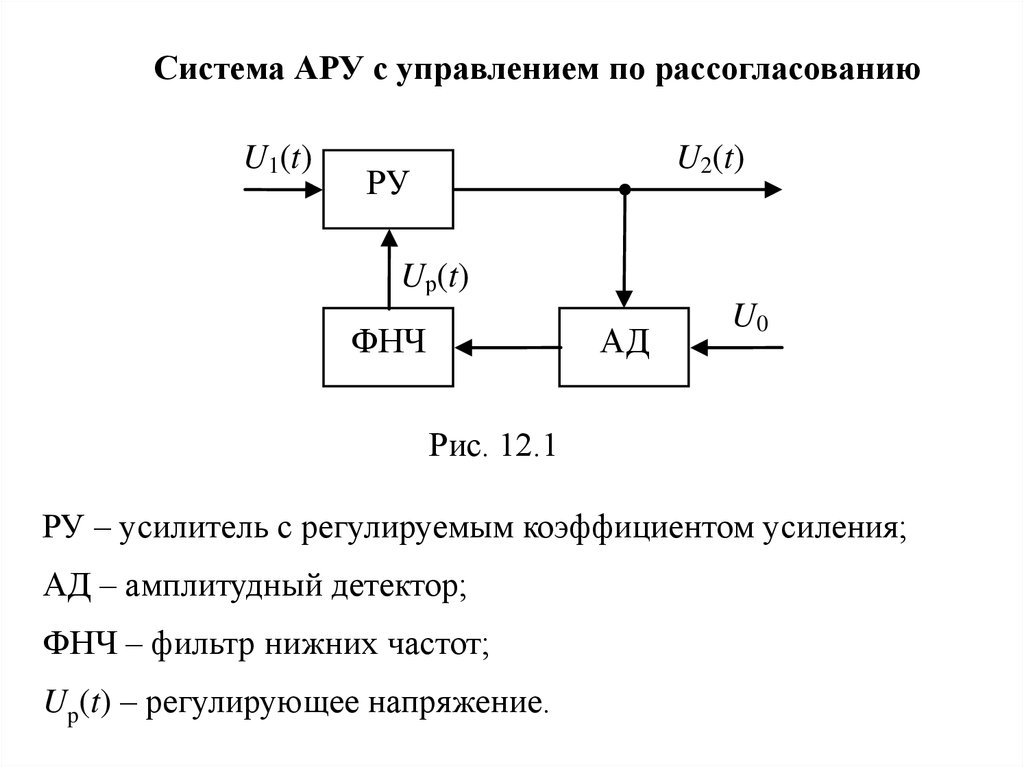
Система АРУ с управлением по рассогласованию
U1(t)
U2(t)
РУ
Uр(t)
ФНЧ
АД
U0
Рис. 12.1
РУ – усилитель с регулируемым коэффициентом усиления;
АД – амплитудный детектор;
ФНЧ – фильтр нижних частот;
Up(t) – регулирующее напряжение.

83.

Амплитудные характеристики РУ
U2
1
2
4
U0
3
U1min
Рис. 12.2
Кривая 1 – линейный (идеальный) усилитель;
кривая 2 – реальный усилитель без АРУ;
кривая 3 – усилитель с АРУ;
кривая 4 – усилитель с «задержанной АРУ».
U1

84.

Математическое описание системы АРУ
Амплитудная характеристика ,линейного усилителя:
U2(t)=kU1(t).
Регулировочная характеристика усилителя:
k (U p ) k0 kpU p
где k p
dk U p
k0 k U p
dU p
U p 0
обратной связи.
крутизна регулировочной характеристики,
U p 0
коэффициент усиления при разомкнутой цепи

85.

Характеристика АД при линейном детектировании:
kД U 2 U 0 , при U 2 U 0 ,
UД
при U 2 U 0 ,
0,
dU д (U 2 )
где kд
dU 2
U2 U0
передачи) детектора.
– крутизна характеристики (коэффициент
Регулирующее напряжение связано с выходным напряжением
детектора дифференциальным уравнением (в операторной форме)
Up(t)=Kф(р)Uд(t).
Общее уравнение системы АРУ для режима сильного сигнала,
когда U2 U0:
U2(t)=[k0+k0kд(U0 - U2)Kф(p)]U1(t).

86.

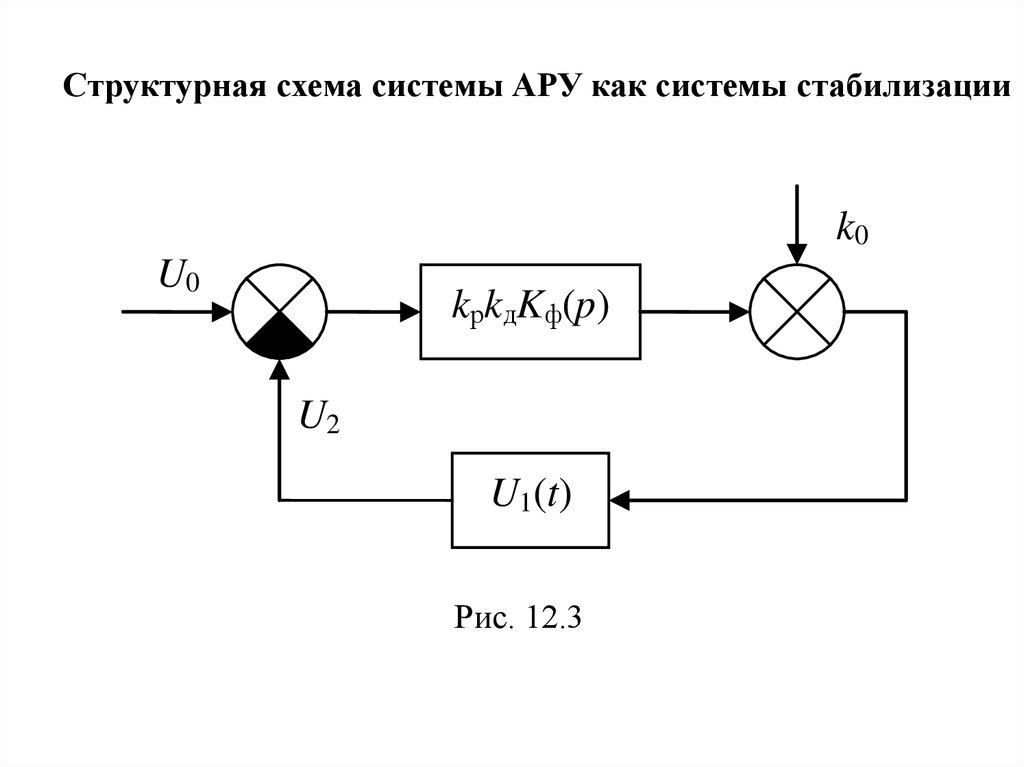
Структурная схема системы АРУ как системы стабилизации
k0
U0
kрkдKф(p)
U2
U1(t)
Рис. 12.3

87.

Тема 3: «Системы частотной автоподстройки (ЧАП)»
Содержание
1. Функциональная схема системы частотной автоподстройки
2. Принцип действия системы ЧАП

88.

Функциональная схема системы частотной автоподстройки
Выход АМ
Uп(t)
Uс(t)
См
Выход
СФ
УПЧ
ЧД
Uг(t)
ПГ
Uу(t)
ФНЧ
ФНЧ
Выход ЧМ
(неследящий
прием)
U(t)
Выход ЧМ
(следящий прием)
Рис. 13.1
См – смеситель, ПГ – подстраиваемый генератор, УПЧ – усилитель
промежуточной частоты, ЧД – частотный дискриминатор, ФНЧ –
фильтр нижних частот.

89.

Принцип действия системы ЧАП
Пример. Стабилизация промежуточной частоты
супергетеродинного приемника
uc(t) – принятый сигнал;
uг(t) – опорное колебание, вырабатываемое гетеродином;
fc0 – номинальная частота сигнала;
fc = fc – fc0;
fп = fc – fг;
f = fп – f0 – частотная расстройка.

90.

fг
U
fгmax
Uош
Δf0
0 Δf0
fг0
Δf
2Δfу
fгmin
Uу
– Uуmax
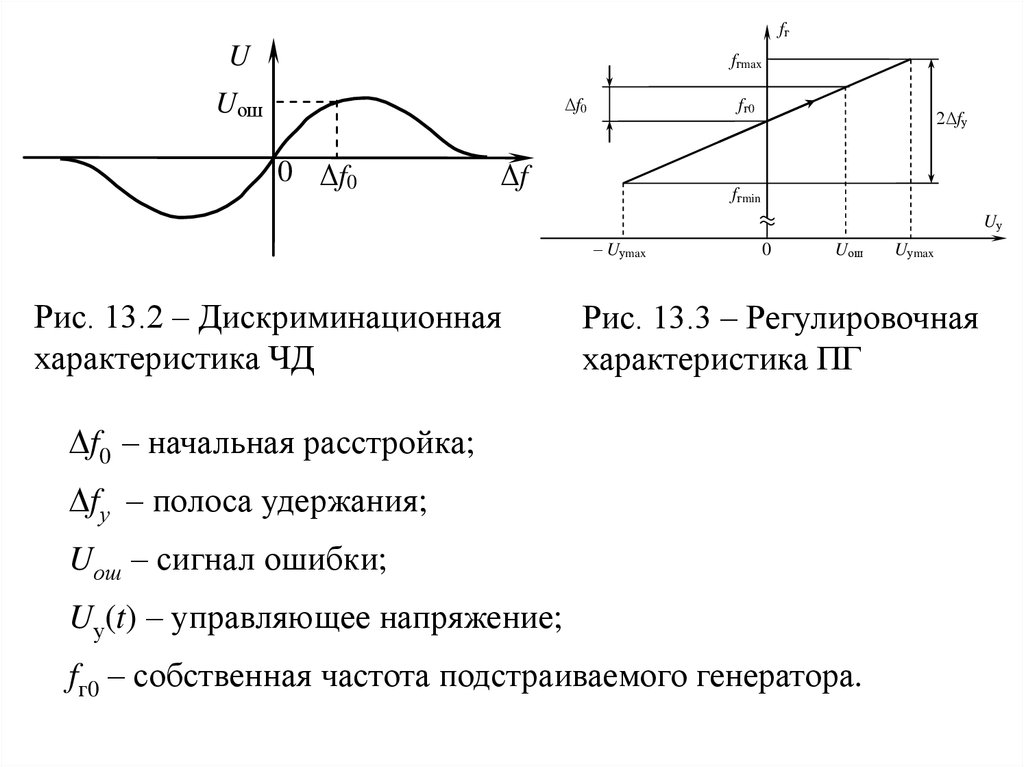
Рис. 13.2 – Дискриминационная
характеристика ЧД
0
Uош
Uуmax
Рис. 13.3 – Регулировочная
характеристика ПГ
f0 – начальная расстройка;
fу – полоса удержания;
Uош – сигнал ошибки;
Uу(t) – управляющее напряжение;
fг0 – собственная частота подстраиваемого генератора.

91.

Тема 4: «Системы фазовой автоподстройки (ФАП)»
Содержание
1. Применение системы ФАП
2.
Функциональная схема системы фазовой автоподстройки
3.
Дискриминационная характеристика фазового дискриминатора
4.
Примеры использования системы ФАП

92.

Применение системы ФАП
• следящие фильтры доплеровских систем измерения скорости;
• стабилизация промежуточной частоты приёмников;
• синхронное детектирование сигналов;
• демодуляторы ЧМ- и ФМ-сигналов;
• синтезаторы частот;
• следящие измерители координат (дальности, угла);
• когерентное сложение сигналов в фазированных антенных
решётках.

93.

Функциональная схема системы фазовой автоподстройки
Uс(t)
ФД
ФНЧ
Uг(t)
Uу(t)
ПГ
Рис. 14.1
ФД – фазовый дискриминатор;
ПГ – подстраиваемый генератор;
ФНЧ – фильтр нижних частот.

94.

Дискриминационная характеристика фазового дискриминатора
U
Umax
φ
–π
π
2
0
π
2
π
–Umax
Рис. 14.2
uc(t)=umcsin c(t)=umcsin( ct+ c0),
uг(t)=umгcos г(t)=umгcos( гt+ г0).

95.

Uд(t)
Δf0 = fс – fг0
t
Uу
а
Uд(t)
Δf0 = fг0 – fс
Uу
б
Рис. 14.3
tз – время захвата;
стационарный режим (режим слежения или удержания) – режим,
при котором частотная расстройка f = 0 ( fс = fг ), фазовый сдвиг
сигнала относительно колебания генератора ст= – /2+ , где –
фазовая ошибка.
t

96.

fг
fгmax
fс+
2Δfу
fг0
fс–
fгmin
Uу
–Uуmax
–Uу–
0
Uу+
Uуmax
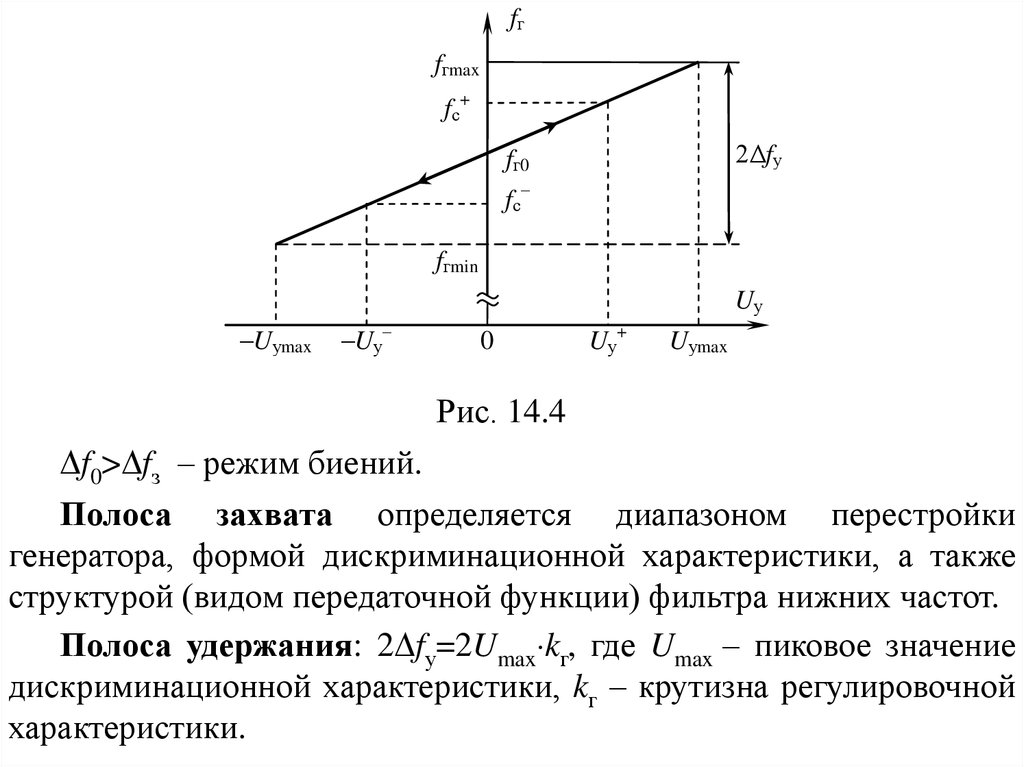
Рис. 14.4
f0> fз – режим биений.
Полоса захвата определяется диапазоном перестройки
генератора, формой дискриминационной характеристики, а также
структурой (видом передаточной функции) фильтра нижних частот.
Полоса удержания: 2 fу=2Umax kг, где Umax – пиковое значение
дискриминационной характеристики, kг – крутизна регулировочной
характеристики.

97.

fг
Режим
биений
Режим
слежения
fг
fс
Режим
биений
Режим
слежения
fг0
fг0
t
0
tз
fс
t
0
tз
а
б
φ
fг
Режим биений
fс
4π
2π
fг0
t
0
t
0
в
г
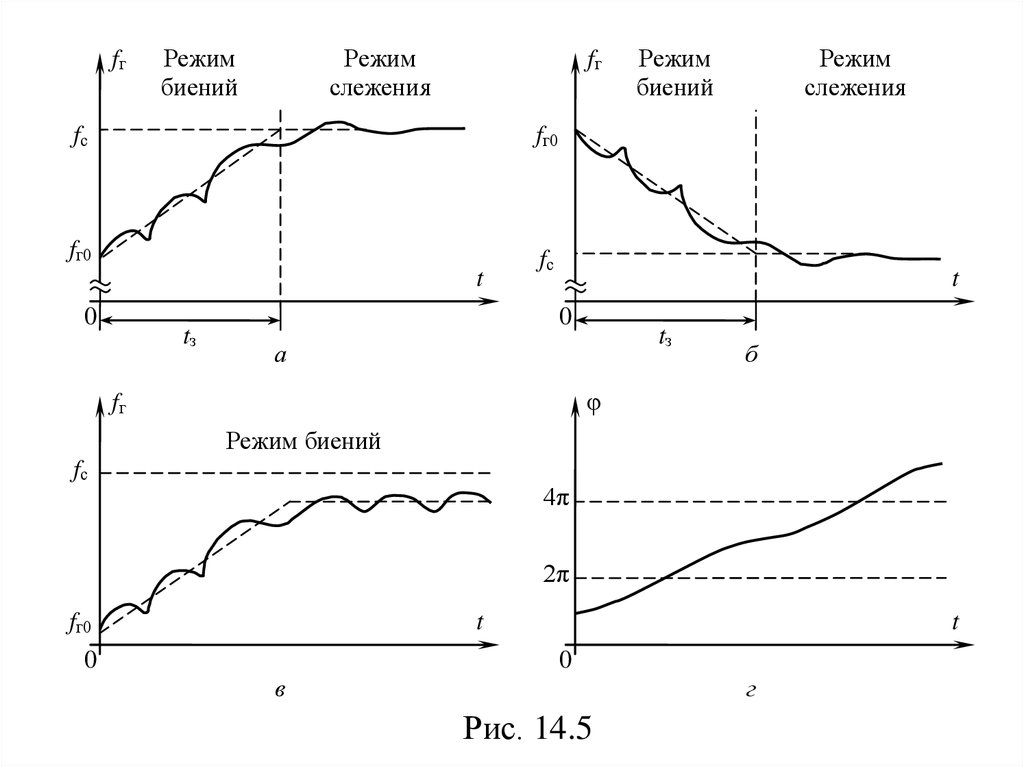
Рис. 14.5

98.

Примеры использования системы ФАП
Uc(t)
См
УПЧ
f0
ФД
f0
Выход АМ
КГ
ФД
Uг(t)
ПГ
ФНЧ
π/2
Рис. 14.6 – Функциональная схема супергетеродинного приёмника
См – смеситель; ПГ – подстраиваемый генератор; УПЧ –
усилитель промежуточной частоты; ФНЧ – фильтр нижних частот;
ФД – фазовый дискриминатор; КГ – кварцевый генератор.
Следящий фильтр на базе системы ФАП: выход фильтра – выход
подстраиваемого генератора.

99.

Линейная модель системы ФАП
Линейная аппроксимация дискриминационной характеристики:
U( ) kд
( << ).
kд – крутизна дискриминационной характеристики в точке =0,
[рад/В];
K(p)=kг KФ(p) – передаточная функция ФНЧ и ПГ;
с и г – фазовые сдвиги сигнала и колебания генератора,
обусловленные отклонениями частот относительно номинального
значения fс0 =fг0.
n(t)
φ
kд
K(p)
φг
Рис. 14.7

100.

Тема 5: «Системы слежения за задержкой
сигнала (ССЗ)»
Содержание
1. Дискриминационная характеристика временного
дискриминатора
2. Временной дискриминатор
3. Формирование дискриминационной характеристики
4. Структурная схема системы слежения за задержкой

101.

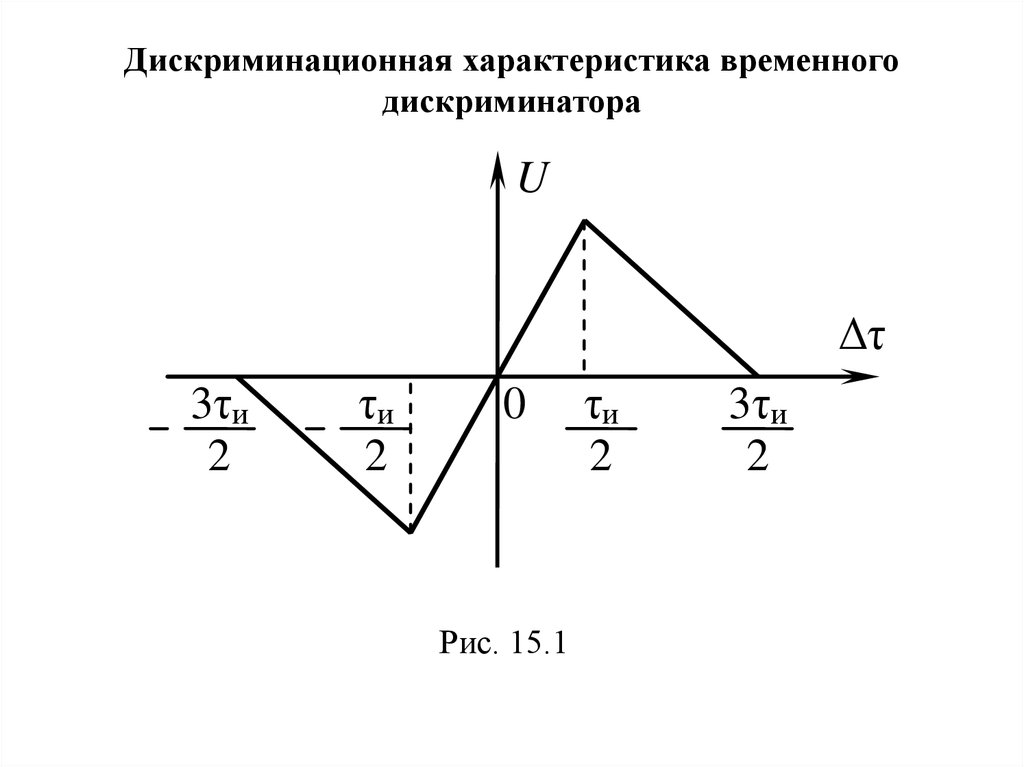
Дискриминационная характеристика временного
дискриминатора
U
Δτ
3τи
2
τи
2
0
Рис. 15.1
τи
2
3τи
2

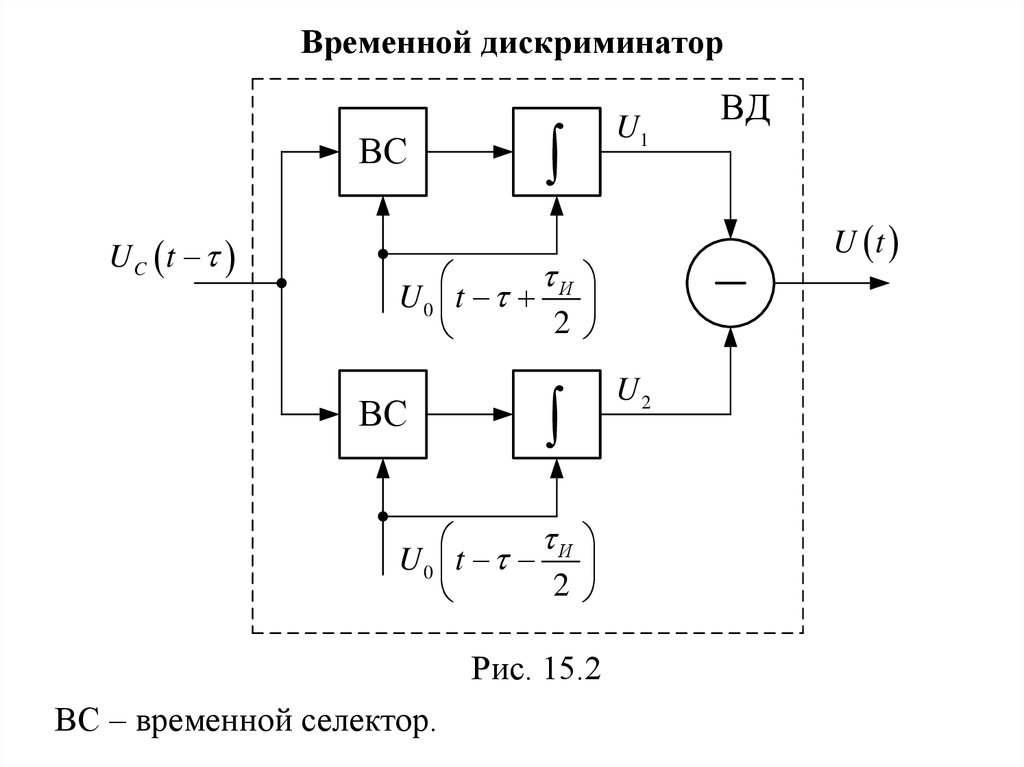
102.

Временной дискриминатор
ВС
UC t
U1
U t
И
U0 t
2
ВС
И
U0 t
2
Рис. 15.2
ВС – временной селектор.
ВД
U2

103.

Формирование дискриминационной характеристики
U1
U2
а
б
U
0
в
Рис. 15.3
U1, U2 – выходные напряжения
каналов 1 и 2.
τ – временное рассогласование.

104.

Структурная схема системы слежения за задержкой
Временное рассогласование
Δτ=τ τˆ
(15.1)
Выходное напряжение дискриминатора
U д (t ) U ( τ) n(t , τ)
(15.2)
где U ( τ) – полезная составляющая; n(t , τ) – помеха.
Зависимость управляющего напряжения
Uу(t)=Kф(p)Uд(t),
где KФ(p) – передаточная функция ФНЧ.
(15.3)

105.

Регулировочная характеристика схемы управляемой задержки
ˆ t ) τˆ 0 kpU y (t )
τ(
(15.4)
где τˆ 0 – значение задержки Uу=0,
kp
dτˆ (U y )
dU y
U y 0
– крутизна регулировочной характеристики
(коэффициент передачи СУЗ, имеющая размерность мкс/В.
Аппроксимиация зависимости U( ) при малых рассогласованиях
U ( τ) kд τ
где
dU ( τ)
kд
d ( τ )
τ 0
(15.5)

106.

n(t,Δτ)
τ
Δτ
Kф(p)
U(Δτ)
τ
kp
τ0
К(p)=kPKФ(p)
–
передаточная
функция,
описывающая
схему управляемой
задержки и ФНЧ.
Рис. 15.4
n(t)
τ
Δτ
kд
τ
Рис. 15.5
K(p)
Линейная модель
ССЗ позволяет
решать задачи
определения запаса
устойчивости,
быстродействия,
точности.

107.

Тема 6: «Системы слежения за направлением прихода
сигналов (ССН)»
Содержание
1. Амплитудный пеленгатор, использующий суммарноразностный метод пеленгования.
2. Структурная схема ССН

108.

Амплитудный пеленгатор, использующий суммарноразностный метод пеленгования.
Uс(t)
Пр
А
АРУ
О1
2d
УД
Uсn(t)
ВМ
Гет
ФД
О2
Uр(t)
Ред
Пр
Uрn(t)
Ид
Uу
У
Рис. 16.1
О1 и О2 – облучатели; ВМ – волноводный мост; uc(t), uр(t) –
суммарный и разностный сигналы; ФД – фазовый детектор; ucп(t)
– опорное колебание; РСН – равносигнальное направление; ИД –
исполнительный двигатель; Uу – управляющее напряжение.

109.

Диаграмма направленности
антенны
Дискриминационная
характеристика
U
Направление
на цель
f2(α)
Umax
α
РСН
α=0
kдα
α
0
0,1Umax
αц
Направление
на Север
αц
f1(α)
а
2Δα
б
Рис. 16.2
f1( ) и f2( ) – парциальные диаграммы; – угловое
рассогласование; D/ – относительный размер антенны (D –
диаметр отражателя, – длина волны).

110.

Угловое рассогласование
α α ц αˆ ц
(16.1)
где ц – азимут (пеленг) цели, αˆ ö – оценка азимута.
Напряжение на выходе УД (углового дискриминатора)
Uд(t)=U( )+n(t, ),
(16.2)
где U( ) –дискриминационная характеристика; n(t, ) – помеха.
U( )=kфUpп(t, )Ucп(t).
U cп U 0 const(α),
U pп
U0
U p (α)
U c (α)
U0
f p (α)
f c (α)
(16.3)
.
(16.4)
U0 – амплитуда сигнала на выходе суммарного канала; Up( ) и
Uc( ) – зависимости амплитуды сигнала на входе от
соответственно для разностного и суммарного каналов; fp( )=f2( ) –
f1( ) и fc( )=f1( )+f2( ).

111.

U (α) kфU
2
0
f p (α)
f c (α)
(16.5)
Управляющее напряжение
Uу(t)=kуUд(t),
(16.6)
d д (t )
Tд
д (t ) kдU y (t )
dt
где д(t) – управляемая переменная (скорость вращения ротора
двигателя); kд – коэффициент передачи, рад/сВ; Тд – постоянная
времени.
д (t ) K д ( p)U у (t )
(16.7)
kид
где K д ( p)
1 Tд p
kp
(16.8)
αˆ ц (t )
д (t )
p
где kP – коэффициент передачи редуктора (интегрирующего звена).
U (α) n(t , α)
ˆαц (t ) k у kp K д ( p)
(16.9)
p

112.

Структурная схема ССН
n(t,α)
αц
α
n(t)
αц
α
U(α)
αц
αц
kp/p
Kд(p)
а
K ( p)
kд
k у kp K д ( p )
p
kу
Рис. 16.3
K(p)
б
. Линейная модель ССН: задачи определения запаса
устойчивости, качества переходного процесса (быстродействия,
перерегулирования), точности слежения.