Похожие презентации:
Устойчивость узла нагрузки
1. Устойчивость узла нагрузки
12. Статическая и динамическая устойчивость
Статическая устойчивость ???Устойчивость в малом. Устойчивость при малых
возмущениях. Применительно к ЭЭС, статическая
устойчивость - это способность электроэнергетической
системы восстанавливать исходное состояние (режим)
после малых его возмущений.
Динамическая устойчивость ???
Устойчивость в большом. Устойчивость при больших
возмущениях. Применительно к ЭЭС, динамическая
устойчивость - это способность электроэнергетической
системы восстанавливать исходное состояние (режим)
после больших возмущений.
2
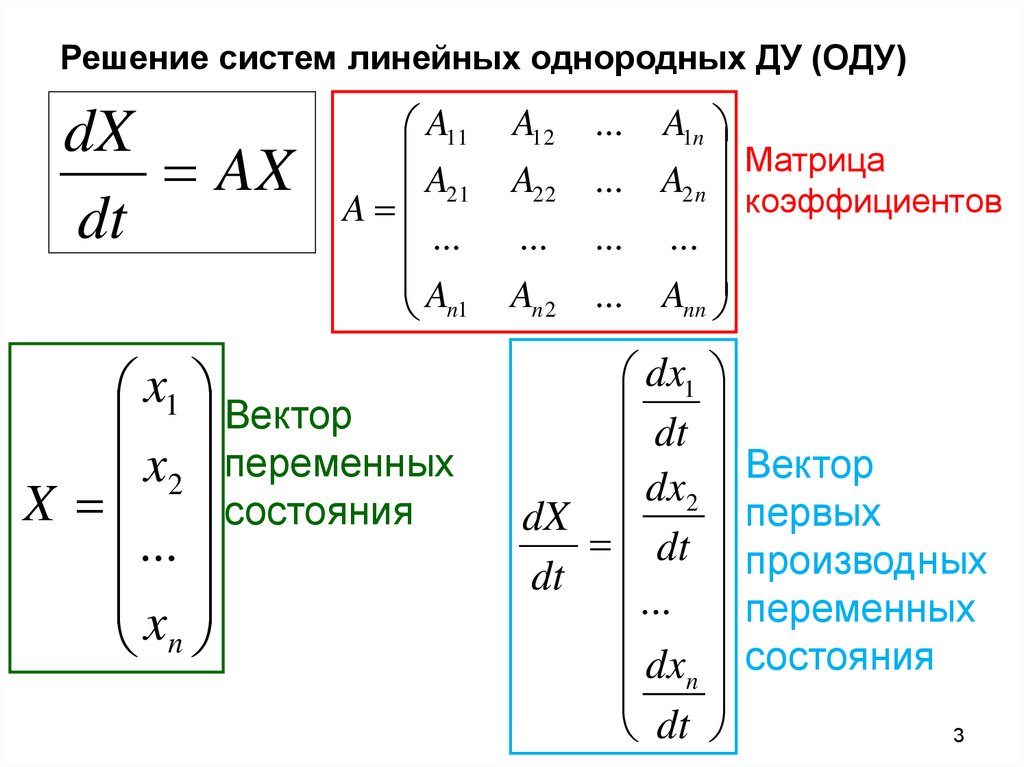
3. Решение систем линейных однородных ДУ (ОДУ)
dXAX
dt
A11
A21
A
...
A
n1
x1 Вектор
x2 переменных
X состояния
...
x
n
A12
A22
...
An 2
A1n
Матрица
... A2 n
коэффициентов
... ...
... Ann
...
dx1
dt
dx2
dX
dt
dt
...
dx
n
dt
Вектор
первых
производных
переменных
состояния
3
4. Решение систем линейных ОДУ
dXAX
dt
Решение системы ОДУ ищется в следующем виде:
n
X Nie
i 1
( λi ) t
N1e
( λ1 ) t
N 2e
( λ2 ) t
... N n e
( λn ) t
λ собственные числа
N -собственные вектора
4
5. Собственные числа и вектора
• Собственный вектор матрицы – вектор,умножение матрицы на который дает тот же
вектор, умноженный на некоторое число,
называемое собственным числом матрицы.
• A – матрица ОДУ;
• N – собственный вектор;
• λ – собственное число.
1 6 2
2
2 • [-1 -6; 2 6] – матрица;
6 1
2
1
• [-2;1], [-3;2] –
1 6 3 3
собственные вектора;
3
6 2 2 • 2 и 3 – собственные числа.
2
AN λN
5
6. Поиск собственных чисел и векторов
AN λNA Eλ N 0
det A Eλ 0
A – матрица ОДУ;
N – собственный вектор;
λ – собственное число.
E – единичная матрица
6
7. Решение систем линейных ОДУ
x t Neλt
x t Ne
t i t
λ ,
λ ,
λ 0.
0.
λ ,
λ ,
λ 0.
0.
t i t
Ne
7
8. Устойчивость системы линейных ОДУ
• Линейная система устойчива, если всесобственные числа имеют отрицательные
действительные части.
• Линейная система неустойчива, если хотя
бы одно собственное число имеет
положительную действительную часть.
• Состояние линейной системы не
определено, если одно или более
собственных чисел имеют действительную
часть равную нулю, а все остальные
собственные числа имеют отрицательные
действительные части.
8
9. Анализ устойчивости системы нелинейных ДУ
dXAX
dt
dX
dt
f1 X 0
x1
f X
f X 0 2 0
x1
X
...
f n X 0
x
1
dX
f X
dt
f X 0
X
f1 X 0
x2
f 2 X 0
x2
...
f n X 0
x2
X
f1 X 0
xn
f 2 X 0
...
xn
...
...
f n X 0
...
xn
...
Матрица Якоби
Якобиан
9
10. Устойчивость системы НЕлинейных ДУ
• Если все собственные значенияякобиана имеют отрицательные действительные
части, то нулевое решение X = 0 исходной системы
и линеаризованной является устойчивым.
• Если хотя бы одно собственное значение
якобиана имеет положительную действительную
часть, то нулевое решение X = 0 исходной системы
и линеаризованной системы вляется неустойчивым.
10
11. Реактивная нагрузка узла
• Пренебрегая зависимостью реактивноймощности от частоты (Kqf=0), а также
полагая, что β=0 (Q=const), получим:
dV
QG K qf f K qu V Tqu
dt
dV
dV
QG K qu K quTqu
QL
dt
dt
dV 1
QG QL
dt
11
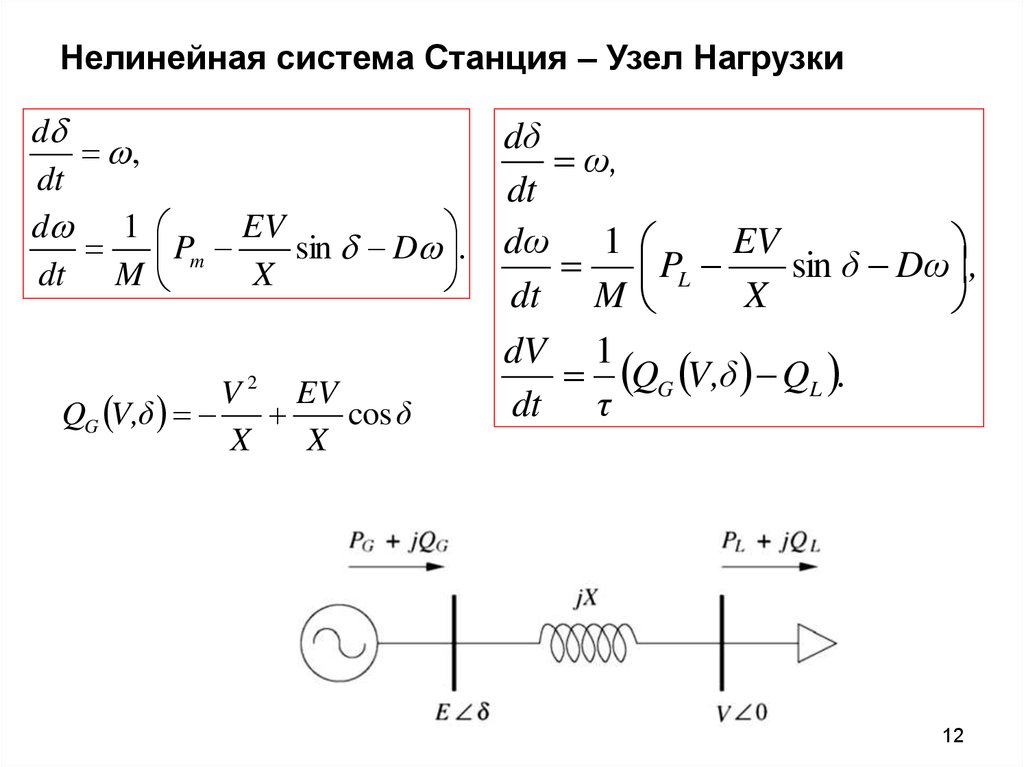
12. Нелинейная система Станция – Узел Нагрузки
d,
dt
d 1
dt M
dδ
ω,
dt
EV
dω
1
EV
P
sin
D
m
.
P
sin
δ
Dω
L
,
X
dt M
X
dV 1
QG V,δ QL .
V 2 EV
dt τ
QG V,δ
cos δ
X
X
12
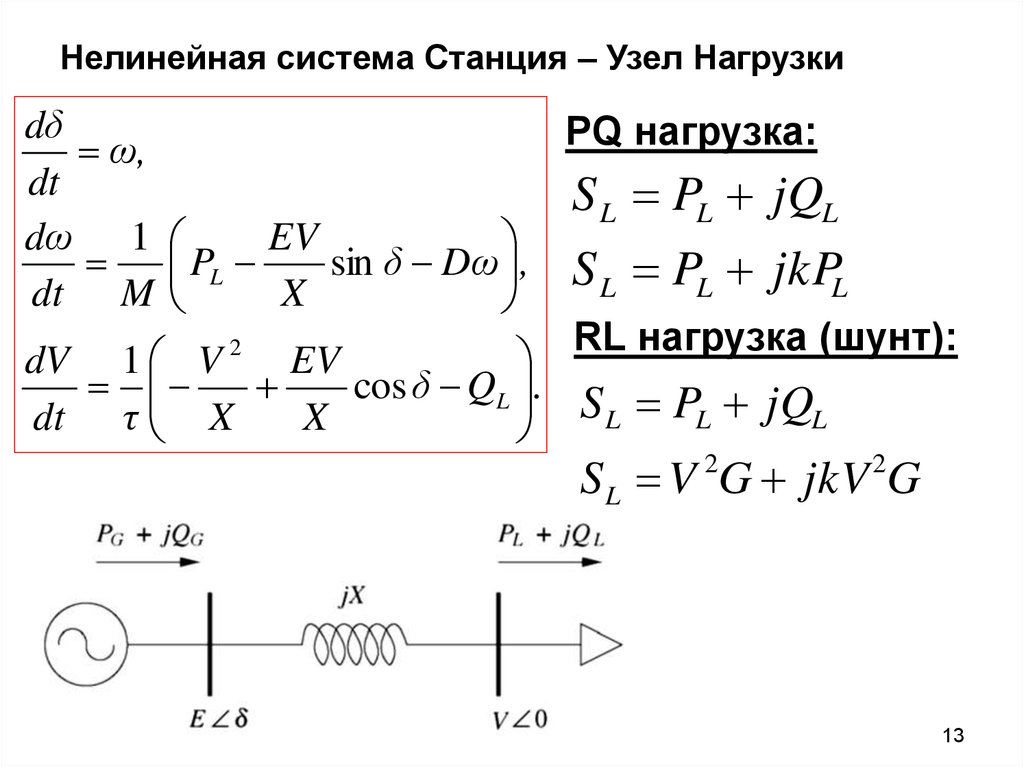
13. Нелинейная система Станция – Узел Нагрузки
dδPQ нагрузка:
ω,
dt
S L PL jQL
dω 1
EV
sin δ Dω , S P jkP
PL
L
L
L
dt M
X
RL нагрузка (шунт):
2
dV 1 V
EV
cos δ QL . S P jQ
L
L
L
dt τ X
X
S L V 2G jkV 2G
13
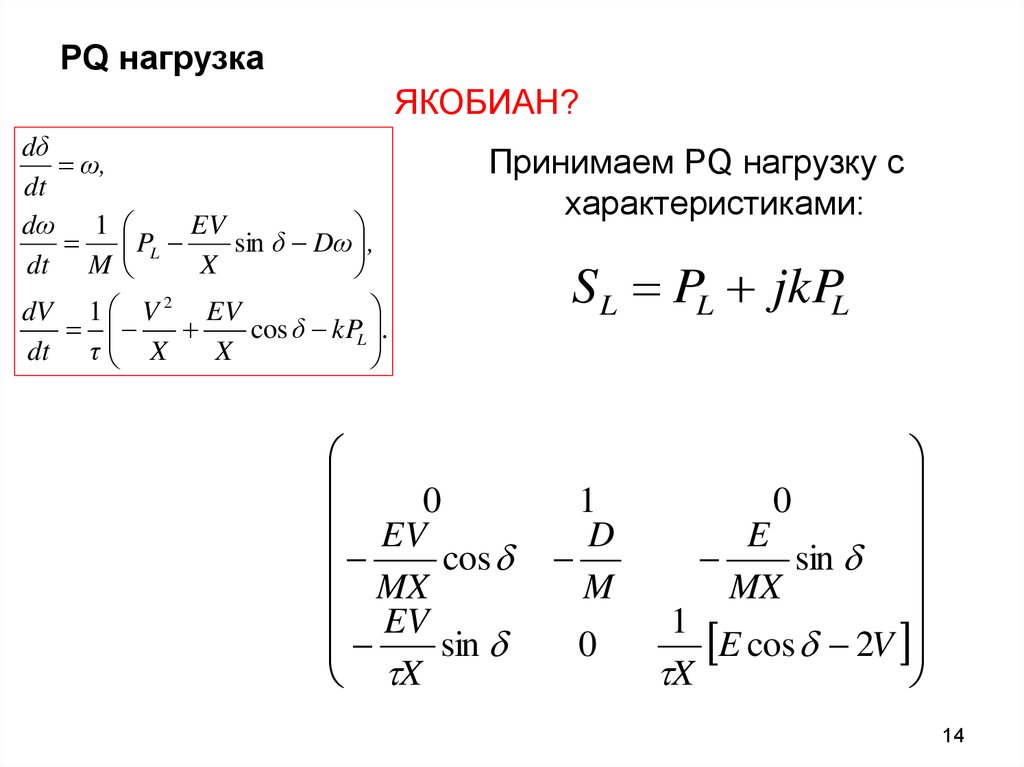
14. PQ нагрузка
ЯКОБИАН?dδ
ω,
dt
dω 1
EV
sin δ Dω ,
PL
dt M
X
Принимаем PQ нагрузку с
характеристиками:
dV 1 V 2 EV
cos δ kPL .
dt τ X
X
0
EV cos
MX
EV
sin
X
S L PL jkPL
1
D
M
0
0
E
sin
MX
1
E cos 2V
X
14
15. Исследование системы уравнений. Поиск предельной точки.
Поиск предельной точки ведется, как и при исследованиипараллельной устойчивости, путем последовательного
увеличения нагрузки приемной системы.
Параметры системы:
M0=0.1; D0=0.1; X0=0.5; E0=1; tau0=0.001;k0=0.5;
Предельные значения:
omega0=0; delta0=0.5535; V0=0.5877; P=0.61805
ОБРАТИТЕ ВНИМАНИЕ: (SL=0.618+j*0.5*0.618)
Каковы критерии предельного режима????
15
16. Исследование системы уравнений. Поиск предельной точки.
Необходимые и достаточные условия?1. Условие необходимое, но недостаточное.
Должно существовать решение системы
нелинейных алгебраических уравнений.
0 ω,
1
0
M
EV
sin δ Dω ,
PL
X
1 V 2 EV
0
cos δ kPL .
τ X
X
2. Необходимое и
достаточное:
выполнение
условия 1, а
также:
Re 0
16
17. Поиск предельной точки. Метод деления (шага) пополам.
1. Выполняем расчеты для некоторого исходногозначения мощности нагрузки P0.
2. Задаем некоторую величину шага dP.
3. Выполняем расчет для следующей точки
Pn=P(n-1)+dP. (На первом шаге P(n-1)=P0).
4. Если решение существует, то при неизменном
dP переходим к расчету следующей точки
(пункт 3).
5. Если решение не существует, то принимаем
dP=dP/2 и аналогично переходим к расчету
следующей точки (пункт 3).
6. Каков критерий остановки?
17
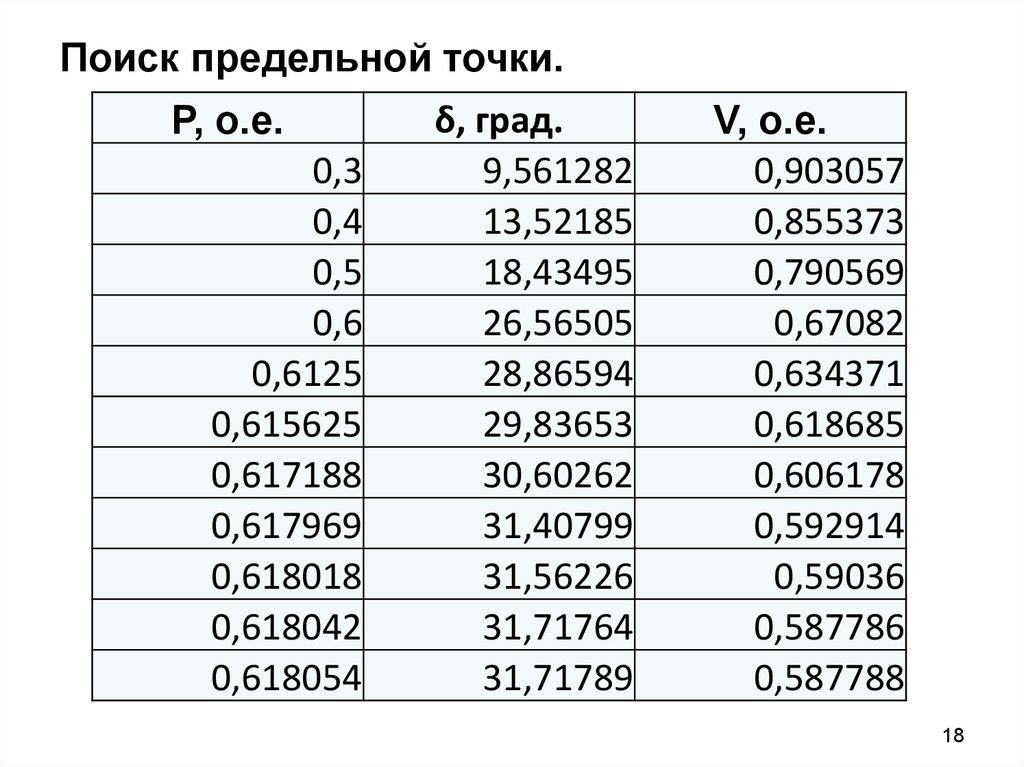
18. Поиск предельной точки.
P, о.е.0,3
0,4
0,5
0,6
0,6125
0,615625
0,617188
0,617969
0,618018
0,618042
0,618054
δ, град.
9,561282
13,52185
18,43495
26,56505
28,86594
29,83653
30,60262
31,40799
31,56226
31,71764
31,71789
V, о.е.
0,903057
0,855373
0,790569
0,67082
0,634371
0,618685
0,606178
0,592914
0,59036
0,587786
0,587788
18
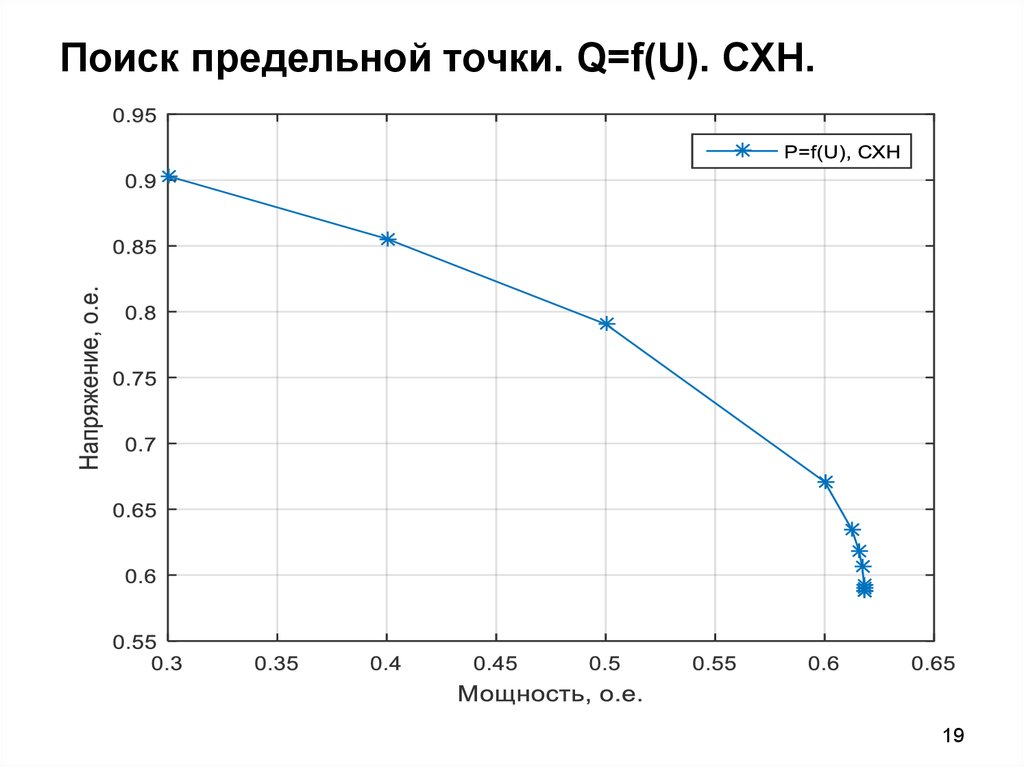
19. Поиск предельной точки. Q=f(U). СХН.
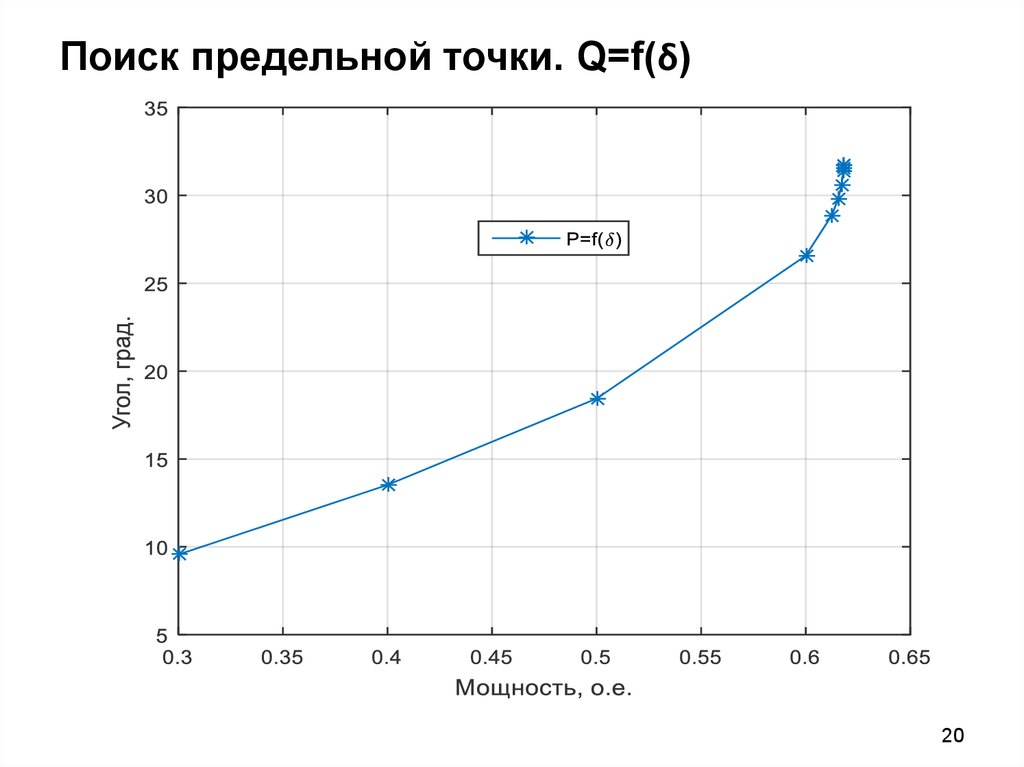
1920. Поиск предельной точки. Q=f(δ)
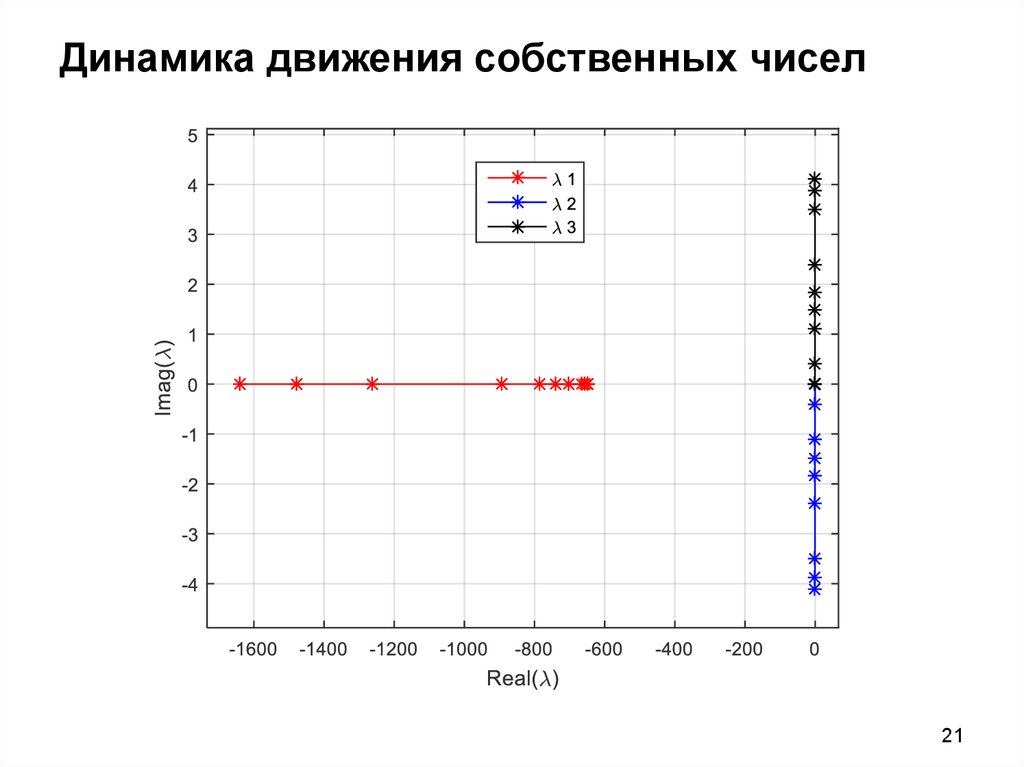
2021. Динамика движения собственных чисел
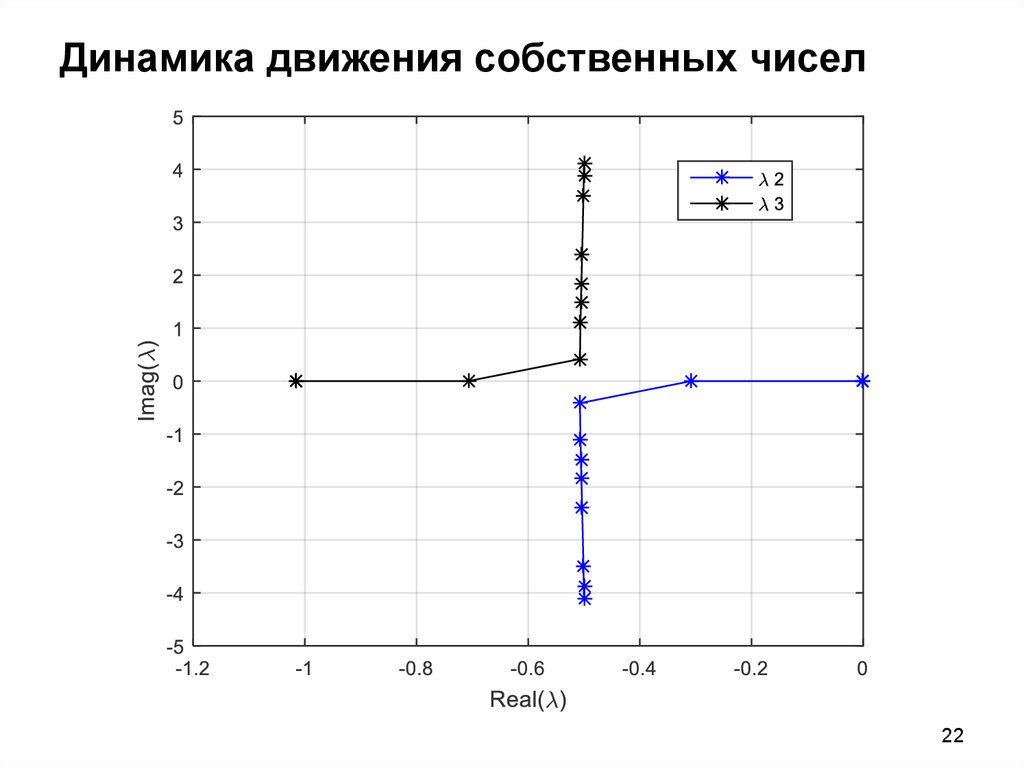
2122. Динамика движения собственных чисел
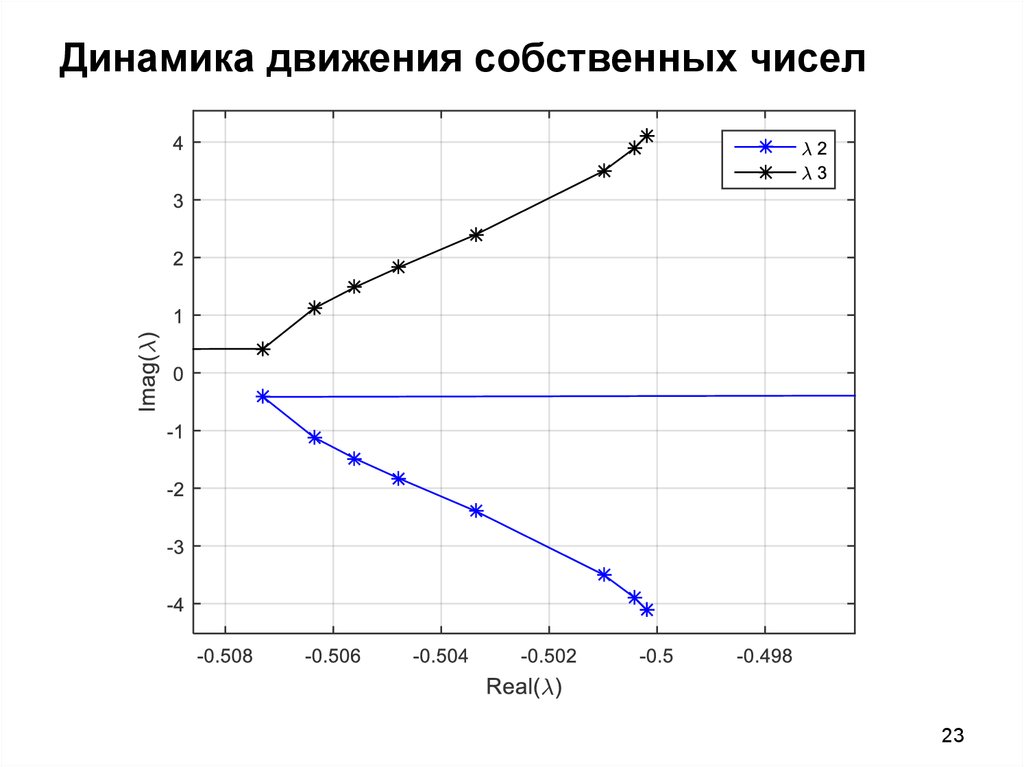
2223. Динамика движения собственных чисел
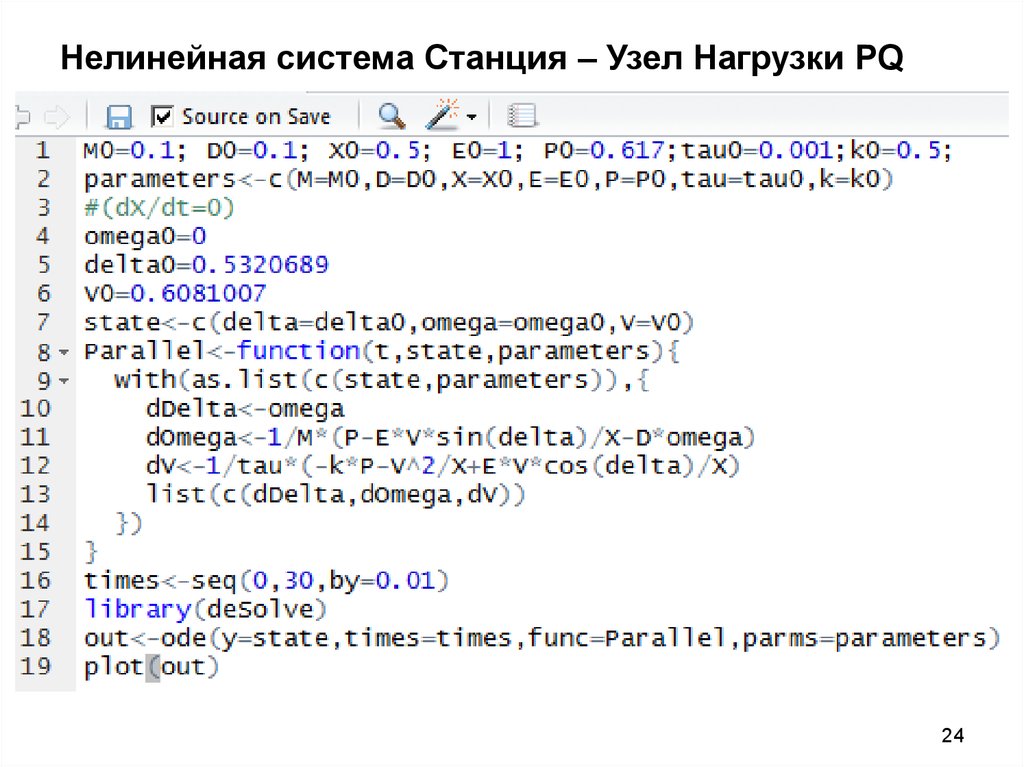
2324. Нелинейная система Станция – Узел Нагрузки PQ
2425. Задание на понедельник!!!
Записать Якобиан для шунтовой нагрузки!Система нелинейных уравнений:
dδ
ω,
dt
dω 1
dt M
EV
2
sin δ Dω ,
V G
X
dV 1 V 2 EV
2
cos δ kV G .
dt τ X
X
25














 Математика
Математика








