Похожие презентации:
Особенности расчета прямозубых конических передач
1.
ОСОБЕННОСТИ РАСЧЕТАПРЯМОЗУБЫХ
КОНИЧЕСКИХ ПЕРЕДАЧ
Разработал: доцент каф. 202
Ковеза Юрий Владимирович
ауд. 227 МК
khai202.ho.ua
Лектор: ассистент каф. 202
Светличный Сергей Петрович
ауд. 246
2.
Содержание лекции:1. Общие положения.
2. Геометрические параметры конического колеса.
3. Осевая форма зуба.
3. Силы действующие в зацеплении.
4. Проектировочный расчет.
5. Проверочный расчет на прочность.
3.
Общие положенияКонические передачи имеют большие габариты,
массу, сложнее в изготовлении и монтаже (надо
выдерживать и регулировать зазор), но без них
не обойтись при необходимости передать
движение с поворотом.
4.
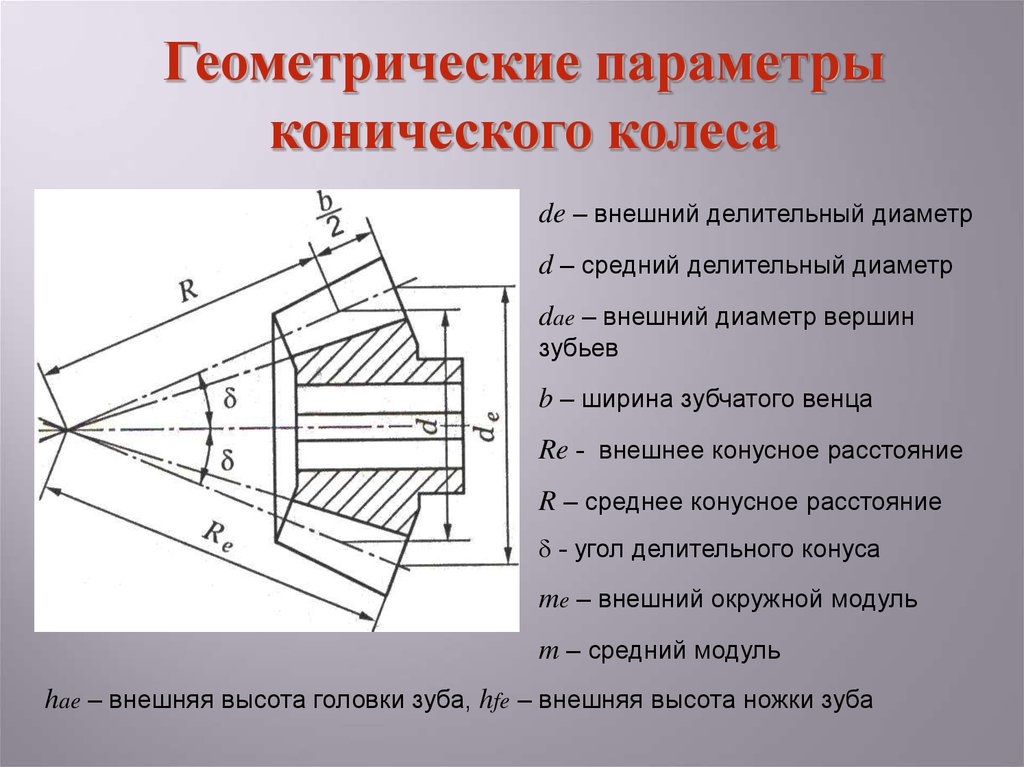
Геометрические параметрыконического колеса
de – внешний делительный диаметр
d – средний делительный диаметр
dae – внешний диаметр вершин
зубьев
b – ширина зубчатого венца
Re - внешнее конусное расстояние
R – среднее конусное расстояние
- угол делительного конуса
me – внешний окружной модуль
m – средний модуль
hae – внешняя высота головки зуба, hfe – внешняя высота ножки зуба
5.
Осевая форма зубаПрименяют три формы зуба:
1 – пропорционально понижающийся зуб, конусы
делительный и впадин имеют одну вершину. Единственная
форма для прямых зубьев.
2 – толщина зуба по делительному конусу увеличивается
пропорционально расстоянию от вершины, вершины
делительного и впадин не совпадают, ширина дна впадины
одинакова. Используют в круговых и тангенциальных.
3 – все три конуса параллельны.
6.
Осевая форма зуба7.
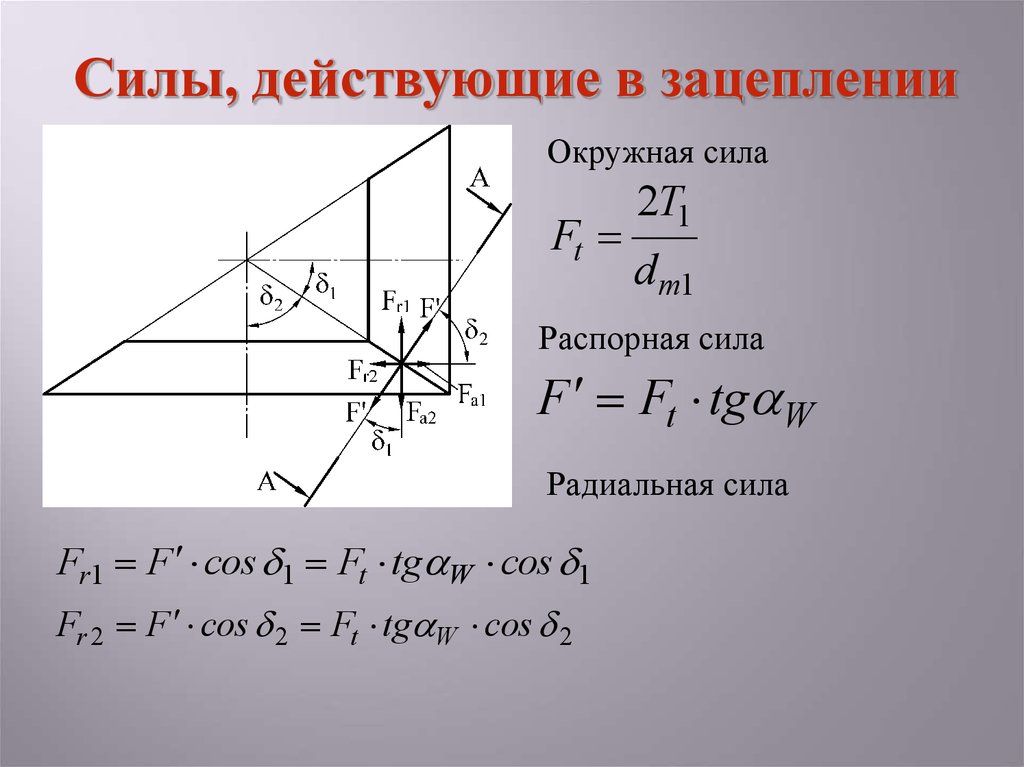
Силы, действующие в зацепленииОкружная сила
Ft
2T1
d m1
Распорная сила
F Ft tg W
Радиальная сила
Fr1 F cos 1 Ft tg W cos 1
Fr 2 F cos 2 Ft tg W cos 2
8.
Силы, действующие в зацепленииОсевая сила
Fa1 F sin 1 Ft tg W sin 1
Fa 2 F sin 2 Ft tg W sin 2
Ft
Нормальная сила Fn
cos W
Допускаем, что нагрузка равномерно распределяется по длине
зуба. Заменяем ее равнодействующей, приложенной в
среднем сечении зуба.
9.
Проектировочный расчет1. Делительный диаметр шестерни на внешнем торце
d e1 K d
Кd = 1013
K be
Re
H ( 1 kbe )kbe 2H u
- вспомогательный коэффициент
1 2
bW
3
T1 K H sin
- межосевой угол передачи
- коэффициент ширины зубчатого венца
относительно внешнего конусного расстояния
H - коэффициент, учитывающий форму зуба
10. Проектировочный расчет
2. Окружной модуль на внешнем торце- принимают равным не более 10
11.
Проектировочный расчетd e1
1. Определяют окружной модуль на торце: mte
z1
2. Определяют число зубьев колеса: z2 z1u12
Если z 2 дробное, то его округляют до ближайшего целого и
уточняют передаточное отношение.
3. Пересчитывают делительные диаметры:
de1 mte z1 de 2 mte z2
zc z12 z22
4. Находят число зубьев плоского колеса
( с точностью до трех знаков после запятой)
5. Рассчитывают внешнее конусное расстояние Re 0.5mte zc
6. Определяют ширину венца и округляют до целого
b kbe Re
7. Пересчитывают величину kbe b / Re
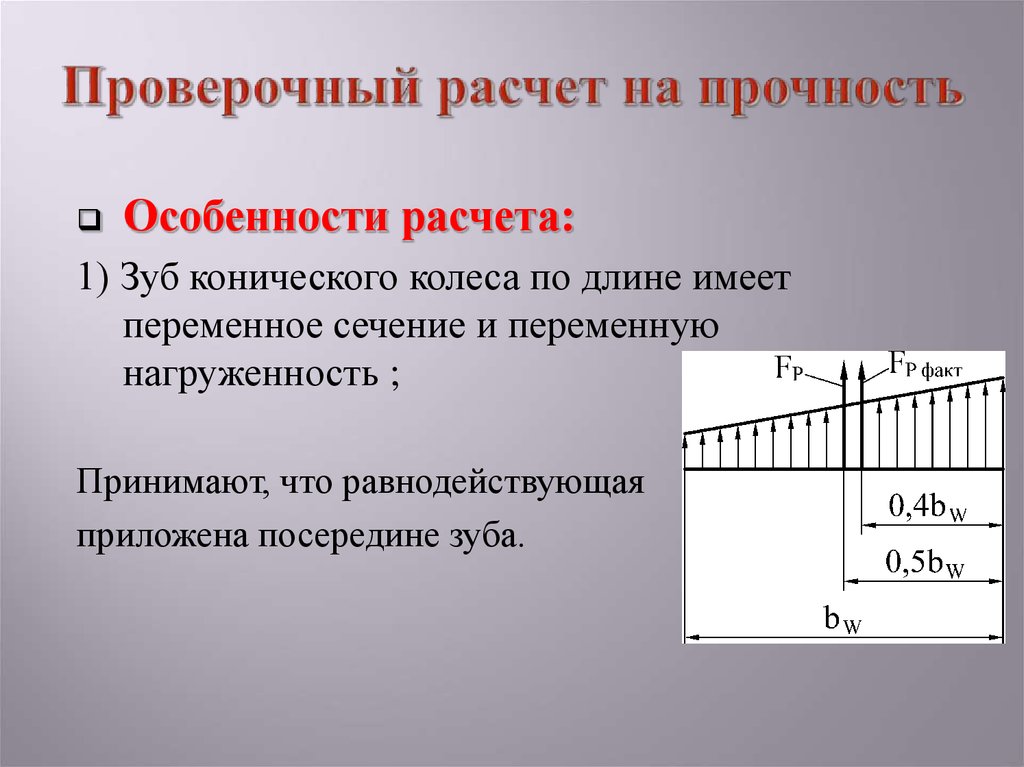
12. Проверочный расчет на прочность
Особенности расчета:1) Зуб конического колеса по длине имеет
переменное сечение и переменную
нагруженность ;
Принимают, что равнодействующая
приложена посередине зуба.
13.
Проверочный расчет на прочность2) При расчетах на прочность конические колеса
заменяют эквивалентными цилиндрическими,
диаметры начальных окружностей и модуль
которых равны диаметрам начальных окружностей
и модулю в среднем сечении зубьев конических
колес.
Эквивалентные колеса получают разворачиванием
дополнительных конусов на плоскость.
Диаметры эквивалентных колес:
dV 1
dm1
cos 1
dV 2
d m2
cos 21
cos 1
u
2
u 1
cos 2
1
u2 1
14.
Проверочный расчет на прочность15. Проверочный расчет на прочность
Окружная сила:d e 1 1 0 ,5 K be d m 1
Ft
2T1
d e1 1 0,5Kbe
K be
bW
Re
Контактные напряжения:
H 32240
T1 K H sin
[ H ]
3
d e 1 ( 1 kbe ) kbe u H
H 1 для прямозубых передач без модификации
H 1,16 – с модификацией
H 1, 5 – для круговых зубьев
16.
Проверочный расчет на прочностьПри определении K Hv в формулу вместо a w
следует подставить величину d1 u 1
K H определяют по графикам в зависимости от
kbe u / 2 kbe
Расчет зубьев конических колес на изгиб аналогичен
цилиндрическим колесам:
F
1
2280T1 K F
YFS1 F 1
bw me
F
2
F
1
YFS 1
YFS 2 F













 Механика
Механика








