Шар, вписанный в цилиндр и конус

1.

называется
(а
), если шар касается основания
конуса и каждой его образующей.
В прямой круговой конус всегда
можно вписать шар
Центр вписанного в конус шара
лежит на высоте конуса.

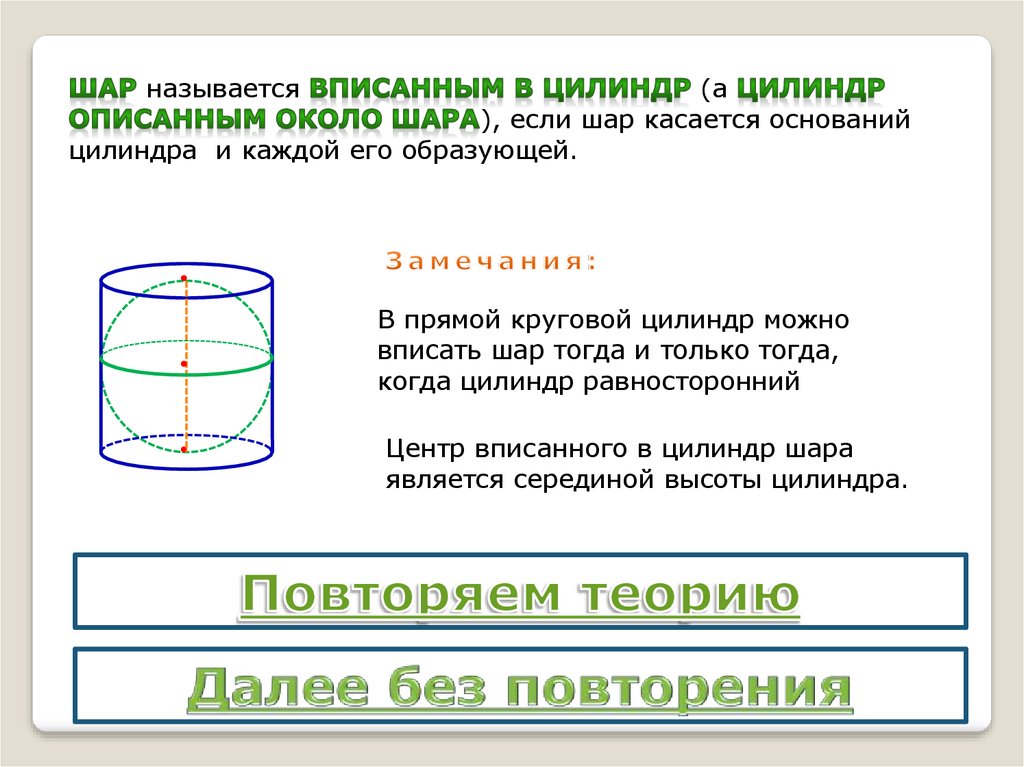
2.

называется
(а
), если шар касается оснований
цилиндра и каждой его образующей.
В прямой круговой цилиндр можно
вписать шар тогда и только тогда,
когда цилиндр равносторонний
Центр вписанного в цилиндр шара
является серединой высоты цилиндра.

3.

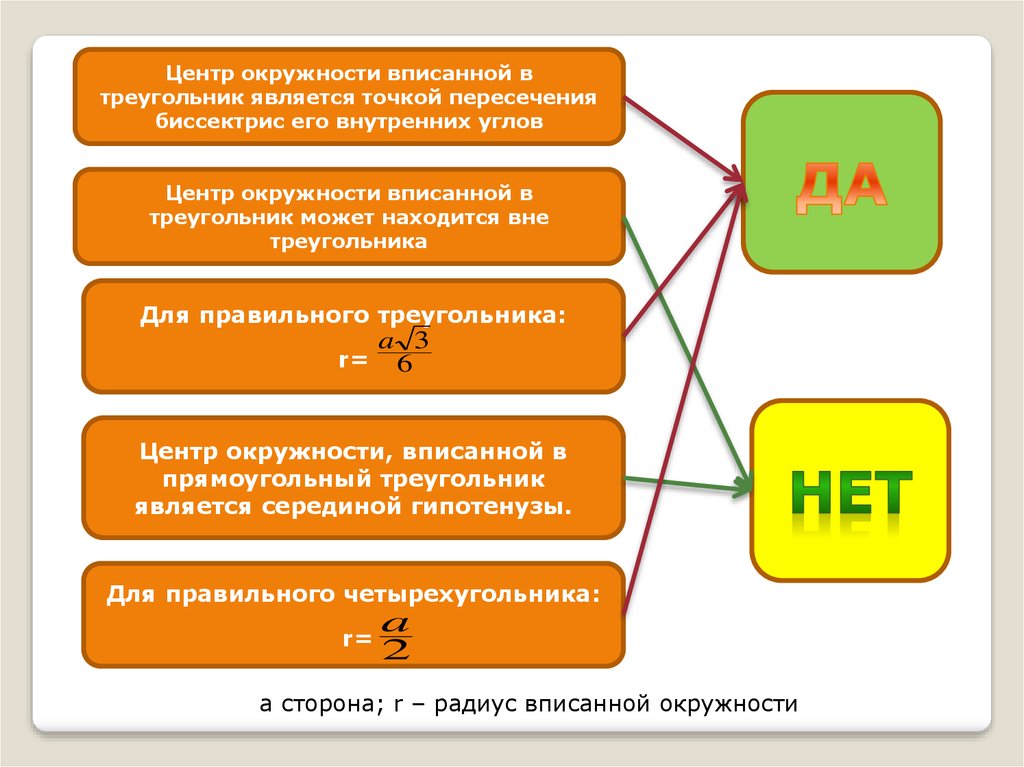
Центр окружности вписанной в
треугольник является точкой пересечения
биссектрис его внутренних углов
Центр окружности вписанной в
треугольник может находится вне
треугольника
Для правильного треугольника:
r=
a 3
6
Центр окружности, вписанной в
прямоугольный треугольник
является серединой гипотенузы.
Для правильного четырехугольника:
r=
a
2
a сторона; r – радиус вписанной окружности

4.

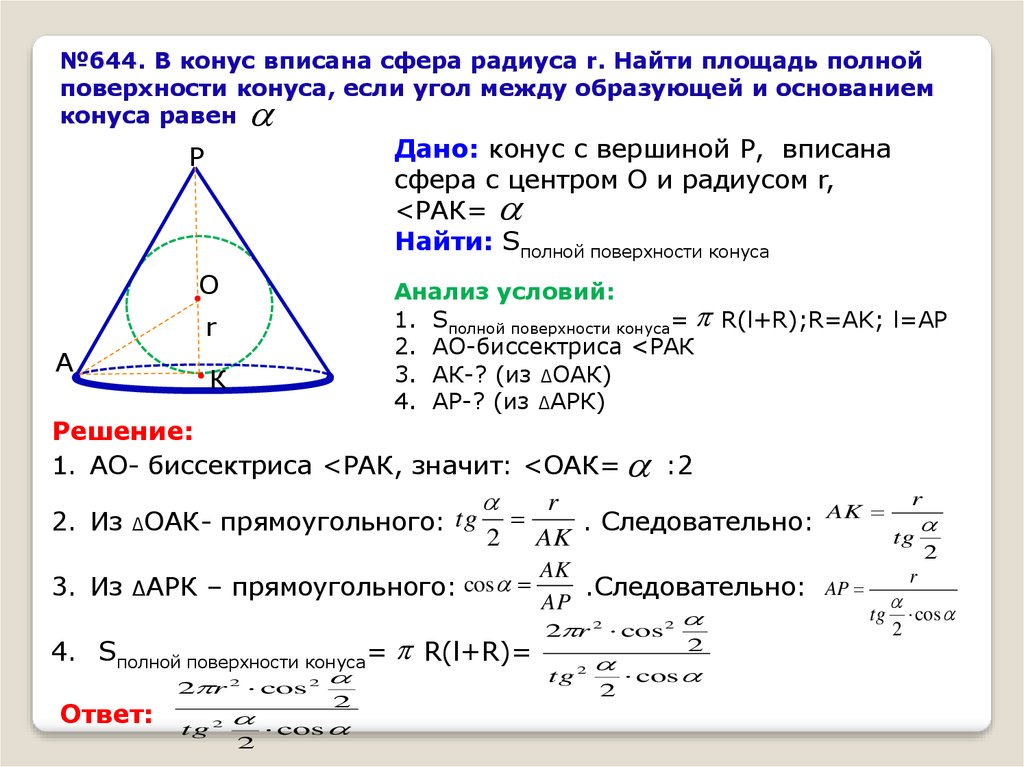
№644. В конус вписана сфера радиуса r. Найти площадь полной
поверхности конуса, если угол между образующей и основанием
конуса равен
Дано: конус с вершиной Р, вписана
сфера с центром О и радиусом r,
<РАК=
Найти: Sполной поверхности конуса
Р
О
Анализ условий:
1. Sполной поверхности конуса= R(l+R);R=AK; l=AP
2. AO-биссектриса <РАК
3. АК-? (из ∆ОАК)
4. АР-? (из ∆АРК)
r
А
К
Решение:
1. АО- биссектриса <РАК, значит: <ОАК= :2
r
tg
2. Из ∆ОАК- прямоугольного:
. Следовательно:
2 AK
r
AK
tg
2
AK
r
3. Из ∆АРК – прямоугольного: cos
.Следовательно: AP
AP
tg cos
2
2
4. Sполной поверхности конуса=
Ответ:
2 r
tg
2
2
cos
2
2
2
cos
R(l+R)=
2 r
tg 2
cos
2
2
cos
2

5.

№642. Сфера вписана в цилиндр. Найти отношение площади
сферы к площади полной поверхности цилиндра.
Дано: цилиндр, вписана сфера с
центром
О
sсферы
Найти:
sпол ной
пов ерхности
цил индра
Анализ условий:
1. Sсферы= 4 R
2
2. Sполной поверхности цилиндра =
Решение:
2 R( R H )
3. H=2R
2
1. Sсферы= 4 R
2. Sполной поверхности цилиндра =
2 R( R H )
3. Т.к. сфера вписана, то Н=2R. Следовательно:
sсферы
sполной
поверхности
2
Ответ: 3
4 R 2
2
2 R( R 2 R) 3
цилиндра

6.

7.

1. Геометрия: Учебник для 10-11 классов средней школы/
Л.С. Атанасян и др.-М.:Просвещение, 1994
2. Зив Б.Г. И др. Задачи по геометрии для 7-11 классов /Б.Г.
Зив, В.М. Мейлер, А.Г. Баханский.-М.:Просвещение, 1991
3. Фотография футбольного мяча, размещенная на слайде 6:
http://www.realbrest.by/images/2(28).jpg