Техническая термодинамика. Законы термодинамики

1. Техническая термодинамика

Законы термодинамики

2. ПАРАМЕТРЫ СОСТОЯНИЯ

Свойства веществ бывают интенсивные и
экстенсивные.
Интенсивные – не зависят от количества вещества
(температура, плотность и т.д.)
Экстенсивные – зависят от количества вещества
(масса, объём, вес, теплоёмкость, внутренняя
энергия и т.д.)
Экстенсивные свойства, отнесённые к количеству
вещества, становятся интенсивными ( удельный
вес, удельный объем, удельная теплоёмкость,
удельная внутренняя энергия и т.д.)

3. ПАРАМЕТРЫ СОСТОЯНИЯ

Интенсивные свойства, определяющие
состояние вещества, называются
параметрами состояния.
Основные параметры состояния:
а) температура T , К (t , oC ) характеризует
тепловое состояние вещества;
б) давление ( p=N/F, Па ) – это отношение
силы N, действующей по нормали к
поверхности F, к площади этой поверхности
кГс
1бар 10 Па 750, 24 мм. рт.ст. 1, 02 2
в) удельный объем ( v ) – это отношение см
объема тела к его массе, м3 / кг
,
5

4. ПАРАМЕТРЫ СОСТОЯНИЯ

Состояние любого вещества однозначно
определяется любой парой параметров состояния:
p, v , p, t , t, v
Для каждого вещества существует функция
состояния, которая называется уравнением
состояния данного вещества:
График этой функции – термодинамическая
поверхность.
F p, v, t 0

5. ТЕРМОДИНОМИЧЕСКИЙ ПРОЦЕСС

Термодинамическая система – это тело или
совокупность тел, взаимодействующих между
собой и окружающей средой.
Термодинамический процесс – это такой процесс,
при котором изменяется хотя бы один из
параметров состояния термодинамической
системы.
Термодинамические процессы бывают
равновесными и неравновесными.
В равновесных термодинамических процессах во
всех точках термодинамической системы
параметры состояния одинаковые.

6. ТЕРМОДИНОМИЧЕСКИЙ ПРОЦЕСС

Частные случаи термодинамического
процесса:
p=const – изобарный процесс;
v=const – изохорный процесс;
T=const – изотермический процесс;
q=0 – адиабатный процесс.

7. ТЕПЛОЁМКОСТЬ

Теплоёмкость – это количество теплоты,
которое нужно подвести к телу для того,
чтобы нагреть его на 1K.
Теплоёмкость – это экстенсивное свойство.
Теплоёмкость, отнесённая к количеству
вещества, называется удельной
теплоёмкостью.
Дж
c
,
кгК
Удельная массовая теплоемкость
Удельная объемная теплоемкость Дж
c`, 3
м К

8. ТЕПЛОЁМКОСТЬ

Средняя теплоёмкость – это теплоёмкость,
измеренная в интервале температур.
c1 2
q
q1 2
,
T2 T1
где 1 2 - это количество теплоты, которое нужно
подвести к 1 кг тела для того, чтобы нагреть его от
.
Т до
1
Т2

9. ТЕПЛОЁМКОСТЬ

Истинная теплоемкость это теплоёмкость при
конкретном значении температуры .
q , x const
cx
T x
где x - индекс процесса.
Изобарная:
Изохорная:
q
cv
T v
q
cp
T p

10. ТЕПЛОЁМКОСТЬ

Для газов справедливо:
cp
cv
k,
где k -показатель адиабаты.
k=1,4 для двухатомных газов ( H , N , O , воздух)
2
2
2
Уравнение Майера :
c p cv R,
где R- газовая постоянная для данного вещества.
Для твердых и жидких тел c p cv (не зависит от
вида процесса).

11. ВНУТРЕННЯЯ ЭНЕРГИЯ

Внутренняя энергия включает в себя:
• энергию поступательного и вращательного
движения молекул,
• внутримолекулярную энергию,
• энергию взаимодействия между молекулами,
• внутриатомную и внутриядерную энергию.
В теплотехнических расчетах используют не
абсолютное значение внутренней энергии, а
величину её изменения в конкретном процессе.
Внутренняя энергия U, Дж
Удельная внутренняя энергия u U , Дж
G кг

12. ВНУТРЕННЯЯ ЭНЕРГИЯ

Внутренняя энергия – это функция состояния, т.е. её
изменение не зависит от пути процесса, а
определяется лишь начальным и конечным
состоянием тела.
Внутренняя энергия определяется однозначно любой
парой параметров состояния:
u p, v
u p, t
u v, t

13. РАБОТА РАСШИРЕНИЯ

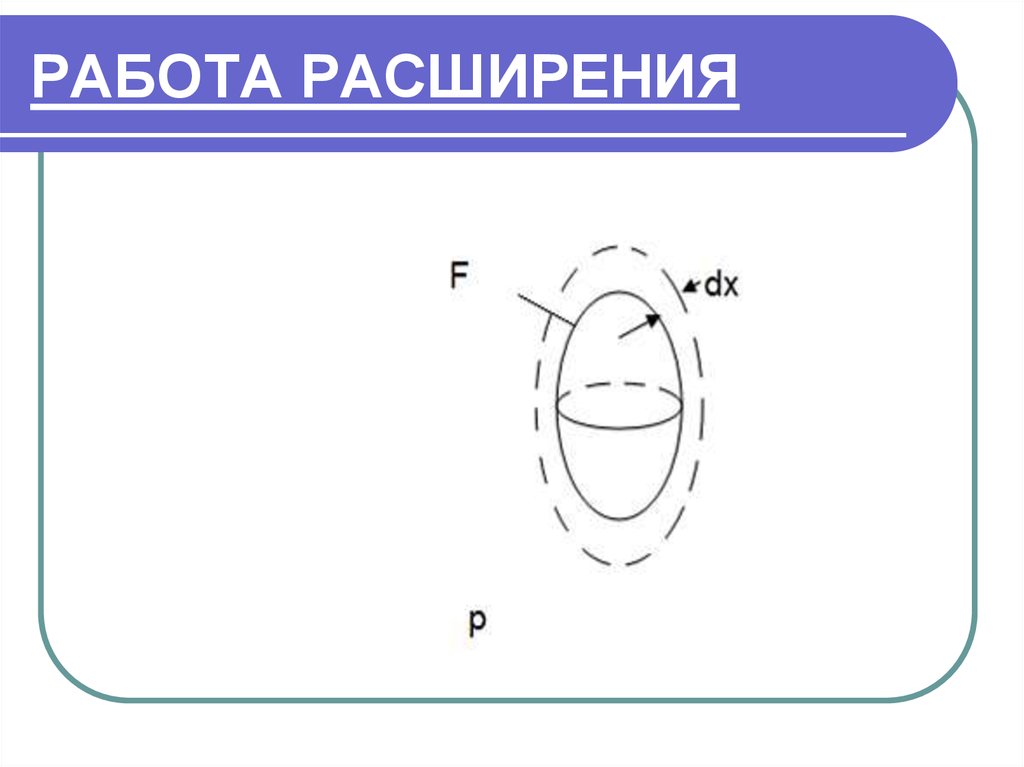
14. РАБОТА РАСШИРЕНИЯ

F-площадь поверхности данного тела.
Тело помещено в среду с давлением р. Преодолевая
это давление, тело расширяется на величину dx.
При этом тело совершило работу расширения:
dL Ndx pFdx pdV , Дж
Удельная работа расширения:
dL pdV
Дж
dl
pdv,
G
G
кг

15. РАБОТА РАСШИРЕНИЯ

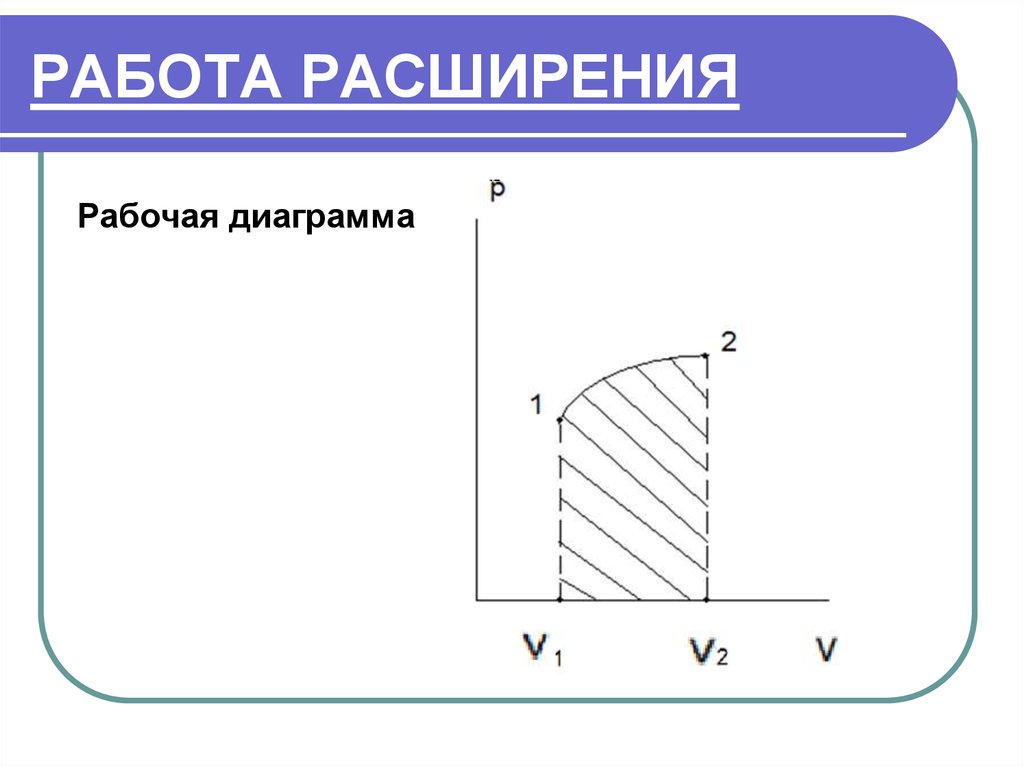
Рабочая диаграмма

16. РАБОТА РАСШИРЕНИЯ

Тело переходит из состояния 1 в состояние 2.
При этом тело совершает работу расширения
l
v2
dl pdv
1 2
v1

17. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

ФОРМУЛИРОВКА ПЕРВОГО ЗАКОНА
ТЕРМОДИНАМИКИ:
Теплота, подведенная к телу, расходуется на
изменение его внутренней энергии и на
совершение работы.
(1)
1 2
1 2
1 2
где Q1 2- количество теплоты, подведённой к телу;
Q
U
L ,
U1 2 - изменение внутренней энергии тела;
L1 2
- работа, совершенная телом

18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

Правило знаков :
«+» - теплота поводится к телу;
«- » - теплота отводится от тела;
«+» - работа, совершаемая телом;
«- » - работа, совершаемая над телом.

19. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

Запишем уравнение (1) первого закона
термодинамики:
в удельной форме:
q1 2 u1 2 l1 2
(2)
в дифференциальной форме:
dQ dU dL
(3)
уравнение (2) в дифференциальной форме
(уравнение (3) в удельной форме) :
dq du dl
(4)

20. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

Если единственным видом работы является работа
расширения, то уравнение (4) примет вид:
dq du pdv
при изохорном процессе (dv=0)
dq du,
т.е. в изохорном процессе вся теплота, подведенная
к телу, расходуется на изменение его внутренней
энергии. Тогда:
q u
cv
T v T v

21. ЭНТАЛЬПИЯ

Энтальпия – это функция состояния, определяемая
уравнением:
I U pV , Дж
Удельная энтальпия:
Дж
i u pv,
кг
Величина изменения энтальпии не зависит от пути
процесса, т.к. она функция состояния. Ее величина
определяется начальным и конечным состоянием
тела. Значение энтальпии однозначно
определяется любой парой параметров
состояния:
i p, v , i p, T , i v, T

22. ЭНТАЛЬПИЯ

Выведем уравнение первого закона термодинамики
через энтальпию. dq du dl du pdv,
d pv pdv vdp
pdv d pv vdp
Тогда:
dq du d pv vdp
dq d u pv vdp di vdp
уравнение первого закона термодинамики,
выраженное через энтальпию:
dq di vdp

23. ЭНТАЛЬПИЯ

Если изобарный процесс (dp=0), то :
dq di,
т.е. вся теплота, подведённая к телу,
расходуется на изменение его
энтальпии. Тогда:
q i
cp
T p T p

24. Второй закон термодинамики

Обратимыми называются такие процессы, при совершении
которых как в прямом, так и в обратном направлении не
происходит ни каких остаточных изменений, как в самой
системе, так и в окружающей среде, в противном случае
процесс будет необратимый.
Формулировка второго закона термодинамики в наиболее
общей форме:
Все реальные самопроизвольные процессы являются
необратимыми.
Частная формулировка Клаузиуса:
Теплота не может самопроизвольно переходить от более
холодного тела к более нагретому.

25. Понятие о циклах

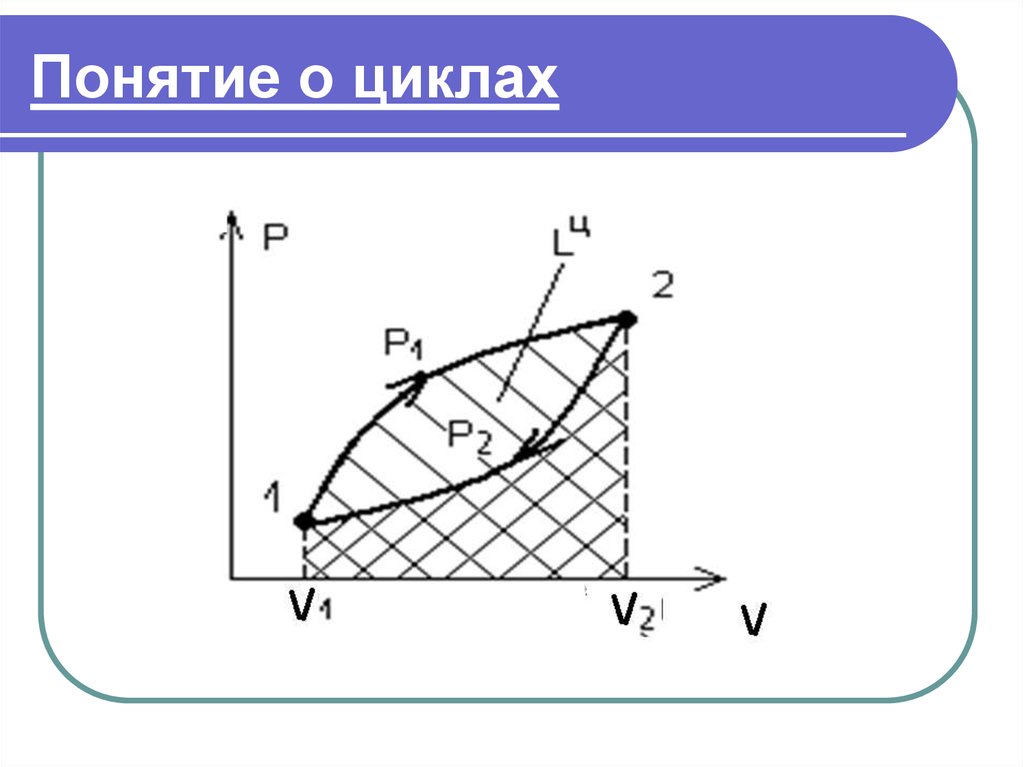
26. Понятие о циклах

Тело переходит из состояния 1 в
состояние 2. При этом совершается
работа расширения, затем тело
возвращается в исходное состояние.
Таким образом тело совершает
круговой процесс - цикл.

27. Понятие о циклах

V2
Работа расширения:
L1P 2 PdV
V1
V1
Работа сжатия:
Работа цикла:
Lц L1P 2 LC2 1
LС2 1 PdV
V2
V2
V1
V2
V2
V1
V2
V1
V1
pdV pdV pdV pdV 0
Уравнение второго закона термодинамики для цикла:
Q
U L Q L
ц
ц
0
ц
ц
ц

28. Цикл Карно

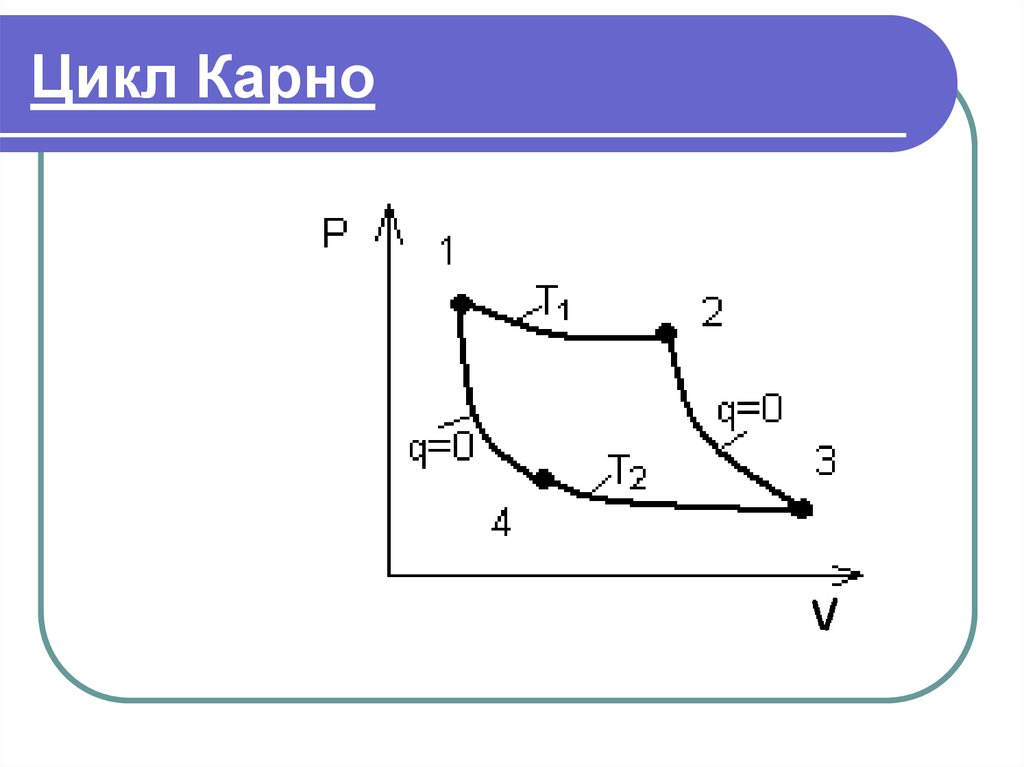
29. Цикл Карно

Процессы: 1-2, 3-4 - изотермические,
2-3;4-1 - адиабатные;
1-2 - расширение тела в изотермическом режиме при
T1,при этом к телу от горячего источника
подводится теплота Q1, в соответствии со вторым
законом термодинамики (Тг > Т1);
2-3 - расширение тела в адиабатном режиме;
3-4 - сжатие тела в изотермическом режиме, при этом
от тела к холодному источнику отводится теплота
Q2 , в соответствии со вторым законом
термодинамики (Тх < Т2);
4-1 - сжатие тела в адиабатном режиме.

30. Цикл Карно

Рассмотрим осуществление цикла Карно в обратном
направлении.
Процессы:
1-4 - возможен;
4-3 - невозможен, т.к. противоречит второму закону
термодинамики, в формулировке Клаузиуса;
3-2- возможен;
2-1- невозможен т.к. противоречит второму закону
термодинамики, в формулировке Клаузиуса;
Таким образом цикл Карно в данной постановке
является необратимым.

31. Цикл Карно

Обратимый цикл Карно.
Пусть в процессе 1-2: Т
Г
Т1 dT
TГ Т 1
0
- второму закону термодинамики процесс не
противоречит.
При совершении процесса 3-4:
Т х Т 2 dT
Tх Т 2
0
- второму закону термодинамики процесс не
противоречит.

32. Цикл Карно

Пусть при совершении цикла в обратном
направлении:
Т х Т 2 dT
Tх Т 2
0
Т Г Т1 dT
TГ Т 1
0
Таким образом процессы 2-1 и 4-3 уже не
противоречат второму закону термодинамики.

33. Энтропия

Термический КПД цикла определяется формулой:
Q1 Q2
,
Q1
Т
(1)
где Q1 и Q2 – количество теплоты, подведенной к телу
за время цикла и отведенной от него
соответственно.

34. Энтропия

Можно доказать, что для обратимого цикла Карно
термический КПД определяется по формуле:
Т1 Т 2
,
Т1
Т
(2)
где Т1 и Т2 –температура тела, при изотермическом
расширении и изотермическом сжатии.

35. Энтропия

Формула (1) справедлива для любого цикла
Из (1) и (2) получим:
Q1 Q2 Т1 Т 2
Q1
Т1
Эта формула справедлива только для обратимого
цикла Карно.

36. Энтропия

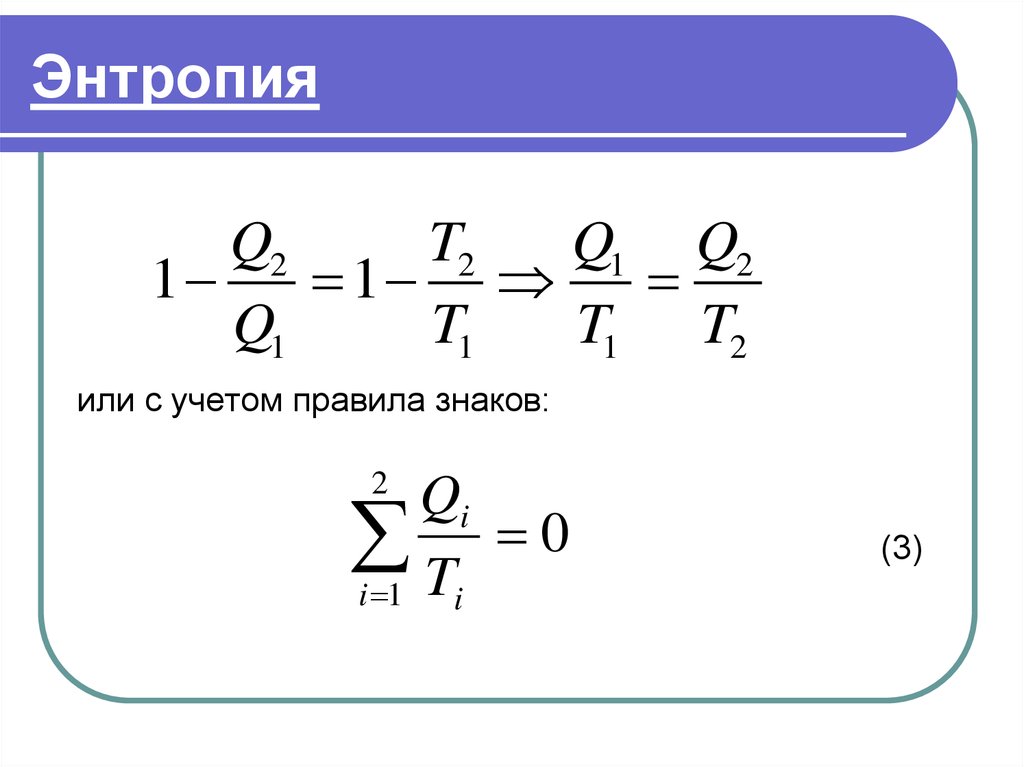
Q2
T2
Q1 Q2
1
1
Q1
T1
T1 T2
или с учетом правила знаков:
2
Qi
0
i 1 Ti
(3)

37. Энтропия

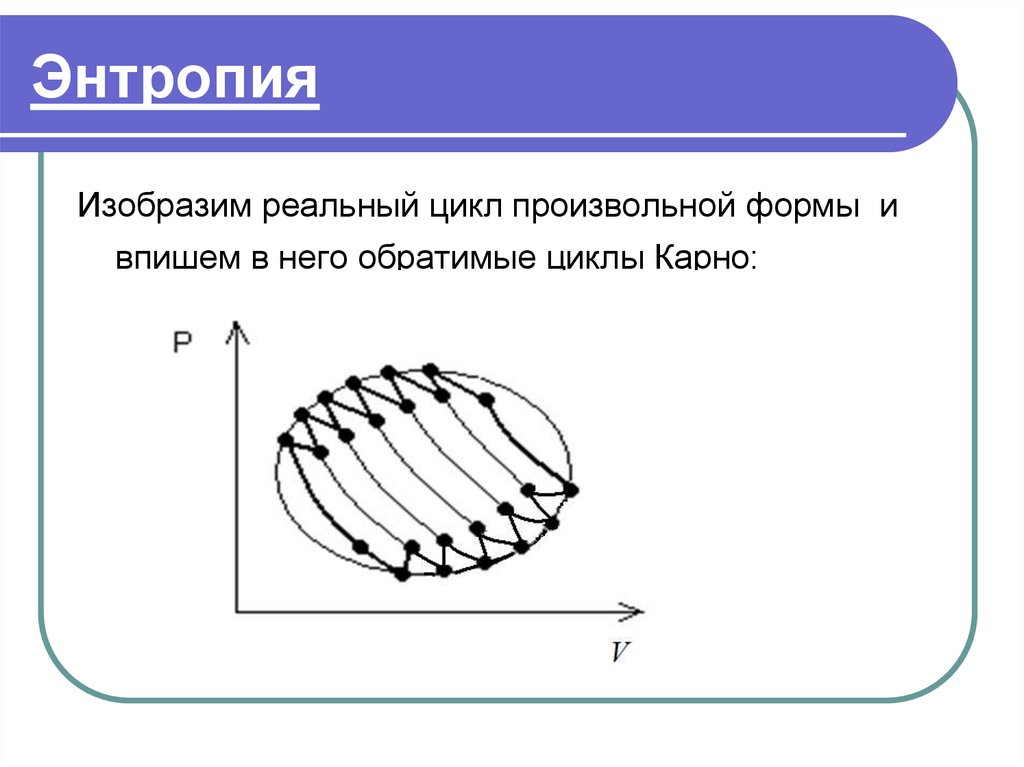
Изобразим реальный цикл произвольной формы и
впишем в него обратимые циклы Карно:

38. Энтропия

В реальный цикл произвольной формы вписали n
обратимых циклов Карно с n пар тепловых
источников.
Тогда формула (3) примет вид:
Qi
0
i 1 Ti
n
Чем больше количество вписанных обратимых
циклов Карно, тем в большей степени они
заменяют реальный цикл.
(4)

39. Энтропия

Пусть
n
, тогда формула (4) примет вид:
Qi
0,
im
n i 1 Ti
n
(5)
т.е. интеграл по замкнутой кривой:
dQ
T 0
(6)

40. Энтропия

Тогда для любого реального цикла
справедлива формула (6). Обозначим
подынтегральное выражение:
dQ
dS
,
T
где S- энтропия , Дж/К

41. Энтропия

dQ
T
- интеграл Клаузиуса.
1
T
- интегрирующий множитель, он превращает функцию
процесса в функцию состояния.
Удельная энтропия:
dq
ds
dq Tds
T

42. Энтропия

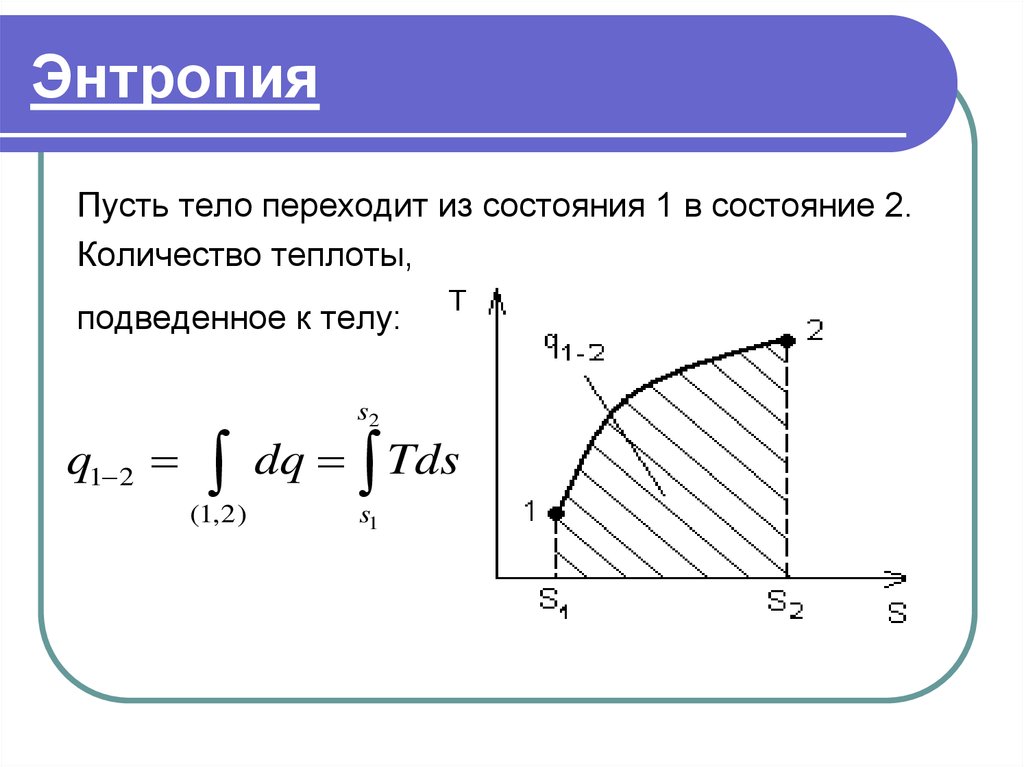
Пусть тело переходит из состояния 1 в состояние 2.
Количество теплоты,
подведенное к телу:
q1 2
(1,2)
s2
dq Tds
s1

43. Энтропия

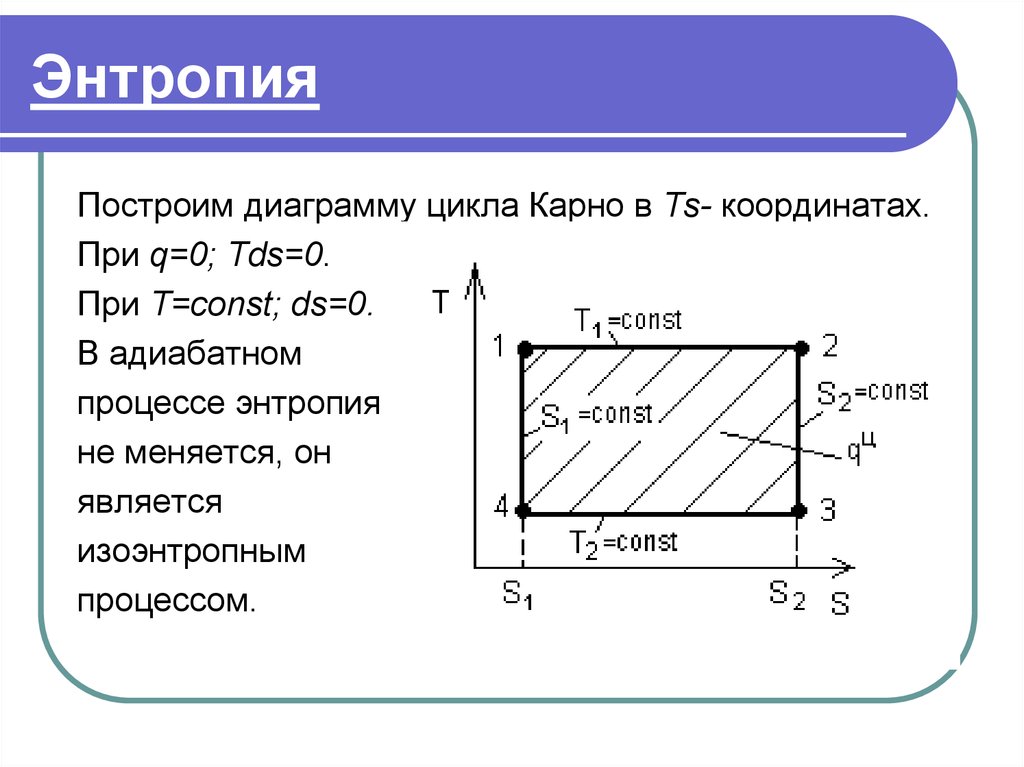
Построим диаграмму цикла Карно в Тs- координатах.
При q=0; Тds=0.
При T=const; ds=0.
В адиабатном
процессе энтропия
не меняется, он
является
изоэнтропным
процессом.

44. ЭКСЕРГИЯ

Основываясь
на
втором
начале
термодинамики, установим количественное
соотношение между работой, которая могла бы
быть совершена системой при данных внешних
условиях в случае протекания в ней равновесных
процессов, и действительной работой,
производимой в тех же условиях, при
неравновесных процессах.
Рассмотрим изолированную систему, состоящую из
горячего источника с температурой Т1, холодного
источника (окружающей среды)
с температурой
То и рабочего тела, совершающего цикл.

45. ЭКСЕРГИЯ

Работоспособностью
(и л и
э к с е р г и е й) т е л л о т ы
Qi,
отбираемой от горячего источника с
температурой Ti, называется максимальная
полезная работа , которая может быть
получена за счет этой теплоты при условии,
что холодным источником является
окружающая среда с температурой То.

46. ЭКСЕРГИЯ

Из предыдущего ясно, что максимальная
полезная работа теплоты
Q,
представляет собой работу равновесного
цикла Кapнo, осуществляемого в
диапазоне температур Ti — To:
LI макс t Q1 ,
где
t 1 T0 / T1

47. ЭКСЕРГИЯ

Таким образом, эксергия теплоты Q1:
L макс Q1 (1 T0 / T1 ),
I
т. е работоспособность теплоты тем
больше, чем меньше отношение То/Т1.
При Т1= То она равна нулю.

48. ЭКСЕРГИЯ

Полезную
работу, полученную за
счет теплоты
Q1 горячего
источника, можно представить в
виде:
L1 = Q1 - Q2,
где Q2 — теплота, отдаваемая в цикле
холодному источнику (окружающей
среде) с температурой То.

49. ЭКСЕРГИЯ

S хол обозначить приращение
Если через
энтропии холодного источника, то
Q2 T0 S хол ,
тогда
L Q1 T0 S хол
I

50. ЭКСЕРГИЯ

Если бы в рассматриваемой изолированной
системе протекали только равновесные
процессы, то энтропия системы оставалась
бы неизменной, а увеличение энтропии
холодного источника равнялось бы
уменьшению энтропии горячего. В этом
случае за счет теплоты Q1 можно было бы
получить максимальную полезную работу:
L макс Q1 T0 Sгор
I

51. ЭКСЕРГИЯ

Величина
L L макс L
I
I
определяет п о т е р ю
р а б от ы,
обусловленную рассеиванием
энергии вследствие неравновесности
протекающих в системе процессов.
Чем больше неравновесность процессов,
мерой которой, является увеличение
энтропии изолированной системы, тем
меньше производимая системой работа.