Похожие презентации:
Случайные события. Понятие вероятности события
1. Тема: Случайные события. Понятие вероятности события.
План:1. Испытания и события.
2. Виды случайных событий.
3. Классическое определение вероятности.
4. Статистическое определение вероятности.
5. Алгебра событий.
2. 1. Испытания и события
• Чтобы каким-то образом оценитьсобытие, необходимо учесть или
специально организовать условия, в
которых оно происходит.
• Выполнение определенных условий или
действий
для
выявления
рассматриваемого
события
носит
название опыта или эксперимента.
3.
• Событиерассматривают,
как
результат испытания (опыта).
• События обозначают заглавными
буквами латинского алфавита
A, B, C и т.д.
4. Виды событий
событие называется случайным,
если в результате опыта оно может
произойти, либо не произойти;
событие называется достоверным,
если оно обязательно произойдет в
результате данного опыта;
событие называется невозможным,
если оно не может произойти в
данном опыте.
5.
Пример.Испытание - подбрасывание
игральной кости.
События (исходы):
А – выпало четное число очков;
В – выпало 8 очков;
С – выпало менее 7 очков.
6. 2. Виды случайных событий
События называются несовместными,если они вместе не могут наблюдаться
в одном и том же опыте (т.е. появление
одного из них исключает появление
других событий в одном и том же
опыте).
7.
Событияназываются
единственно возможными,
если в результате опыта
появление одного из них,
есть событие достоверное.
8.
Событияназываются
равновозможными, если ни у
одного
из
них
нет
преимущества для появления
перед другими.
9.
Событияобразуют полную
группу событий, если хотя бы
одно из них обязательно
произойдет в опыте.
10.
Пример.В аптеку принимаются на
реализацию
лекарственные
препараты от двух поставщиков.
11.
События:A- отсутствие поставок;
B- поступление товара от одного из
поставщиков;
C - поступление товара от двух
поставщиков;
образуют полную группу.
12.
Противоположныминазываются два единственно
возможных
события,
образующих полную группу.
13.
Если одно из противоположных событийобозначить через A, то другое
обозначают
A
14.
Пример.Брошена монета.
События:
A - «появился герб»;
A -«появилась надпись».
15. 3. Классическое определение вероятности
• Одной из главных задач в теориивероятностей является задача определения
количественной
меры,
возможности
появления события.
• Количественной
мерой
возможности
появления
рассматриваемого
события
является вероятность.
16.
• Вероятностью события А называетсячисло,
равное
отношению
числа
исходов,
благоприятствующих наступлению
события А к общему числу
возможных исходов.
17.
mP ( A)
n
• где m-число исходов благоприятствующих
наступлению события А;
• n – общее число возможных исходов.
18. Свойства вероятности
• Вероятность достоверного событияравна единице;
• Вероятность невозможного события
равна нулю;
• Вероятность случайного события есть
положительное число, заключенное
между нулем и единицей;
19. 4. Статистическое определение вероятности
Относительнойчастотой
события называют отношение
числа испытаний, в которых
событие появилось, к общему
числу фактически произведенных
испытаний.
20.
• Относительная частота события Аопределяется формулой
m
W ( A)
n
• где m-число появлений события, n – общее
число испытаний.
21.
Пример.Среди
1000
новорожденных
оказалось 517 мальчиков. Чему равна
частота рождения мальчиков?
Событие А – рождение мальчика.
517
W ( A)
0,517
1000
22.
Сопоставляя определение вероятности иотносительной частоты, делаем вывод:
определение вероятности не требует, чтобы
испытания
производились
в
действительности;
определение
же
относительной частоты предполагает, что
испытания были произведены фактически.
Другими
словами,
вероятность
вычисляют до опыта, а относительную
частоту – после опыта.
23.
Вероятностьюсобытия
А
называется
число,
около
которого
группируются
значения
относительной
частоты данного события в различных сериях
большого числа испытаний
m
P( A) lim
n n
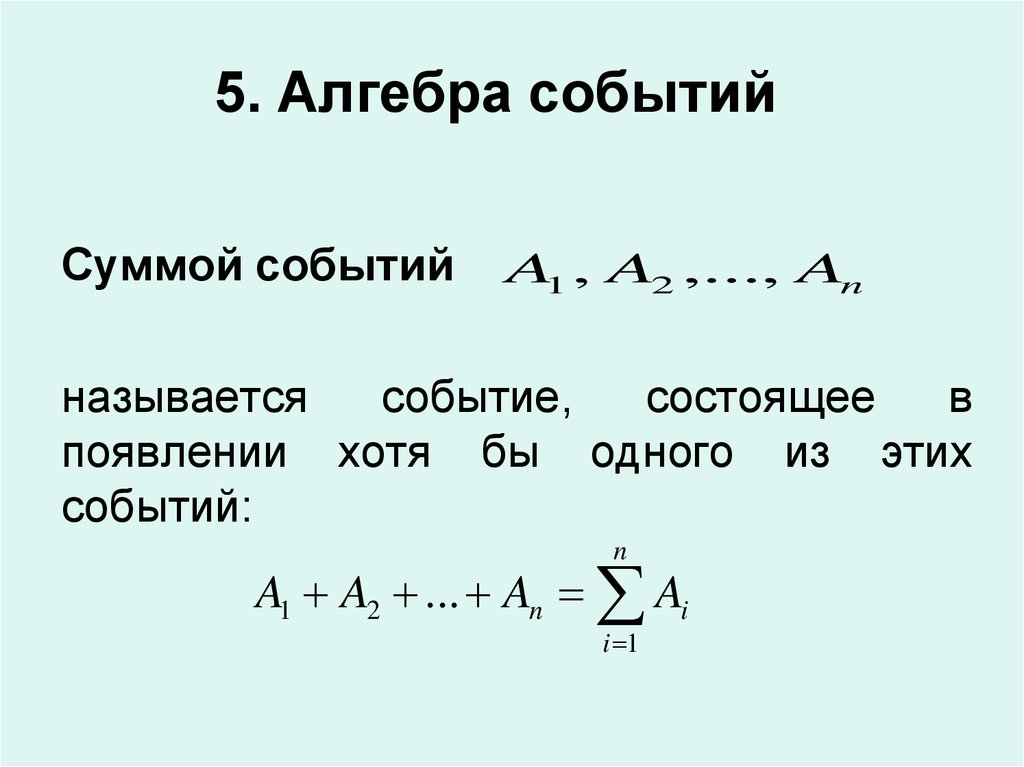
24. 5. Алгебра событий
Суммой событийA1 , A2 ,..., An
называется
событие,
состоящее
в
появлении хотя бы одного из этих
событий:
n
A1 A2 ... An Ai
i 1
25.
Если А и В совместныесобытия, то их сумма
A+В
обозначает наступление события А
или события В или обоих событий
вместе.
Если А и В несовместные
события,
то
их
сумма
A+В
обозначает
наступление
или
события А или события В.
26.
Пример.Победитель соревнования награждается призом
(событие А), денежной премией (событие В).
Что представляют собой события A+B?
27.
Пример.Победитель соревнования награждается призом
(событие А), денежной премией (событие В).
Что представляют собой события A+B?
Решение.
Событие А+В состоит в награждении победителя
или призом или денежной премией, или тем и
другим.
28.
Произведением событийA1 , A2 ,..., An
называется событие, состоящее в
одновременном появлении всех этих
событий:
A1 A2 ... An
n
ПA
i 1
i
29.
Пример.Событие,
состоящее
в
одновременной продаже в аптеке
двух
препаратов,
является
произведением событий А и В, где
А - продажа одного препарата,
В - продажа другого препарата.
30.
Вероятность наступления события А,вычисленная в предположении, что событие В
уже
произошло,
называется
условной
вероятностью события А при условии В и
обозначается
PB A
31.
Пример.В коробке содержится 3 белых и 3
желтых шара. Из коробки дважды
вынимают наугад по одному шару, не
возвращая их в коробку.
Найти вероятность появления белых
шаров при втором испытании (событие В),
если при первом испытании был извлечен
желтый шар (событие А).
32. Решение. После первого испытания в коробке осталось 5 шаров, из них 3 белых. Искомое условие вероятности:
3PA B 0,6
5
33. Тема. Основные формулы для вычисления вероятностей событий
План:1. Формула полной вероятности.
2. Формулы Байеса.
3. Формула Бернулли.
4. Формула Пуассона.
34. 1. Формула полной вероятности
Теорема. Вероятность события А, котороеможет наступить лишь при условии
появления одного из несовместных
событий B1 , B2 ,..., Bn
образующих полную группу, равна сумме
произведений вероятностей каждого из
этих
событий
на
соответствующую
условную вероятность события А:
35.
P A P B1 PB1 A P B2 PB2 A ... P Bn PBn A36.
Пример.На
склад
поступили
хирургические зажимы с трех станков.
На первом станке изготовлено 40%
зажимов от их общего количества, на
втором – 35% и на третьем 25%,
причем на первом станке было
изготовлено 90% зажимов высшего
сорта, на втором 80% и на третьем
70%.
Какова вероятность того, что взятый
наугад зажим окажется высшего сорта?
37.
Решение.Введем обозначения:
А – выбранный наугад хирургический зажим
оказался высшего сорта;
B1- зажим изготовлен на первом станке;
B2- зажим изготовлен на втором станке;
B3- зажим изготовлен на третьем станке;
P A P B1 PB1 A P B2 PB2 A P B3 PB3 A
38.
P(B1)=0,4;P(B2)=0,35;
P(B3)=0,25;
PB1 A 0,9;
PB2 A 0,8;
PB3 A 0,7.
P A 0,4 0,9 0,35 0,8 0,25 0,7 0,815
39. 2. Формулы Байеса
Пусть событие А происходитодновременно
с
одним
из
n
несовместных событий B1 , B2 ,..., Bn ,
образующих полную группу.
Поскольку заранее не известно,
какое из этих событий наступит, их
называют гипотезами.
40.
Вероятность появления события Аопределяется по формуле полной
вероятности.
Требуется
найти
вероятность
события Bi если известно, что событие
А произошло:
PA Bi
P Bi PBi A
P A
41.
Полученные формулы называютформулами
Байеса,
по
имени
английского
священника
и
математика (1702-1761 гг.), который
их вывел; опубликованы в 1764 г.
Формулы
Байеса
позволяют
переоценить вероятности гипотез
после того, как становится известным
результат
испытания,
в
итоге
которого появилось событие А.
42.
Пример.В первом ящике имеются 8 белых и
6 черных шаров, а во втором 10- белых и
4 черных.
Наугад выбирают ящик и шар.
Известно, что вынутый шар – черный.
Найти вероятность того, что был
выбран первый ящик.
43.
Решение.А – при проведении двух
последовательных испытаний выбора
ящика и выбора шара, был вынут
черный шар;
B1- был выбран первый ящик;
B2 - был выбран второй ящик.
P(B1)=0,5 и P(B2)=0,5.
44.
Вероятность извлечения черного шара после того,как выбран первый ящик, составляет
6
3
PB1 A
;
14 7
Вероятность извлечения черного шара после
того, как выбран второй ящик, составляет
4 2
PB2 A
;
14 7
45.
Вероятность того, что вынутый шароказался черным:
P A P B1 PB1 A P B2 PB2 A
1 3 1 2 1 3 2 1 5
5
P A
;
2 7 2 7 2 7 7 2 7 14
46.
Искомая вероятность, того что черныйшар был вынут из первого ящика
составит:
PA B1
P B1 PB1 A
P A
1 3
3 14
3
2
7
PA B1
0,6.
5
14 5
5
14
47. 3. Формула Бернулли
Если производятся испытания,при которых вероятность появления
события А в каждом испытании не
зависит
от
исходов
других
испытаний, то такие испытания
называются
независимыми
относительно события А.
48.
Вероятность того, что в n независимыхиспытаниях, в каждом из которых
вероятность появления события А равна p
(где 0<p<1) событие А наступит ровно k
раз, вычисляется по формуле Бернулли:
Pn k C p q
k
n
Где
q 1 p
k
n k
49.
Пример.Вероятность попадания в цель
при одном выстреле составляет
р=0,8.
Найти вероятность четырех
попаданий при шести выстрелах.
50.
Решение.n=6; k=4; p=0,8; q=0,2.
P6 4 C 0,8 0,2
4
6
4
2
6!
4
2
0,8 0,2 0,246.
4! 6 4 !
51. 4. Формула Пуассона
Теорема. Если вероятность p наступлениясобытия А в каждом испытании постоянна и
мала, а число независимых испытаний n
достаточно велико, то вероятность того, что
событие А наступит m раз приближенно равна:
Pn m
m
m!
e , где n p
52.
Пример.Предприятие
изготовило
и
отправило
заказчику
100000
пробирок.
Вероятность того, что пробирка
может оказаться битой, равна
0,0001.
Найти вероятность того, что в
отправленной партии будет три
битых пробирки.
53.
Решение.По условию, n=100000; p=0,0001; m=3.
100000 0,0001 10
54.
Решение.По условию, n=100000; p=0,0001; m=3.
100000 0,0001 10
Воспользуемся формулой Пуассона:
10
1000 0,000045
10
P100000 3
e
0,0075.
3!
6
3
















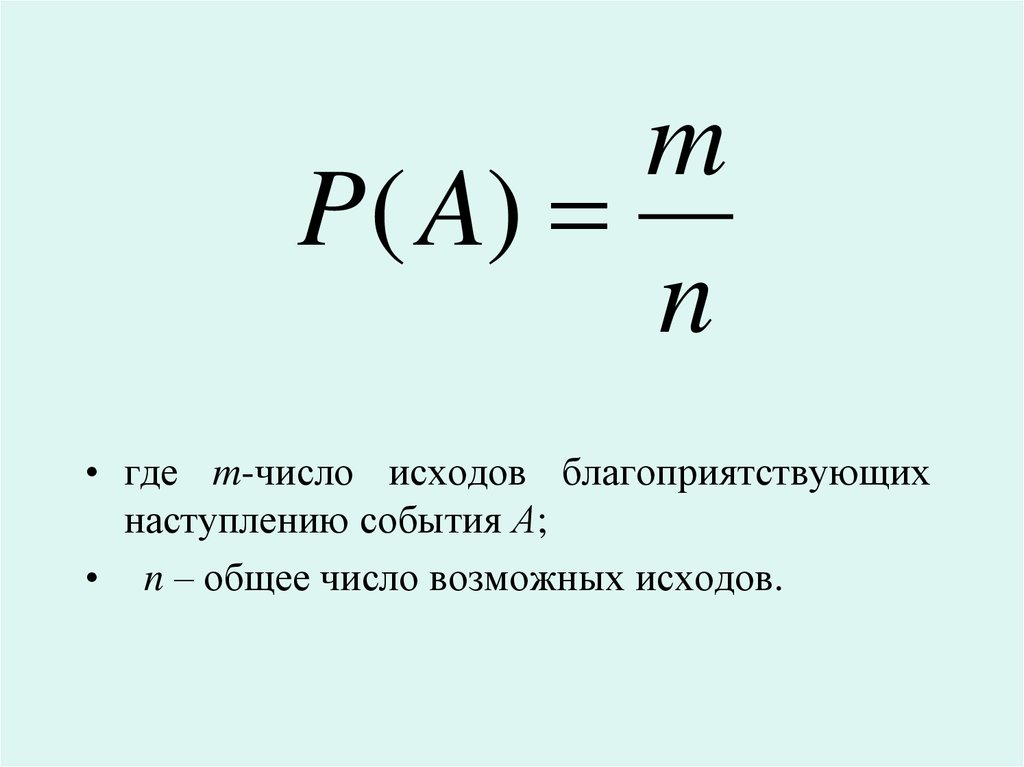
















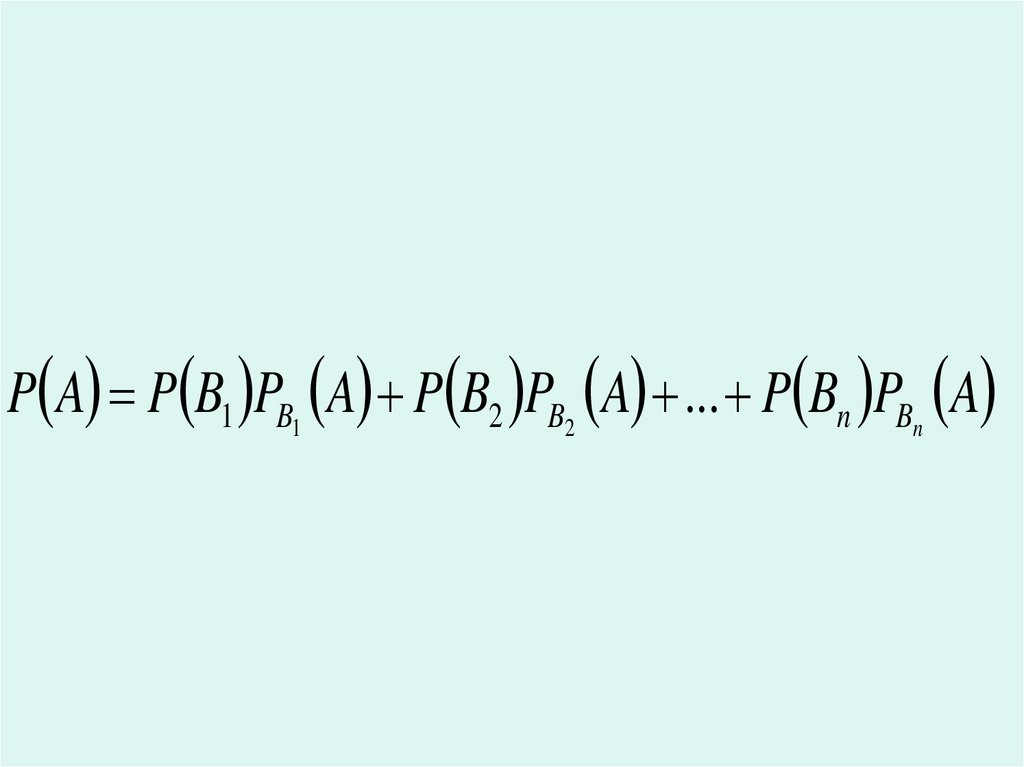



















 Математика
Математика








