Похожие презентации:
Основы выборочного метода
1. Раздел 2. Математическая статистика Лектор: старший преподаватель кафедры математики Константиновская Наталья Валерьевна
2. Тема. Основы выборочного метода
План:1. Основные понятия математической
статистики.
2. Числовые характеристики выборки.
3. Оценка параметров генеральной
совокупности по ее выборке.
3. 1. Основные понятия математической статистики
Математическая статистика – этораздел математики, изучающий способы
сбора статистической информации и
методы ее обработки.
4.
В математической статистике выделяют дваосновных направления исследований:
1.
Оценка
параметров
генеральной
совокупности.
2.
Проверка статистических гипотез.
5.
Генеральная совокупность – этомножество всех изучаемых объектов.
Выборочная
совокупность
(выборка) – это часть генеральной
совокупности,
выбранная
некоторым
(случайным) образом.
Объемом совокупности (выборочной
или генеральной) называют число объектов
этой совокупности.
6.
Например, из десяти тысяч студентовотобрано для обследования 100 человек.
Объем генеральной совокупности N=10000;
объем выборки n=100.
7.
Выборкадолжна
быть
репрезентативной,
то
есть
давать
правильное представление о пропорциях
генеральной совокупности.
Выборка будет репрезентативной,
если ее осуществить случайно, все
объекты имеют одинаковую вероятность
попасть в выборку.
8.
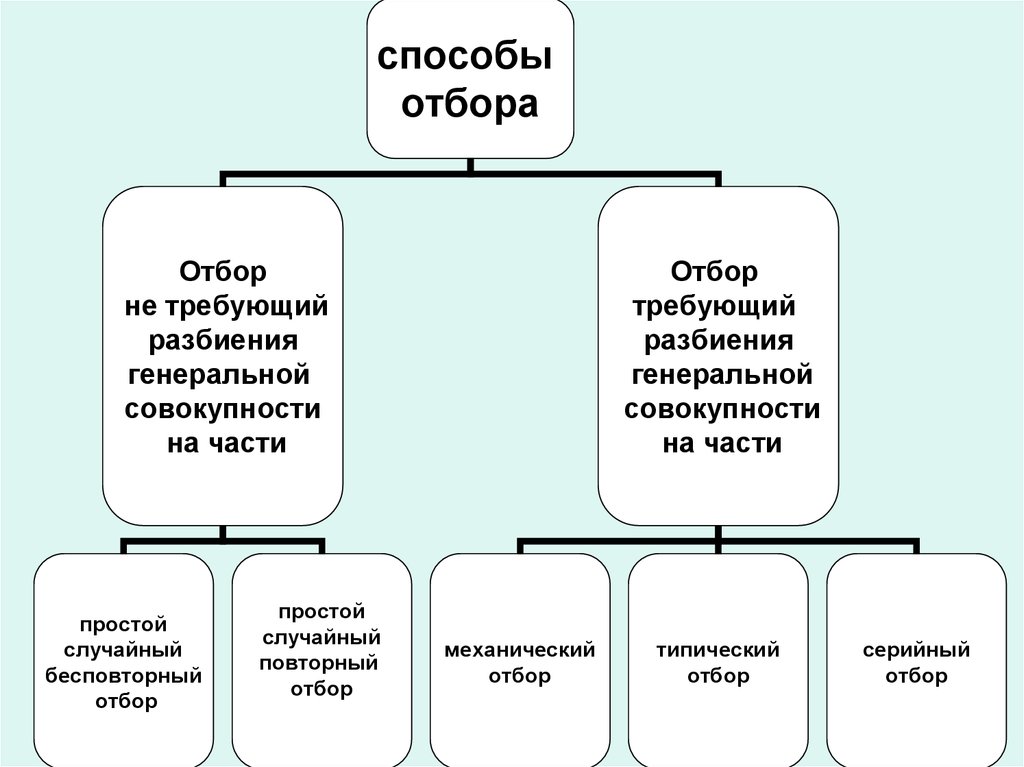
способыотбора
Отбор
не требующий
разбиения
генеральной
совокупности
на части
простой
случайный
бесповторный
отбор
простой
случайный
повторный
отбор
Отбор
требующий
разбиения
генеральной
совокупности
на части
механический
отбор
типический
отбор
серийный
отбор
9.
Каждый элемент выборкиxi
называется вариантой.
Число наблюдений варианты ni
называется частотой встречаемости
(частотой).
Относительная
частота
–
это
отношение частоты к объему выборки
ni
Wi
n
10.
Статистическим распределениемвыборки называют перечень вариант и
соответствующих им частот или
относительных частот.
xi
x1
x2
…
xk
ni
n1
n2
…
nk
11.
Гистограмма частот – это ступенчатаяфигура,
состоящая
из
смежных
прямоугольников, построенных на одной
прямой, основаниями которых служат
частичные интервалы длины h, а высоты
равны отношению ni к h .
Полигон частот – ломаная линия, отрезки
которой соединяют точки с координатами
(xi; ni).
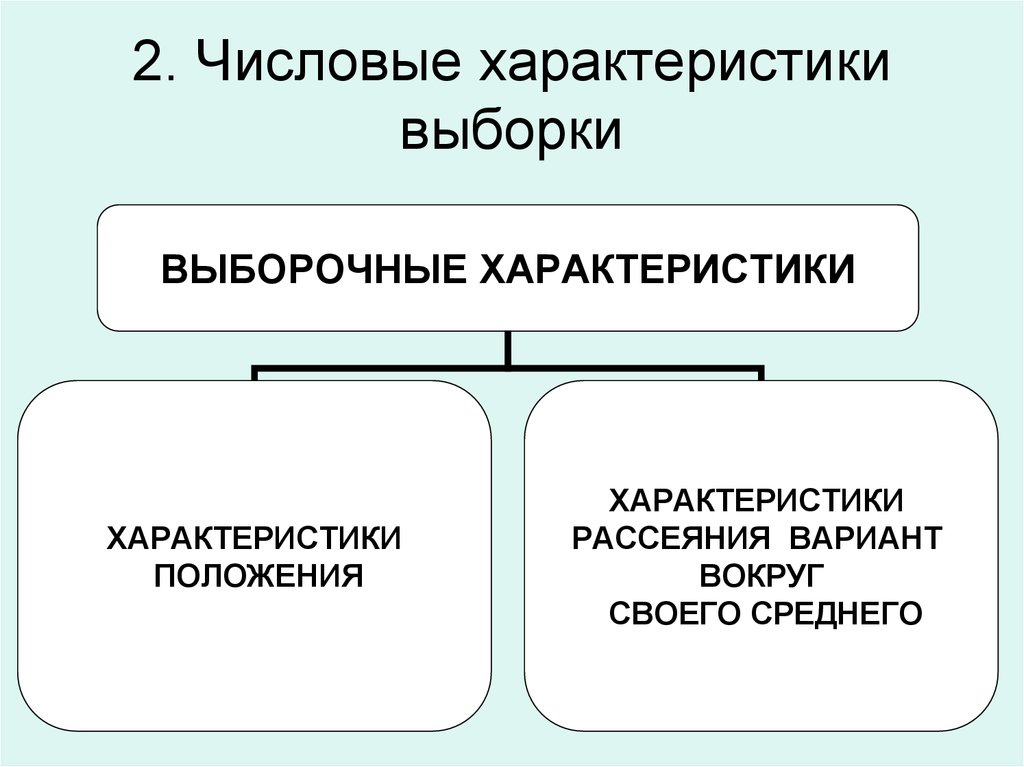
12. 2. Числовые характеристики выборки
ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИХАРАКТЕРИСТИКИ
ПОЛОЖЕНИЯ
ХАРАКТЕРИСТИКИ
РАССЕЯНИЯ ВАРИАНТ
ВОКРУГ
СВОЕГО СРЕДНЕГО
13. Характеристики положения
Мода (М0) – это такое значениеварианты,
что
предшествующее
и
следующее за ним значения имеют меньшие
частоты встречаемости.
Для одномодальных распределений
мода – это наиболее часто встречающаяся
варианта в данной совокупности.
14.
Медиана (МЕ) - это значение признака,относительно которого ряд распределения
делится на 2 равные по объему части.
15.
Выборочная средняя – это среднееарифметическое
значение
вариант
статистического ряда
k
xB
1
x
n
i i
n i 1
16. Характеристики рассеяния вариант вокруг своего среднего
Выборочная дисперсия – среднееарифметическое квадратов отклонения
вариант от их среднего значения
k
1
2
DB xi xB ni
n i 1
17.
Выборочная дисперсия может бытьподсчитана по формуле
n
1
2
2
D B x i ni x B
n i 1
18.
Среднее квадратическое отклонение –это квадратный корень из выборочной
дисперсии
B
DB
19. 3. Оценка параметров генеральной совокупности по ее выборке
Числовыезначения,
характеризующие
генеральную
совокупность, называются параметрами.
Одна из задач математической
статистики – определение параметров
большого массива по исследованию его
части.
20.
Статистическое оценивание можетвыполняться двумя способами:
1). Точечная оценка – оценка, которая
дается для некоторой определенной точки.
2). Интервальная оценка – по данным
выборки оценивается интервал, в котором
лежит истинное значение с заданной
вероятностью.
21.
Несмещенной оценкойсредней
(математического
служит выборочная средняя
генеральной
ожидания)
x ГЕН xB
22.
Выборочная дисперсия не обладаетсвойством несмещенности.
Это смещенная оценка генеральной
дисперсии .
23.
Напрактике
используют
исправленную
выборочную
дисперсию,
которая является несмещенной оценкой
дисперсии генеральной совокупности:
n DB
S
n 1
2
DГЕН S
2
24.
Кроме того, в расчетах используют S исправленное среднее квадратическоеотклонение, называемое стандартным
отклонением
ГЕН S
25.
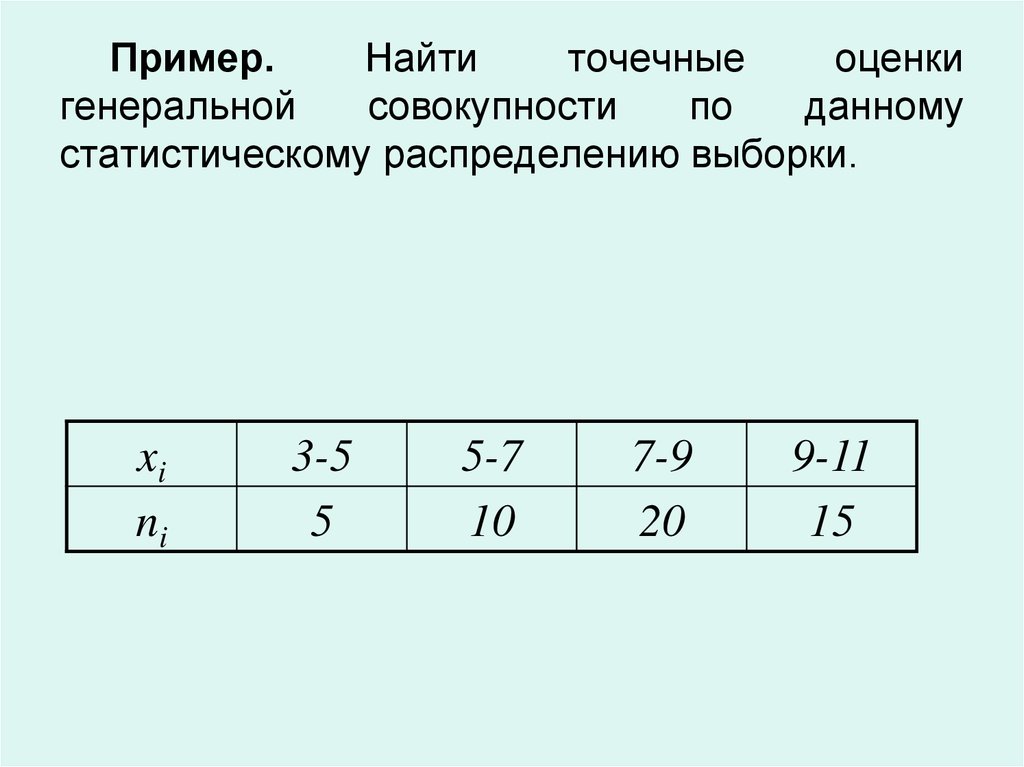
Пример.Найти
точечные
оценки
генеральной
совокупности
по
данному
статистическому распределению выборки.
xi
ni
3-5
5
5-7
10
7-9
20
9-11
15
26.
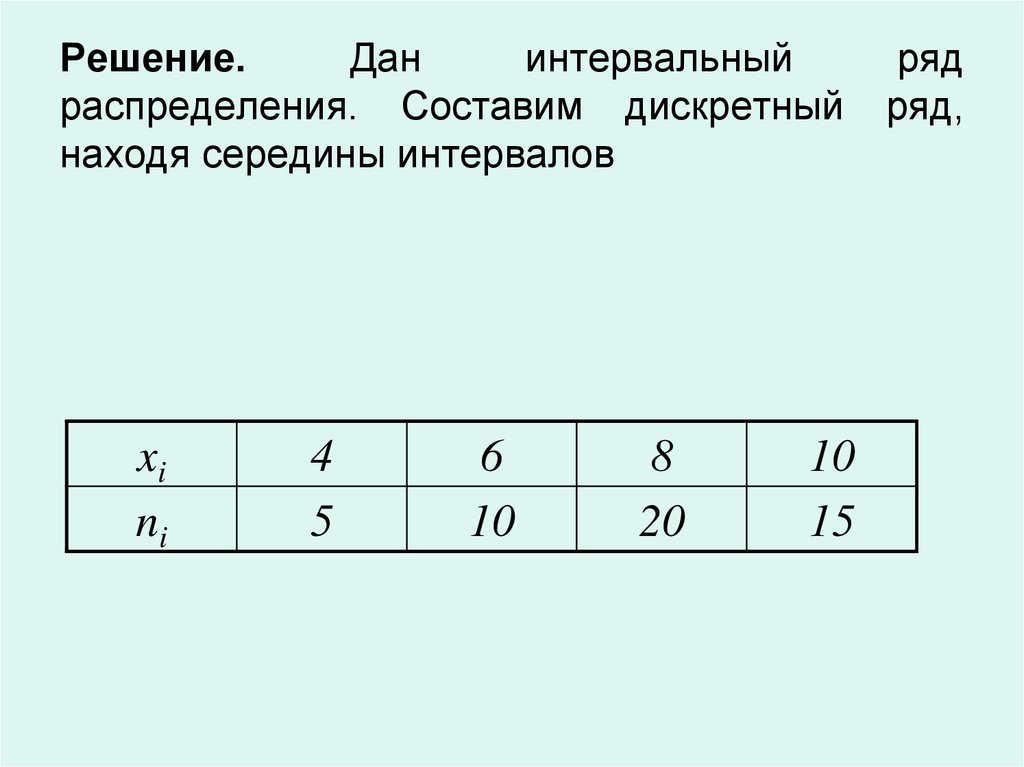
Решение.Дан
интервальный
распределения. Составим дискретный
находя середины интервалов
xi
ni
4
5
6
10
8
20
10
15
ряд
ряд,
27.
4 5 6 10 8 20 10 15xB
7,8
50
x Г 7,8
4 5 6 10 8 20 10 15
2
DB
7,8 3,56
50
2
2
2
2
28.
50 3,56S
3,63
50 1
2
DГ 3,63
Г 3,63 1,906
29. Тема. Проверка статистических гипотез
План:1.
Основные
понятия
теории
статистических гипотез.
2. Общая постановка задачи проверки
гипотез.
3.
Проверка
гипотез
относительно
средних (критерий Стьюдента).
4.
Проверка
гипотез
о
законах
распределения.
30. 1. Основные понятия теории статистических гипотез
Статистическая гипотеза – это любоепредположение
о
виде
неизвестного
распределения или о параметрах известных
распределений.
Статистическая гипотеза – это всякое
высказывание о генеральной совокупности,
проверяемое по выборке.
31.
Процедурасопоставления
высказанного
предположения
(гипотезы)
с
выборочными
данными называется проверкой
гипотез.
32.
Гипотезы будем обозначать буквой Н синдексами. Будем предполагать, что у нас
имеется 2 непересекающиеся гипотезы H0 и
H 1.
H0 – нулевая гипотеза (или основная).
H1 – альтернативная или конкурирующая
гипотеза.
33.
Выдвинутая гипотеза может бытьправильной или неправильной, поэтому
возникает необходимость ее проверки.
Задача проверки статистических
гипотез состоит в том, чтоб на основе
выборки
x1 , x2 , x3 ,..., xn
принять
(т.
е.
считать
справедливой) либо нулевую гипотезу ,
либо конкурирующую гипотезу .
34.
При проверке гипотезы может быть принятонеправильное решение, то есть могут быть
допущены ошибки двух родов:
Ошибка первого рода состоит в том, что
отвергается нулевая гипотеза H0, когда на
самом деле она верна.
Ошибка второго рода состоит в том, что
отвергается альтернативная гипотеза H1,
когда на самом деле она верна.
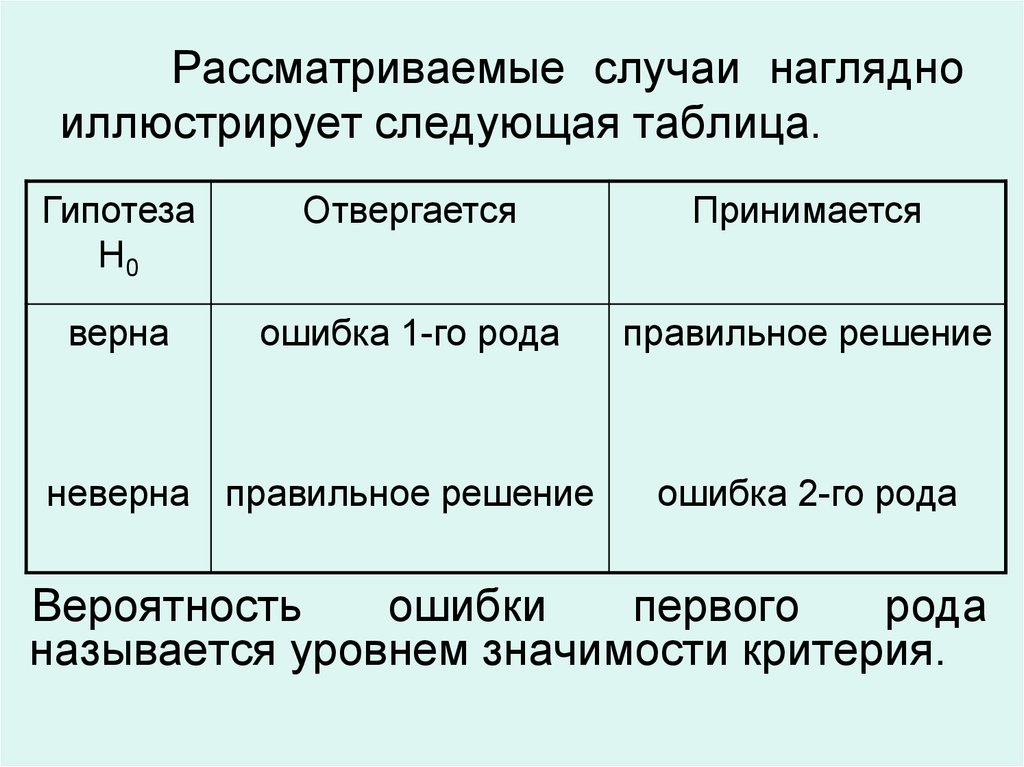
35. Рассматриваемые случаи наглядно иллюстрирует следующая таблица.
ГипотезаH0
Отвергается
Принимается
верна
ошибка 1-го рода
правильное решение
неверна правильное решение
ошибка 2-го рода
Вероятность
ошибки
первого
рода
называется уровнем значимости критерия.
36.
Для проверки принятой гипотезыиспользуют статистический критерий – это
правило, позволяющее, основываясь только
на выборке
, принять либо
x1 , x2 , x3 ,..., xn
отвергнуть нулевую гипотезу .
Различают
два
вида
критериев:
параметрические и непараметрические.
37.
Параметрическиекритерии
представляют собой функции параметров
данной совокупности и используются, если
совокупности, из которых взяты выборки,
подчиняются
нормальному
закону
распределения.
Непараметрические
критерии
применяются,
если
нет
подчинения
распределения нормальному закону.
38. 2. Общая постановка задачи проверки гипотез
1. Формулируют (выдвигают) нулевуюгипотезу об отсутствии различий между
группами, об отсутствии существенного
отличия фактического распределения от
некоторого
заданного,
например,
нормального, экспоненциального и др.
39.
2. Формулируют противоположнуюнулевой альтернативную гипотезу .
3. Задают уровень значимости .
Уровень значимости
- это
вероятность
ошибки
отвергнуть
нулевую гипотезу , если на самом деле
эта гипотеза верна.
При 0,05 ошибка возможна в 5%
случаев.
40.
4. Для проверки выдвинутой гипотезыиспользуют критерии.
Критерий – это случайная величина К,
которая служит для проверки H0. Эти
функции
распределения
известны
и
табулированы.
Критерий зависит от двух параметров: от
числа степеней свободы и от уровня
значимости. Фактическую величину критерия
получают по данным наблюдения K НАБЛ .
41.
5.По
таблице
определяют
критическое
значение,
превышение
которого при справедливости гипотезы
маловероятно К КРИТ , f
6. Сравнивают K НАБЛ и ККРИТ , f .
Если К НАБЛ К КРИТ , f , то отвергают H0 и
принимают H1.
Если К НАБЛ К КРИТ , f , то отвергают H1 и
принимают H0.
7. Вывод: различие статистически
значимо (0,05) или незначимо .
42.
3. Проверка гипотезотносительно средних
Сравнивают друг с другом две независимые
выборки объемов n1 и n2 , взятые из нормально
распределенных совокупностей с параметрами M(X1) и
M(X2) . Дополнительно предполагаем, что неизвестные
генеральные дисперсии равны между собой. По этим
выборкам найдены соответствующие выборочные
средние x1 и x2
и исправленные дисперсии S12 и S22. Уровень
значимости задан.
43. 3. Проверка гипотез относительно средних
1. Нулевая гипотеза H0: M(X1) = M(X2) ;2. Альтернативная гипотеза H1: M X 1 M X 2
3. 0,05
4. Для проверки нулевой гипотезы в этом
случае можно использовать критерий
Стьюдента сравнения средних.
Величину критерия находим по формуле:
t НАБЛ
n1 n2 n1 n2 2
2
2
n1 n2
n1 1 S1 n2 1 S2
x1 x2
44.
Доказано, что величина t НАБЛ присправедливости нулевой гипотезы имеет
t – распределение Стьюдента с
f n1 n2 2
степенями свободы.
45.
5. По таблице находим tКРИТ , f n1 n2 26. Сравниваем tКРИТ и tНАБЛ .
Если tНАБЛ tКРИТ , f H0
Если t НАБЛ tКРИТ , f H1 различие
достоверно
46.
Пример.По двум независимым малым выборкам
объемов n1=5 и n2=6 , извлеченным из
нормальных генеральных совокупностей X1 и
X2, вычислены выборочные средние:
x1 3,3
и
x2 2,48 .
Известно, что генеральные дисперсии
примерно равны, т. е. D ГЕН D ГЕН .
При уровне значимости 0,05 проверить
нулевую гипотезу H0: M(X1) = M(X2) если
t НАБЛ 3,27 .
1
2
47.
Решение.tКРИТ 0,05, f n1 n2 2 5 6 2 9 2,26.
tНАБЛ tКРИТ , f отвергаемH 0
Вывод: выборочные средние различаются
значимо 0,05
.
48. Решение.
4. Проверка гипотез о законахраспределения
Во многих практических задачах закон
распределения случайных величин заранее не
известен,
и
надо
выбрать
модель,
согласующуюся с результатами наблюдений.
Выдвигают
нулевую
гипотезу:
неизвестная
функция
распределения
исследуемой
случайной
величины
X
распределена по некоторому теоретическому
закону, например, по нормальному закону
H 0 : F x FТЕОР x
49. 4. Проверка гипотез о законах распределения
В качестве этой теоретической моделиможет быть рассмотрен любой закон,
например,
экспоненциальный
или
биномиальное распределение.
Это
определяется
сущностью
изучаемого явления, а также результатами
предварительной обработки наблюдений:
формой
графика
распределения,
соотношениями
между
выборочными
данными.
50.
Выдвигается альтернативная гипотеза, чтоданная
генеральная
совокупность
не
распределена по закону
FТЕОР x :
H 1 : F x FТЕОР x
Задается уровень значимости, например,
0,05
Если
хотим
проверить,
согласуются
эмпирические данные с нашим гипотетическим
предположением относительно теоретической
функции
распределения
или
нет,
то
используем критерий согласия.
51.
Критерий согласия – это критерийпроверки гипотезы о предполагаемом законе
неизвестного распределения.
Рассмотрим один из них, использующий
2
распределение
и получивший
название критерий согласия Пирсона.
2
Применим критерий
к проверке
нулевой гипотезы , что генеральная
совокупность распределена нормально.
52.
Критерий предполагает, что результатынаблюдений
сгруппированы
в
вариационный ряд и разбиты на классы.
По выборке объема n построим
эмпирическое распределение FЭМП x :
варианты:
x1 , x2 ,..., xk ;
эмпирические частоты: n1 , n2 ,..., nk
;
и сравним его с предполагаемым
теоретическим
распределением,
вычисленным
в
предположении
нормального закона распределения.
Теоретические частоты: n1 , n2 ,..., nk .
53.
То есть фактическиH 0 : nЭМП nТЕОР
В качестве критерия проверки нулевой
гипотезы примем случайную величину:
2
k
n
n
2
ТЕОР
,
НАБЛ
ЭМП
i 1
nТЕОР
где k – число классов.
2
Из таблиц находим КРИТ 0,05; f k. 3
2
2
Сравниваем, если НАБЛ КРИТ , f H 0
- расхождение теоретических и эмпирических
частот незначимое. Следовательно, данные
наблюдений
согласуются
с
гипотезой
о
нормальном законе распределения генеральной
совокупности.
54.
Пример.При уровне значимости 0,05 проверить
гипотезу о нормальном распределении
генеральной совокупности, если известны
эмпирические и теоретические частоты.
эмпирические частоты:
6 13 38 74 106 85 30 14;
теоретические частоты:
3 14 42 82 99 76 37 13.
55. Пример.
Решение.2
НАБЛ
7,19
2
0,05, f 8 3 5 11,1
КРИТ
Найдем
2
2
Сравниваем:
НАБЛ
КРИТ , f H 0
- расхождение теоретических и эмпирических
частот незначимое.
Следовательно,
данные
наблюдений
согласуются с гипотезой о нормальном законе
распределения генеральной совокупности.























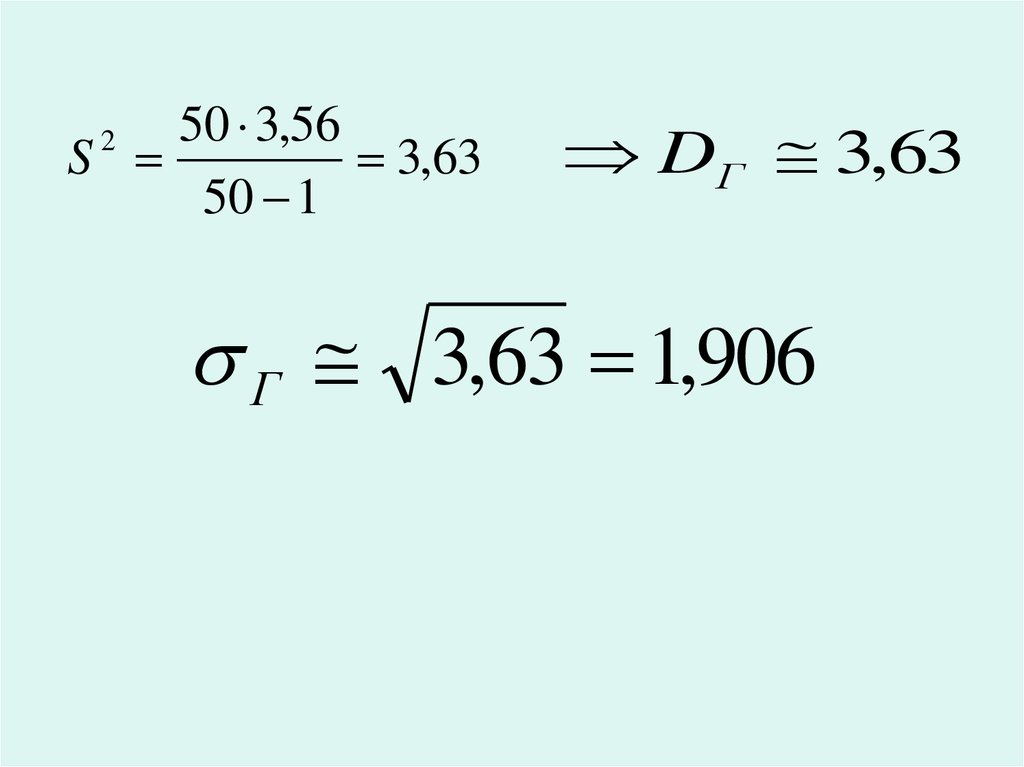


























 Математика
Математика








