Похожие презентации:
Производная сложной функции
1. Производная
2.
Производной функции f(x) вточке х0 называется предел отношения
приращения функции к приращению
аргумента при Δx→0, если этот предел
существует.
Функцию, имеющую производную в точке х0
называют дифференцируемой в этой точке.
3.
Физический смысл производнойv(t ) S (t )
a(t ) v (t ) S (t )
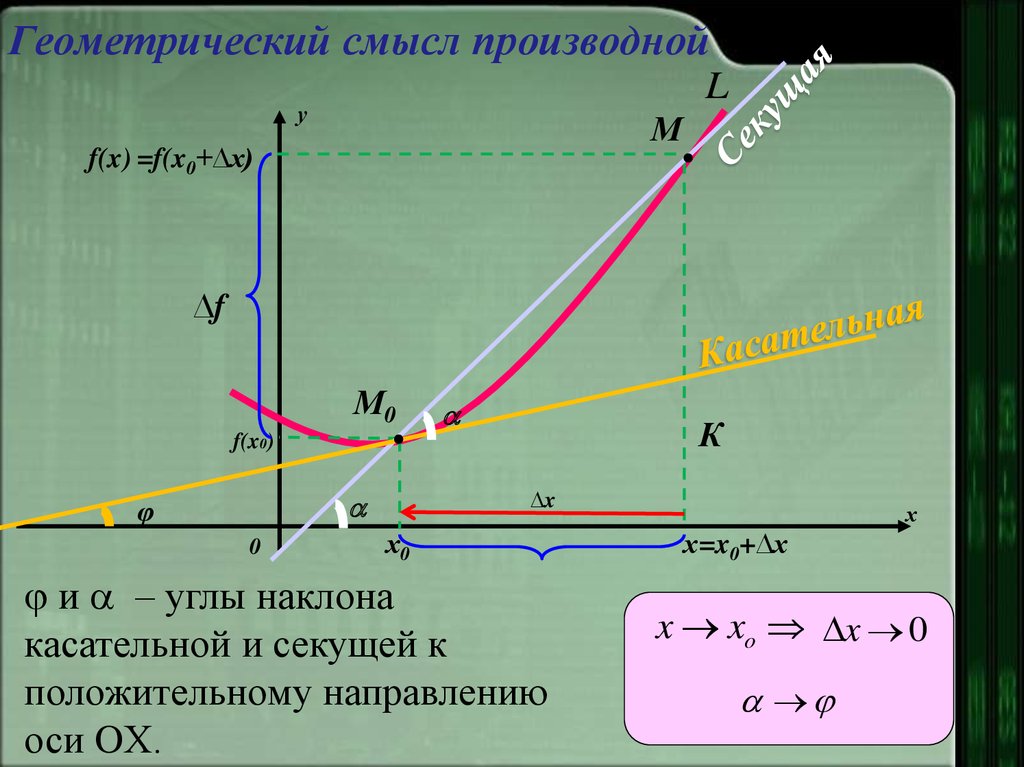
Геометрический смысл производной
Касательной к кривой L
называется предельное положение
секущей MM0, когда точка М
стремится к точке М0 по кривой L.
4. Геометрический смысл производной
Lу
М
f(x) =f(x0+∆x)
∆f
М0
К
f(x0)
φ
0
∆x
х0
и – углы наклона
касательной и секущей к
положительному направлению
оси OХ.
х
х =x0+∆x
x xo x 0
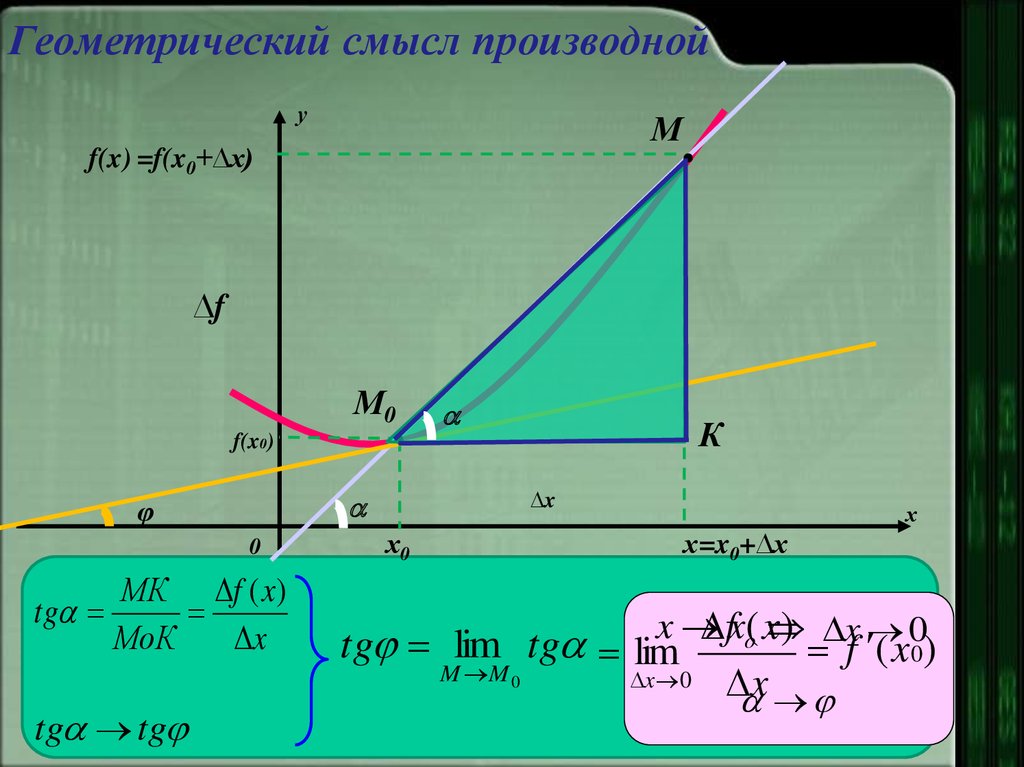
5. Геометрический смысл производной
уМ
f(x) =f(x0+∆x)
∆f
М0
К
f(x0)
φ
0
МК f ( x)
tg
МоК
x
tg tg
∆x
х0
х
х =x0+∆x
x
fxo( x
) x 0
tg lim tg lim
f ( x 0)
M M 0
x 0 x
6.
Геометрический смысл производной –это тангенс угла наклона касательной,
проведённой к графику функции в данной
точке (угловой коэффициент касательной).
Уравнение
касательной
Уравнение прямой, проходящей через точку х0
f(x) - f(x 0 )
k tg
x - x0
f ( x) f ( x0 )
f ( x0 )
x x0
k tg f ( x0 )
f ( x) f ( x0 ) f ( x0 )( x x0 )
f ( x) f ( x0 ) f ( x0 )( x x0 )
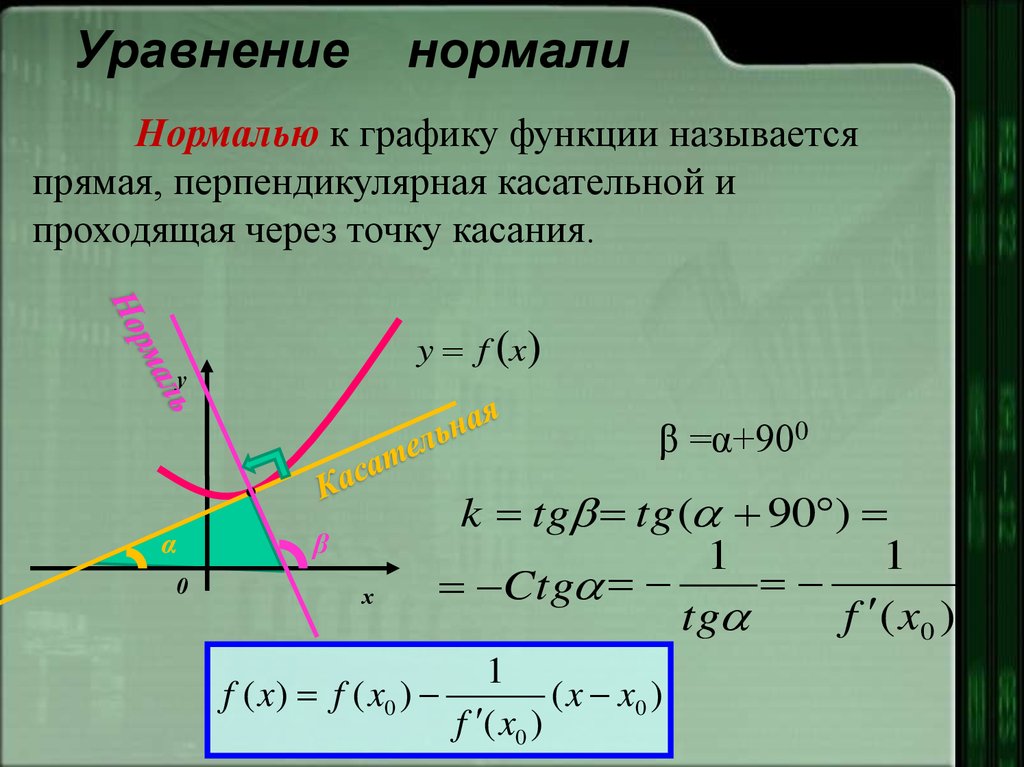
7. Уравнение нормали
Нормалью к графику функции называетсяпрямая, перпендикулярная касательной и
проходящая через точку касания.
y f x
у
β =α+900
α
β
0
х
k tg tg ( 90 )
1
1
Ctg
f ( x0 )
tg
1
f ( x) f ( x0 )
( x x0 )
f ( x0 )
8. Составить уравнение касательной и нормали к графику функции y=2x3+x2-x+3 в точке x0=2
f ( x) f ( x0 ) f ( x0 )( x x0 )1
f ( x) f ( x0 )
( x x0 )
f ( x0 )
f (2) 2 23 22 2 3 21
f ( x) 6 x 2 2 x 1
f (2) 6 22 4 1 27
f ( x) 21 27( x 2)
1
f ( x) 21 ( x 2)
27
f ( x) 21 27 x 54
f ( x) 27 x 33
уравнение касательной
1
2
f ( x)
x 21
27
27
уравнение нормали
9.
Правила дифференцированияu=f(x)
Производная
суммы и разности
Производная
произведения
Постоянный
множитель
выносится за знак
производной
Производная
частного
v=g(x)
• (u±v)’=u’ ±v’
• (u•v)’=u’ v+v’u
• (Cu)’=Cu’
u v v u
v2
v
• u
u
u
C
C
10. Производная сложной функции
Функция является сложной, если оназависит от аргумента через одну или несколько
других функций.
Определите является ли функция сложной:
2
u
x
3
u
sin
x
2
да
1) y sin x
да
6
)
y
sin(
x
3)
y u g sin u
2) y cos x
3) y x
3
нет
y
ln x
7) y
3
нет
4 x нет
4) y log 3 ( x нет
1) да
3
1
5) y cos
x
g
u x3 1
y log 3 u
8) y
4
x
3
1
4
u
u
x
3x
да
4
3
x
9
)
y
(
x
3
x
)
y да
cos uy u 3
11. Теорема о производной сложной функции:
Если функция Z(y(х))дифференцируема по y, а у(х)
дифференцируема по х, то Z'(x)=Z'y·y'x
y sin x
y
u
sin x
u sin x
u cos x
1
u
cos x
2 u
2 sin x
1
cos x
2 sin x
12. Примеры:
1) (eSin2 5 x
5e
)' (e )' e u e
Sin2 5 x
u
u
sin2 5 x
(sin 5x)
2
2 Sin5 x Cos5x 5Sin10 x e
Sin2 5 x
u Sin 2 5 x
( Sin 5 x)' ( g )' 2 g g 2 Sin 5 x( Sin 5 x)'
2 Sin5x 5 Cos5x
2
2
g Sin 5 x
( Sin5 x) 5Cos5 x
13.
12) Ln(tg x Sinx ) ' Lnu ' u
u
1
3
tg x Sinx
3
tg x Sinx
3
1
tg x 3 Sinx Cos
u tg x 3 Sinx b
1
2
3x 2 Cosx
x Sinx 2 x 3 Sinx
3
x3 Sinx
1
1
tg x Sinx tgb
b
2
2
3
Cos b
Cos x Sinx
3
x Sinx
3
1
2 x Sinx
3
x3 Sinx
3x 2 Cosx
2 x 3 Sinx
x Sinx
3
14.
12) Ln(tg x Sinx ) ' Lnu ' u
u
1
3
tg x Sinx
3
tg x Sinx
3
1
tg x 3 Sinx
1
Cos
3x 2 Cosx
x Sinx 2 x Sinx
2
3
3
3x 2 Cosx
tg ( x Sinx ) Cos ( x Sinx ) 2 x Sinx
3
2
3
3
Cos ( x 3 Sinx ) (3 x 2 Cosx)
Sin( x Sinx ) Cos ( x Sinx ) 2 x Sinx
3
2
3
3
(3x 2 Cosx)
x3 Sinx Sin(2 x3 Sinx )











 Математика
Математика








