Специальная теория относительности (СТО)

1. Специальная теория относительности (СТО)

2. Постулаты Эйнштейна (1905 г.)

Постулаты Эйнштейна (1905 г.)
• Принцип
• Принцип постоянства
относительности: все
скорости света:
законы природы
скорость света в вакууме
инвариантны по
не зависит от скорости
отношению к переходу от
движения источника
одной инерциальной
света или наблюдателя и
системы отсчета к
одинакова во всех
другой.
инерциальных системах
отсчета.
Эйнштейн Альберт
1879 – 1955

3. Принцип существования предельной скорости материальных объектов

Фундаментальный закон природы:
существует предельная скорость движения
материальных объектов, она одинакова во
всех ИСО и численно равна скорости света
в вакууме.

4.

Понятно, что одновременно удовлетворять
принципам относительности Эйнштейна и
принципу постоянства скорости света
преобразования Галилея не могут.
Но этим условиям удовлетворяют
преобразования Лоренца, с которых начинается
специальная теория относительности и из
которых вытекает ряд необычных с точки зрения
ньютоновской механики следствий.

5. Преобразования Лоренца

Получим преобразования Лоренца, опираясь на
постулаты Эйнштейна.
Учитывая однородность пространства и времени,
можно предположим, что новые преобразования
линейны, тогда
x x' vt'
По принципу относительности все инерциальные
системы отсчета равноправны, следовательно,
можно записать
x ( x vt )

6. Преобразования Лоренца

• Пусть в момент t 0 , когда начала систем отсчета
К и K’ совпадали, произошла вспышка света. Тогда
распространение света будет происходить по
законам:
x ct ,
x ct
Следовательно,
ct c v t '
ct (c v)t

7. Преобразования Лоренца

• Подставив значение
первое, получим
t из второго уравнения в
t
ct c v
c
2
• откуда
, 2
2
1
2
v
1 2
c

8. Преобразования Лоренца

• Подставив значение
x x' vt'
или
в одну из формул
x ( x vt )
и решив полученное уравнение относительно t,
получим
vx'
t t ' 2
c

9. Преобразования Лоренца

y
z
к
y'
{x',y',z'}
к'
V
x
x'
z'
V /c
1/ 1 V 2 / c2 1/ 1 2
x x V t
x
x V t
y y
V2
1 2
c
z z
t
V
x
2
c
V2
1 2
c
t
t t x / c

10. Относительность одновременности

y
к
y'
к'
V
x
z
z'
x
x V t
2
; t
V
1 2
c
1
Пусть в системе к'
2
x1
x2
x'
V
x
2
c
V2
1 2
c
t1 t2 ,
x x V t
t t x / c
x1 x2
Покажем, что в системе
к
t1 t2
t
или
но
Доказательство:
t1 t 2 t x1 t 2 x2
c
c
c
x 0

11. Пространство и время в движущихся ИСО

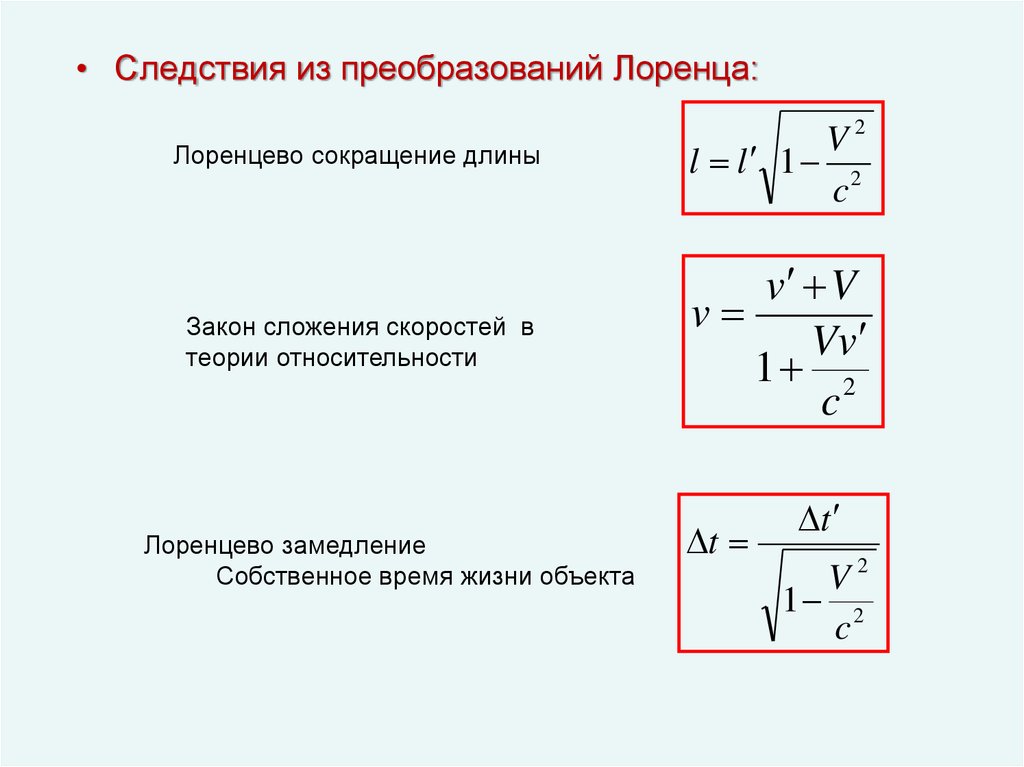
• Следствия из преобразований
Лоренца:
Лоренцево сокращение длины

12.

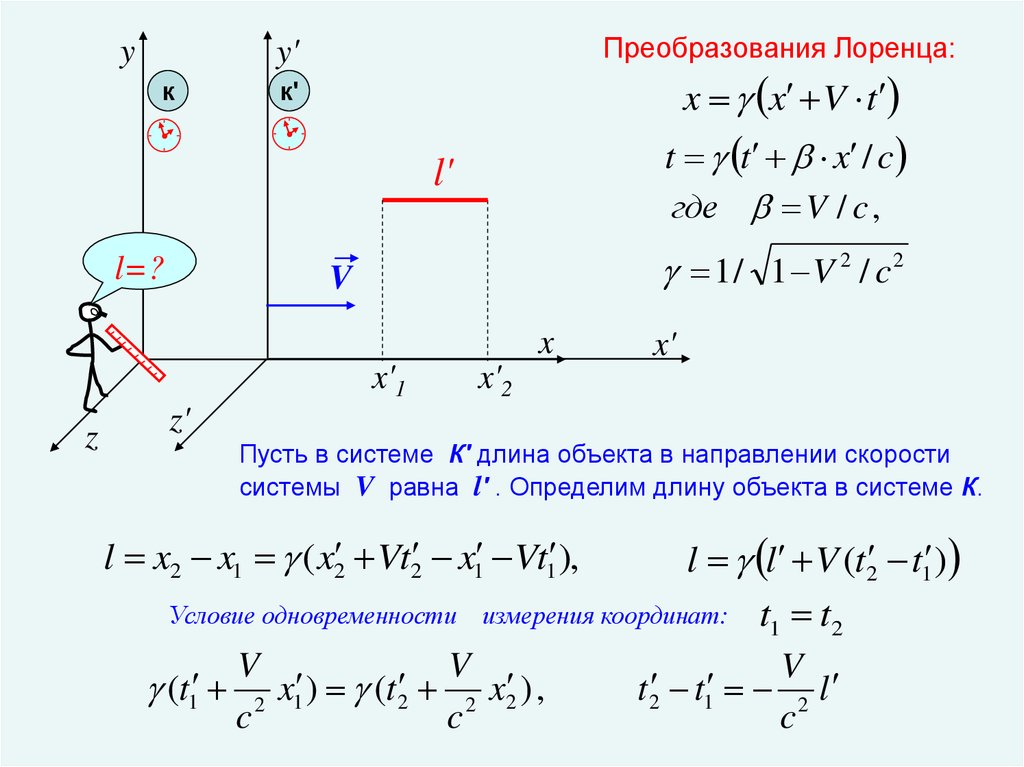
y
Преобразования Лоренца:
y'
к
x x V t
к'
t t x / c
где V / c ,
l'
l=?
1/ 1 V 2 / c2
V
x
x'1
z
x'
x'2
z'
Пусть в системе К' длина объекта в направлении скорости
системы V равна l' . Определим длину объекта в системе К.
l l V (t2 t1 )
Условие одновременности измерения координат: t1 t2
V
V
V
(t1 2 x1 ) (t 2 2 x2 ) ,
t 2 t1 2 l
c
c
c
l x2 x1 ( x2 Vt2 x1 Vt1 ),

13.

y
y'
к
к'
l l V (t2 t1 )
l'
t 2 t1
l=?
V
x
x'1
z
x'2
z'
V2
l l 1 2
c
V2
l l 1 2
c
x'
l
V2
1 2
V2 c
1 2
c
l l
!
V
l
2
c

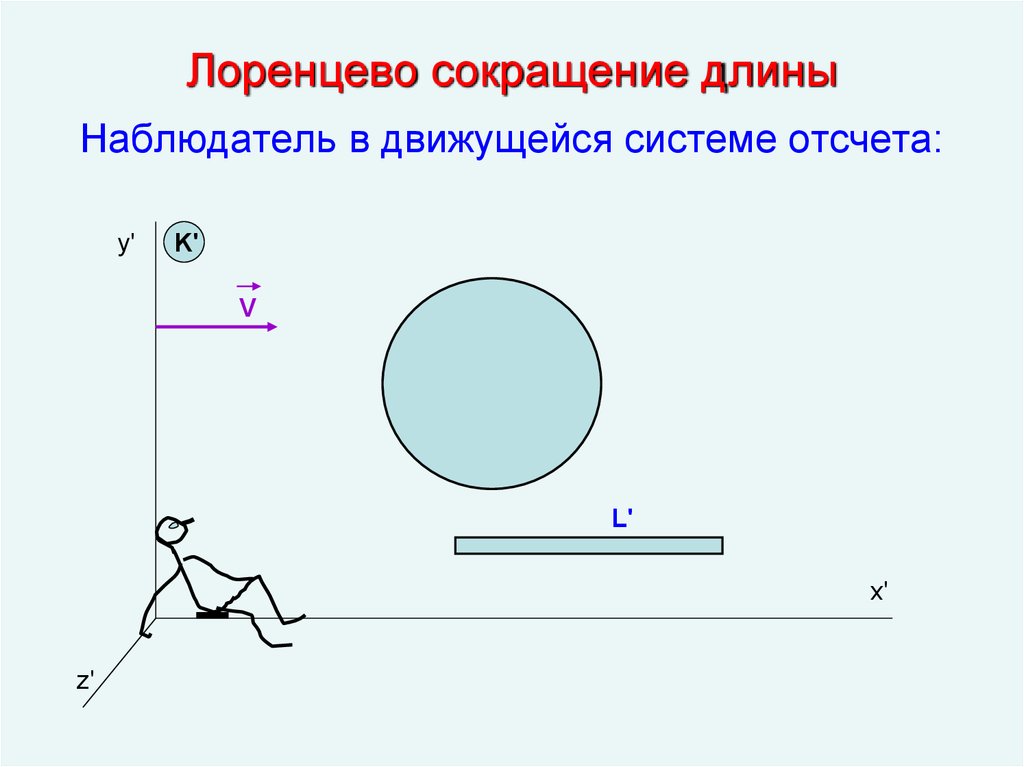
14. Лоренцево сокращение длины

Наблюдатель в движущейся системе отсчета:
y'
K'
V
L'
x'
z'

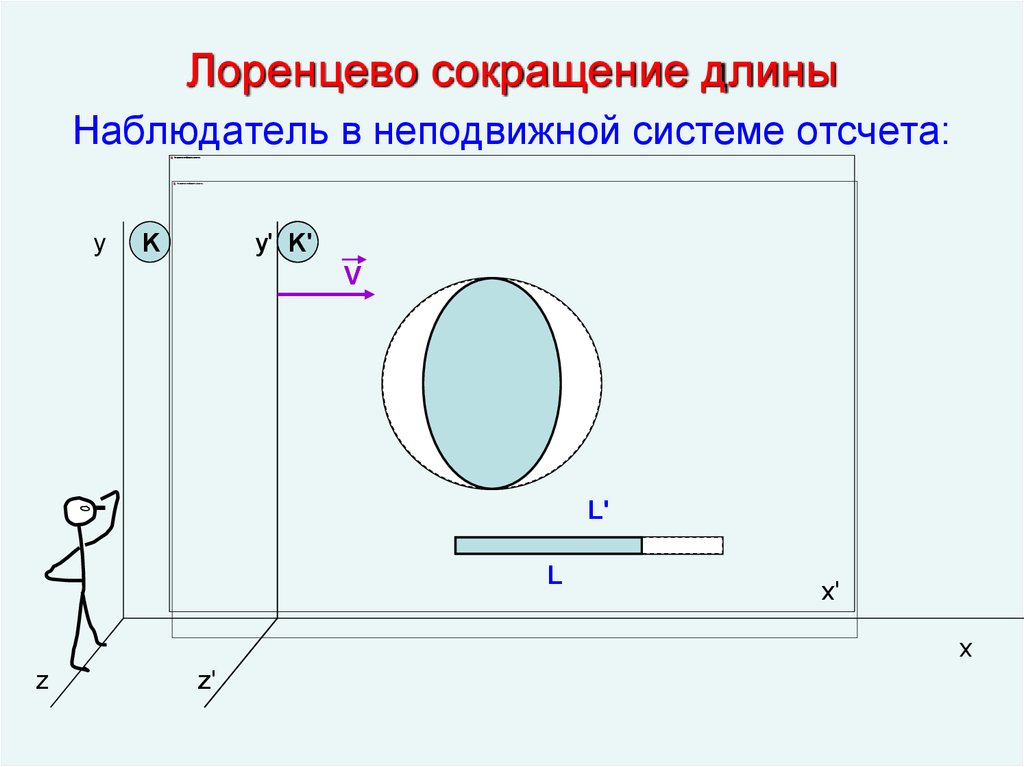
15. Лоренцево сокращение длины

Наблюдатель в неподвижной системе отсчета:
y
K
y' K'
V
L'
L
x'
x
z
z'

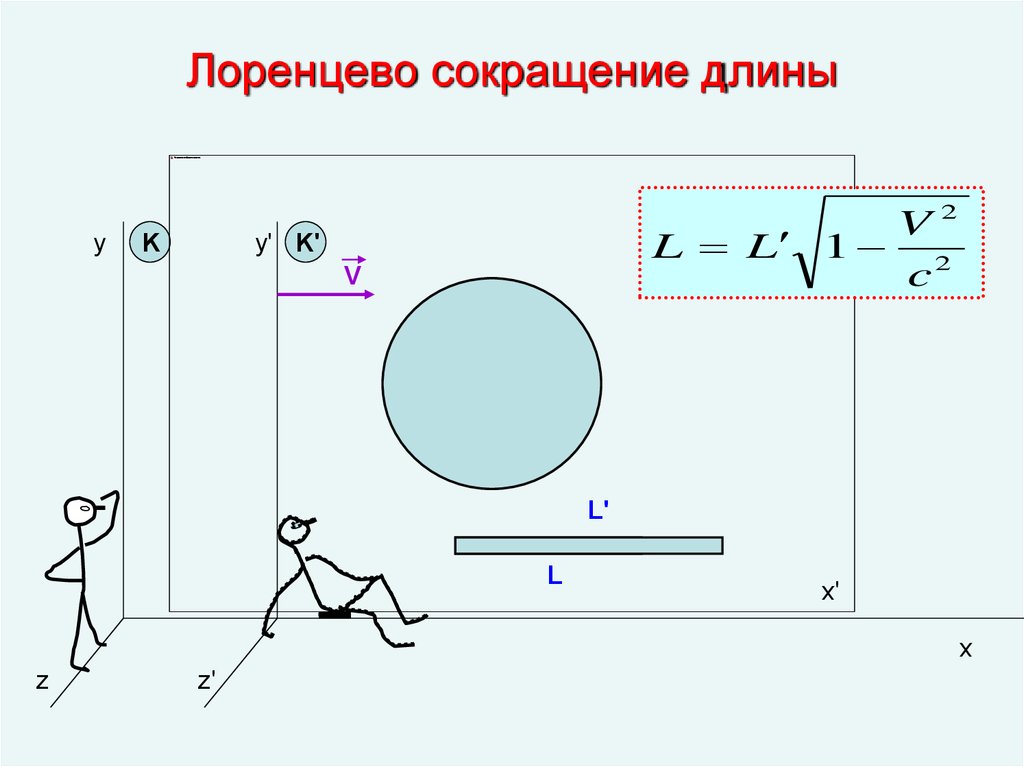
16. Лоренцево сокращение длины

y
K
V2
L L 1 2
c
y' K'
V
L'
L
x'
x
z
z'

17. Пространство и время в движущихся ИСО

• Следствия из преобразований
Лоренца:
Закон сложения скоростей
в теории относительности

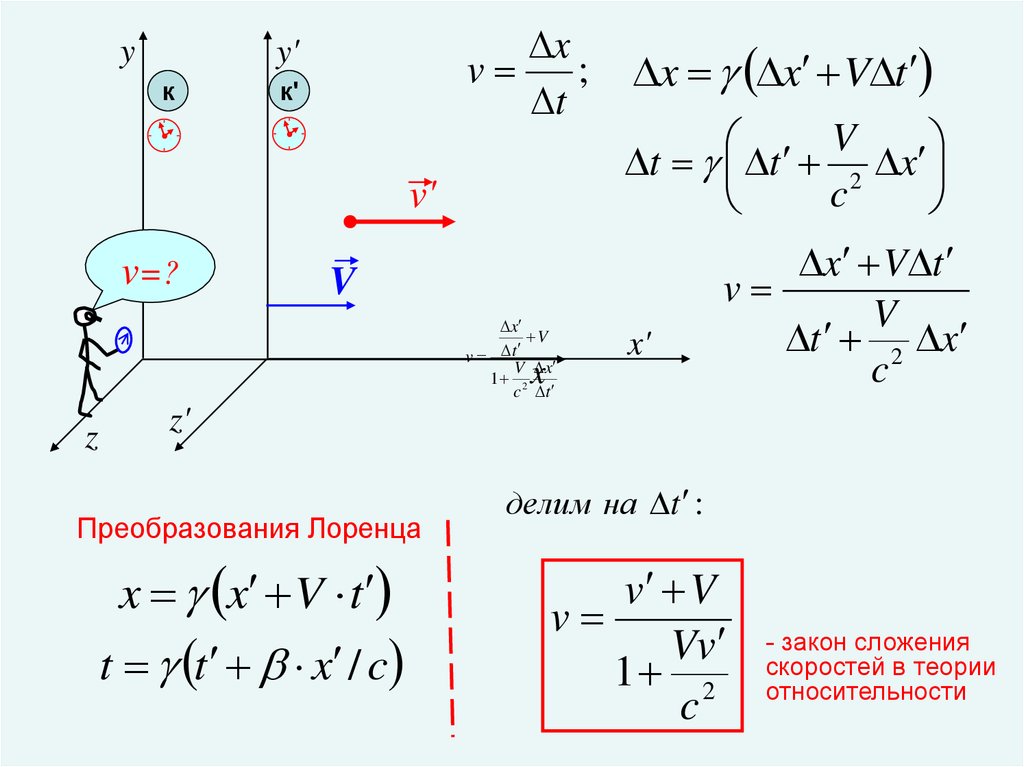
18.

y
x
v
;
t
y'
к
к'
v'
v=?
V
t t 2 x
c
V
x
V
v t
V x
1 2
c t
x
z
x x V t
x'
x V t
v
V
t 2 x
c
z'
Преобразования Лоренца
x x V t
t t x / c
делим на t :
v V
v
Vv
1 2
c
- закон сложения
скоростей в теории
относительности

19. Пространство и время в движущихся ИСО

• Следствия из преобразований
Лоренца:
Лоренцево замедление
Собственное время жизни объекта

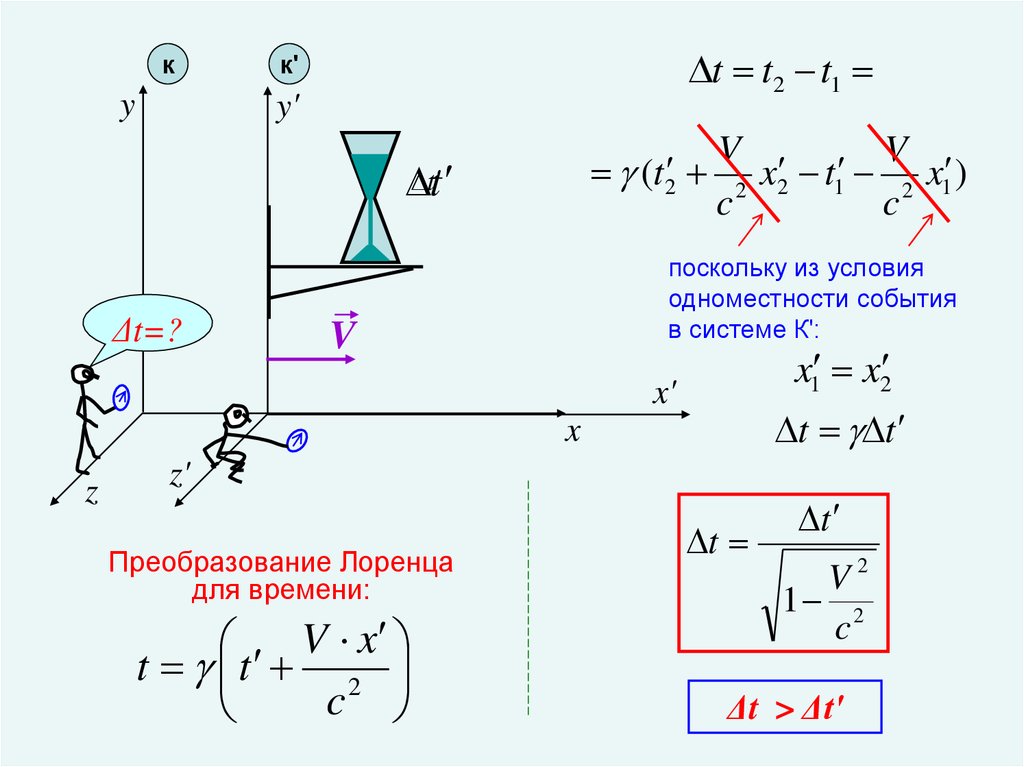
20.

к
y
t t2 t1
к'
y'
V
V
(t 2 2 x2 t1 2 x1 )
c
c
tt
Δt=?
поскольку из условия
одноместности события
в системе К':
V
x1 x2
x'
t t
x
z
z'
Преобразование Лоренца
для времени:
V x
t t 2
c
t
t
V2
1 2
c
Δt > Δt′

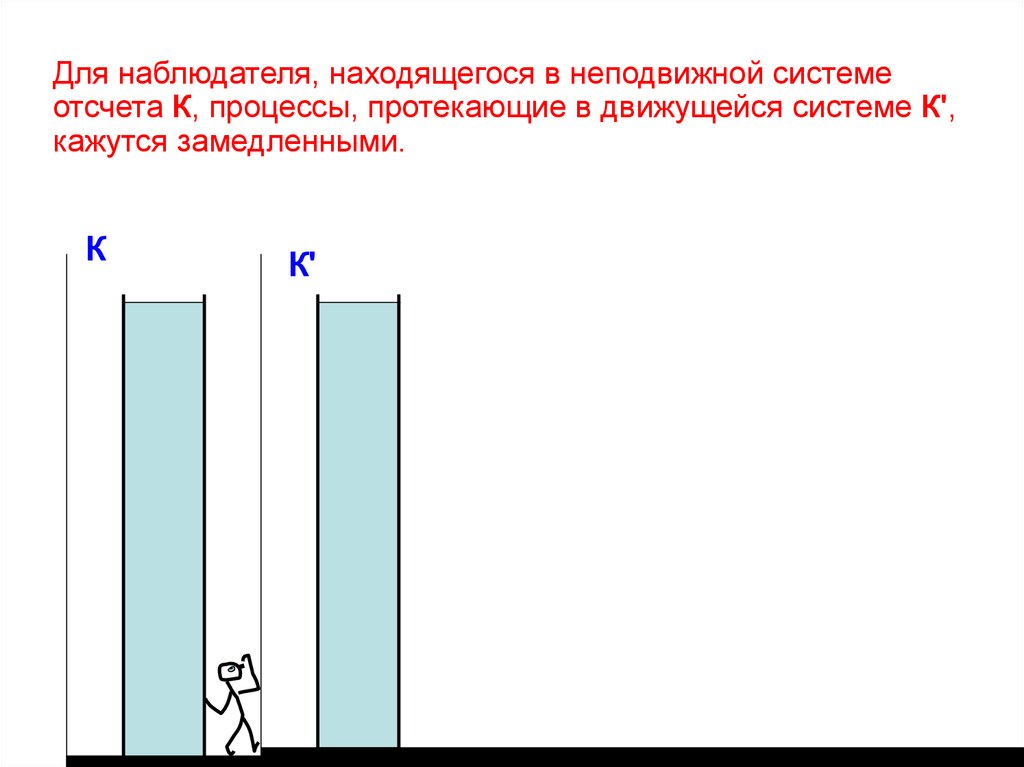
21.

Для наблюдателя, находящегося в неподвижной системе
отсчета К, процессы, протекающие в движущейся системе К',
кажутся замедленными.
К
К'

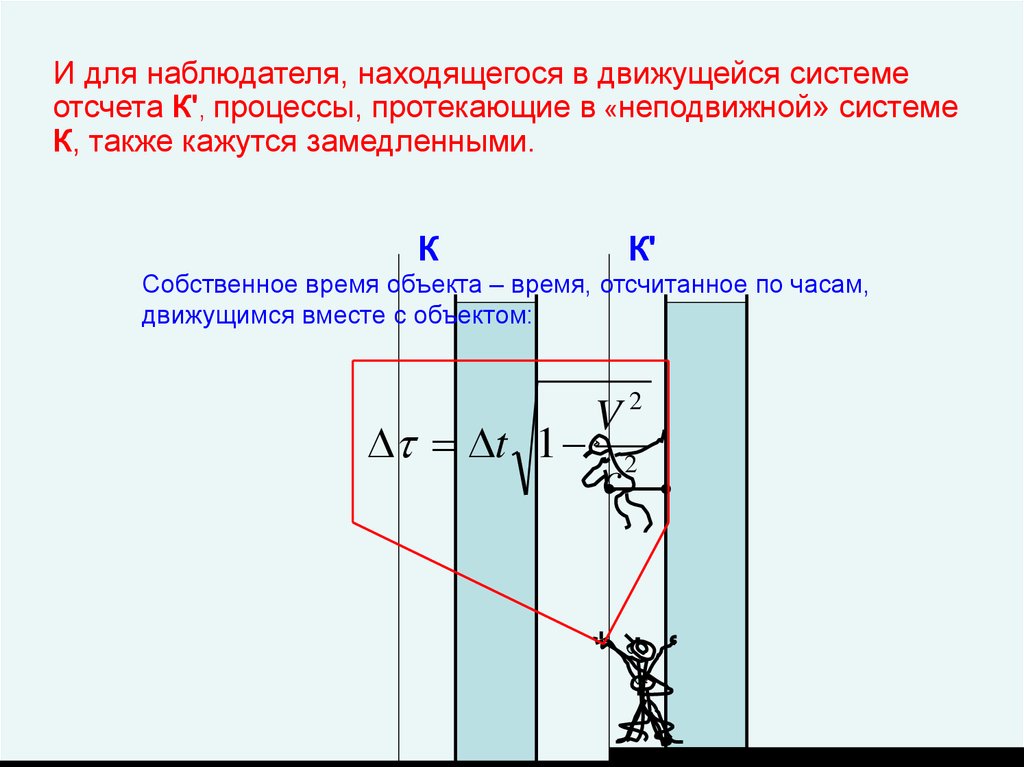
22.

И для наблюдателя, находящегося в движущейся системе
отсчета К', процессы, протекающие в «неподвижной» системе
К, также кажутся замедленными.
К
К'
Собственное время объекта – время, отсчитанное по часам,
движущимся вместе с объектом:
V2
t 1 2
c

23. Пространство и время в движущихся ИСО

Единое пространственновременное описание. Интервал

24.

x'=f(x,t),
t'=φ(x,t)
Δr ≠ inv,
Δt ≠ inv
с = inv
(доказать самостоятельно!)

25.

• Следствия из преобразований Лоренца:
Лоренцево сокращение длины
V2
l l 1 2
c
Закон сложения скоростей в
теории относительности
v V
v
Vv
1 2
c
Лоренцево замедление
Собственное время жизни объекта
t
t
V2
1 2
c

26. Энергия и импульс

• Релятивистская энергия и релятивистский импульс
будут определяться следующими выражениями:
E
mc 2
p
2
v
1 2
c
mv
v2
1 2
c
Закон взаимосвязи массы и энергии был установлен
Эйнштейном и является фундаментальным законом природы
E mc 2
E
mc 2
1 2
c
2
-энергия покоя
-энергия движения

27. Связь между релятивистским импульсом и энергией

• Запишем выражения для импульса и энергии и
исключим из них скорость
E
p
mc 2
2
v
1 2
c
mv
v2
1 2
c
• После преобразований получим
E m c p c
2
2
4
2
2
• Можно записать еще одну формулу
pc 2
E
v

28. Кинетическая энергия

• Кинетическая энергия релятивистской
частицы определяется
Ek
mc 2
2
1 2
c
mc 2

29. Уравнение динамики

• Основное уравнение динамики
d mv
F
2
dt
v
1
2
c