Похожие презентации:
Математическая логика. Логика высказываний
1. МАТЕМАТИЧЕСКАЯ ЛОГИКА
2.
Основная литература1. Молчанов, В. А. Логика высказываний. –
Саратов, 2014.
2. Ю. Л. Ершов, Е. А. Палютин. Математическая
логика. – М., 2011.
3. Игошин, В. И. Математическая логика и теория
алгоритмов. – М., 2010.
4. Игошин, В. И. Сборник задач по математической
логике и теории алгоритмов. – М., 2008.
3. Предмет математической логики
4.
Логика возникла в VI—IV вв. до н. э. как«анализ мышления», т.е. анализ принципов
правильных рассуждений.
Основоположник
логики
–
древнегреческий ученый Аристотель (384322 гг. до н. э.), который в сочинениях
«Аналитики» впервые изложил идею
дедуктивного вывода.
5.
ЛОГИКА (ФОРМАЛЬНАЯ)изучает
формы,
в
которых
проявляются
законы
причинноследственных
связей,
вне
зависимости от содержания (смысла)
тех явлений (предметов), к которым
эти законы относятся.
6.
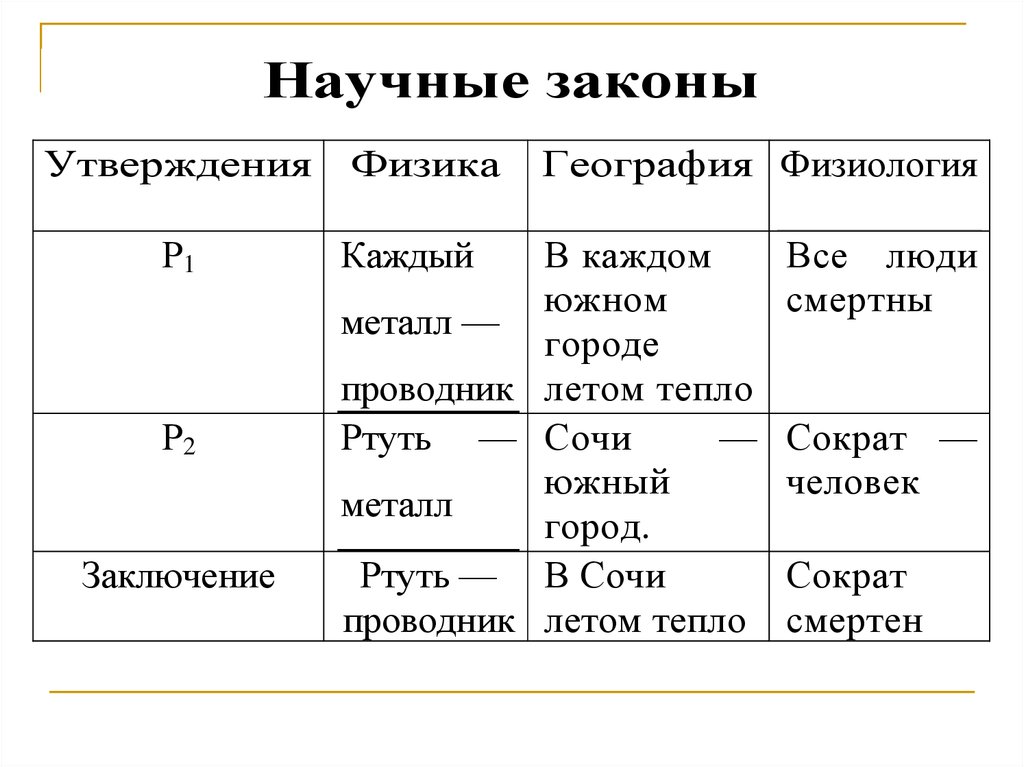
Научные законыУтверждения
Р1
Р2
Заключение
Физика
Каждый
География Физиология
В каждом
южном
металл —
городе
проводник летом тепло
Ртуть — Сочи
—
южный
металл
город.
Ртуть — В Сочи
проводник летом тепло
Все люди
смертны
Сократ —
человек
Сократ
смертен
7.
Общая форма всех этих законов- закон формальной логики
Р1. Каждый предмет, обладающий
свойством R, обладает свойством Q.
Р2: Предмет a обладает свойством R.
Заключение:
Предмет
a
обладает
свойством Q.
8.
Закон формальной логикив символьном виде
Р1:
Р2:
.
9.
Одна из основных задач логики - изучениеправильных способов рассуждений.
В общем случае рассуждение это
последовательность умозаключений.
Умозаключение - способ получения новых
суждений из ранее известных суждений
1 ,..., n . Схематически это изображается
диаграммой:
1 ,..., n
1 ,..., n – посылки и –
,
где
заключение умозаключения.
10.
Математическаялогика
занимается
задачами формализации правильных способов
рассуждений с помощью математического
аппарата.
Главная цель – изучение математических
рассуждений с целью точного определения
понятия «математическое доказательство».
Первый исследователь этого направления немецкий математик Г.Лейбниц (1646—1716).
11.
Этапы развития математической логики:Английский математик Дж.Буль (1815—1864)
создал алгебру логики.
Немецкий математик Г.Фреге (1848—1925)
разработал логико-математические языки и
теорию их осмысления (так называемую
семантику).
Итальянский математик Дж.Пеано (1858—
1932)
изложил
арифметику
на
языке
математической логики.
12.
В XIX веке математическая логикастала основой всех наук:
открытие неевклидовой геометрии,
поиски
обоснования
математического анализа,
открытие
парадоксов,
т.е.
рассуждений,
приводящих
к
противоречиям.
13.
Анализ парадоксов привел к созданиюпрограммы
Д.Гильберта
(1862—1943)
обоснования
математики
на
основе
аксиоматического подхода.
Систематический подход к математике на
основе
математической
логики
впервые
изложили английские математики Б.Рассел
(1872—1970) и А.Уайтхед (1861—1947) в работе
«Основания математики» (1910—1913).
К.Гедель (1906-1978) показал ограниченность
аксиоматического
подхода
к
обоснованию
математики.
14.
Бурное развитие математической логики итеории алгоритмов в наше время обусловлено:
распространением
информационнокоммуникационных технологий,
необходимостью создания теоретических
основ обработки и передачи информации,
математического
моделирования
разнообразных задач и процессов.
15.
Знания — это представление информации ввиде формальных высказываний.
Законы формальной логики преобразуют одни
высказывания в другие, т.е. преобразуют
информацию из одной формы представления в
другую.
Законы формальной логики — это
инструмент
преобразования
информации!
16.
Основнаялогики.
задача
формальной
База знаний:
Предложение:
Задача (формальная): проверить, что
выводится из
по законам формальной
логики.
Задача
(неформальная):
выяснить,
является ли предложение
следствием
утверждений базы знаний Г.
17.
Приложение 1.Базы знаний
(экспертные системы, Big Data и др.)
База знаний
Предложение
— база знаний системы.
— запрос к базе знаний.
Аппарат логического вывода — ядро
системы анализа данных.
18.
Приложение 2.Семантический Web
База знаний
Предложение
— ресурсы Интернет.
— запрос к базе знаний.
Аппарат логического вывода — ядро
системы анализа ресурсов.
19.
Приложение 3.Автоматизация научных исследований
(логическое программирование)
База знаний
Предложение
— система аксиом.
— утверждение.
Аппарат логического вывода — ядро
автоматической системы доказательства
теорем.
20.
Для реализации приложений необходимо:Создать
формальный
язык
для
представления знаний.
Выделить необходимую систему законов
формальной логики.
Проверить
корректность
логических
законов.
Проверить полноту построенной системы
логических законов.
Разработать
алгоритм
проверки
выводимости одних предложений из других
по заданным логическим законам.
21. Логика высказываний
22.
Высказываниеповествовательное
предложение, о котором можно судить,
истинное оно или ложное.
Обозначаются высказывания A,B,C,…
Истинностное значение высказывания A
обозначается символом (A) и определяется по
формуле:
(A)=1, если высказывание A истинно, и
(A)=0, если A ложно.
23. Алгебра высказываний
24.
Из высказываний путем соединения ихразличными способами (с помощью связок
«не», «и», «или», «следует», «равносильно»)
можно составлять новые, более сложные
высказывания.
При этом главное внимание уделяется
истинностно-функциональным комбинациям, в
которых истинность или ложность новых
высказываний определяется истинностью или
ложностью составляющих их высказываний.
Определение.
Алгеброй
высказываний
называется множество всех высказываний P с
логическими операциями , , , , .
25. Формулы алгебры высказываний
26.
Свойстваалгебры
высказываний
P
описываются с помощью формул, которые
строятся из переменных символов с помощью
знаков логических операций. Такие формулы
приято называть также пропозициональными
формулами
Cимволы логических операций , , , , ,
которые называются пропозициональными
связками.
Переменные символы X,Y,Z,…, которые
используются для обозначения высказываний и
которые называются пропозициональными
переменными.
27.
Определение.Формулы
алгебры
высказываний индуктивно определяются по
правилам:
1) каждая пропозициональная переменная
является формулой,
2) если , – формулы, то формулами
являются также выражения
( ), , , , .
Множество
всех
формул
высказываний обозначим FАВ .
алгебры
28.
Если в формулу входят переменныеX 1 ,..., X n , то записывают ( X 1 ,..., X n ) .
Из индуктивного определения формул
следует, что если в формулу вместо
переменных X1,..., X n подставить произвольные
конкретные высказывания A1 ,..., An , то получится
некоторое сложное высказывание ( A1,..., An ) .
Истинностное значение
высказывания
( ( A1 ,..., An ))
определяется истинностными
значениями
исходных
высказываний
( A1 ),..., ( An ) согласно таблицам истинностных
значений логических операций , , , , .
29.
Формула определяет функцию nF ,
переменных
которая
каждому
упорядоченному набору ( ( X 1 ),..., ( X n )) n
элементов
множества
{0,1}
ставит
в
соответствие элемент ( ( X 1 ,..., X n )) этого же
множества.
Функция F называется истинностной
функцией
формулы
и
графически
представляется истинностной таблицей.
Такая таблица содержит 2n строк и имеет
2n
2 возможных
одно
из
распределений
значений 0 и 1 в последнем столбце.
30.
Пример.Формула ( X Y X Y )
имеет следующую истинностную таблицу:
X
0
0
1
1
Y
0
1
0
1
X
1
1
0
0
Y X Y X Y X Y X Y
1
1
1
1
0
0
0
1
1
0
1
0
0
0
1
0
31.
Определение. Формула называется:тавтологией
(или
тождественно
истинной формулой) и обозначается | ,
если
ее
истинностная
функция
тождественно равна 1;
противоречием
(или
тождественно
ложной формулой), если ее истинностная
функция тождественно равна 0;
выполнимой, если ее истинностная функция
не равна тождественно 0;
опровержимой, если ее истинностная
функция не равна тождественно 1.
32.
Тавтологии являются общими схемамипостроения истинных высказываний и в этом
смысле выражают некоторые логические законы.
Примеры таких законов являются:
| X X – закон исключенного третьего,
| X X – закон двойного отрицания,
| ( X X ) – закон противоречия,
| ( X Y ) ( Y X ) – закон контрапозиции.
33.
Новые тавтологии можнопомощью следующих правил.
получить
Правило отделения:
если | , | , то | .
Правило подстановки:
если | ( X1,..., X n ) , то для любых формул
1 ,..., n
тавтологией
является
формула
( 1 ,..., n ) .
с
































 Математика
Математика








