Формальные теории

1. Лекция 12. Формальные теории

Содержание лекции:
1.
2.
3.
4.
Определение формальной теории
Интерпретация формальной теории
Теоремы ограничения
Понятие изоморфизма в терминах теории формальных систем
Формальные теории
© Н.М. Светлов, 2006-2010
1/10

2. Литература

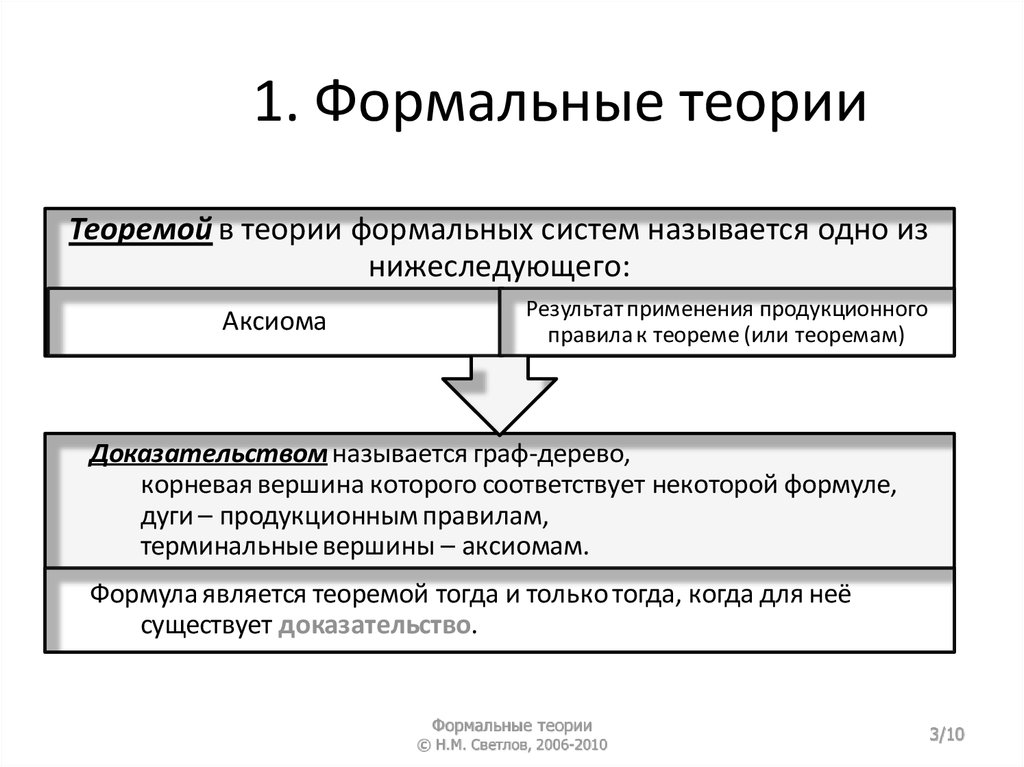
1. Формальные теории
Теоремой в теории формальных систем называется одно из
нижеследующего:
Аксиома
Результат применения продукционного
правила к теореме (или теоремам)
Доказательством называется граф-дерево,
корневая вершина которого соответствует некоторой формуле,
дуги – продукционным правилам,
терминальные вершины – аксиомам.
Формула является теоремой тогда и только тогда, когда для неё
существует доказательство.
Формальные теории
© Н.М. Светлов, 2006-2010
3/10

3. 1. Формальные теории

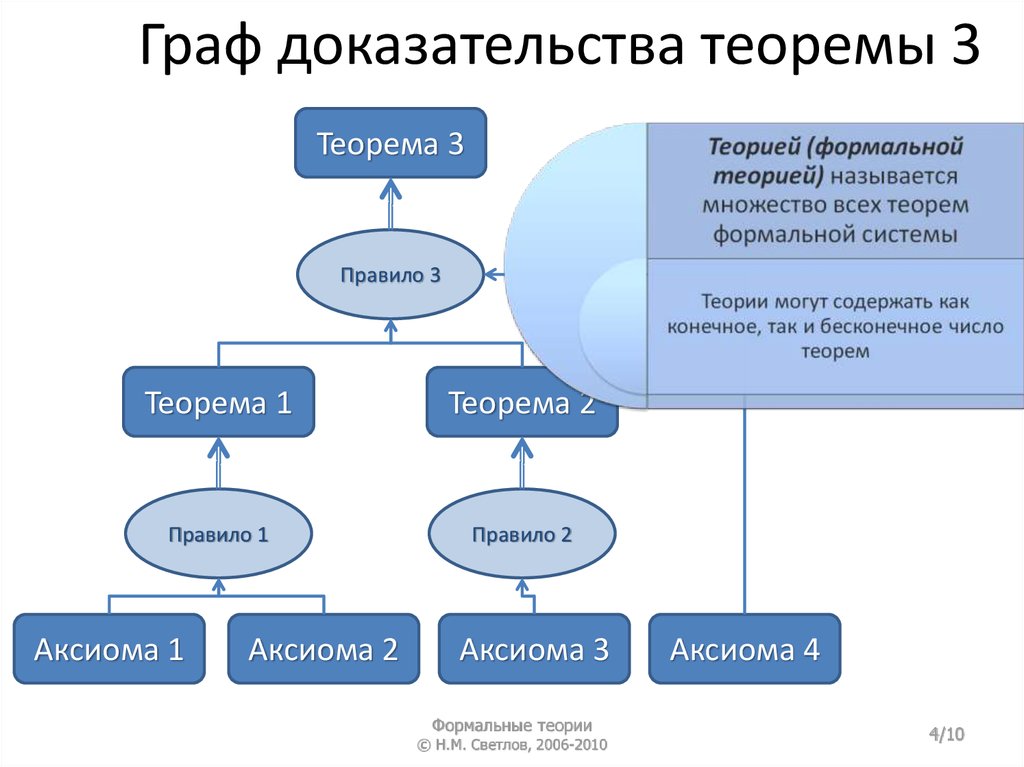
Граф доказательства теоремы 3
Теорема 3
Правило 3
Теорема 1
Теорема 2
Правило 1
Правило 2
Аксиома 1
Аксиома 2
Аксиома 3
Формальные теории
© Н.М. Светлов, 2006-2010
Аксиома 4
4/10

4. Граф доказательства теоремы 3

2. Интерпретация формальной
теории
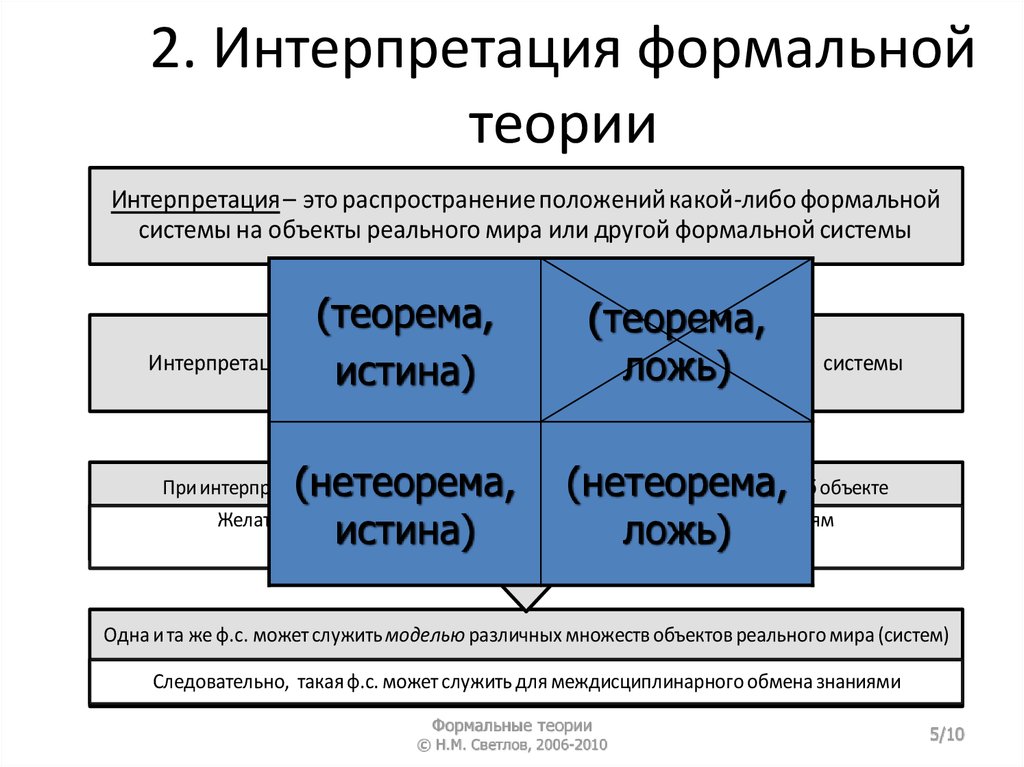
Интерпретация – это распространение положений какой-либо формальной
системы на объекты реального мира или другой формальной системы
(теорема,
(теорема,
Интерпретация наделяет смыслом символы и формулы
формальной системы
ложь)
истина)
(нетеорема, (нетеорема,
истина)
ложь)
не во всех интерпретациях это достижимо
При интерпретации теоремы ф.с. соответствуют истинным утверждениям об объекте
Желательно, чтобы нетеоремы соответствовали ложным утверждениям
Одна и та же ф.с. может служить моделью различных множеств объектов реального мира (систем)
Следовательно, такая ф.с. может служить для междисциплинарного обмена знаниями
Формальные теории
© Н.М. Светлов, 2006-2010
5/10

5. 2. Интерпретация формальной теории

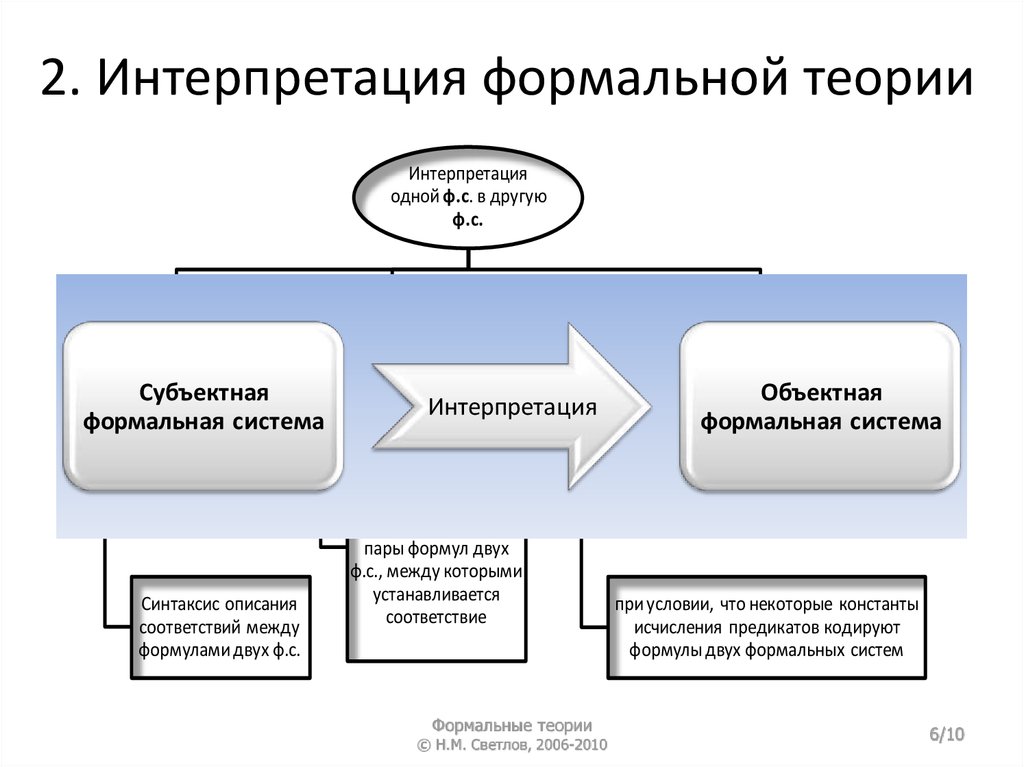
Интерпретация
одной ф.с. в другую
ф.с.
Требует задания
третьей ф.с.,
содержащей:
Субъектная
формальная система
Алфавиты
и синтаксис
обеих ф.с.
Синтаксис описания
соответствий между
формулами двух ф.с.
Может быть
осуществлена с
помощью:
Представляет
собой:
Интерпретация
Правила построения
формул, рекурсивно
перечисляющие все
пары формул двух
ф.с., между которыми
устанавливается
соответствие
Объектная
формальная система
исчисления
предикатов I порядка
Формальные теории
© Н.М. Светлов, 2006-2010
любого другого
универсального
метаязыка
при условии, что некоторые константы
исчисления предикатов кодируют
формулы двух формальных систем
6/10

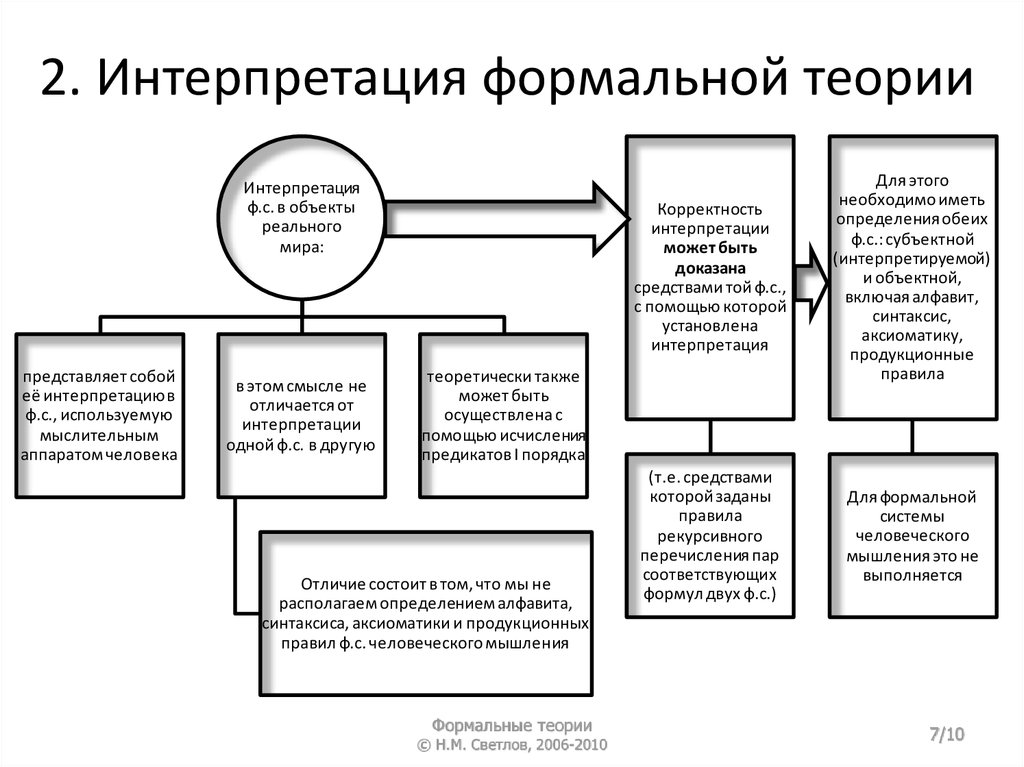
6. 2. Интерпретация формальной теории

Интерпретация
ф.с. в объекты
реального
мира:
представляет собой
её интерпретацию в
ф.с., используемую
мыслительным
аппаратом человека
в этом смысле не
отличается от
интерпретации
одной ф.с. в другую
Корректность
интерпретации
может быть
доказана
средствами той ф.с.,
с помощью которой
установлена
интерпретация
Для этого
необходимо иметь
определения обеих
ф.с.: субъектной
(интерпретируемой)
и объектной,
включая алфавит,
синтаксис,
аксиоматику,
продукционные
правила
(т.е. средствами
которой заданы
правила
рекурсивного
перечисления пар
соответствующих
формул двух ф.с.)
Для формальной
системы
человеческого
мышления это не
выполняется
теоретически также
может быть
осуществлена с
помощью исчисления
предикатов I порядка
Отличие состоит в том, что мы не
располагаем определением алфавита,
синтаксиса, аксиоматики и продукционных
правил ф.с. человеческого мышления
Формальные теории
© Н.М. Светлов, 2006-2010
7/10

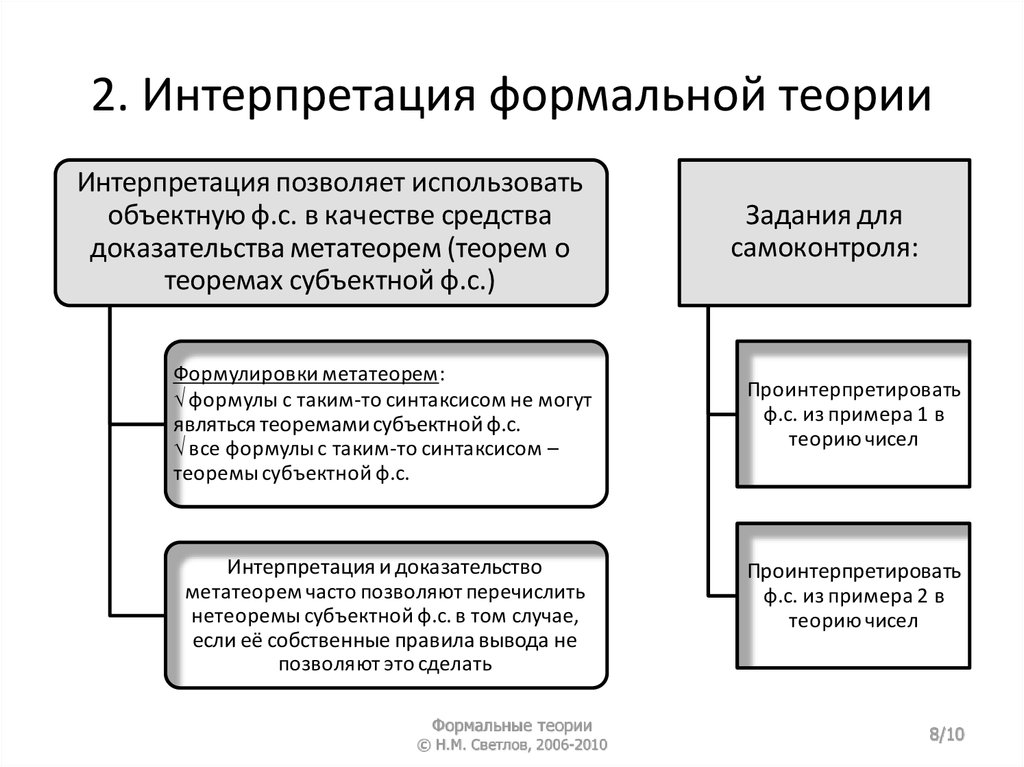
7. 2. Интерпретация формальной теории

Интерпретация позволяет использовать
объектную ф.с. в качестве средства
доказательства метатеорем (теорем о
теоремах субъектной ф.с.)
Формулировки метатеорем:
формулы с таким-то синтаксисом не могут
являться теоремами субъектной ф.с.
все формулы с таким-то синтаксисом –
теоремы субъектной ф.с.
Интерпретация и доказательство
метатеорем часто позволяют перечислить
нетеоремы субъектной ф.с. в том случае,
если её собственные правила вывода не
позволяют это сделать
Формальные теории
© Н.М. Светлов, 2006-2010
Задания для
самоконтроля:
Проинтерпретировать
ф.с. из примера 1 в
теорию чисел
Проинтерпретировать
ф.с. из примера 2 в
теорию чисел
8/10

8. 2. Интерпретация формальной теории

3. Теоремы ограничения
• Вторая теорема Гёделя
– В формальной арифметике существуют такие формулы
p, что ни p, ни ¬p не являются теоремами (1931 г.)
• Теорема Тарского
– Не все истинные формулы формальной арифметики
являются её теоремами (1935 г.)
• В арифметике понятие истинности неформализуемо
• Теорема Чёрча
– Исчисление предикатов первого порядка неразрешимо
(1936 г.)
Формальные теории
© Н.М. Светлов, 2006-2010
9/10

9. 3. Теоремы ограничения

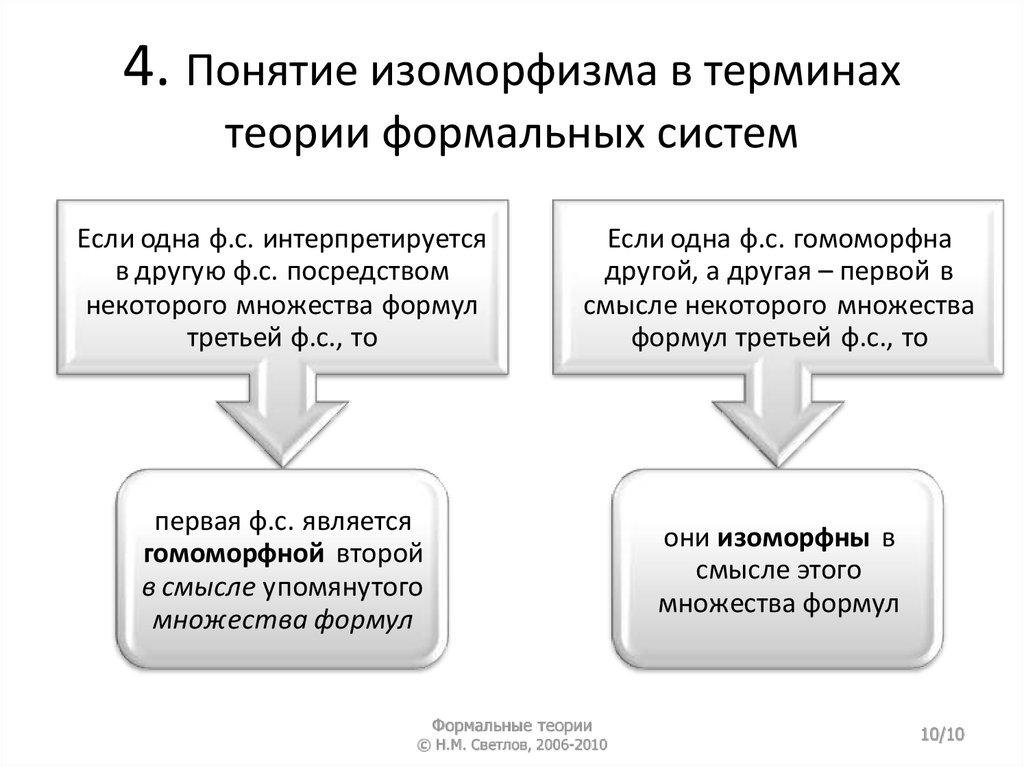
4. Понятие изоморфизма в терминах
теории формальных систем
Если одна ф.с. интерпретируется
в другую ф.с. посредством
некоторого множества формул
третьей ф.с., то
Если одна ф.с. гомоморфна
другой, а другая – первой в
смысле некоторого множества
формул третьей ф.с., то
первая ф.с. является
гомоморфной второй
в смысле упомянутого
множества формул
они изоморфны в
смысле этого
множества формул
Формальные теории
© Н.М. Светлов, 2006-2010
10/10