Геометрическая оптика

1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА

ЕГЭ. ФИЗИКА
РЕПЕТИЦИЯ ПО ФИЗИКЕ
Владимир Петрович Сафронов
г. Ростов-на-Дону, 2015
Звоните: т. 8 928 111 7884
Пишите: [email protected]

2. ОПТИКА

изучает явления, связанные с возникновением, распространением и взаимодействием
с веществом световых электромагнитных волн в диапазоне (кожзгсф)
фиолетовый 0,4 (400) 0,76 (760) красный мкм нм .
ГЕОМЕТРИЧЕСКАЯ ОПТИКА
Прямолинейное распространение света
В геометрической оптике считается, что свет распространяется вдоль световых лучей,
т.е. прямолинейно.
Не учитываются волновые свойства света (интерференция, дифракция).
Для этого длина световой волны должна быть намного меньше размеров
препятствий d: << d.
Скорость света в вакууме (воздухе) является максимально c 3 108 м/с 300 000 км/с.
возможной скоростью распространения сигнала:
В любой оптической среде скорость света v меньше, чем в вакууме.
с
Абсолютный показатель преломления n определяет, во сколько раз
v
скорость света в вакууме с больше скорости света в оптической среде v
n c v 1.
Относительный показатель преломления n21 показывает, во сколько
n1
v1
раз скорость света в первой среде v1 отличается скорости во второй v2:
v2
n2
v1 n2
n21
.
v2 n1
где n1 , n2 — абсолютные показатели преломления первой и второй сред.
В.П. Сафронов 2015 [email protected]

3. Законы отражения и преломления света (Синеллиус):

1) Падающий, отраженный и преломленный лучи лежат в одной
плоскости с перпендикуляром, опущенным в точку падения (рис.). n1
2) Угол падения равен углу отражения .
3) Отношение синусов углов падения и преломления равно
n
>
n
2
1
относительному показателю преломления двух данных сред:
sin( )
sin( ) n2
n1 .
n21 . Первая среда —воздух n1 = 1
sin( )
sin( ) n1
Полное отражение.
Происходит при переходе лучей из оптически более плотной среды в менее плотную (n1 > n2).
В этом случае, угол падения меньше угла преломления
Поэтому, при углах падения > ПРЕД преломление света
не происходит, свет полностью отражается от поверхности.
Предельный угол полного отражения
определяется из условия: 900 sin 1
sin( пред) = n21
в воздухе:
В.П. Сафронов 2015 [email protected]
sin( пред) = 1/ n1 .

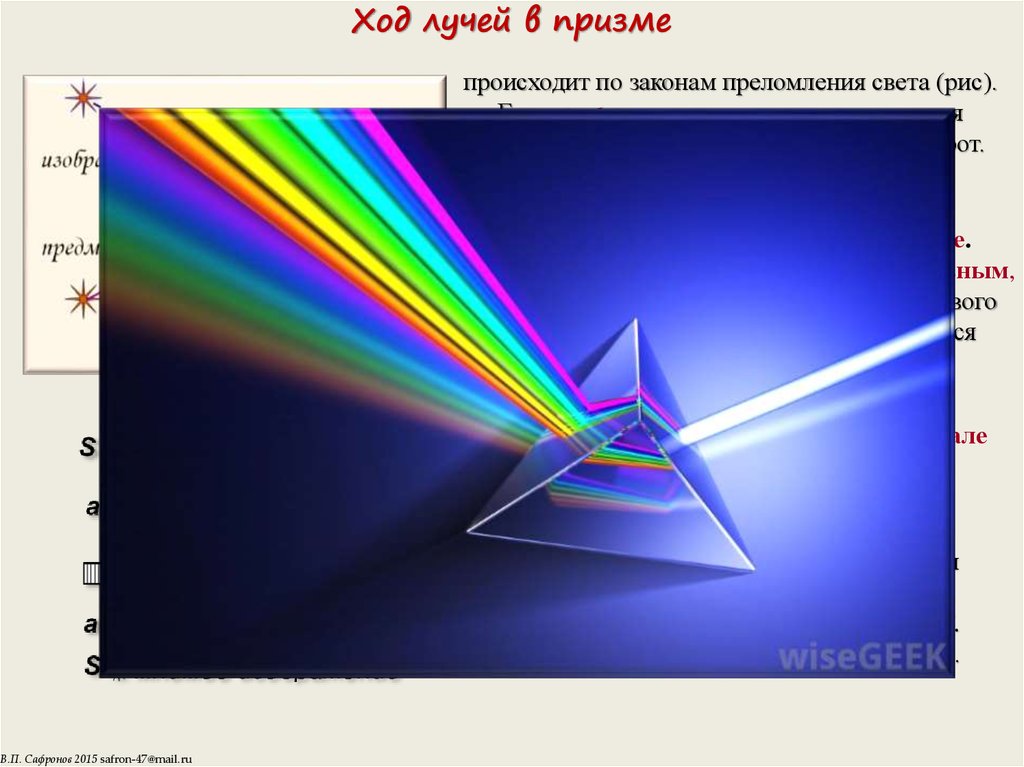
4. Ход лучей в призме

происходит по законам преломления света (рис).
Если n1 < n2 луч света после преломления
отклоняется к основанию призмы и наоборот.
Призма дает мнимое изображение.
Действительное и мнимое изображение.
Изображение точки называется действительным,
если в этой точке пересекаются лучи светового
пучка и мнимым, если в ней пересекаются
продолжения этих лучей.
Построение изображения в плоском зеркале
основано на законе отражения света.
S — источник света,
S′ — мнимое изображение S.
Положение изображения S′ определяется
пересечением продолжений двух любых
лучей, попадающих в глаз, причем a = a′.
В плоском зеркале мнимое изображение.
В.П. Сафронов 2015 [email protected]

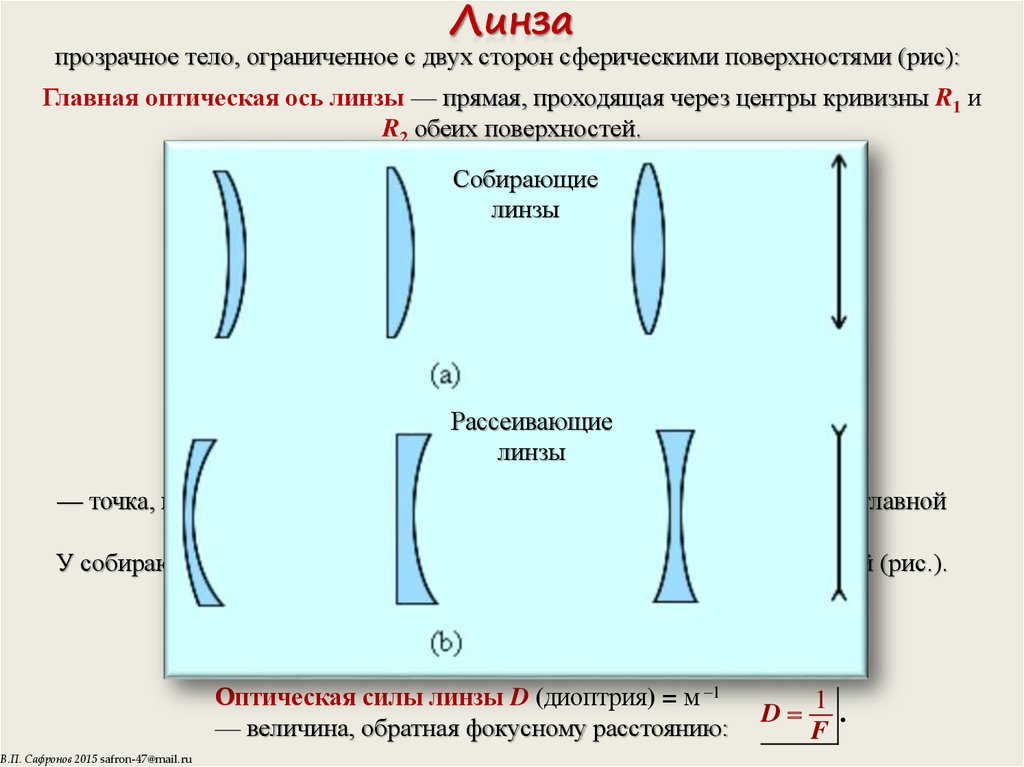
5. Линза

прозрачное тело, ограниченное с двух сторон сферическими поверхностями (рис):
Главная оптическая ось линзы — прямая, проходящая через центры кривизны R1 и
R2 обеих поверхностей.
Оптический центр линзы О
Собирающие
— точка, проходя через которую лучи не преломляются.
линзы
2F
F
O
F
F
O
Рассеивающие
линзы
Главный фокус линзы
— точка, в которой пересекаются лучи, падающие на линзу параллельно главной
оптической оси (или их продолжения).
У собирающей линзы фокус действительный, у рассеивающей — мнимый (рис.).
Фокусное расстояние линзы F, м
— расстояние от оптического центра до точки фокуса.
F > 0 — собирающая, F < 0 — рассеивающая.
Оптическая силы линзы D (диоптрия) = м –1
1
D .
— величина, обратная фокусному расстоянию:
F
В.П. Сафронов 2015 [email protected]

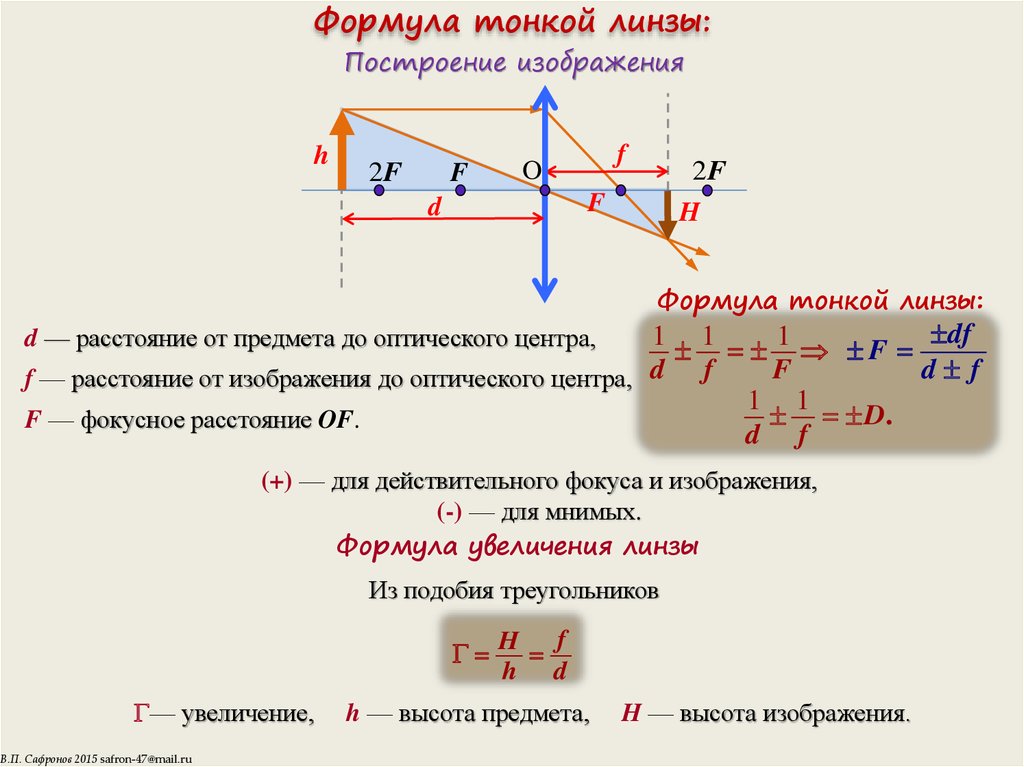
6. Формула тонкой линзы:

Построение изображения
h
2F
F
f
O
2F
H
F
d
Формула тонкой линзы:
df
1 1
1
F
F
d f
f — расстояние от изображения до оптического центра, d f
1 1
D.
F — фокусное расстояние OF.
d f
d — расстояние от предмета до оптического центра,
(+) — для действительного фокуса и изображения,
(-) — для мнимых.
Формула увеличения линзы
Из подобия треугольников
— увеличение,
В.П. Сафронов 2015 [email protected]
H f
h d
h — высота предмета,
H — высота изображения.

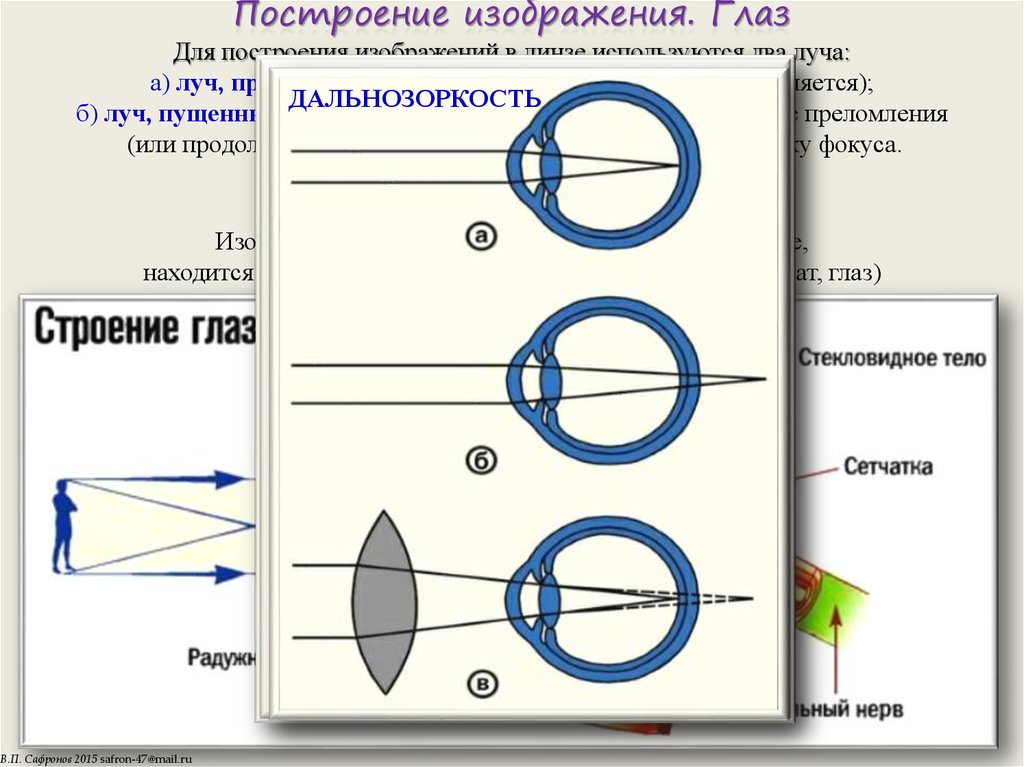
7. Построение изображения. Глаз

Для построения изображений в линзе используются два луча:
а) луч, проходящий через оптический центр (не преломляется);
ДАЛЬНОЗОРКОСТЬ
БЛИЗОРУКОСТЬ
б) луч, пущенный параллельно главной оптической оси после преломления
(или продолжение преломленного луча), проходит через точку фокуса.
СОБИРАЮЩАЯ ЛИНЗА
Предмет — за двойным фокусом.
Изображение действительное обратное уменьшенное,
находится между фокусом и двойным фокусом (фотоаппарат, глаз)
h
2F
F
F
d
В.П. Сафронов 2015 [email protected]
f
O
H f
1
h d
2F
H

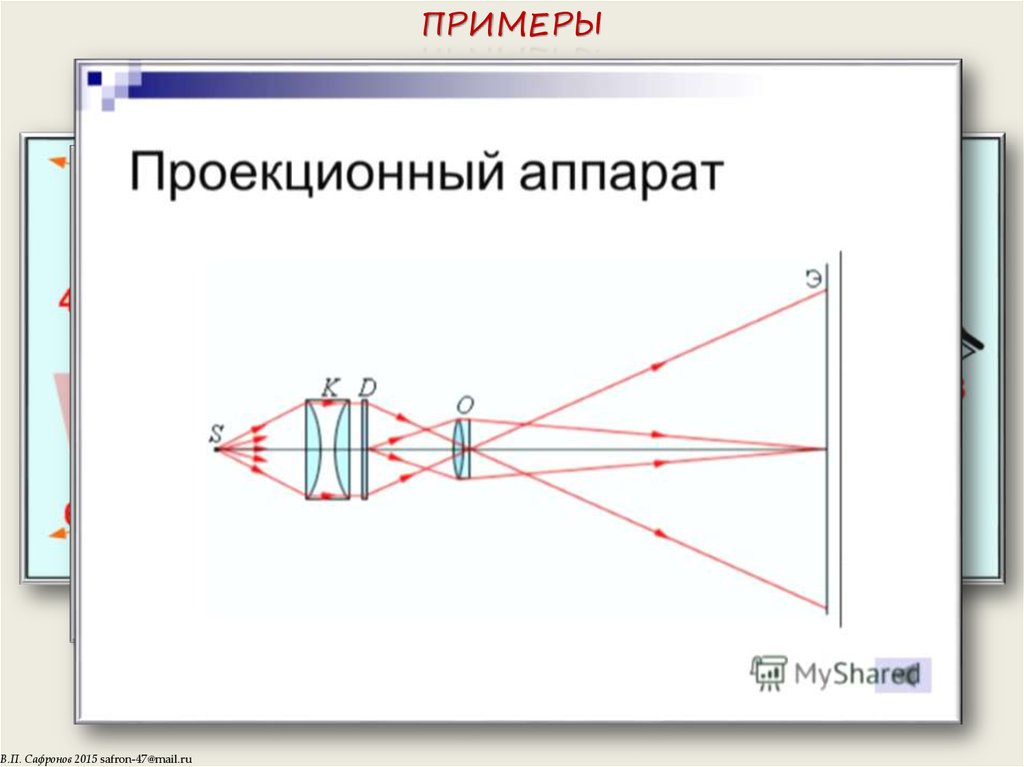
8. Построение изображения. Проектор

СОБИРАЮЩАЯ ЛИНЗА
Предмет — между фокусом и двойным фокусом.
Изображение действительное обратное УВЕЛИЧЕННОЕ,
находится за двойным фокусом (ПРОЕКТОР)
2F
h
f
O
F
d
2F
F
H
В.П. Сафронов 2015 [email protected]
H f
1
h d

9. Построение изображения. Двойной фокус

СОБИРАЮЩАЯ ЛИНЗА
Предмет — НА двойнОм фокусЕ.
Изображение действительное обратное ОДИНАКОВОЕ,
находится НА двойнОм фокусЕ
h
2F
F
2F
F
d
H
В.П. Сафронов 2015 [email protected]
f
O
H f
1
h d

10. Построение изображения. Лупа

СОБИРАЮЩАЯ ЛИНЗА
Предмет — между фокусом и оптическим центром.
Изображение мнимое, прямое, УВЕЛИЧЕННОЕ
находится ПЕРЕД ЛИНЗОЙ (ЛУПА)
f 0
H
2F
F
h
O
d
В.П. Сафронов 2015 [email protected]
H f
0, 1
h d
F
2F

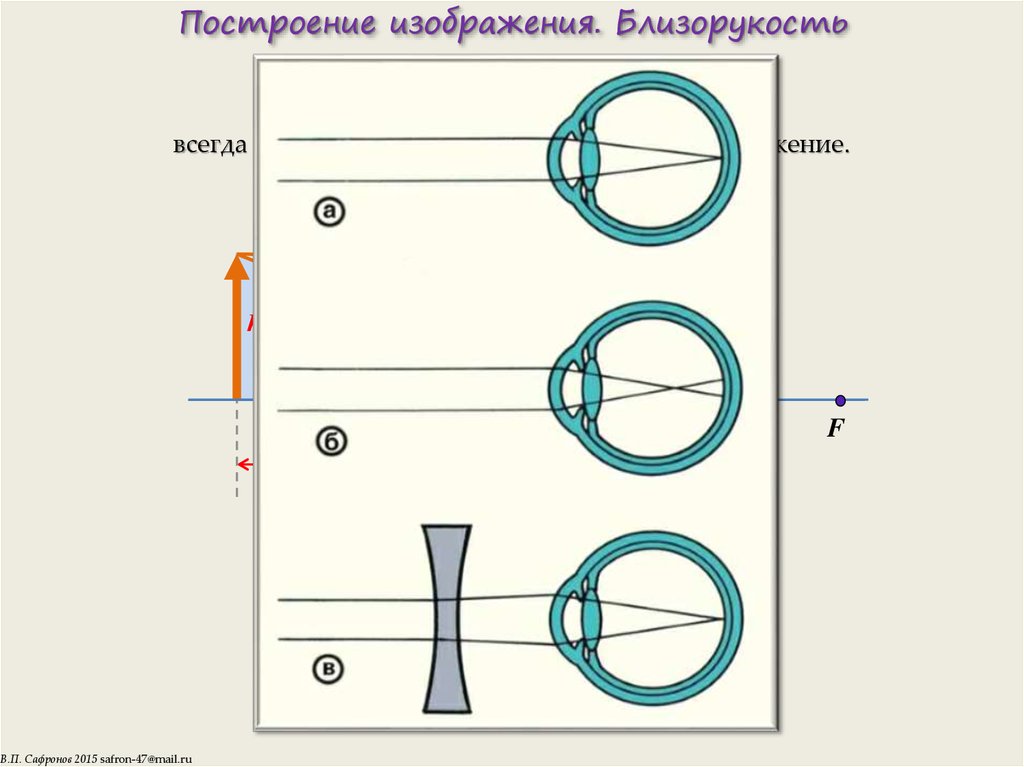
11. Построение изображения. Близорукость

РАССЕИВАЮЩАЯ ЛИНЗА
всегда дает мнимое прямое уменьшенное изображение.
h
H
O
f 0
F 0
d
В.П. Сафронов 2015 [email protected]
H f
0, 1
h d
F

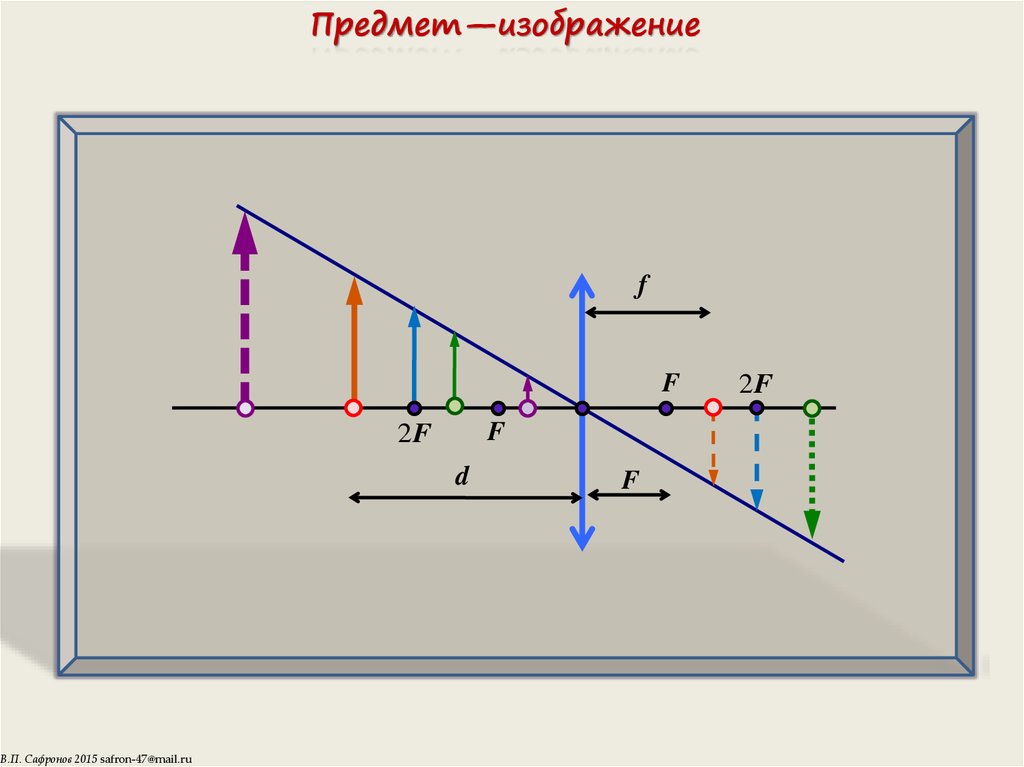
12. Предмет—изображение

f
F
F
2F
d
В.П. Сафронов 2015 [email protected]
F
2F

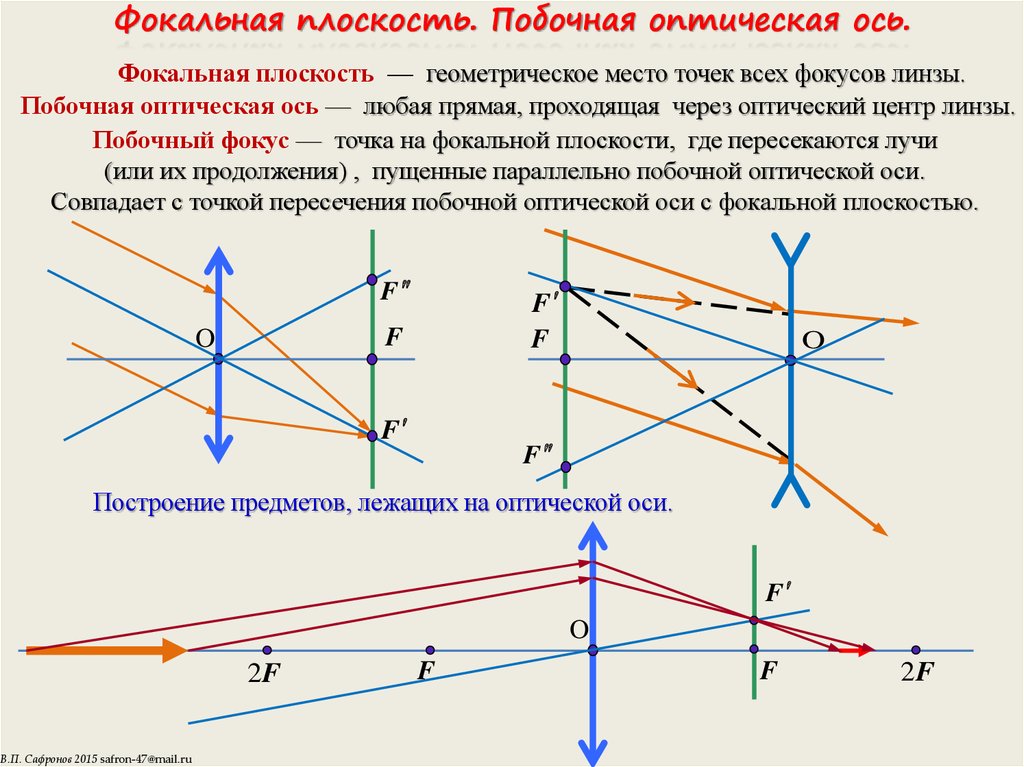
13. Фокальная плоскость. Побочная оптическая ось.

Фокальная плоскость — геометрическое место точек всех фокусов линзы.
Побочная оптическая ось — любая прямая, проходящая через оптический центр линзы.
Побочный фокус — точка на фокальной плоскости, где пересекаются лучи
(или их продолжения) , пущенные параллельно побочной оптической оси.
Совпадает с точкой пересечения побочной оптической оси с фокальной плоскостью.
F
F
F
F
O
F
O
F
Построение предметов, лежащих на оптической оси.
F
O
2F
В.П. Сафронов 2015 [email protected]
F
F
2F

14. ПРИМЕРЫ

Оптический телескоп
Оптический микроскоп
В.П. Сафронов 2015 [email protected]

15. КОНЕЦ ГЕОМЕТРИЧЕСКАЯ ОПТИКА

В.П. Сафронов 2015 [email protected]